Traveling Wave Reactor and Condition of Existence of Nuclear Burning Soliton-Like Wave in Neutron-Multiplying Media

Abstract

Physical fundamentals of traveling wave reactor are considered. We show that the condition of existence of nuclear burning soliton-like wave in a neutron-multiplying medium is determined in general by two conditions. The first condition (necessary) is determined by relationship between the equilibrium concentration and critical concentration of active (fissionable) isotope that is a consequence of the Bohr–Sommerfeld quantization condition. The second condition (sufficient) is set by the so-called Wigner quantum statistics, or more accurately, by a statistics of the Gaussian simplectic ensembles with respect to the parameter that describes the squared width of burning wave front of nuclear fuel active component.

1. Introduction

In spite of obvious efficiency of the nuclear power engineering of new generation, the main difficulties of its acceptance are predetermined by non-trivial properties which a future ideal nuclear reactor must possess. At first, the natural, i.e., unenriched uranium or thorium must be used as a nuclear fuel. Secondly, the traditional control rods must be completely absent in the control system of nuclear reactor. Thirdly, in spite of the absence of control rods a reactor must possess the property of so-called internal safety. It means that a reactor core must always be in the critical state, i.e., the normal operation of reactor is automatically provided not as a result of personnel activity, but by virtue of underlying physical laws, which prevent the explosive development of chain reaction in a natural way. Figuratively speaking, the reactor with internal safety it is “the nuclear installation which never explodes” [1]. It seems to be strange, but the reactors satisfying such unusual requirements are really possible. For the first time the idea of such self-regulating fast reactor in general terms (so-called breed-and-burn mode) was proposed by Russian physicists Feinberg and Kunegin in 1958 at II Genevan conference [2] and relatively recently was “resuscitated” as an idea of the self-regulating fast reactor in traveling-wave mode by Russian physicist L. Feoktistov [3] and independently by American physicists Teller, Ishikawa and Wood [4].

The main idea of reactor with internal safety consists in the selection of fuel composition so that, at first, the characteristic time ${\tau }_{\beta }$ of the nuclear burning of fuel active (fissionable) component is considerably greater than the characteristic time of delayed neutrons production and, secondly, necessary self-regulation conditions are maintained during the reactor operation (that always take place, when the equilibrium concentration ${\tilde{n}}_{fiss}$ of fuel active component is greater than its critical concentration [5] $n_{crit}$ [3]). These very important conditions can practically always to be attained, if in the reactor the chain of nuclear transformations of the Feoktistov uranium-plutonium cycle type [3]

$${}^{238}U(n,\gamma )\to {}^{239}U\stackrel{{\beta }^{-}}{\to }{}^{239}Np\stackrel{{\beta }^{-}}{\to }{}^{239}Pu(n,fission)$$

(1)

or the Teller-Ishikawa-Wood thorium-uranium cycle type [4]

$${}^{232}Th(n,\gamma )\to {}^{233}Th\stackrel{{\beta }^{-}}{\to }{}^{233}Pa\stackrel{{\beta }^{-}}{\to }{}^{233}U(n,fission)$$

(2)

will be present at sufficient level.

In both cases the produced fissionable isotopes ${}^{239}Pu$ in (1) or ${}^{233}U$ in (2) are the active components of nuclear fuel. The characteristic time of such a reaction corresponds to the proper β-decays time and is approximately equal to ${\tau }_{\beta }=2.3/ln2\simeq 3.3days$ for the reaction (1) and ${\tau }_{\beta }\simeq 39.5days$ for the reaction (2). This is several orders greater than the time of delayed neutron production.

The self-regulation of nuclear burning process consists in the fact that such a system left by itself can not pass from a critical state to reactor runaway mode, because a critical concentration is bounded above by the finite equilibrium concentration of nuclear fuel fissionable component (plutonium in (1) or uranium in (2)), i.e., ${\tilde{n}}_{fiss}>n_{crit}$ (the condition for existence of Feoktistovs wave mode [3]). At phenomenological level the self-regulation of nuclear burning is manifested as follows. The increase of neutron flux for some reason or other leads to the rapid burn-up of nuclear fuel fissionable component (plutonium in (1) or uranium in (2)), i.e., its concentration and, as a result, the neutron flux will decrease, while the new nuclei of corresponding fissionable component of nuclear fuel are produced with the same rate of production during time ${\tau }_{\beta }$. And vice versa, when the neutron flux is sharply decreased due to external action, the fuel burn-up rate decreases too, and the accumulation rate of fuel fissionable component will increase as well as the number of neutron production in a reactor during the same time ${\tau }_{\beta }$. However, as is known [3], the Feoktistov condition for existence of wave mode is only necessary but not sufficient condition. Therefore complete generalization of the condition for existence of wave mode for critical waves of nuclear burning in neutron-multiplying media is the purpose of this article.

2. The Features of Condition for Existence of Wave Mode of Nuclear Burning Critical Wave According to Feoktistov

As is known, to verify any physical hypothesis one can use simplified models. One of the possible simplifications consists in a separate consideration of neutron-nuclear processes and heat removal process. Such a simplification is especially justified at a long control time. At the same time, neutron processes can be studied in the one-dimensional geometry rather than in the three-dimensional geometry and also can be considered in the diffusion approximation and one-group approximation. This means that neutron spectral characteristics are averaged in an appropriate manner over the fixed neutron energy interval, and the problem is solved at the fixed neutron energy.

Following References [3,6], let us consider the kinetics of self-regulating fast uranium-plutonium reactor, where the Feoktistov self-propagating neutron-fission wave of nuclear burning is generated. Such a wave mode meets all requirements, which are appropriate to the nuclear reactor with internal safety.

Main transmutation chain corresponds to the uranium-plutonium fuel cycle (1). We consider the ${}^{238}U$-filled half-space, which is irradiated by neutrons from the open surface. We also assume for simplicity that the neutron spectrum and fission spectrum are identical. The typical neutron energy in the medium strongly depends on moderator properties. Following Feoktistov [3,7], we will consider the case, when the moderator is absent or is present in small amounts and the neutron spectrum practically coincides with initial one.

The main goal of such a simplified model consists in finding of an autowave solution for the transmutation chain (1) under the indispensable condition $n_{crit}<{\tilde{n}}_{Pu}$.

The balance equation for plutonium concentration looks like

$$\frac{d{N}_{Pu}}{dt}=vn\left[{}^8{\sigma }_a{N}_8-{(}^{Pu}{\sigma }_a{+}^{Pu}{\sigma }_f)N_{Pu}\right]$$

(3)

where $N_{Pu}$ is the ${}^{239}Pu$ concentration, $N_8$ is the ${}^{238}U$ concentration, n is the neutron concentration, v is the neutron velocity in the one-group approximation, ${\sigma }_a$ and ${\sigma }_f$ are the neutron-capture cross-section and fission cross-section, respectively.

From here it follows that the plutonium relative equilibrium concentration, when the derivative becomes zero, has the form

$${\tilde{n}}_{Pu}=\frac{{\tilde{N}}_{Pu}}{N_8}=\frac{{}^8{\sigma }_a}{{}^{Pu}{\sigma }_a{+}^{Pu}{\sigma }_f}$$

(4)

Here $N_{Pu}{\mid }_{t=0}=0$ and the current concentration $N_{Pu}\left(t\right)$ cannot exceed ${\tilde{N}}_{Pu}$.

Recall that the value of constant ${\tilde{n}}_{Pu}$ strongly varies depending on the neutron energy, for example, for a thermal reactor ${\tilde{n}}_{Pu}=0.25\%$, while for a fast reactor ${\tilde{n}}_{Pu}\approx 10\%$.

The other characteristic of the uranium-plutonium medium is the plutonium critical concentration $n_{crit}$. At $n_{Pu}>n_{crit}$ the system becomes supercritical and capable of self-multiplication, and, conversely, at $n_{Pu}<n_{crit}$ the system becomes subcritical and the neutron flux density attenuates with time.

The value $n_{crit}$ can be obtained from the neutron balance

$$\frac{dn}{dt}=nv{N}_8\left[{(\nu -1)}^{Pu}{\sigma }_f{n}_{Pu}-\sum _n{}^i{\sigma }_a{n}_i\right]$$

(5)

where $n_i$ are the relative concentrations of the elements taking part in the reaction, ν is the average number of prompt neutrons per ${}^{239}Pu$ fission, ${}^i{\sigma }_a$ is the absorption cross-section for i-th element including U and Pu (neutron escape can be also included).

The magnitude

$$n_{Pu}=n_{crit}^{Pu}=\frac{{\displaystyle \sum _n}{}^i{\sigma }_a{n}_i}{{(\nu -1)}^{Pu}{\sigma }_f}$$

(6)

determines the plutonium concentration when the multiplying medium is in critical state. The magnitude $n_{crit}$ is also a function of neutron energy. Since the two dimensionless numbers ${\tilde{n}}_{Pu}$ and $n_{crit}$ are composed from the different combinations of constants, the following variants ${\tilde{n}}_{Pu}>n_{crit}$, ${\tilde{n}}_{Pu}<n_{crit}$ and ${\tilde{n}}_{Pu}=n_{crit}$ are possible. It appeared that for thermal neutrons ${\tilde{n}}_{Pu}<n_{crit}$ and for fast neutrons ${\tilde{n}}_{Pu}>n_{crit}$. In the first case the system is viable only in the presence of neutron source. If this external source will be switched off, the reaction immediately stops. In other case, which we will consider below, the asymptotical and independent of initial conditions solution in the form of stationary traveling wave is possible. This is not paradoxical, if to take into account the foregoing explanation of physical sense of Equation (1).

Thus, in case of ${}^{238}U$ slow burning induced by fast neutrons it is impossible to overstep the criticality threshold. On formal level this makes possible to neglect the partial time derivative in the neutron transport equation. Further developments can be presented in the following way. Neutrons from the external source are absorbed in the nuclear fuel layer, whose thickness does not exceed the neutron free path, and due to fission the uranium is transmuted into the plutonium. With the plutonium accumulation the fission process intensifies, the neutron number grows and fission reaction begins to develop farther. In time the center of energy release shifts away from the neutron source, whose influence decreases, and the system comes to the stationary traveling-wave mode. In other words, all functions become depending on the argument $z=x+ut$ (the wave is directed from right to left and u is its velocity). At the same time the wave velocity u is of order $L/\tau$, where $L\approx 5cm$ is the neutron diffusion length and $\tau =2.3/ln2=3.3days$ is the ${}^{239}Pu$-production time from ${}^{238}U$.

To obtain the system of kinetic equations for neutrons and nuclei taking part in the transmutation chain (1) with respect to the autowave variable $z=x+ut$, we will write down at first this system of equations in the traditional coordinates $\left\{x;t\right\}$.

So, the kinetic equation for neutrons has the form

$$\frac{d\tilde{n}(x,t)}{dt}=D\Delta \tilde{n}(x,t)+q(x,t)$$

(7)

where $\tilde{n}(x,t)$ is a neutron density; $D=v/3{\Sigma }_S$ is the neutron diffusion coefficient, $c{m}^2/s$; v is the neutron velocity in one-group approximation, $cm/s$; ${\Sigma }_S$ is the neutron macroscopic scattering cross-section, $c{m}^{-1}$; q is the neutron source strength, $c{m}^{-3}{s}^{-1}$.

It is obvious that within the framework of our problem the expression for the neutron source strength looks like

$$q(x,t)=\tilde{n}(x,t)v\left[{(\nu -1)}^{Pu}{\sigma }_f{N}_{Pu}-\sum _i{}^i{\sigma }_a{N}_i\right]$$

(8)

where $N_i$ is the concentration of i-th isotope in the reaction chain (2), ${}^{Pu}{\sigma }_f$ is the microscopic fission cross-section for ${}_{94}^{239}Pu$, ${}^i{\sigma }_a$ is the neutron-capture cross-section by i-th isotope, ν is the average number of prompt neutrons per ${}_{94}^{239}Pu$ fission.

Using Equation (6) for the plutonium relative critical concentration and normalizing the neutron concentration and isotope concentration to the ${}^{238}U$ concentration, we obtain the diffusion Equation (7) in the following form

$$\frac{1}{D}\frac{dn(x,t)}{dt}=\Delta n(x,t)-\frac{N_8}{D}v\sum _i{}^i{\sigma }_a{n}_i(x,t),\left[1-\frac{n_{Pu}(x,t)}{n_{crit}^{Pu}(x,t)}\right]n(x,t)$$

(9)

where

$$n(x,t)=\frac{\tilde{n}(x,t)}{N_8(x,t)},n_i(x,t)=\frac{N_i(x,t)}{N_8(x,t)},n_{Pu}(x,t)=\frac{N_{Pu}(x,t)}{N_8(x,t)},n_{crit}^{Pu}(x,t)=\frac{N_{crit}^{Pu}(x,t)}{N_8(x,t)}$$

(10)

or, in other words, $n(x,t)$ and $n_i(x,t)$ are the relative concentration of neutrons and isotopes, respectively, $n_{Pu}$ and $n_{crit}^{Pu}$ are the plutonium relative equilibrium and critical concentration, respectively.

We have mentioned above, that the inequality ${\tilde{n}}_{Pu}>n_{crit}$ formally predetermines the stationary form of the kinetic equation. So long as for qualitative analysis of Equation (7) it is sufficient to find an approximate solution of steady-state equation in the region in front of wave [3,7], i.e., in the asymptotical region $x⟶-\infty$ we can neglect the summands $n_9$ and $n_{Pu}$, which are finding together with $n_8\cong 1$ . This means that the stationary form of the kinetic Equation (9) in the simplified form looks like

$$\frac{d^{2}n(x,t)}{d{x}^2}=C_{\infty }\left[1-\frac{n_{Pu}(x,t)}{n_{crit}^{Pu}(x,t)}\right]n(x,t)$$

(11)

where the constant $C_{\infty }$ is equal to

$$C_{\infty }=\frac{v}{D}{(}^8{\sigma }_a)N_8(x,0)=\frac{1}{D\tau }=\frac{1}{L^2}$$

(12)

τ is the neutron lifetime, $D=L^2/\tau$ is the neutron diffusion coefficient, $c{m}^2{s}^{-1}$ and concentration $N_8(x,t)$ is equal to the initial concentration $N_8(x,0)$.

Following Refs. [3,7], we will seek the approximate solution of the steady-state Equation (11) in the region in front of wave $(x⟶-\infty )$.

Now we write down the kinetic equations for each of isotopes taking part in the reaction chain (1). First we write down an equation for the ${}_{92}^{238}U$ isotope

$$\frac{d{n}_8(x,t)}{dt}=-vn(x,t)N_8(x,0){(}^8{\sigma }_a{+}^8{\sigma }_f)N_8(x,t)+vn(x,t)N_8(x,0)\sum _{9,Pu}{}^i{\sigma }_a{n}_i(x,t)$$

(13)

In References [3,7] the second summand on the right-hand-side of Equation (13) is introduced under the assumptions that the ${}^{238}U$-neutron and ${}^{239}Pu$-neutron capture leads to ${}^{240}Pu$ production, whose properties are assumed to be identical to the properties of ${}^{238}U$ initial nucleus. Obviously, this is done to simplify the problem or, in other words, to satisfactorily close the systems of kinetic equations for neutrons and nuclei taking part in the reaction chain (1).

Assuming that ${}^8{\sigma }_f{\ll }^8{\sigma }_a$ [3,7], the kinetic equation for ${}^{238}U$ takes the following form

$$\frac{d{n}_8(x,t)}{dt}=-\left[c_8{n}_8(x,t)-c_9{n}_9(x,t)-c_{Pu}{n}_{Pu}(x,t)\right]n(x,t)$$

(14)

where

$$c_i=v{N}_8{(x,0)}^i{\sigma }_a,i=8,9,Pu$$

(15)

The kinetic equation for ${}^{239}U$ looks like

$$\frac{d{N}_9(x,t)}{dt}=vn(x,t)N_8{(x,0)}^8{\sigma }_a{N}_8(x,t)-vn(x,t)N_8(x,0){(}^9{\sigma }_a{+}^9{\sigma }_f)N_9(x,t)-\frac{N_9(x,t)}{{\tau }_{\beta }}$$

(16)

where ${\tau }_{\beta }={\tau }_{\beta }^9+{\tau }_{\beta }^{Np}$ is the ${}^{239}U$ lifetime which is equal by assumption [3,7] to the sum of half-lives of ${}^{239}U$ and ${}^{239}Np$ β-radioactive nuclei.

Taking into account that ${}^9{\sigma }_f{\ll }^9{\sigma }_a$ and normalizing to initial concentration $N_8(x,0)$ we obtain Equation (16) in the following form

$$\frac{d{n}_9(x,t)}{dt}=c_{8}n(x,t)n_8(x,t)-c_{9}n(x,t)n_9(x,t)-\frac{n_9(x,t)}{{\tau }_{\beta }}$$

(17)

Finally we write down the kinetic equation for ${}^{239}Pu$ as

$$\frac{d{N}_{Pu}(x,t)}{dt}=\frac{N_9(x,t)}{{\tau }_{\beta }}-vn(x,t)N_8(x,0){(}^{Pu}{\sigma }_a{+}^{Pu}{\sigma }_f)N_{Pu}(x,t)$$

(18)

Taking into consideration the expression for the plutonium equilibrium concentration (4) and normalizing to the initial concentration $N_8(x,0)$, we have Equation (18) in the form

$$\frac{d{n}_{Pu}(x,t)}{dt}=\frac{n_9(x,t)}{{\tau }_{\beta }}-c_{8}n(x,t)\frac{n_{Pu}(x,t)}{{\tilde{n}}_{Pu}}$$

(19)

Now we are ready to write down the system of kinetic equations for neutrons and nuclei that take part in the transmutation chain (2) with respect to the dimensionless autowave variable $z=\xi /L=(x+ut)/L$, where u is the velocity of steady-state traveling wave going from left to right (as in References [3,7]) and L is the neutron average diffusion length.

For this we use the following operators

$$\frac{\partial }{\partial x}=\frac{d}{d\xi },\frac{\partial }{\partial t}=u\frac{d}{d\xi }$$

(20)

Following [3,7], we assume, without loss of generality, that ${}^8{\sigma }_a\cong {}^9{\sigma }_a\cong {}^{Pu}{\sigma }_a$. From here it follows that $c_8=c_9=c_{Pu}$. Then, introducing the dimensionless constant $\Lambda =u{\tau }_{\beta }/L$ and the variable $n_{*}\left(z\right)=c_1{\tau }_{\beta }n\left(z\right)$, and simultaneously performing the transformation of coordinates in Equations (11), (14), (17) and (19)

$$z=\frac{\xi }{L}=\frac{x+ut}{L},$$

(21)

we obtain the system of kinetic equations for neutrons and nuclei taking part in the reaction chain (1) with respect to the dimensionless autowave variable z

$$\frac{d^2{n}_{*}}{d{z}^2}=\left[1-\frac{n_{Pu}}{n_{crit}^{Pu}}\right]n_{*}$$

(22)

$$\Lambda \frac{d{n}_8}{dz}=-\left[n_8-n_9-n_{Pu}\right]n_{*}$$

(23)

$$\Lambda \frac{d{n}_9}{dz}=\left(n_8-n_9\right)n_{*}-n_9$$

(24)

$$\Lambda \frac{d{n}_{Pu}}{dz}=n_9-\frac{n_{Pu}}{{\tilde{n}}_{Pu}}{n}_{*}$$

(25)

where u is the phase velocity of stationary traveling wave, L is the neutron average diffusion length, $n_{*}(z,t)$ is the neutron flux density, $D=v/3{\Sigma }_s=L^2/\tau$ is neutron diffusion constant, $c{m}^2·s^{-1}$; v is the neutron velocity in the one-group approximation, $cm·s^{-1}$; ${\Sigma }_s$ is the the neutron macroscopic scattering cross-section, $c{m}^{-1}$; $\tau =1/v\sum {\sigma }_a^i{N}_i$ is the neutron lifetime in medium, $N_i$ is the nucleus concentration of $8{(}^{238}U)$, $9{(}^{239}Np)$ and ${}^{239}Pu$; $\Lambda =u{\tau }_{\beta }/L$ is the dimensionless constant, $n_{crit}^{Pu}=N_{crit}/N_8(-\infty )=\sum \left({\sigma }_a^i{n}_i\right)/(\nu -1){\sigma }_f^{Pu}$ is the plutonium relative critical concentration, $n_i$ is the nucleus concentration of $8{(}^{238}U)$ and $9{(}^{239}Np)$ normalized to ${}^{238}U$ initial concentration, i.e., to $N_8(-\infty )$, ${\sigma }_a$ and ${\sigma }_f$ are the microscopic neutron capture cross-section and fission cross-section, respectively, ν is the average number of prompt neutrons produced per plutonium nucleus fission.

Solving these equations Feoktistov has used the analogy between the diffusion equation and the Schrödinger steady-state equation in the quasi-classical approximation [3]. Naturally, in this case (see Equation (22)) the solution stationarity condition is satisfied integrally, because there are points where $n_{Pu}>n_{crit}$, and there are points where $n_{Pu}<n_{crit}$. In this sense, the region $n_{Pu}>n_{crit}$ corresponds to kind of allowed region, whereas the region $n_{Pu}<n_{crit}$ corresponds to subbarrier region. In other words, the inverted profile of plutonium concentration in the ${}^{238}U$ medium plays the role of potential well (Figure 1 [8]).

Figure 1. Time dependence of neutron concentration. Propagating wave (a) and locked wave; (b) a segment of the curve $n_{Pu}\left(z\right)$ above the $n_{cr}$ line is the reactor core; the scales of $n_{cr}$ and $n_{Pu}$ are given with $a\times 10$ magnification [8]; t is expressed in arbitrary units.

Figure 1. Time dependence of neutron concentration. Propagating wave (a) and locked wave; (b) a segment of the curve $n_{Pu}\left(z\right)$ above the $n_{cr}$ line is the reactor core; the scales of $n_{cr}$ and $n_{Pu}$ are given with $a\times 10$ magnification [8]; t is expressed in arbitrary units.

For the region in front of wave $(z=-\infty )$ the approximate solution looks like

$$n=Cexpz$$

(26)

$$n_8=exp\left(-\frac{C}{\Lambda }expz\right)$$

(27)

$$n_9=\frac{C}{1+\Lambda }expz$$

(28)

$$n_{Pu}=\frac{{\tilde{n}}_{Pu}}{1+\Lambda }\left[1-exp\left(-\frac{C}{\Lambda {\tilde{n}}_{Pu}}expz\right)\right]$$

(29)

It will be recalled that searching this solution, we have neglected summands $n_9$ and $n_{Pu}$ whose values are determined by edge condition $n_8\cong 1$. Then, assuming that the subbarrier region ends at $z=0$, we have $n_{Pu}=n_{crit}$ at this point. This makes it possible to determinate the constant C. According to the Bohr–Sommerfeld quantization condition, we have the following equality at the point $z=a$

$$\underset{0}{\overset{a}{\int }}\sqrt{\frac{n_{Pu}}{n_{crit}^{Pu}}-1}dz=\frac{\pi }{2}$$

(30)

where the integral is taken over the supercritical region $(n_{Pu}>n_{crit})$.

At the same time the condition (30) plays also the role of condition for finding the point a at $n_{Pu}=n_{crit}$, i.e., when the transition into subbarrier region happens due to burn-up (see Figure 1a [8] and Figure 2) [9].

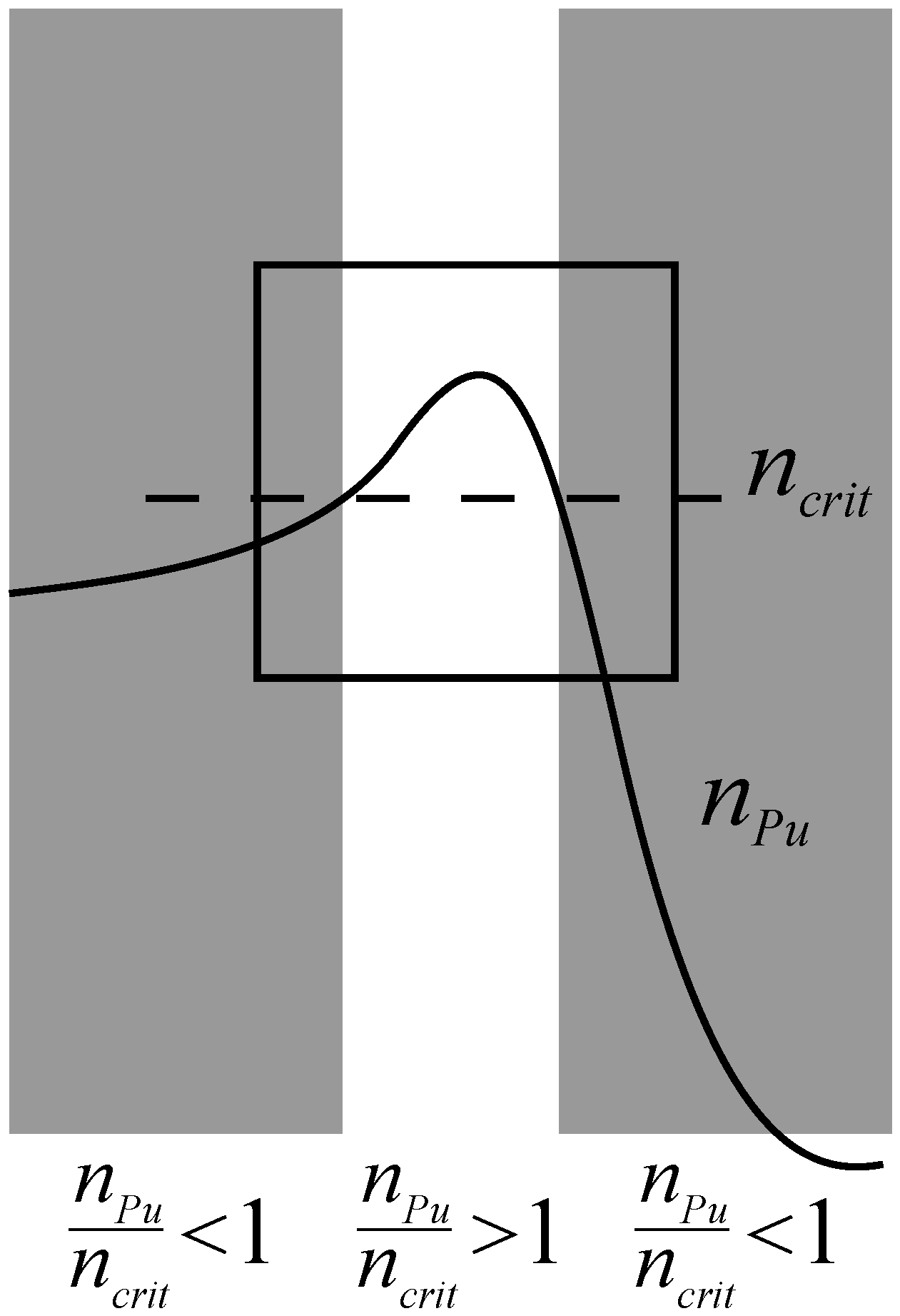
Figure 2. The schematic view of the permitted and subbarier (gray colored) region corresponding to the conditions $n_{Pu}>n_{crit}$ and $n_{Pu}<n_{crit}$, respectively. The delineated by square region is considered more particularly in Figure 3.

Figure 2. The schematic view of the permitted and subbarier (gray colored) region corresponding to the conditions $n_{Pu}>n_{crit}$ and $n_{Pu}<n_{crit}$, respectively. The delineated by square region is considered more particularly in Figure 3.

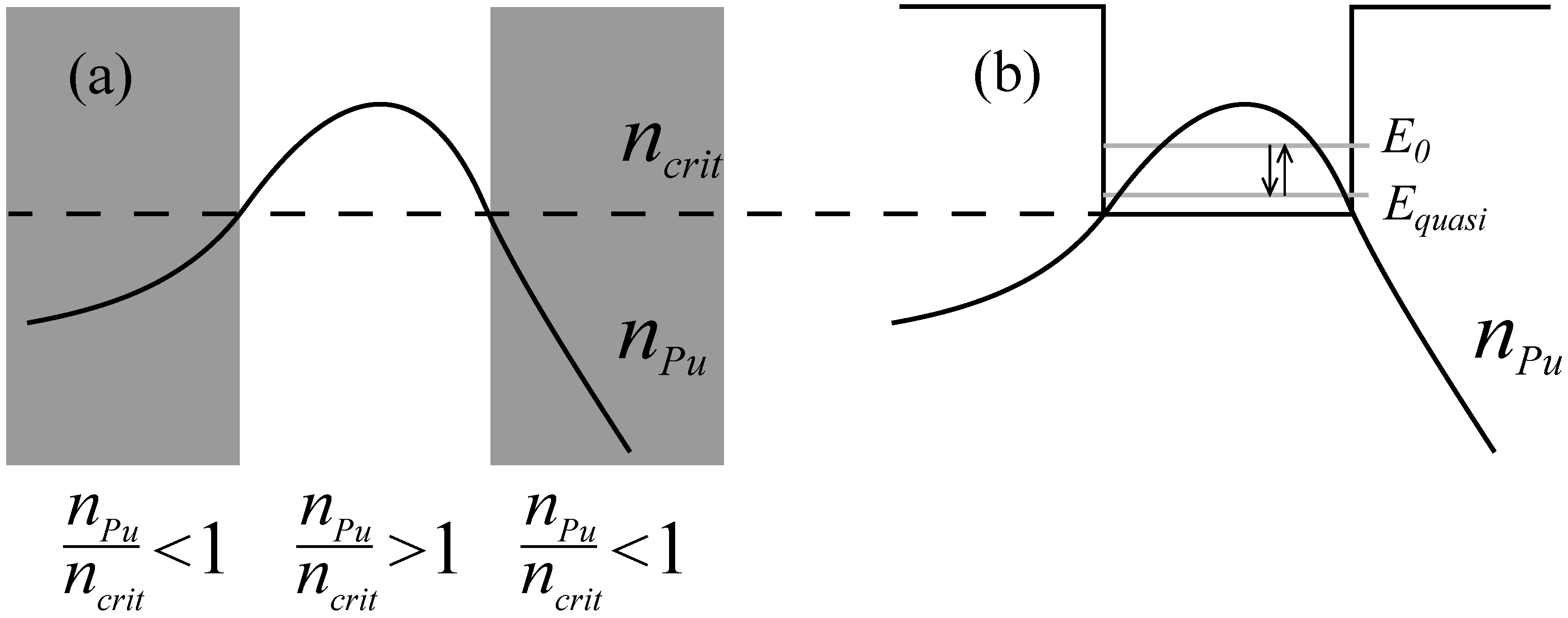
Figure 3. Schematic description of the permitted and forbidden region boundaries of nuclear burning according to the Borh-Sommerfeld condition (a) and the corresponding quasi-equivalent two-level scheme (b).

Figure 3. Schematic description of the permitted and forbidden region boundaries of nuclear burning according to the Borh-Sommerfeld condition (a) and the corresponding quasi-equivalent two-level scheme (b).

Performing the ordinary for quasi-classical approximation matching with the supercriticality region $(n_{Pu}>n_{crit})$, we come to calculation of Λ.

As a critical state is automatically maintained at $n_{Pu}>n_{crit}$ [3] (that is the direct consequence of the Bohr–Sommerfeld quantization condition), we can use this fact for generalization of the following inequality:

$${\tilde{n}}_{Pu}>n_{Pu}>n_{crit}^{Pu}$$

(31)

where ${\tilde{n}}_{Pu}$ is the plutonium equilibrium concentration (see Figure 1).

Thus, Feoktistov have shown for the first time that the soliton-like propagation of neutron-fission wave of nuclear burning is possible in ${}^{238}U$ medium only at definite ratio between the equilibrium and critical plutonium concentrations $({\tilde{n}}_{Pu}>n_{crit})$, which is imposed by the Bohr–Sommerfeld quantization condition. In other words, only in this case the critical (quasi-stationary) state of system (reactor core) can automatically maintained without any external intervention, and, consequently, only in this case the reactor completely and unambiguously possesses the property of internal safety.

It is appropriate here to pay an attention to very important Feoktistovs parameter, which, as shown below, is basis for the existence of soliton-like wave of nuclear burning:

$$\Lambda \left(a\right)=\frac{u{\tau }_{\beta }}{L}$$

(32)

where a is the width of allowed range of integration in the Bohr–Sommerfeld condition (30), where the inequality $n_{Pu}>n_{crit}$ (Figure 2) and ${\tilde{n}}_{Pu}>n_{crit}$, respectively, are satisfied; $\Lambda \left(a\right)$ is the dimensionless coefficient, which appears within the framework of simplified diffusion model of the Feoktistov reactor (22)–(25).

It is obvious that Equation (30) due to its physical meaning is a key factor, which predetermines the phase velocity of soliton-like burning wave. Therefore, this equation exists regardless of level of idealization of reactor core model and should appear in the explicit or implicit form in any model in which the system of kinetics equations for neutrons and nuclei has soliton-like solutions for neutrons. At the same time, as the average width of soliton wave is about $2L$, the maximum values for the dimensionless coefficient $\Lambda \left(a\right)$ and wave velocity u are determined by the following approximate equality

$$\frac{1}{b}{\Lambda }_{max}\left(a\right)=\frac{u_{max}{\tau }_{\beta }}{bL}=1$$

(33)

where the coefficient b is about 2, although a final estimate will be given below.

From analysis of Equation (33) it follows that the velocity of soliton-like wave propagation does not always equal to the diffusion speed $u=L/{\tau }_{\beta }$. It can be considerably slower or faster due to very strong domination of the nonlinearity parameter or, conversely, the variance parameter, which reflect the peculiarities of nuclear transformation kinetics (for example, in the chain (1) and/or in (2)). In practice, they manifest itself as different degree of fuel burn-up.

In other words, when the wave velocity and consequently the degree of fuel burn-up are low, the wave stops due to the following reasons. Neutrons from an external source, which take place in the initial stage of wave initiation, burn out the plutonium on the medium boundary and simultaneously transmute the uranium into ${}^{239}Np$. Neptunium with time begins to produce the plutonium, but it can not create the required high concentration, while the ${}^{239}Pu$ accumulation decreases due to the uranium burn-up. More and more thick layer without both ${}^{238}U$ and ${}^{239}Pu$ grows near to the medium boundary. The neutron diffusion through this layer does not provide the increase of plutonium concentration in next layers, and the wave does not arise even at $n_{Pu}(x,0)=n_{crit}$. And, vice versa, when the wave velocity and consequently degree of fuel burn-up are high, the wave stops also because of the scarce (or more exactly, delayed) plutonium production which takes place due to another reason. Figuratively speaking, the situation resembles the forest fire by strong wind, when only crown posts burn. When the wind velocity increases, it could extinguish the fire at all. We have the similar situation, when there is a velocity, at which in the early stage (when $x\approx 0$) the neutron soliton wave front outruns the plutonium (sigmoid) wave front, and this advance exceeds the neutron diffusion length. This leads, in fact, to transformation of fast wave into slow wave or to its full stop. It is interesting to note that this case is not discussed in the literature (with the exception of [8,10]), but it is possible to assume that it corresponds to some hypothetical situation, when the nuclear burning wave forms in highly enriched fuel which has the ultra-low critical concentration of fuel fissionable component.

Thus, when the lag (Figure 1b [8]) or advance of neutron wave front relative to the plutonium wave front is considerably greater than the neutron diffusion length, these waves stop and totally degrade. This means that the degradation of waves with very low or very high initial phase velocity will exhibit in the fact that Equation (32) tends to zero at some low or very high values of a. Therefore taking into account Equation (33), we can conclude that Equation (32) is true in the range $0⩽(1/b)\Lambda \left(a\right)⩽1$. Based on this generalization, we can make an important assumption that the expression $(1/b)\Lambda \left(a\right)$ means the certain probability density distribution $p\left(a\right)$ with respect to a:

$$\frac{u{\tau }_{\beta }}{bL}=p\left(a\right)$$

(34)

Let us consider and substantiate the type and main properties of such a statistics and also show the results of its verification based on the known computational experiments on simulation of nuclear burning wave in the U-Pu (1) and Th-U (2) fuel cycles.

3. Chaos and Integrability in Nonlinear Dynamics of Reactor Core

In order to solve the assigned task we use the known analogy between the neutron diffusion equation and the Schrödinger steady-state equation in quasi-classical approximation. We would remind that earlier we have used this analogy to search the solution of the system of kinetics equation for neutrons and nuclei (22)–(25) in the reaction chain (1) of the U-Pu fuel cycle. Since the system of equations for neutrons and nuclei in the Th-U fuel cycle (2) is structurally identical to the system equation for the U-Pu fuel cycle (1), the computed “quantum mechanical” solution, which describes the statistics (34), will be general for both fuel cycles, except for a few inessential details.

So, due to mentioned analogy we use the Bohr–Sommerfeld quantization condition, which in the case of the one-dimensional systems determines the energy eigenvalues $E_n$ in the explicit form

$$\oint p\left(x\right)dx=\oint \sqrt{2m\left(E_n-V\left(x\right)\right)}dx=2\pi \hslash \left(n+\frac{1}{2}\right),n=0,1,2,\dots$$

(35)

where m and $p\left(x\right)$ are the particle mass and particle momentum in the field of some smooth potential $V\left(x\right)$.

For the Feoktistov nearly integrable system of the equations (22)–(25) or for the similar Teller system of equations, for which it is assumed that $m=1/2$, $\hslash =1$, $V\left(x\right)=1$ and $n=0$, this condition is applied in the following form

$$\underset{0}{\overset{a}{\int }}\sqrt{E_0-1}dz=\frac{\pi }{2},E_0=\frac{n_{fiss}}{n_{crit}^{fiss}}$$

(36)

where index $fis$ signifies the fissionable isotope, for example, the ${}^{239}Pu$ in the Feoktistov U-Pu fuel cycle (1) or the ${}^{233}U$ in the Teller Th-U fuel cycle (2).

However, in describing the real evolution of fast reactor core, the corresponding systems of equations for neutrons and nuclei are non-integrable almost without exception. This, in its turn, means that according to the Kolmogorov–Arnold–Moser theorem [11,12] quasi-classical quantization formulas are inapplicable for the system, where the motion in phase space is not restricted by multidimensional tori. This is caused by the fact that in the Hamiltonian non-integrable systems the more and more number of tori is collapsed in phase space with perturbation (non-integrability) growth. As a result, the trajectories of majority of coupled states get entangled in phase space, the motion becomes mainly chaotic, and coupled states themselves and their energies can not be described by the rules of quasi-classical quantization, for example, such as the Einstein–Brillouin–Keller (EBK) quantization rule for multidimensional case [12,13], which generalizes the Bohr–Sommerfeld quantization rule. Note that now a notion “quantum chaos” joins the range of problems related to quantum-mechanical description of systems chaotic in a classic limit [14,15].

Since the results of random matrices theory will be used for research of chaotic properties of the statistics (30), we give in advance an overview of the main concepts of this theory.

First, following [14,15], let us shortly consider a nature of so-called universality classes and kinds of the Gaussian ensembles. It is known, if the Hamilton operator matrix has any symmetry, it can be reduced to the block-diagonal form. At the same time, the matrix elements in each block are specified by a certain quantum number set. For simplicity, we assume below that the Schrödinger equation $i\hslash \left(\partial \psi /\partial t\right)=\widehat{H}\psi$ describes the states belonging only to the one block. At the same time, the size of the operator matrix $\widehat{H}$ is finite and equals to some integer.

As shown in [14,15], these universality classes divide physical systems into groups depending on their relation to orthogonal, unitary or symplectic transformations, after which the matrix $\widehat{H}$ remains invariant. In other words, as it ascertained in [14]:

• the Hamiltonian of spinless system, which is symmetrical with respect to time inversion, is invariant under orthogonal transformations and can be represented by a real matrix;
• the Hamiltonian of spinless system, which is not symmetrical with respect to time inversion, is invariant under unitary transformations and can be represented by the Hermitian matrix;
• the Hamiltonian of the system with the spin of 1/2, which is symmetrical with respect to time inversion, is invariant under symplectic transformations and can be represented by a quaternion real matrix.

Now let us talk about the Gaussian ensembles. If the matrix element distribution function is invariant under one of mentioned transformations, this means that the sets of all matrices with elements, which are described by these distribution functions, form the Gaussian orthogonal ensemble (GOE), the Gaussian unitary ensemble (GUE) and the Gaussian symplectic ensemble (GSE), respectively.

At the same time it should be noted the one very important detail. The matrix element distribution function of the Gaussian ensembles can not be directly measured, because the experiment can give us information about the energy levels of investigated quantum-mechanical system only. In other words, just the distribution function of energy eigenvalues is of greater interest from the practical point of view.

Derivation of corresponding equations for the considered types of the Gaussian ensembles can be found in [15]. At the same time, the correlated distribution function of energy eigenvalues for all ensemble types it is possible to write down in the sufficiently universal form:

$$P\left(E_1,\dots ,E_N\right)\sim \prod _{n>m}{\left(E_n-E_m\right)}^{\nu }exp\left(-A\sum _n{E}_n^2\right)$$

(37)

where ν is the universality index, which takes on the value of 1, 2 and 4 for GOE, GUE and GSE statistics, respectively. At $\nu =0$ the energy eigenvalues are not correlated. In this case, the energy level spacing distribution function is described by the Poisson statistics, and the matrix ensemble itself is called the Poisson ensemble.

So long as the energy level spacing distribution function is the most studied characteristic of chaotic systems, following [14], we give a calculation only for relatively simple case of the Gaussian ensemble of the matrices $2\times 2$ in size. We calculate the energy level spacing distribution function $p_W\left(s\right)$ substituting the function $P(E1,E2)$ into (37):

$$\begin{array}{ccc}\hfill p_W\left(s\right)& =& \underset{-\infty }{\overset{+\infty }{\int }}d{E}_1\underset{-\infty }{\overset{+\infty }{\int }}d{E}_{2}P\left(E_1,E_2\right)\delta \left(s-|E_1-E_2|\right)\hfill \\ & =& C\underset{-\infty }{\overset{+\infty }{\int }}d{E}_1\underset{-\infty }{\overset{+\infty }{\int }}d{E}_2{|E_1-E_2|}^{\nu }exp\left(-A\sum _n{E}_n^2\right)\delta \left(s-|E_1-E_2|\right)\hfill \end{array}$$

(38)

Constants A and C are determined by the two normalization conditions:

$$\underset{0}{\overset{\infty }{\int }}{p}_W\left(s\right)ds=1$$

(39)

$$\underset{0}{\overset{\infty }{\int }}s{p}_W\left(s\right)ds=1$$

(40)

The first condition is the total probability normalization to unit, and the second condition is the average energy level spacing normalization to unit. Integration of (38) gives the so-called Wigner energy level spacing distribution functions, which correspond to the different Gaussian ensembles:

$$p_W\left(s\right)=\left\{\begin{array}{cc}\frac{\pi }{2}sexp\left(-\frac{\pi }{4}{s}^2\right),\hfill & \nu =1\left(GOE\right)\hfill \\ \frac{32}{\pi }{s}^{2}exp\left(-\frac{\pi }{4}{s}^2\right),\hfill & \nu =2\left(GUE\right)\hfill \\ {\left(\frac{8}{3\sqrt{\pi }}\right)}^6{s}^{4}exp\left(-\frac{64}{9\pi }{s}^2\right),\hfill & \nu =4\left(GSE\right)\hfill \end{array}\right.$$

(41)

Despite the fact that these functions were obtained for the Gaussian ensembles of matrices $2\times 2$ in size, they describe with good accuracy the spectra of arbitrary size matrices [14].

Note that random matrix theory at first was developed to find some regularities for heavy nucleus energy spectra [15,16], but it attracted keen interest after the Bohigas, Giannoni and Schmit conclusion [17] that this theory is applicable to any chaotic system.

Returning to our problem, we will attempt to use the considered statistical properties of the Gaussian ensembles to determine the Equation (34) statistics type.

4. The Wigner Quantum Statistics and Generalized Condition for Existence of Traveling Wave Mode of Nuclear Burning

To apply the results of previous section, in the framework of nearly integrable system, to which the system of equations describing the kinetics of nuclear burning in the Feoktistov U-Pu fuel cycle (1) or the Taylor Th-U fuel cycle (2) belongs, we use some formal quantum analogy of this system [18].

It is obvious that to research the Wigner statistics type a two-level quantum system is needed, at least. Therefore we assume that a quantum energy system equivalent to the analyzed area of nuclear burning is two-level (Figure 2) and formally introduce the “energy” eigenvalue of stationary ground state as ${\left(n_{fiss}\right)}_0/n_{crit}=E_0$ and “energy” eigenvalue of quasistationary state as ${\left(n_{fiss}\right)}_{quasi}/n_{crit}=E_{quasi}$ (Figure 3). At the same time $E_0>E_{quasi}$ and ${\left(n_{fiss}\right)}_0$ is some specified value of fissionableisotope concentration limited from above by the fissionable isotope equilibrium concentration, i.e., ${\left(n_{fiss}\right)}_0<{\tilde{n}}_{fiss}$. We assume also that the quasistationary level is situated near the potential well bottom, i.e., $E_{quasi}\to 1$ (see Figure 3), and is strongly unstable [19]. Therefore, the nuclear burning mode “lives” most of the time in the ground energy state, i.e., on the level $E_0$.

So, to describe the wave mode of nuclear burning we use below the quantum-mechanical analogy, in the framework of which the “energy” spectrum of nuclear burning in allowed region is described by some quasiequivalent two-level scheme (Figure 3).

Then, for the nearly integrable system which describes the kinetics of nuclear transformations in the Feoktistov (1) or the Teller (2) fuel cycle in general case we can use the Bohr–Sommerfeld approximate condition in the following form

$$\underset{0}{\overset{a}{\int }}\sqrt{\frac{n_{fiss}}{n_{crit}^{fiss}}-1}dz\approx a\sqrt{E_0-E_{quasi}}\sim \frac{\pi }{2}$$

(42)

From here the obvious and important assertion follows: by virtue of the Bohr–Sommerfeld condition (42) the type of the Wigner energy level spacing statistics unambiguously predetermines the analogous statistics type of parameter, which characterizes the squared width $\left(a^2\right)$ of concentration wave front of active (fissionable) material.

Note that we have not any information about the value of “energy” $E_0$ before the experiment, whereas it is possible to consider that $E_{quasi}=1$. If, additionally, in the steady-state mode all wave kinetic parameters are predetermined by the equilibrium ${\tilde{n}}_{fiss}$ and critical $n_{crit}^{fiss}$ concentration of active (fissionable) isotope (whose values are known before experiment), the physical meaning and the necessity of following change

$$a\sqrt{E_0-E_{quasi}}=a_{*}\sqrt{\frac{{\tilde{n}}_{fiss}}{n_{crit}}-1}$$

(43)

become apparent.

Table 1. The parameters of nuclear burning wave.

Parameter	U-Pu Cycle						Th-U Cycle
	References
	Present paper	[20]	[21]	[21]	[22]	[4]	[23]	${}^{*}$
$\frac{{\tilde{n}}_{equil}^{fiss}}{n_{crit}^{fiss}}$	$\frac{0.100}{0.017}$	$\frac{2.585}{1.750}$	$\frac{0.145}{0.080}$	$\frac{0.024}{0.015}$	$\frac{0.240}{0.105}$	$\frac{0.10}{0.05}$	$\frac{0.071}{0.032}$	$\frac{0.070}{0.035}$
$a_{*}$	0.704	2.274	1.743	2.028	1.385	1.571	1.423	1.571
$u_{theor}/u_{simul}$	1030/1012	2.9/3.1	125/130	21/22	622/620	293/331	46/50	25
$\left[cm/year\right]$

${}^{*}$ Forecast for the Th-U fuel cycle in infinite medium at the 10% enrichment of ${}^{233}U$.

Table 1. The parameters of nuclear burning wave.

Parameter	U-Pu Cycle						Th-U Cycle
	References
	Present paper	[20]	[21]	[21]	[22]	[4]	[23]	${}^{*}$
$\frac{{\tilde{n}}_{equil}^{fiss}}{n_{crit}^{fiss}}$	$\frac{0.100}{0.017}$	$\frac{2.585}{1.750}$	$\frac{0.145}{0.080}$	$\frac{0.024}{0.015}$	$\frac{0.240}{0.105}$	$\frac{0.10}{0.05}$	$\frac{0.071}{0.032}$	$\frac{0.070}{0.035}$
$a_{*}$	0.704	2.274	1.743	2.028	1.385	1.571	1.423	1.571
$u_{theor}/u_{simul}$	1030/1012	2.9/3.1	125/130	21/22	622/620	293/331	46/50	25
$\left[cm/year\right]$

${}^{*}$ Forecast for the Th-U fuel cycle in infinite medium at the 10% enrichment of ${}^{233}U$.

It is obvious that the conditions (42) and (43) make it possible to obtain the expression for the parameter $a_{*}$:

$$a_{*}^2\sim \frac{{\pi }^2}{4}\frac{n_{crit}}{{\tilde{n}}_{Pu}-n_{crit}}$$

(44)

The next step for determining the statistics $p\left(a_{*}\right)$ of Equation (34) type consists in the experimental verification of proposed hypothesis. With that end in view we have compared the Gaussian ensemble statistics (41) with well-known computational experimental data [8,23,24,25,26,27] and have obtained a good accordance of calculation data with the theoretical dependence, which is described by the Gaussian symplectic ensemble statistics (see Table 1 and Figure 4).

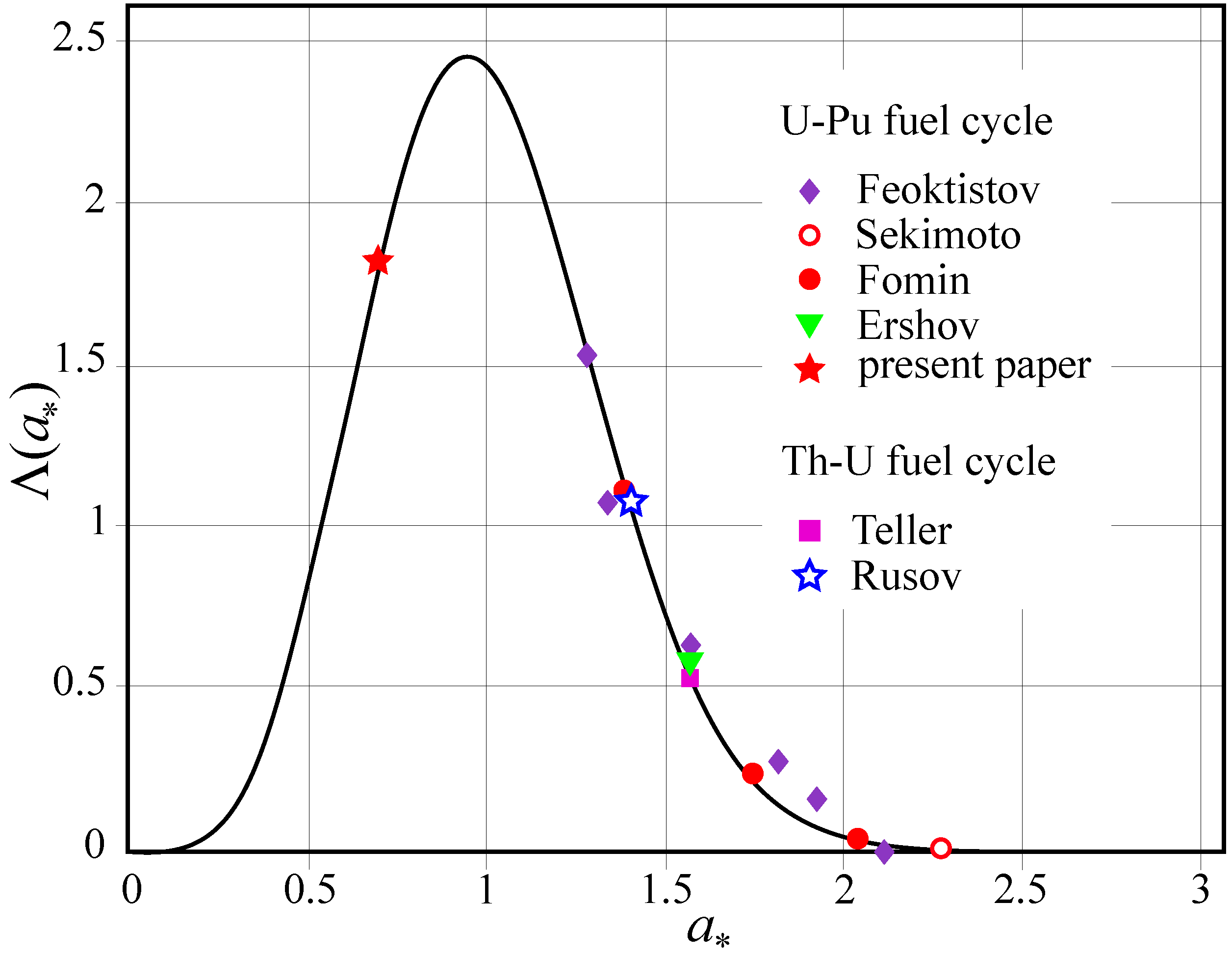
Figure 4. The theoretical (solid line) and calculational (points) dependence of $\Lambda \left(a_{*}\right)$ on the parameter $a_{*}$.

Figure 4. The theoretical (solid line) and calculational (points) dependence of $\Lambda \left(a_{*}\right)$ on the parameter $a_{*}$.

Thus, we can conclude that the wave velocity u (see Equation (34)) is predetermined by the following approximate equality

$$\frac{u{\tau }_{\beta }}{2L}\simeq p_W^s\left(a_{*}\right)={\left(\frac{8}{3\sqrt{\pi }}\right)}^6{a}_{*}^{4}exp\left(-\frac{64}{9\pi }{a}_{*}^2\right),a_{*}^2\simeq \frac{{\pi }^2}{4}·\frac{n_{crit}^{Pu}}{{\tilde{n}}_{Pu}-n_{crit}^{Pu}},$$

(45)

where coefficient $b=2$ (see Equation (34)); ${\tau }_{\beta }$ is the delay time caused by active (fissionable) isotope production, which is equal to the β-decay period of compound nuclei in the Feoktistov (1) or the Teller (2) fuel cycle; $p_W^s\left(a_{*}\right)$ is the Wigner symplectic statistics.

Thus, based on the verification results of Equation (45) we can make a conclusion, which generalizes the physical conditions for existence of Feoktistovs wave mode. The velocity of soliton-like wave propagation in neutron-multiplying medium must be determined in general case by the two conditions. The first condition (necessary) is predetermined by relationship between the equilibrium concentration and critical concentration of active (fissionable) isotope $({\tilde{n}}_{Pu}/n_{crit}>1)$ or, more exactly, by the corresponding Bohr–Sommerfeld quantization condition. The second condition (sufficient) is set by statistics of the Gaussian symplectic ensembles with respect to the parameter a, which describes the burning wave thickness of active (fissionable) component of nuclear fuel.

5. Computation 3D-Experiment and Verification of the Wigner Quantum Statistics

We consider here the simplified diffusion model for neutrons and nuclei kinetics in the chain (1) in the one-group approximation (neutrons energy is ∼1$MeV$) and cylindrical geometry. The corresponding system of differential equations, which describes the kinetics of Feoktistovs U-Pu fuel cycle with consideration of delayed neutrons, i.e., the kinetics of initiation and propagation of neutron-fission wave $n(x,t)$, is as follows [23]

$$\frac{\partial n(x,t)}{\partial t}=D\Delta n(x,t)+q(x,t)$$

(46)

where

$$\begin{array}{ccc}\hfill q(x,t)& =& \left[\nu (1-p)-1\right]·n(x,t)·v_n·{\sigma }_f^{Pu}·N_{Pu}(x,t)+\sum _{i=1}^6\frac{{\tilde{N}}_{i}ln2}{T_{1/2}^i}-\hfill \end{array}$$

$$\begin{array}{ccc}\hfill & & n(x,t)·v_n·\left[\sum _{8,9,Pu}{\sigma }_a^i·N_i(x,t)+\sum _{i=1}^6{\sigma }_a^i·{\tilde{N}}_i(x,t)+\sum _{i=fragments}{\sigma }_a^i·{\overline{N}}_i(x,t)\right]\hfill \end{array}$$

$$\frac{\partial N_8(x,t)}{\partial t}=-v_n·n(x,t)·{\sigma }_a^8·N_8(x,t)$$

(47)

$$\frac{\partial N_9(x,t)}{\partial t}=v_n·n(x,t)·{\sigma }_a^8·N_8(x,t)-\frac{1}{{\tau }_{\beta }}{N}_9(x,t)$$

(48)

$$\frac{\partial N_{Pu}(x,t)}{\partial t}=\frac{1}{{\tau }_{\beta }}{N}_9(x,t)-v_n·n(x,t)·\left({\sigma }_a^{Pu}+{\sigma }_f^{Pu}\right)·N_{Pu}(x,t)$$

(49)

$$\frac{\partial {\tilde{N}}_i}{\partial t}=p_i·v_n·n(x,t)·{\sigma }_f^{Pu}·N_{Pu}(x,t)-\frac{ln2·{\tilde{N}}_i}{T_{1/2}^i},i=1,6$$

(50)

To specify the last term $q(x,t)$ on the right-hand-side of Equation (46), we use the approach of effective additional neutron absorber:

$$n(x,t)v_n\sum _{i=fragments}{\sigma }_a^i·{\overline{N}}_i(x,t)=n(x,t)v_n{\sigma }_a^{eff}\overline{N}(x,t)$$

(51)

Taking into account the fact that fission with two fragment formation is most probable, the kinetic equation for $\overline{N}(x,t)$ becomes

$$\frac{\partial \overline{N}(x,t)}{\partial t}=2\left(1-\sum _{i=1}^6{p}_i\right)·n(x,t)·v_n·{\sigma }_f^{Pu}·N_{Pu}(x,t)+\sum _{i=1}^6\frac{{\tilde{N}}_{i}ln2}{T_{1/2}^i}$$

(52)

$n(x,t)$ is the neutron density; D is the neutron diffusion constant; $v_n$ is the neutron velocity($E_n=1MeV$, the one-group approximation); ${\tilde{N}}_i$ are the concentrations of neutron-rich fission fragments of ${}^{239}Pu$ nuclei; $N_8$, $N_9$, $N_{Pu}$ are the concentrations of ${}^{238}U$ , ${}^{239}U$, ${}^{239}Pu$, respectively; ${\overline{N}}_i$ are the concentrations of remaining fission fragments of ${}^{239}Pu$ nuclei; ${\sigma }_a$ is the neutron-capturemicrocross-section; ${\sigma }_f$ is the fission microcross-section; ${\tau }_{\beta }$ is the nucleus life time with respect to the β-decay; $p_i$ are the parameters characterizing delayed neutron groups for main fuel fissionable nuclides [27].

The boundary conditions for the system of differential Equations (46)–(50) are

$${n(x,t)|}_{x=0}={\Phi }_0/v_n{,n(x,t)|}_{x=l}=0$$

(53)

where ${\Phi }_0$ is the neutron density of plane diffusion neutron source, which is located on the boundary $x=0$; l is the uranium bar length.

An estimation of the neutron flux density from the inner source on the boundary ${\Phi }_0$ can be obtained from an estimation of the $Pu$ critical concentration which is of order of 10%:

$$4{\tau }_{\beta }{\Phi }_0{\sigma }_a^8{N}_8(x,t){{|}_{t=0}=0.1N_8(x,t)|}_{t=0}$$

(54)

and therefore we have

$${\Phi }_0\approx 0.1/4{\tau }_{\beta }{\sigma }_a^8$$

(55)

Note that Equation (55) is only an estimation of ${\Phi }_0$. The results of the computational experiment show that it can be substantially smaller in reality.

In general, different boundary conditions can be used, depending on the physical conditions under which nuclear burning is initiated by the neutron source, for example, the Dirichlet condition of (29) type, the Neumann condition or a so-called third-kind boundary condition, which generalizes first two conditions. The use of the third-kind boundary condition is recommended in neutron transport theory [27]. In the simple case this condition (which is known as the Milne problem) is a linear combination of the neutron concentration $n(x,t)$ and its spatial derivative $\partial n/\partial x(x,t)$ on the boundary

$$n(0,t)-0.7104\lambda n^{(1,0)}(0,t)=0$$

(56)

where λ is the neutron free path and $n^{(1,0)}(0,t)\equiv \partial n/\partial x(0,t)$.

Although the “neutron source-nuclear fuel” system behavior depends on the boundary conditions near the boundary, computational experiments show that inside the reactor core, i.e., far from the boundary, the system behavior is asymptotically invariant. This confirms the independence of wave propagation in reactor volume on the boundary conditions and the way in which the nuclear burning is initiated. In this sense, the problem of determining the optimum parameters of nuclear fuel “ignition” in the “neutron source-nuclear fuel” system is a nontrivial and extraordinarily vital issue, which requires a separate examination.

The initial conditions for the system of differential Equations (46)–(50) are

$${n(x,t)|}_{x,t=0}={\Phi }_0/v_n{,n(x,t)|}_{x,t=0}=0$$

(57)

$$N_8{(x,t)|}_{t=0}=\frac{{\rho }_8}{{\mu }_8}{N}_A\approx \frac{19}{238}{N}_A$$

(58)

$$N_9{(x,t)|}_{t=0}=0,N_{Pu}{(x,t)|}_{t=0}=0,{\tilde{N}}_i(x,t){{|}_{t=0}=0,{\overline{N}}_i(x,t)|}_{t=0}=0$$

(59)

where ${\rho }_8$ is the density, $g·c{m}^{-3}$; ${\mu }_8$ is the gram-molecular weight, $g·mol{e}^{-1}$; $N_A$ is the Avogadro number.

The following values of constants were used for the simulation:

$${\sigma }_f^{Pu}=2.0·{10}^{-24}c{m}^2;{\sigma }_f^8=0.55·{10}^{-24}c{m}^2$$

(60)

$${\sigma }_a^8={\sigma }_a^i={\sigma }_a^{fragments}=5.38·{10}^{-26}c{m}^2;{\sigma }_a^9={\sigma }_a^{Pu}=2.12·{10}^{-26}c{m}^2$$

(61)

$$\nu =2.9;{\tau }_{\beta }\sim 3.3days;v_n\approx {10}^{9}cm·s^{-1};D\approx 2.8·{10}^{9}c{m}^2·s^{-1}$$

(62)

The system of Equations (46)–(51) with the boundary conditions (53)–(56), initial conditions (57)–(59) and the values of constants (60)–(62) is solved numerically using the software package Fortran Power Station 4.0. At the same time we use the DMOLCH subprogram from the IMSL Fortran Library. The DMOLCH subprogram solves a system of partial differential equations of the form $u_t=f(x,t,u_x,u_{xx})$ by the method of straight lines [23,28]. The solutions for diffusion model of neutrons and nuclei kinetics in the chain (1) in the one-group approximation and cylindrical geometry are presented in Figure 5.

Verification of the Wigner symplectic statistics consists in comparison of the experimental velocity of nuclear burning wave obtained by a computational 3D-experiment with its theoretical value obtained by Equation (45). For this purpose we at first find the plutonium critical concentration $n_{crit}$ from the profile of its experimental concentration distribution (Figure 5). It is obvious that the absolute value of critical concentration approximately equals to $N_{crit}^{Pu}\cong 8·{10}^{20}c{m}^{-3}$ (see Figure 6b). It follows from here that the plutonium normalized critical concentration is

$$n_{crit}^{fiss}=N_{crit}^{Pu}/N_8(x,0)=0.0167$$

(63)

where by virtue of Equation (58) the initial uranium concentration is $N_8(x,0)=4.79·{10}^{22}c{m}^{-3}$ and the value of $a_{*}$ is equal to $0.704$ by virtue of Equation (44). In other words, the important case when $a_{*}<1$ takes a place (see Figure 4).

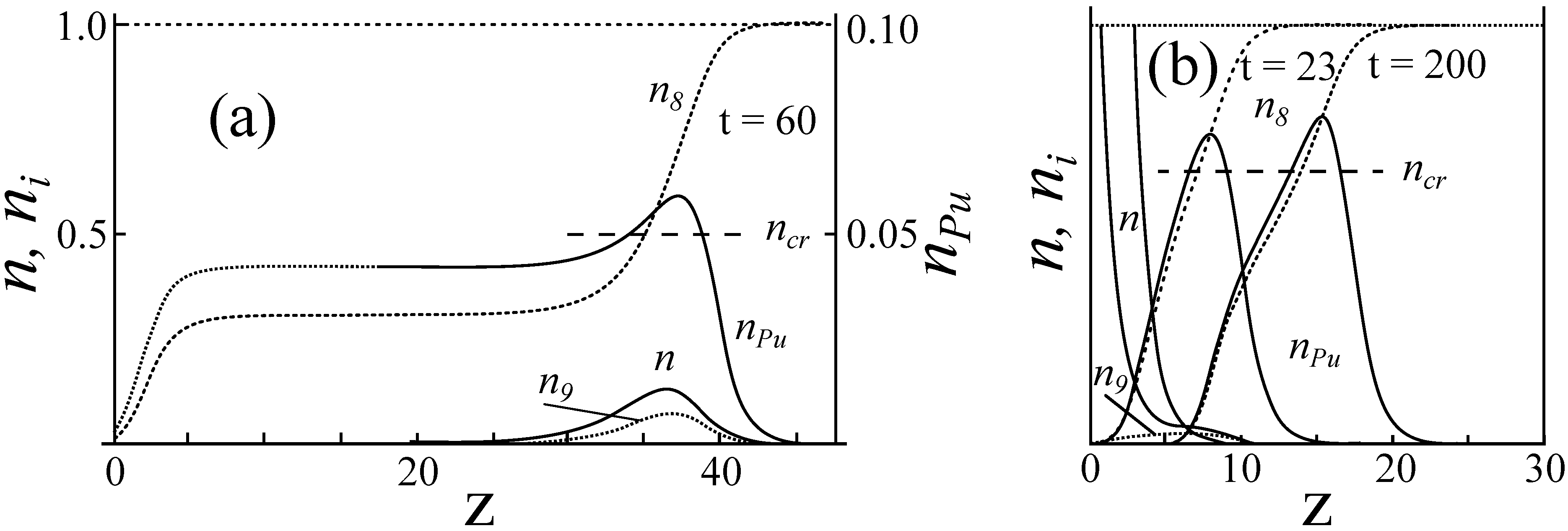
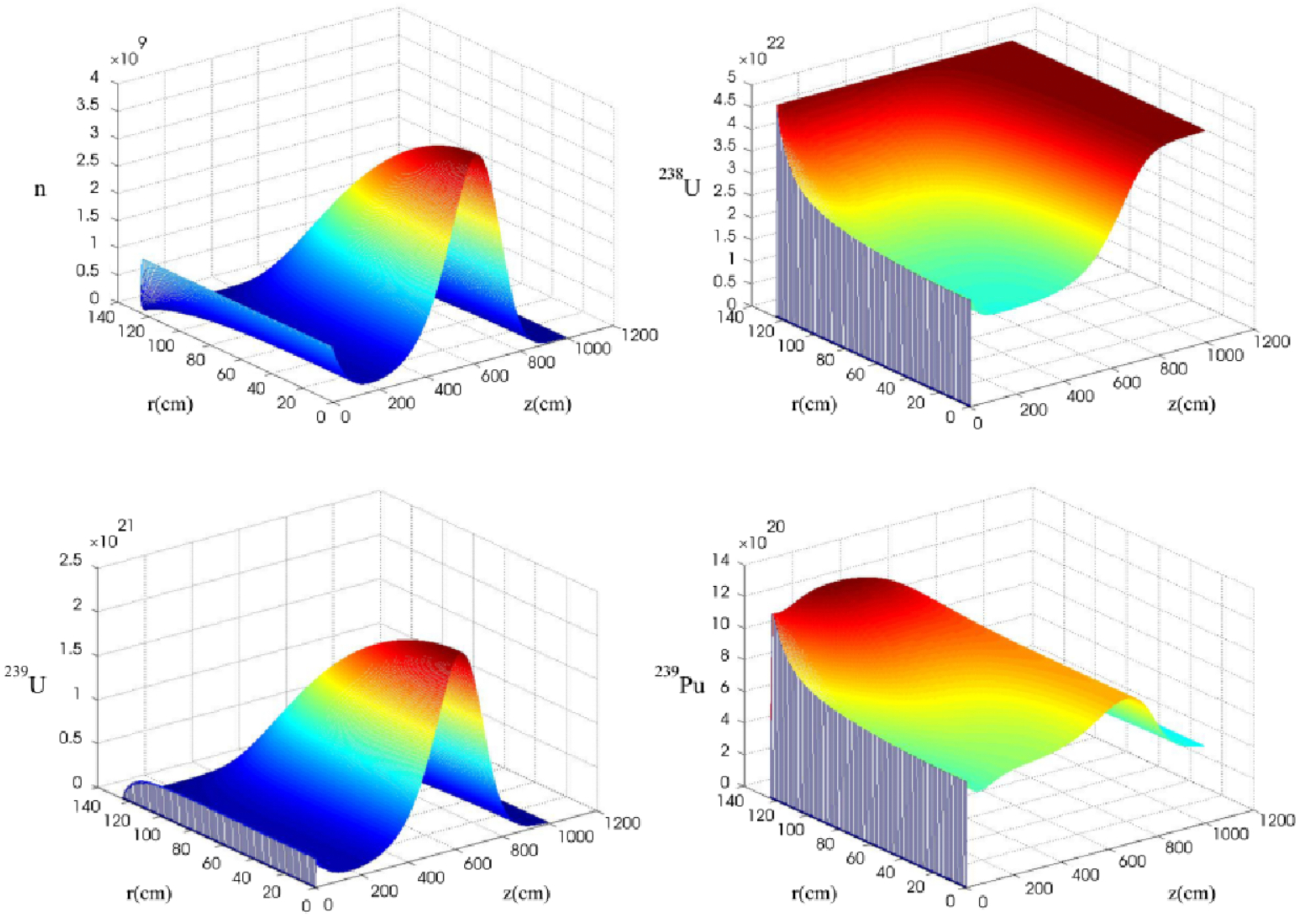
Figure 5. Concentration kinetics of neutrons, ${}^{238}U$, ${}^{239}U$ and ${}^{239}Pu$ in the cylindrical reactor core with radius of 125 cm and 1000 cm long over the time 240 days. Here r is transverse spatial coordinate axis (cylinder radius), z is longitudinal spatial coordinate axis (cylinder length).

Figure 5. Concentration kinetics of neutrons, ${}^{238}U$, ${}^{239}U$ and ${}^{239}Pu$ in the cylindrical reactor core with radius of 125 cm and 1000 cm long over the time 240 days. Here r is transverse spatial coordinate axis (cylinder radius), z is longitudinal spatial coordinate axis (cylinder length).

Taking into account the plutonium normalized equilibrium concentration ${\tilde{n}}_{fiss}=0.1$, by virtue of Equation (45) we obtain the Wigner theoretical symplectic probability:

$$\frac{1}{2}\Lambda \left(a_{*}\right)=p_W^s\left(a_{*}\right)=0.9303$$

(64)

which corresponds to the nuclear burning wave velocity $u_{theor}=2.82cm/day$ at given parameters $L=5cm$ and ${\tau }_{\beta }=3.3days$.

Now it is easy to determine the experimental value of nuclear burning wave velocity and, accordingly, the Wigner symplectic probability. In Figure 6a the profile of experimental concentration distribution of neutrons is shown. We can see that the wave crest has covered the distance of $600cm$ during$t=217days$. Thus, the velocity of nuclear burning neutron wave is

$$u_{simul}=600/217\simeq 2.77cm/day$$

(65)

This, in its turn, corresponds to the value of $1/2\Lambda \left(a_{*}\right)=p_W^s\left(a_{*}\right)=0.9141$.

Thus, the approximate equality of the experimental and theoretical velocity of nuclear burning wave ($u_{theor}\cong u_{simul}$) makes it possible to conclude that the Wigner quantum (symplectic) statistics verified by computing 3D-experiment (see Figure 4) satisfactorily describes experimental data characterized by the parameter $\Lambda \left(a_{*}\right)$.

Figure 6. The concentration distribution of neutrons at the velocity of wave propagation $u_{simul}\approx 2.77cm/day$ (a) and ${}^{239}Pu$ at ${\tilde{n}}_{Pu}=0.1$ and $n_{crit}^{Pu}=0.0167$ (b) along the axis of a cylinder over the period $t=217days$.

Figure 6. The concentration distribution of neutrons at the velocity of wave propagation $u_{simul}\approx 2.77cm/day$ (a) and ${}^{239}Pu$ at ${\tilde{n}}_{Pu}=0.1$ and $n_{crit}^{Pu}=0.0167$ (b) along the axis of a cylinder over the period $t=217days$.

Here we note that computing experiments show that the conditions of wave blocking, which describe the degradation and subsequent stop of wave, are predetermined by the degree of burn-up of the main nonfissionable (${}^{238}U$) and fissionable (${}^{239}Pu$) components of nuclear fuel in front of the wave by neutrons from an external source in the initial stage of wave “ignition”. This process is very important, since when the degree of fuel burn-up in front of the wave is high, the wave can not overcome this “scorched” region just like a fire in the steppe can not overcome the plowed stripe of the land in front of combustion wave. It is obvious that in the initial stage of wave initiation the degree of fuel burn-up is determined, first of all, by the energy and intensity of neutrons from the external source and by the properties of nuclear fuel. The most important of these properties is the delay time ${\tau }_{\beta }$ of active (fissionable) isotope production, which is equal to the effective period of β-decay of compound nuclei in the Feoktistov U-Pu fuel cycle (1) or the Teller Th-U fuel cycle (2).

In spite of the general understanding of physics of nuclear burning wave blocking, it is obvious that indicated above difficulties in the describing this process testify to nontriviality of given problem. Unfortunately, the solving of this problem exceeds the scope of this work, but it will be a subject of future research.

6. On the Depth of Analogy between Diffusion Equation for Neutrons and the Schrödinger Equation in the WKB Approximation

It is known [29], that the solution of differential equation of the form

$$\frac{d^2\omega }{d{x}^2}=f\left(x\right)·\omega$$

(66)

in the Liouville–Green approximation looks like

$$\omega =A{f}^{-1/4}exp\left(\int f^{1/2}dx\right)+B{f}^{-1/4}exp\left(-\int f^{1/2}dx\right)$$

(67)

where $|f^{-1/4}|$ is the sufficiently small and slowly varying function, A and B are arbitrary constants.

From Equation (67) the famous expression for the phase with consideration of turning point follows

$$\oint f^{1/2}dx=2\pi \left(n+\frac{1}{2}\right),n=0,1,2,\dots$$

(68)

Note that physicists often name Equation (67) the WKB approximation after Wentzel, Kramers and Brillouin, who had developed a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients. However, as is known [29], their contribution consists not in construction of the Liouville–Green approximation which had been already obtained by that time, but in establishing of the equations which connect exponential and oscillatory solutions in turning points on real axis.

Thus, it is obvious that to obtain the necessary condition for existence of the nuclear burning wave (31) the use of the Bohr–Sommerfeld quantization condition (30) or, more precisely, the analogy between the diffusion equation and the Schrödinger equation in the WKB approximation was not quite obligatory. The use of Equation (68) is quite enough in this case, because, as is well-known [29], this equation is the independent result of the asymptotic decomposition theory and exists regardless of goals and ideology of the mathematical apparatus of quantum mechanics.

However the purpose of our research consists in finding of the generalized condition for existence of nuclear burning wave including both the necessary condition and sufficient condition. In this sense a question arises: “How will the nuclear burning wave velocity change, when the values of current concentration $n_{fiss}$ and critical concentration $n_{crit}^{fiss}$ of nuclear fuel active components in Equation (22) change in a random manner?” It is obvious that in this case formulation of the problem (with consideration of Equations (34) and (68)) comes to finding the probability density distribution function $p\left(a_{*}\right)$ of the random value of effective thickness of a nuclear burning concentration wave. This function, in its turn, is predetermined by a “random” nature of the equilibrium ${\tilde{n}}_{fiss}$ and critical $n_{crit}^{fiss}$ concentration of nuclear fuel active component, and thereby sets a random nature of wave velocity (see Equation (34)):

$$a_{*}=\frac{\pi }{2}\sqrt{\frac{n_{crit}^{fiss}}{{\tilde{n}}_{fiss}-n_{crit}^{fiss}}}\Rightarrow p\left(a_{*}\right)\simeq \frac{u{\tau }_{\beta }}{2L}$$

(69)

And here is the key moment of the article. To avoid the use of random matrix theory by “brute force” in researching the random process in (22), we have applied its results in the form of quantum analogy stated above. In this sense there are not serious reasons to search any hidden physical sense of the found analogy. In other words, interpreting the results of present paper, it is not advisable to talk about some real quantum effects and, all the more, about observation of the so-called quantum chaos mode in our case. Indeed we show that the probabilistic nature of nuclear burning wave velocity (see Equation (45) and Figure 4) is immediately predetermined by random nature of the initial values of the equilibrium ${\tilde{n}}_{fiss}$ and critical $n_{crit}^{fiss}$ concentration of nuclear fuel active component.

In this connection, a natural question arises, how in such a neutron-multiplying system, on the one hand, dynamic and chaotic modes coexist and, on the other hand, the chaotic mode in the form of the Wigner statistics is observed, although we have considered, at first sight, absolutely different fuel media, which in addition have the different initial fuel composition (see Figure 4).

Indeed it is known that the dynamic and chaotic modes can be observed under certain conditions in the same nonlinear dynamic system. This is easy to show on an example of the evolution of motion phase trajectories of the following hypothetical system.

Let us imagine some cylinder volume which is ${}^{238}U$ filled. We mentally divide it into identical disks. Each of these disks is described by the eigenvalue of equilibrium concentration ${\tilde{n}}_{fiss}$ and critical concentration $n_{crit}^{fiss}$ of ${}^{239}Pu$ under the obligatory condition ${\tilde{n}}_{fiss}>n_{crit}^{fiss}$. More specifically, each of the disks is described by the eigenvalue $a_{*n}=\Delta ·n$ (where $n=0,1,2,\dots ,n_{max}=3/\Delta$ (see Figure 4) and Δ is the subinterval of the segment $\left[0,a_{*max}=3\right]$). At the same time, the disks with the different values ałn are equally spaced in a cylinder. Then for the traveling wave of nuclear burning the dynamic mode takes place in each of disks, but when the wave passes from one disk to another, the change of the dynamic modes which are characterized by the different pair of equilibrium ${\tilde{n}}_{fiss}$ and critical $n_{crit}^{fiss}$ concentration of ${}^{239}Pu$ takes place due to the chaotic mode. In this sense, such an example visually demonstrates the random nature of changes of the different modes of motion phase trajectories, when the chaotic mode (strange as it may seem) plays the role of constructive chaos [30], which “instantly” transfers the system from one dynamic mode to another.

Another question related to the different fuel media and their initial composition can be reformulated in the following way: “What does the nuclear burning wave velocity mainly depend on in the uranium-thorium cycle (1) and thorium-uranium cycle (2)?” An answer is obvious and rather simple. In both cycles the nuclear burning wave velocity (far from a source which initiates the firing process) is fully characterized by the equilibrium ${\tilde{n}}_{fiss}$ and critical $n_{crit}^{fiss}$ concentration of nuclear fuel active component.

First of all, this is explained by the fact that the equilibrium ${\tilde{n}}_{fiss}$ and critical $n_{crit}^{fiss}$ concentration of nuclear fuel active component completely identify the neutron-multiplying properties of fuel medium, because they are the conjugate pair of integral parameters, which due to their physical content completely and sufficiently characterize all physics of nuclear transformations predetermined by initial fuel composition. This also follows from the simple analysis of the solutions of the system of kinetic equations for neutrons and nuclei (22)–(25). From this it follows that regardless of the type of nuclear cycle and initial fuel composition the nuclear burning wave velocity will be determined by the values of the equilibrium ${\tilde{n}}_{fiss}$ and critical $n_{crit}^{fiss}$ concentration of nuclear fuel active component and, consequently, as calculating experiments show (Figure 4), will obey the Wigner statistics.

7. Conclusions

The solutions of the system of diffusion type equations for neutrons and concomitant kinetic equations for nuclei obtained by numerical 3D-simulation persistently point to the regions, where the stable soliton-like solutions for neutrons and solitary wave solutions for nuclei are existed. This is no wonder for nearly intergrable systems, to which the investigated system of equations for neutrons and nuclei belongs, whereas the existence of stable soliton-like solutions in three spatial dimensions causes a surprise for the following reason.

As is known, the derivation and solution of integrable nonlinear evolution partial differential equations in three spatial dimensions has been the Holy Grail in the field of integrability since the late 1970s. The celebrated Korteveg–de Vries and nonlinear Schrödinger equations, as well as Kadomtsev–Petviashvili and Davey–Stewertson equations, are prototypical examples of integrable evolution equations in the one and two spatial dimensions, respectively. Do there integrable analogs of these equations in three spatial dimensions exist?

As it has turned out, quite recently, in 2006, the method for finding of analytical solutions of indicated above partial differential equations in three spatial dimensions was developed [31]. Therefore, the natural question arises: “To which from this equations does the diffusion equation for neutrons correspond, or, maybe, his is perfectly a new type of soliton partial differential equations in three spatial dimensions?”