Effect of Various Excitation Conditions on Vibrational Energy in a Multi-Degree-of-Freedom Torsional System with Piecewise-Type Nonlinearities
Abstract
:1. Introduction
2. Problem Formulation

3. Nonlinear Analysis with Harmonic Balance Method and Piecewise-Type Nonlinearities
3.1. Harmonic Balance Method with Multi-Staged Clutch Dampers
| Property | Stage | Value |
|---|---|---|
| Torsional stiffness, kC (linearized in a piecewise manner) (N·m/rad) | 1 | 10.1 |
| 2 | 61.8 | |
| 3 | 595.8 | |
| 4 | 1838.0 | |
| Hysteresis, Hi (N·m) | 1 | 0.98 |
| 2 | 1.96 | |
| 3 | 19.6 | |
| 4 | 26.5 | |
| Transition angle at positive side (δi > 0), (rad) | 1 | 0.05 |
| 2 | 0.16 | |
| 3 | 0.30 | |
| 4 | 0.39 | |
| Transition angle at negative side (δi < 0), (rad) | 1 | −0.04 |
| 2 | −0.05 | |
| 3 | −0.09 | |
| 4 | −0.15 |
| Torque Component | Case I | Case II | Case III | |
|---|---|---|---|---|
| Magnitude (N·m) | TM | 160.8 | 192.3 | 195.9 |
| Tp1 | 357.6 | 589.6 | 1378.6 | |
| Phase (rad) | −1.86 | −1.71 | −1.64 | |
| Torque Component | Case I | Case II | Case III |
|---|---|---|---|
| TDi (N·m) | 14.9 | 46.5 | 50.1 |
| TDv (N·m) | 145.8 | 145.8 | 145.8 |

3.2. Examination of System Responses of Severe Excitation Condition
 , harmonic balance method (HBM) (stable solution);
, harmonic balance method (HBM) (stable solution);  , HBM (unstable solution).
, HBM (unstable solution).
 , harmonic balance method (HBM) (stable solution);
, harmonic balance method (HBM) (stable solution);  , HBM (unstable solution).
, HBM (unstable solution).
 , HBM (unstable solution).
, HBM (unstable solution).
 , HBM (unstable solution).
, HBM (unstable solution).
 , HBM (unstable solution).
, HBM (unstable solution).
 , HBM (unstable solution).
, HBM (unstable solution).
 , NS by frequency up-sweeping;
, NS by frequency up-sweeping;  , NS by frequency down-sweeping; , flow of numerical solution under frequency up-sweeping; , flow of numerical solution under frequency down-sweeping.
, NS by frequency down-sweeping; , flow of numerical solution under frequency up-sweeping; , flow of numerical solution under frequency down-sweeping.
 , NS by frequency up-sweeping;
, NS by frequency up-sweeping;  , NS by frequency down-sweeping; , flow of numerical solution under frequency up-sweeping; , flow of numerical solution under frequency down-sweeping.
, NS by frequency down-sweeping; , flow of numerical solution under frequency up-sweeping; , flow of numerical solution under frequency down-sweeping.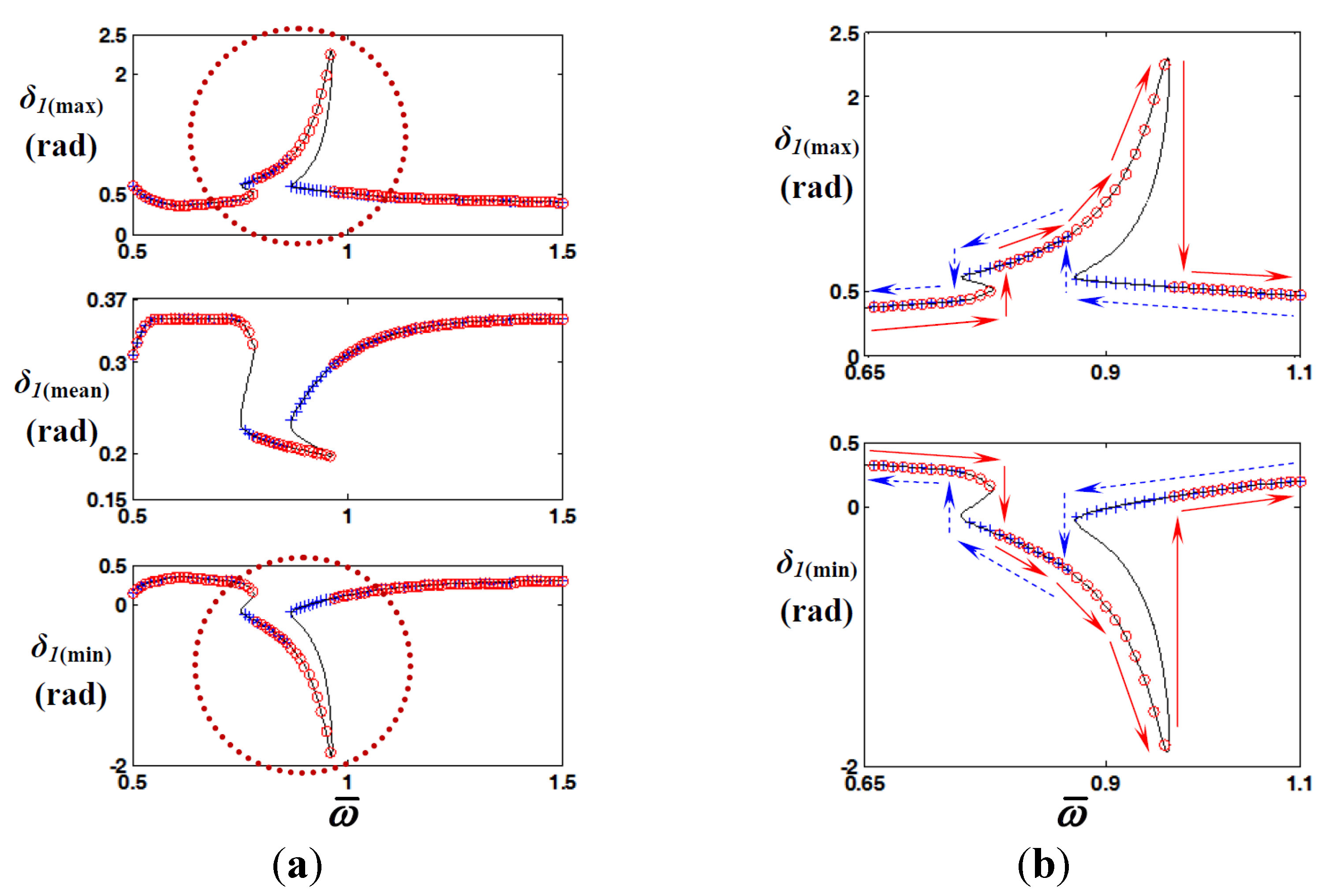
 , NS by frequency up-sweeping;
, NS by frequency up-sweeping;  , NS by frequency down-sweeping.
, NS by frequency down-sweeping.
 , NS by frequency up-sweeping;
, NS by frequency up-sweeping;  , NS by frequency down-sweeping.
, NS by frequency down-sweeping.
4. Nonlinear Dynamic Responses along with Various Excitation Conditions
4.1. Nonlinear Dynamic Characteristics with Various Excitation Conditions
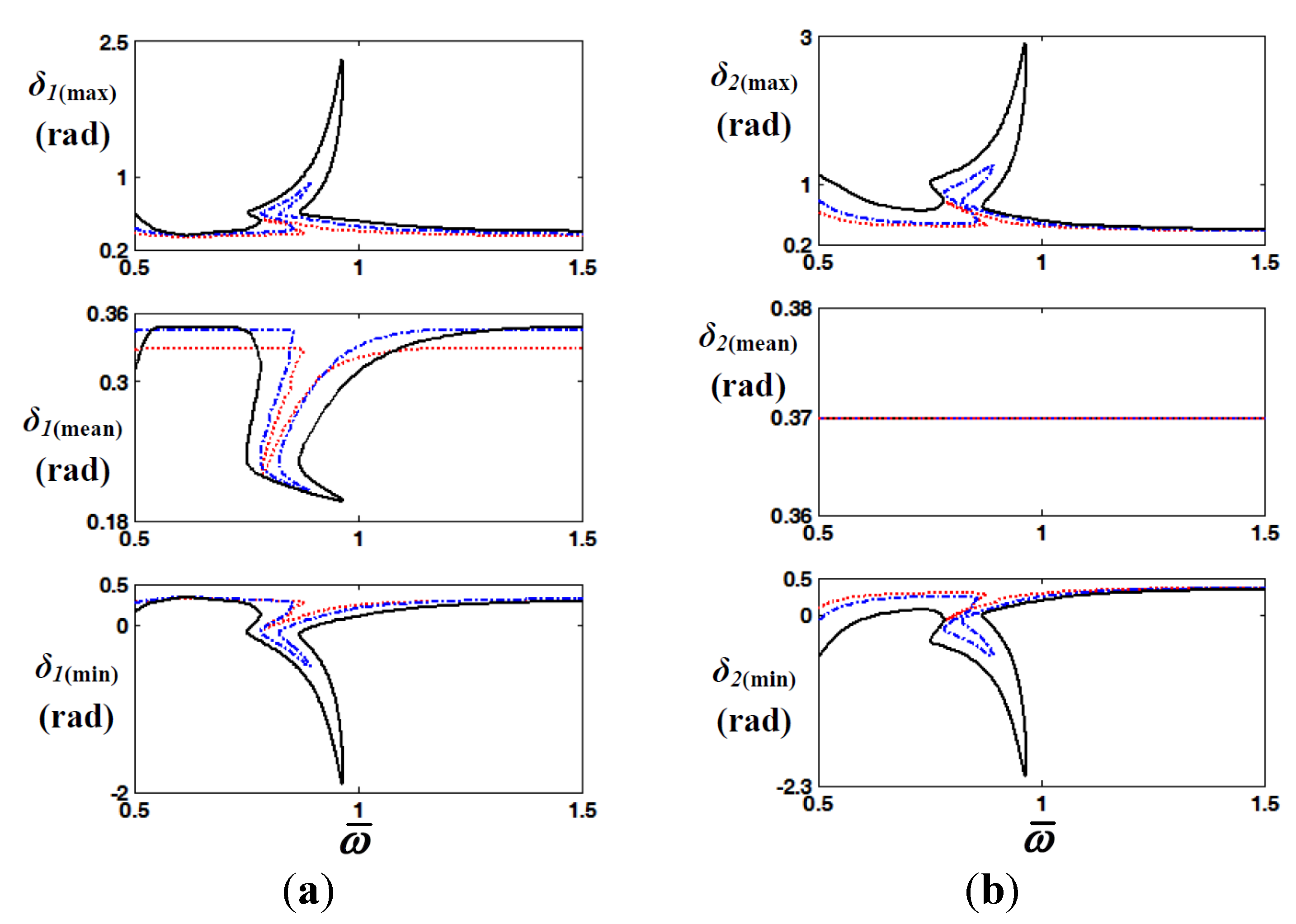


4.2. Investigation of Quasi-Periodic Responses Using Poincaré Map
 , HBM with stable regime (or NS by frequency up-sweeping);
, HBM with stable regime (or NS by frequency up-sweeping);  , HBM with unstable regime (or NS by frequency down-sweeping).
, HBM with unstable regime (or NS by frequency down-sweeping).
 , HBM with stable regime (or NS by frequency up-sweeping);
, HBM with stable regime (or NS by frequency up-sweeping);  , HBM with unstable regime (or NS by frequency down-sweeping).
, HBM with unstable regime (or NS by frequency down-sweeping).
 , HBM; , NS.
, HBM; , NS.
 , HBM; , NS.
, HBM; , NS.


5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yoon, J.Y.; Singh, R. Effect of multi-staged clutch damper characteristics on transmission gear rattle under two engine conditions. J. Automob. Eng. 2013, 227, 1273–1294. [Google Scholar] [CrossRef]
- Yoon, J.Y.; Lee, I.J. Nonlinear analysis of vibro-impacts for unloaded gear pairs with various excitation and system parameters. J. Vib. Acoust. 2014, 136. [Google Scholar] [CrossRef]
- Yoon, J.Y. Effect of multi-staged clutch damper characteristics on vibro-impacts within a geared system. Master’s Thesis, Ohio State University, Columbus, OH, USA, 2003. [Google Scholar]
- Peng, Z.K.; Lang, Z.Q.; Billings, S.A.; Tomlinson, G.R. Comparison between harmonic balance and nonlinear output frequency response function in nonlinear system analysis. J. Sound Vib. 2008, 311, 56–73. [Google Scholar] [CrossRef]
- Al-shyyab, A.; Kahraman, A. Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: Sub-harmonic motions. J. Sound Vib. 2005, 279, 417–451. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, J.K.; Meng, G. Incremental harmonic balance method for nonlinear flutter of an airfoil with uncertain-but-bounded parameters. Appl. Math. Model. 2012, 36, 657–667. [Google Scholar] [CrossRef]
- Genesio, R.; Tesi, A. Harmonic balance methods for the analysis of chaotic dynamics in nonlinear systems. Automatica 1992, 28, 531–548. [Google Scholar] [CrossRef]
- Masiani, R.; Capecchi, D.; Vestroni, F. Resonant and coupled response of hysteretic two-degree-of-freedom systems using harmonic balance method. Int. J. Non-Linear Mech. 2002, 37, 1421–1434. [Google Scholar] [CrossRef]
- Raghothama, A.; Narayanan, S. Bifurcation and chaos in geared rotor bearing system by incremental harmonic balance method. J. Sound Vib. 1999, 226, 469–492. [Google Scholar] [CrossRef]
- Raghothama, A.; Narayanan, S. Bifurcation and chaos of an articulated loading platform with piecewise non-linear stiffness using the incremental harmonic balance method. Ocean Eng. 2000, 27, 1087–1107. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, S.; Liu, X. Nonlinear dynamics of a spur gear pair with time-varying stiffness and backlash based on incremental harmonic balance method. Int. J. Mech. Sci. 2006, 48, 1256–1263. [Google Scholar] [CrossRef]
- Wong, C.W.; Zhang, W.S.; Lau, S.L. Periodic forced vibration of unsymmetrical piecewise-linear systems by incremental harmonic balance method. J. Sound Vib. 2006, 48, 1256–1263. [Google Scholar] [CrossRef]
- Padmanabhan, C.; Singh, R. Spectral coupling issues in a two-degree-of-freedom system with clearance non-linearities. J. Sound Vib. 1992, 155, 209–230. [Google Scholar] [CrossRef]
- Kim, T.C.; Rook, T.E.; Singh, R. Super- and sub-harmonic response calculation for a torsional system with clearance nonlinearity using the harmonic balance method. J. Sound Vib. 2005, 281, 965–993. [Google Scholar] [CrossRef]
- Kim, T.C.; Rook, T.E.; Singh, R. Effect of nonlinear impact damping on the frequency response of a torsional system with clearance. J. Sound Vib. 2005, 281, 995–1021. [Google Scholar] [CrossRef]
- Comparin, R.J.; Singh, R. Non-linear frequency response characteristics of an impact pair. J. Sound Vib. 1989, 134, 259–290. [Google Scholar] [CrossRef]
- Kim, T.C.; Rook, T.E.; Singh, R. Effect of smoothening functions on the frequency response of an oscillator with clearance non-linearity. J. Sound Vib. 2003, 263, 665–678. [Google Scholar] [CrossRef]
- Rook, T.E.; Singh, R. Dynamic analysis of a reverse-idler gear pair with concurrent clearance. J. Sound Vib. 1995, 182, 303–322. [Google Scholar] [CrossRef]
- Comparin, R.J.; Singh, R. Frequency response characteristics of a multi-degree-of-freedom system with clearance. J. Sound Vib. 1990, 142, 101–124. [Google Scholar] [CrossRef]
- Duan, C.; Singh, R. Forced vibration of a torsional oscillator with Coulomb friction under a periodically varying normal load. J. Sound Vib. 2009, 325, 499–506. [Google Scholar] [CrossRef]
- Duan, C.; Singh, R. Dynamic analysis of preload nonlinearity in a mechanical oscillator. J Sound Vib. 2007, 301, 963–978. [Google Scholar] [CrossRef]
- Ben-Gal, N.; Moore, K.S. Bifurcation and stability properties of periodic solutions to two nonlinear spring-mass systems. Nonlinear Anal. Theory Method Appl. 2005, 61, 1015–1030. [Google Scholar] [CrossRef]
- Wang, C.C. Application of a hybrid method to the nonlinear dynamic analysis of a flexible rotor supported by a spherical gas-lubricated bearing system. Nonlinear Anal. Theory Method Appl. 2009, 70, 2035–2053. [Google Scholar] [CrossRef]
- Yoon, J.Y.; Yoon, H.S. Nonlinear frequency response analysis of a multi-stage clutch damper with multiple nonlinearities. J. Comput. Nonlinear Dyn. 2014, 9. [Google Scholar] [CrossRef]
- Sundararajan, P.; Noah, S.T. Dynamics of forced nonlinear systems using shooting/arc-length continuation method-application to rotor systems. J. Vib. Acoust. 1997, 119, 9–20. [Google Scholar] [CrossRef]
- Sundararajan, P.; Noah, S.T. An algorithm for response and stability of large order non-linear systems-application to rotor systems. J. Sound Vib. 1998, 214, 695–723. [Google Scholar] [CrossRef]
- Royston, T.J.; Singh, R. Periodic response of mechanical systems with local non-linearities using an enhanced Galerkin technique. J. Sound Vib. 1996, 194, 243–263. [Google Scholar] [CrossRef]
- Lee, J.H.; Singh, R. Nonlinear frequency responses of quarter vehicle models with amplitude-sensitive engine mounts. J. Sound Vib. 2008, 313, 784–805. [Google Scholar] [CrossRef]
- Von Groll, G.; Ewins, D.J. The harmonic balance method with arc-length continuation in rotor/stator contact problems. J. Sound Vib. 2001, 241, 223–233. [Google Scholar] [CrossRef]
- Deconinck, B.; Nathan Kutz, J. Computing spectra of linear operators using the Floquet-Fourier-Hill method. J. Comp. Physics 2006, 219, 296–321. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.-Y.; Kim, B. Effect of Various Excitation Conditions on Vibrational Energy in a Multi-Degree-of-Freedom Torsional System with Piecewise-Type Nonlinearities. Energies 2015, 8, 10861-10882. https://doi.org/10.3390/en81010861
Yoon J-Y, Kim B. Effect of Various Excitation Conditions on Vibrational Energy in a Multi-Degree-of-Freedom Torsional System with Piecewise-Type Nonlinearities. Energies. 2015; 8(10):10861-10882. https://doi.org/10.3390/en81010861
Chicago/Turabian StyleYoon, Jong-Yun, and Byeongil Kim. 2015. "Effect of Various Excitation Conditions on Vibrational Energy in a Multi-Degree-of-Freedom Torsional System with Piecewise-Type Nonlinearities" Energies 8, no. 10: 10861-10882. https://doi.org/10.3390/en81010861





