Sensitivity-Based Model of Low Voltage Distribution Systems with Distributed Energy Resources
Abstract
:1. Introduction
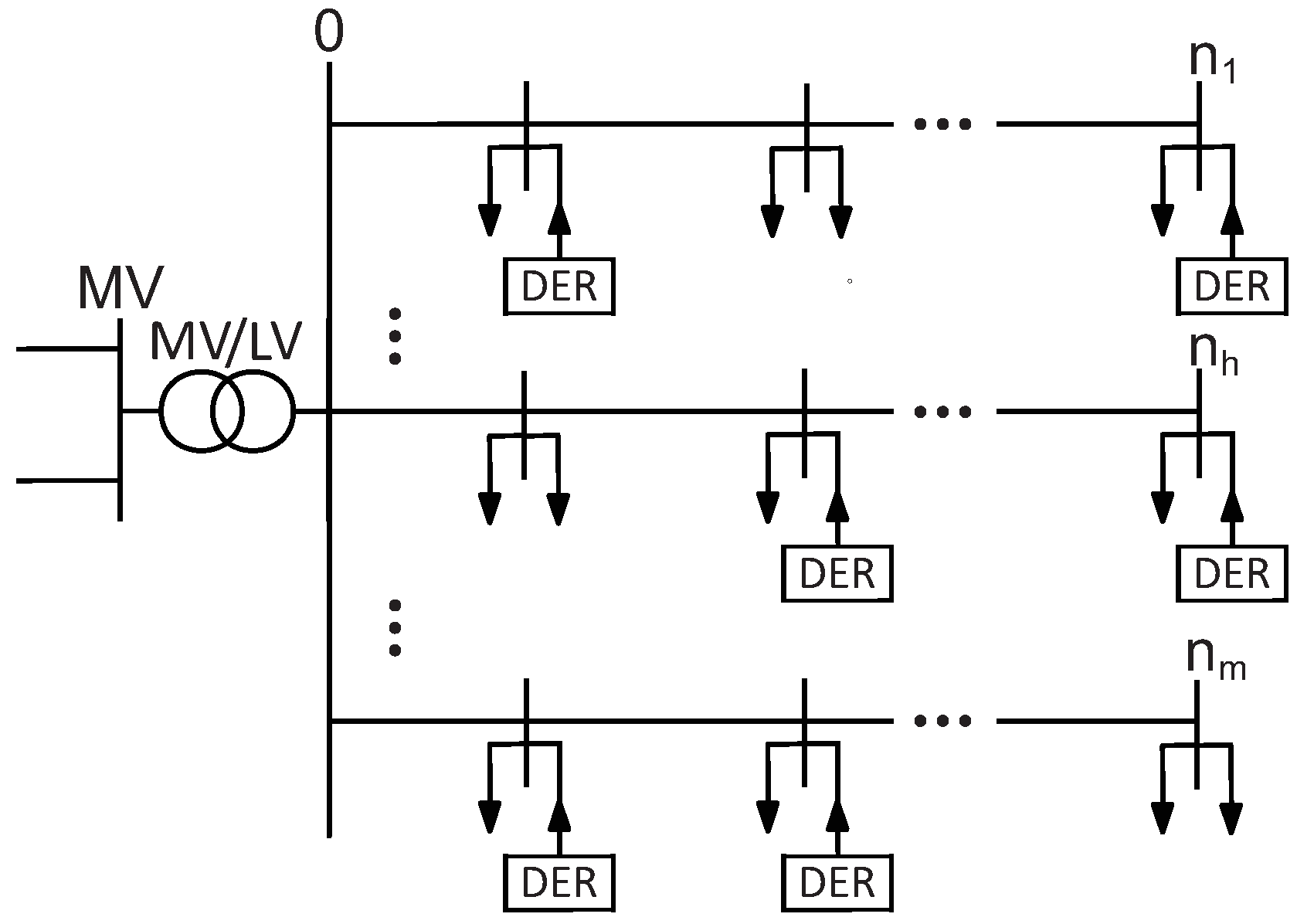
2. Distribution System Modeling
2.1. Branch Model
- the vector of the variation of the electrical variables at the supplying node , with respect to the initial operating point , through the Jacobian matrix ; and
- the vector of the DERs active and reactive power injections at the receiving node, which are assumed to be assigned enforcements.
2.2. Feeder Model
- The vectors of the DERs active and reactive power injections in all the nodes of the feeder through the matrices ; and
- The variation of the squared voltage amplitude at the LV busbar of the supplying substation through the vectors .
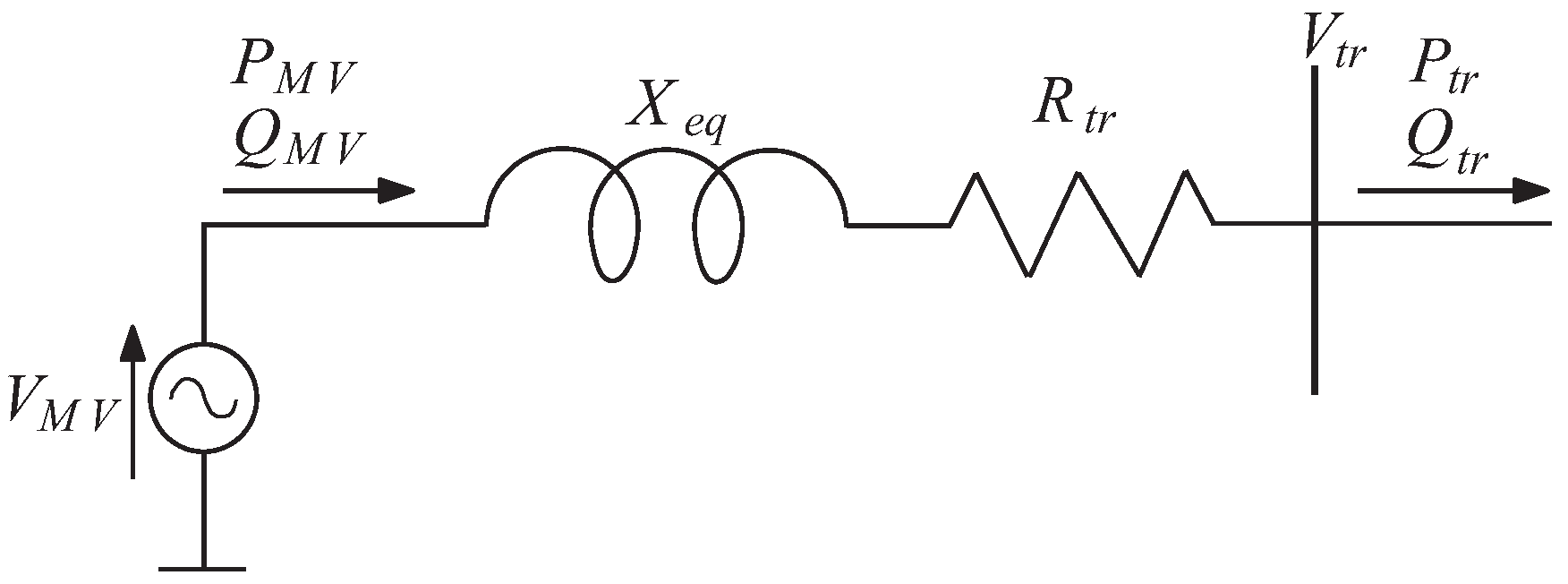
2.3. Medium/Low Voltage Supplying System
2.4. Low Voltage Distribution System Model
- The vectors of the DERs active and reactive power injections in all the nodes of the h-th feeder through the matrices ; and
- The vectors of the DERs active and reactive power injections in all the nodes of the other feeders through the matrices .
- Calculate the Jacobian matrices for the MV/LV supplying system and for each j-th branch of each h-th feeder, from the analytic derivatives of Equation (1) evaluated in the initial operating point;
- Calculate the matrices and for each j-th node of each h-th feeder, according to Equations (5) and (6);
- Calculate the matrices and the vectors through , , which are provided by Equation (11), for each h-th feeder;
- Calculate the matrices and the vectors for each j-th node of each h-th feeder according to Equation (14);
- Calculate the vector through which is provided by Equation (23);
- Calculate the matrices and according to Equation (26), for each j-th node of each h-th feeder.
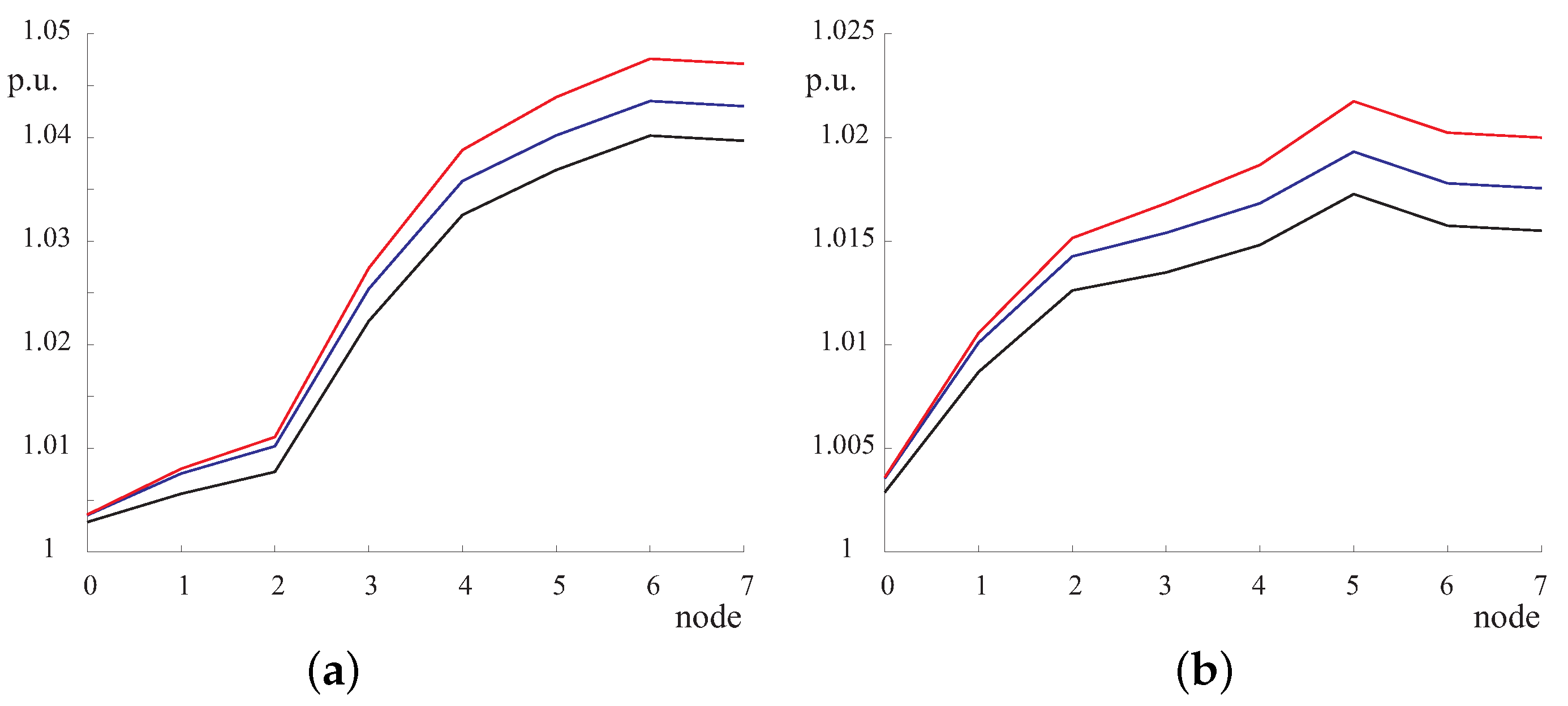
3. Case Study
3.1. Model Application
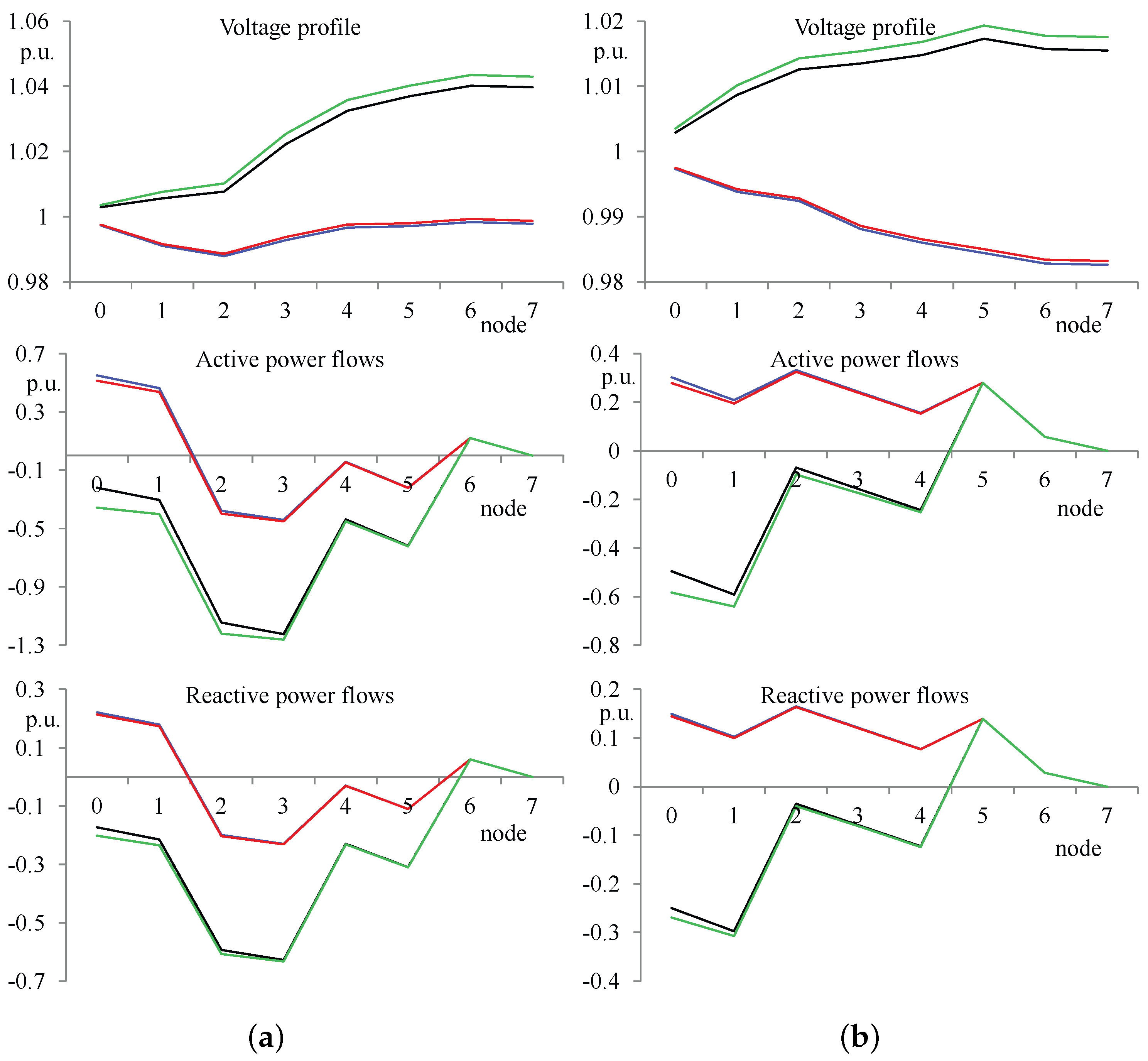
3.2. Model Validation
- Case A: kW and kVAr for ,
- Case B: kW and kVAr for .
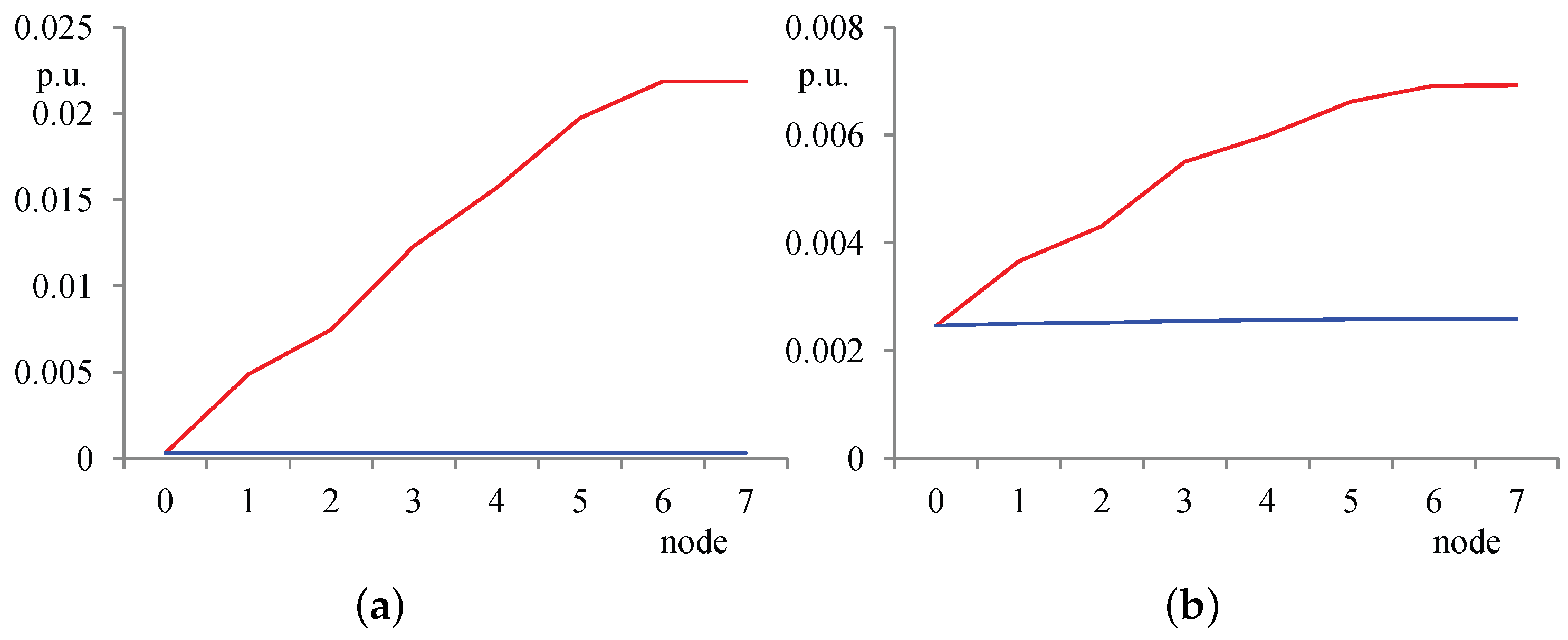
3.3. Comparison with a Perturb-and-Observe Method
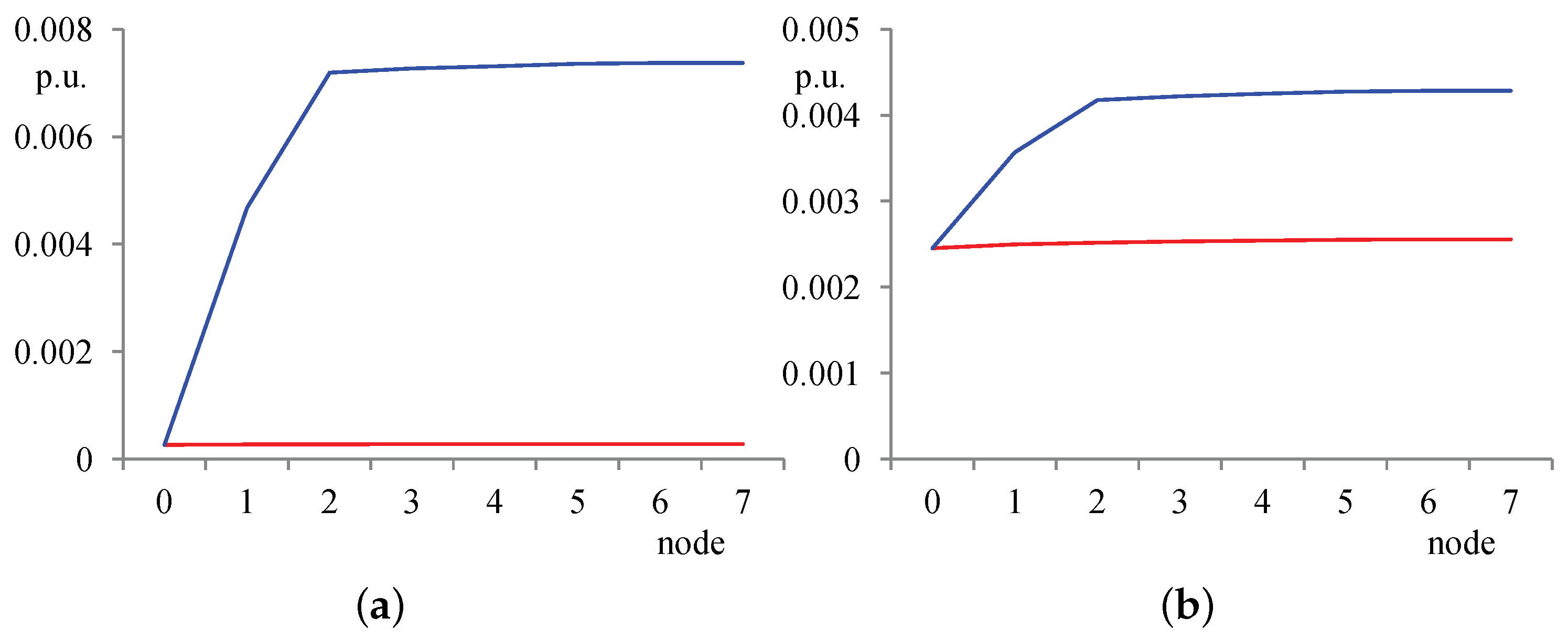
3.4. Distributed Energy Resources Impact Evaluation
- Quantify the interaction between the voltage regulation devices that are installed in a VM [17]: e.g., if a VM is defined along feeder 1, the voltage variation at node 4 caused by and the voltage variation at node 6 caused by represent the interaction between the voltage regulators acting on and .
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Bouhafs, F.; Mackay, M.; Merabti, M. Links to the future: Communication requirements and challenges in the smart grid. IEEE Power Energy Mag. 2013, 58, 2818–2833. [Google Scholar] [CrossRef]
- Belhomme, R.; Cerero Real De Asua, R.; Valtorta, G.; Paice, A.; Bouffard, F.; Rooth, R.; Losi, A. ADDRESS—Active demand for the smart grids of the future. In Proceedings of the CIRED Seminar: SmartGrids for Distribution, Frankfurt, Germany, 23–24 June 2008.
- Casolino, G.M.; Losi, A. Load areas in distribution systems. In Proceedings of the 15th IEEE International Conference on Environment and Electrical Engineering (EEEIC 2015), Rome, Italy, 10–13 June 2015.
- Di Fazio, A.R.; Erseghe, T.; Ghiani, E.; Murroni, M.; Siano, P.; Silvestro, F. Integration of renewable energy sources, energy storage systems, and electrical vehicles with smart power distribution networks. J. Ambient Intell. Humaniz. Comput. 2013, 4, 663–671. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; Zwaenepoel, B.; Kooning, J.D.M.D.; Meersman, B.; Vandevelde, L. Smart microgrids and virtual power plants in a hierarchical control structure. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies (ISGT Europe), Manchester, UK, 5–7 December 2011.
- Arefifar, S.A.; Mohamed, Y.; El-Fouly, T. Optimized multiple microgrid-based clustering of active distribution systems considering communication and control requirements. IEEE Trans. Ind. Electr. 2015, 62, 711–723. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Fusco, G.; Russo, M. Decentralised voltage regulation in smart grids using reactive power from renewable DG. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON 2012), Florence, Italy, 9–12 September 2012.
- Huang, J.; Jiang, C.; Xu, R. A review on distributed energy resources and MicroGrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar]
- Brenna, M.; Berardinis, E.D.; Carpini, L.D.; Foiadelli, F.; Paulon, P.; Petroni, P.; Sapienza, G.; Scrosati, G.; Zaninelli, D. Optimal distributed voltage regulation for secondary networks with DGs. IEEE Trans. Smart Grid 2013, 4, 877–885. [Google Scholar] [CrossRef]
- Kumar, V.; Gupta, I.; Gupta, H.; Agarwal, C. Voltage and current sensitivities of radial distribution network: A new approach. IEE Proc. Gener. Transm. Distrib. 2005, 152, 813–818. [Google Scholar] [CrossRef]
- Khatod, D.K.; Pant, V.; Sharma, J. A novel approach for sensitivity calculations in the radial distribution system. IEEE Trans. Power Deliv. 2006, 21, 2048–2057. [Google Scholar] [CrossRef]
- Zhou, Q.; Bialek, J.W. Simplified calculation of voltage and losses sensitivity factors in distribution networks. In Proceedings of the 16th Power Systems Computation Conference (PSCC2008), Glasgow, Scotland, UK, 14–18 July 2008.
- Weckx, S.; D’Hulst, R.; Driesen, J. Voltage sensitivity analysis of a laboratory distribution grid with incomplete Data. IEEE Trans. Smart Grid 2015, 6, 1271–1280. [Google Scholar] [CrossRef]
- Gurram, R.; Subramanyyam, B. Sensitivity analysis of radial distribution network—Adjoint network method. Int. J. Electr. Power Energy Syst. 1999, 21, 323–326. [Google Scholar] [CrossRef]
- Tamp, F.; Ciufo, P. A Sensitivity analysis toolkit for the simplification of MV distribution network voltage management. IEEE Trans. Smart Grid 2014, 5, 559–568. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; Valeri, S.; De Santis, M. LV distribution system modeling for distributed energy resources. In Proceedings of the 2016 16th IEEE International Conference on Environment and Electrical Engineering (EEEIC 2016), Florence, Italy, 7–10 June 2016.
- Di Fazio, A.R.; Fusco, G.; Russo, M. Decentralized voltage control of distributed generation using a distribution system structural MIMO model. Control Eng. Pract. 2016, 47, 81–90. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Optimal sizing of capacitors placed on a radial distribution system. IEEE Trans. Power Deliv. 1989, 4, 735–743. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 1–19. [Google Scholar] [CrossRef]

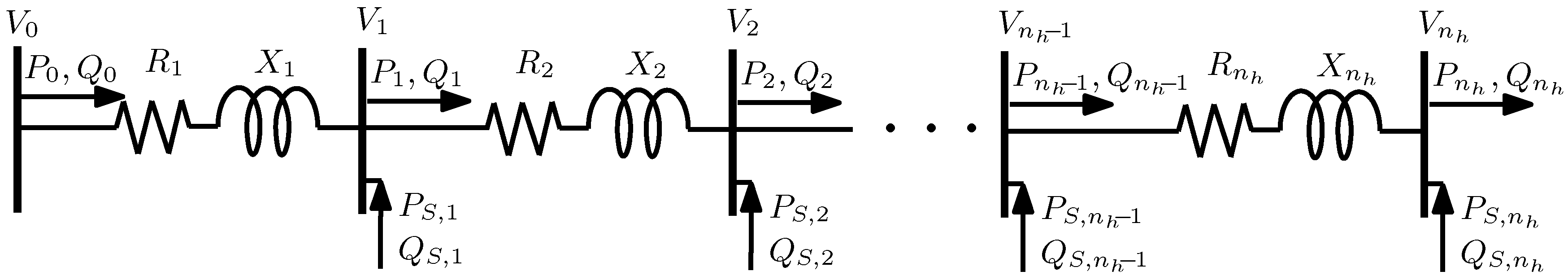

| From Node | To Node | Both Feeders | Feeder 1 | Feeder 2 | |||
|---|---|---|---|---|---|---|---|
| R (p.u.) | X (p.u.) | PL (p.u.) | QL (p.u.) | PL (p.u.) | QL (p.u.) | ||
| 0 | 1 | 0.0105 | 0.0025 | 0.0832 | 0.0416 | 0.0928 | 0.0464 |
| 1 | 2 | 0.0060 | 0.0014 | 0.8400 | 0.3780 | 0.2756 | 0.1376 |
| 2 | 3 | 0.0114 | 0.0027 | 0.0600 | 0.0300 | 0.0872 | 0.0436 |
| 3 | 4 | 0.0080 | 0.0011 | 0.0 | 0.0 | 0.0872 | 0.0436 |
| 4 | 5 | 0.0095 | 0.0014 | 0.1776 | 0.0800 | 0.2756 | 0.1376 |
| 5 | 6 | 0.0052 | 0.0007 | 0.0600 | 0.0300 | 0.2220 | 0.1112 |
| 6 | 7 | 0.0040 | 0.0006 | 0.1200 | 0.0600 | 0.0572 | 0.0284 |
| Case | Feeder Number | Maximum Errors (%) on the Variations of | ||
|---|---|---|---|---|
| Voltage Amplitudes | Active Power Flows | Reactive Power Flows | ||
| A | 1 | 3.3 | 4.4 | 1.9 |
| 2 | 3.1 | 2.8 | 1.3 | |
| B | 1 | 6.5 | 8.5 | 3.6 |
| 2 | 5.5 | 5.4 | 2.4 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Fazio, A.R.; Russo, M.; Valeri, S.; De Santis, M. Sensitivity-Based Model of Low Voltage Distribution Systems with Distributed Energy Resources. Energies 2016, 9, 801. https://doi.org/10.3390/en9100801
Di Fazio AR, Russo M, Valeri S, De Santis M. Sensitivity-Based Model of Low Voltage Distribution Systems with Distributed Energy Resources. Energies. 2016; 9(10):801. https://doi.org/10.3390/en9100801
Chicago/Turabian StyleDi Fazio, Anna Rita, Mario Russo, Sara Valeri, and Michele De Santis. 2016. "Sensitivity-Based Model of Low Voltage Distribution Systems with Distributed Energy Resources" Energies 9, no. 10: 801. https://doi.org/10.3390/en9100801





