Forecasting Crude Oil Price Using EEMD and RVM with Adaptive PSO-Based Kernels
Abstract
:1. Introduction
2. Methodology
2.1. Ensemble Empirical Mode Decomposition
- Step 1:
- Specify the number of ensemble M and the standard deviation of Gaussian white noises σ, with ;
- Step 2:
- ; Add a Gaussian white noise ∼ to crude oil price series to construct a new series , as follows:
- Step 3:
- Decompose into m IMFs and a residue , as follows:where is the j-th IMF in the i-th trial, and J is the number of IMFs, determined by the size of crude oil price series N with [30].
- Step 4:
- If , go to Step 2 to perform EMD again; otherwise, go to Step 5;
- Step 5:
- Calculate the average of corresponding IMFs of M trials as final IMFs:
2.2. Particle Swarm Optimization
2.3. Relevance Vector Machine
2.4. Adaptive PSO for Parameter Optimization in RVM
- Step 1:
- Setting parameters. Set the following parameters for running APSO, population size P, maximal iteration times T, the maximal and minimal inertia weights and , the range of the ten parameters to be optimized;
- Step 2:
- Encoding. Encode the ten parameters into a particle (vector) to represent , , , , a, b, c, d, e, and f accordingly;
- Step 3:
- Defining the fitness function. The fitness function is defined by root mean square error (RMSE):where N is the size of training samples, is the true target of the input , and is the predicted target associated with and the parameter ;
- Step 4:
- Initializing. Set ; randomly generate initial speed and position for each particle; use the value of particle to compose the kernel for RVM in Equation (22), and then evaluate each particle; is selected as , while the particle with the optimal fitness is selected as ;
- Step 5:
- Step 6:
- Evaluating particles. Evaluate each particle by fitness function;
- Step 7:
- Updating the historical best particle, if necessary. If , then ;
- Step 8:
- Updating the global best particle, if necessary. If , then ;
- Step 9:
- Judging whether the iteration terminates or not. If , go to Step 5. Otherwise, stop the iteration and output as the optimized parameters for the combined kernel in RVM. The optimal RVM predictor is obtained at this point.
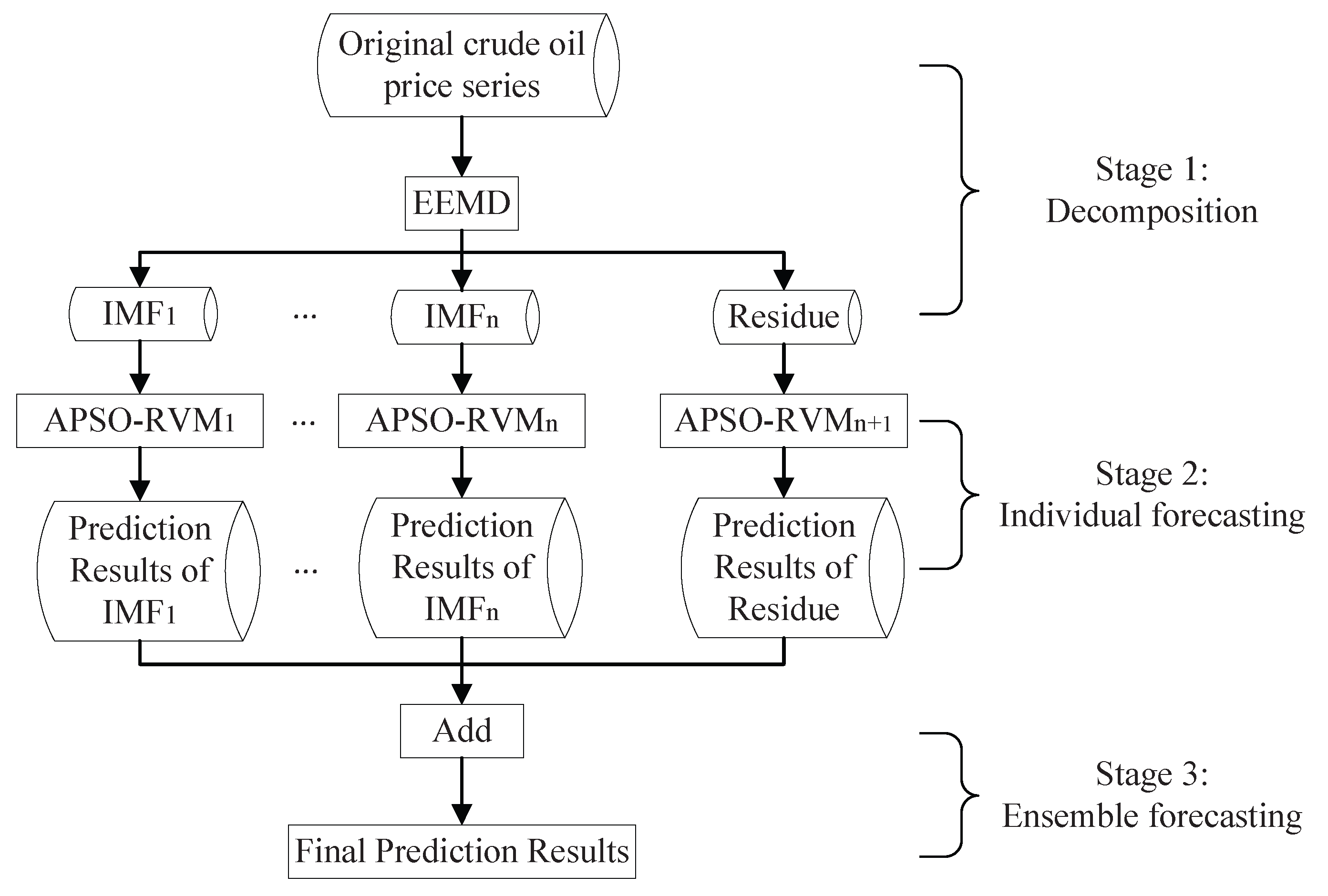
2.5. The Proposed EEMD–APSO–RVM Model
- Stage 1:
- Decomposition. The original crude oil price series is decomposed into with intrinsic mode function (IMF) components and one residue component using EEMD;
- Stage 2:
- Individual forecasting. RVM with the combined kernel optimized by APSO is used to forecast each component in Stage 1 independently, resulting in the predicted values of IMFs and that of the residue , respectively;
- Stage 3:
- Ensemble forecasting. The final predicted results can be obtained by simply adding the predicted results of all IMF components and the residue; i.e., .
3. Numerical Example
3.1. Data Description
3.2. Evaluation Criteria
3.3. Experimental Settings
3.4. Results and Analysis
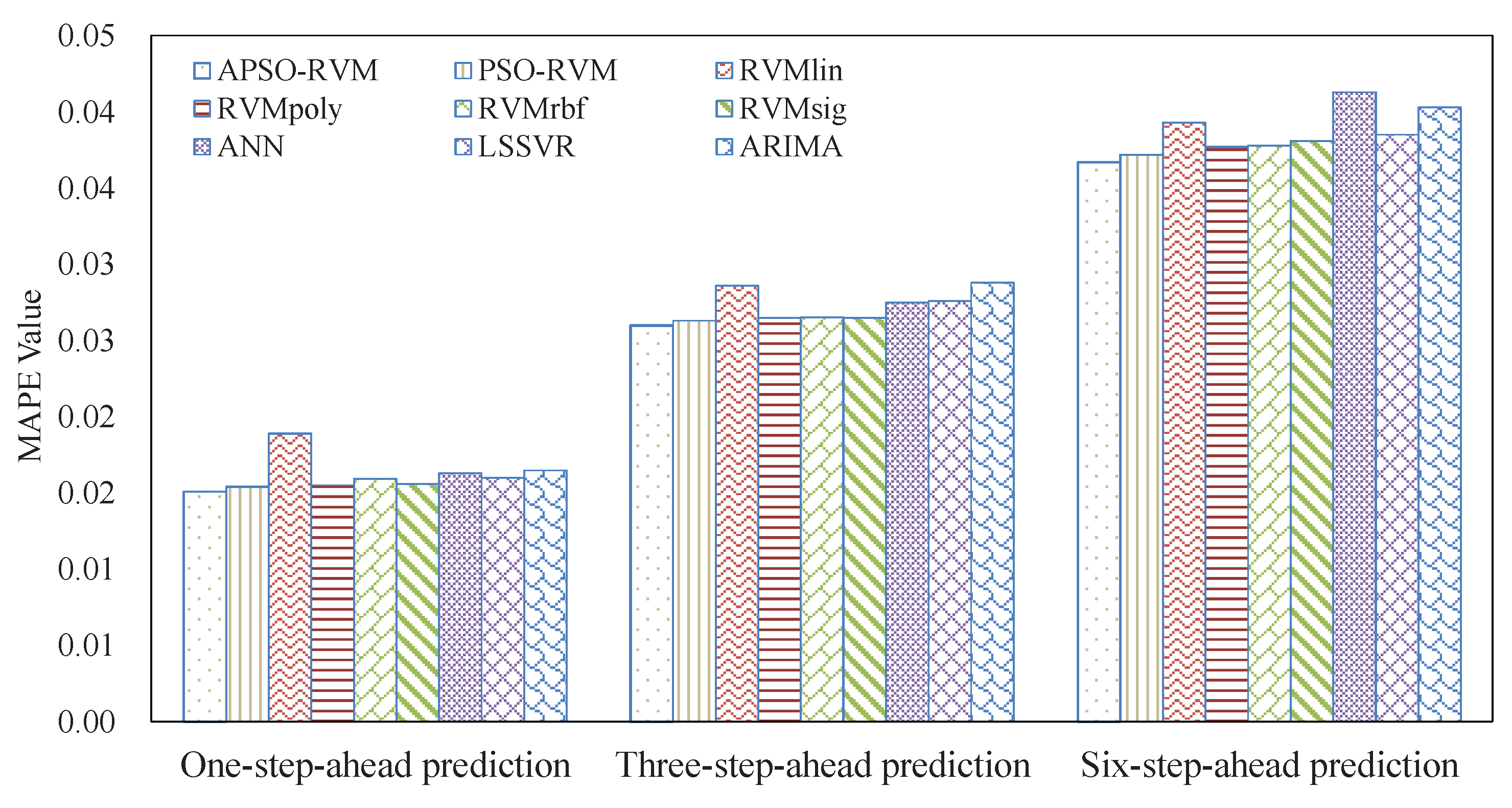
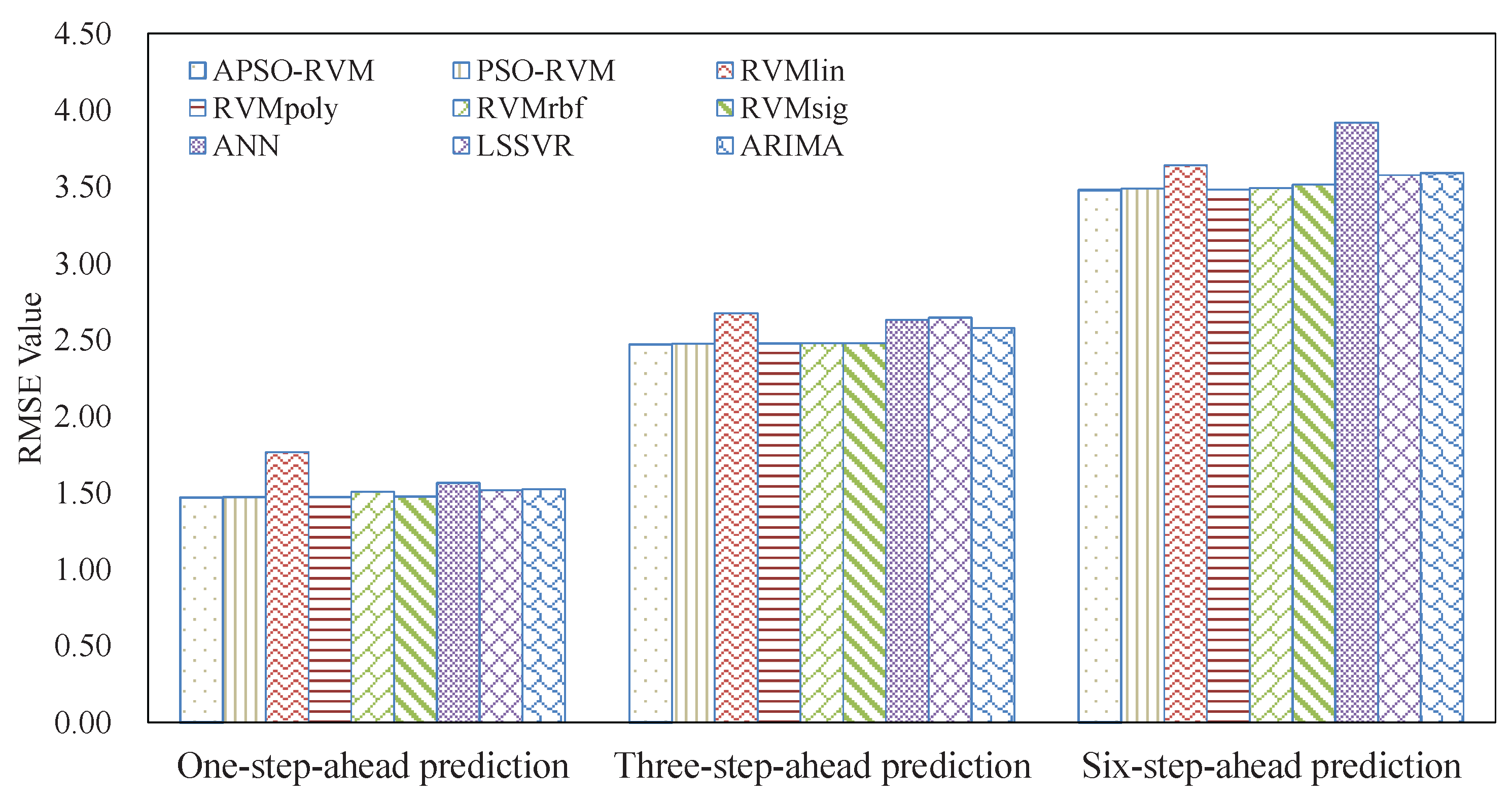
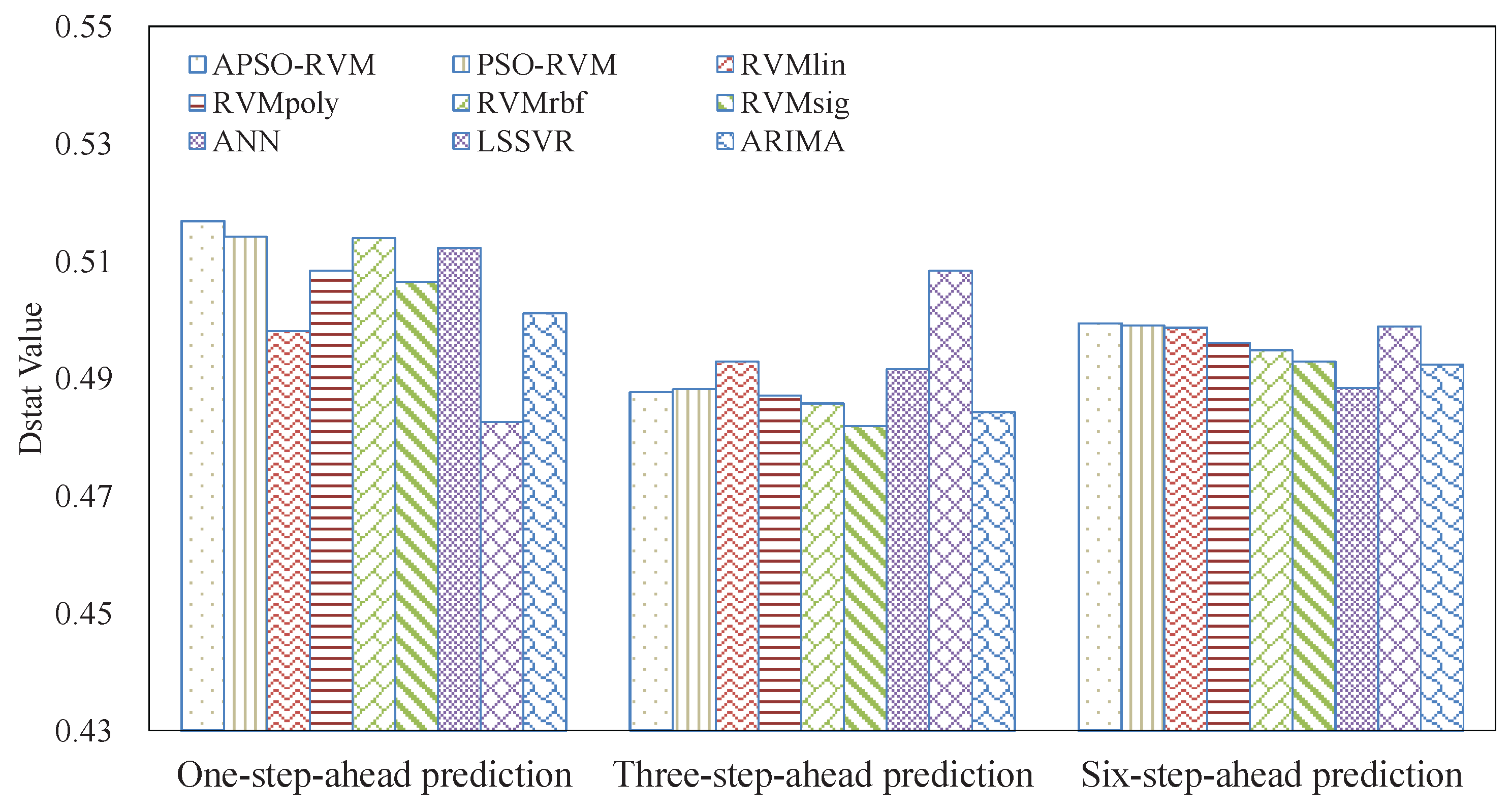
3.4.1. Results of Single Models
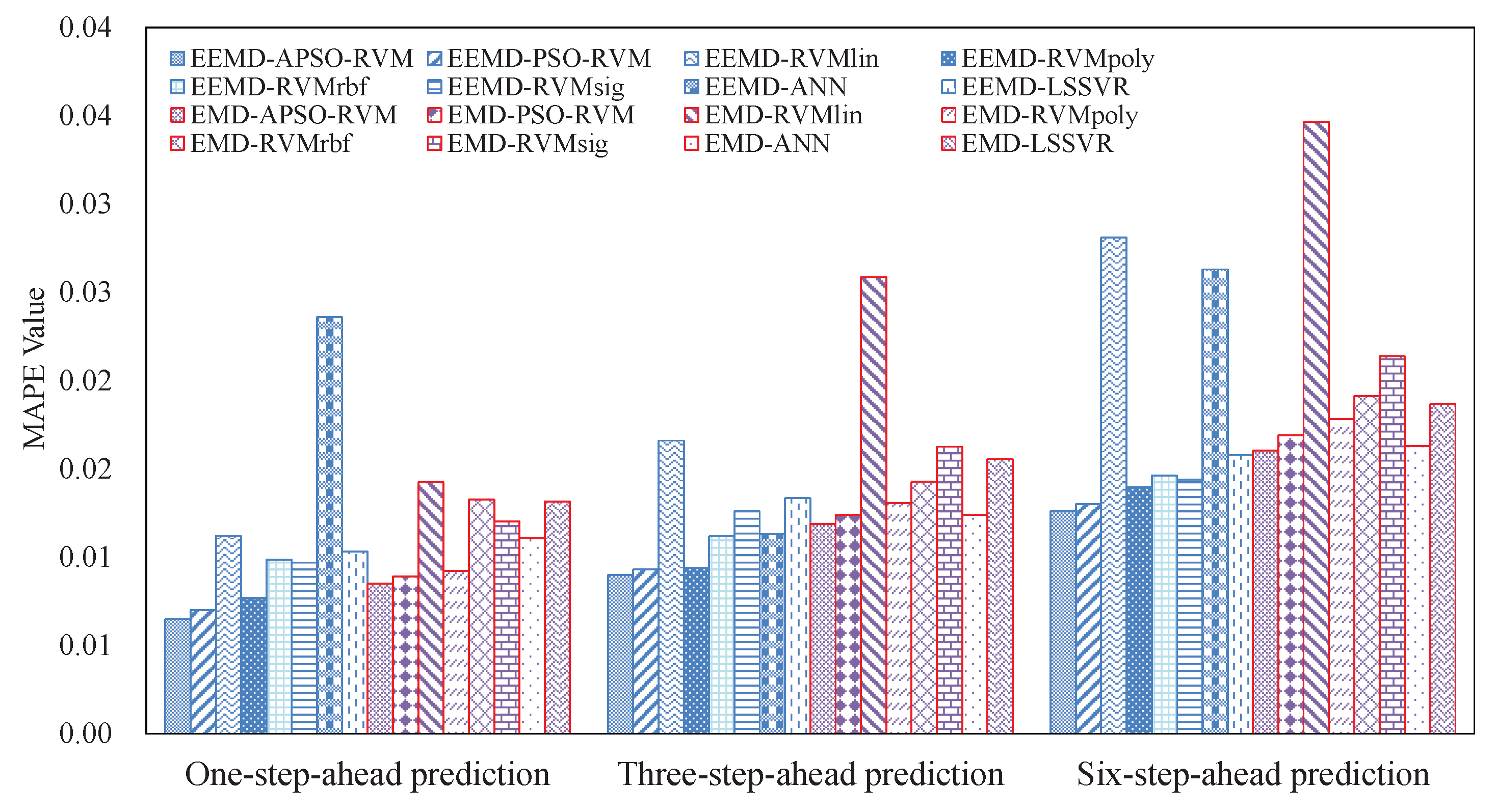
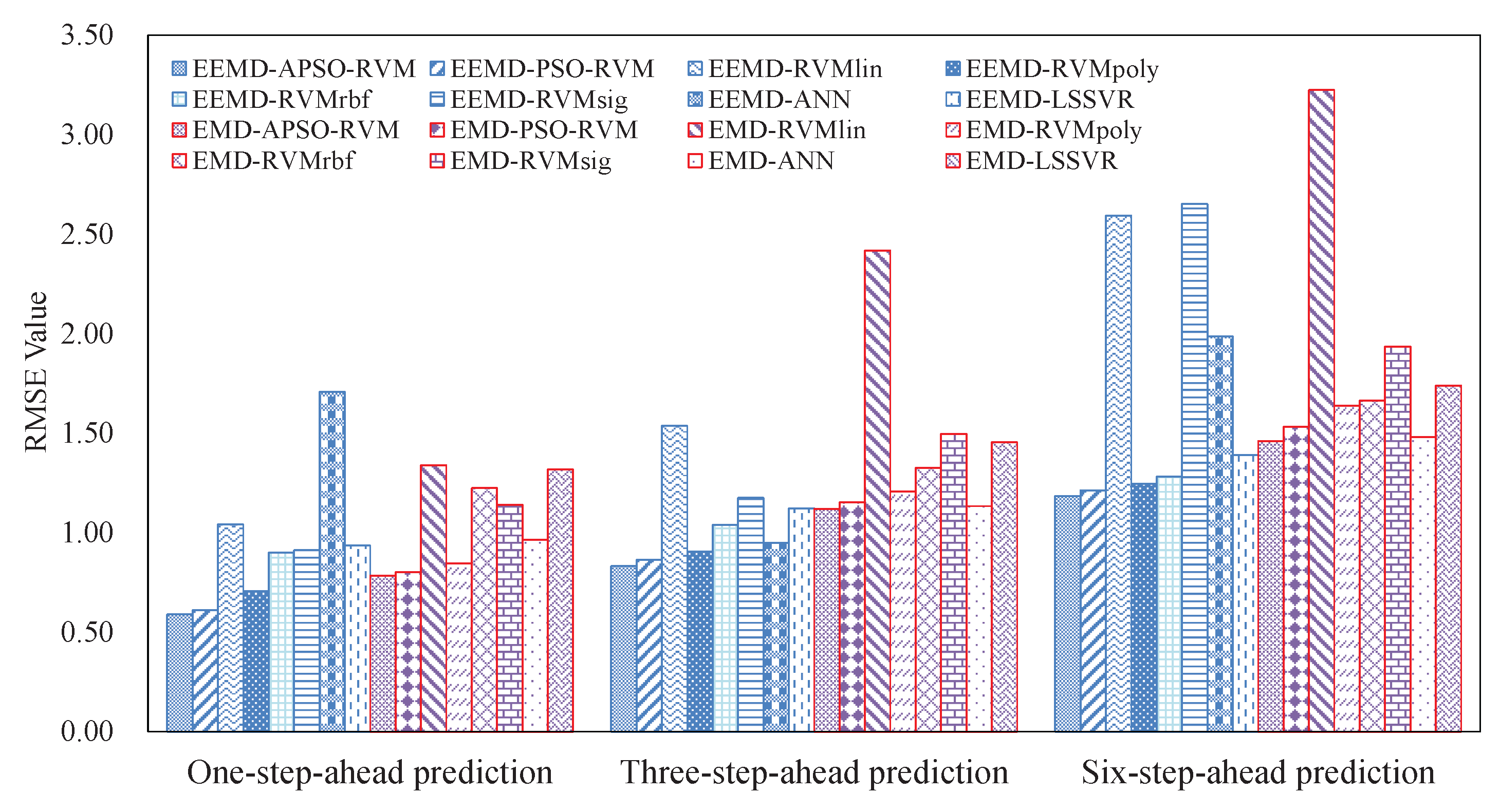
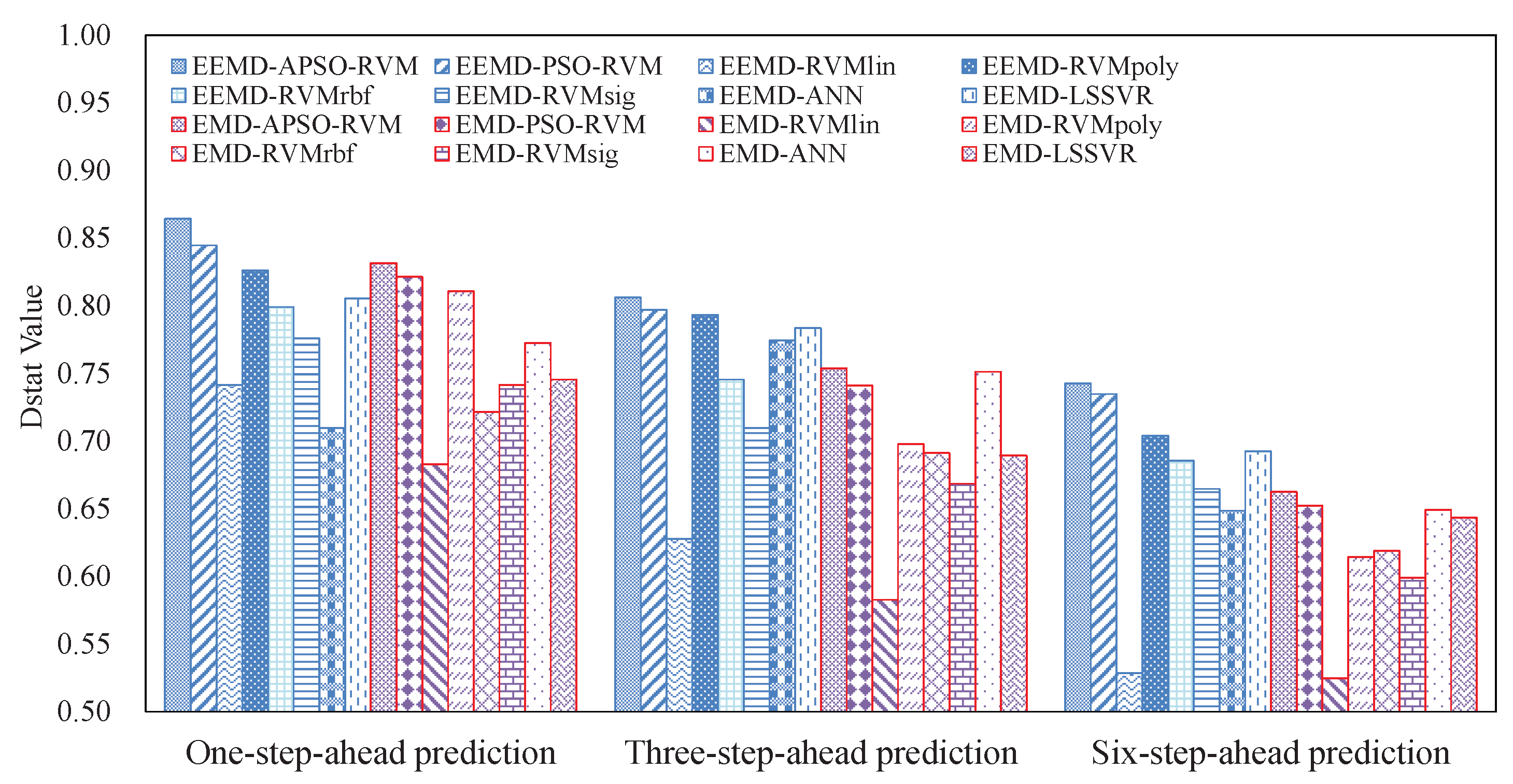
3.4.2. Results of Ensemble Models
3.5. Analysis of Robustness and Running Time
3.6. Summarizations
- (1)
- Due to nonlinearity and nonstationarity, it is difficult for single models to accurately forecast crude oil price.
- (2)
- The RVM has a good ability to forecast crude oil price. Even with a single kernel, SVM may outperform LSSVM, ANN, and ARIMA in many cases.
- (3)
- The combined kernel can further improve the accuracy of RVM. PSO can be applied to optimize the weights and parameters of the single kernels for the combined kernel in RVM. In this case, the proposed APSO outperforms the traditional PSO.
- (4)
- The EEMD-related methods achieve better results than the counterpart EMD-related methods, showing that EEMD is more suitable for decomposing crude oil price.
- (5)
- With the benefits of EEMD, APSO, and RVM, the proposed ensemble EEMD–APSO–RVM significantly outperforms any other compared models listed in this paper in terms of MAPE, RMSE, and Dstat. At the same time, it is a stable and effective forecasting method in terms of robustness and running time. These all show that the EEMD–APSO–RVM is promising for crude oil price forecasting.
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- British Petroleum. 2016 Energy Outlook. 2016. Available online: https://www.bp.com/content/dam/bp/pdf/energy-economics/energy-outlook-2016/bp-energy-outlook-2016.pdf (accessed on 28 August 2016).
- Wang, Y.; Wei, Y.; Wu, C. Detrended fluctuation analysis on spot and futures markets of West Texas Intermediate crude oil. Phys. A 2011, 390, 864–875. [Google Scholar] [CrossRef]
- He, K.J.; Yu, L.; Lai, K.K. Crude oil price analysis and forecasting using wavelet decomposed ensemble model. Energy 2012, 46, 564–574. [Google Scholar] [CrossRef]
- Yu, L.A.; Dai, W.; Tang, L. A novel decomposition ensemble model with extended extreme learning machine for crude oil price forecasting. Eng. Appl. Artif. Intell. 2016, 47, 110–121. [Google Scholar] [CrossRef]
- Hooper, V.J.; Ng, K.; Reeves, J.J. Quarterly beta forecasting: An evaluation. Int. J. Forecast. 2008, 24, 480–489. [Google Scholar] [CrossRef]
- Murat, A.; Tokat, E. Forecasting oil price movements with crack spread futures. Energy Econ. 2009, 31, 85–90. [Google Scholar] [CrossRef]
- Baumeister, C.; Kilian, L. Real-time forecasts of the real price of oil. J. Bus. Econ. Statist. 2012, 30, 326–336. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhuang, X.H. Application of ARIMA model in short-term prediction of international crude oil price. Adv. Mater. Res. 2013, 798, 979–982. [Google Scholar] [CrossRef]
- Yu, L.A.; Wang, S.Y.; Lai, K.K. Forecasting crude oil price with an EMD-based neural network ensemble learning paradigm. Energy Econ. 2008, 30, 2623–2635. [Google Scholar] [CrossRef]
- He, A.W.; Kwok, J.T.; Wan, A.T. An empirical model of daily highs and lows of West Texas Intermediate crude oil prices. Energy Econ. 2010, 32, 1499–1506. [Google Scholar] [CrossRef]
- Li, S.; Ge, Y. Crude Oil Price Prediction Based on a Dynamic Correcting Support Vector Regression Machine. Abstr. Appl. Anal. 2013, 2013, 528678. [Google Scholar]
- Morana, C. A semiparametric approach to short-term oil price forecasting. Energy Econ. 2001, 23, 325–338. [Google Scholar] [CrossRef]
- Arouri, M.E.H.; Lahiani, A.; Lévy, A.; Nguyen, D.K. Forecasting the conditional volatility of oil spot and futures prices with structural breaks and long memory models. Energy Econ. 2012, 34, 283–293. [Google Scholar] [CrossRef]
- Mohammadi, H.; Su, L. International evidence on crude oil price dynamics: Applications of ARIMA-GARCH models. Energy Econ. 2010, 32, 1001–1008. [Google Scholar] [CrossRef]
- Shambora, W.E.; Rossiter, R. Are there exploitable inefficiencies in the futures market for oil? Energy Econ. 2007, 29, 18–27. [Google Scholar] [CrossRef]
- Mirmirani, S.; Li, H.C. A comparison of VAR and neural networks with genetic algorithm in forecasting price of oil. Adv. Econom. 2004, 19, 203–223. [Google Scholar]
- Azadeh, A.; Moghaddam, M.; Khakzad, M.; Ebrahimipour, V. A flexible neural network-fuzzy mathematical programming algorithm for improvement of oil price estimation and forecasting. Comput. Ind. Eng. 2012, 62, 421–430. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, J. A multiple adaptive wavelet recurrent neural network model to analyze crude oil prices. J. Econ. Bus. 2012, 64, 275–286. [Google Scholar]
- Haidar, I.; Kulkarni, S.; Pan, H. Forecasting model for crude oil prices based on artificial neural networks. In Proceedings of the IEEE International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP 2008), Sydney, Australia, 15–18 December 2008; pp. 103–108.
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2013. [Google Scholar]
- Xie, W.; Yu, L.; Xu, S.; Wang, S. A new method for crude oil price forecasting based on support vector machines. In Computational Science—ICCS 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 444–451. [Google Scholar]
- Chiroma, H.; Abdulkareem, S.; Abubakar, A.I.; Herawan, T. Kernel functions for the support vector machine: Comparing performances on crude oil price data. In Recent Advances on Soft Computing and Data Mining; Springer: Basel, Switzerland, 2014; pp. 273–281. [Google Scholar]
- Guo, X.; Li, D.; Zhang, A. Improved support vector machine oil price forecast model based on genetic algorithm optimization parameters. AASRI Procedia 2012, 1, 525–530. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Yu, Y.L.; Li, W.; Sheng, D.R.; Chen, J.H. A novel sensor fault diagnosis method based on Modified Ensemble Empirical Mode Decomposition and Probabilistic Neural Network. Measurement 2015, 68, 328–336. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Liang, Y.T.; Zhou, J.Z.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Tang, L.; Dai, W.; Yu, L.; Wang, S. A novel CEEMD-based EELM ensemble learning paradigm for crude oil price forecasting. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 141–169. [Google Scholar] [CrossRef]
- Yu, L.; Wang, Z.; Tang, L. A decomposition–ensemble model with data-characteristic-driven reconstruction for crude oil price forecasting. Appl. Energy 2015, 156, 251–267. [Google Scholar] [CrossRef]
- He, K.J.; Zha, R.; Wu, J.; Lai, K.K. Multivariate EMD-Based Modeling and Forecasting of Crude Oil Price. Sustainability 2016, 8, 387. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Fan, L.; Pan, S.; Li, Z.; Li, H. An ICA-based support vector regression scheme for forecasting crude oil prices. Technol. Forecast. Soc. Chang. 2016, 112, 245–253. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Chen, S.; Gunn, S.R.; Harris, C.J. The relevance vector machine technique for channel equalization application. IEEE Trans. Neural Netw. 2002, 12, 1529–1532. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Suga, Y.; Won, S. A new approach to fuzzy modeling of nonlinear dynamic systems with noise: Relevance vector learning mechanism. IEEE Trans. Fuzzy Syst. 2006, 14, 222–231. [Google Scholar]
- Tolambiya, A.; Kalra, P.K. Relevance vector machine with adaptive wavelet kernels for efficient image coding. Neurocomputing 2010, 73, 1417–1424. [Google Scholar] [CrossRef]
- De Martino, F.; de Borst, A.W.; Valente, G.; Goebel, R.; Formisano, E. Predicting EEG single trial responses with simultaneous fMRI and Relevance Vector Machine regression. Neuroimage 2011, 56, 826–836. [Google Scholar] [CrossRef] [PubMed]
- Mehrotra, H.; Singh, R.; Vatsa, M.; Majhi, B. Incremental granular relevance vector machine: A case study in multimodal biometrics. Pattern Recognit. 2016, 56, 63–76. [Google Scholar] [CrossRef]
- Gupta, R.; Laghari, K.U.R.; Falk, T.H. Relevance vector classifier decision fusion and EEG graph-theoretic features for automatic affective state characterization. Neurocomputing 2016, 174, 875–884. [Google Scholar] [CrossRef]
- Kiaee, F.; Sheikhzadeh, H.; Mahabadi, S.E. Relevance Vector Machine for Survival Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 648–660. [Google Scholar] [CrossRef] [PubMed]
- Fei, H.; Xu, J.W.; Min, L.; Yang, J.H. Product quality modelling and prediction based on wavelet relevance vector machines. Chemom. Intell. Lab. Syst. 2013, 121, 33–41. [Google Scholar] [CrossRef]
- Wang, F.; Gou, B.C.; Qin, Y.W. Modeling tunneling-induced ground surface settlement development using a wavelet smooth relevance vector machine. Comput. Geotech. 2013, 54, 125–132. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Martinez-Ramon, M.; Rojo-Alvarez, J.L.; Munoz-Mari, J. Nonlinear system identification with composite relevance vector machines. IEEE Signal. Process. Lett. 2007, 14, 279–282. [Google Scholar] [CrossRef]
- Psorakis, I.; Damoulas, T.; Girolami, M.A. Multiclass Relevance Vector Machines: Sparsity and Accuracy. IEEE Trans. Neural Netw. 2010, 21, 1588–1598. [Google Scholar] [CrossRef] [PubMed]
- Fei, S.W.; He, Y. A Multiple-Kernel Relevance Vector Machine with Nonlinear Decreasing Inertia Weight PSO for State Prediction of Bearing. Shock Vib. 2015, 2015. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Zhou, W.D.; Yuan, S.S. Multifractal Analysis and Relevance Vector Machine-Based Automatic Seizure Detection in Intracranial EEG. Int. J. Neural Syst. 2015, 25, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Wang, K.; Yu, T.; Fang, M.L. Integrating relevance vector machines and genetic algorithms for optimization of seed-separating process. Eng. Appl. Artif. Intell. 2007, 20, 970–979. [Google Scholar] [CrossRef]
- Fei, S.W.; He, Y. Wind speed prediction using the hybrid model of wavelet decomposition and artificial bee colony algorithm-based relevance vector machine. Int. J. Electr. Power Energy Syst. 2015, 73, 625–631. [Google Scholar] [CrossRef]
- Liu, D.T.; Zhou, J.B.; Pan, D.W.; Peng, Y.; Peng, X.Y. Lithium-ion battery remaining useful life estimation with an optimized Relevance Vector Machine algorithm with incremental learning. Measurement 2015, 63, 143–151. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Liu, B.Y.; Zhang, Z.L. Combining ensemble empirical mode decomposition with spectrum subtraction technique for heart rate monitoring using wrist-type photoplethysmography. Biomed. Signal Process. Control 2015, 21, 119–125. [Google Scholar] [CrossRef]
- Huang, S.C.; Wu, T.K. Combining wavelet-based feature extractions with relevance vector machines for stock index forecasting. Expert Syst. 2008, 25, 133–149. [Google Scholar] [CrossRef]
- Huang, S.C.; Hsieh, C.H. Wavelet-Based Relevance Vector Regression Model Coupled with Phase Space Reconstruction for Exchange Rate Forecasting. Int. J. Innov. Comput. Inf. Control 2012, 8, 1917–1930. [Google Scholar]
- Liu, F.; Zhou, J.Z.; Qiu, F.P.; Yang, J.J.; Liu, L. Nonlinear hydrological time series forecasting based on the relevance vector regression. In Proceedings of the 13th International Conference on Neural Information Processing (ICONIP’06), Hong Kong, China, 3–6 October 2006; pp. 880–889.
- Sun, G.Q.; Chen, Y.; Wei, Z.N.; Li, X.L.; Cheung, K.W. Day-Ahead Wind Speed Forecasting Using Relevance Vector Machine. J. Appl. Math. 2014, 2014, 437592. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Bargiotas, D.; Bourbakis, N.G.; Tsoukalas, L.H. Genetic Optimal Regression of Relevance Vector Machines for Electricity Pricing Signal Forecasting in Smart Grids. IEEE Trans. Smart Grid 2015, 6, 2997–3005. [Google Scholar] [CrossRef]
- Zhang, X.; Lai, K.K.; Wang, S.Y. A new approach for crude oil price analysis based on empirical mode decomposition. Energy Econ. 2008, 30, 905–918. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert Spectrum 1. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, New York, NY, USA, 4–6 October 1995; Volume 1, pp. 39–43.
- Nickabadi, A.; Ebadzadeh, M.M.; Safabakhsh, R. A novel particle swarm optimization algorithm with adaptive inertia weight. Appl. Soft Comput. 2011, 11, 3658–3670. [Google Scholar] [CrossRef]
- EIA Website. Available online: http://www.eia.doe.gov (accessed on 20 September 2016).
- Liu, H.; Tian, H.Q.; Li, Y.Q. Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction. Appl. Energy 2012, 98, 415–424. [Google Scholar] [CrossRef]
- Yu, L.; Zhao, Y.; Tang, L. A compressed sensing based AI learning paradigm for crude oil price forecasting. Energy Econ. 2014, 46, 236–245. [Google Scholar] [CrossRef]

| Type | Name | Descriptions | ||
|---|---|---|---|---|
| Decomposition | Forecasting | Ensemble | ||
| Single | APSO-RVM | - | RVM with a combined kernel optimized by APSO | - |
| PSO-RVM | - | RVM with a combined kernel optimized by standard PSO | - | |
| RVMlin | - | RVM with a linear kernel | - | |
| RVMpoly | - | RVM with a polynomial kernel | - | |
| RVMrbf | - | RVM with a radial basic function kernel | - | |
| RVMsig | - | RVM with a sigmoid kernel | - | |
| ANN | - | Back propagation neural network | - | |
| LSSVR | - | Least squares support vector regression | - | |
| ARIMA | - | Autoregressive integrated moving average | - | |
| Ensemble | EEMD-APSO-RVM | EEMD | RVM with a combined kernel optimized by APSO | Addition |
| EEMD-PSO-RVM | EEMD | RVM with a combined kernel optimized by standard PSO | Addition | |
| EEMD-RVMlin | EEMD | RVM with a linear kernel | Addition | |
| EEMD-RVMpoly | EEMD | RVM with a polynomial kernel | Addition | |
| EEMD-RVMrbf | EEMD | RVM with a radial basic function kernel | Addition | |
| EEMD-RVMsig | EEMD | RVM with a sigmoid kernel | Addition | |
| EEMD-ANN | EEMD | Back propagation neural network | Addition | |
| EEMD-LSSVR | EEMD | Least squares support vector regression | Addition | |
| EMD-APSO-RVM | EMD | RVM with a combined kernel optimized by APSO | Addition | |
| EMD-PSO-RVM | EMD | RVM with a combined kernel optimized by standard PSO | Addition | |
| EMD-RVMlin | EMD | RVM with a linear kernel | Addition | |
| EMD-RVMpoly | EMD | RVM with a polynomial kernel | Addition | |
| EMD-RVMrbf | EMD | RVM with a radial basic function kernel | Addition | |
| EMD-RVMsig | EMD | RVM with a sigmoid kernel | Addition | |
| EMD-ANN | EMD | Back propagation neural network | Addition | |
| EMD-LSSVR | EMD | Least squares support vector regression | Addition | |
| Description | Symbol | Range / Value |
|---|---|---|
| Population size | P | 20 |
| Maximal iterations | T | 40 |
| Particle dimension | D | 10 |
| Maximal, minimal inertia weight | 0.9, 0.4 | |
| Accelerate constants | 1.49, 1.49 | |
| Kernel weight | [0, 1] | |
| Coefficient in Kpoly | a | [0, 2] |
| Constant in Kpoly | b | [0, 10] |
| Exponent in Kpoly | c | [1, 4] |
| Width in Krbf | d | [] |
| Coefficient in Ksig | e | [0, 4] |
| Constant in Ksig | f | [0, 8] |
| Horizon | MAPE | RMSE | Dstat |
|---|---|---|---|
| One | 0.0065 ± 0.0001 | 0.5905 ± 0.0110 | 0.8643 ± 0.0032 |
| Three | 0.0091 ± 0.0001 | 0.8324 ± 0.0340 | 0.8062 ± 0.0037 |
| Six | 0.0126 ± 0.0003 | 1.1843 ± 0.0702 | 0.7028 ± 0.0028 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Zhou, M.; Guo, C.; Luo, M.; Wu, J.; Pan, F.; Tao, Q.; He, T. Forecasting Crude Oil Price Using EEMD and RVM with Adaptive PSO-Based Kernels. Energies 2016, 9, 1014. https://doi.org/10.3390/en9121014
Li T, Zhou M, Guo C, Luo M, Wu J, Pan F, Tao Q, He T. Forecasting Crude Oil Price Using EEMD and RVM with Adaptive PSO-Based Kernels. Energies. 2016; 9(12):1014. https://doi.org/10.3390/en9121014
Chicago/Turabian StyleLi, Taiyong, Min Zhou, Chaoqi Guo, Min Luo, Jiang Wu, Fan Pan, Quanyi Tao, and Ting He. 2016. "Forecasting Crude Oil Price Using EEMD and RVM with Adaptive PSO-Based Kernels" Energies 9, no. 12: 1014. https://doi.org/10.3390/en9121014






