Input Forces Estimation for Nonlinear Systems by Applying a Square-Root Cubature Kalman Filter
Abstract
:1. Introduction
2. Problem Formulation
2.1. Discretization of a Nonlinear System
2.2. Square-Root Cubature Kalman Filter [14,15]
2.2.1. Initialization
2.2.2. Time Update
2.2.3. Measurement Update
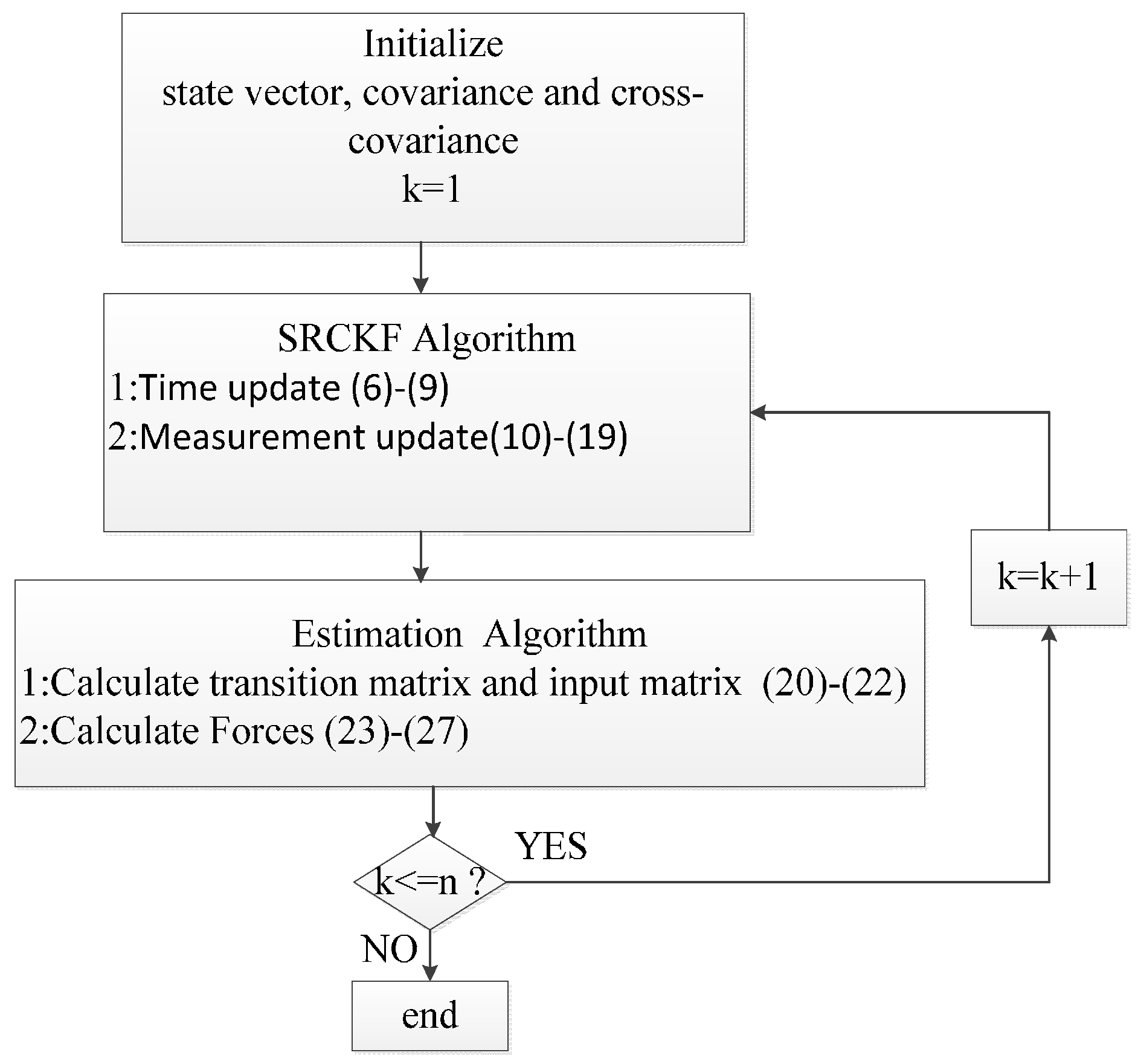
2.3. The Nonlinear Estimator
3. Numerical Simulations and Discussions
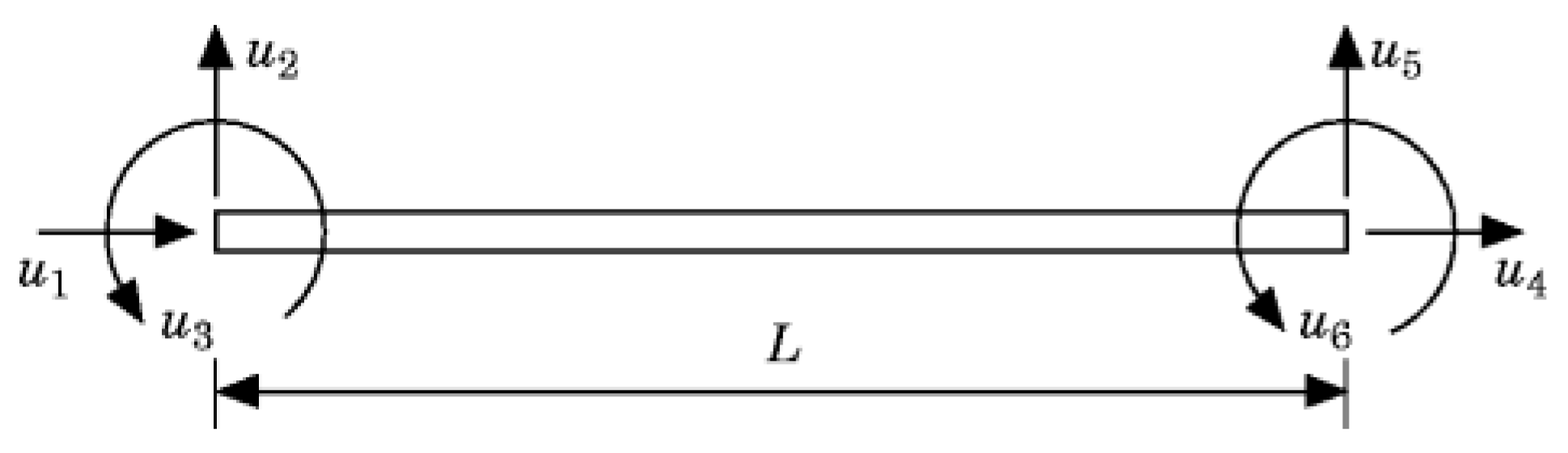
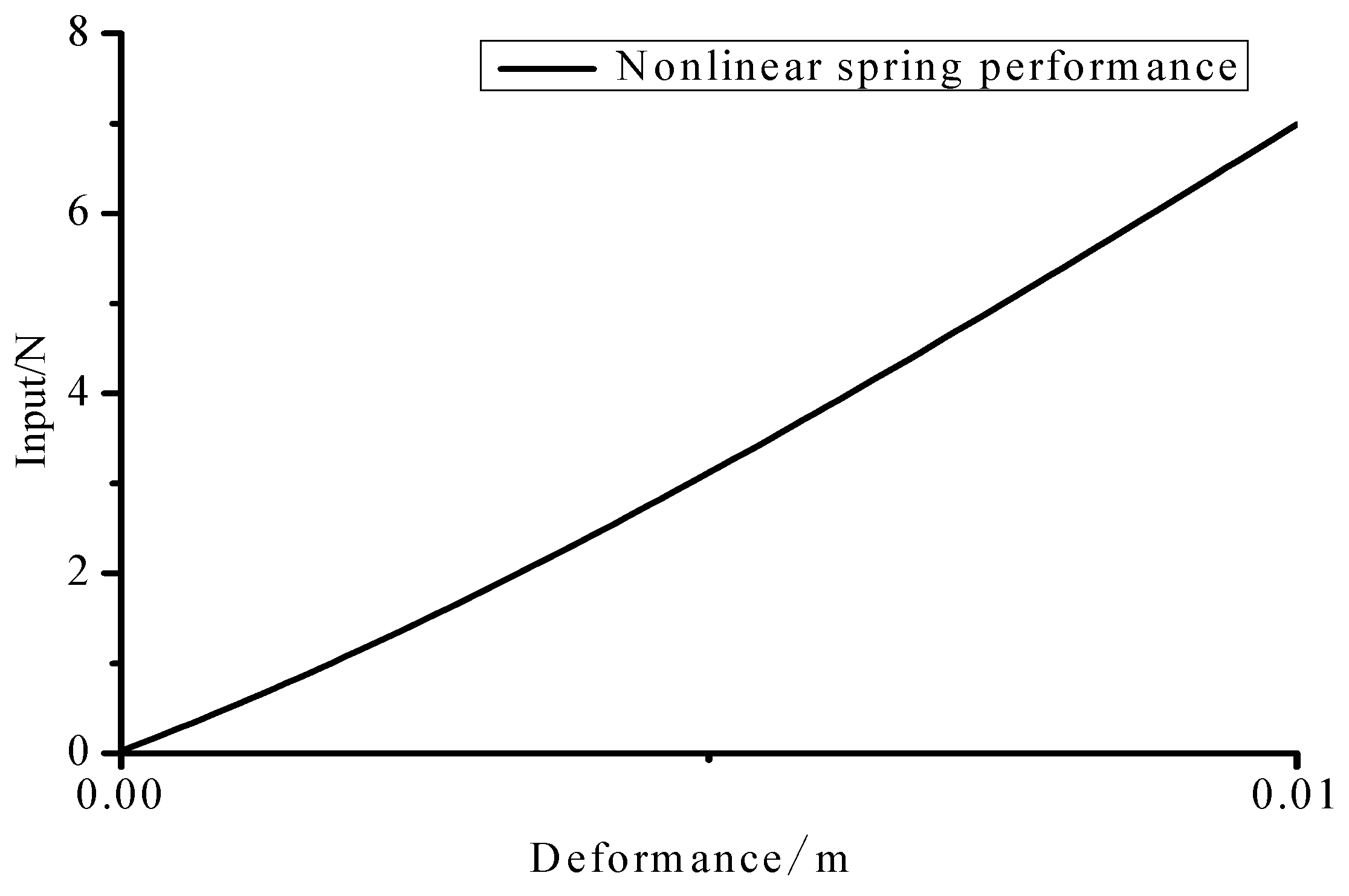
3.1. Simulation Model
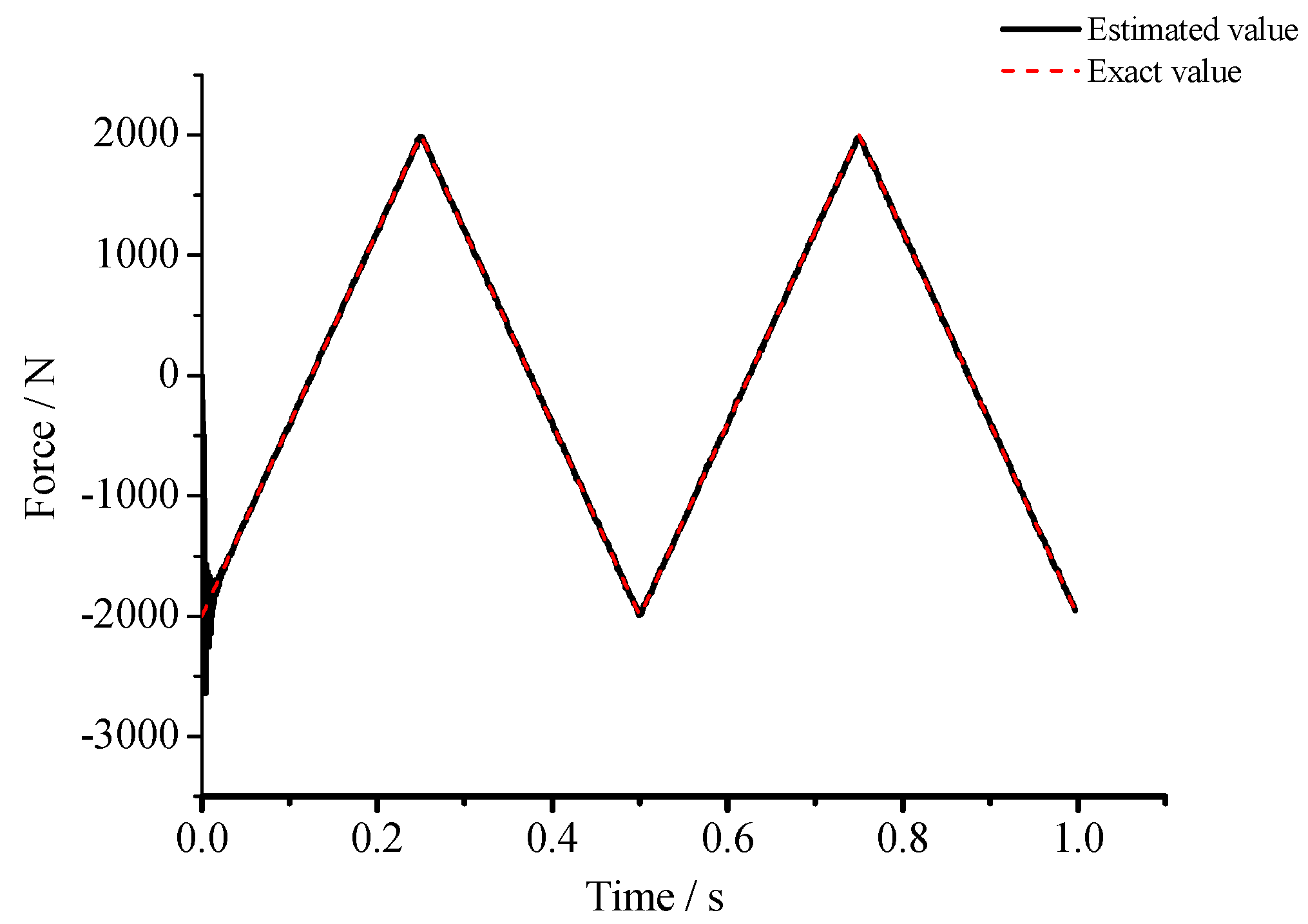
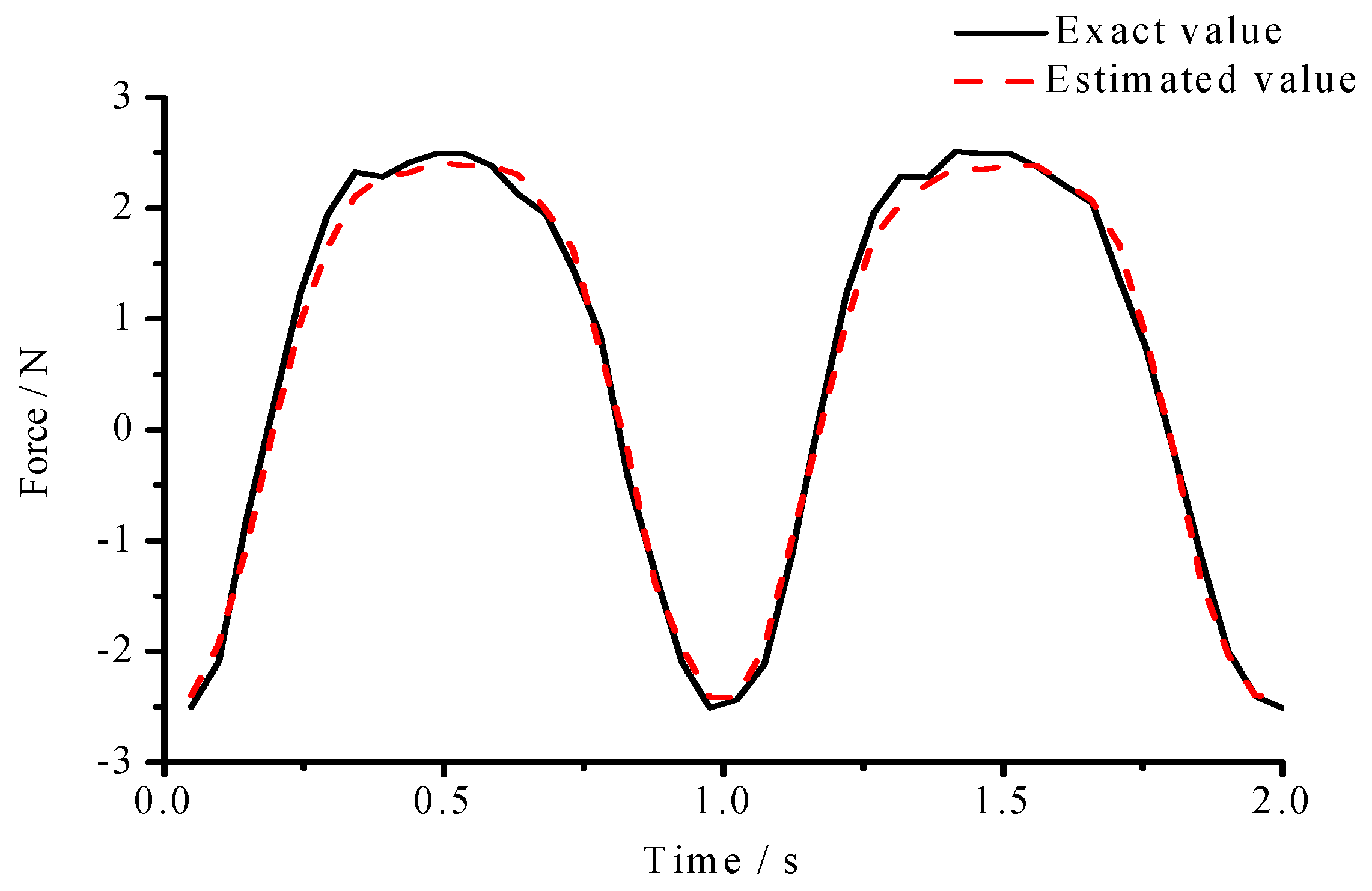
3.2. Simulation Results
3.3. Discussions of the Simulations
4. Experiment and Results
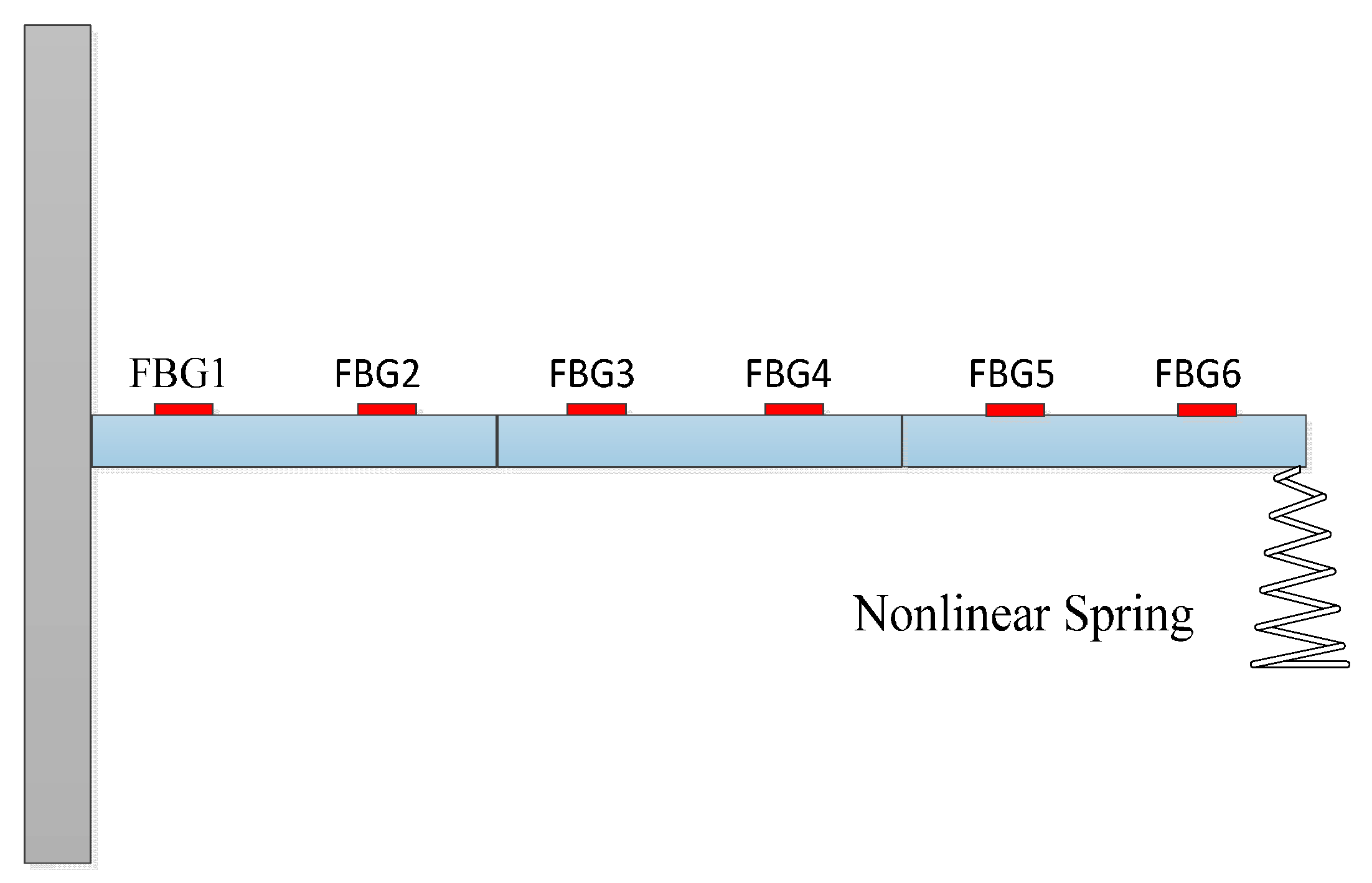
4.1. Experimental Model and Measurement Principle
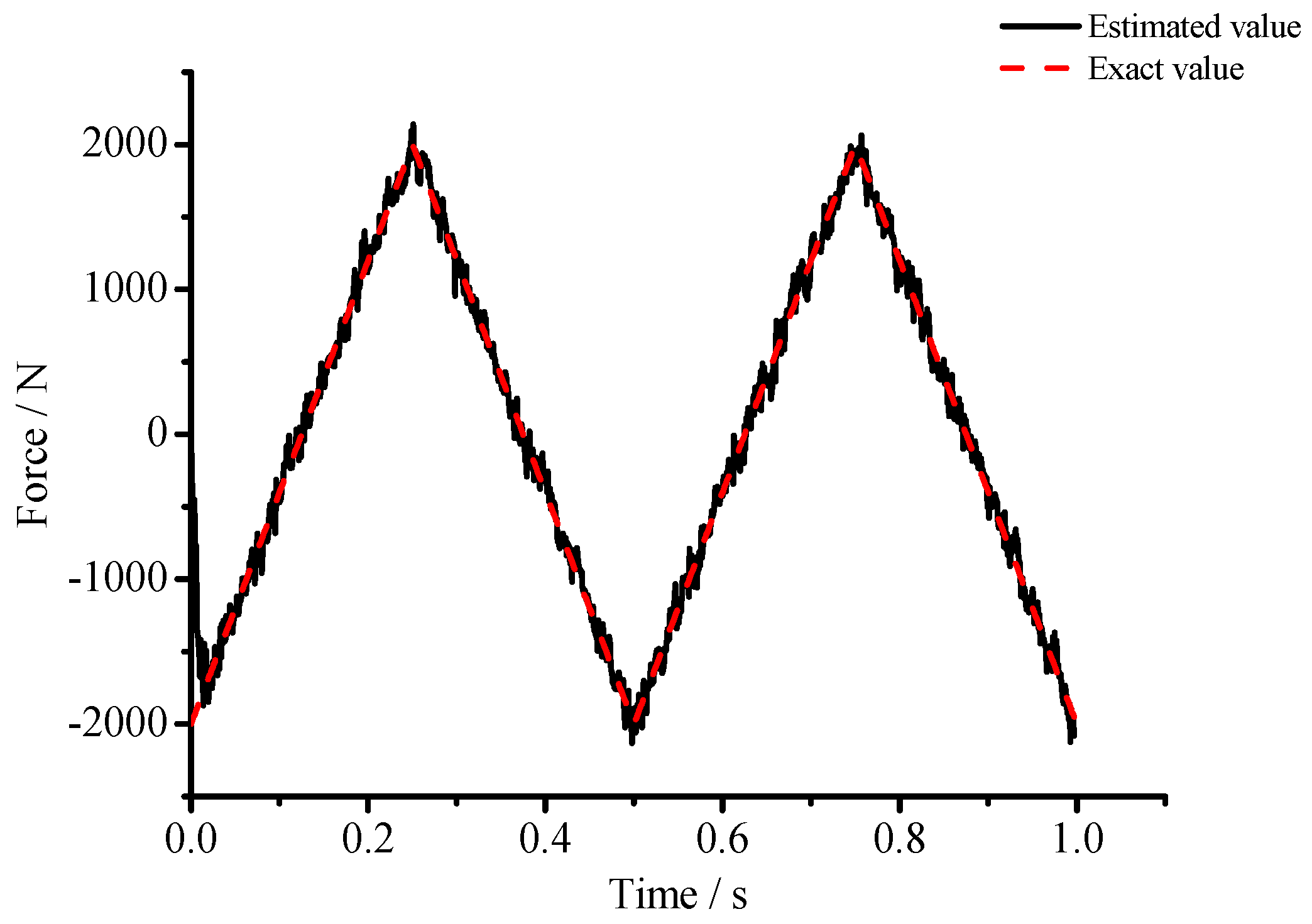
4.2. Experimental Procedure and Results
4.3. Discussions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Noor, A.K.; Venneri, S.L.; Paul, D.B.; Hopkins, M.A. Structures technology for future aerospace systems. Comput. Struct. 2000, 74, 507–519. [Google Scholar] [CrossRef]
- Airoldi, A.; Sala, G.; Evenblij, R.; Koimtzoglou, C.; Loutas, T.; Carossa, G.M.; Mastromauro, P.; Kanakis, T. Load Monitoring by means of optical fibers and strain gages. In Smart Intelligent Aircraft Structures (SARISTU); Springer: Cham, Switzerland, 2016. [Google Scholar]
- Liu, J.; Sun, X.; Li, K.; Jiang, C.; Han, X. A probability density function discretization and approximation method for the dynamic load identification of stochastic structures. J. Sound Vib. 2015, 357, 74–94. [Google Scholar] [CrossRef]
- Liu, J.; Sun, X.; Han, X.; Jiang, C.; Yu, D. Dynamic load identification for stochastic structures based on Gegenbauer polynomial approximation and regularization method. Mech. Syst. Signal Process. 2015, 56–57, 35–54. [Google Scholar] [CrossRef]
- Zhou, P.; Xu, S.; Wang, Z.; Yan, Y.; Kang, R.; Guo, D. A load identification method for the grinding damage induced stress (GDIS) distribution in silicon wafers. Int. J. Mach. Tools Manuf. 2016, 107, 1–7. [Google Scholar] [CrossRef]
- Xue, X.; Chen, X.; Zhang, X.; Qiao, B. Hermitian plane wavelet finite element method: Wave propagation and load identification. Comput. Math. Appl. 2016, 72, 2920–2942. [Google Scholar] [CrossRef]
- Song, H.; Yu, K.; Li, X.; Han, J. Error estimation of load identification based on linear sensitivity analysis and interval technique. Struct. Multidiscip. Optim. 2017, 55, 432–436. [Google Scholar] [CrossRef]
- Ma, C.; Tuan, P.; Lin, D.; Liu, C. A study of an inverse method for the estimation of impulsive loads. Int. J. Syst. Sci. 1998, 29, 663–672. [Google Scholar] [CrossRef]
- Ma, C.K.; Ho, C.C. An inverse method for the estimation of input forces acting on non-linear structural systems. J. Sound Vib. 2004, 275, 953–971. [Google Scholar] [CrossRef]
- Chopin, N.; Jacob, P.E.; Papaspiliopoulos, O. Smc2: An efficient algorithm for sequential analysis of state space models. J. R. Stat. Soc. 2013, 75, 397–426. [Google Scholar] [CrossRef]
- Dan, C.; Miguez, J. Nested particle filters for online parameter estimation in discrete-time state-space markov models. arXiv, 2013; arXiv:1308.1883. [Google Scholar]
- Martino, L.; Read, J.; Elvira, V.; Louzada, F. Cooperative parallel particle filters for online model selection and applications to urban mobility. Digit. Signal Process. 2017, 60, 172–185. [Google Scholar] [CrossRef]
- Drovandi, C.C.; Mcgree, J.M.; Pettitt, A.N. A sequential monte carlo algorithm to incorporate model uncertainty in bayesian sequential design. J. Comput. Graph. Stat. 2014, 23, 3–24. [Google Scholar] [CrossRef] [Green Version]
- Arasaratnam, I.; Haykin, S.; Hurd, T.R. Cubature kalman filtering for continuous-discrete systems: Theory and simulations. IEEE Trans. Signal Process. 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Yu, T.; Jian, H.; Liu, T. Design of adaptive robust square-root cubature Kalman filter with noise statistic estimator. Appl. Math. Comput. 2015, 256, 352–367. [Google Scholar] [CrossRef]
- Bakr, E.M.; Shabana, A.A. Geometrically nonlinear analysis of multibody systems. Comput. Struct. 1986, 23, 739–751. [Google Scholar] [CrossRef]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis; McGraw-Hill: New York, NY, USA, 1900. [Google Scholar]
- Ma, A.J.; Chen, S.H.; Li, X.N. Design sensitivity analysis of non-linear response for large deflection forced vibrations of beams. J. Sound Vib. 1995, 187, 683–693. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, X.; Wang, L.; Zhu, Y.; Dong, H.; Chen, W.; Li, J.; Ji, B.; Ding, Y. Research of concrete residual strains monitoring based on WLI and FBG following exposure to freeze–thaw tests. Cold Reg. Sci. Technol. 2015, 116, 40–48. [Google Scholar] [CrossRef]
- Dong, L.; Ma, J.; Ibrahim, Z.; Ismail, Z. Etched FBG coated with polyimide for simultaneous detection the salinity and temperature. Opt. Commun. 2017, 392, 218–222. [Google Scholar]
- Woyessa, G.; Fasano, A.; Markos, C.; Rasmussen, H.; Bang, O. Low loss polycarbonate polymer optical fiber for high temperature FBG humidity sensing. IEEE Photonics Technol. Lett. 2017, 29, 575–578. [Google Scholar] [CrossRef]


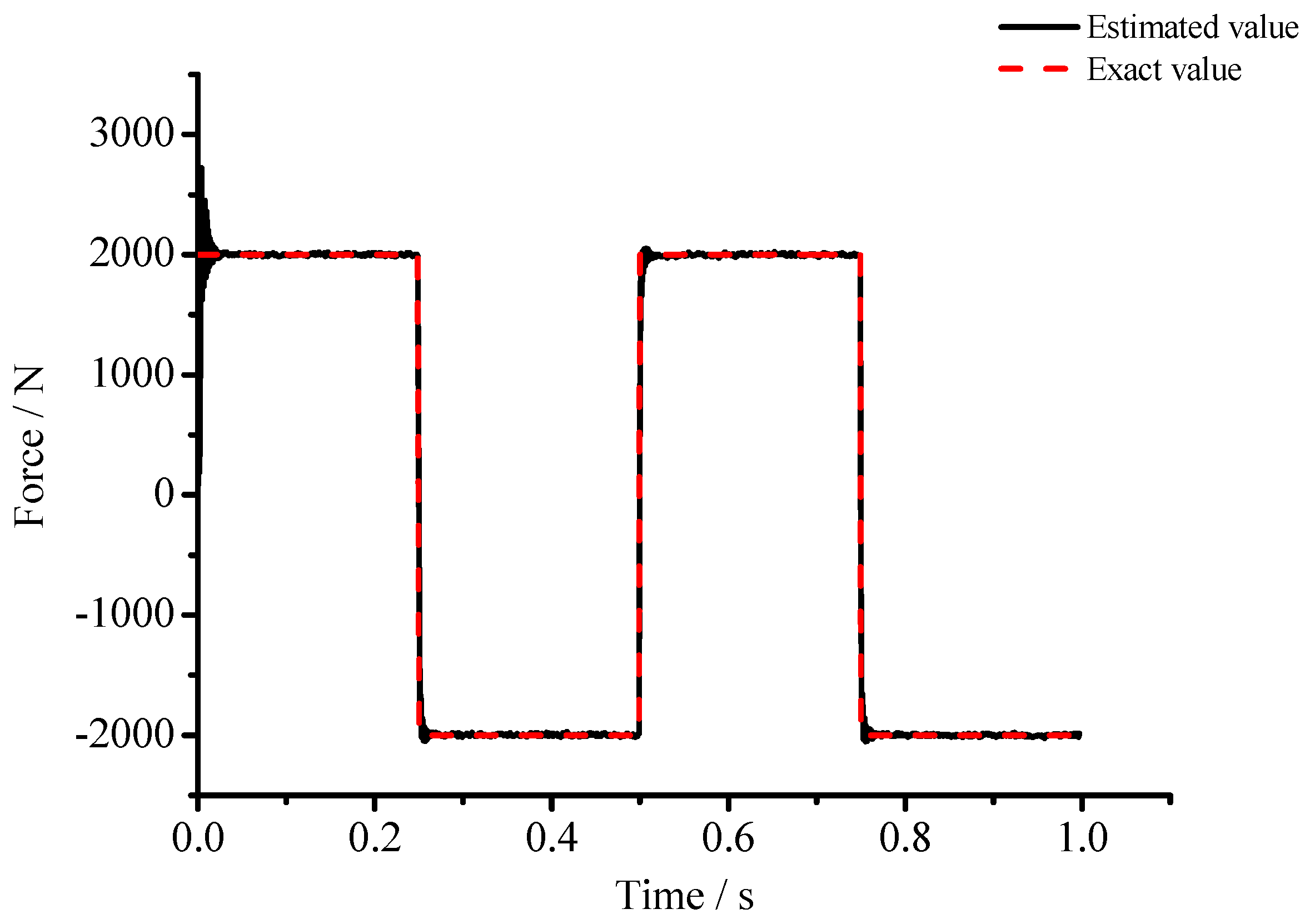
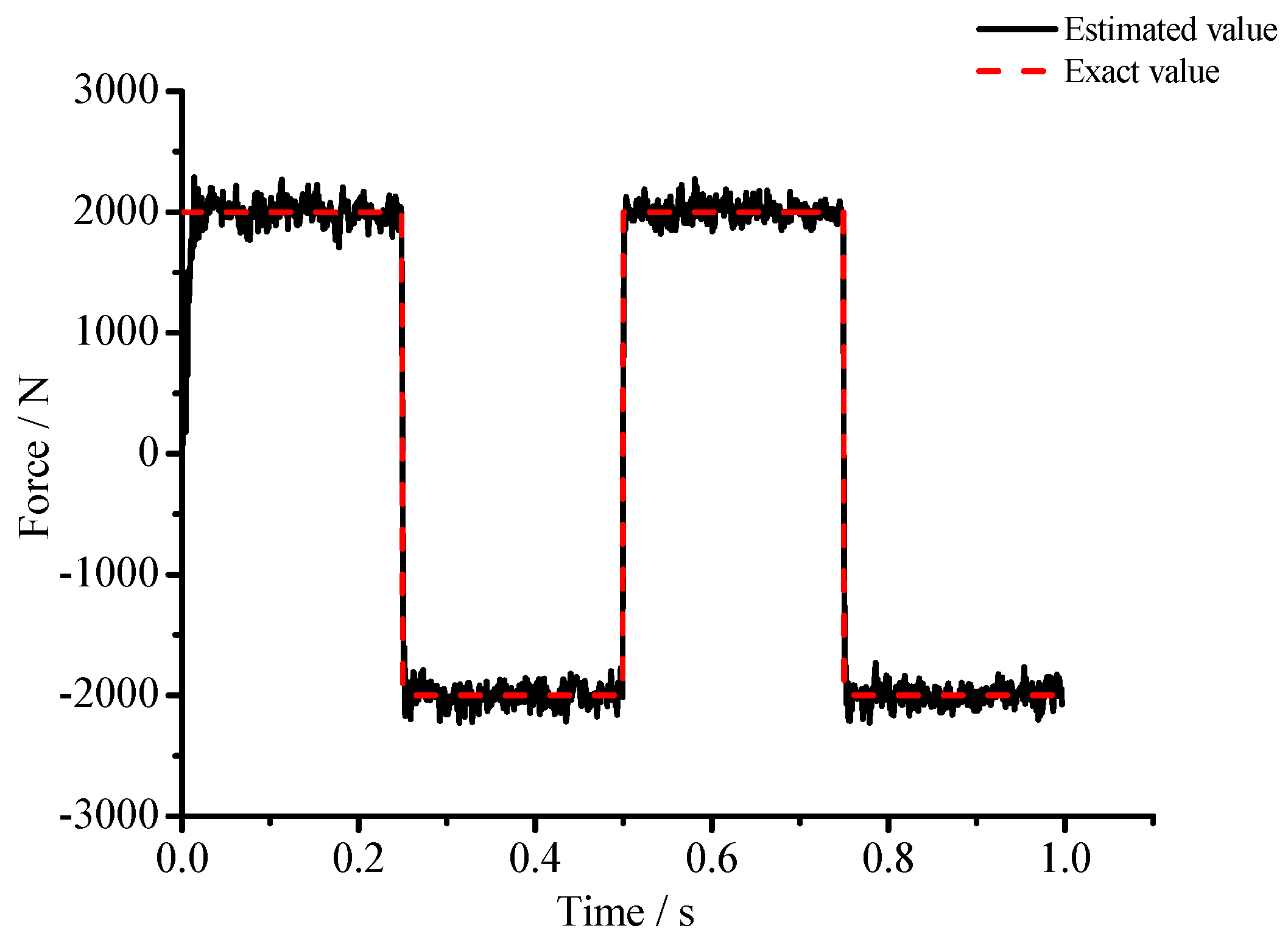

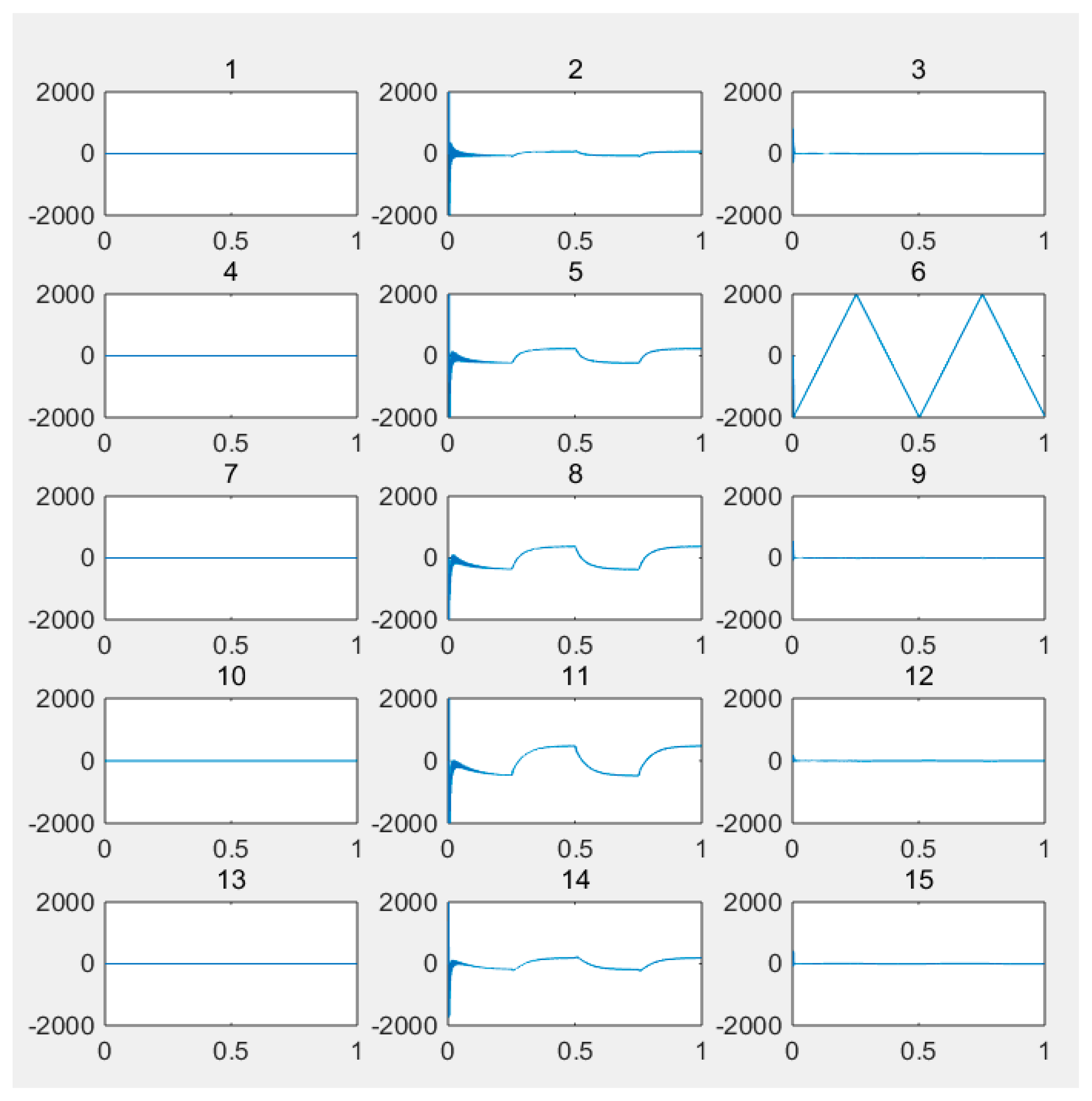


| Force Type | Sinusoidal | Rectangular | Triangular | |||
|---|---|---|---|---|---|---|
| 1 × | 1 × | 1 × | 1 × | 1 × | 1 × | |
| Mean () | 9.61 | 1.72 | 60.1 | 50.1 | 25.5 | 16.4 |
| RMSE (%) | 0.46 | 0.43 | 6.61 | 5.41 | 5.27 | 3.62 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Zhang, Y.; Liang, D. Input Forces Estimation for Nonlinear Systems by Applying a Square-Root Cubature Kalman Filter. Materials 2017, 10, 1162. https://doi.org/10.3390/ma10101162
Song X, Zhang Y, Liang D. Input Forces Estimation for Nonlinear Systems by Applying a Square-Root Cubature Kalman Filter. Materials. 2017; 10(10):1162. https://doi.org/10.3390/ma10101162
Chicago/Turabian StyleSong, Xuegang, Yuexin Zhang, and Dakai Liang. 2017. "Input Forces Estimation for Nonlinear Systems by Applying a Square-Root Cubature Kalman Filter" Materials 10, no. 10: 1162. https://doi.org/10.3390/ma10101162




