The Stability Analysis Method of the Cohesive Granular Slope on the Basis of Graph Theory
Abstract
:1. Introduction
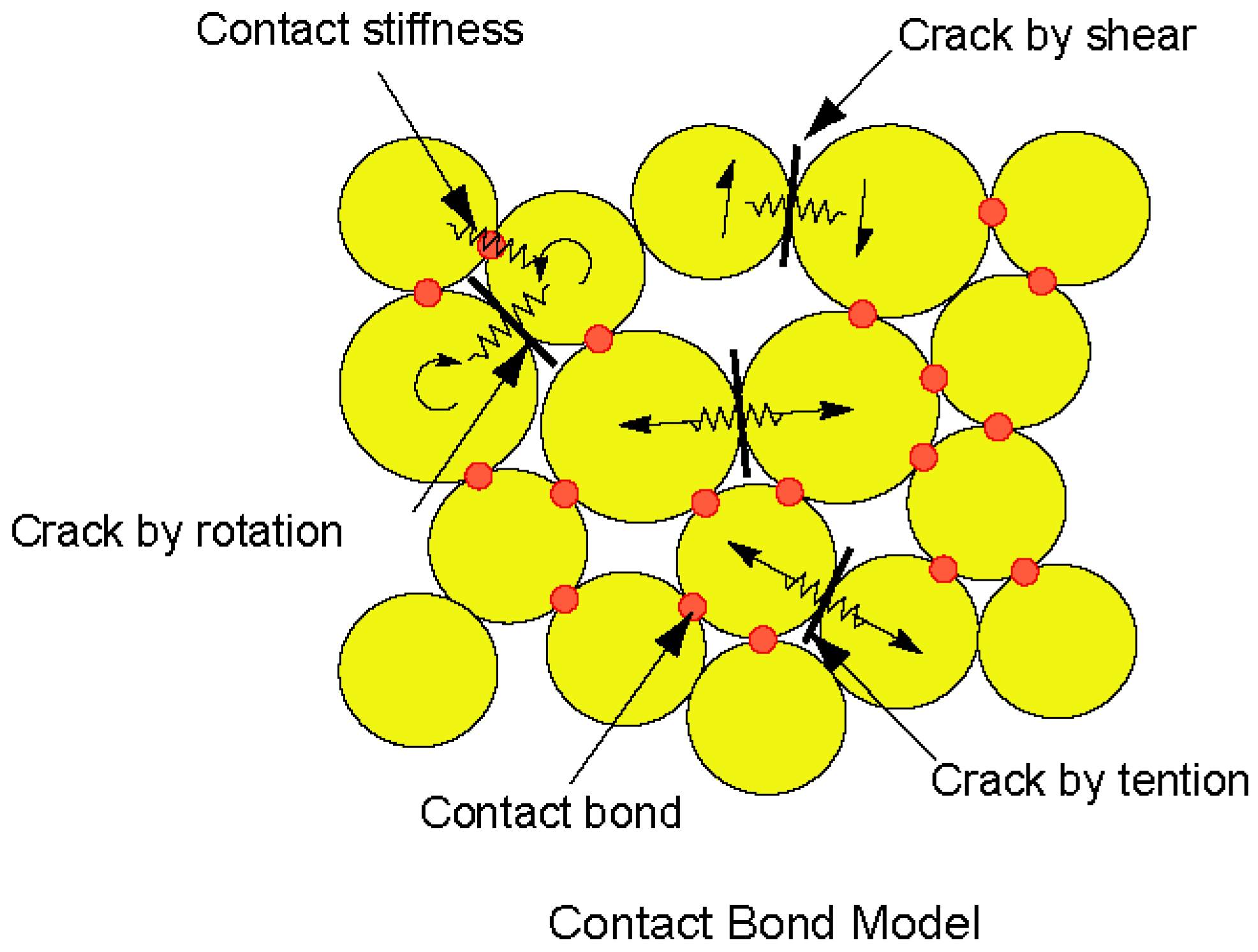
2. The Characterization Method of Macro Contact in Two Dimensional DEM
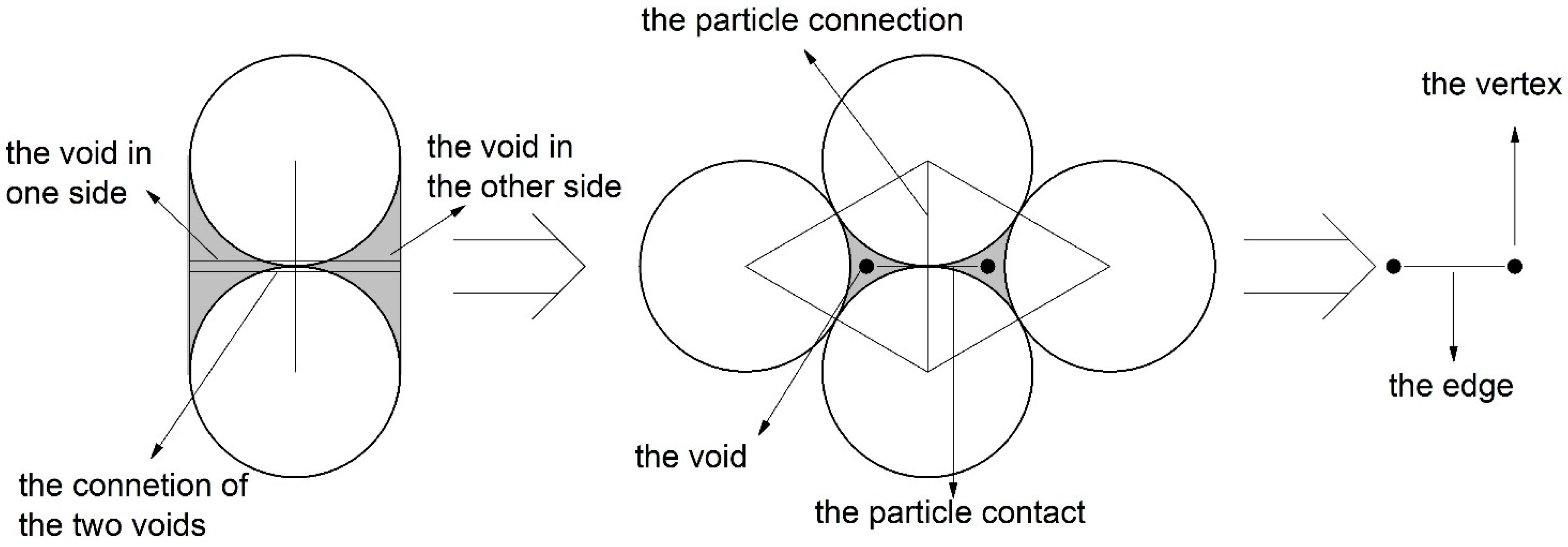
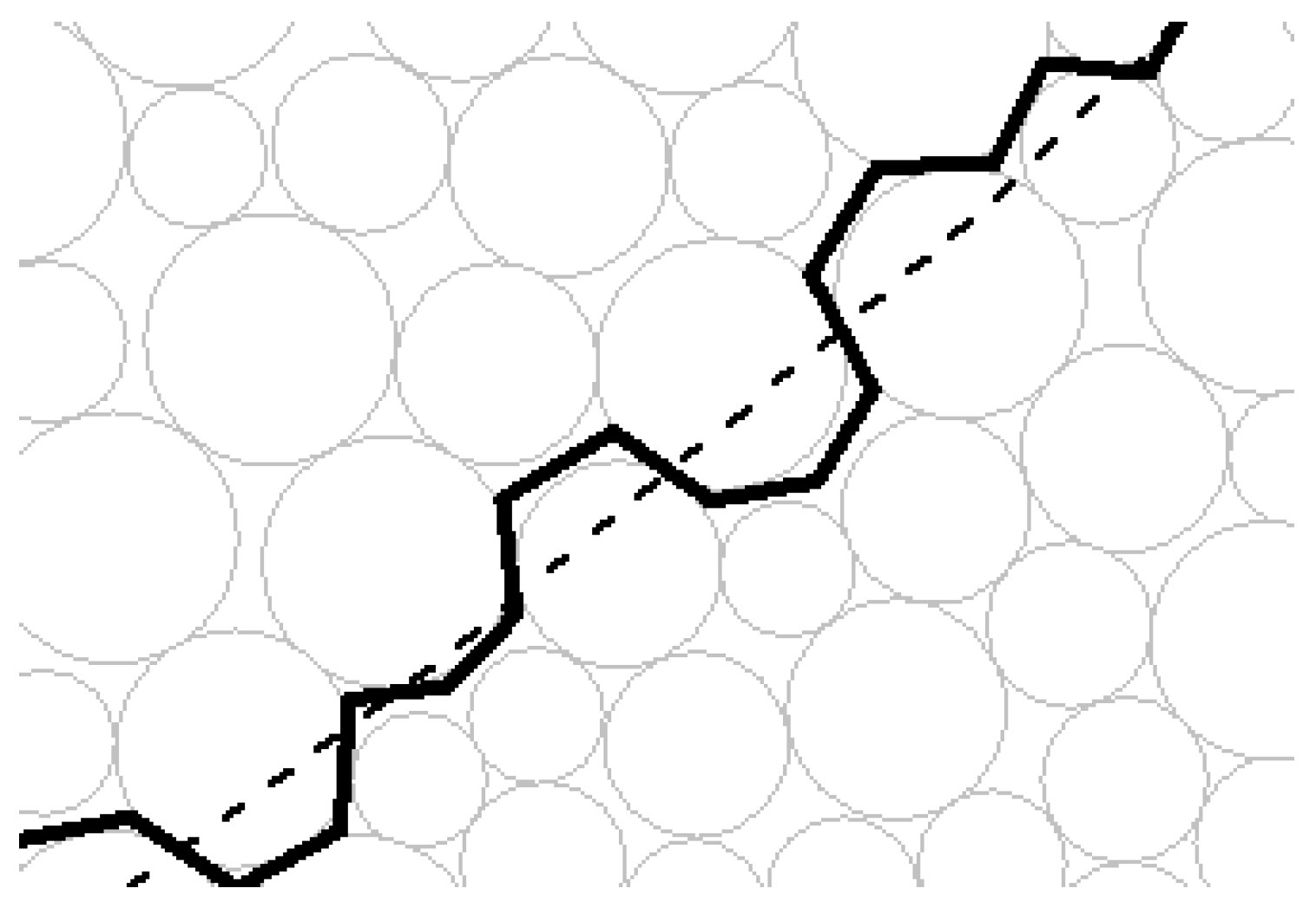
2.1. The Characterization Method of the Particle Contact
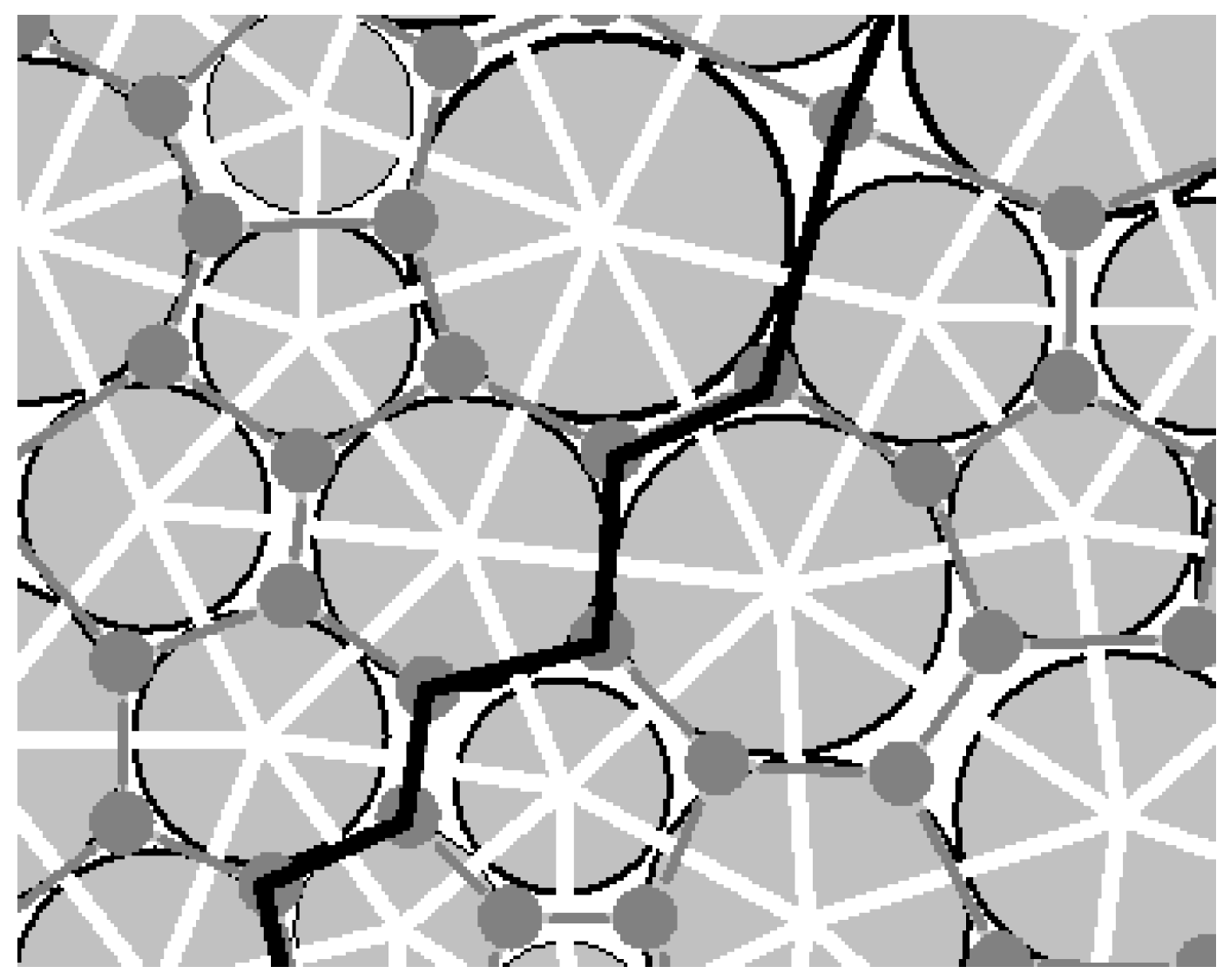
2.2. The Characterization Method of the Macro-Contact
3. The Computing Method of the Slope Stability
3.1. A Simple Introduction to DEM
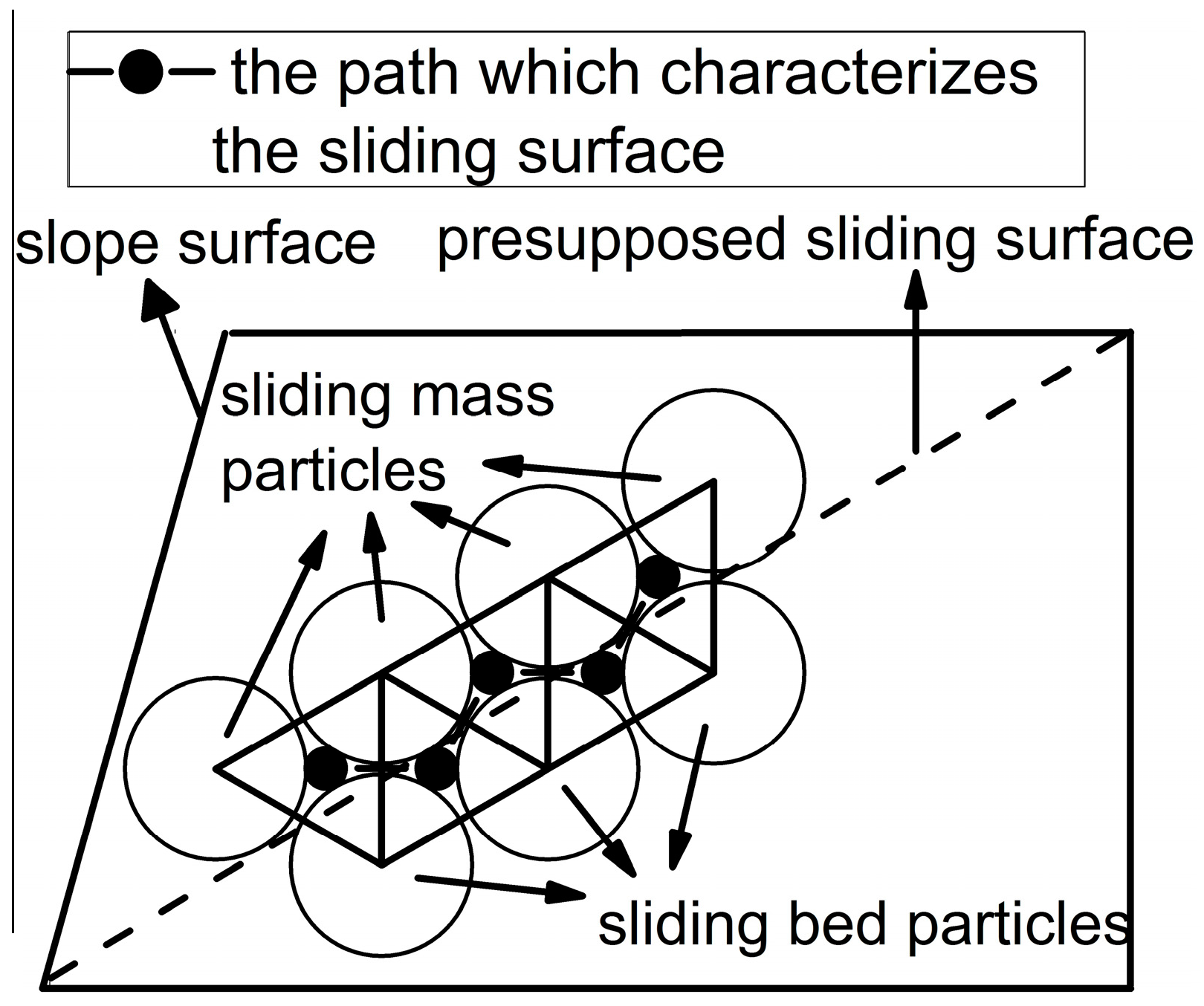
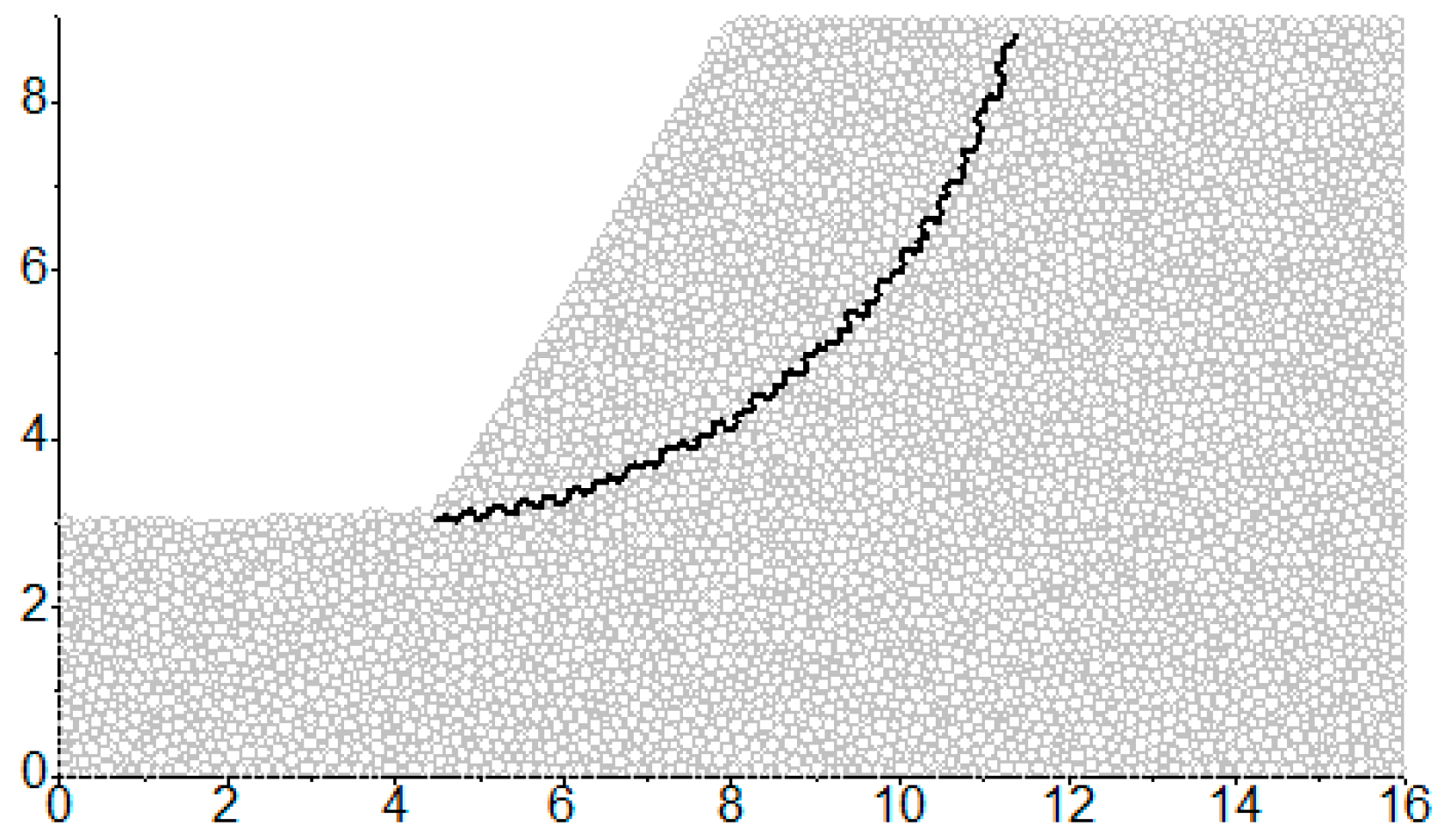
3.2. The Detailed Method to Characterize the Sliding Surface
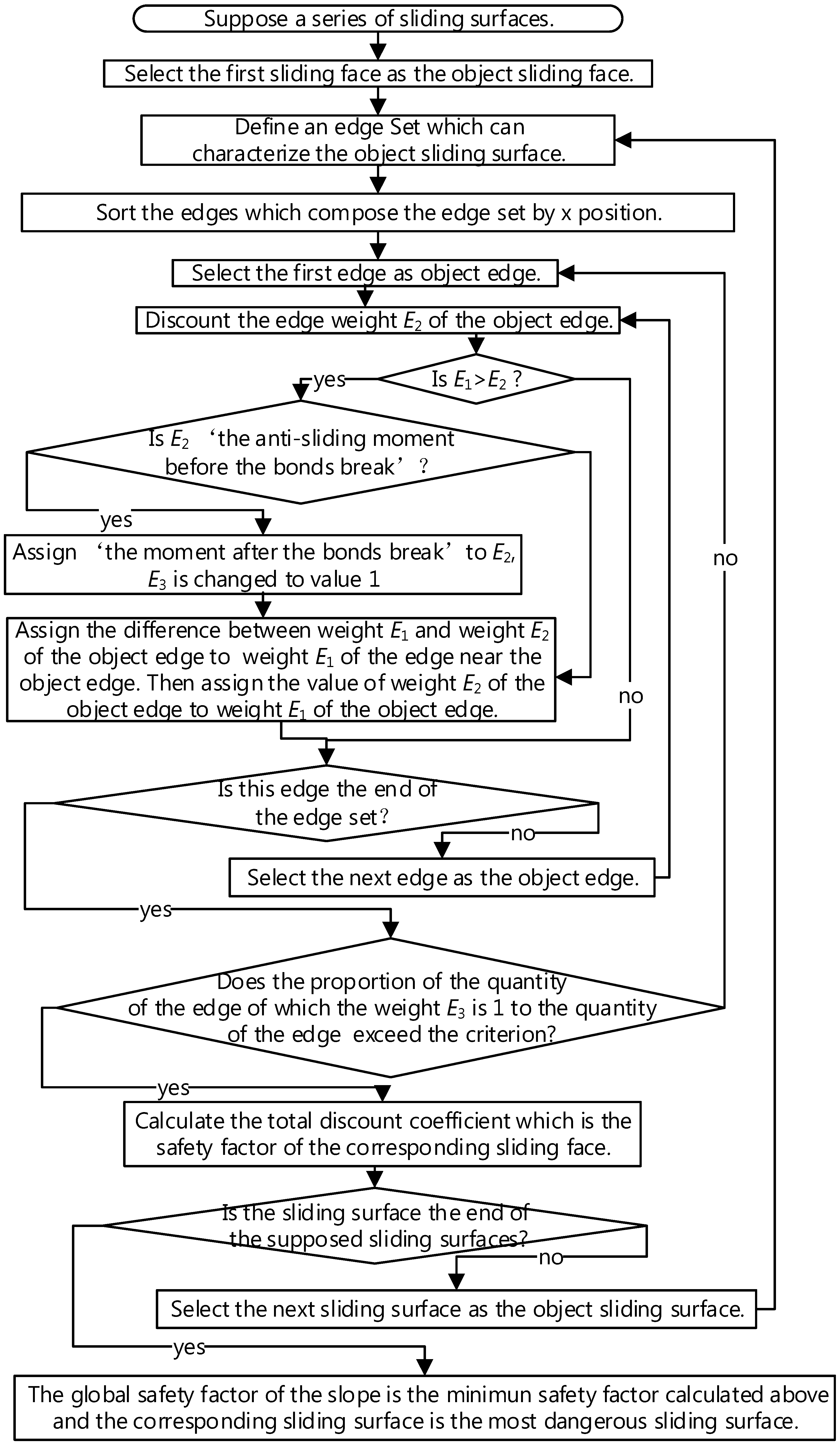
3.3. The Computing Method of the Cohesive Soil Slope Stability
3.4. The Computing Method of the Edge Weight
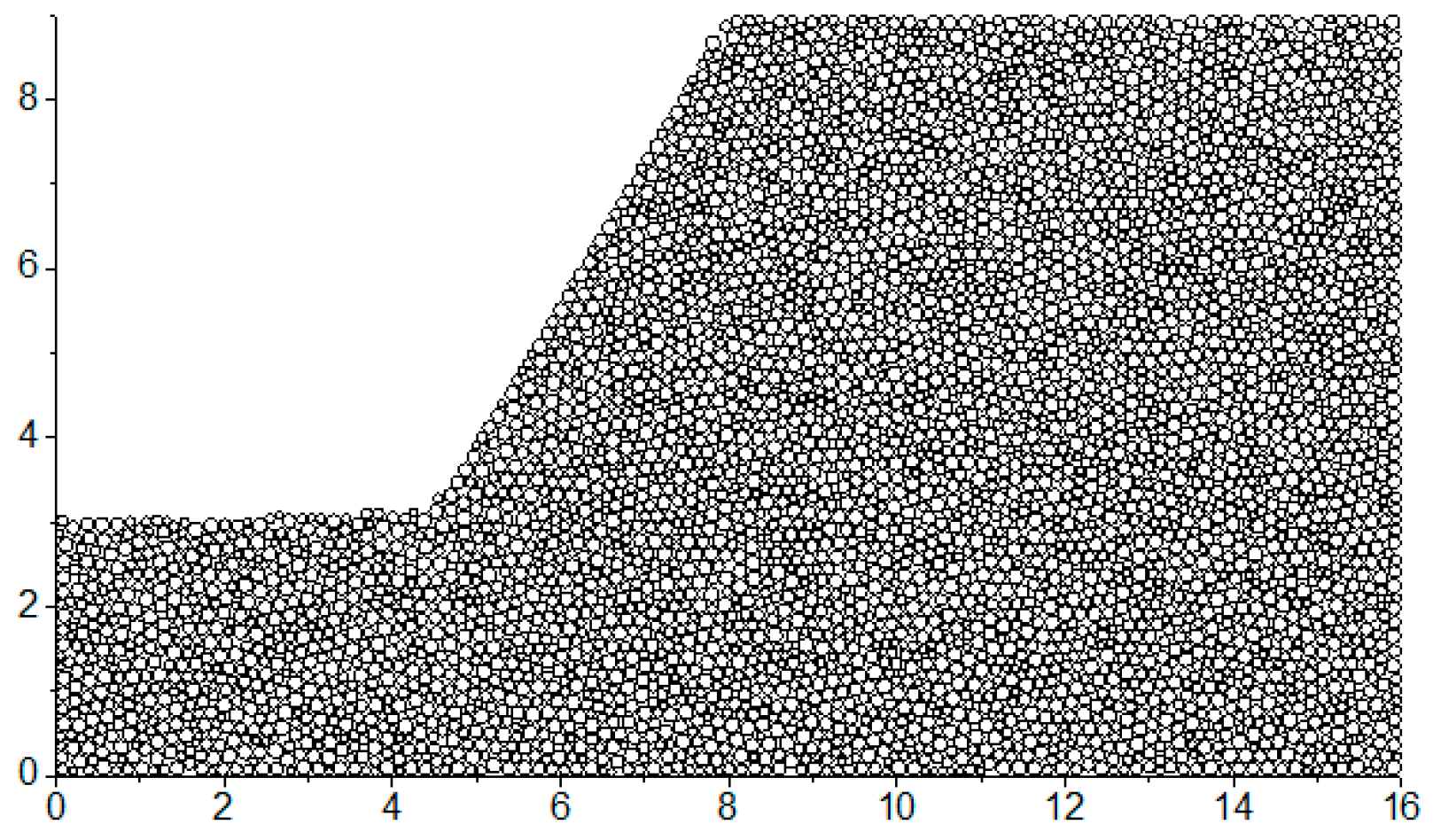
4. Case Study and the Corresponding Result
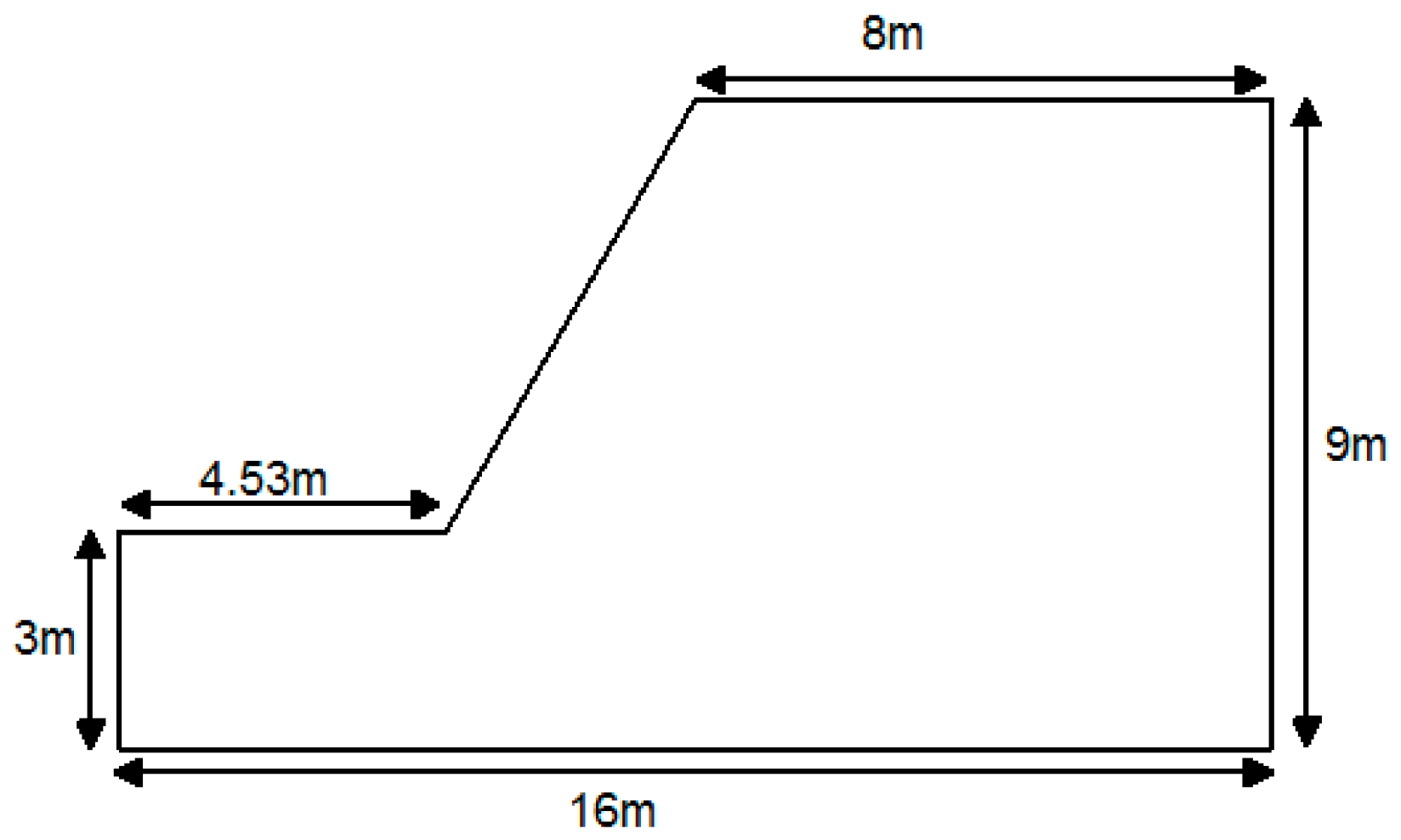
4.1. Case Study
4.2. The Detailed Parameters
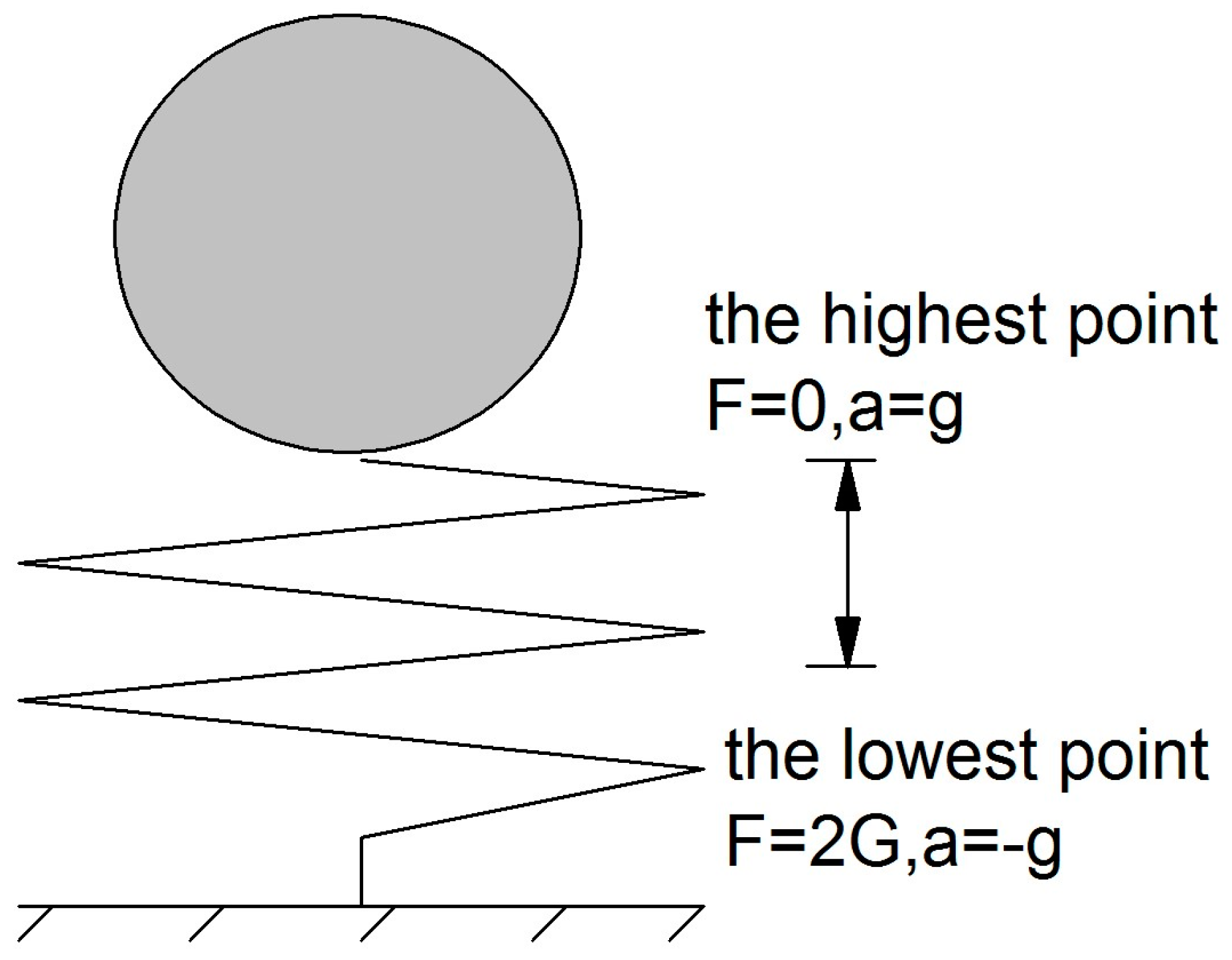
4.2.1. The Impact Load Caused by the Bond Break
4.2.2. The Friction
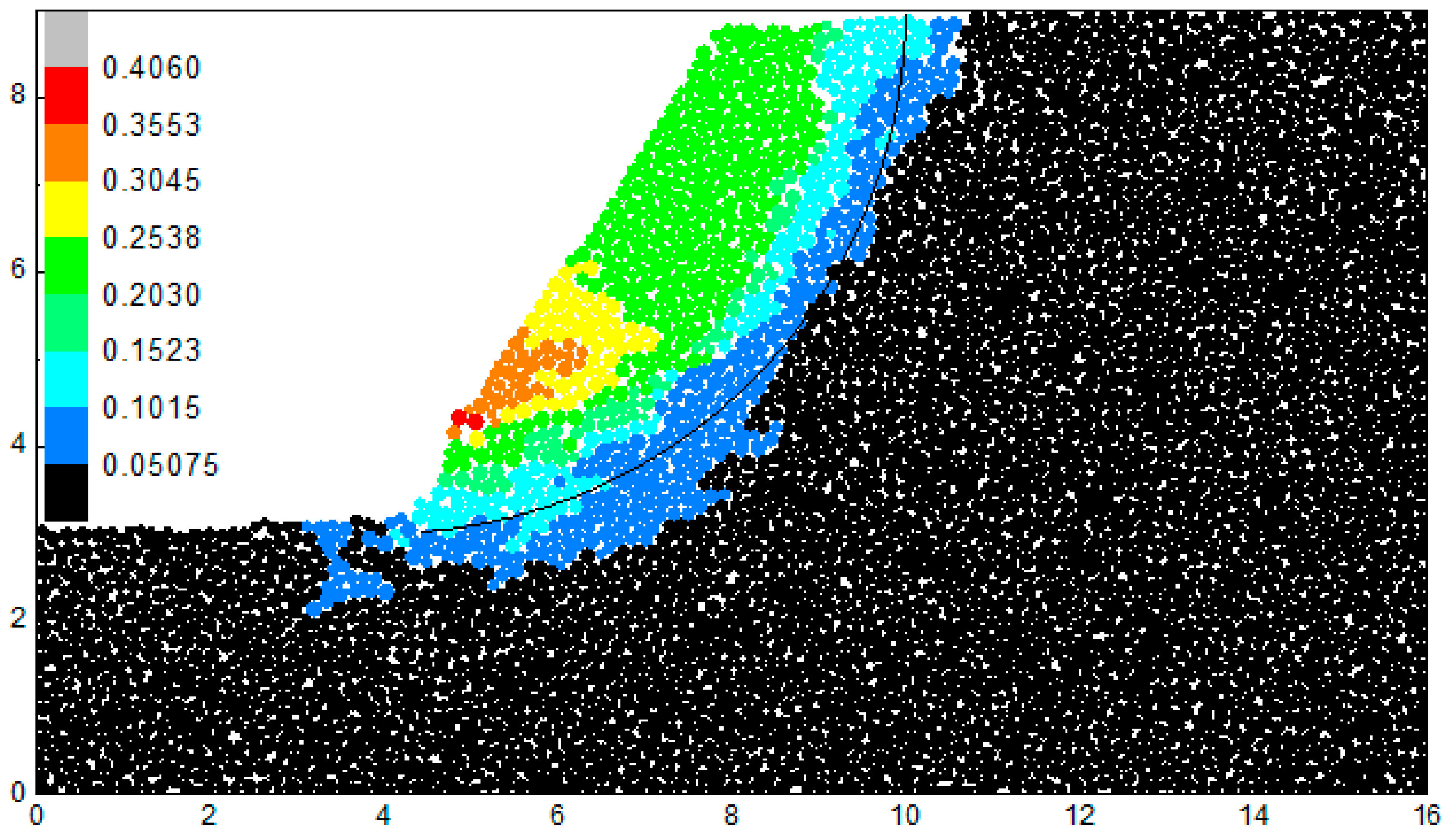
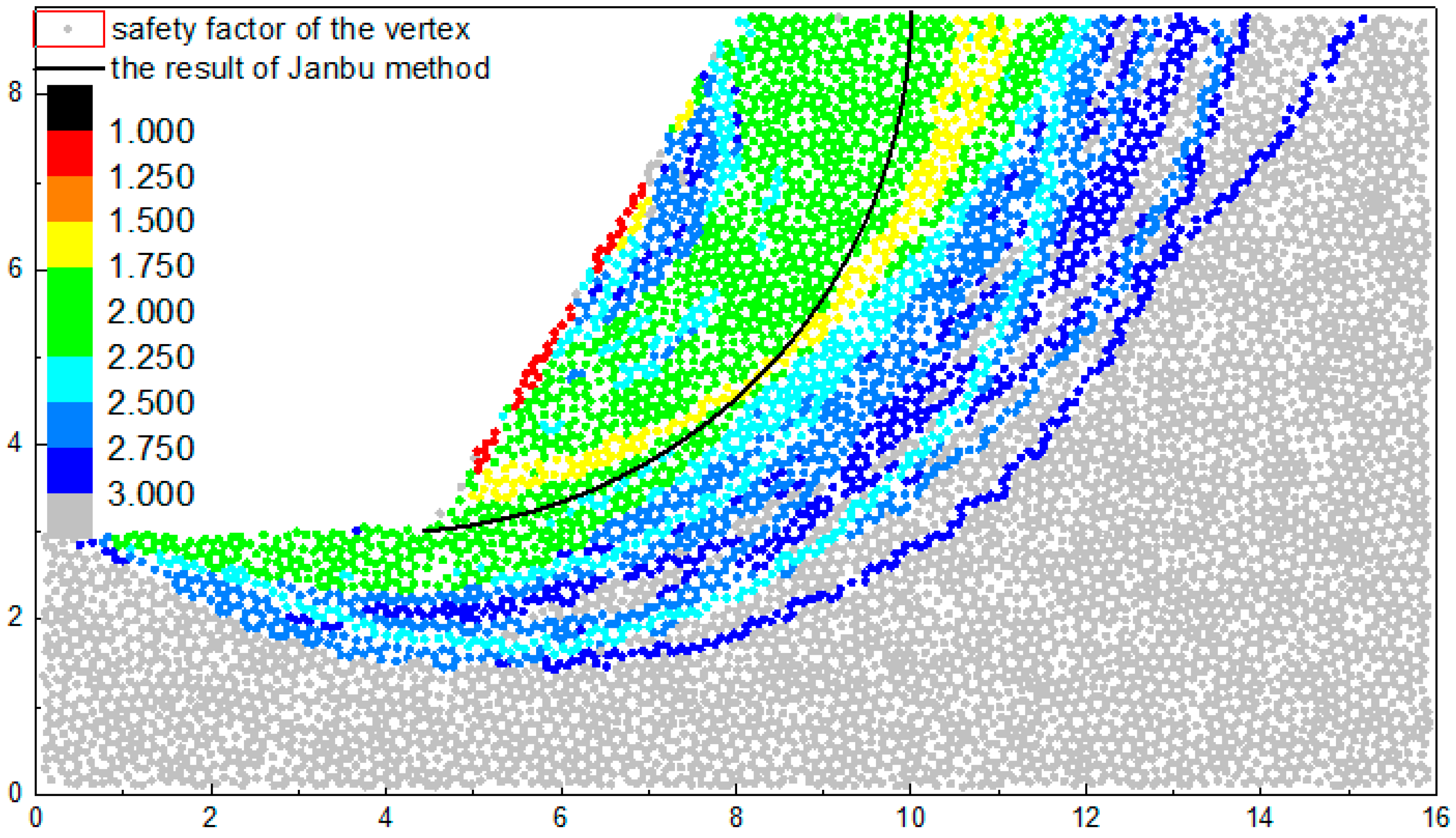
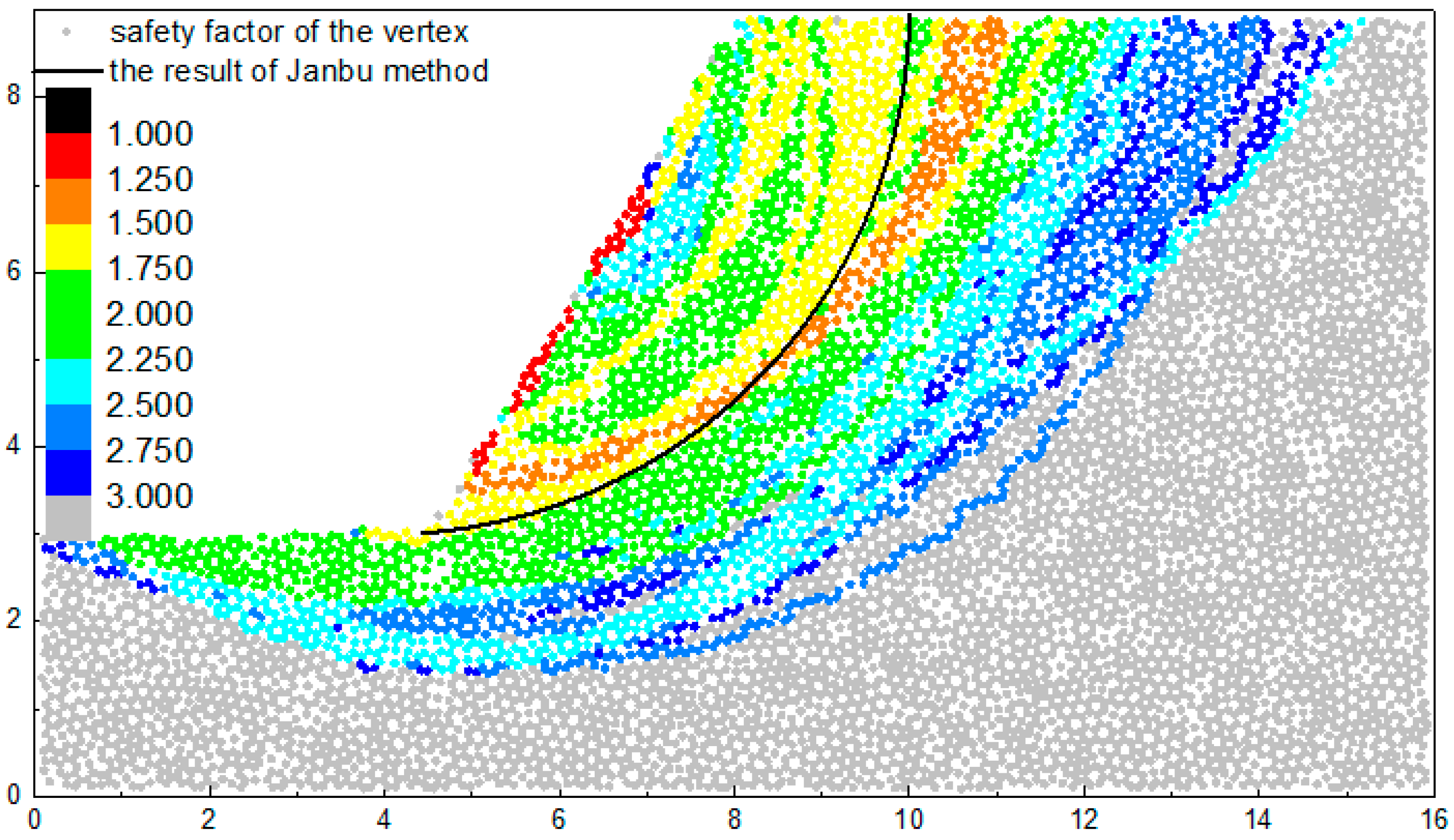
4.3. The Result
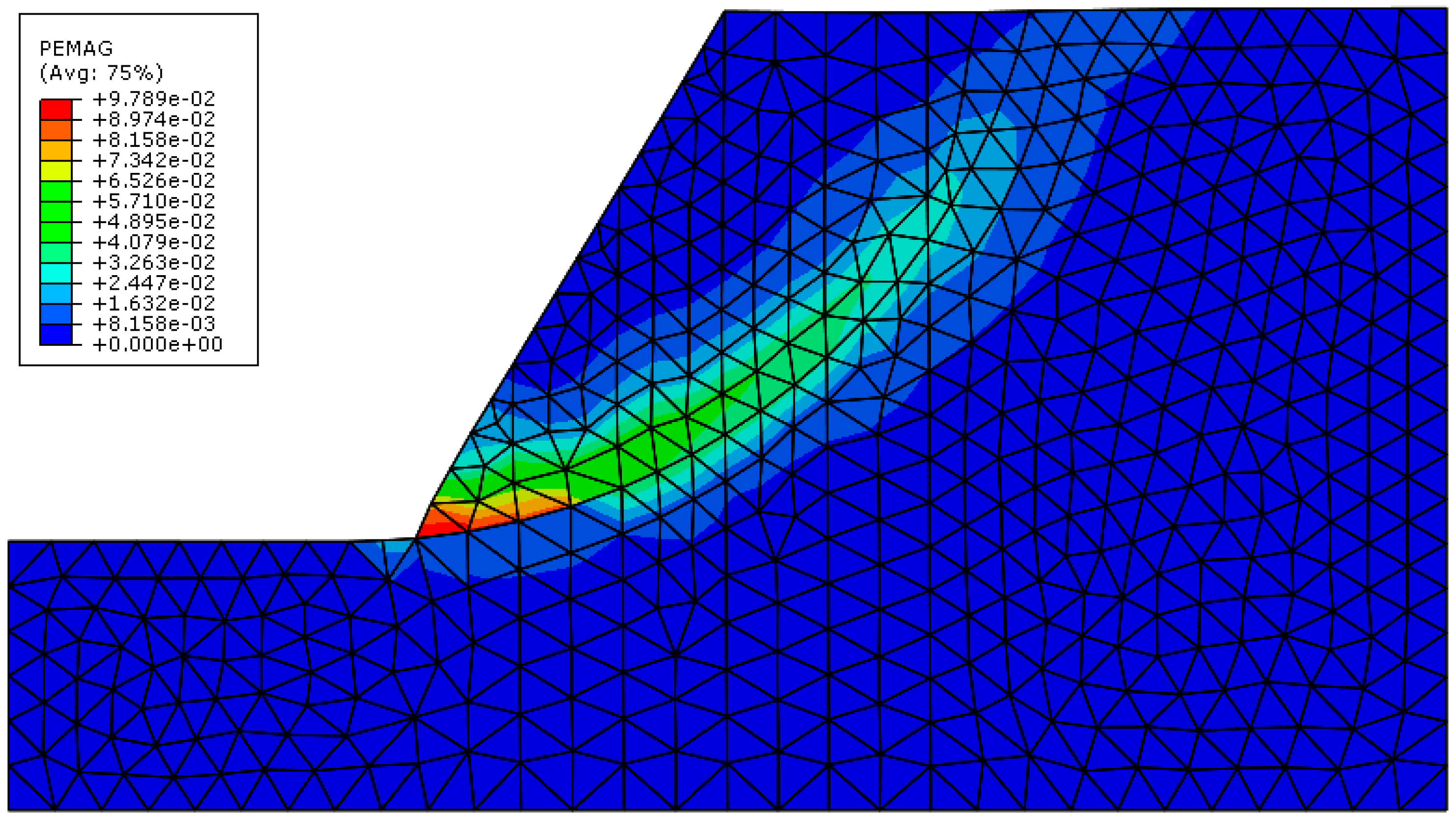
4.3.1. The Failure after Reducing the Strength Parameters
4.3.2. The Safety Factor
4.3.3. The Case Considering Dilatation Softening
5. Discussion
5.1. The Comparison with Strength Reduction Method of Continuum Method
5.2. The Comparison with Strength Reduction Method of DEM
5.3. The Comparsion with Gravity Increase Method of DEM
5.4. The Comparison with Slip Circle Method
5.5. The Softening and the Instability Criterion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bishop, A.W. The use of the slip circle in stability analysis of slope. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Géotechnique 1999, 51, 653–654. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Zheng, Y.R.; Shi, W.M. Analysis on safety factor of slope by strength reduction FEM. Chin. J. Geotech. Eng. 2002, 24, 343–346. (In Chinese) [Google Scholar]
- Li, E.; Zhuang, X.; Zheng, W.; Cai, Y. Effect of graph generation on slope stability analysis based on graph theory. J. Rock Mech. Geotech. Eng. 2014, 6, 380–386. [Google Scholar] [CrossRef]
- Zheng, W.; Zhuang, X.; Tannant, D.D.; Cai, Y.; Nunoo, S. Unified continuum/discontinuum modeling framework for slope stability assessment. Eng. Geol. 2014, 179, 90–101. [Google Scholar] [CrossRef]
- Wang, C.; Tannant, D.D.; Lilly, P.A. Numerical analysis of the stability of heavily jointed rock slopes using PFC2D. Int. J. Rock Mech. Min. Sci. 2003, 40, 415–424. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Li, S.; Yin, Y.P.; Qian, H.T. Study of seismic response of colluvium accumulation slope by particle flow code. Granul. Matter 2010, 12, 483–490. [Google Scholar] [CrossRef]
- Camones, L.A.M.; Vargas, E.D.A.; Figueiredo, R.P.D.; Velloso, R.Q. Application of the discrete element method for modeling of rock crack propagation and coalescence in the step-route failure mechanism. Eng. Geol. 2013, 153, 80–94. [Google Scholar] [CrossRef]
- Huang, D.; Cen, D.; Ma, G.; Huang, R.Q. Step-route failure of rock slopes with intermittent joints. Landslides 2015, 12, 1–16. [Google Scholar] [CrossRef]
- Satake, M. Tensorial form definitions of discrete-mechanical quantities for granular assemblies. Int. J. Solids Struct. 2004, 41, 5775–5791. [Google Scholar] [CrossRef]
- Bagi, K. Microstructural stress tensor of granular assemblies with volume forces. J. Appl. Mech. 1999, 66, 934–936. [Google Scholar] [CrossRef]
- Bagi, K. Analysis of microstructural strain tensor for granular assemblies. Int. J. Solids Struct. 2006, 43, 3166–3184. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 2015, 30, 331–336. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Dondi, G.; Simone, A.; Vignali, V.; Manganelli, G. Numerical and experimental study of granular mixes for asphalts. Powder Technol. 2012, 232, 31–40. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Markauskas, D.; Kačianauskas, R. Compacting of particles for biaxial compression test by the discrete element method. J. Civ. Eng. Manag. 2006, 12, 153–161. [Google Scholar]
- Zhou, J.; Wang, J.Q.; Zeng, Y. Slope safety factor by methods of particle flow code strength reduction and gravity increase. Rock Soil Mech. 2000, 22, 701–704. (In Chinese) [Google Scholar]
- Zhou, B.; Wang, H.B.; Zhao, W.F. Analysis of relationship between particle mesoscopic and macroscopic mechanical parameters of cohesive materials. Rock Soil Mech. 2012, 32, 3171–3178. (In Chinese) [Google Scholar]
- Li, L.; Tang, C.; Zhu, W.; Liang, Z. Numerical analysis of slope stability based on the gravity increase method. Comput. Geotech. 2009, 36, 1246–1258. [Google Scholar] [CrossRef]
- Tang, F.; Zheng, Y.R.; Zhao, S.Y. Discussion on two safety factors for progressive failure of soil slope. Chin. J. Rock Mech. Eng. 2007, 26, 1402–1407. (In Chinese) [Google Scholar]
- Vandamme, J.; Zou, Q.; Ellis, E. Novel particle method for modelling the episodic collapse of soft coastal bluffs. Geomorphology 2012, 138, 295–305. [Google Scholar] [CrossRef]
- Vandamme, J.; Zou, Q. Investigation of slope instability induced by seepage and erosion by a particle method. Comput. Geotech. 2013, 48, 9–20. [Google Scholar] [CrossRef]
- Li, L.; Holt, R.M. Particle scale reservoir mechanics. Oil Gas Sci. Technol. 2002, 57, 525–538. [Google Scholar] [CrossRef]
- Liu, X.L.; Wang, S.J.; Wang, S.Y.; Wang, E.Z. Fluid-driven fractures in granular materials. Bull. Eng. Geol. Environ. 2015, 74, 621–636. [Google Scholar] [CrossRef]
- Huang, H.; Detournay, E. Discrete element modeling of tool-rock interaction II: Rock indentation. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1913–1929. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wong, L.N.Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression: A numerical study based on parallel bonded-particle model approach. Rock Mech. Rock Eng. 2012, 45, 711–737. [Google Scholar] [CrossRef]
- Luo, S.; Zhao, Z.; Peng, H.; Pu, H. The role of fracture surface roughness in macroscopic fluid flow and heat transfer in fractured rocks. Int. J. Rock Mech. Min. Sci. 2016, 87, 29–38. [Google Scholar] [CrossRef]
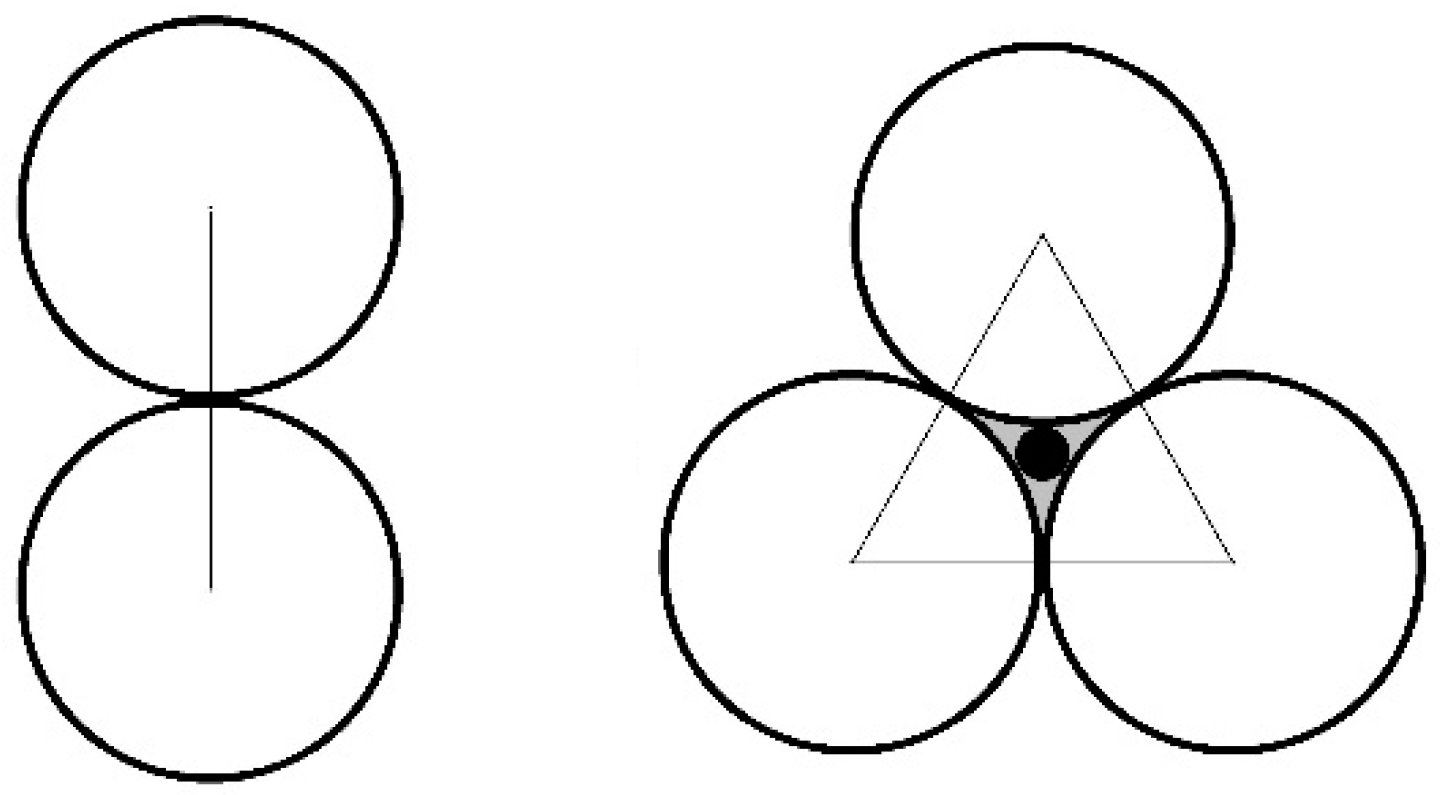
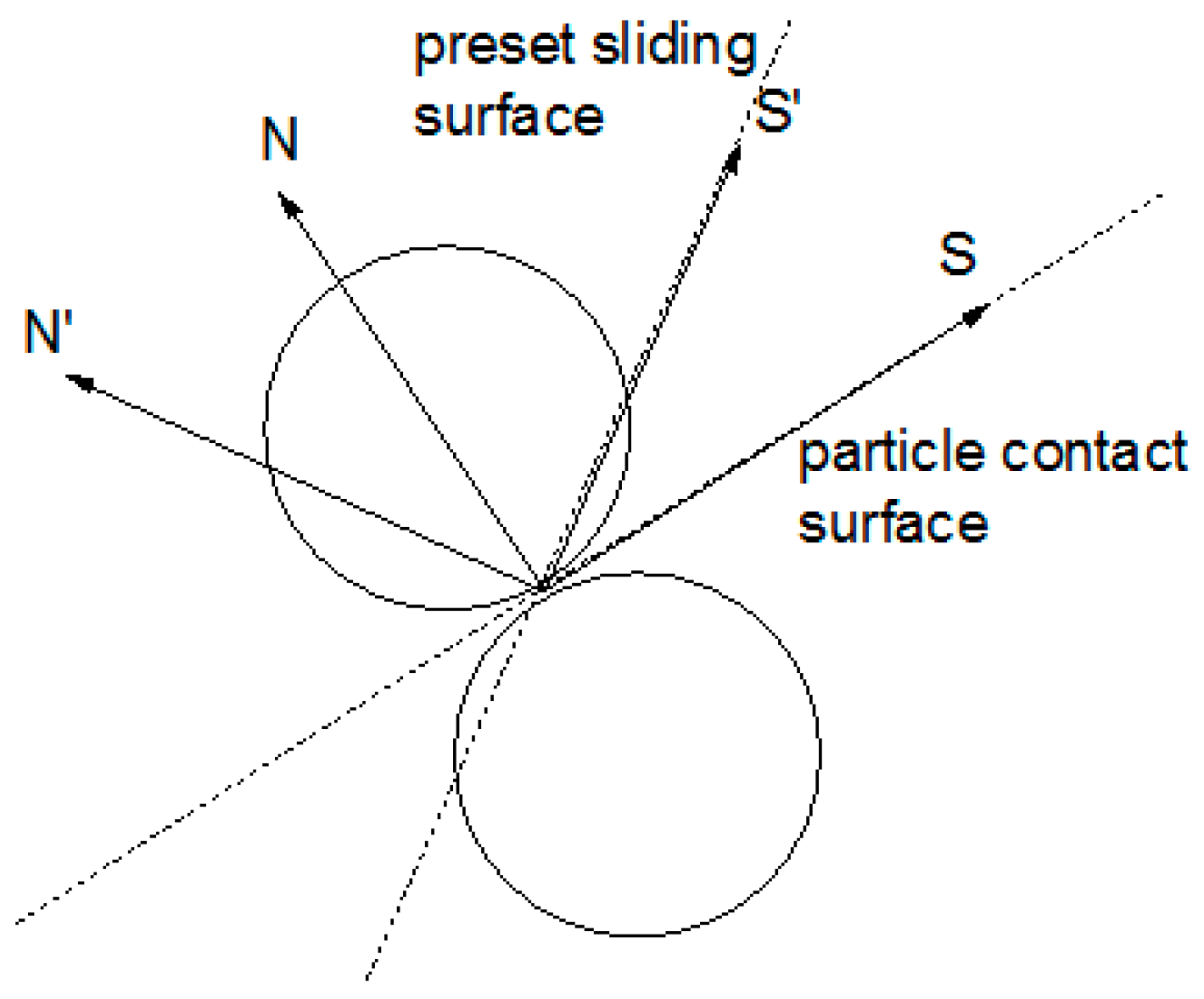
| The shear force in the preset sliding surface | |
| The normal force in the preset sliding surface | |
| The distance from the circle center of the sliding surface to the contact point | |
| The unit vector in the tangential direction of the particle contact surface | |
| The unit vector in the normal direction of the particle contact surface | |
| The unit vector in the tangential direction of preset sliding surface | |
| The unit vector in the normal direction of preset sliding surface | |
| The macro friction |
| Marco Parameters | Values |
|---|---|
| Soil unit weight | 18.5 kN/m3 |
| Cohesion | 20 kPa |
| Internal friction angle | 15° |
| Elastic modulus | 20 MPa |
| Poisson’s ratio | 0.2 |
| Mesoscopic Parameters | Values |
|---|---|
| Particle density | 2170 kg/m3 |
| Particle radius | 0.05 m~0.1 m |
| Normal bond strength | 6 kPa |
| Shear bond strength | 6 kPa |
| Normal contact stiffness | 2.0 × 107 N/m |
| Shear contact stiffness | 0.4 × 107 N/m |
| Friction coefficient of the particle surface | 0.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Liu, X.; Wang, E.; Wang, S. The Stability Analysis Method of the Cohesive Granular Slope on the Basis of Graph Theory. Materials 2017, 10, 240. https://doi.org/10.3390/ma10030240
Guan Y, Liu X, Wang E, Wang S. The Stability Analysis Method of the Cohesive Granular Slope on the Basis of Graph Theory. Materials. 2017; 10(3):240. https://doi.org/10.3390/ma10030240
Chicago/Turabian StyleGuan, Yanpeng, Xiaoli Liu, Enzhi Wang, and Sijing Wang. 2017. "The Stability Analysis Method of the Cohesive Granular Slope on the Basis of Graph Theory" Materials 10, no. 3: 240. https://doi.org/10.3390/ma10030240






