Generalized GW+Boltzmann Approach for the Description of Ultrafast Electron Dynamics in Topological Insulators
Abstract
:1. Introduction
2. Methods
2.1. Theory
2.2. Experiment
3. Results and Discussion
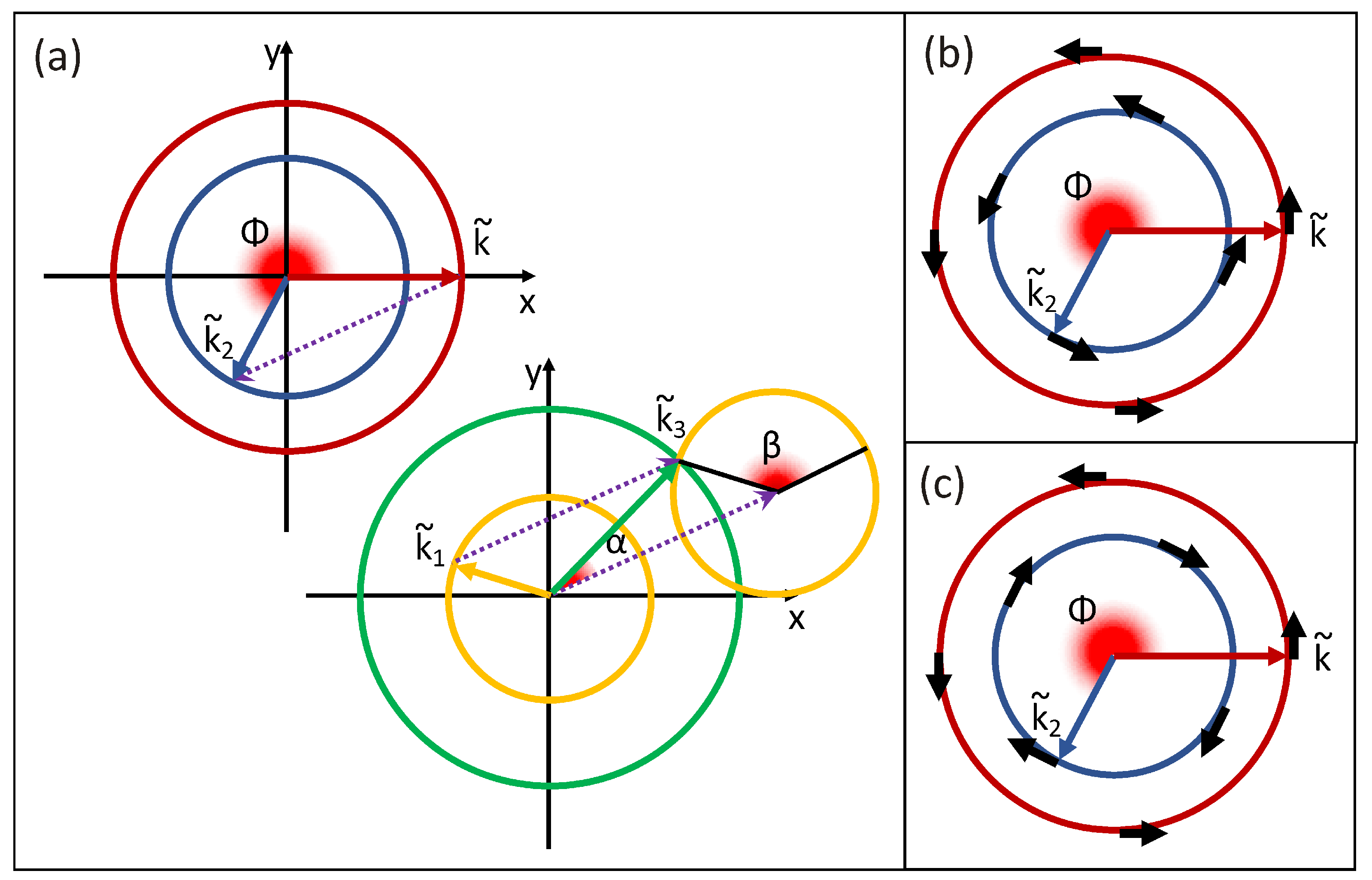
3.1. Generalized Boltzmann Approach for Ultrafast Dynamics in Topological Insulators
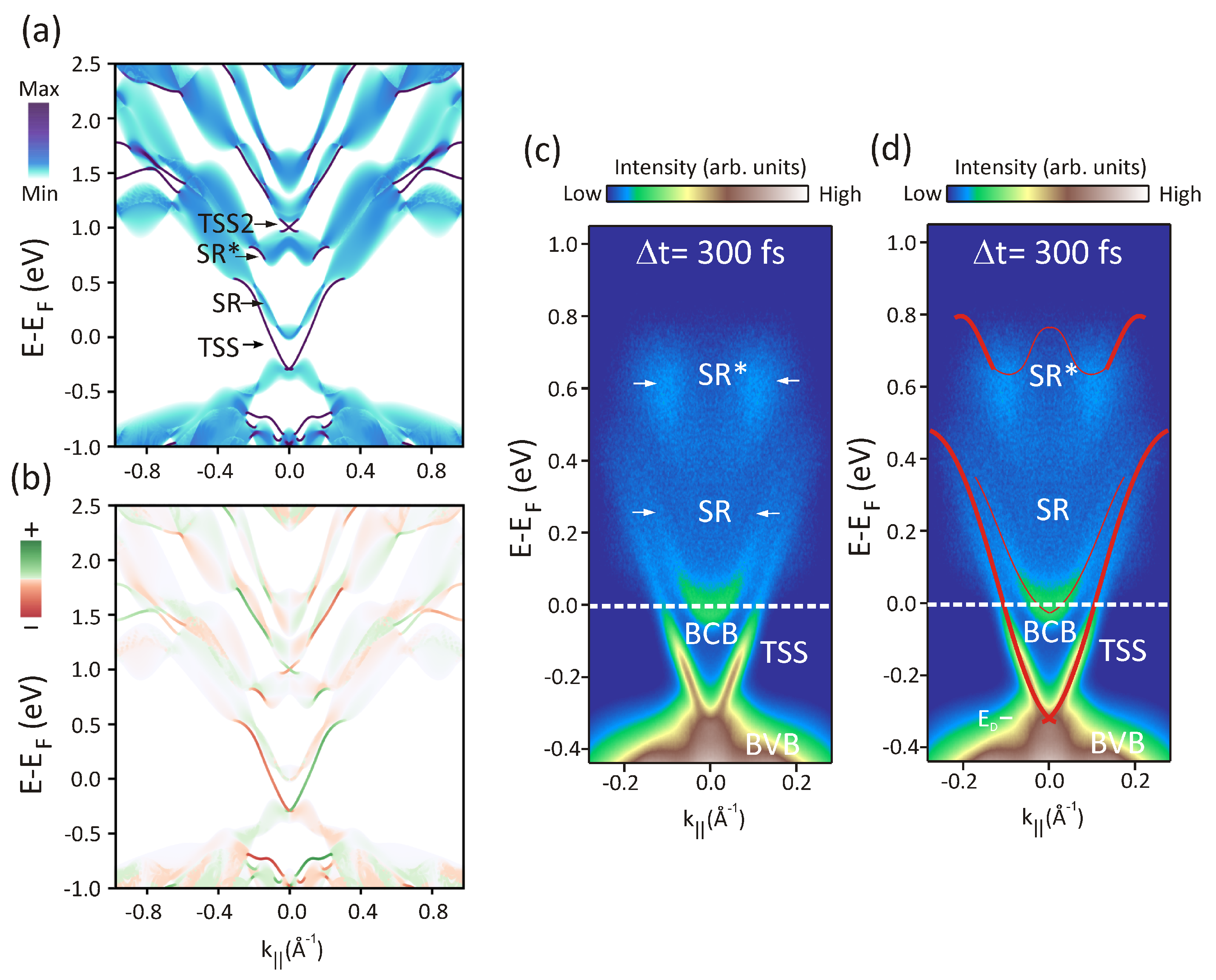
3.2. Calculations in Equilibrium: Application to BiTe
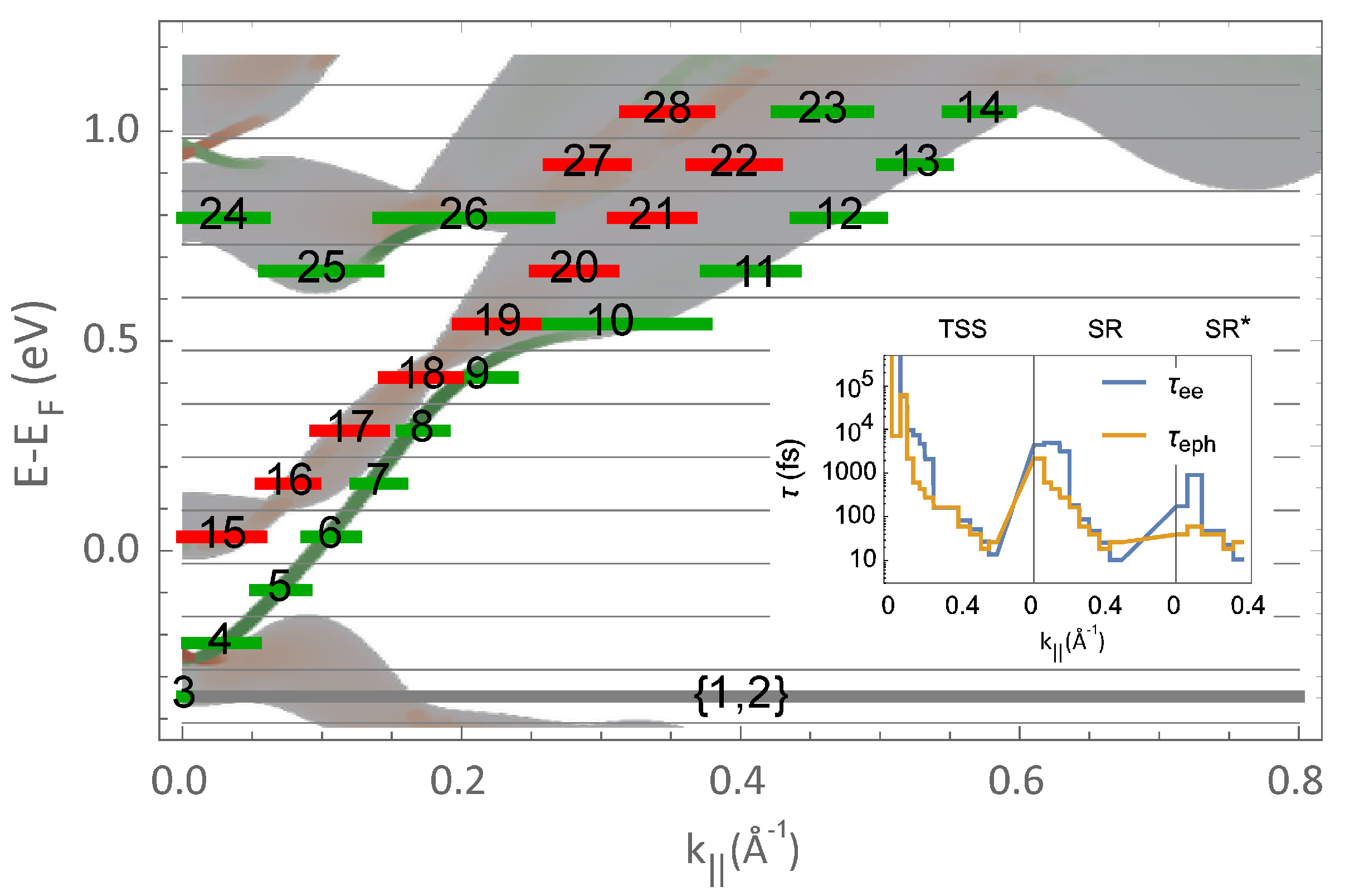
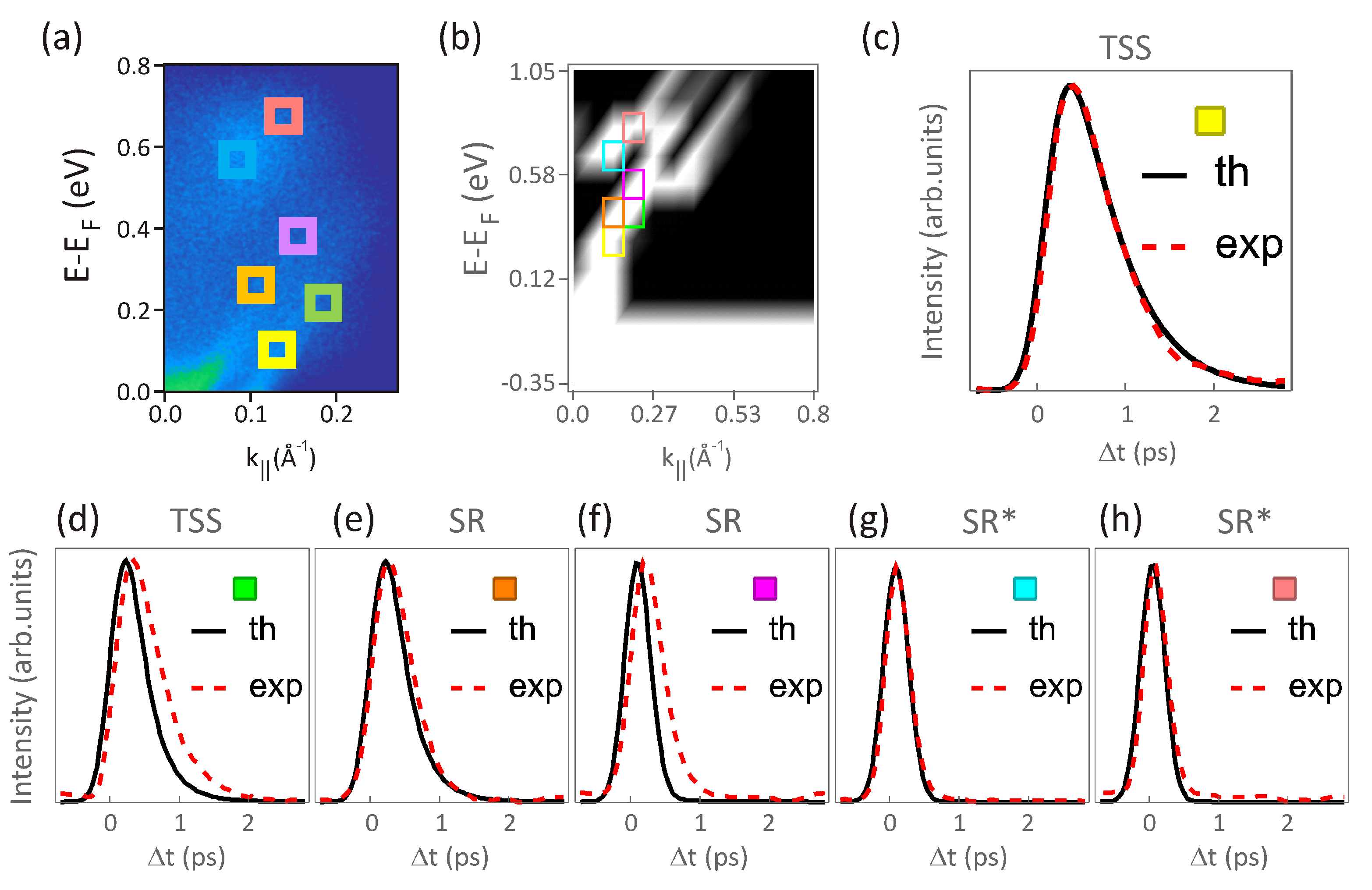
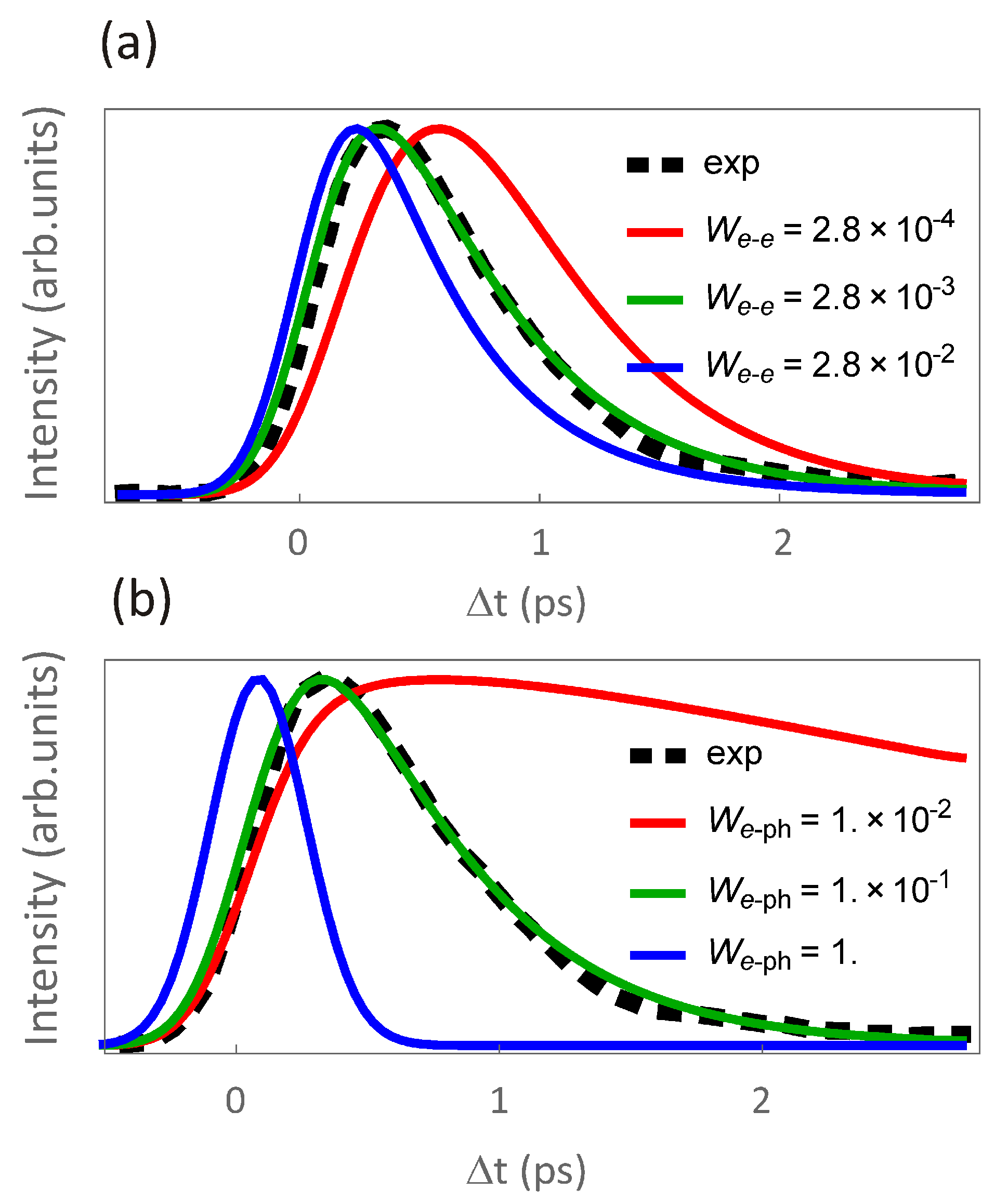
3.3. Parameter-Sensitive +Boltzmann Approach for the Description of Subpicosecond Electron Dynamics in BiTe
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Crane, D.G., Ed.; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Kang, M.; Kim, B.; Ryu, S.H.; Jung, S.W.; Kim, J.; Moreschini, L.; Jozwiak, Ch.; Rotenberg, E.; Bostwick, A.; Kim, K.S. Universal mechanism of band-gap engineering in transition-metal dichalcogenides. Nano Lett. 2017, 17, 1610–1615. [Google Scholar] [CrossRef]
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039–1263. [Google Scholar] [CrossRef]
- Terada, Y.; Yoshida, S.; Okubo, A.; Kanazawa, K.; Xu, M.; Takeuchi, O.; Shigekawa, H. Optical doping: Active control of metal-insulator transition in nanowire. Nano Lett. 2008, 8, 3577–3581. [Google Scholar] [CrossRef]
- Garcia, G.; Buonsanti, R.; Runnerstrom, E.L.; Mendelsberg, R.J.; Llordes, A.; Anders, A.; Richardson, T.J.; Milliron, D.J. Dynamically modulating the surface plasmon resonance of doped semiconductor nanocrystals. Nano Lett. 2011, 11, 4415–4420. [Google Scholar] [CrossRef] [PubMed]
- Crepaldi, A.; Ressel, B.; Cilento, F.; Zacchigna, M.; Grazioli, C.; Berger, H.; Bugnon, P.; Kern, K.; Grioni, M.; Parmigiani, F. Ultrafast photodoping and effective Fermi–Dirac distribution of the Dirac particles in Bi2Se3. Phys. Rev. B 2012, 86, 205133. [Google Scholar] [CrossRef]
- Tiberj, A.; Rubio-Roy, M.; Paillet, M.; Huntzinger, J.-R.; Landois, P.; Mikolasek, M.; Contreras, S.; Sauvajol, J.-L.; Dujardin, E.; Zahab, A.-A. Reversible optical doping of graphene. Sci. Rep. 2013, 3, 2355. [Google Scholar] [CrossRef] [PubMed]
- Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Z2 Topological order and the quantum spin Hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological insulators in three dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Dil, J.H.; Meier, F.; Osterwalder, J.; Patthey, L.; Checkelsky, J.G.; Ong, N.P.; et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 2009, 460, 1101–1105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jozwiak, C.; Chen, Y.L.; Fedorov, A.V.; Analytis, J.G.; Rotundu, C.R.; Schmid, A.K.; Denlinger, J.D.; Chuang, Y.-D.; Lee, D.-H.; Fisher, I.R.; et al. Widespread spin polarization effects in photoemission from topological insulators. Phys. Rev. B 2011, 84, 165113. [Google Scholar] [CrossRef]
- Pan, Z.-H.; Vescovo, E.; Fedorov, A.V.; Gardner, D.; Lee, Y.S.; Chu, S.; Gu, G.D.; Valla, T. Electronic structure of the topological insulator Bi2Se3 using angle-resolved photoemission spectroscopy: Evidence for a nearly full surface spin polarization. Phys. Rev. Lett. 2011, 106, 257004. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Barriga, J.; Varykhalov, A.; Braun, J.; Xu, S.-Y.; Alidoust, N.; Kornilov, O.; Minár, J.; Hummer, K.; Springholz, G.; Bauer, G.; et al. Photoemission of Bi2Se3 with circularly polarized light: Probe of spin Polarization or means for spin manipulation? Phys. Rev. X 2014, 4, 011046. [Google Scholar]
- Pesin, D.; MacDonald, A.H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 2012, 11, 409–416. [Google Scholar] [CrossRef] [PubMed]
- McIver, J.W.; Hsieh, D.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Control over topological insulator photocurrents with light polarization. Nat. Nanotech. 2012, 7, 96–100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kastl, C.; Karnetzky, C.; Karl, H.; Holleitner, A.W. Ultrafast helicity control of surface currents in topological insulators with near-unity fidelity. Nat. Commun. 2015, 6, 6617. [Google Scholar] [CrossRef] [PubMed]
- Dankert, A.; Geus, J.; Kamalakar, M.V.; Charpentier, S.; Dash, S.P. Room temperature electrical detection of spin polarized currents in topological insulators. Nano Lett. 2015, 15, 7976–7981. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, J.; Qi, X.-L.; Zhang, S.-C. Dynamical axion field in topological magnetic insulators. Nat. Phys. 2010, 6, 284–288. [Google Scholar] [CrossRef]
- Sobota, J.A.; Yang, S.; Analytis, J.G.; Chen, Y.L.; Fisher, I.R.; Kirchmann, P.S.; Shen, Z.-X. Ultrafast optical excitation of a persistent surface-state population in the topological insulator Bi2Se3. Phys. Rev. Lett. 2012, 108, 117403. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Hsieh, D.; Sie, E.J.; Steinberg, H.; Gardner, D.R.; Lee, Y.S.; Jarillo-Herrero, P.; Gedik, N. Measurement of intrinsic Dirac fermion cooling on the surface of the topological insulator Bi2Se3 using time-resolved and angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2012, 109, 127401. [Google Scholar] [CrossRef] [PubMed]
- Sobota, J.A.; Yang, S.-L.; Leuenberger, D.; Kemper, A.F.; Analytis, J.G.; Fisher, I.R.; Kirchmann, P.S.; Devereaux, T.P.; Shen, Z.-X. Distinguishing bulk and surface electron–phonon coupling in the topological insulator Bi2Se3 using time-resolved photoemission spectroscopy. Phys. Rev. Lett. 2014, 113, 157401. [Google Scholar] [CrossRef] [PubMed]
- Cacho, C.; Crepaldi, A.; Battiato, M.; Braun, J.; Cilento, F.; Zacchigna, M.; Richter, M.C.; Heckmann, O.; Springate, E.; Liu, Y.; et al. Momentum-resolved spin dynamics of bulk and surface excited states in the topological insulator Bi2Se3. Phys. Rev. Lett. 2015, 114, 097401. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Barriga, J.; Golias, E.; Varykhalov, A.; Braun, J.; Yashina, L.V.; Schumann, R.; Minár, J.; Ebert, H.; Kornilov, O.; Rader, O. Ultrafast spin-polarization control of Dirac fermions in topological insulators. Phys. Rev. B 2016, 93, 155426. [Google Scholar] [CrossRef]
- Golias, E.; Sánchez-Barriga, J. Observation of antiphase coherent phonons in the warped Dirac cone of Bi2Te3. Phys. Rev. B 2016, 94, 161113. [Google Scholar] [CrossRef]
- Neupane, M.; Xu, S.-Y.; Ishida, Y.; Jia, S.; Fregoso, B.M.; Liu, C.; Belopolski, I.; Bian, G.; Alidoust, N.; Durakiewicz, T.; et al. Gigantic surface lifetime of an intrinsic topological insulator. Phys. Rev. Lett. 2015, 115, 116801. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Barriga, J.; Battiato, M.; Golias, E.; Varykhalov, A.; Yashina, L.V.; Kornilov, O.; Rader, O. Laser-induced persistent photovoltage on the surface of a ternary topological insulator at room temperature. Appl. Phys. Lett. 2017, 110, 141605. [Google Scholar] [CrossRef]
- Wang, Y.H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 2013, 342, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Dahlhaus, J.P.; Fregoso, B.M.; Moore, J.E. Magnetization signatures of light-induced quantum Hall edge states. Phys. Rev. Lett. 2015, 114, 246802. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Barriga, J.; Varykhalov, A.; Springholz, G.; Steiner, H.; Kirchschlager, R.; Bauer, G.; Caha, O.; Schierle, E.; Weschke, E.; Ünal, A.A.; et al. Nonmagnetic band gap at the Dirac point of the magnetic topological insulator (Bi1−xMnx)2Se3. Nat. Commun. 2016, 7, 10559. [Google Scholar] [CrossRef] [PubMed]
- Battiato, M.; Held, K. Ultrafast and gigantic spin injection in semiconductors. Phys. Rev. Lett. 2016, 116, 196601. [Google Scholar] [CrossRef] [PubMed]
- Battiato, M.; Maldonado, P.; Oppeneer, P.M. Treating the effect of interface reflections on superdiffusive spin transport in multilayer samples. J. Appl. Phys. 2014, 115, 172611. [Google Scholar] [CrossRef]
- Sánchez-Barriga, J.; Battiato, M.; Krivenkov, M.; Golias, E.; Varykhalov, A.; Romualdi, A.; Yashina, L.V.; Minár, J.; Ebert, H.; Kornilov, O.; et al. Subpicosecond spin dynamics of excited states in the topological insulator Bi2Te3. Phys. Rev. B 2017, 95, 125405. [Google Scholar]
- Battiato, M.; Carva, K.; Oppeneer, P.M. Superdiffusive spin transport as a mechanism of ultrafast demagnetization. Phys. Rev. Lett. 2010, 105, 027203. [Google Scholar] [CrossRef] [PubMed]
- Kioupakis, E.; Tiago, M.L.; Louie, S.G. Quasiparticle electronic structure of bismuth telluride in the GW approximation. Phys. Rev. B 2010, 82, 245203. [Google Scholar]
- Yazyev, O.V.; Kioupakis, E.; Moore, J.E.; Louie, S.G. Quasiparticle effects in the bulk and surface-state bands of Bi2Se3 and Bi2Te3 topological insulators. Phys. Rev. B 2012, 85, 161101. [Google Scholar] [CrossRef]
- Nechaev, I.A.; Chulkov, E.V. Quasiparticle band gap in the topological insulator Bi2Te3. Phys. Rev. B 2013, 88, 165135. [Google Scholar] [CrossRef]
- Michiardi, M.; Aguilera, I.; Bianchi, M.; de Carvalho, V.E.; Ladeira, L.O.; Gomes Teixeira, N.; Avellar Soares, E.; Friedrich, C.; Blügel, S.; Hofmann, P. Bulk band structure of Bi2Te3. Phys. Rev. B 2014, 90, 075105. [Google Scholar] [CrossRef]
- Förster, T.; Krüger, P.; Rohlfing, M. GW calculations for Bi2Te3 and Sb2Te3 thin films: Electronic and topological properties. Phys. Rev. B 2016, 93, 205442. [Google Scholar]
- Friedrich, C.; Blügel, S.; Schindlmayr, A. Efficient implementation of the GW approximation within the all-electron FLAPW method. Phys. Rev. B 2010, 81, 125102. [Google Scholar] [CrossRef]
- FLEUR: The Jülich FLAPW Code Family. Available online: www.flapw.de.
- Li, C.; Freeman, A.J.; Jansen, H.J.F.; Fu, C.L. Magnetic anisotropy in low-dimensional ferromagnetic systems: Fe monolayers on Ag(001), Au(001), and Pd(001) substrates. Phys. Rev. B 1990, 42, 5433–5442. [Google Scholar] [CrossRef]
- Sakuma, R.; Friedrich, C.; Miyake, T.; Blügel, S.; Aryasetiawan, F. GW calculations including spin–orbit coupling: Application to Hg chalcogenides. Phys. Rev. B 2011, 84, 085144. [Google Scholar] [CrossRef]
- Aguilera, I.; Friedrich, C.; Blügel, S. Spin-orbit coupling in quasiparticle studies of topological insulators. Phys. Rev. B 2013, 88, 165136. [Google Scholar] [CrossRef]
- Kotani, T.; van Schilfgaarde, M. All-electron GW approximation with the mixed basis expansion based on the full-potential LMTO method. Solid State Commun. 2002, 121, 461–465. [Google Scholar] [CrossRef]
- Godby, R.W.; Schlüter, M.; Sham, L.J. Self-energy operators and exchange-correlation potentials in semiconductors. Phys. Rev. B 1988, 37, 10159–10175. [Google Scholar] [CrossRef]
- Aryasetiawan, F. Electronic structure calculations. In Advances in Condensed Matter Science; Anisimov, V.I., Ed.; Gordon and Breach: New York, NY, USA, 2000; p. 33. [Google Scholar]
- Aguilera, I.; Friedrich, C.; Bihlmayer, G.; Blügel, S. GW study of topological insulators Bi2Se3, Bi2Te3 and Sb2Te3: Beyond the perturbative one-shot approach. Phys. Rev. B 2013, 88, 045206. [Google Scholar] [CrossRef]
- Friedrich, C.; Schindlmayr, A.; Blügel, S.; Kotani, T. Elimination of the linearization error in GW calculations based on the linearized augmented-plane-wave method. Phys. Rev. B 2006, 74, 045104. [Google Scholar] [CrossRef]
- Friedrich, C.; Müller, M.C.; Blügel, S. Band convergence and linearization error correction of all-electron GW calculations: The extreme case of zinc oxide. Phys. Rev. B 2011, 83, 081101. [Google Scholar] [CrossRef]
- Wyckoff, R.W.G. Structures of complex binary compounds RnXm. In Crystal Structures; J. Wiley and Sons: New York, NY, USA, 1964; Volume 2. [Google Scholar]
- Mostofi, A.A.; Yates, J.R.; Lee, Y.-S.; Souza, I.; Vanderbilt, D.; Marzari, N. Wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2008, 175, 685–699. [Google Scholar] [CrossRef]
- Bahramy, M.S.; King, P.D.C.; de la Torre, A.; Chang, J.; Shi, M.; Patthey, L.; Balakrishnan, G.; Hofmann, P.; Arita, R.; Nagaosa, N.; et al. Emergent quantum confinement at topological insulator surfaces. Nat. Commun. 2012, 3, 1159. [Google Scholar] [CrossRef] [PubMed]
- Del Fatti, N.; Voisin, C.; Achermann, M.; Tzortzakis, S.; Christofilos, D.; Vallée, F. Nonequilibrium electron dynamics in noble metals. Phys. Rev. B 2000, 61, 16956. [Google Scholar] [CrossRef]
- Rethfeld, B.; Kaiser, A.; Vicanek, M.; Simon, G. Ultrafast dynamics of nonequilibrium electrons in metals under femtosecond laser irradiation. Phys. Rev. B 2002, 65, 214303. [Google Scholar] [CrossRef]
- Mueller, B.Y.; Rethfeld, B. Relaxation dynamics in laser-excited metals under nonequilibrium conditions. Phys. Rev. B 2013, 87, 035139. [Google Scholar] [CrossRef]
- Shtanov, V.I.; Yashina, L.V. On the Bridgman growth of lead-tin selenide crystals with uniform tin distribution. J. Cryst. Growth 2009, 311, 3257–3264. [Google Scholar] [CrossRef]
- Jozwiak, C.; Sobota, J.A.; Gotlieb, K.; Kemper, A.F.; Rotundu, C.R.; Birgeneau, R.J.; Hussain, Z.; Lee, D.-H.; Shen, Z.-X.; Lanzara, A. Spin-polarized surface resonances accompanying topological surface state formation. Nat. Commun. 2016, 7, 13143. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Barriga, J.; Vergniory, M.G.; Evtushinsky, D.; Aguilera, I.; Varykhalov, A.; Blügel, S.; Rader, O. Surface Fermi arc connectivity in the type-II Weyl semimetal candidate WTe2. Phys. Rev. B 2016, 94, 161401. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battiato, M.; Aguilera, I.; Sánchez-Barriga, J. Generalized GW+Boltzmann Approach for the Description of Ultrafast Electron Dynamics in Topological Insulators. Materials 2017, 10, 810. https://doi.org/10.3390/ma10070810
Battiato M, Aguilera I, Sánchez-Barriga J. Generalized GW+Boltzmann Approach for the Description of Ultrafast Electron Dynamics in Topological Insulators. Materials. 2017; 10(7):810. https://doi.org/10.3390/ma10070810
Chicago/Turabian StyleBattiato, Marco, Irene Aguilera, and Jaime Sánchez-Barriga. 2017. "Generalized GW+Boltzmann Approach for the Description of Ultrafast Electron Dynamics in Topological Insulators" Materials 10, no. 7: 810. https://doi.org/10.3390/ma10070810




