On Critical States, Rupture States and Interlocking Strength of Granular Materials
Abstract
:1. Introduction
2. Results
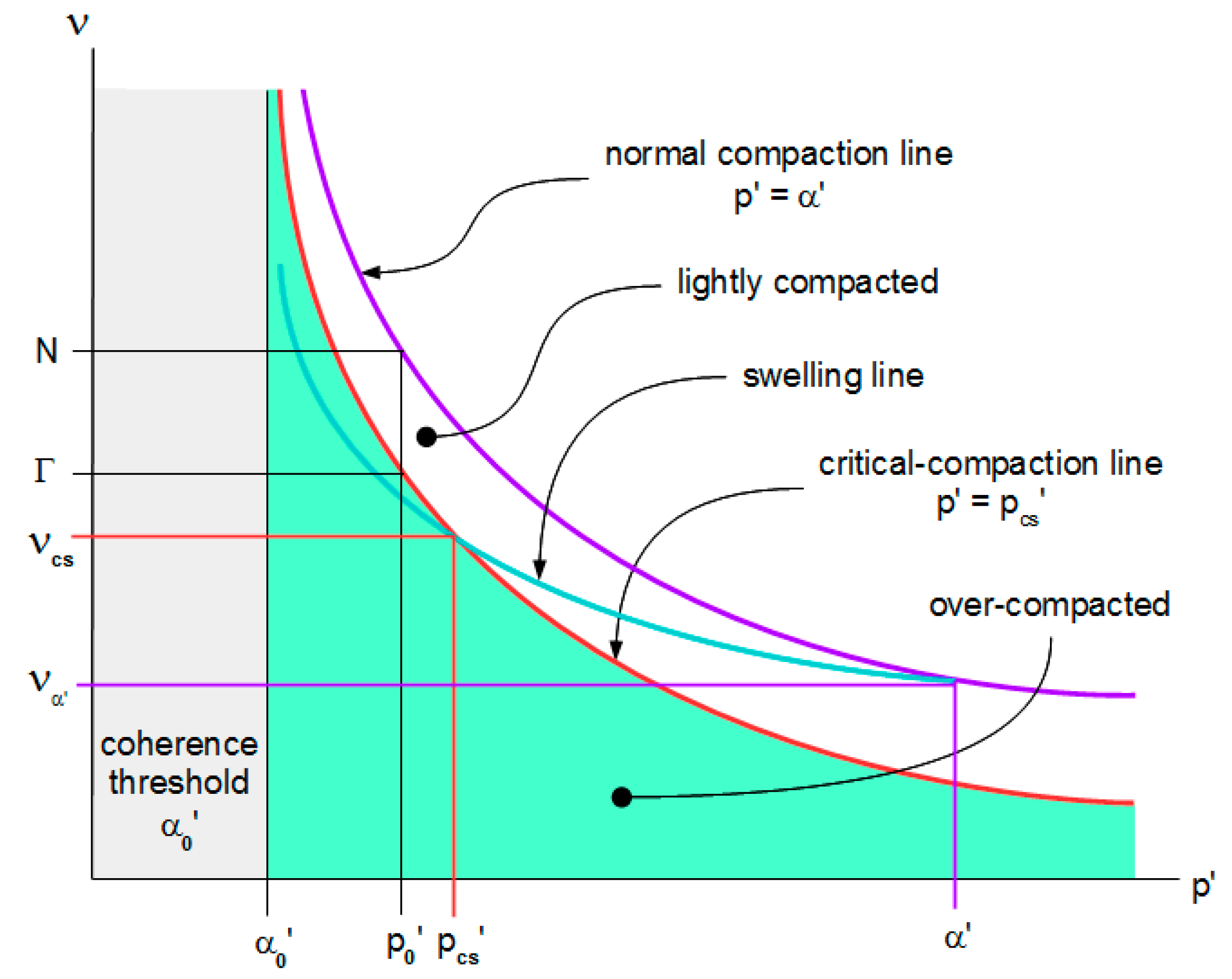
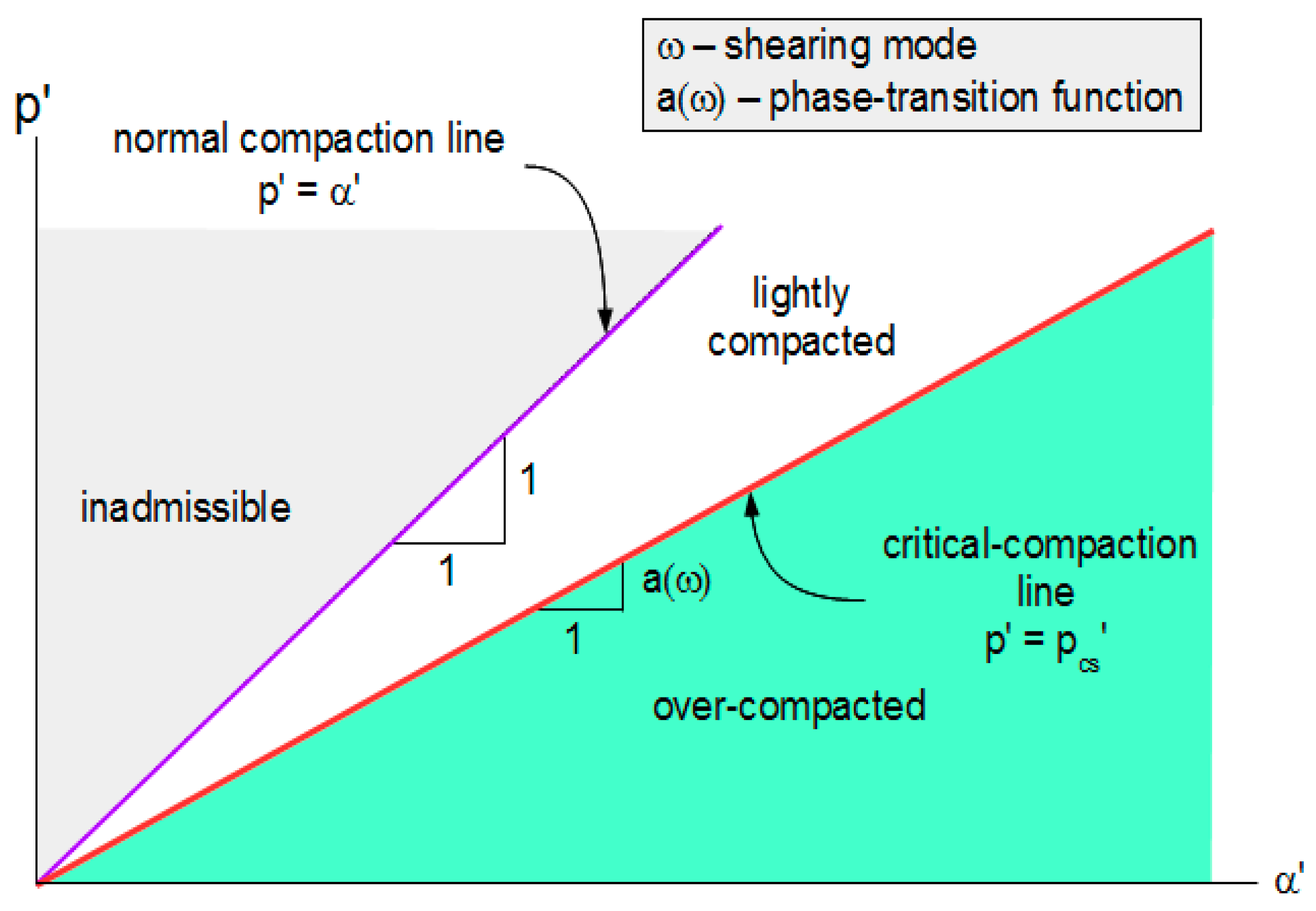
2.1. Critical-Compaction Surface
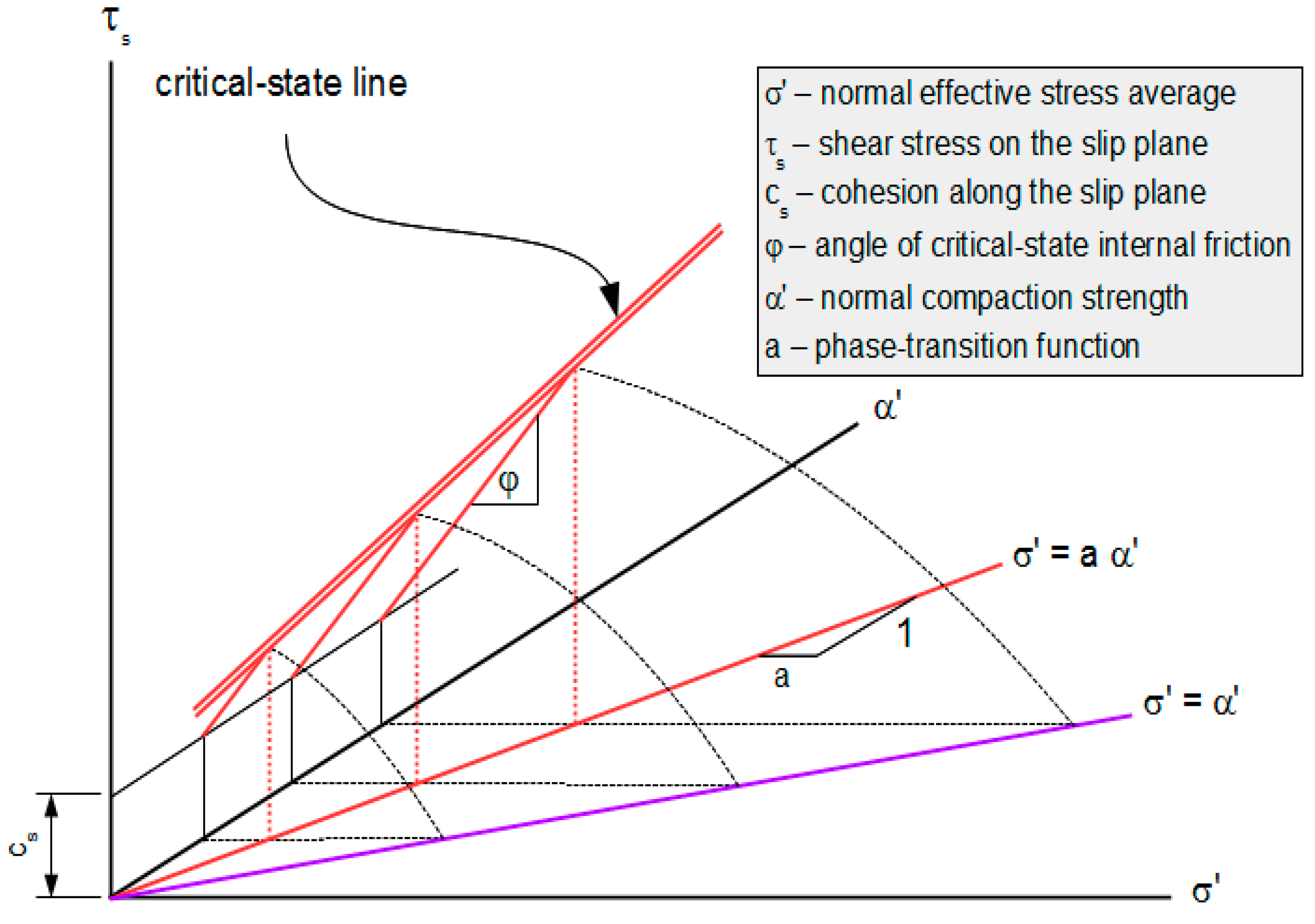
2.2. Critical-State Surface
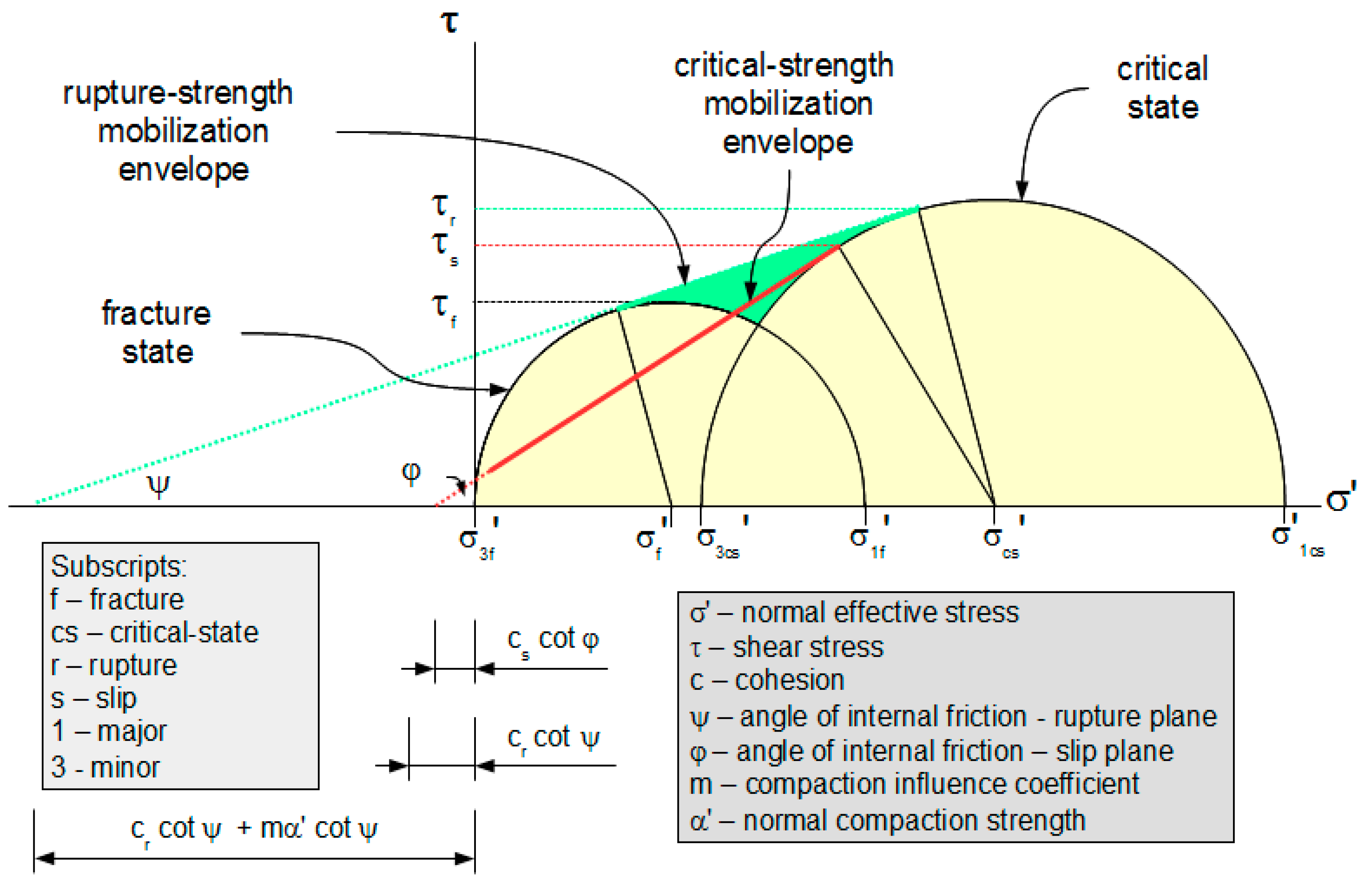
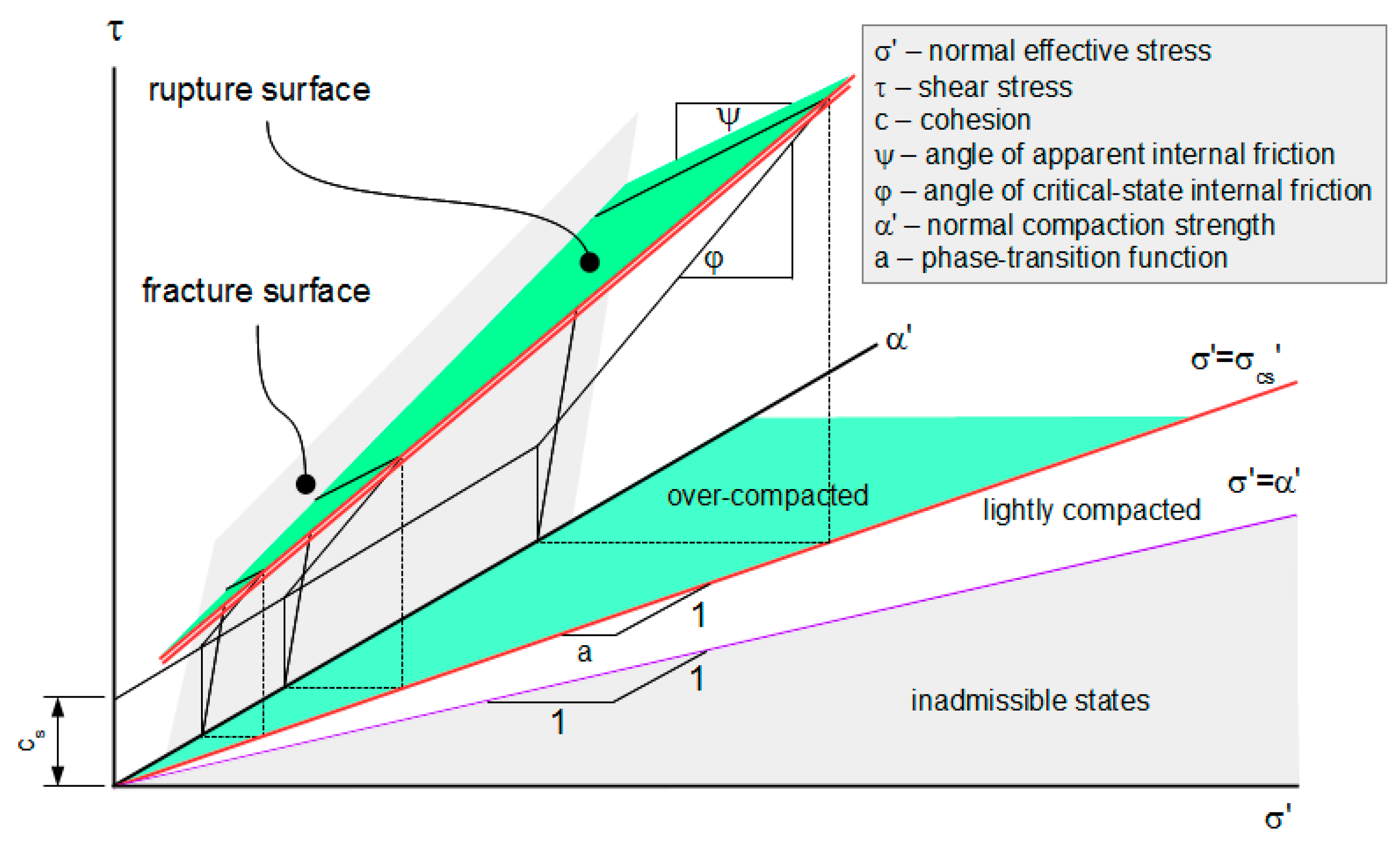
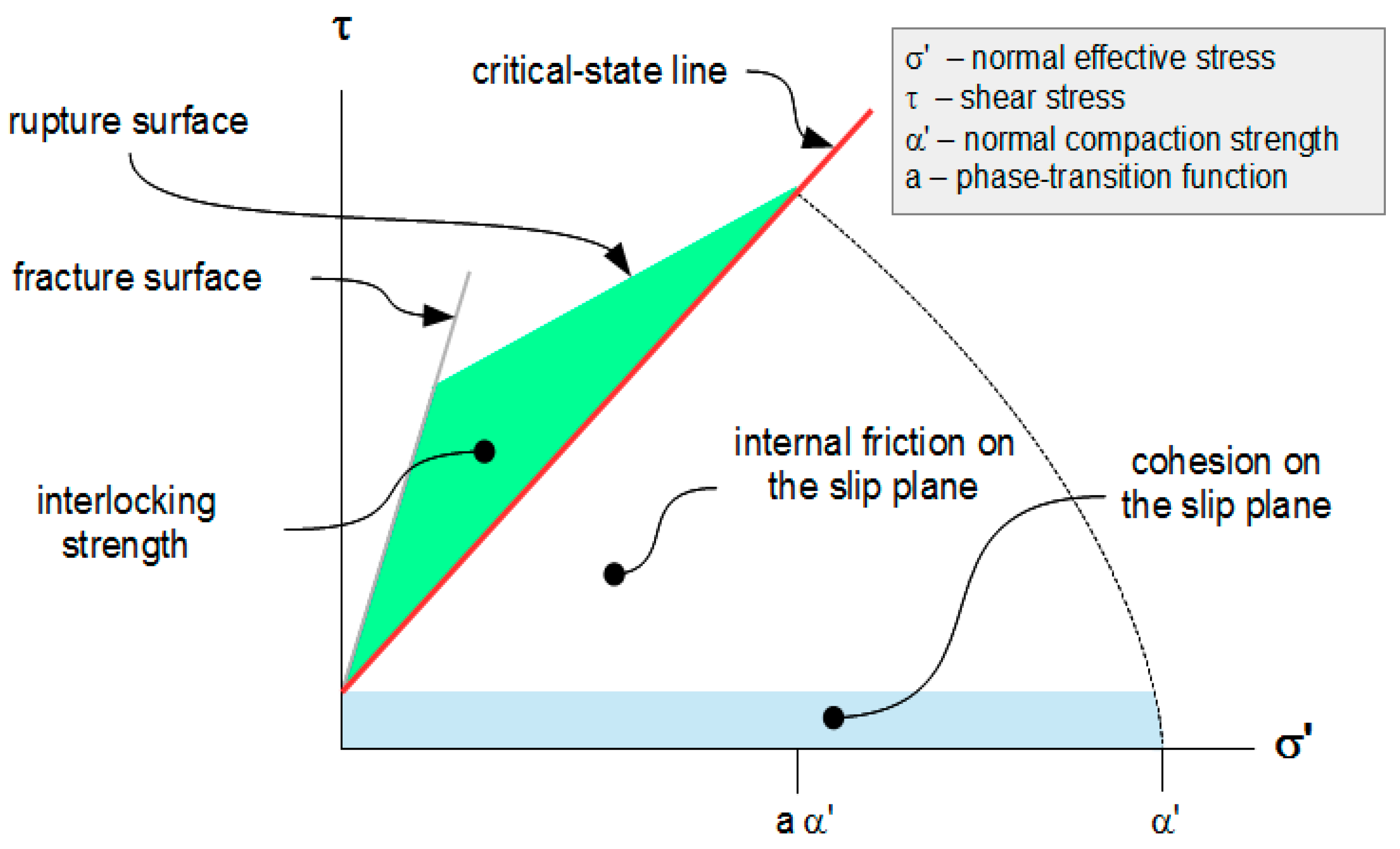
2.3. Rupture Surface
− [m − a(ω)·g(ω)·χ]cos ψ·α0’ − g(ω)·χ·cos ψ·α0’,
for pf’ ≤ p’ ≤ pcs’.
3. Discussion
3.1. Strength
3.2. Dilation
- Define interlocking in terms of the difference between the critical mean-normal effective stress and the mean-normal effective stress in place of Taylor’s ratio.
- Distinguish any virtual cohesion from the contributions due to over-compaction.
3.3. Comparison
4. Materials and Methods
5. Conclusions
Acknowledgments
Conflicts of Interest
Glossary/Nomenclature/Abbreviation
| Parameters | |
| α’ | normal compaction strength, maximum mean-normal effective stress |
| α0’ | minimum mean-normal effective stress for well-defined flexibilities |
| ν | specific volume |
| νcs | specific volume at critical compaction |
| σ1’ | major principal effective stress |
| σ2’ | intermediate principal effective stress |
| σ3’ | minor principal effective stress |
| σ’ | average of the major and minor principal effective stresses |
| σf’ | σ’ at the intersection of the fracture and rupture surfaces |
| σnr’ | normal effective stress component on the rupture plane |
| σns’ | normal effective stress component on the slip plane |
| σcs’ | average of major and minor principal effective stresses at critical state |
| τr | shear strength component along the rupture plane |
| τs | shear strength component along the slip plane |
| ω | shearing mode |
| p’ | mean-normal effective stress |
| p0’ | reference mean-normal effective stress |
| pf’ | p’ at the intersection of the fracture and rupture surfaces |
| pcs’ | critical-compaction strength—p’ at critical state |
| r | radius of Mohr’s circle of stress |
| Material Properties | |
| β | index of ln-ln normal compaction line in ν-p’ space |
| Γ(ω) | specific volume at p0’ on the continuous-flow line for ω |
| Γ | specific volume at p0’ on the continuous-flow line—a material constant |
| ξ | index of ln-ln swelling line in ν-p’ space |
| κ | index of semi-ln swelling line in ν-p’ space |
| λ | index of semi-ln normal compaction line in ν-p’ space |
| φ | angle of internal friction on the slip plane |
| ψ | angle of internal friction on the rupture plane |
| χ | coefficient of interlocking strength |
| a(ω) | phase-transition function |
| cr | virtual cohesion along the rupture plane |
| cs | virtual cohesion along the slip plane |
| f(p’,ν) | apparent flexibility—slope of the normal compaction line |
| fc(p’,ν) | centric flexibility—slope of the swelling line |
| g(ω) | intermediate principal effective stress factor |
| m | coefficient of compaction influence |
| M | coefficient of internal friction on the slip plane—Cambridge research program |
| N | specific volume at p0’ on the normal compaction line |
| P | coefficient of interlocking—Cambridge research program |
| R | coefficient of internal friction on the rupture plane—Cambridge research program |
| Χ | coefficient of interlocking strength—Cambridge research program |
| Terzaghi’s Implementation—equivalent terms are shown in parentheses | |
| α | normal compaction strength |
| α0 | coherence threshold for well-defined flexibilities |
| σ | normal stress under normally compacted conditions (σns) |
| σ’ | normal stress under over-compacted conditions (σnr) |
| σ1 | major principal stress |
| σ3 | minor principal stress |
| σcs | average of major and minor principal stresses at critical state |
| τ | shear strength under normally compacted conditions (τs) |
| τ’ | shear strength under over-compacted conditions (τr) |
| φ | angle of internal friction under normally compacted conditions (φ) |
| φ’ | angle of internal friction under over-compacted conditions (‘true’) (ψ) |
| φf | angle of internal friction in Terzaghi’s Equation (5.3) [5] |
| c | cohesion under normally compacted conditions (cs) |
| c’ | effective cohesion under over-compacted conditions (‘true’) (cr + m·(α − α0)) |
| c0’ | virtual cohesion under over-compacted conditions (cr) |
| N | gradient of the effective cohesion relation in Terzaghi’s Equation (5.3) [5] |
| s | shear strength in Terzaghi’s implementation |
Appendix A. Terzaghi’s Theory of Strength
= c0’·cos φ’ + [m·cos φ’ − a(ω)·g(ω)·(sin φ − sin φ’)]·α
− [m·cos φ’ − a(ω)·g(ω)·(sin φ − sin φ’)]·α0
− g(ω)·(sin φ − sin φ’)·α0.
+ g(ω)·(sin φ − sin φ’)·α0.
+ a(ω)·g(ω)·(sin φ − sin φ’)·(α − α0)·cos φ’.
cos φ·cos φ’.
References
- Yu, M. Advances in strength theories for materials under complex stress state in the 20th century. Appl. Mech. Rev. 2002, 55, 169–218. [Google Scholar] [CrossRef]
- Coulomb, C.A. Essai sur une Application des Règles de Maximis et Minimis à Quelques Problèmes de Statique, Relatifs à l’Architecture; Mémoirs de Mathématique et de Physique, présentés à l’Académie Royale des Sciences par divers Savans et lûs dans ses Assemblées: Paris, France, 1776; Volume 7, pp. 343–382. (In French) [Google Scholar]
- Heyman, J. Coulomb’s Memoir on Statics: An Essay in the History of Civil Engineering; Cambridge University Press: London, UK, 1972; Imperial College Press: London, UK, 1997; p. 132. [Google Scholar]
- Mohr, O. Welche Umstande bedingen die Elastizitatsgrenze und den Bruch eines Materials. Z. Ver. Deutsch. Ing. Band 1900, 44, 1524–1530. [Google Scholar]
- Terzaghi, K. Stress Conditions for Failure in Soils. In Theoretical Soil Mechanics; John Wiley and Sons: New York, NY, USA, 1943; pp. 7–11. [Google Scholar]
- Reynolds, O. On the dilatancy of media composed of rigid particles in contact. Philos. Mag. 1885, 20, 469–481. [Google Scholar] [CrossRef]
- Taylor, D.W. The Fundamentals of Soil Mechanics; John Wiley and Sons: New York, NY, USA, 1948. [Google Scholar]
- Roscoe, K.H.; Schofield, A.N.; Wroth, C.P. On the Yielding of Soils. Geotechnique 1958, 8, 22–53. [Google Scholar] [CrossRef]
- Jenike, A.W.; Shield, R.T. On the plastic flow of Coulomb solids beyond original failure. ASME J. Appl. Mech. 1959, 27, 599–602. [Google Scholar]
- Rowe, P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. A 1962, 269, 500–527. [Google Scholar] [CrossRef]
- Schofield, A.N.; Wroth, C.P. Critical State Soil Mechanics; McGraw-Hill: Maidenhead, UK, 1968. [Google Scholar]
- Parry, R.H.G. Triaxial compression and extension tests on remoulded saturated clay. Geotechnique 1960, 10, 166–180. [Google Scholar] [CrossRef]
- Jenike, A.W. Personal Communication with the Author; Jenike and Johanson, Inc.: North Billerica, MA, USA, 1988. [Google Scholar]
- Prager, W. Recent Developments in the Mathematical Theory of Plasticity. J. Appl. Phys. 1949, 20, 235–241. [Google Scholar] [CrossRef]
- Collins, I.F.; Muhunthan, B.; Qu, B. Thermomechanical state parameter models for sands. Geotechnique 2010, 60, 611–622. [Google Scholar] [CrossRef]
- Schofield, A.N. A note on Taylor’s interlocking and Terzaghi’s “true cohesion” error. In Geotechnical News; Bi-Tech Publishers, Ltd.: Richmond, BC, Canada, 1999; Volume 17. [Google Scholar]
- Schofield, A.N. Interlocking, and peak and design strengths. Geotechnique 2006, 56, 357–358. [Google Scholar] [CrossRef]
- Burland, J.B.; Dean, E.T.R.; Gudehus, G.; Muhunthan, B.; Collins, I. F. Discussion: Interlocking, and peak and design strengths. Geotechnique 2008, 58, 527–532. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis for limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Jenike, A.W. A theory of flow of particulate solids in converging and diverging channels based on a conical yield function. Powder Technol. 1987, 50, 229–236. [Google Scholar] [CrossRef]
- Yin, Z.; Chang, C.S. Non-uniqueness of critical state line in compression and extension conditions. Int. J. Numer. Anal. Meth. Geomech. 2009, 33, 1315–1338. [Google Scholar] [CrossRef]
- Kanatani, K.-I. Mechanical foundation of the plastic deformation of granular materials. In Proceedings of the IUTAM Conference on Deformation and Failure of Granular materials, Delft, The Netherlands, 31 August–3 September 1982; pp. 119–127. [Google Scholar]
- Goddard, J.D.; Bashir, Y.M. On Reynolds dilatancy. In Recent Developments in Structured Continua; DeKee, D., Kaloni, P.N., Eds.; Longman: White Plains, NY, USA, 1990; Volume 2, pp. 23–35. [Google Scholar]
- Houlsby, G.T. Interpretation of dilation as a kinematic constraint. In Modern Approaches to Plasticity; Kolymbas, D., Ed.; Elsevier: New York, NY, USA, 1993; pp. 119–138. [Google Scholar]
- Dafalias, Y.F. An anisotropic critical state clay plasticity model. Mech. Res. Commun. 1986, 13, 341–347. [Google Scholar] [CrossRef]
- Collins, I.F.; Muhunthan, B.; Tai, A.T.T.; Pender, M.J. The concept of a ‘Reynolds-Taylor state’ and the mechanics of sands. Geotechnique 2007, 57, 437–447. [Google Scholar] [CrossRef]
- Wroth, C.P.; Bassett, R.H. A stress-strain relationship for the shearing behavior of a sand. Geotechnique 1965, 15, 32–56. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M.G. A state parameter for sands. Geotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
- Poole, C.P., Jr. (Ed.) Encyclopedia of Condensed Matter Physics; Elsevier: Amsterdam, The Netherlands, 2004; p. 229. [Google Scholar]
- Schofield, A.N. Disturbed Soil Properties and Geotechnical Design; Thomas Telford Publishing: London, UK, 2005. [Google Scholar]
- Noll, W. A mathematical theory of the mechanical behavior of continuous media. Arch. Ration. Mech. Anal. 1958, 2, 197–226. [Google Scholar] [CrossRef]
- Truesdell, C. Constitutive Relations. In A First Course in Rational Continuum Mechanics; Academic Press, Inc. (London) Ltd.: London, UK, 1977; pp. 160–162. [Google Scholar]



| Feature | Present Theory | Jenike–Shield | Schofield | Collins et al. |
|---|---|---|---|---|
| Non-teleological | Yes | Yes | No | No |
| Reference stress | α’ | α’ = pcs’ = σcs’ | pcs’ | pcs’ |
| Shearing mode | Yes | Yes | No | No |
| Cohesion | Yes | Yes | No | No |
| Range of σ2’ | σ 3’ ≤ σ2’ ≤ σ1’ | σ2’ = (σ1’ + σ3’)/2 | σ2’ = σ3’ | σ2’ = σ3’ |
| Locus of critical states is a | Surface | Surface | Line | Line |
| Strain rates at critical state | Uncoupled | Uncoupled | Coupled | Coupled |
| Allows rate dependence | Yes | Yes | No | No |
| Elasto-plastic, rigid-plastic | Elasto-plastic | Rigid-plastic | Elasto-plastic | Elasto-plastic |
| Parallel flow | Yes | Yes | Yes | Yes |
| Non-parallel flow | Yes | Yes | No | No |
| New state parameter | α’ | α’ | ? | ξ |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szalwinski, C.M. On Critical States, Rupture States and Interlocking Strength of Granular Materials. Materials 2017, 10, 865. https://doi.org/10.3390/ma10080865
Szalwinski CM. On Critical States, Rupture States and Interlocking Strength of Granular Materials. Materials. 2017; 10(8):865. https://doi.org/10.3390/ma10080865
Chicago/Turabian StyleSzalwinski, Chris M. 2017. "On Critical States, Rupture States and Interlocking Strength of Granular Materials" Materials 10, no. 8: 865. https://doi.org/10.3390/ma10080865





