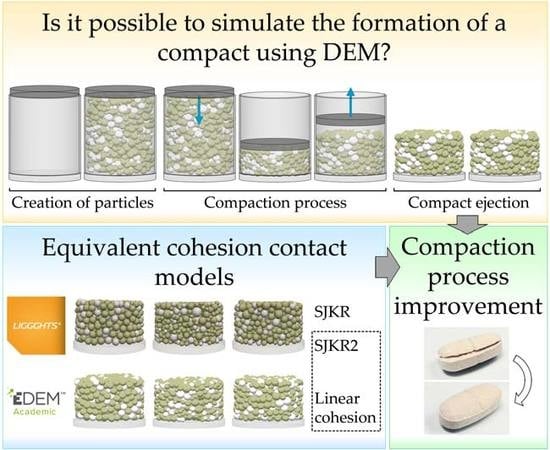
Comparison of Cohesive Models in EDEM and LIGGGHTS for Simulating Powder Compaction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Discrete Element Method (DEM)
2.2. DEM Simulations
2.3. Methodology
3. Results and Discussion
3.1. Effect of the Timestep
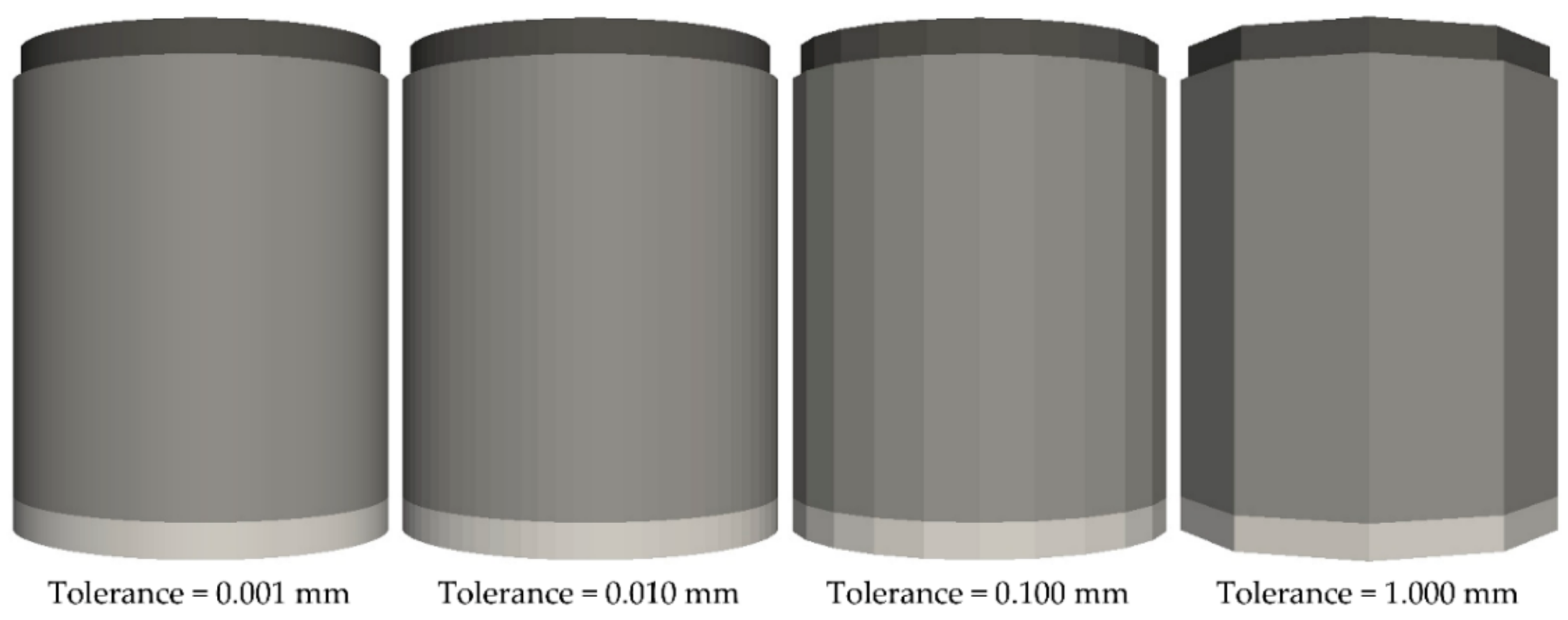
3.2. Effect of Conversion Tolerance
3.3. Effect of Punch Speed
3.4. Effect of the PSD
3.5. Comparison between the Contact Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cronin, K.; Ring, D.; Sheehan, L.; Foulon, A. Probabilistic analysis of weight variability in tablets & capsules arising from the filling of a cavity with powder of a poly-dispersed size. Powder Technol. 2015, 270, 287–295. [Google Scholar] [CrossRef]
- Furukawa, R.; Shiosaka, Y.; Kadota, K.; Takagaki, K.; Noguchi, T.; Shimosaka, A.; Shirakawa, Y. Size-induced segregation during pharmaceutical particle die filling assessed by response surface methodology using discrete element method. J. Drug Deliv. Sci. Technol. 2016, 35, 284–293. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; Curtis, J.S.; Wassgren, C.R.; Kong, A.; Narayan, P.J.; Hancock, B.C. Granular segregation in discharging cylindrical hoppers: A discrete element and experimental study. Chem. Eng. Sci. 2007, 62, 6423–6439. [Google Scholar] [CrossRef]
- Yu, Y.; Saxén, H. Experimental and DEM study of segregation of ternary size particles in a blast furnace top bunker model. Chem. Eng. Sci. 2010, 65, 5237–5250. [Google Scholar] [CrossRef]
- Yang, S.C. Density effect on mixing and segregation processes in a vibrated binary granular mixture. Powder Technol. 2006, 164, 65–74. [Google Scholar] [CrossRef]
- Jiang, M.; Zhao, Y.; Liu, G.; Zheng, J. Enhancing mixing of particles by baffles in a rotating drum mixer. Particuology 2011, 9, 270–278. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, Y.; Bao, C.; Hou, Q.; Yu, A. Optimisation of a circularly vibrating screen based on DEM simulation and Taguchi orthogonal experimental design. Powder Technol. 2017, 310, 307–317. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, Y.; Bao, C.; Hou, Q.; Yu, A. Laboratory-scale validation of a DEM model of screening processes with circular vibration. Powder Technol. 2016, 303, 269–277. [Google Scholar] [CrossRef]
- Barbabela e Silva, B.; da Cunha, E.R.; de Carvalho, R.M.; Tavares, L.M. Modeling and simulation of green iron ore pellet classification in a single deck roller screen using the discrete element method. Powder Technol. 2018, 332, 359–370. [Google Scholar] [CrossRef]
- Ghodki, B.M.; Charith Kumar, K.; Goswami, T.K. Modeling breakage and motion of black pepper seeds in cryogenic mill. Adv. Powder Technol. 2018, 29, 1055–1071. [Google Scholar] [CrossRef]
- Metzger, M.J.; Glasser, B.J. Simulation of the breakage of bonded agglomerates in a ball mill. Powder Technol. 2013, 237, 286–302. [Google Scholar] [CrossRef]
- Obermayr, M.; Dressler, K.; Vrettos, C.; Eberhard, P. A bonded-particle model for cemented sand. Comput. Geotech. 2013, 49, 299–313. [Google Scholar] [CrossRef]
- Manso, J.; Marcelino, J.; Caldeira, L. Crushing and oedometer compression of rockfill using DEM. Comput. Geotech. 2018, 101, 11–22. [Google Scholar] [CrossRef]
- Janda, A.; Ooi, J.Y. DEM modeling of cone penetration and unconfined compression in cohesive solids. Powder Technol. 2016. [Google Scholar] [CrossRef]
- Thakur, S.C.; Ahmadian, H.; Sun, J.; Ooi, J.Y. An experimental and numerical study of packing, compression, and caking behaviour of detergent powders. Particuology 2014. [Google Scholar] [CrossRef]
- Aranda-Sánchez, L.D. Simulación numérica de las propiedades del refractario libre de carbono; Polythecnic University of Madrid: Madrid, Spain, 2016. [Google Scholar]
- Nordström, J.; Alderborn, G.; Frenning, G. Compressibility and tablet forming ability of bimodal granule mixtures: Experiments and DEM simulations. Int. J. Pharm. 2018. [Google Scholar] [CrossRef] [PubMed]
- Wiącek, J.; Molenda, M. Effect of particle size distribution on micro-and macromechanical response of granular packings under compression. Int. J. Solids Struct. 2014. [Google Scholar] [CrossRef]
- Wiacek, J.; Molenda, M.; Horabik, J.; Ooi, J.Y. Influence of grain shape and intergranular friction on material behavior in uniaxial compression: Experimental and DEM modeling. Powder Technol. 2012. [Google Scholar] [CrossRef]
- He, Y.; Evans, T.J.; Shen, Y.S.; Yu, A.B.; Yang, R.Y. Discrete modelling of the compaction of non-spherical particles using a multi-sphere approach. Miner. Eng. 2018. [Google Scholar] [CrossRef]
- Šmilauer, V.; Catalano, E.; Chareyre, B.; Dorofeenko, S.; Duriez, J.; Dyck, N.; Eliáš, J.; Er, B.; Eulitz, A.; Gladky, A.; et al. Yade Documentation 2nd ed. The Yade Project. 2015. Available online: http://yade-dem.org/doc/ (accessed on 9 November 2018).
- Jiménez-Herrera, N.; Barrios, G.K.P.; Tavares, L.M. Comparison of breakage models in DEM in simulating impact on particle beds. Adv. Powder Technol. 2018, 29, 692–706. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, Y.; Zhang, J.; Saxén, H.; Yu, Y. LIGGGHTS and EDEM application on charging system of ironmaking blast furnace. Adv. Powder Technol. 2017. [Google Scholar] [CrossRef]
- Markauskas, D.; Ramírez-Gómez, Á.; Kacianauskas, R.; Zdancevicius, E. Maize grain shape approaches for DEM modelling. Comput. Electron. Agric. 2015, 118, 247–258. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Papanicolopulos, S.A.; Kloss, C.; Pirker, S.; Ooi, J.Y. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Kozhar, S.; Dosta, M.; Antonyuk, S.; Heinrich, S.; Bröckel, U. DEM simulations of amorphous irregular shaped micrometer-sized titania agglomerates at compression. Adv. Powder Technol. 2015, 26, 767–777. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- DEM Solutions. EDEM 2.6 Theory Reference Guide; DEM Solutions: Edinburgh, UK, 2014.
- Weisstein, E.W. Sphere-Sphere Intersection. Available online: http://mathworld.wolfram.com/Sphere-SphereIntersection.html (accessed on 23 October 2018).
- Wang, W.; Qi, H.; Liu, P.; Zhao, Y.; Chang, H. Numerical simulation of densification of Cu–Al mixed metal powder during axial compaction. Metals 2018. [Google Scholar] [CrossRef]
- Nunes de Barros, F.; Bhaskar, A.; Singh, R. A Validated Model for Design and Evaluation of Control Architectures for a Continuous Tablet Compaction Process. Processes 2017. [Google Scholar] [CrossRef]
- Olmos, L.; Martin, C.L.; Bouvard, D. Sintering of mixtures of powders: Experiments and modelling. Powder Technol. 2009, 190, 134–140. [Google Scholar] [CrossRef]
- Wang, H.; Glaser, B.; Sichen, D. Improvement of Resistance of MgO-Based Refractory to Slag Penetration by In Situ Spinel Formation. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2015, 46, 749–757. [Google Scholar] [CrossRef] [Green Version]
- Thakur, S.C.; Ooi, J.Y.; Ahmadian, H. Scaling of discrete element model parameters for cohesionless and cohesive solid. Powder Technol. 2016. [Google Scholar] [CrossRef]







| Material Property | Material 1 | Material 2 | Wall |
|---|---|---|---|
| Mean diameter (mm) | 2.1 | 2.1 | - |
| Density (kg/m3) | 3500 | 3000 | 8000 |
| Young’s modulus (Pa) | 2.5 × 108 | 2.5 × 108 | 2.0 × 108 |
| Poisson’s ratio | 0.25 | 0.25 | 0.25 |
| Setup Number | Timestep (s) | Timestep (% Rayleigh) | Conversion Tolerance (mm) | Speed of Punch (m/s) | Total Simulation Time (Compaction + Ejection) (s) | ||
|---|---|---|---|---|---|---|---|
| MP | UD/ND | ||||||
| 1 | 1.0 × 10−6 | 5.0 × 10−7 | ~5 | 0.01 | 0.2 | 0.175 | (0.125 + 0.05) |
| 2 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.2 | 0.175 | (0.125 + 0.05) |
| 3 | 3.125 × 10−6 | 2.0 × 10−6 | ~15 | 0.01 | 0.2 | 0.175 | (0.125 + 0.05) |
| 4 | 4.0 × 10−6 | 2.5 × 10−6 | ~20 | 0.01 | 0.2 | 0.175 | (0.125 + 0.05) |
| 5 | 5.0 × 10−6 | 3.125 × 10−6 | ~25 | 0.01 | 0.2 | 0.175 | (0.125 + 0.05) |
| 6 | 6.25 × 10−6 | 4.0 × 10−6 | ~30 | 0.01 | 0.2 | 0.175 | (0.125 + 0.05) |
| 7 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.001 | 0.2 | 0.175 | (0.125 + 0.05) |
| 8 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.1 | 0.2 | 0.175 | (0.125 + 0.05) |
| 9 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 1.0 | 0.2 | 0.175 | (0.125 + 0.05) |
| 10 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.0001 | 250.05 | (50 + 0.05) |
| 11 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.0005 | 50.05 | (50 + 0.05) |
| 12 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.001 | 25.05 | (25 + 0.05) |
| 13 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.005 | 5.05 | (5 + 0.05) |
| 14 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.01 | 2.55 | (2.5 + 0.05) |
| 15 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.05 | 0.55 | (0.5 + 0.05) |
| 16 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.1 | 0.3 | (0.25 + 0.05) |
| 17 | 2.0 × 10−6 | 1.0 × 10−6 | ~10 | 0.01 | 0.5 | 0.1 | (0.05 + 0.05) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Aragón, C.; Ordieres-Meré, J.; Alba-Elías, F.; González-Marcos, A. Comparison of Cohesive Models in EDEM and LIGGGHTS for Simulating Powder Compaction. Materials 2018, 11, 2341. https://doi.org/10.3390/ma11112341
Ramírez-Aragón C, Ordieres-Meré J, Alba-Elías F, González-Marcos A. Comparison of Cohesive Models in EDEM and LIGGGHTS for Simulating Powder Compaction. Materials. 2018; 11(11):2341. https://doi.org/10.3390/ma11112341
Chicago/Turabian StyleRamírez-Aragón, Cristina, Joaquín Ordieres-Meré, Fernando Alba-Elías, and Ana González-Marcos. 2018. "Comparison of Cohesive Models in EDEM and LIGGGHTS for Simulating Powder Compaction" Materials 11, no. 11: 2341. https://doi.org/10.3390/ma11112341