Auxeticity of Concentric Auxetic-Conventional Foam Rods with High Modulus Interface Adhesive
Abstract
:1. Introduction
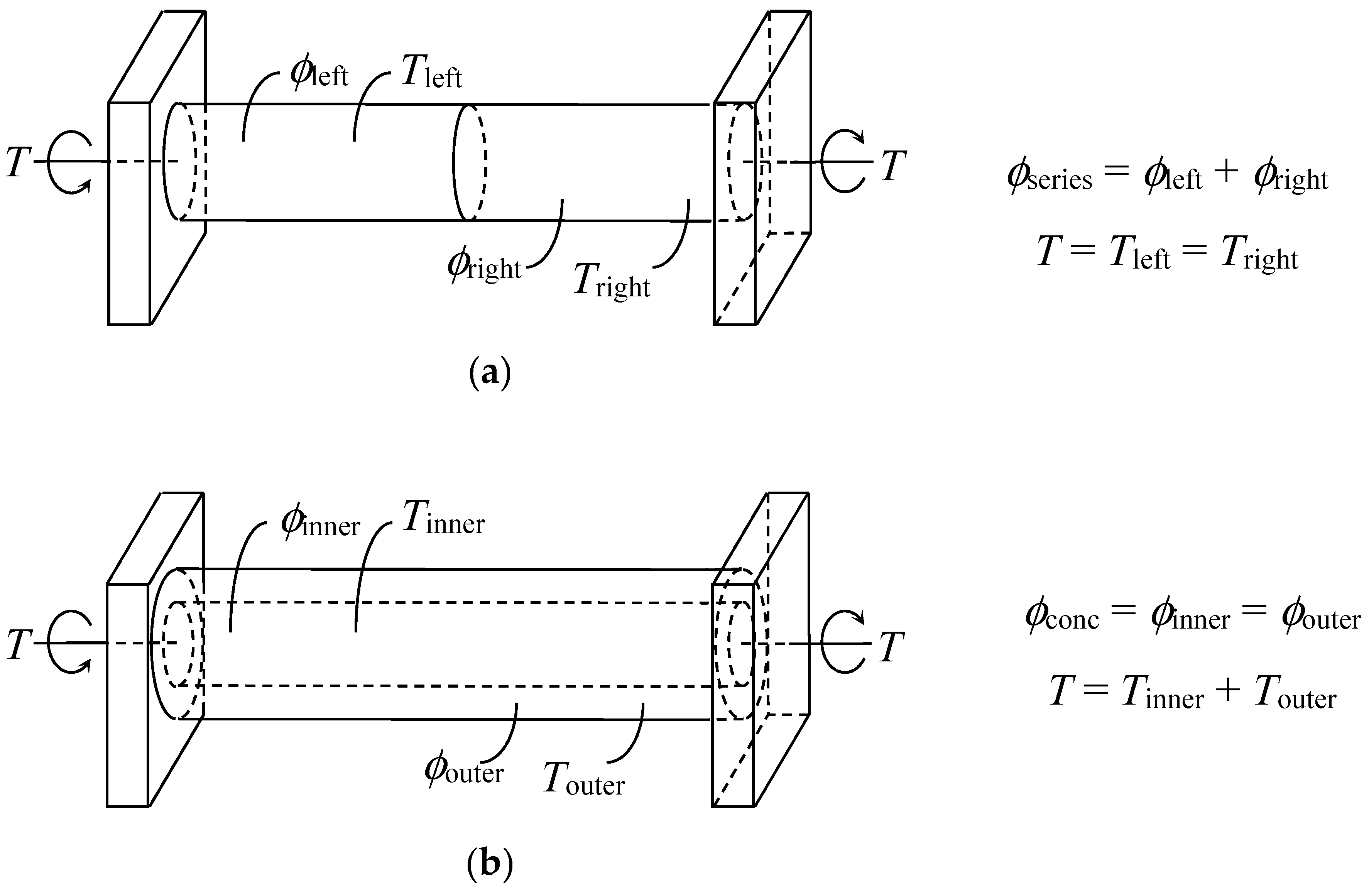
2. Theory and Formulation
2.1. Single Solid Rods
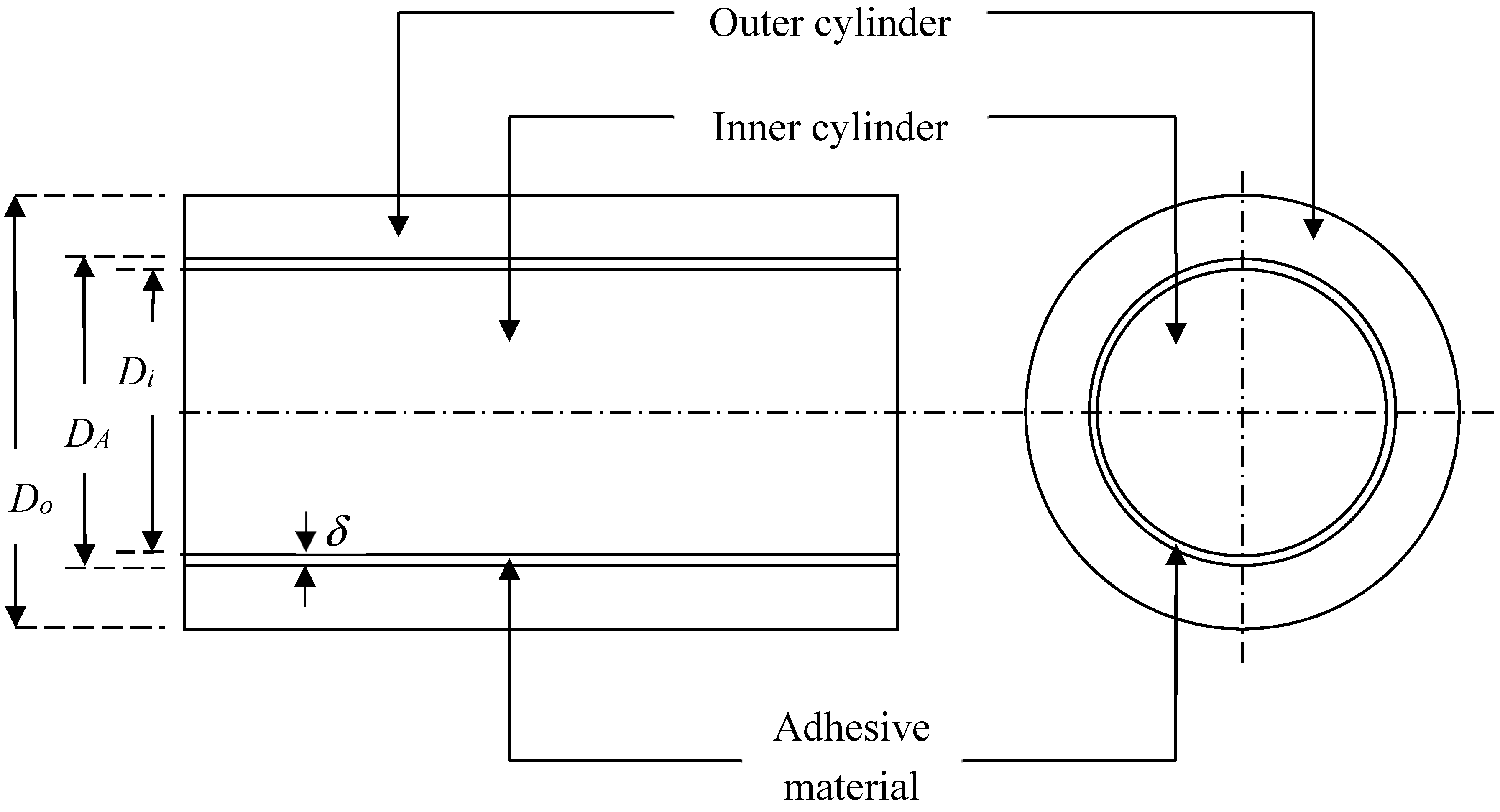
2.2. Bi-Layered Concentric Rods
2.3. Tri-Layered Concentric Rods
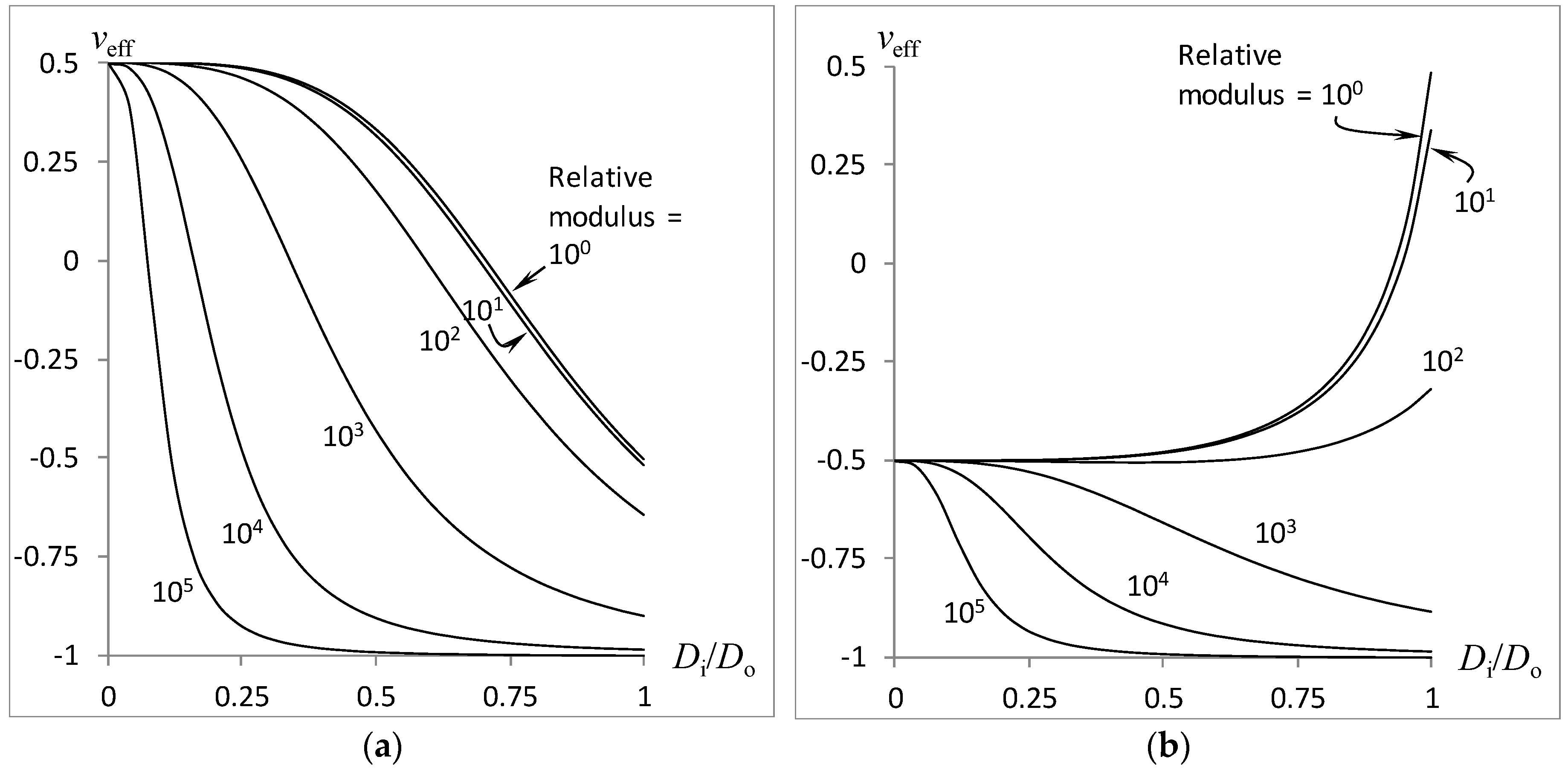
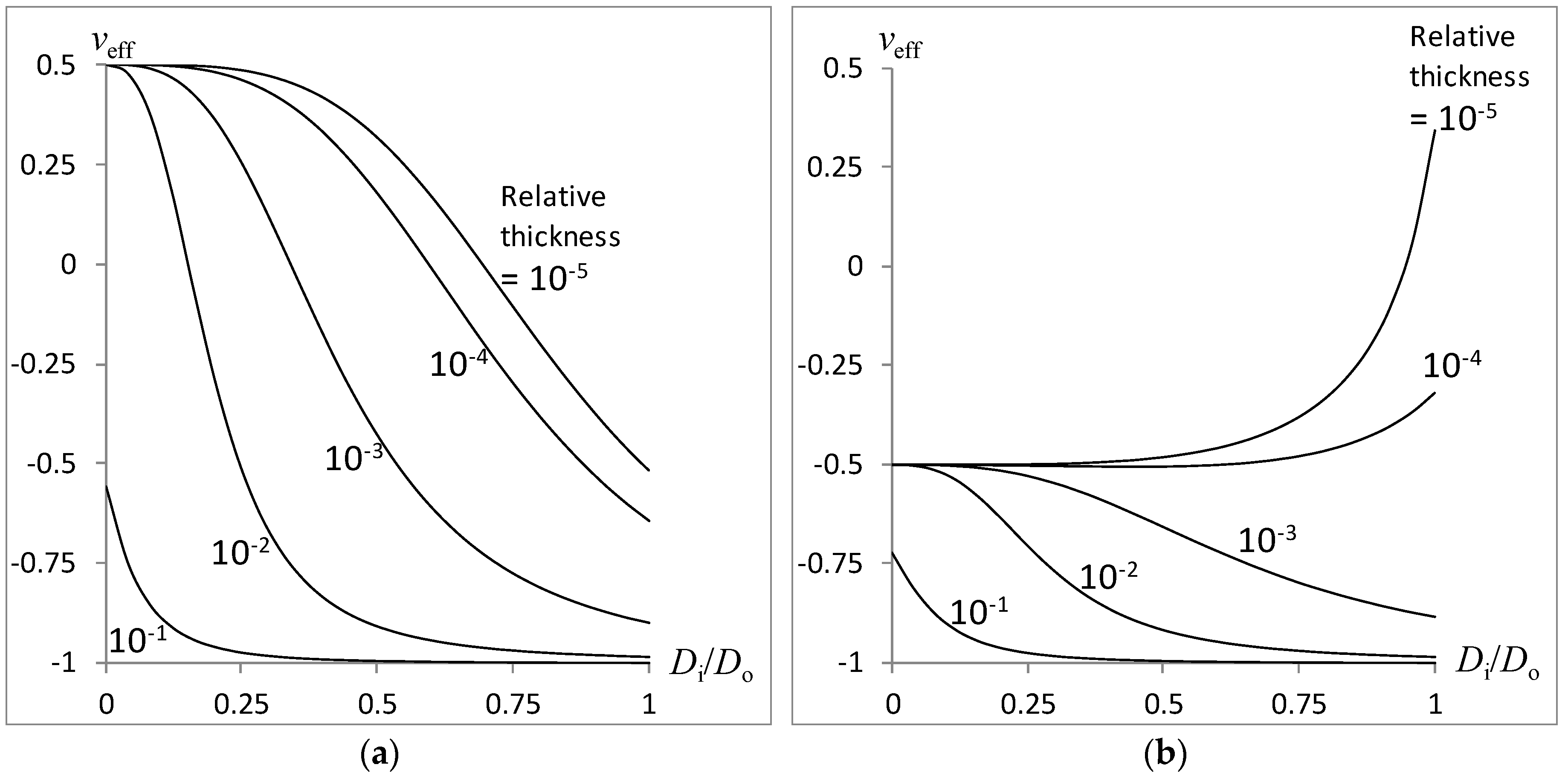
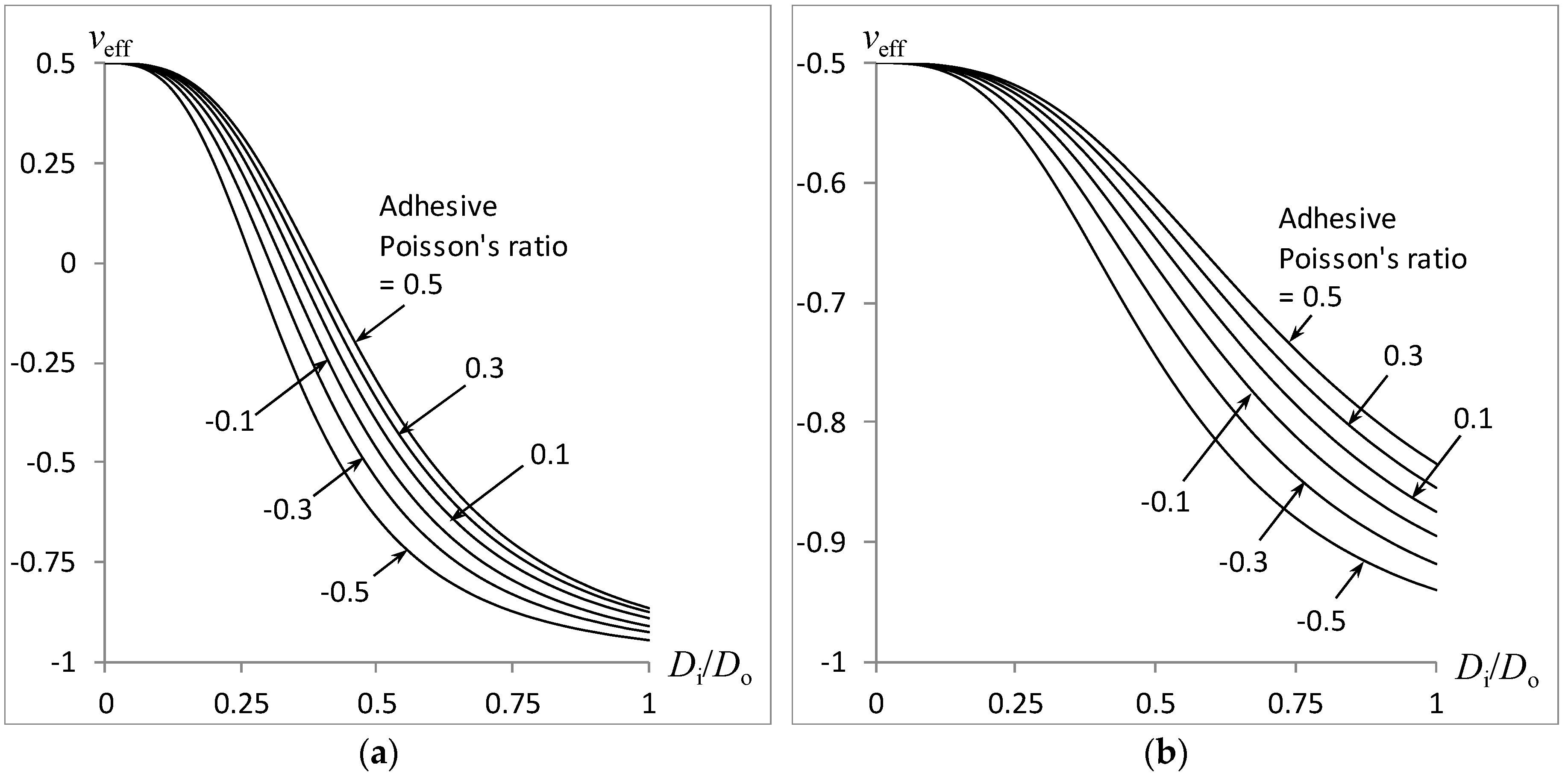
3. Results and Discussion
- (a)
- less pronounced effective Poisson’s ratio if the magnitudes are equal and less than 0.5,
- (b)
- the outer shell plays a larger role than the inner core in influencing the effective Poisson’s ratio under bending and especially torsion, but is directly proportional to the cross-sectional area for the axial load,
- (c)
- the foam with a larger Poisson’s ratio magnitude will exert a greater effect on the sign of the effective Poisson’s ratio.
4. Conclusions
Conflicts of Interest
References
- Ely, J.F.; Zienkiewicz, O.C. Torsion of compound bars—A relaxation solution. Int. J. Mech. Sci. 1960, 1, 356–365. [Google Scholar] [CrossRef]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotropic Body; Holden-Day: San Francisco, CA, USA, 1963; ISBN 978-071-471-657-2. [Google Scholar]
- Hashin, Z.; Rosen, B.W. The elastic moduli of fiber-reinforced materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Packham, B.A.; Shail, R. St. Venant torsion of composite cylinders. J. Elast. 1978, 8, 393–407. [Google Scholar] [CrossRef]
- Tsukrov, I.; Drach, B. Elastic deformation of composite cylinders with cylindrically orthotropic layers. Int. J. Solids Struct. 2010, 47, 25–33. [Google Scholar] [CrossRef]
- Maksymuk, A.V.; Shcherbina, N.N. Torsion of laminated cylindrical shells with adhesive interlayers. Mech. Compos. Mater. 1998, 34, 363–368. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, C.L. Magnetoelectric effect in a circumferentially polarized composite cylinder. Smart Mater. Struct. 2013, 22, 105018. [Google Scholar] [CrossRef]
- Levin, V.A.; Zubov, L.M.; Zingerman, K.M. The torsion of a composite, nonlinear-elastic cylinder with an inclusion having initial large strains. Int. J. Solids Struct. 2014, 51, 1403–1409. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R. Negative Poisson’s ratio materials. Science 1987, 238, 551. [Google Scholar] [CrossRef] [PubMed]
- Popereka, M.Y.A.; Balagurov, V.G. Ferromagnetic films having a negative Poisson ratio. Fiz. Tverd. Tela 1969, 11, 3507–3513. [Google Scholar]
- Milstein, F.; Huang, K. Existence of a negative Poisson ratio in fcc crystals. Phys. Rev. B 1979, 19, 2030–2033. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Almgren, R.F. An isotropic three-dimensional structure with Poisson’s ratio = −1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Kolpakov, A.G. The determination of averaged characteristics for elastic skeletons. Prikl. Mat. Mekh. 1985, 49, 969–977. [Google Scholar]
- Wojciechowski, K.W. Constant thermodynamic tension Monte-Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Branka, A.C. Negative Poisson ratio in a two-dimensional ‘‘isotropic’’ solid. Phys. Rev. A 1989, 40, 7222–7225. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Design of a fastener based on negative Poisson’s ratio foam. Cell. Polym. 1991, 10, 205–212. [Google Scholar]
- Caddock, B.D.; Evans, K.E. Negative Poisson ratios and strain-dependent mechanical properties in arterial prostheses. Biomaterials 1995, 16, 1109–1115. [Google Scholar] [CrossRef]
- Martz, E.O.; Lakes, R.S.; Goel, V.K.; Park, J.B. Design of an artificial intervertebral disc exhibiting a negative Poisson’s ratio. Cell. Polym. 2005, 24, 127–138. [Google Scholar]
- Dolla, W.J.S.; Fricke, B.A.; Becker, B.R. Structural and drug diffusion models of conventional and auxetic drug-eluting stents. J. Med. Dev. 2007, 1, 47–55. [Google Scholar] [CrossRef]
- Scarpa, F. Auxetic materials for bioprostheses. IEEE Signal Process. Mag. 2008, 25, 125–126. [Google Scholar] [CrossRef]
- Lakes, R.S.; Lowe, A. Negative Poisson’s ratio foam as seat cushion material. Cell. Polym. 2000, 19, 157–167. [Google Scholar]
- Wang, Y.C.; Lakes, R.S. Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s ratio foam cushions. Int. J. Solids Struct. 2002, 39, 4825–4838. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Bag, S.; Mullarkey, P.G.; Perrie, W.; Evans, K.E. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–655. [Google Scholar] [CrossRef]
- Alderson, A.; Davies, P.J.; Evans, K.E.; Alderson, K.L.; Grima, J.N. Modelling of the mechanical and mass transport properties of auxetic molecular sieves: An idealised inorganic (zeolitic) host-guest system. Mol. Simul. 2005, 31, 889–896. [Google Scholar] [CrossRef]
- Alderson, A.; Davies, P.J.; Williams, M.R.; Evans, K.E.; Alderson, K.L.; Grima, J.N. Modelling of the mechanical and mass transport properties of auxetic molecular sieves: An idealised organic (polymeric honeycomb) host-guest system. Mol. Simul. 2005, 31, 897–905. [Google Scholar] [CrossRef]
- Lim, T.C.; Acharya, R.U. Performance Evaluation of Auxetic Molecular Sieves with Re-Entrant Structures. J. Biomed. Nanotechnol. 2010, 6, 718–724. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, F.; Giacomin, J.; Zhang, Y.; Pastorino, P. Mechanical performance of auxetic polyurethane foam for antivibration glove applications. Cell. Polym. 2005, 24, 253–268. [Google Scholar]
- Alderson, A.; Alderson, K.L. Expanding materials and applications: Exploiting auxetic textiles. Tech. Text. Int. 2005, 14, 29–34. [Google Scholar]
- Park, K.O.; Choi, J.B.; Lee, S.J.; Choi, H.H.; Kim, J.K. Polyurethane foam with Negative Poisson’s ratio for diabetic shoe. Key Eng. Mater. 2005, 288–289, 677–680. [Google Scholar] [CrossRef]
- Ellul, B.; Muscat, M.; Grima, J.N. On the effect of the Poisson’s ratio (positive and negative) on the stability of pressure vessel heads. Phys. Status Solidi B 2009, 246, 2025–2032. [Google Scholar] [CrossRef]
- Salit, V.; Weller, T. On the feasibility of introducing auxetic behavior into thin-walled structures. Acta Mater. 2009, 57, 125–135. [Google Scholar] [CrossRef]
- Whitty, J.P.M.; Henderson, B.; Myler, P.; Chirwa, C. Crash performance of cellular foams with reduced relative density part 2: Rib deletion. Int. J. Crashworthiness 2007, 12, 689–698. [Google Scholar]
- Park, K.O.; Choi, J.B.; Park, J.C.; Park, D.J.; Kim, J.K. An improvement in shock absorbing behavior of polyurethane foam with a negative Poisson effect. Key Eng. Mater. 2007, 342–343, 845–848. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic Materials and Structures; Springer: Singapore, 2015; ISBN 978-981-287-274-6. [Google Scholar]
- Wojciechowski, K.W.; Scarpa, F.; Grima, J.N.; Alderson, A. Auxetics and other systems of anomalous characteristics. Phys. Status Solidi B 2017, 254, 1770266. [Google Scholar] [CrossRef]
- Lim, T.C. 2D structures exhibiting negative area compressibility. Phys. Status Solidi B 2017, 254, 1600682. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic and negative thermal expansion structure based on interconnected array of rings and sliding rods. Phys. Status Solidi B 2017, 254, 1600775. [Google Scholar] [CrossRef]
- Lim, T.C. An accurate design equation for the maximum deflection in a class of auxetic sectorial plates. Phys. Status Solidi B 2017, 254, 1600784. [Google Scholar] [CrossRef]
- Lim, T.C. Shear deformation in a class of thick hexagonal plates. Phys. Status Solidi B 2017, 254, 1700014. [Google Scholar] [CrossRef]
- Jiang, L.; Hu, H. Finite element modeling of multilayer orthogonal auxetic composites under low-velocity impact. Materials 2017, 10, 908. [Google Scholar] [CrossRef] [PubMed]
- Wormser, M.; Wein, F.; Stingl, M.; Körner, C. Design and additive manufacturing of 3D phononic band gap structures based on gradient based optimization. Materials 2017, 10, 1125. [Google Scholar] [CrossRef] [PubMed]
- Czarnecki, S.; Łukasiak, T.; Lewiński, T. The isotropic and cubic material designs. Recovery of the underlying microstructures appearing in the least compliant continuum bodies. Materials 2017, 10, 1137. [Google Scholar] [CrossRef] [PubMed]
- Pigłowski, P.M.; Narojczyk, J.W.; Poźniak, A.A.; Wojciechowski, K.W.; Tretiakov, K.V. Auxeticity of Yukawa systems with nanolayers in the (111) crystallographic plane. Materials 2017, 10, 1338. [Google Scholar] [CrossRef] [PubMed]
- Jopek, H. Finite element analysis of tunable composite tubes reinforced with auxetic structures. Materials 2017, 10, 1359. [Google Scholar] [CrossRef] [PubMed]
- Strek, T.; Jopek, H.; Idczak, E.; Wojciechowski, K.W. Computational modelling of structures with non-intuitive behavior. Materials 2017, 10, 1386. [Google Scholar] [CrossRef] [PubMed]
- Lim, T.C. Functionally graded beam for attaining Poisson-curving. J. Mater. Sci. Lett. 2002, 21, 1899–1901. [Google Scholar] [CrossRef]
- Gatt, R.; Attard, D.; Grima, J.N. On the behaviour of bi-material strips when subjected to changes in external hydrostatic pressure. Scr. Mater. 2009, 60, 65–67. [Google Scholar] [CrossRef]
- Lim, T.C. On simultaneous positive and negative Poisson’s ratio laminates. Phys. Status Solidi B 2007, 244, 910–918. [Google Scholar] [CrossRef]
- Lim, T.C. Mixed auxeticity of auxetic sandwich structures. Phys. Status Solidi B 2012, 249, 1366–1372. [Google Scholar] [CrossRef]
- Donescu, S.; Chiroiu, V.; Munteanu, L. On the Young’s modulus of a auxetic composite structure. Mech. Res. Commun. 2009, 36, 294–301. [Google Scholar] [CrossRef]
- Kocer, C.; McKenzie, D.R.; Bilek, M.M. Elastic properties of a material composed of alternating layers of negative and positive Poisson’s ratio. Mater. Sci. Eng. A 2009, 505, 111–115. [Google Scholar] [CrossRef]
- Lim, T.C. Out-of-plane modulus of semi-auxetic laminates. Eur. J. Mech. A Solids 2009, 28, 752–756. [Google Scholar] [CrossRef]
- Chirima, G.T.; Zied, K.M.; Ravirala, N.; Alderson, K.L.; Alderson, A. Numerical and analytical modelling of multi-layer adhesive–film interface systems. Phys. Status Solidi B 2009, 246, 2072–2082. [Google Scholar] [CrossRef]
- Lim, T.C. In-plane stiffness of semiauxetic laminates. J. Eng. Mech. 2010, 136, 1176–1180. [Google Scholar] [CrossRef]
- Lim, T.C.; Rajendra Acharya, U. Counterintuitive modulus from semi-auxetic laminates. Phys. Status Solidi B 2011, 248, 60–65. [Google Scholar] [CrossRef]
- Grima, J.N.; Oliveri, L.; Ellul, B.; Gatt, R.; Attard, D.; Cicala, G.; Recca, G. Adjustable and negative thermal expansion from multilayered systems. Phys. Status Solidi Rapid Res. Lett. 2010, 4, 133–135. [Google Scholar] [CrossRef]
- Lim, T.C. Coefficient of thermal expansion of stacked auxetic and negative thermal expansion laminates. Phys. Status Solidi B 2011, 248, 140–147. [Google Scholar] [CrossRef]
- Lim, T.C.; Acharya, U.R. Longitudinal modulus of semi-auxetic unidirectional fiber composites. J. Reinf. Plast. Compos. 2010, 29, 1441–1445. [Google Scholar] [CrossRef]
- Lim, T.C. Torsion of semi-auxetic rods. J. Mater. Sci. 2011, 46, 6904–6909. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H. Effective mechanical properties of concentric cylindrical composites with auxetic phase. Phys. Status Solidi B 2012, 249, 1359–1365. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Fraska, A. Torsion of elliptical composite beams with auxetic phase. Phys. Status Solidi B 2016, 253, 1359–1368. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Torsion of a two-phased composite bar with helical distribution of constituents. Phys. Status Solidi B 2017, 254, 1700050. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, T.-C. Auxeticity of Concentric Auxetic-Conventional Foam Rods with High Modulus Interface Adhesive. Materials 2018, 11, 223. https://doi.org/10.3390/ma11020223
Lim T-C. Auxeticity of Concentric Auxetic-Conventional Foam Rods with High Modulus Interface Adhesive. Materials. 2018; 11(2):223. https://doi.org/10.3390/ma11020223
Chicago/Turabian StyleLim, Teik-Cheng. 2018. "Auxeticity of Concentric Auxetic-Conventional Foam Rods with High Modulus Interface Adhesive" Materials 11, no. 2: 223. https://doi.org/10.3390/ma11020223




