Wave Electromechanical Coupling Factor for the Guided Waves in Piezoelectric Composites
Abstract
:1. Introduction
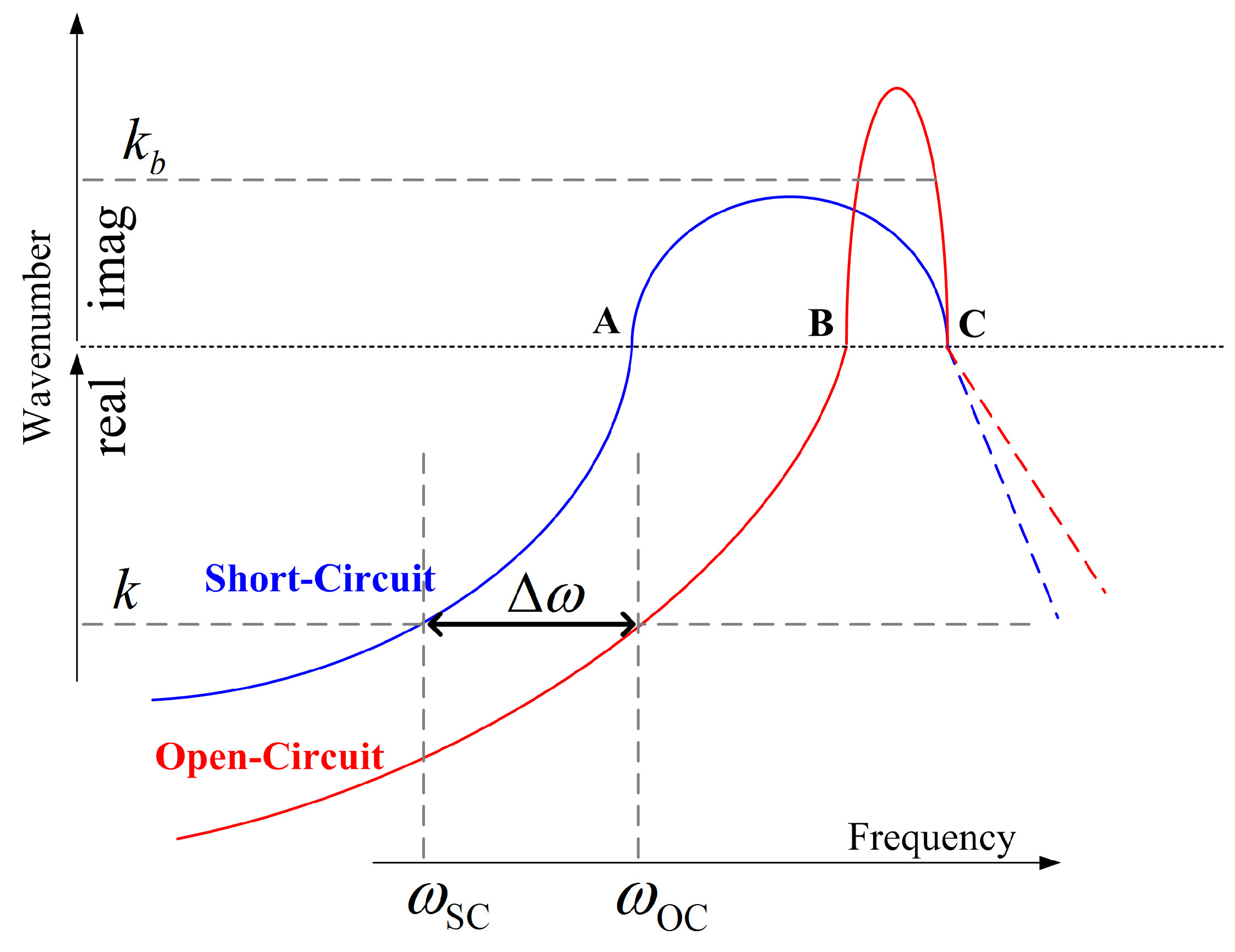
2. Definitions of WEMCF
3. Wave and Finite Element Method (WFEM)
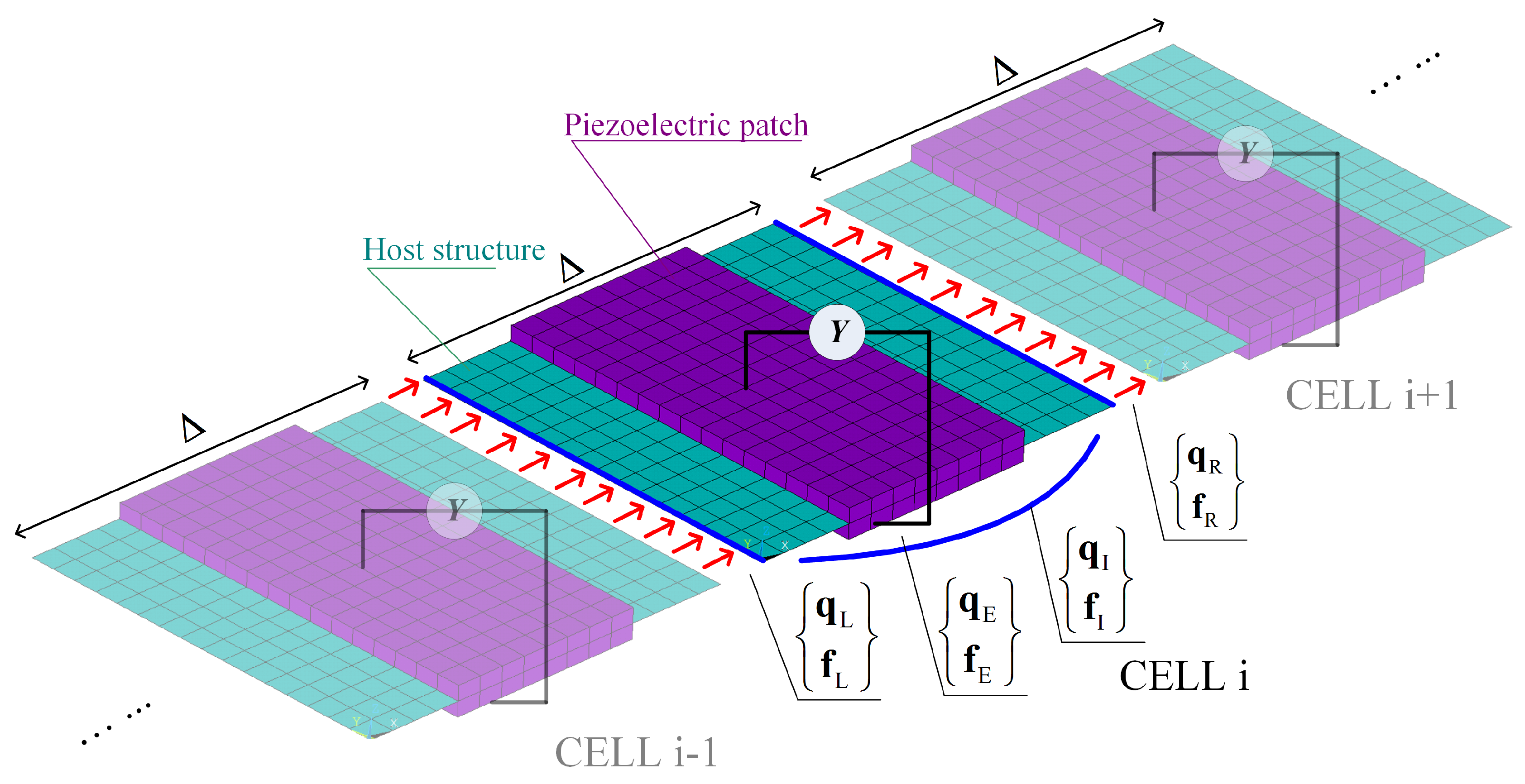
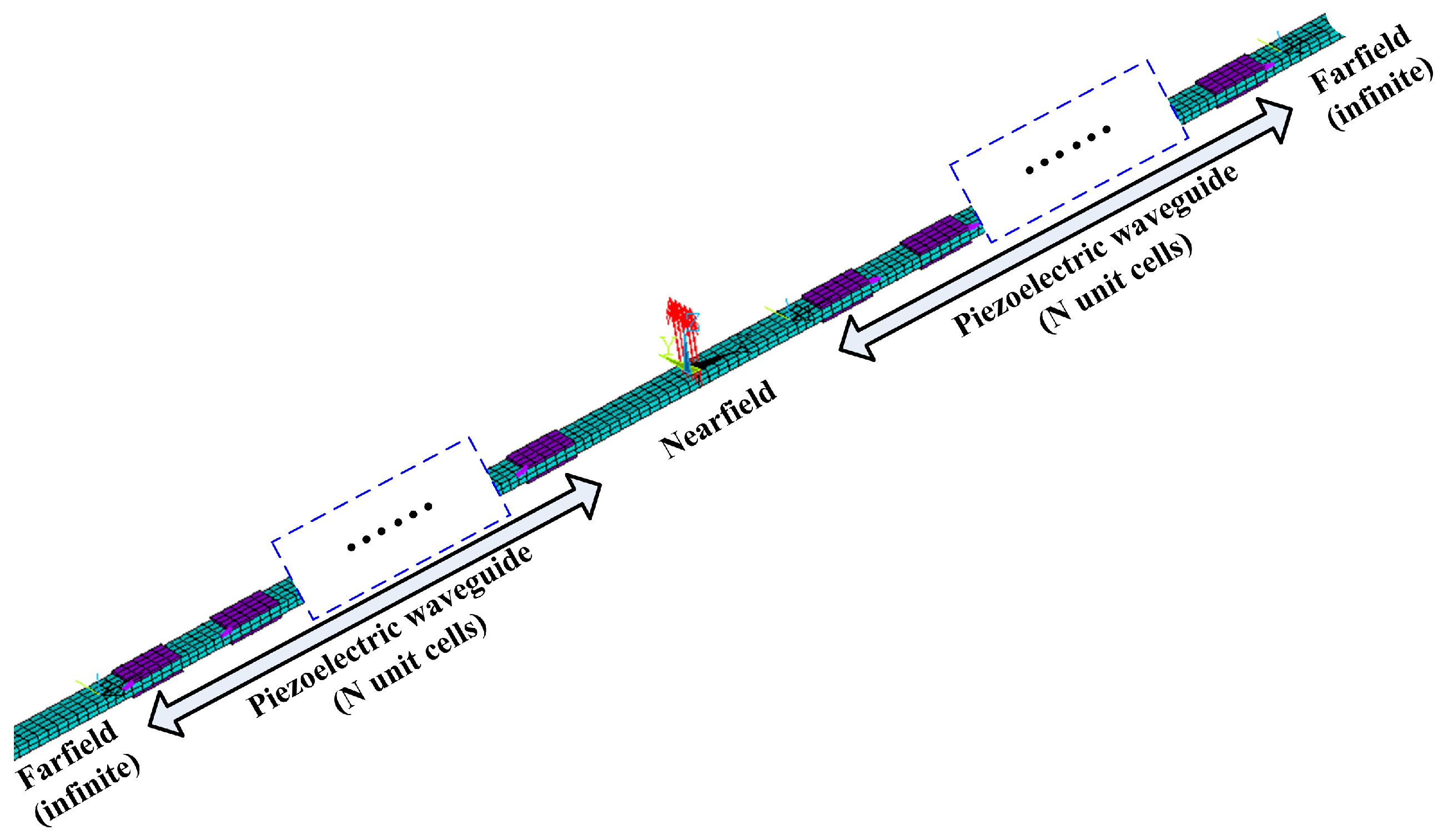
3.1. Basic Procedure
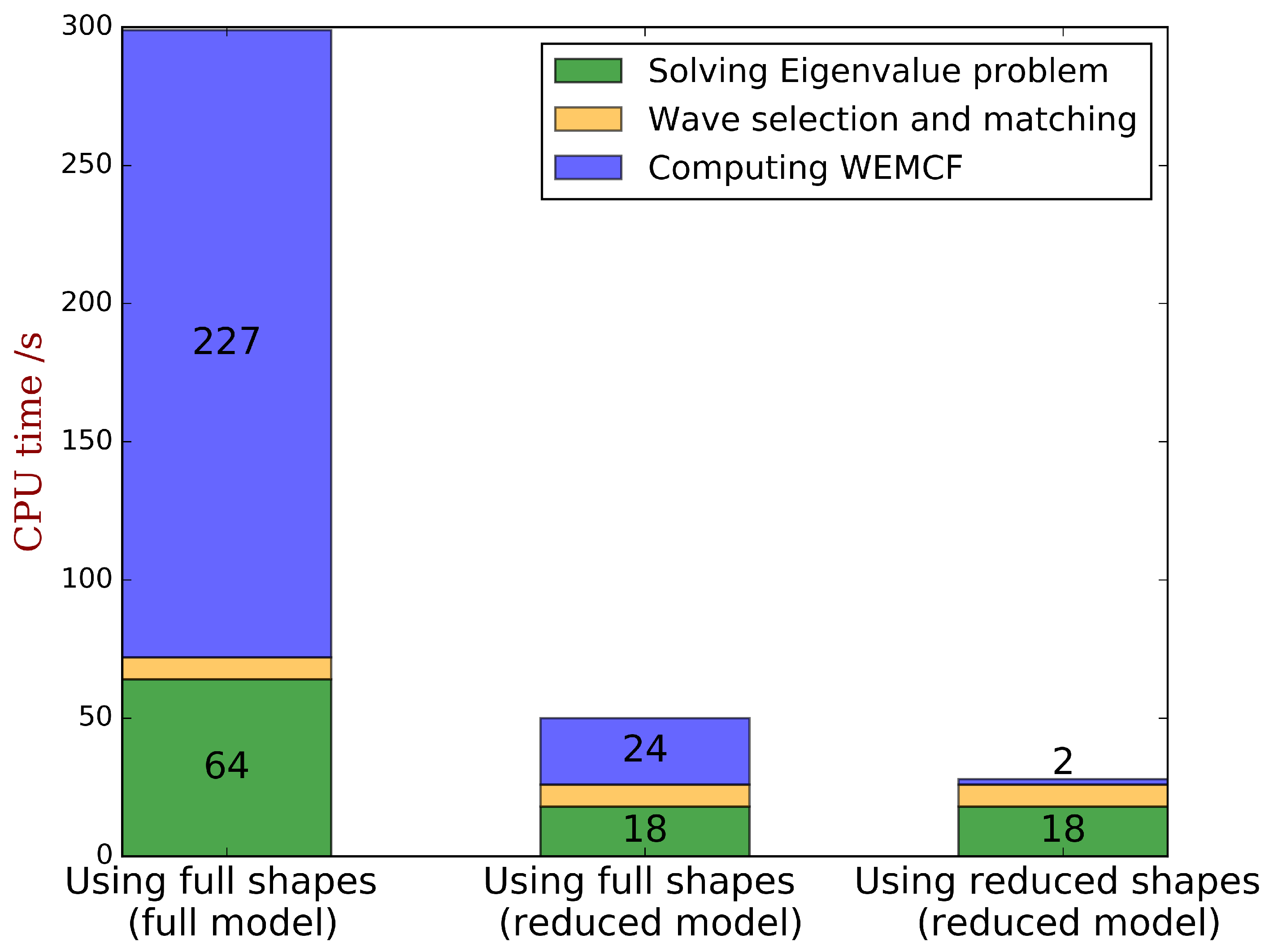
3.2. Reduced Model for the Piezoelectric Composites
4. Energy Formulas of WEMCF
4.1. Two Energy Formulas
4.2. Demonstrations
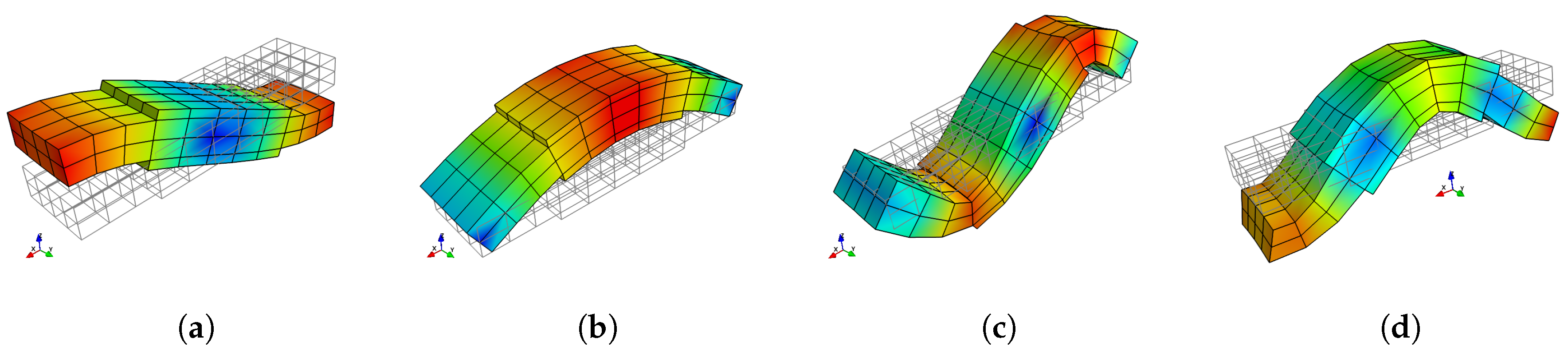
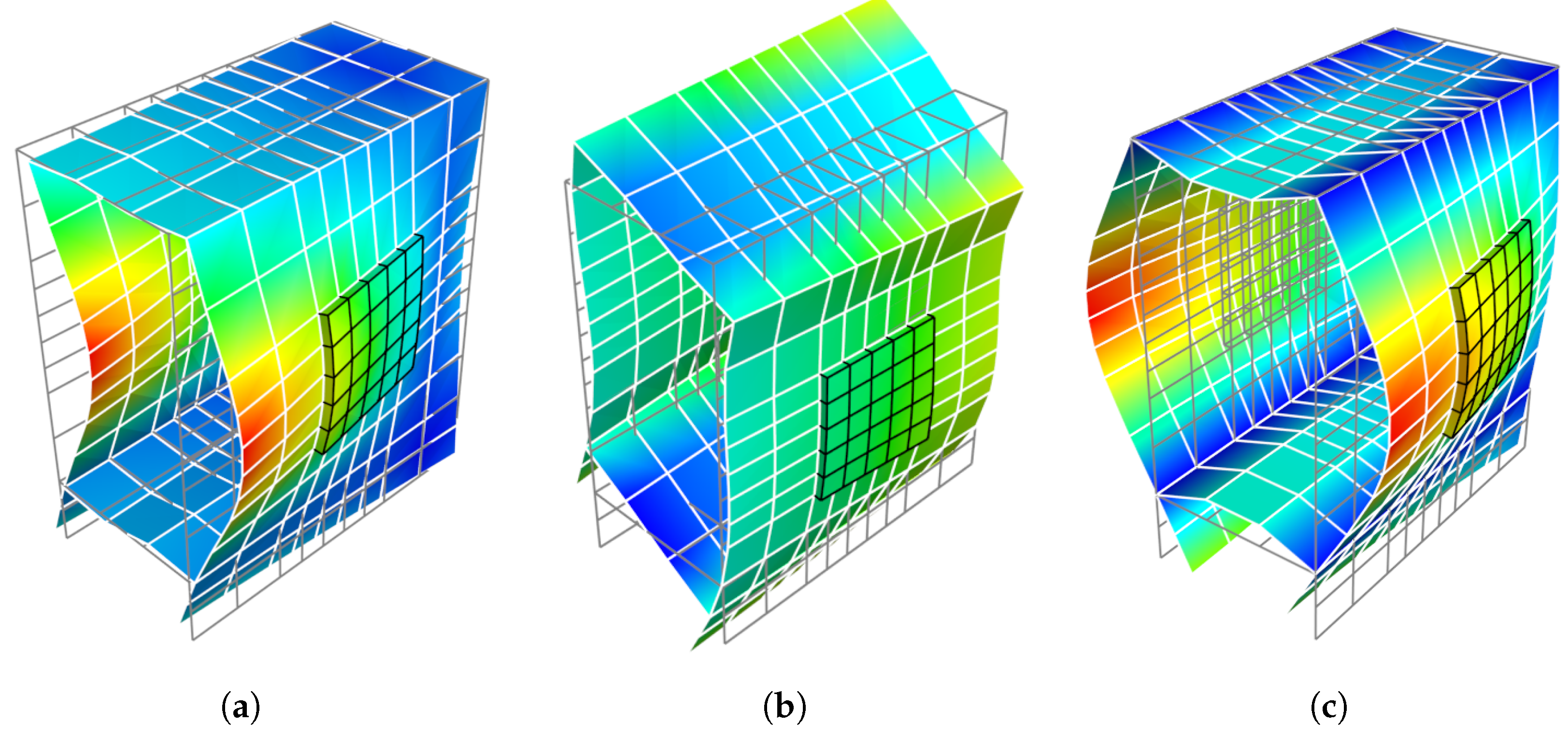
4.2.1. Relationship between the Wavenumber and Wave Shape
4.2.2. Demonstration of Energy Formula
4.2.3. Demonstration of Energy Formula
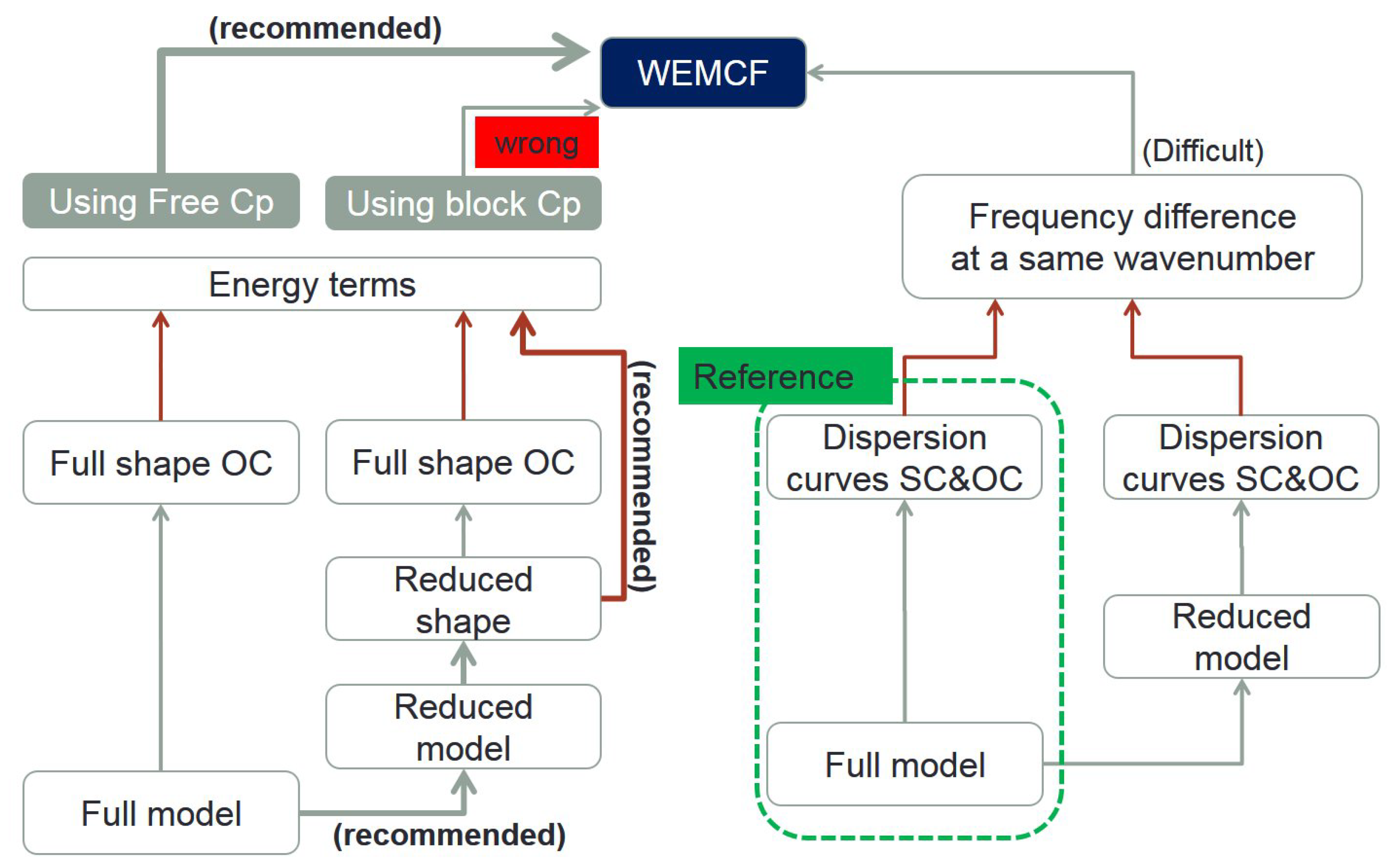
4.3. Implementations
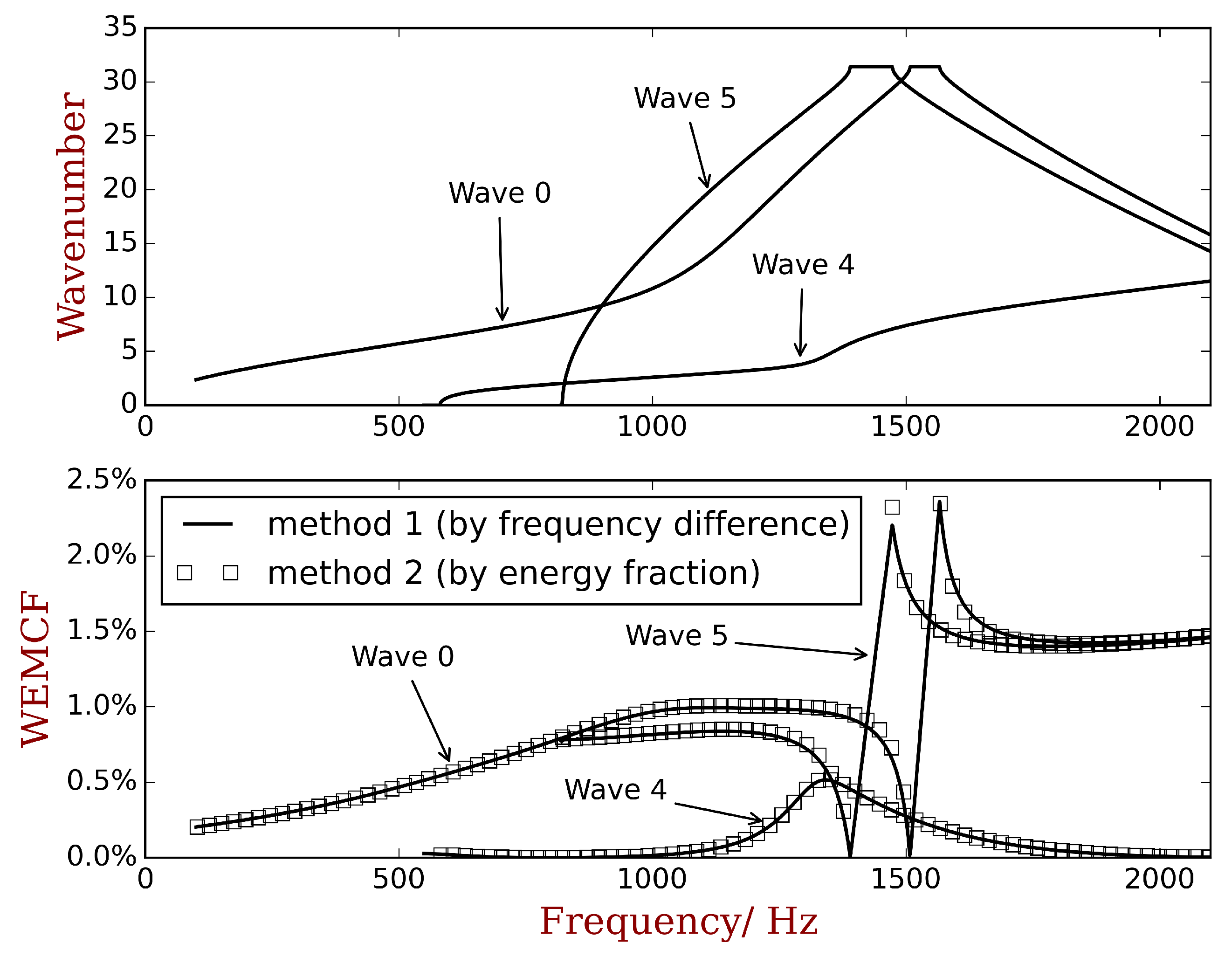
5. Validations
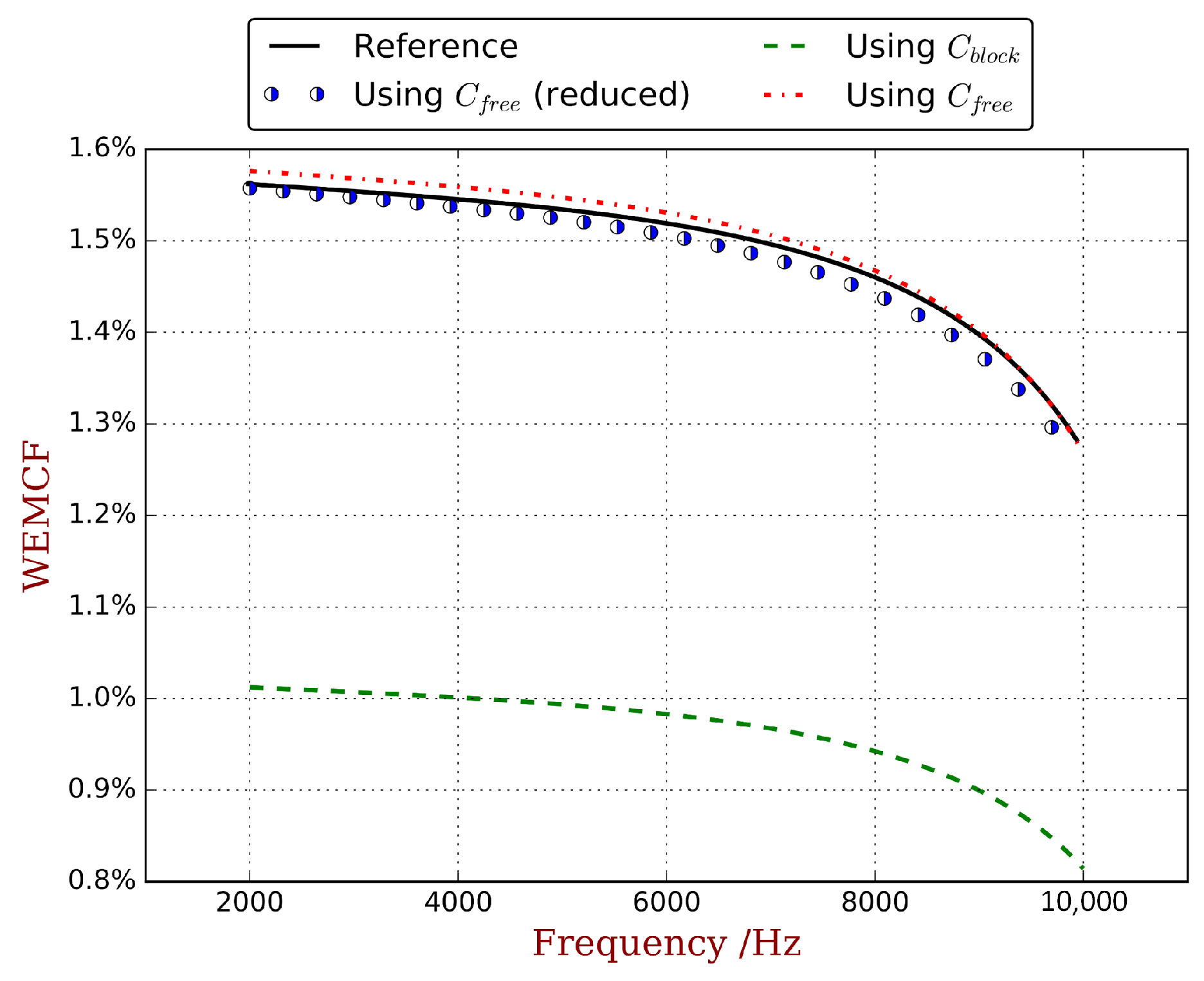
5.1. Validation of the Implementations
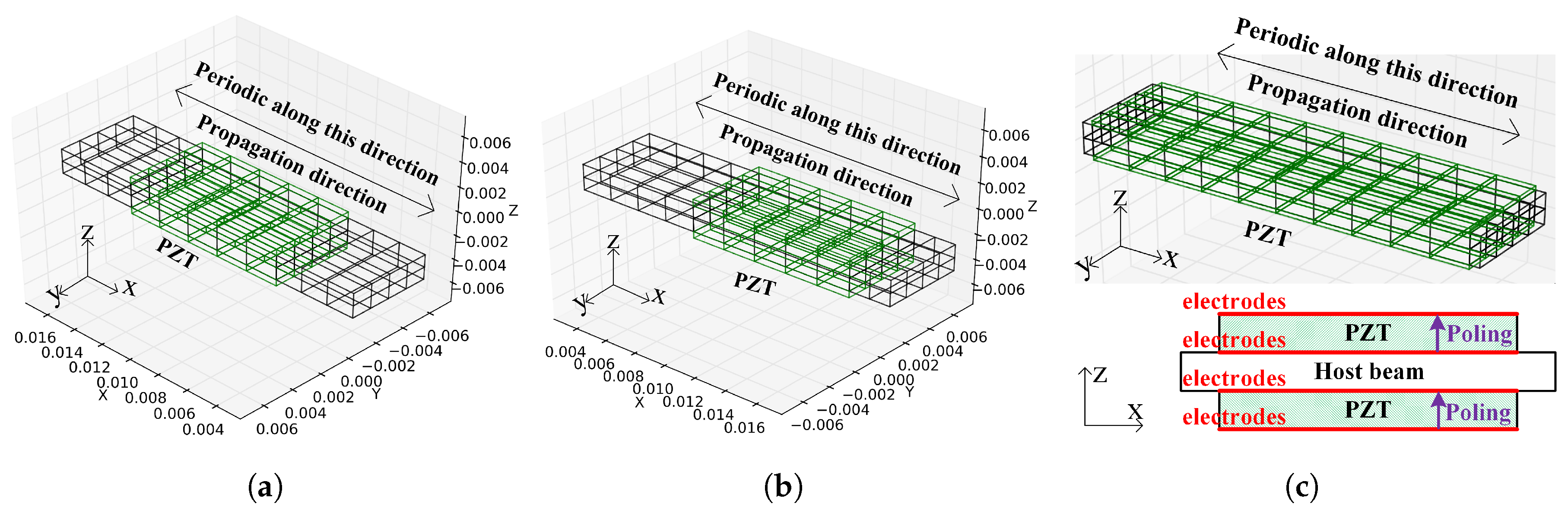
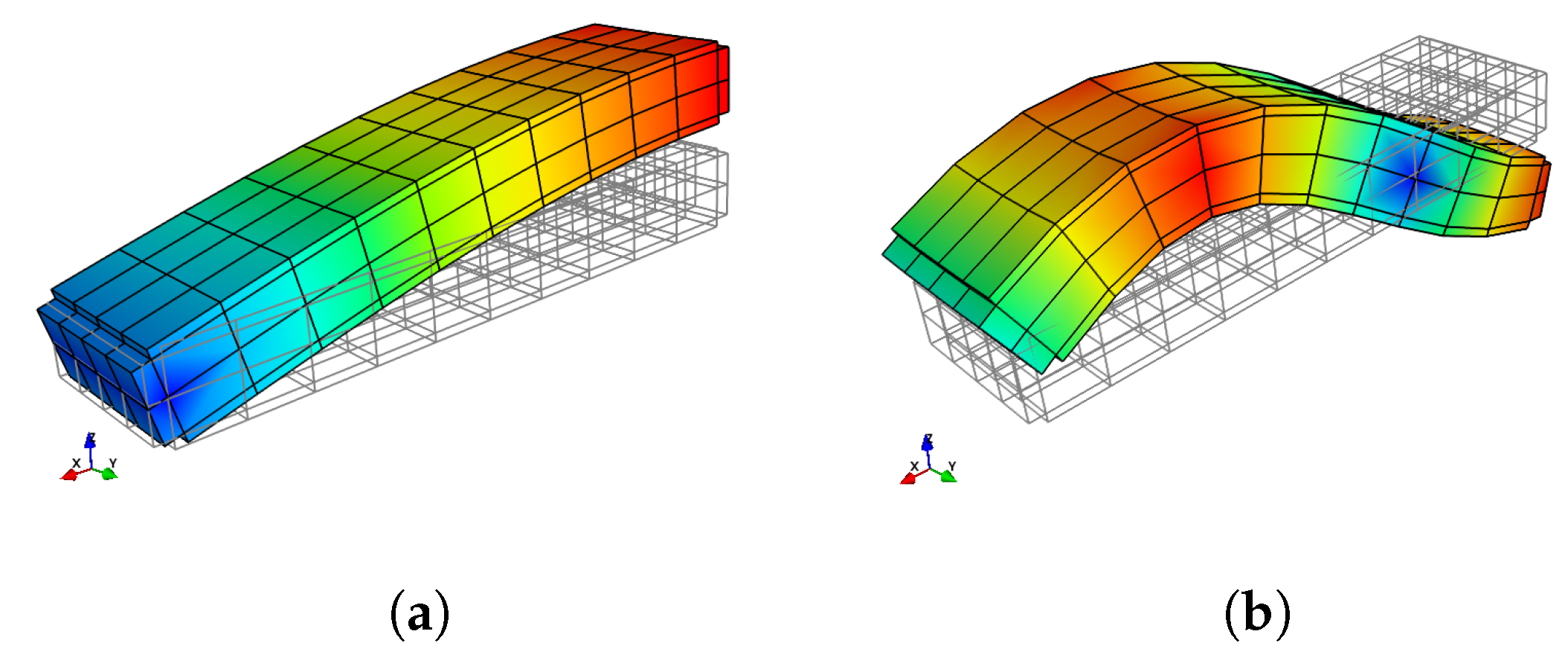
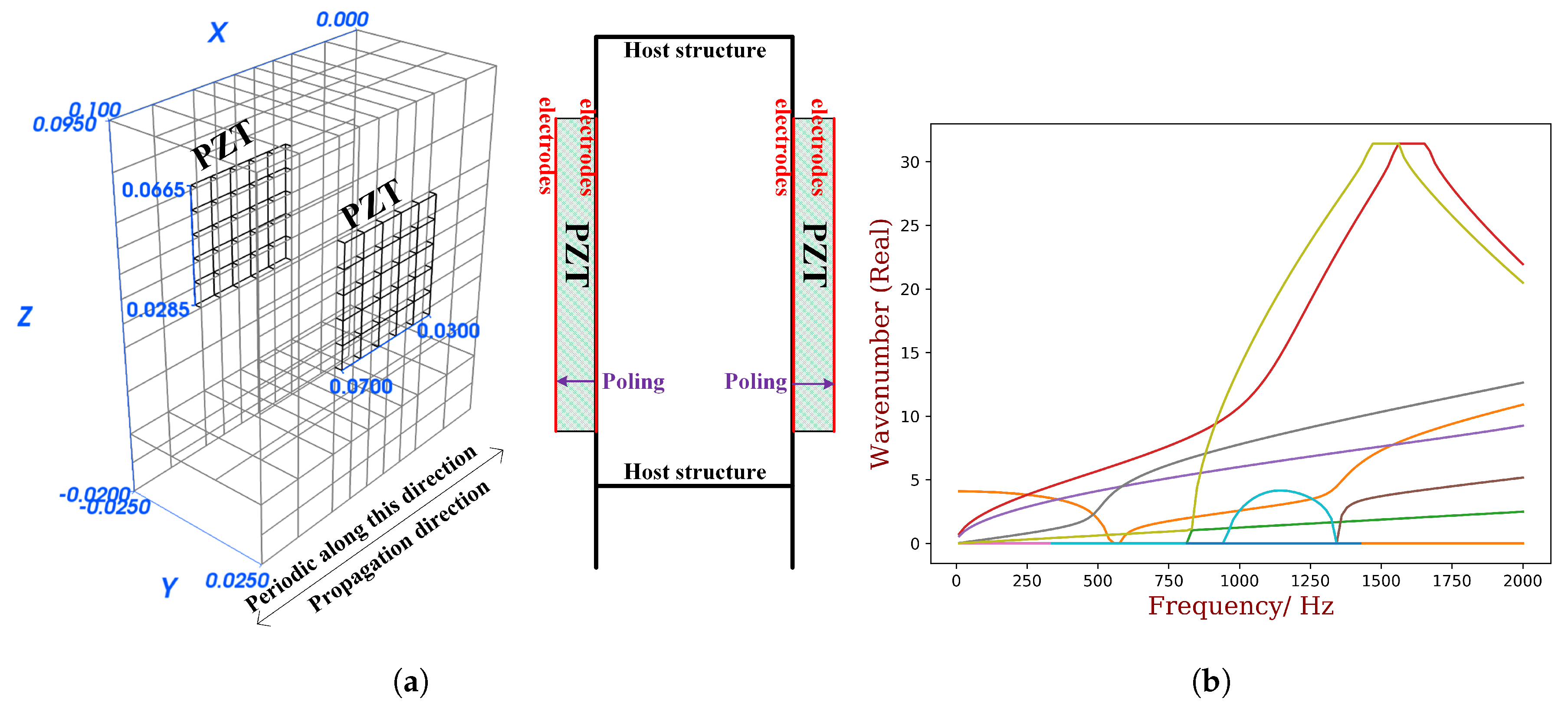
5.2. Validation against a Thin-Wall Piezoelectric Structure
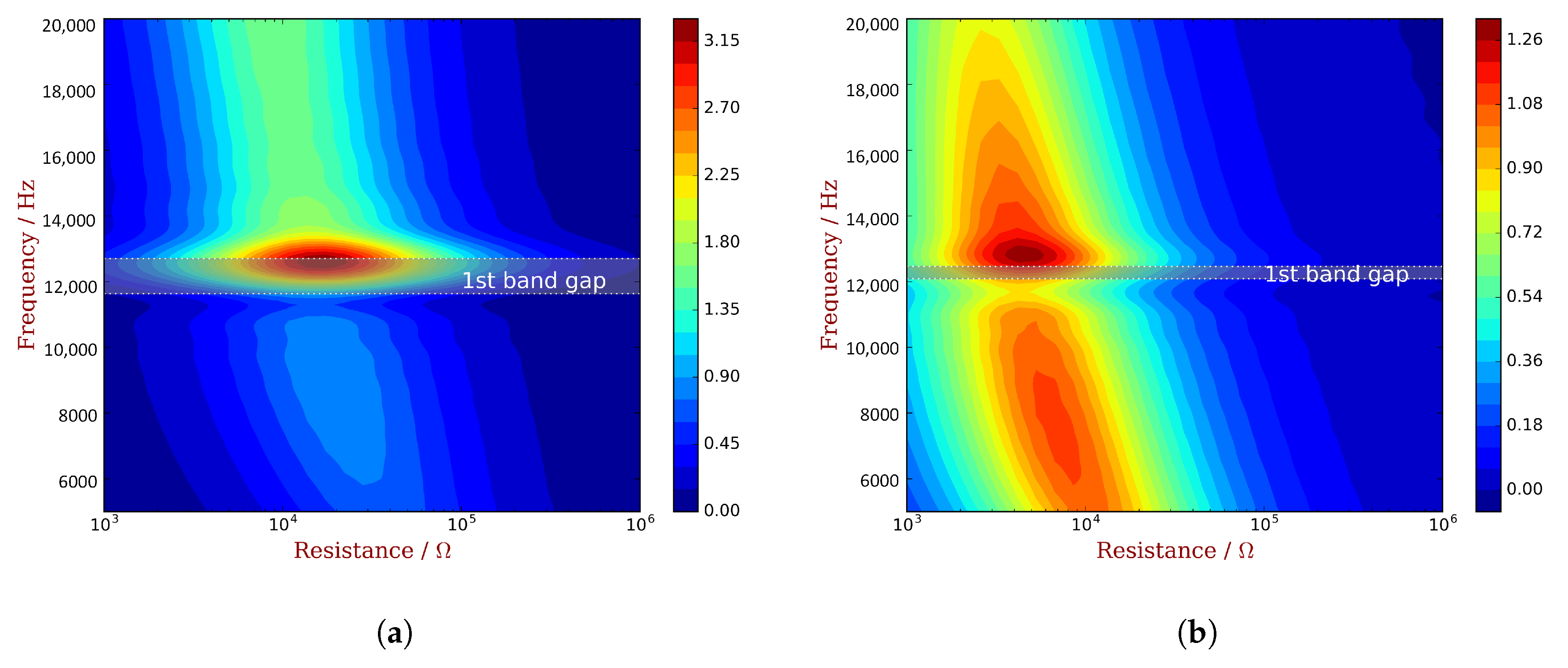
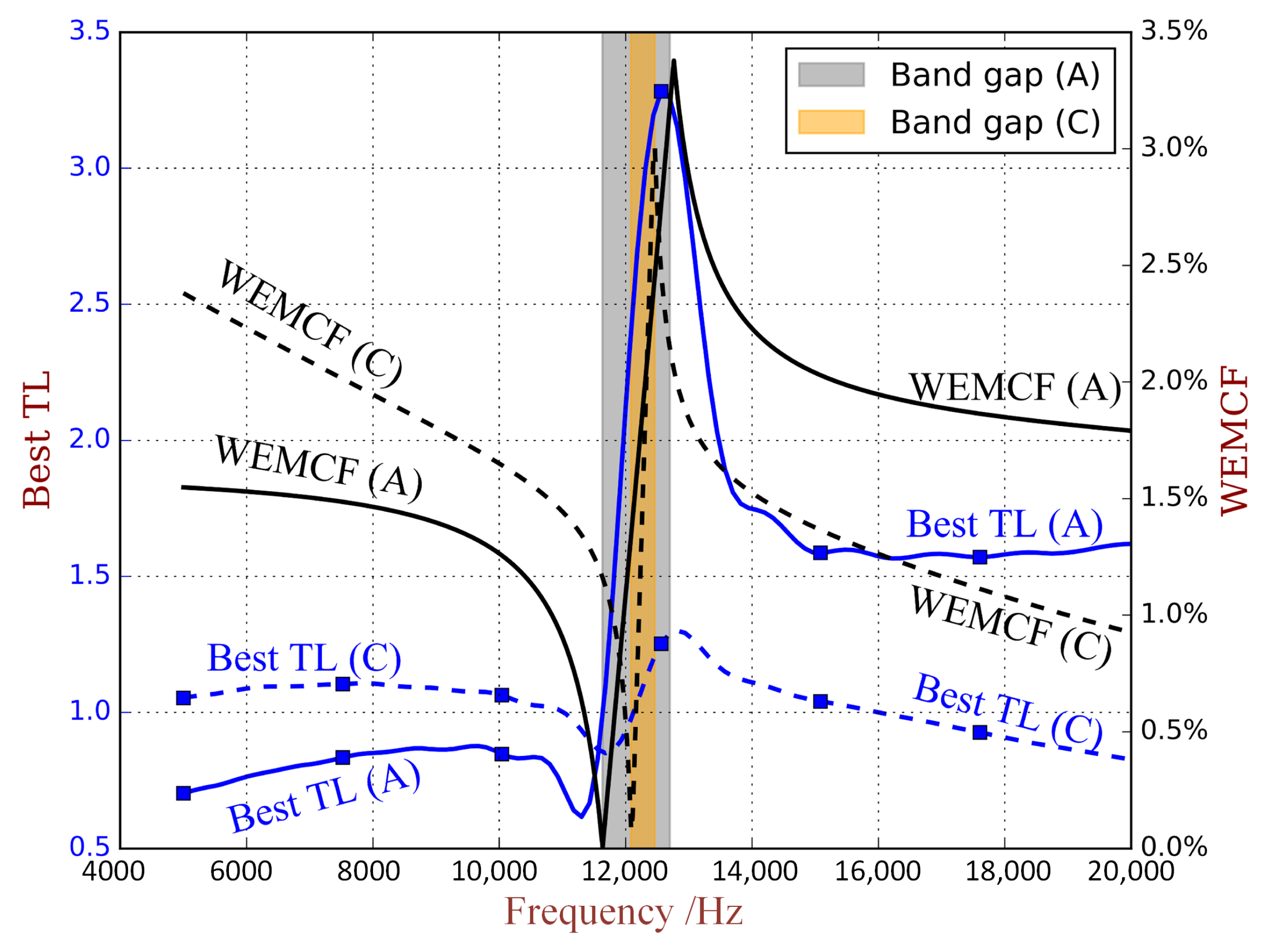
6. Application: Designing the Resistive PZT Waveguide
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EMCF | electromechanical coupling factor |
| WEMCF | wave electromechanical coupling factor |
| MEMCF | modal electromechanical coupling factor |
| WFEM | wave and finite element method |
| FRF | frequency response function |
| TL | transmission loss |
| OC | open circuit |
| SC | short circuit |
| DOF | Degree-of-freedom |
Appendix A. Material Properties of the Piezoelectric Material (PZT4)
References
- Priya, S.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: Boston, MA, USA, 2009; pp. 325–336. [Google Scholar]
- Qin, Q.H. Advanced Mechanics of Piezoelectricity; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Berlincourt, D.A.; Curran, D.R.; Jaffe, H. Piezoelectric and Piezomagnetic Materials and Their Function in Transducers. In Physical Acoustics; Elsevier: New York, NY, USA, 1964; pp. 169–270. [Google Scholar]
- IEEE. IEEE Standard on Piezoelectricity; IEEE: Piscataway, NJ, USA, 1988. [Google Scholar]
- Wasa, K.; Ito, S.; Nakamura, K.; Matsunaga, T.; Kanno, I.; Suzuki, T.; Okino, H.; Yamamoto, T.; Seo, S.H.; Noh, D.Y. Electromechanical coupling factors of single-domain 0.67Pb(Mg1/3Nb2/3)O3-0.33PbTiO3 single-crystal thin films. Appl. Phys. Lett. 2006, 88, 122903. [Google Scholar] [CrossRef] [Green Version]
- Pijolat, M.; Loubriat, S.; Queste, S.; Mercier, D.; Reinhardt, A.; Defaÿ, E.; Deguet, C.; Clavelier, L.; Moriceau, H.; Aïd, M.; et al. Large electromechanical coupling factor film bulk acoustic resonator with X-cut LiNbO3 layer transfer. Appl. Phys. Lett. 2009, 95, 182106. [Google Scholar] [CrossRef]
- Mason, W.P.; Baerwald, H. Piezoelectric Crystals and Their Applications to Ultrasonics. Phys. Today 1951, 4, 23. [Google Scholar] [CrossRef]
- Preumont, A. Dynamics of Electromechanical and Piezoelectric Systems; Springer: Dordrecht, The Netherlands, 2006; p. 224. [Google Scholar]
- Thomas, O.; Ducarne, J.; Deü, J.F. Performance of piezoelectric shunts for vibration reduction. Smart Mater. Struct. 2012, 21, 015008. [Google Scholar] [CrossRef] [Green Version]
- Vasques, C.M.A. Improved passive shunt vibration control of smart piezo-elastic beams using modal piezoelectric transducers with shaped electrodes. Smart Mater. Struct. 2012, 21, 125003. [Google Scholar] [CrossRef]
- Ducarne, J.; Thomas, O.; Deü, J.F. Placement and dimension optimization of shunted piezoelectric patches for vibration reduction. J. Sound Vib. 2012, 331, 3286–3303. [Google Scholar] [CrossRef]
- Li, L.; Yin, S.; Liu, X.; Li, J. Enhanced electromechanical coupling of piezoelectric system for multimodal vibration. Mechatronics 2015, 31, 205–214. [Google Scholar] [CrossRef]
- Mead, D. Waves and Modes in Finite Beams: Application of the Phase-Closure Principle. J. Sound Vib. 1994, 171, 695–702. [Google Scholar] [CrossRef]
- Langley, R. Some perspectives on wave-mode duality in SEA. In Proceedings of the IUTAM International Symposium on Statistical Energy Analysis, Southampton, UK, 8–11 July 1997; pp. 1–12. [Google Scholar]
- Wang, X.; So, R.; Chan, K. Resonant beam vibration: A wave evolution analysis. J. Sound Vib. 2006, 291, 681–705. [Google Scholar] [CrossRef]
- Collet, M.; Cunefare, K.; Ichchou, M. Wave Motion Optimization in Periodically Distributed Shunted Piezocomposite Beam Structures. J. Intell. Mater. Syst. Struct. 2008, 20, 787–808. [Google Scholar] [CrossRef]
- Tateo, F.; Collet, M.; Ouisse, M.; Ichchou, M.; Cunefare, K.; Abbe, P. Experimental characterization of a bi-dimensional array of negative capacitance piezo-patches for vibroacoustic control. J. Intell. Mater. Syst. Struct. 2015, 26, 952–964. [Google Scholar] [CrossRef]
- Chen, S.; Wang, G.; Wen, J.; Wen, X. Wave propagation and attenuation in plates with periodic arrays of shunted piezo-patches. J. Sound Vib. 2013, 332, 1520–1532. [Google Scholar] [CrossRef]
- Dai, L.; Jiang, S.; Lian, Z.; Hu, H.; Chen, X. Locally resonant band gaps achieved by equal frequency shunting circuits of piezoelectric rings in a periodic circular plate. J. Sound Vib. 2015, 337, 150–160. [Google Scholar] [CrossRef]
- Bareille, O.; Kharrat, M.; Zhou, W.; Ichchou, M. Distributed piezoelectric guided-T-wave generator, design and analysis. Mechatronics 2012, 22, 544–551. [Google Scholar] [CrossRef]
- Thien, A.B.; Chiamori, H.C.; Ching, J.T.; Wait, J.R.; Park, G. The use of macro-fibre composites for pipeline structural health assessment. Struct. Control Health Monit. 2008, 15, 43–63. [Google Scholar] [CrossRef]
- Su, Z.; Ye, L. Selective generation of Lamb wave modes and their propagation characteristics in defective composite laminates. Proc. Inst. Mech. Eng. Part L 2004, 218, 95–110. [Google Scholar] [CrossRef]
- Mueller, I.; Fritzen, C.P. Inspection of Piezoceramic Transducers Used for Structural Health Monitoring. Materials 2017, 10, 71. [Google Scholar] [CrossRef] [PubMed]
- Ono, K. On the Piezoelectric Detection of Guided Ultrasonic Waves. Materials 2017, 10, 1325. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Zhang, Y.; Lin, S.; Fu, Z. Study on the electromechanical coupling coefficient of Rayleigh-type surface acoustic waves in semi-infinite piezoelectrics/non-piezoelectrics superlattices. Ultrasonics 2014, 54, 604–608. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Zhang, S.Y.; Zheng, K.; Lin, W.; Gao, H.D. Calculation of electromechanical coupling coefficient of Lamb waves in multilayered plates. Ultrasonics 2006, 44 (Suppl. 1), e849–e852. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Collet, M.; Ichchou, M.; Li, L.; Bareille, O.; Dimitrijevic, Z. A wave-based design of semi-active piezoelectric composites for broadband vibration control. Smart Mater. Struct. 2016, 25, 055032. [Google Scholar] [CrossRef]
- Chang, S.; Rogacheva, N.; Chou, C. Analysis of methods for determining electromechanical coupling coefficients of piezoelectric elements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 630–640. [Google Scholar] [CrossRef]
- Mead, D. Wave propagation and natural modes in periodic systems: II. Multi-coupled systems, with and without damping. J. Sound Vib. 1975, 40, 19–39. [Google Scholar] [CrossRef]
- Fan, Y.; Zhou, C.; Laine, J.; Ichchou, M.; Li, L. Model reduction schemes for the wave and finite element method using the free modes of a unit cell. Comput. Struct. 2018, 197, 42–57. [Google Scholar] [CrossRef]
- Fan, Y.; Collet, M.; Ichchou, M.; Li, L.; Bareille, O.; Dimitrijevic, Z. Energy flow prediction in built-up structures through a hybrid finite element/wave and finite element approach. Mech. Syst. Signal Proc. 2016, 66-67, 137–158. [Google Scholar] [CrossRef]
- Mead, D. The forced vibration of one-dimensional multi-coupled periodic structures: An application to finite element analysis. J. Sound Vib. 2009, 319, 282–304. [Google Scholar] [CrossRef]
- Zhou, C.W.; Lainé, J.P.; Ichchou, M.; Zine, A.M. Wave finite element method based on reduced model for periodic structures. Int. J. Appl. Mech. 2015, 07, 1550018. [Google Scholar] [CrossRef]
- Mencik, J.M. New advances in the forced response computation of periodic structures using the wave finite element (WFE) method. Comput. Mech. 2014, 54, 789–801. [Google Scholar] [CrossRef] [Green Version]
- Waki, Y.; Mace, B.; Brennan, M. Numerical issues concerning the wave and finite element method for free and forced vibrations of waveguides. J. Sound Vib. 2009, 327, 92–108. [Google Scholar] [CrossRef]
- Fan, Y.; Collet, M.; Ichchou, M.; Li, L.; Bareille, O.; Dimitrijevic, Z. Enhanced wave and finite element method for wave propagation and forced response prediction in periodic piezoelectric structures. Chin. J. Aeronaut. 2017, 30, 75–87. [Google Scholar] [CrossRef]
- Benjeddou, A. Advances in piezoelectric finite element modeling of adaptive structural elements: A survey. Comput. Struct. 2000, 76, 347–363. [Google Scholar] [CrossRef]
- Zhou, C. Wave and Modal Coupled Approach for Multi-Scale Analysis of Periodic Structures. Ph.D. Thesis, Ecole Centrale de Lyon, Ecully, France, 2014. [Google Scholar]
- Mead, D. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling. J. Sound Vib. 1973, 27, 235–260. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Collet, M.; Ichchou, M.; Bareille, O.; Li, L. Wave Electromechanical Coupling Factor for the Guided Waves in Piezoelectric Composites. Materials 2018, 11, 1406. https://doi.org/10.3390/ma11081406
Fan Y, Collet M, Ichchou M, Bareille O, Li L. Wave Electromechanical Coupling Factor for the Guided Waves in Piezoelectric Composites. Materials. 2018; 11(8):1406. https://doi.org/10.3390/ma11081406
Chicago/Turabian StyleFan, Yu, Manuel Collet, Mohamed Ichchou, Olivier Bareille, and Lin Li. 2018. "Wave Electromechanical Coupling Factor for the Guided Waves in Piezoelectric Composites" Materials 11, no. 8: 1406. https://doi.org/10.3390/ma11081406





