Transient Thermal Stress Problem of a Functionally Graded Magneto-Electro-Thermoelastic Hollow Sphere
Abstract
:1. Introduction
2. Analysis
2.1. Heat Conduction Problem
2.2. Thermoelastic Problem
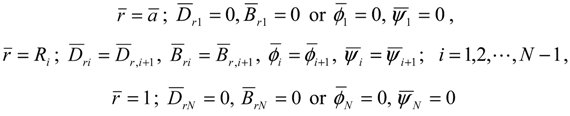
3. Numerical Results

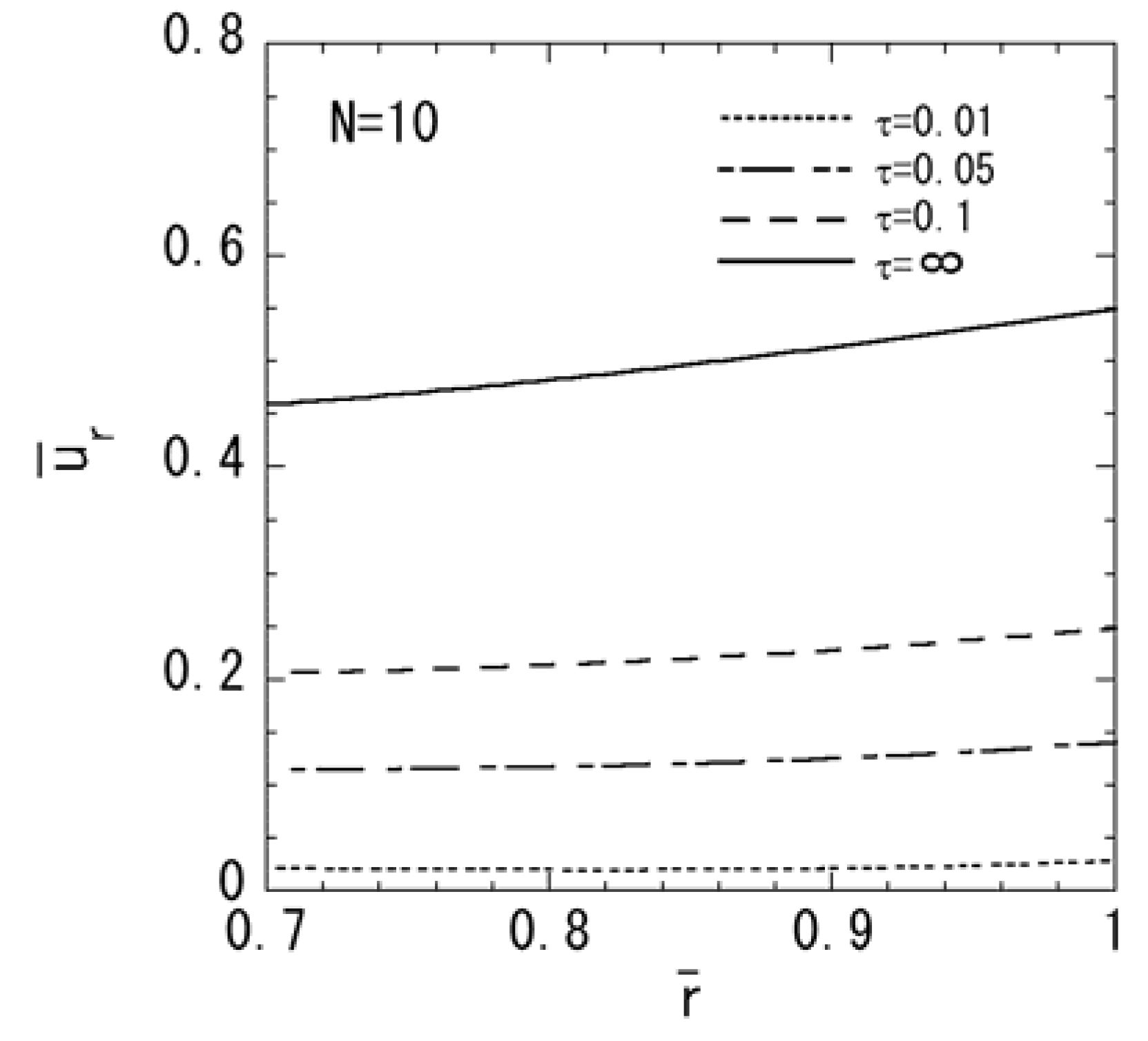
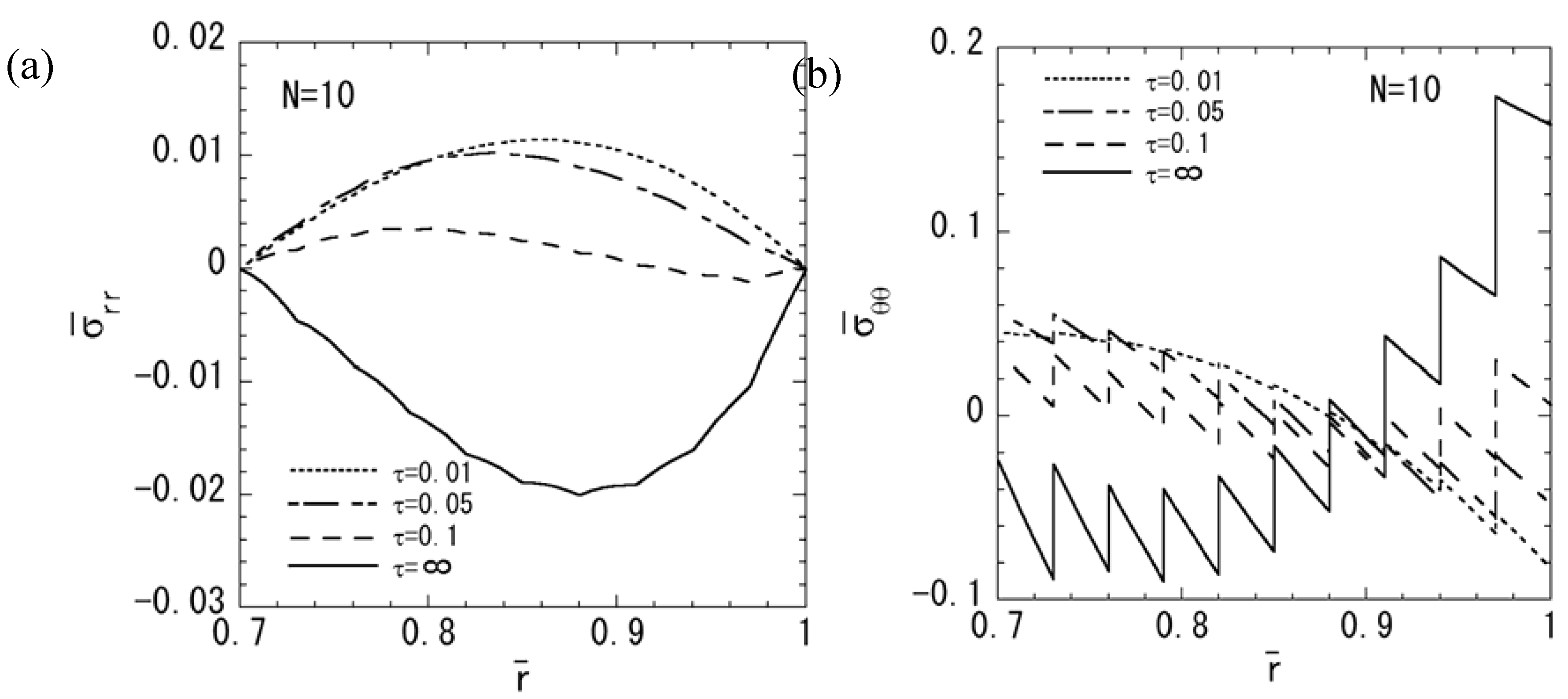
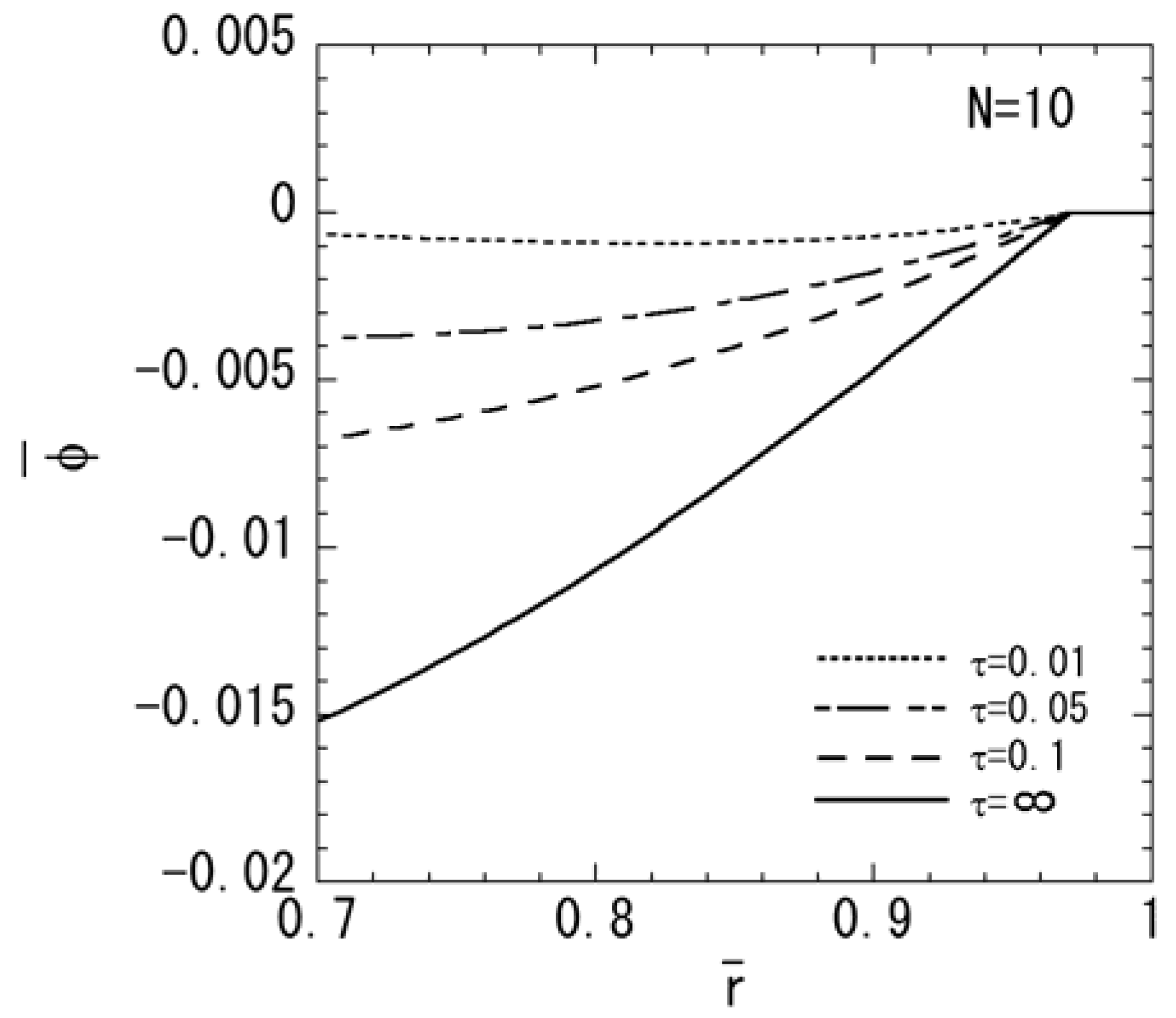

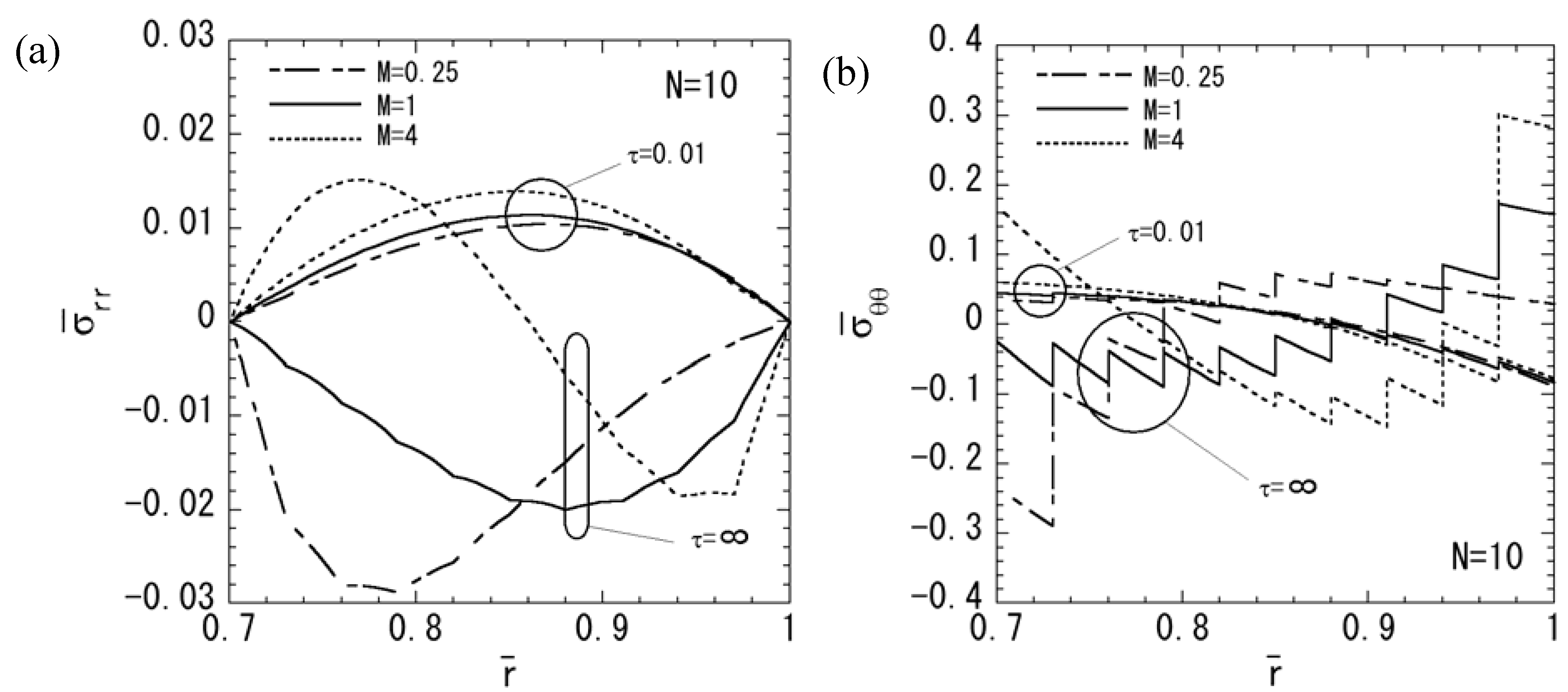
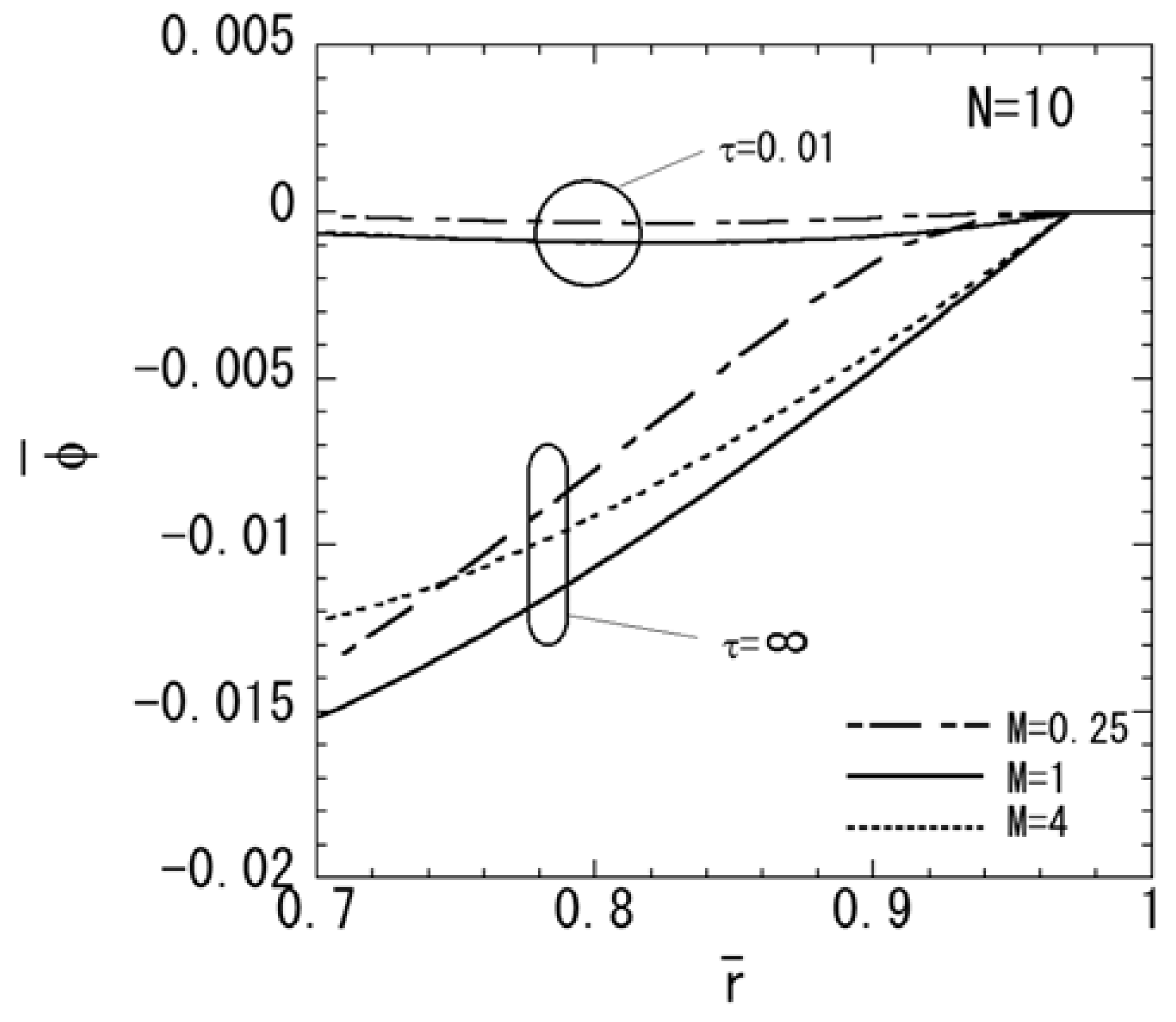
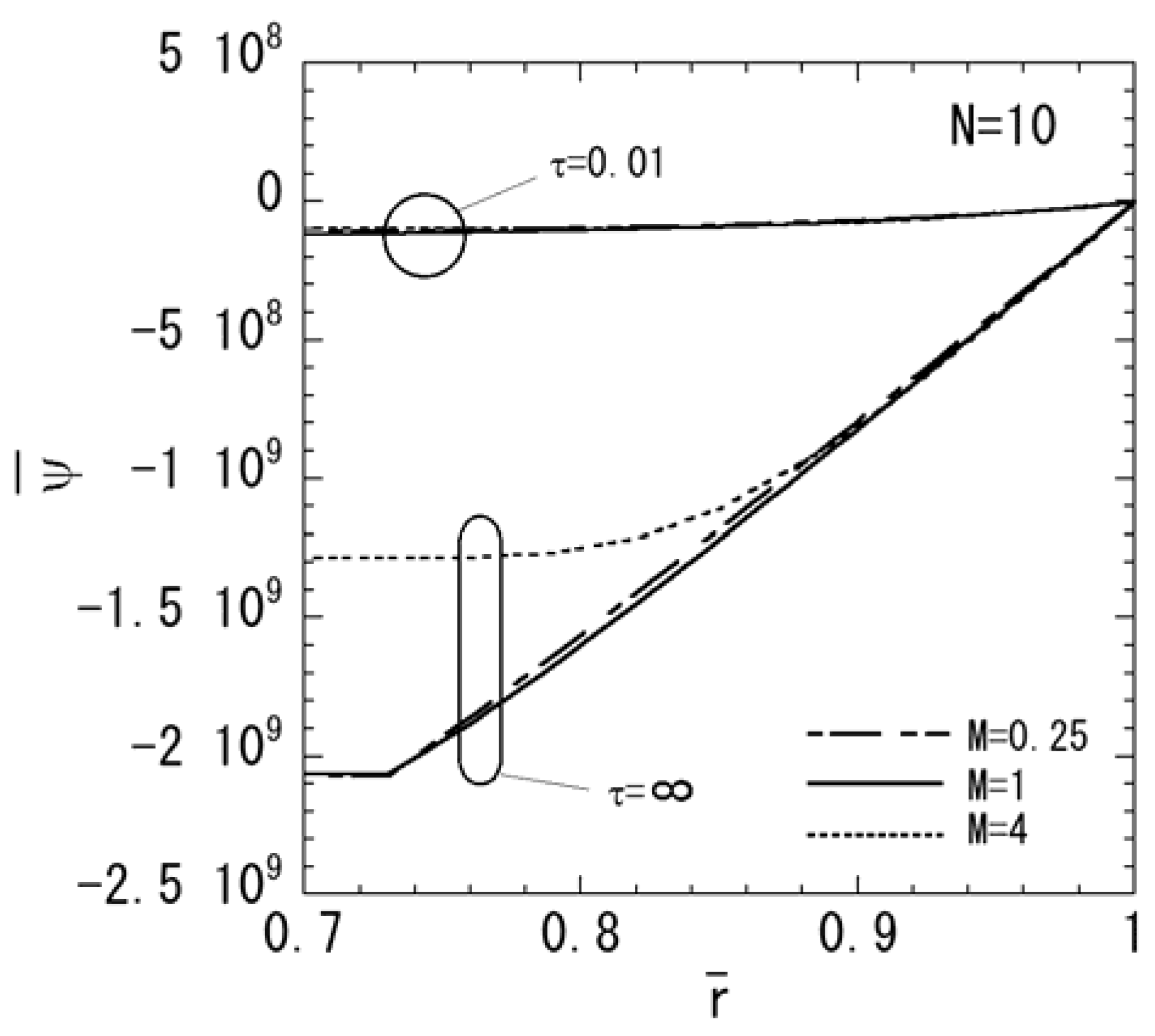
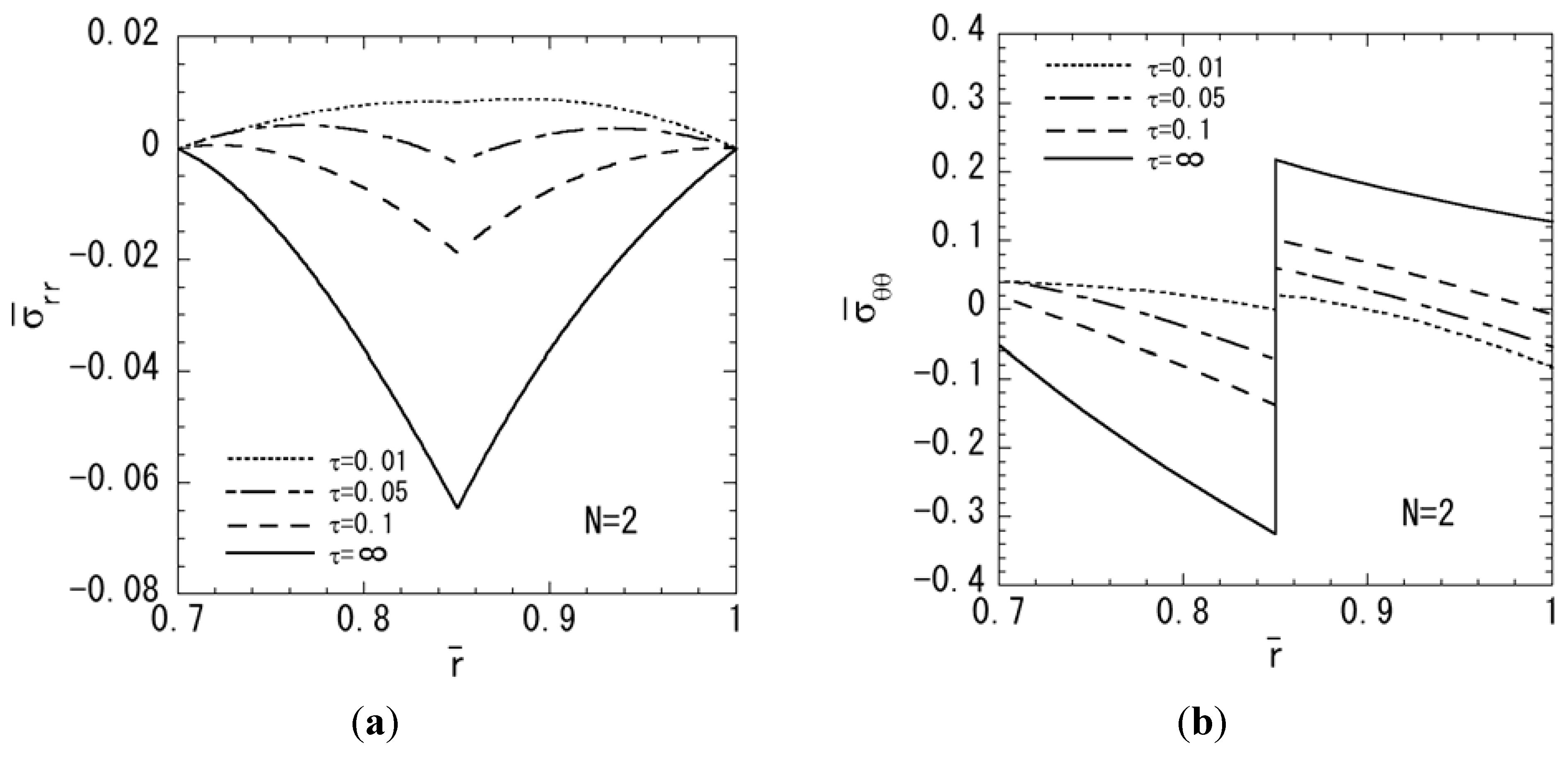
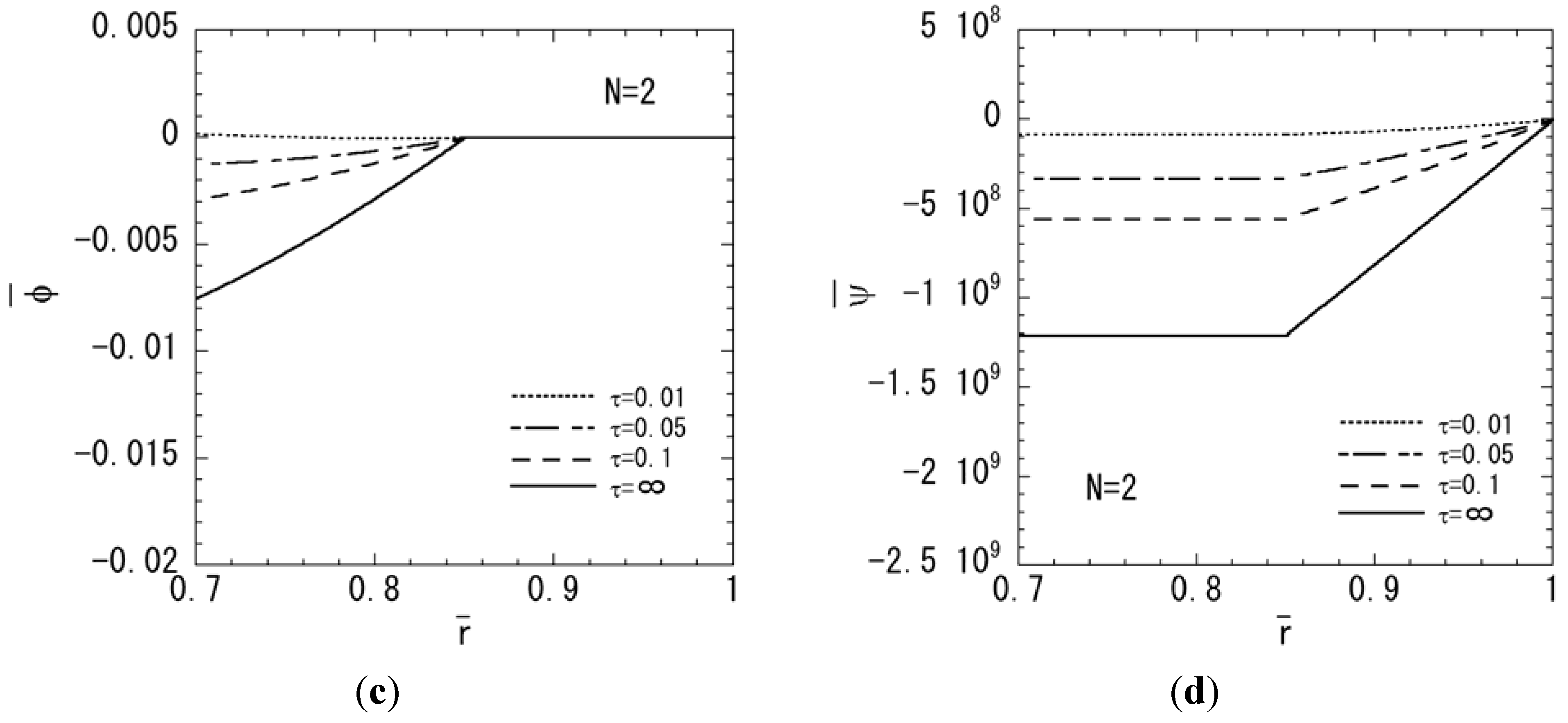
4. Conclusions
References
- Harrshe, G.; Dougherty, J.P.; Newnhan, R.E. Theoretical modeling of multilayer magnetoelectric composite. Int. J. Appl. Electromagn Mater. 1993, 4, 145–159. [Google Scholar]
- Nan, C.W. Magnetoelectric effect in composites of piezoelectric and piezomagnetic phases. Phys. Rev. B 1994, 50, 6082–6088. [Google Scholar]
- Pan, E.; Heyliger, P.R. Exact solutions for magneto-electro-elastic laminates in cylindrical bending. Int. J. Solids Struct. 2003, 40, 6859–6876. [Google Scholar]
- Anandkumar, R.; Annigeri, R.; Ganesan, N.; Swarnamani, S. Free vibration behavior of multiphase and layered magneto-electro-elastic beam. J. Sound Vib. 2007, 299, 44–63. [Google Scholar]
- Wang, R.; Han, Q.; Pan, E. An analytical solution for a multilayered magneto-electro-elastic circular plate under simply supported lateral boundary conditions. Smart Mater. Struc. 2010, 19, 065025. [Google Scholar]
- Babaei, M.H.; Chen, Z.T. Exact solutions for radially polarized and magnetized magnetoelectroelastic rotating cylinders. Smart Mater. Struc. 2008, 17, 025035. [Google Scholar]
- Ying, J.; Wang, H.M. Magnetoelectroelastic fields in rotating multiferroic composite cylindrical structures. J. Zhejiang Univ. Sci. A 2009, 10, 319–326. [Google Scholar]
- Wang, H.M.; Ding, H.J. Transient responses of a magneto-electro-elastic hollow sphere for fully coupled spherically symmetric problem. Eur. J. Mech. A Solids 2006, 25, 965–980. [Google Scholar]
- Wang, H.M.; Ding, H.J. Spherically symmetric transient responces of functionally graded magneto-electro-elastic hollow sphere. Struct. Eng. Mech. 2006, 23, 525–542. [Google Scholar]
- Ma, C.C.; Lee, J.M. Theoretical analysis of in-plane problem in functionally graded nonhomogeneous magnetoelectroelastic bimaterials. Int. J. Solids Struct. 2009, 46, 4208–4220. [Google Scholar]
- Yu, J.; Wu, B. Circumferential wave in magneto-electro-elastic functionally graded cylindrical curved plates. Eur. J. Mech. A Solids 2009, 28, 560–568. [Google Scholar]
- Wu, C.P.; Lu, Y.C. A modified pagano method for 3d dynamic responses of functionally graded magneto-electro-elastic plates. Compount. Struct. 2009, 90, 363–372. [Google Scholar]
- Huang, D.J.; Ding, H.J.; Chen, W.Q. Static analysis of anisotropic functionally graded magneto-electro-elastic beams subjected to arbitrary loading. Eur. J. Mech. A Solids. 2010, 29, 356–369. [Google Scholar]
- Lee, J.M.; Ma, C.C. Analytical solutions for an antiplane problem of two dissimilar functionally graded magnetoelectroelastic half-planes. Acta Mech. 2010, 212, 21–38. [Google Scholar]
- Ganesan, N.; Kumaravel, A.; Sethuraman, R. Finite element modeling of a layered, multiphase magnetoelectroelastic cylinder subjected to an axisymmetric temperature distribution. J. Mech. Mater. Struc. 2007, 2, 655–674. [Google Scholar]
- Kumaravel, A.; Ganesan, N.; Sethuraman, R. Steady-state analysis of a three-layered electro-magneto-elastic strip in a thermal environment. Smart Mater. Struct. 2007, 16, 282–295. [Google Scholar]
- Hou, P.F.; Yi, T.; Wang, L. 2D general solution and fundamental solution for orthotropic electro-magneto-elastic materials. J. Thermal Stresses 2008, 31, 807–822. [Google Scholar]
- Wang, B.L.; Niraula, O.P. Transient thermal fracture analysis of transversely isotropic magneto-electro-elastic materials. J. Thermal Stresses 2007, 30, 297–317. [Google Scholar]
- Ootao, Y.; Tanigawa, Y. Transient analysis of multilayered magneto-electro-thermoelastic strip due to nonuniform heat supply. Compount. Struct. 2005, 68, 471–480. [Google Scholar]
- Ootao, Y.; Ishihara, M. Exact solution of transient thermal stress problem of a multilayered magneto-electro-thermoelastic hollow cylinder. J. Solid Mech. Mater. Eng. 2011, 5, 90–103. [Google Scholar]
- Ootao, Y.; Tanigawa, Y. Transient thermal stress analysis of a nonhomogeneous hollow sphere due to axisymmetric heat supply. Trans. Jpn. Soc. Mech. Eng. 1991, 57A, 1581–1587. [Google Scholar]
- Ootao, Y.; Tanigawa, Y. Three-dimensional transient thermal stress analysis of a nonhomogeneous hollow sphere with respect to rotating heat source. Jpn. Soc. Mech. Eng. 1994, 60A, 2273–2279. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ootao, Y.; Ishihara, M. Transient Thermal Stress Problem of a Functionally Graded Magneto-Electro-Thermoelastic Hollow Sphere. Materials 2011, 4, 2136-2150. https://doi.org/10.3390/ma4122136
Ootao Y, Ishihara M. Transient Thermal Stress Problem of a Functionally Graded Magneto-Electro-Thermoelastic Hollow Sphere. Materials. 2011; 4(12):2136-2150. https://doi.org/10.3390/ma4122136
Chicago/Turabian StyleOotao, Yoshihiro, and Masayuki Ishihara. 2011. "Transient Thermal Stress Problem of a Functionally Graded Magneto-Electro-Thermoelastic Hollow Sphere" Materials 4, no. 12: 2136-2150. https://doi.org/10.3390/ma4122136



