“Property Phase Diagrams” for Compound Semiconductors through Data Mining
Abstract
:1. Introduction
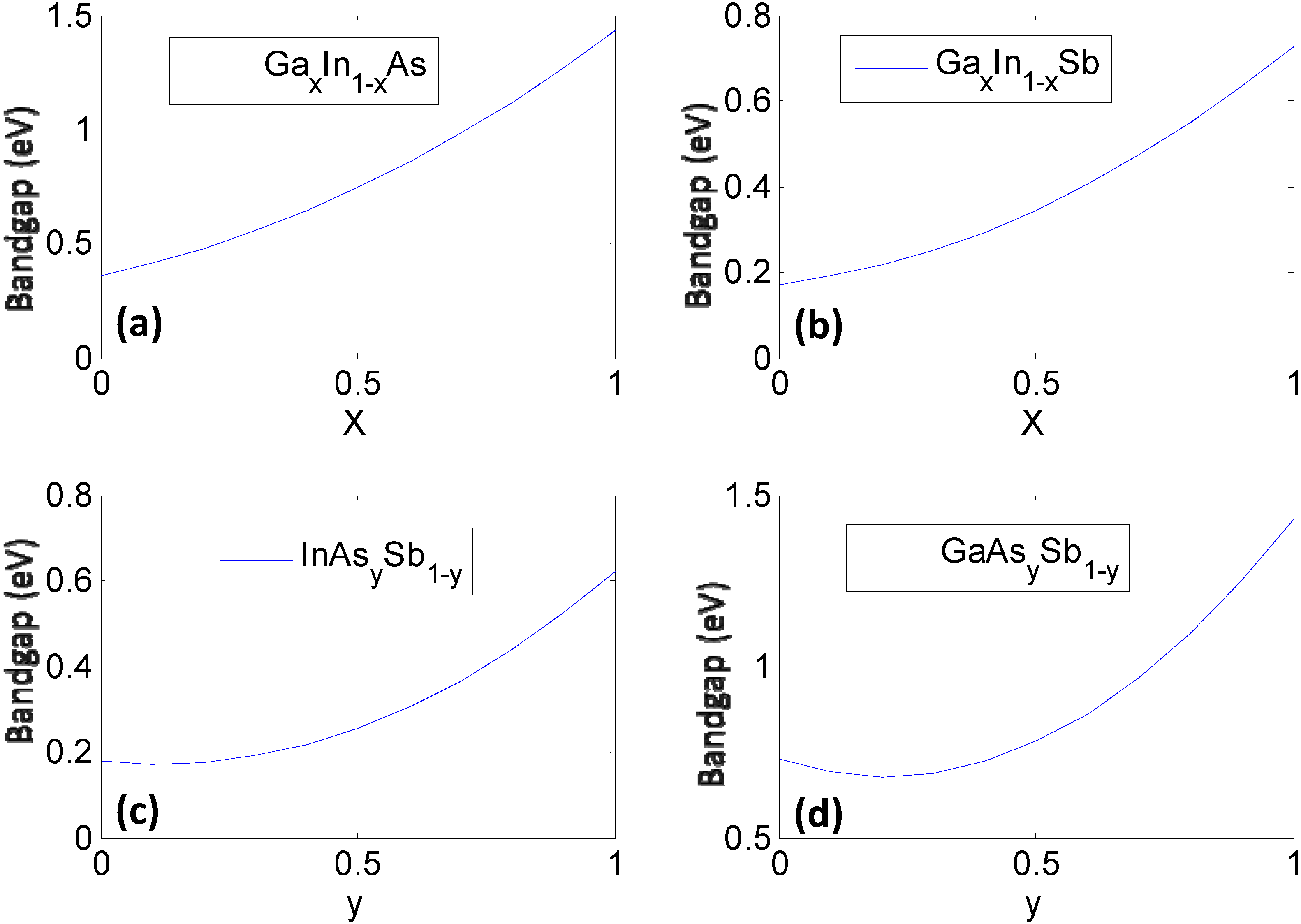
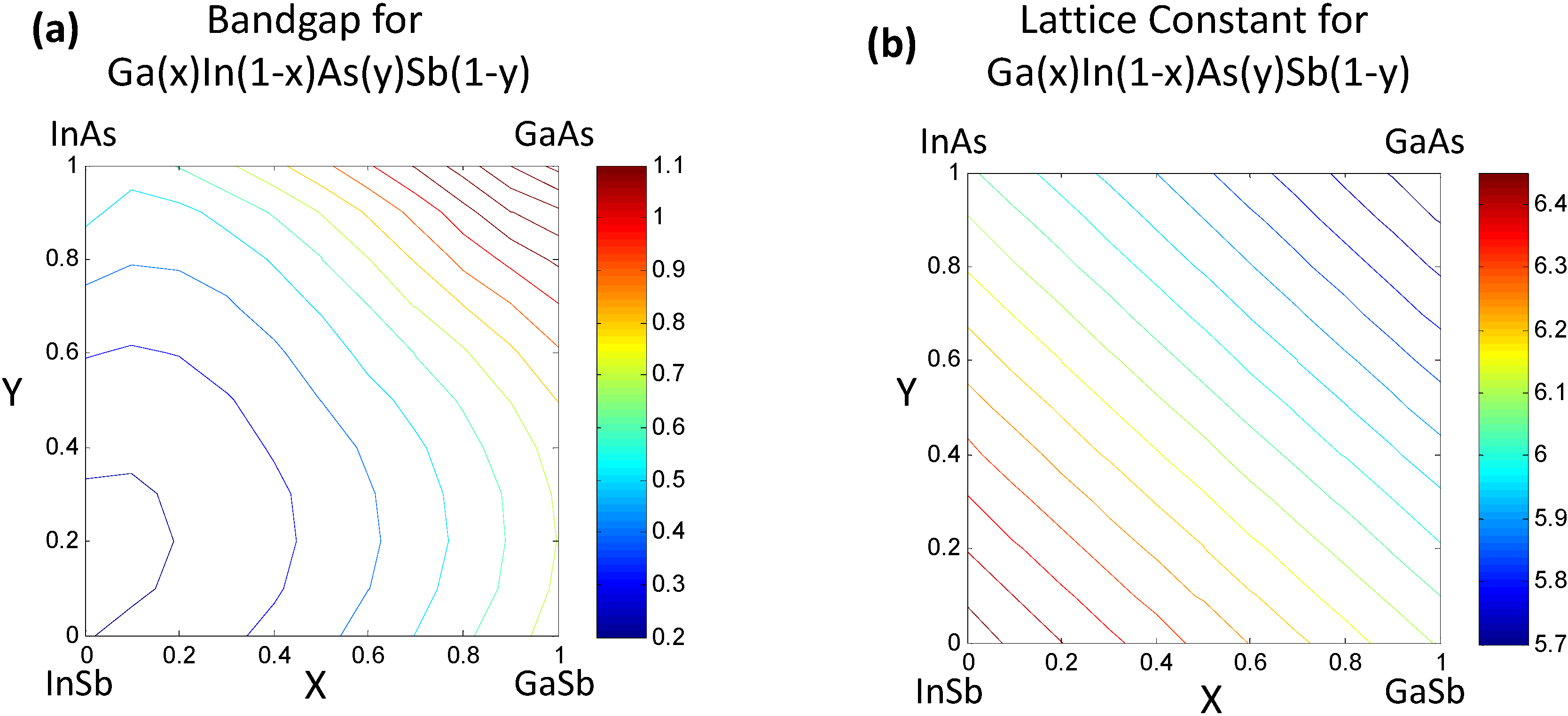
2. A High Dimensional Data Approach to Bandgap Engineering
2.2. Data Mining on Discrete Data
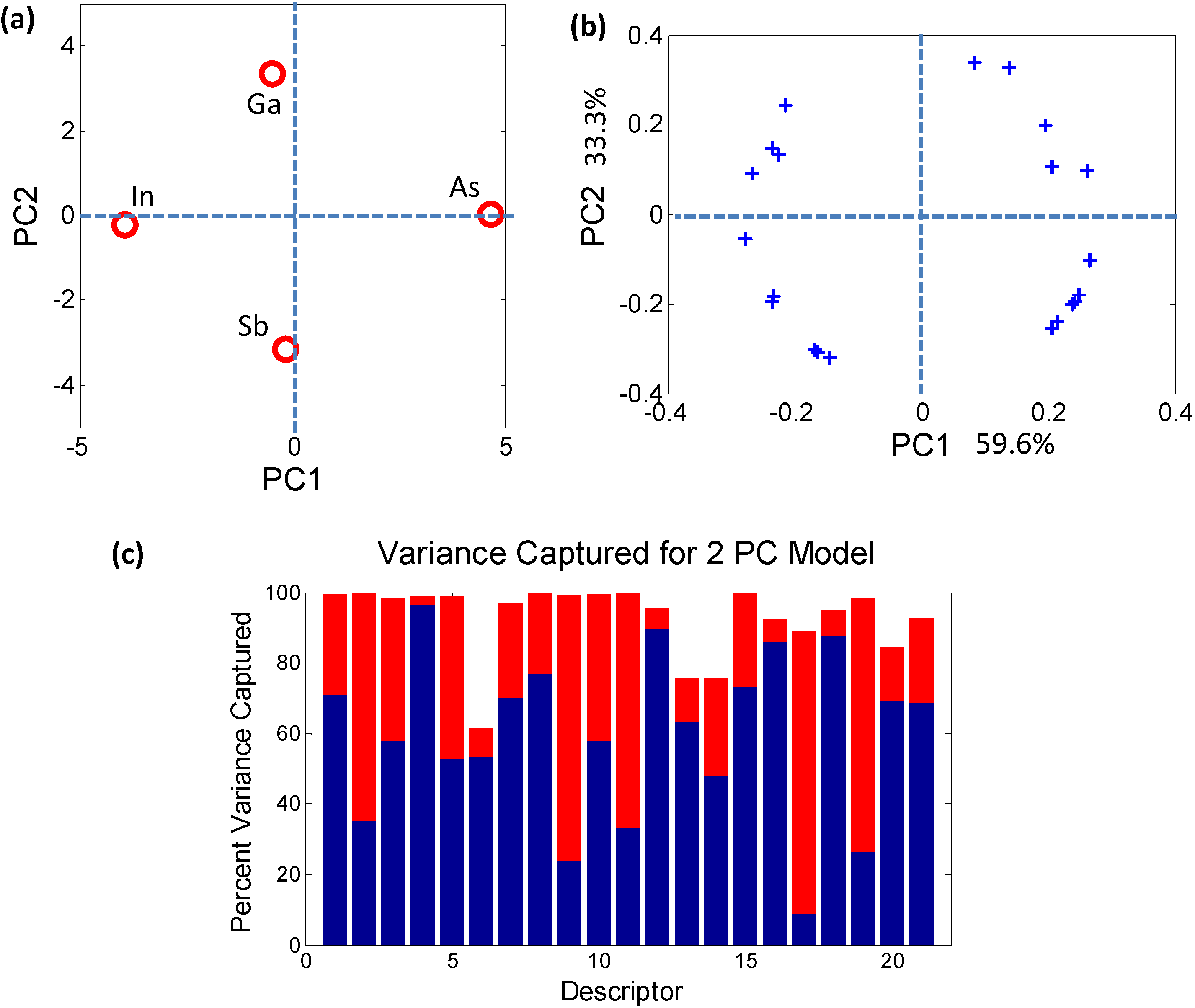
| Element | MB | AN | MP | PR | Nv | RH | CR | PEN | SH | HV | AW |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ga | 1.7 | 31 | 302.93 | 1.695 | 3 | −6.3 | 1.25 | 1.81 | 0.37 | 258.7 | 69.723 |
| In | 1.63 | 49 | 429.32 | 2.05 | 3 | −2.4 | 1.5 | 1.78 | 0.23 | 231.5 | 114.818 |
| Sb | 2.14 | 51 | 903.89 | 1.765 | 5 | −198 | 1.41 | 2.05 | 0.21 | 77.14 | 121.757 |
| As | 2.27 | 33 | 1090 | 1.415 | 5 | 450 | 1.21 | 2.18 | 0.33 | 34.76 | 74.92159 |
| Element | C | Sig | DT | FIP | SIP | EU | WF | AR | BP | D |
|---|---|---|---|---|---|---|---|---|---|---|
| Ga | 25.86 | 0.0678 | 320 | 6 | 26.51 | 20.51 | 4.2 | 1.22 | 2676 | 5.907 |
| In | 26.74 | 0.116 | 108 | 5.78 | 24.64 | 18.86 | 4.12 | 1.63 | 2353 | 7.31 |
| Sb | 25.23 | 0.0288 | 211 | 8.64 | 25.1 | 16.46 | 4.55 | 1.82 | 1908 | 6.691 |
| As | 24.64 | 0.0345 | 282 | 9.81 | 30 | 20.19 | 5.2 | 1.25 | 889 | 5.78 |
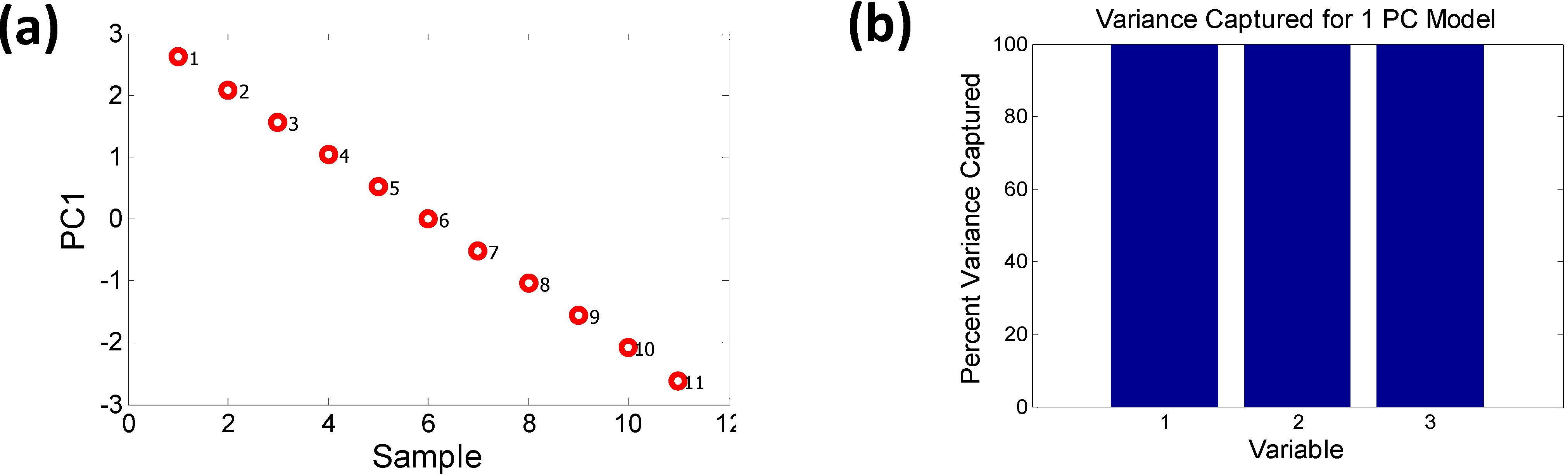
2.2.1. Dimensionality Reduction of Discrete Data—e.g., Principal Component Analysis

2.2.2. Characterizing Ternary Compounds Using the Reduced Set of Elemental Descriptors
- EN = 2x(ENA − ENB) + 2x(ENA − ENC) + 2y(ENB − ENC)
- AN = x(AN)A + y(AN)B + z(AN)C
- MP = x(MP)A + y(MP)B + z(MP)C
- PR = 2x(PRA − PRB) + 2x(PRA − PRC) + 2y(PRB − PRC)
- Nv = x(Nv)A + y(Nv)B + z(Nv)C
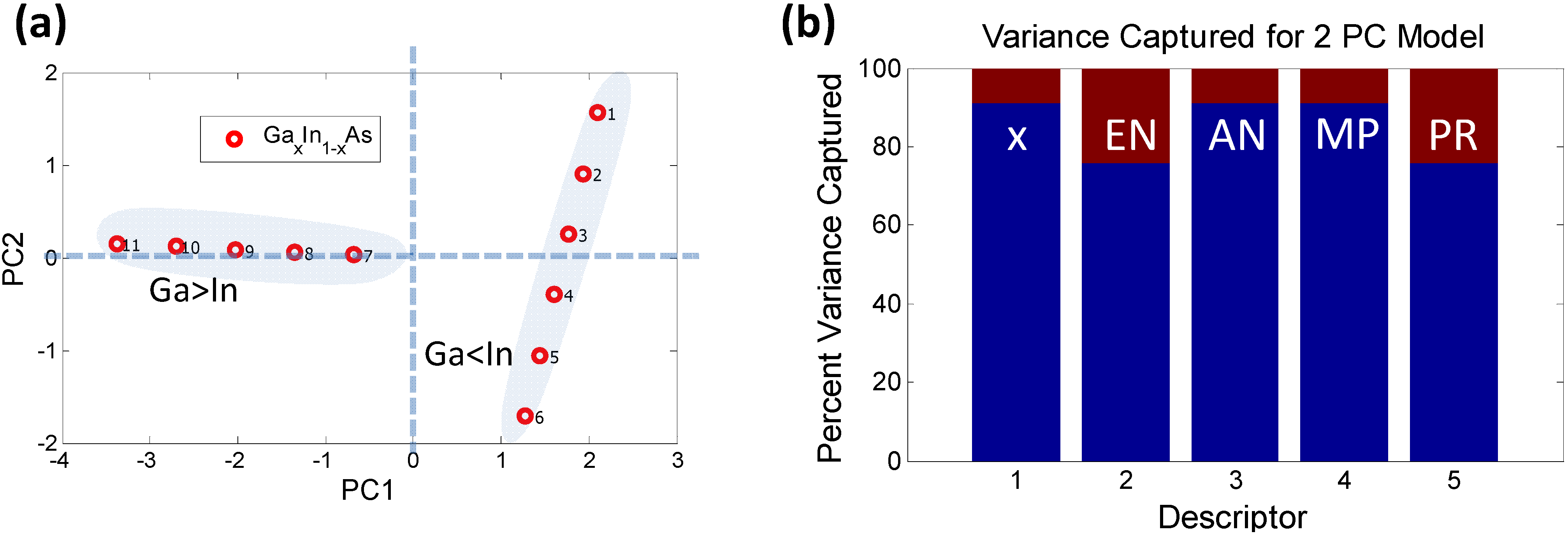
2.3. Relating the Elemental Descriptors to Bandgap Bowing
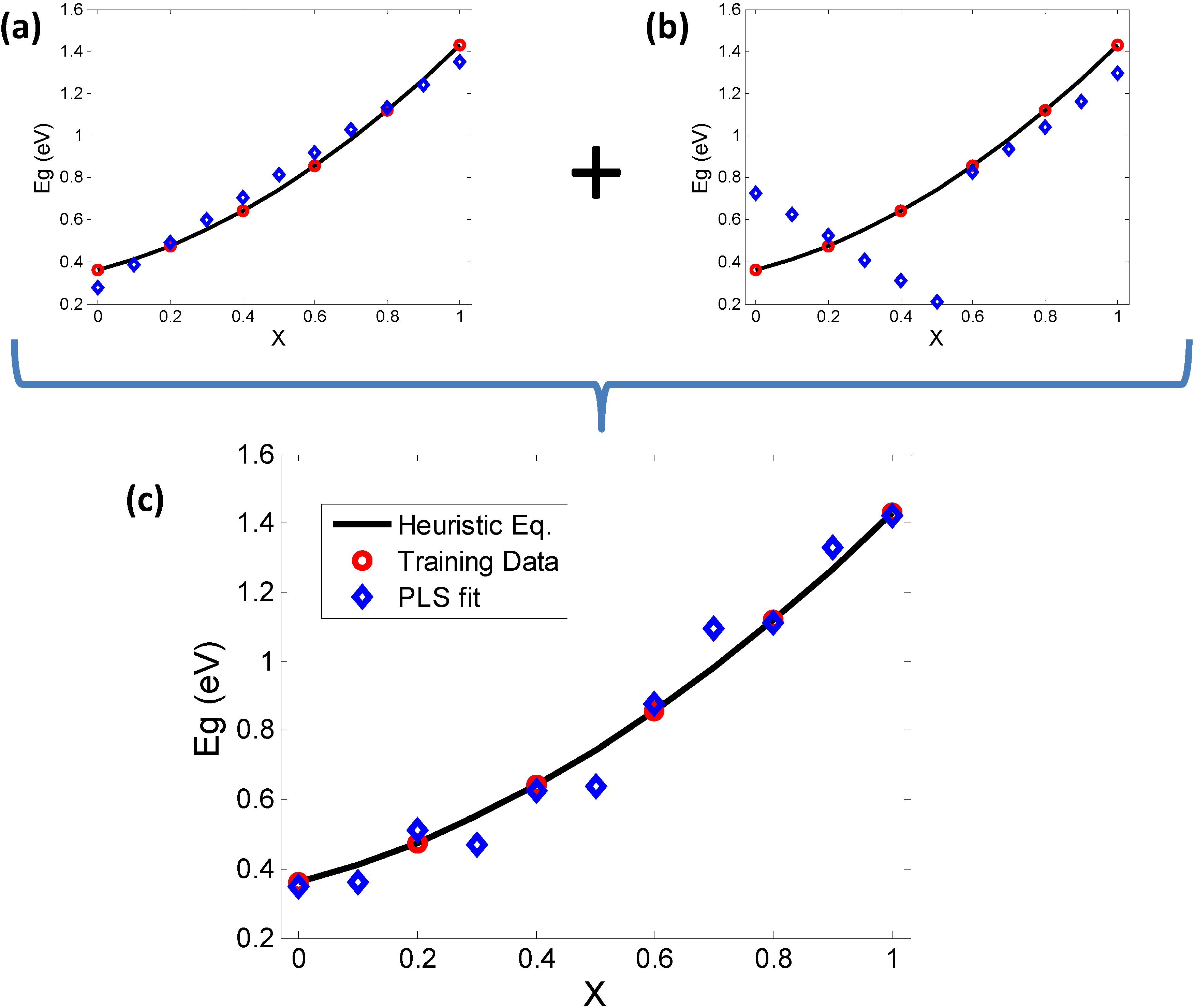
3. Conclusions
Acknowledgments
References
- Connolly, J.A.D. Multivariable phase diagrams: An algorithm based on generalized thermodynamics. Am. J. Sci. 1990, 290, 666–718. [Google Scholar] [CrossRef]
- Jones, H. The Theory of Brillouin Zones and Electronic States in Crystals; North-Holland Publishing Company: Amsterdam, the Netherland, 1960. [Google Scholar]
- Blakemore, J.S. Semiconducting and other major properties of gallium arsenide. J. Appl. Phys. 1982, 53, R123–R181. [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Rajan, K. Combinatorial materials sciences: Experimental strategies for accelerated knowledge discovery. Ann. Rev. Mater. Res. 2008, 38, 299–322. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.R.; Ram-Mohan, L.R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Rabitz, H.; Shim, K. Multicomponent semiconductor material discovery guided by a generalized correlated function expansion. J. Chem. Phys. 1999, 111, 10640–10651. [Google Scholar] [CrossRef]
- Shim, K.; Rabitz, H.; Dutta, P. Band gap and lattice constant of GaxIn1−xAsySb1−y. J. Appl. Phys. 2000, 88, 7157–7161. [Google Scholar] [CrossRef]
- Landolt, H.H.; Börnstein, R.; Hellwege, K.H.; Madelung, O.; Weiss, H.; Bimberg, D. Numerical Data and Functional Relationships in Science and Technology: New Series; Springer: Berlin, Germany, 1982. [Google Scholar]
- Rajan, K.; Suh, C.; Rajagopalan, A.; Li, X. Quantitative structure-activity relationships (QSARs) for materials science. MRS Proc. 2002, 700, 223–232. [Google Scholar]
- Suh, C.; Rajan, K. Combinatorial design of semiconductor chemistry for bandgap engineering: “Virtual” combinatorial experimentation. Appl. Surf. Sci. 2004, 223, 148–158. [Google Scholar] [CrossRef]
- Balachandran, P.V.; Broderick, S.R.; Rajan, K. Identifying the ‘inorganic gene’ for high-temperature piezoelectric perovskites through statistical learning. Proc. R. Soc. A 2011, 467, 2271–2290. [Google Scholar] [CrossRef] [PubMed]
- Broderick, S.R.; Suh, C.; Provine, J.; Roper, C.S.; Maboudian, R.; Howe, R.T.; Rajan, K. Application of principal component analysis to a full profile correlative analysis of FTIR spectra. Surf. Interface Anal. 2012, 44, 365–371. [Google Scholar] [CrossRef]
- Broderick, S.R.; Rajan, K. Eigenvalue decomposition of spectral features in density of states curves. Europhys. Lett. 2011, 95. [Google Scholar] [CrossRef]
- Broderick, S.R.; Nowers, J.R.; Narasimhan, B.; Rajan, K. Tracking chemical processing pathways in combinatorial polymer libraries via data mining. J. Comb. Chem. 2010, 12, 270–277. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C.; McEuen, P. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Emsley, J. The Elements; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Daffertshofer, A.; Lamoth, C.J.C.; Meijer, O.G.; Beek, P.J. PCA in studying coordination and variability: A tutorial. Clin. Biomech. 2004, 19, 415–428. [Google Scholar] [CrossRef]
- Joliffe, I.T.; Morgan, B.J. Principal component analysis and exploratory factor analysis. Stat. Methods Med. Res. 1992, 1, 69–95. [Google Scholar] [CrossRef] [PubMed]
- Berthiaux, H.; Mosorov, V.; Tomczak, L.; Gatumel, C.; Demeyre, U. Principal component analysis for characterising homogeneity in powder mixing using image processing techniques. Chem. Eng. Process 2006, 45, 397–403. [Google Scholar] [CrossRef]
- Villars, P.; Girgis, K.; Hulliger, F. A simple method for the prediction of new intermetallic phases. J. Solid State Chem. 1982, 42, 89–100. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression—A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Sjostrom, M.; Wold, S.; Lindberg, W.; Persson, J.A.; Martens, H. A multivariate calibration-problem in analytical-chemistry solved by partial least-squares models in latent-variables. Anal. Chim. Acta 1983, 150, 61–70. [Google Scholar] [CrossRef]
- Rajagopalan, A.; Suh, C.W.; Li, X.; Rajan, K. “Secondary” descriptor development for zeolite framework design: An informatics approach. Appl. Catal. A 2003, 254, 147–160. [Google Scholar] [CrossRef]
- Kong, C.S.; Luo, W.; Arapan, S.; Villars, P.; Iwata, S.; Ahuja, R.; Rajan, K. Information theoretic approach for the discovery of design rules for crystal chemistry. J. Chem. Inf. Mod. 2012, 52, 1812–1820. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Srinivasan, S.; Rajan, K. “Property Phase Diagrams” for Compound Semiconductors through Data Mining. Materials 2013, 6, 279-290. https://doi.org/10.3390/ma6010279
Srinivasan S, Rajan K. “Property Phase Diagrams” for Compound Semiconductors through Data Mining. Materials. 2013; 6(1):279-290. https://doi.org/10.3390/ma6010279
Chicago/Turabian StyleSrinivasan, Srikant, and Krishna Rajan. 2013. "“Property Phase Diagrams” for Compound Semiconductors through Data Mining" Materials 6, no. 1: 279-290. https://doi.org/10.3390/ma6010279