Interactions and Diffusion of Methane and Hydrogen in Microporous Structures: Nuclear Magnetic Resonance (NMR) Studies
Abstract
:1. Introduction
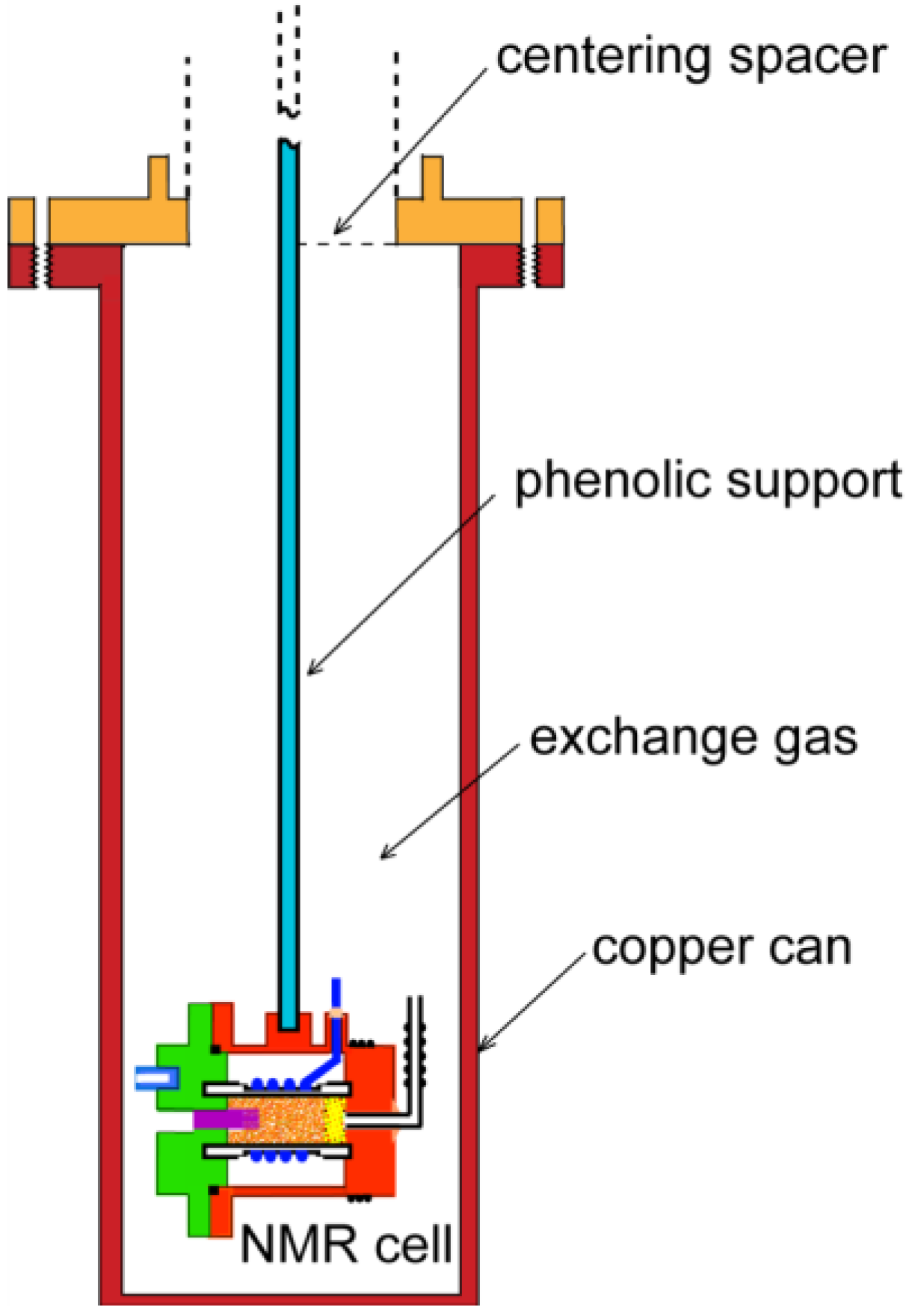
2. Experimental Section

3. Results and Discussion
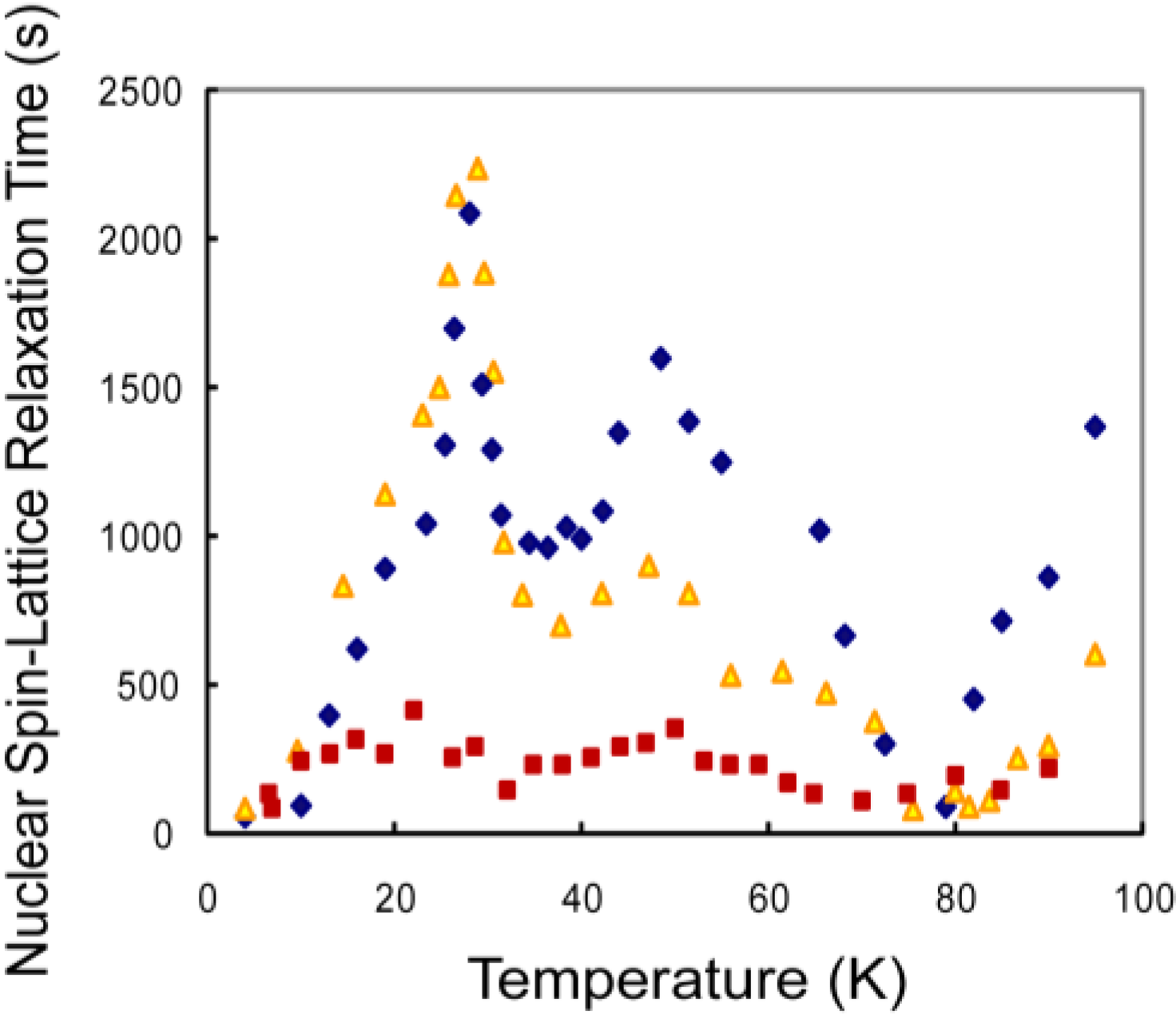
3.1. CH4 Molecules
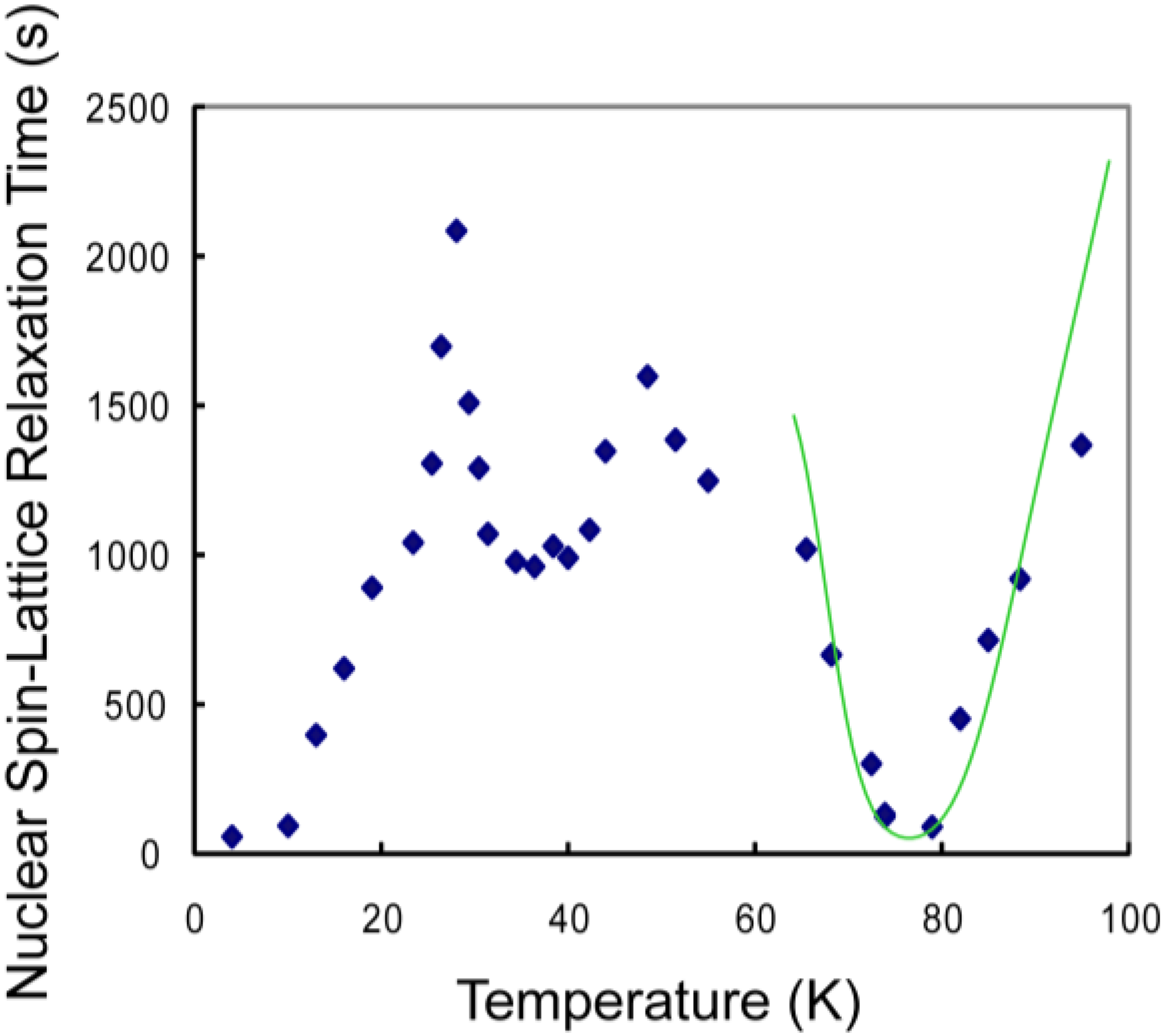
3.2. Hydrogen Deuteride Molecules
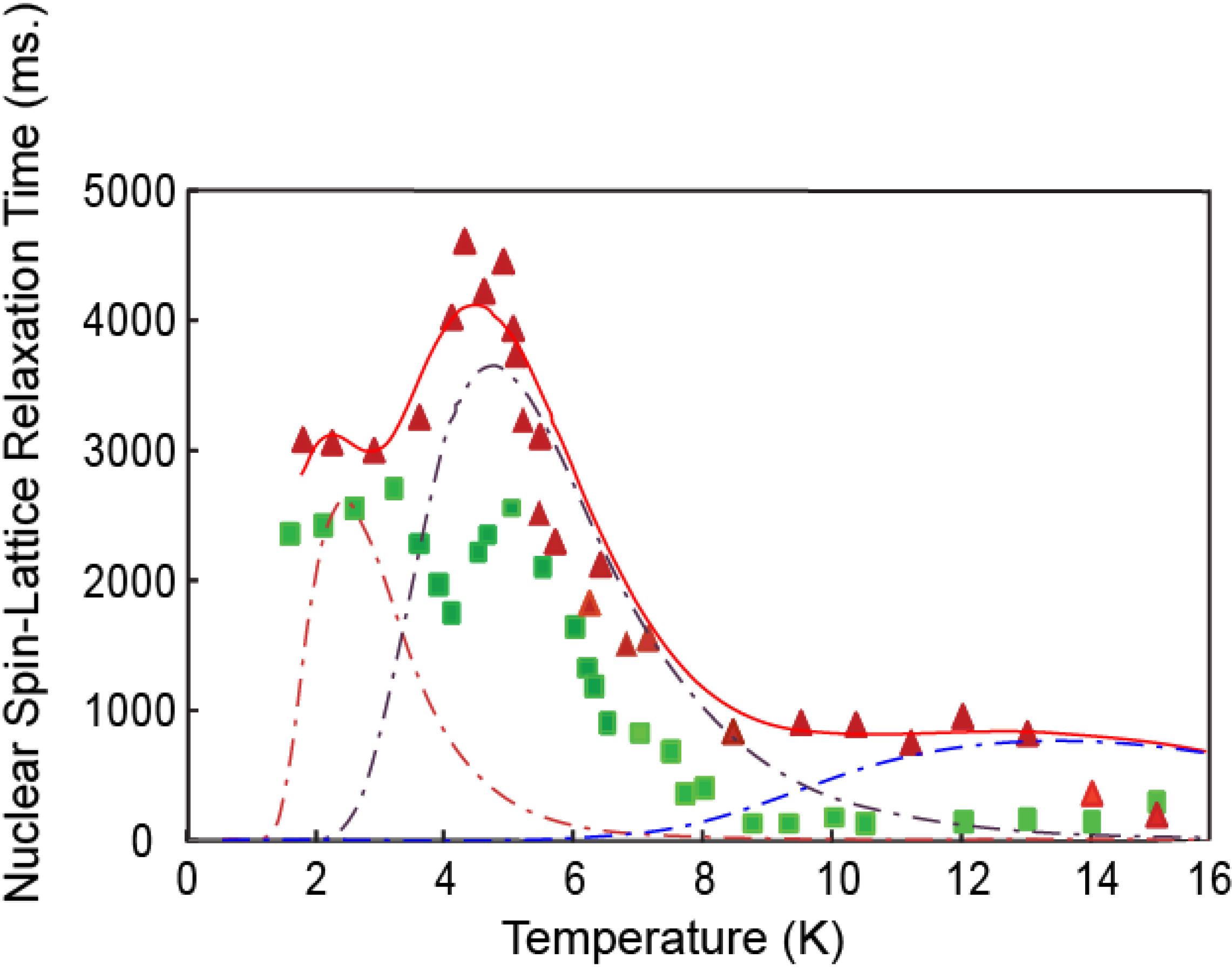
3.3. Discussion
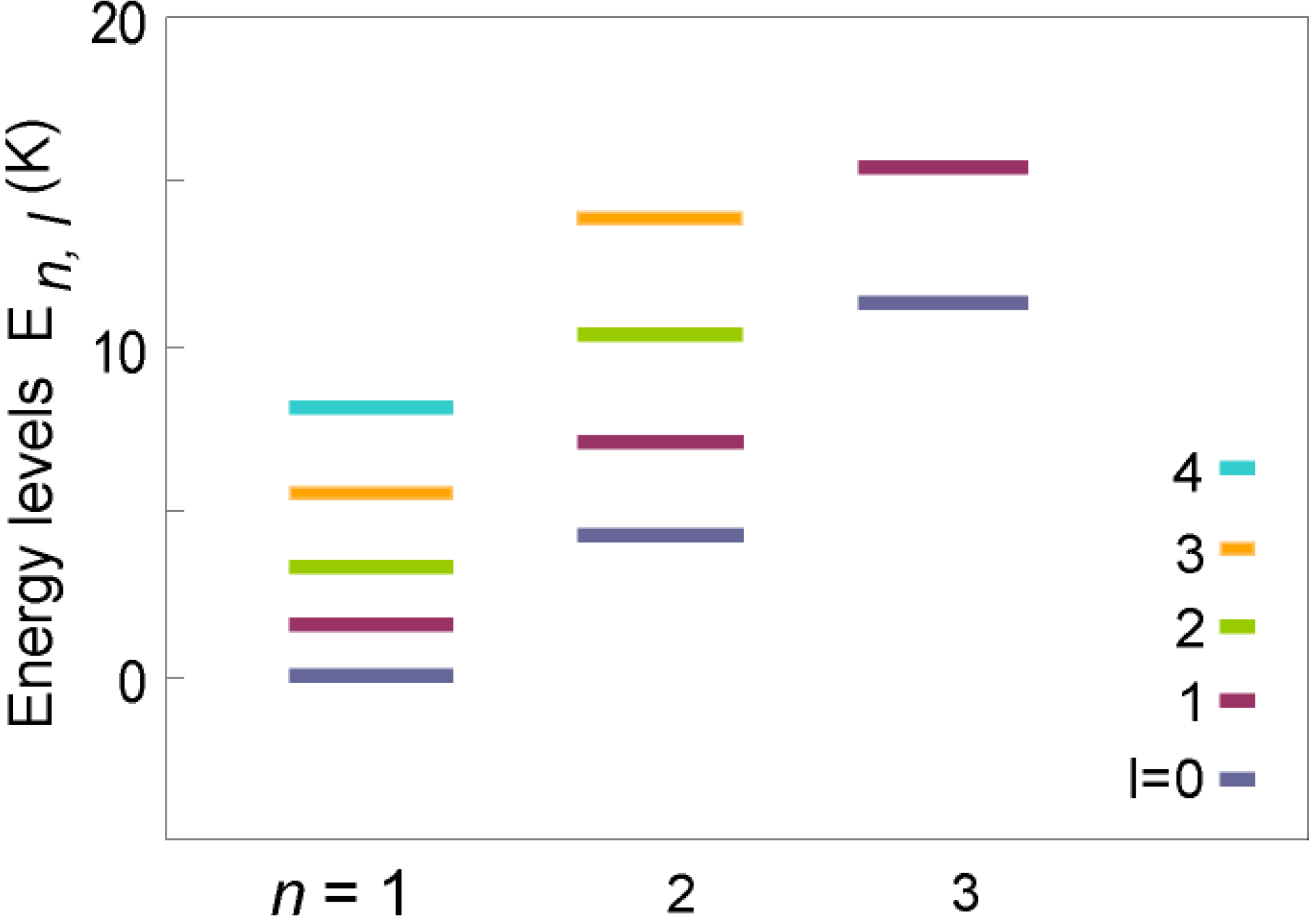

4. Conclusions
Acknowledgments
Appendix A
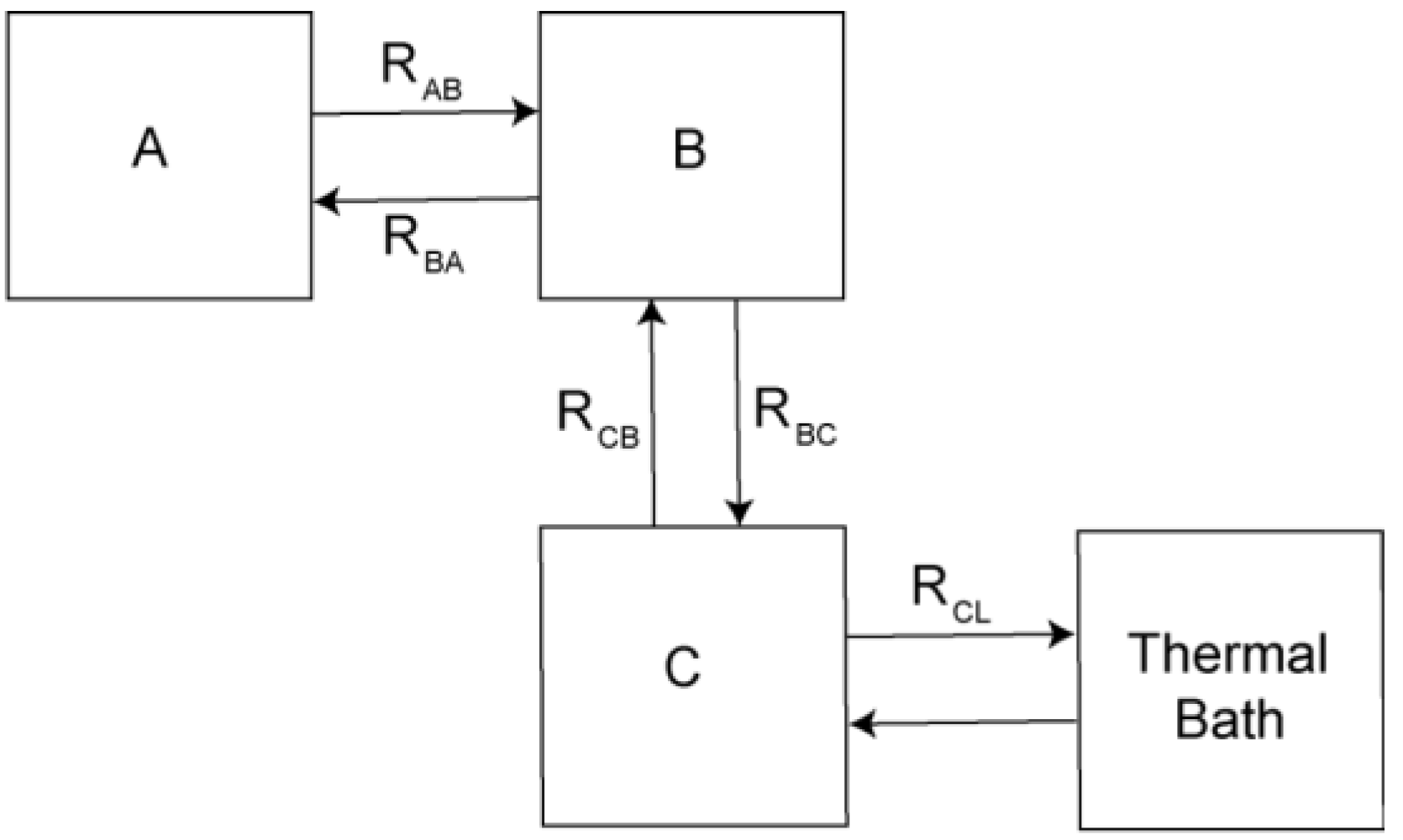
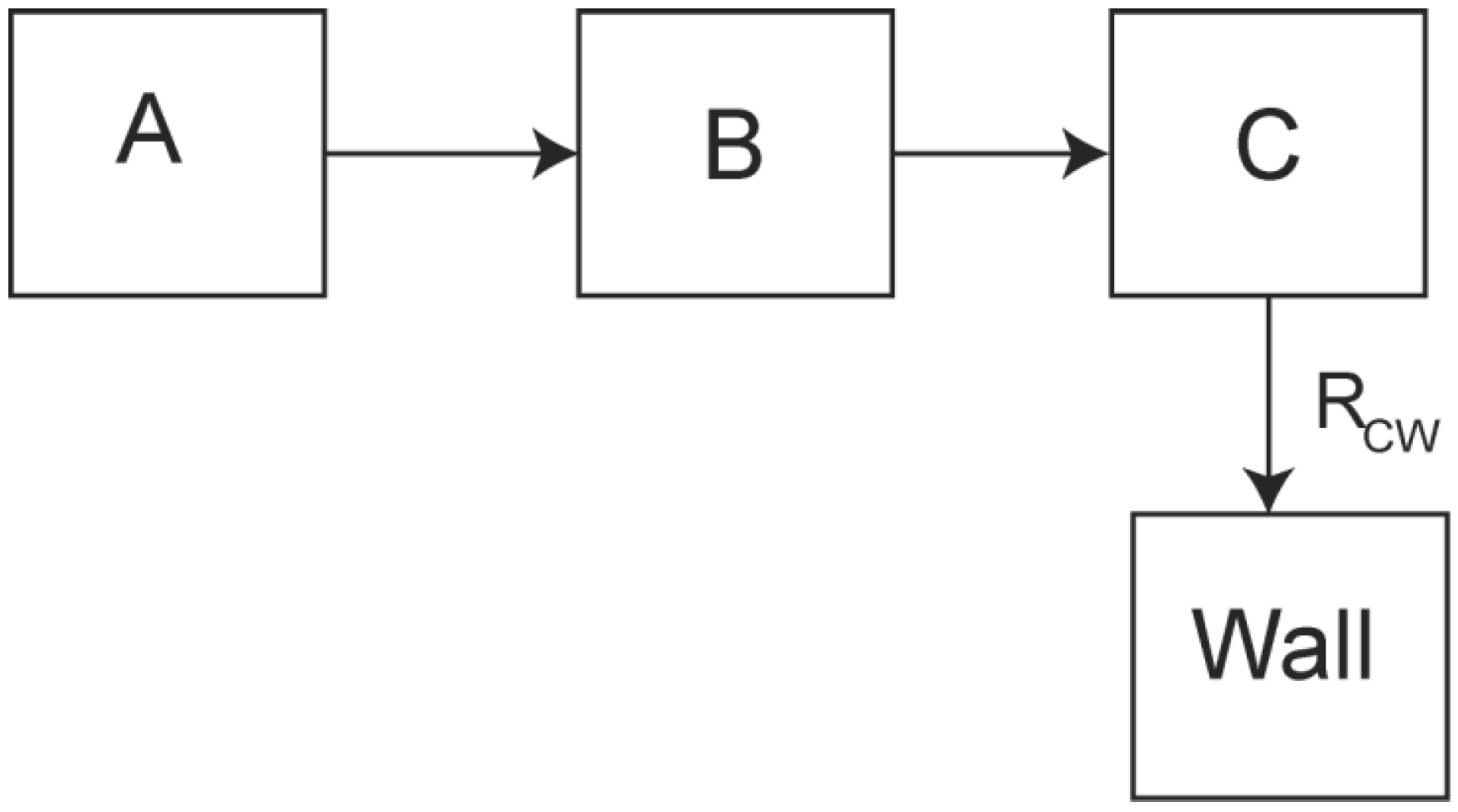
Theoretical Treatment of Relaxation of Coupled Energy Baths
- (i)
- Bath B isolated from the lattice but strongly coupled to bath (A), i.e.,
- (ii)
- Bath A more strongly coupled to the lattice than to bath B, i.e.,
- (a)
- , for the fast relaxing component, and
- (b)
- , for the slow relaxing component.
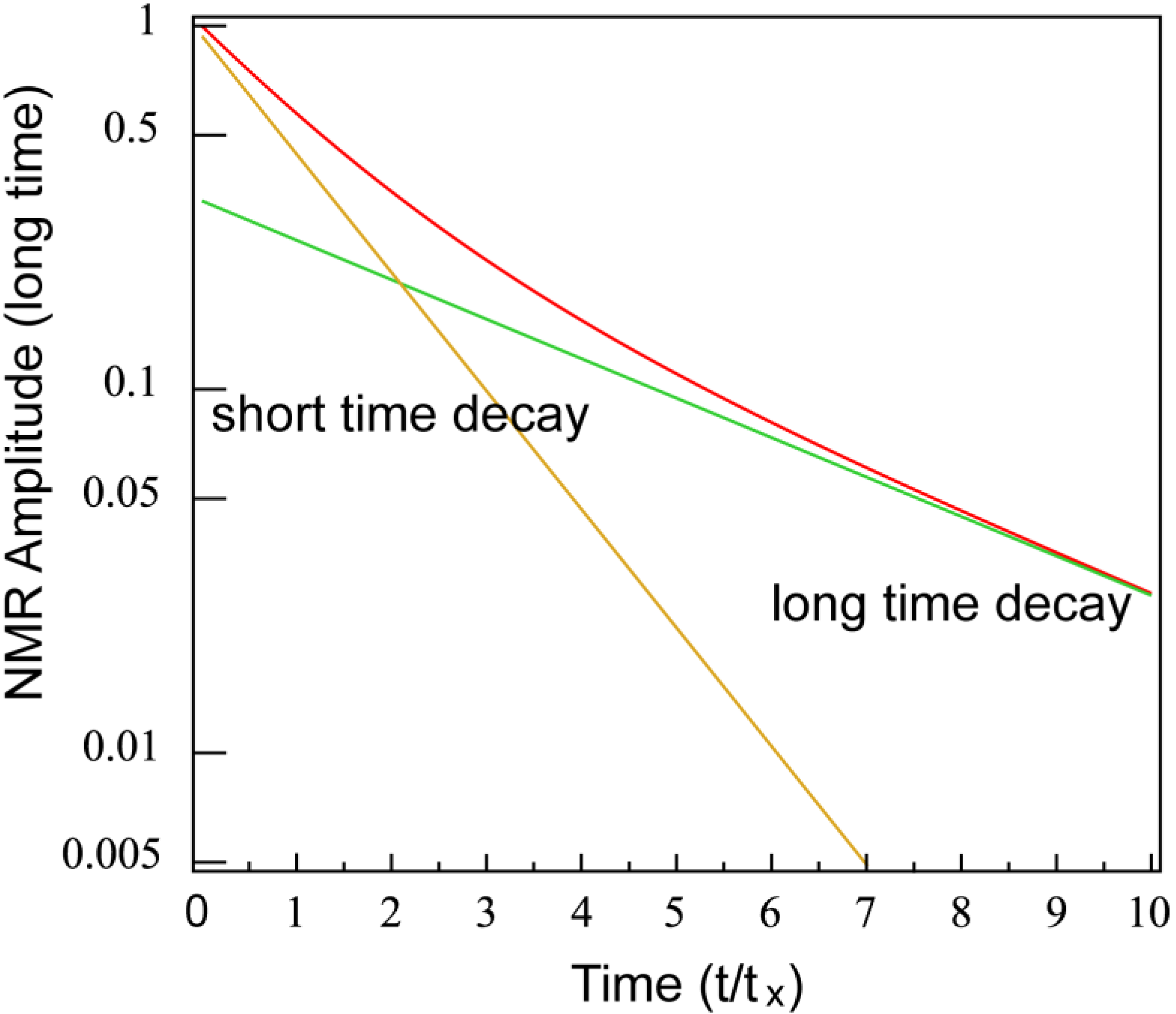
- (a)
- , and
- (b)
- .
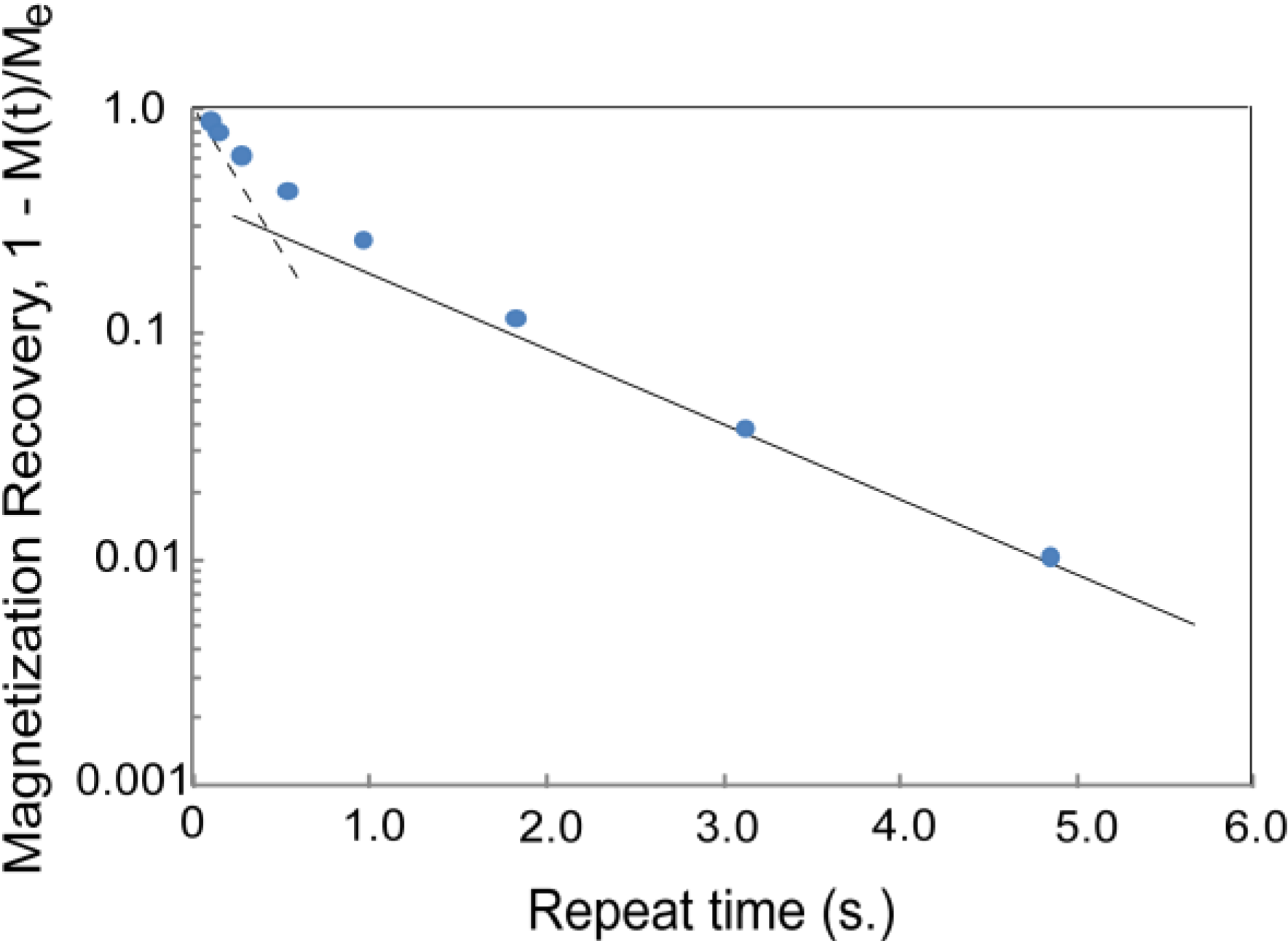
Appendix B
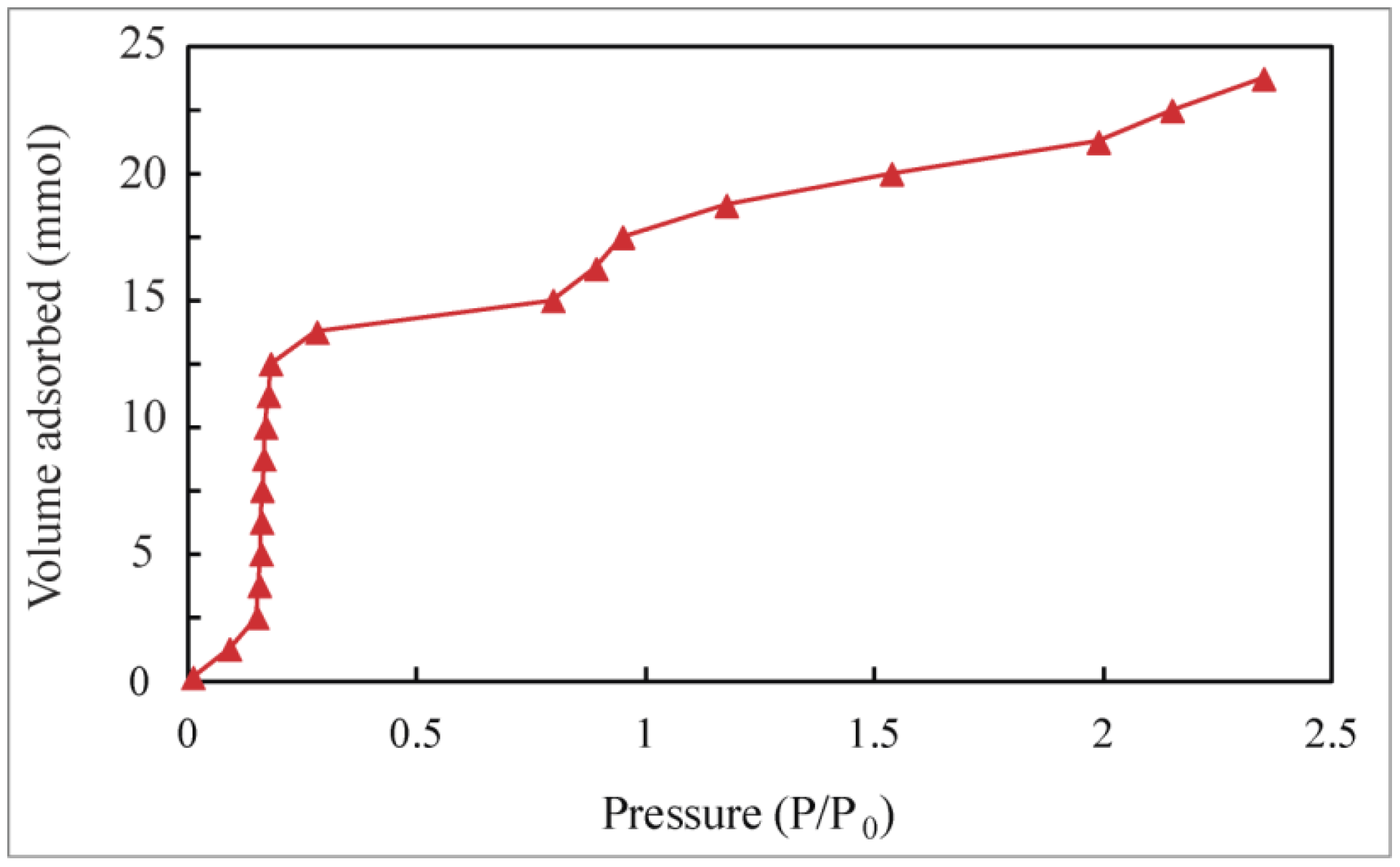
Adsorption Isotherms
References and Notes
- Eddaoudi, M.; Kim, J.; Rosi, N.; Vodak, D.; Wachter, J.; O’Keefe, M.; Yaghi, O.M. Systematic design of pore size and functionality in isoreticular MOFs and their application in methane storage. Science 2002, 295, 469–472. [Google Scholar] [CrossRef]
- Alavi, S. Selective guest docking in metal-organic framework materials. ChemPhysChem 2010, 11, 55–57. [Google Scholar] [CrossRef]
- Yildirim, T.; Hartman, M.R. Direct observation of hydrogen adsorption sites and nanocage formation in metal-organic frameworks. Phys. Rev. Lett. 2005, 95, 215504:1–215504:5. [Google Scholar] [CrossRef]
- Jansen, J.C.; Stoecker, M.; Kange, H.G.; Weitkamp, J. Advanced Zeolite Science and Applications, Volume 85 (Studies in Surface Science and Catalysis; Elsevier Science: Amsterdam, the Netherlands, 1994. [Google Scholar]
- Ma, S.; Sun, D.; Simmons, J.M.; Collier, C.D.; Yuan, D.; Zhou, H.-C. Metal-Organic framework from an anthracene derivative containing nanoscopic cages exhibiting high methane uptake. J. Am. Chem. Soc. 2008, 130, 1012–1016. [Google Scholar] [CrossRef]
- Basic research needs for the Hydrogen Economy: Workshop on Hydrogen Production, Storage and Use. Office of Basic Energy Sciences, U.S. Department of Energy, 13–15 May 2003. Available online: http://www.sc.doe.gov/bes/hydrogen.pdf (accessed on 7 June 2013).
- Pang, J.; Hampsey, J.E.; Wu, Z.; Hu, Q.; Lu, Y. Hydrogen adsorption in mesoporous carbons. Appl. Phys. Lett. 2004, 85, 4887–4889. [Google Scholar] [CrossRef]
- Giraudet, S.; Zhu, Z. hydrogen adsorption in nitrogen enriched ordered mesoporous carbons doped with nickel nanoparticles. Carbon 2011, 49, 398–405. [Google Scholar] [CrossRef]
- Yuan, F.; Li, G. Low temperature catalytic conversion of methane to methanol by barium sulfate nanotubes supporting sulfates: Pt(SO4)2, HgSO4, Ce(SO4)2 and Pb(SO4)2. Chem. Commun. 2005, 2238–2240. [Google Scholar]
- Matsushita, T.; Toda, R.; Hieda, M.; Wada, N. Quantum states of helium atoms confined in nanocage in Na-Y zeolite. J. Low Temp. Phys. 2010, 158, 188–193. [Google Scholar] [CrossRef]
- Wada, N.; Cole, M. Low-Dimensional helium quantum fluids realized under nano-extreme conditions. J. Phys. Soc. Jpn. 2008, 77, 111012:1–111012:11. [Google Scholar] [CrossRef]
- Jee, S.E.; McGaughey, A.J.H.; Scoll, D.S. Molecular simulations of hydrogen and methane permeation through pore mouth modified zeolite membranes. Mol. Simul. 2008, 35, 70–79. [Google Scholar]
- Guyer, R.A.; Richardson, R.C.; Zane, L.I. Excitations in quantum crystals (A Survey of NMR Experiments in Solid Helium). Rev. Mod. Phys. 1971, 43, 532–600. [Google Scholar] [CrossRef]
- Weinhaus, F.; Meyer, H.; Myers, S.M.; Harris, A.B. Nuclear longitudinal relaxation in HCP D2. Phys. Rev. 1971, B3, 626–634. [Google Scholar] [CrossRef]
- Zhou, D.; Rall, M.; Brison, J.P.; Sullivan, N.S. NMR studies of vacancy motion in solid hydrogen. Phys. Rev. 1990, B42, 1929–1939. [Google Scholar] [CrossRef]
- Rall, M.; Zhou, D.; Kisvarsanyi, E.G.; Sullivan, N.S. Nuclear spin-spin relaxation of isotopic impurities in solid hydrogen. Phys. Rev. 1992, B45, 2800–2808. [Google Scholar] [CrossRef]
- Nijman, L. Investigation of Solid Methane by NMR at High Pressure and Low Temperature. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 1977. [Google Scholar]
- Zeolite-13X, Part number MS-1343. Linde Division, Union Carbide Corporation: Danbury, CT, USA.
- Green, S. Nitrogen gas storage in a zeolite. Research Experience for Undergraduates Report, National High. Magnetic Field Laboratory. 2009. Available online: http://www.magnet.fsu.edu/education/reu/program/2009/documents/green.pdf (accessed on 7 June 2013).
- Teflon, E.I.; du Pont de Nemours and Company, Wilmington, DA, USA.
- Ji, Y.; Hamida, J.A.; Sullivan, N.S. NMR Studies of Quantum Rotors Confined in Zeolite. J. Low Temp. Phys. 2010, 158, 509–514. [Google Scholar] [CrossRef]
- Kumar, A.V.A.; Yashonath, S.; Sluiter, M.; Kawazoe, Y. Rotational motion of methane within the confines of zeolite NaCaA: Molecular dynamics and ab initio calculations. Phys. Rev. 2001, E65, 011203:1–011203:7. [Google Scholar]
- Bloembergen, N.; Purcell, E.M.; Pound, R.V. Relaxation effects in nuclear magnetic resonance absorption. Phys. Rev. 1948, 73, 679–712. [Google Scholar] [CrossRef]
- Sullivan, N.S.; Deschamps, P.; Neel, P.; Vaisiere, J.M. Efficient fast-recovery scheme for NMR pulse spectrometers. Revue Phys. Appl. 1983, 18, 253–261. [Google Scholar] [CrossRef]
- Genio, E.B.; Ihas, G.G.; Sullivan, N.S. Ultra-Low temperature thermometry using zeeman perturbed NQR. J. Low Temp. Phys. 1998, 112, 2145–2146. [Google Scholar] [CrossRef]
- Stroud, H.J.F.; Richards, E.; Limcharden, P.; Parsonage, N.F. Thermodynamic study of the linde sieve 5A + methane system. JCS Faraday Trans. 1976, 172, 942–954. [Google Scholar]
- Yashonanth, S.; Thomas, J.M.; Nowak, K.; Cheetham, A.K. The siting, energetics and mobility of saturated hydrocarbons inside zeolitic cages: Methane in zeolite Y. Nature 1988, 331, 601–604. [Google Scholar] [CrossRef]
- Sullivan, N.S. Orientational order–disorder transitions in solid hydrogen. Can. J. Chem. 1988, 66, 908–914. [Google Scholar] [CrossRef]
- DeWall, J.; Dimeno, R.M.; Sokol, P.E. Slow diffusion of molecular hydrogen in zeolite. J. Low Temp. Phys. 2002, 129, 171–194. [Google Scholar] [CrossRef]
- Eckert, J.; Nichol, J.M.; Howard, J.; Trouw, F.R. Adsorption of hydrogen in Ca2+ exchanged zeolite A probed by inelastic neutron scattering, spectroscopy. J. Phys. Chem. 1996, 100, 10646–10651. [Google Scholar] [CrossRef]
- Pulido, A.; Nachtigall, P.; Delgado, M.R.; Arean, C.O. Computational and variable-temperature infrared spectroscopic studies on carbon monoxide adsorption on Zeolite Ca-A. ChemPhysChem 2009, 10, 1058–1065. [Google Scholar] [CrossRef]
- Arean, C.O.; Delgado, M.R.; Bauca, C.L.; Vrbyka, L.; Nachtigall, P. Carbon monoxide adsorption on low-silica zeolites—From single to dual and to multiple cation sites. Phys. Chem. Chem. Phys. 2007, 9, 4657–4661. [Google Scholar] [CrossRef]
- Gasiorowicz, S. The Radial Equation, Quantum Physics; John Wiley & Sons: New York, NY, USA, 1974; p. 187. [Google Scholar]
- Liboff, R.L. The Free Particle Wavefunction, Introductory Quantum Mechanics; Adison Wesley Longman, Inc.: Reading, MA, USA, 1998; p. 429. [Google Scholar]
- Coulomb, J.P.; Flouquet, N.; Dufau, N.; Llewellyn, P.; Andre, G. Structural and dynamic properties of confined hydrogen isotopes (H2, HD, D2) in model porous materials: Silicalite-I, AlPO4-N family (N = 5, 8.11, 54) and MCM-41 (Φ = 25 Å). Microporous Mesoporous Mater. 2007, 101, 271–278. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Clarendon Press: Oxford, UK, 1961; Chapter VIII. [Google Scholar]
- Yates, D.J.C. Studies of the surface area of Zeolites. Can. J. Chem. 1968, 46, 1695–1701. [Google Scholar] [CrossRef]
- Vyas, R.K.; Kumar, S.H.; Kumar, S.U. Determination of volume and surface area of zeolite molecular sieves by D_R and D_A equations—A comparative study. Indian J. Chem. Technol. 2004, 11, 704–709. [Google Scholar]
- Akhtar, F.; Bergstrom, L. Colloidal processing and thermal treatment of binderless hierarchically porous Zeolite-13X Monoliths for CO2 capture. J. Am. Ceram. Soc. 2011, 94, 92–98. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ji, Y.; Sullivan, N.S.; Tang, Y.; Hamida, J.A. Interactions and Diffusion of Methane and Hydrogen in Microporous Structures: Nuclear Magnetic Resonance (NMR) Studies. Materials 2013, 6, 2464-2482. https://doi.org/10.3390/ma6062464
Ji Y, Sullivan NS, Tang Y, Hamida JA. Interactions and Diffusion of Methane and Hydrogen in Microporous Structures: Nuclear Magnetic Resonance (NMR) Studies. Materials. 2013; 6(6):2464-2482. https://doi.org/10.3390/ma6062464
Chicago/Turabian StyleJi, Yu, Neil S. Sullivan, Yibing Tang, and Jaha A. Hamida. 2013. "Interactions and Diffusion of Methane and Hydrogen in Microporous Structures: Nuclear Magnetic Resonance (NMR) Studies" Materials 6, no. 6: 2464-2482. https://doi.org/10.3390/ma6062464



