Effect of Spark Plasma Sintering on the Structure and Properties of Ti1−xZrxNiSn Half-Heusler Alloys
Abstract
:1. Introduction
2. Results
2.1. Structural Properties
| Composition | Conditions | Density (%) | SRT (μV K−1) | ρRT (mΩ cm) | |||
|---|---|---|---|---|---|---|---|
| Pre-SPS | Post-SPS | Pre-SPS | Post-SPS | Pre-SPS | Post-SPS | ||
| Ti0.5Zr0.5NiSn0.95 | 1000 °C/50 MPa | 79 | 84 | – | – | – | – |
| Ti0.5Zr0.5NiSn0.94Sb0.01 | 1050 °C/80 MPa | 78 | 96 | −133 | −117 | 1.2 | 0.6 |
| Ti0.5Zr0.5NiSn(1) | 1050 °C/80 MPa | 76 | 98 | −286 | −113 | 9.5 | 1.8 |
| Ti0.5Zr0.5NiSn0.99Sb0.01 | 1050 °C/80 MPa | 83 | 98 | −141 | −109 | 1.1 | 0.5 |
| Ti0.5Zr0.5NiSn0.98Sb0.02 | 900 °C/50 MPa | 76 | 83 | – | – | – | – |
| Ti0.5Zr0.5NiSn(2) | 900 °C/80 MPa | 81 | 98 | −272 | −168 | 9.7 | 2.7 |
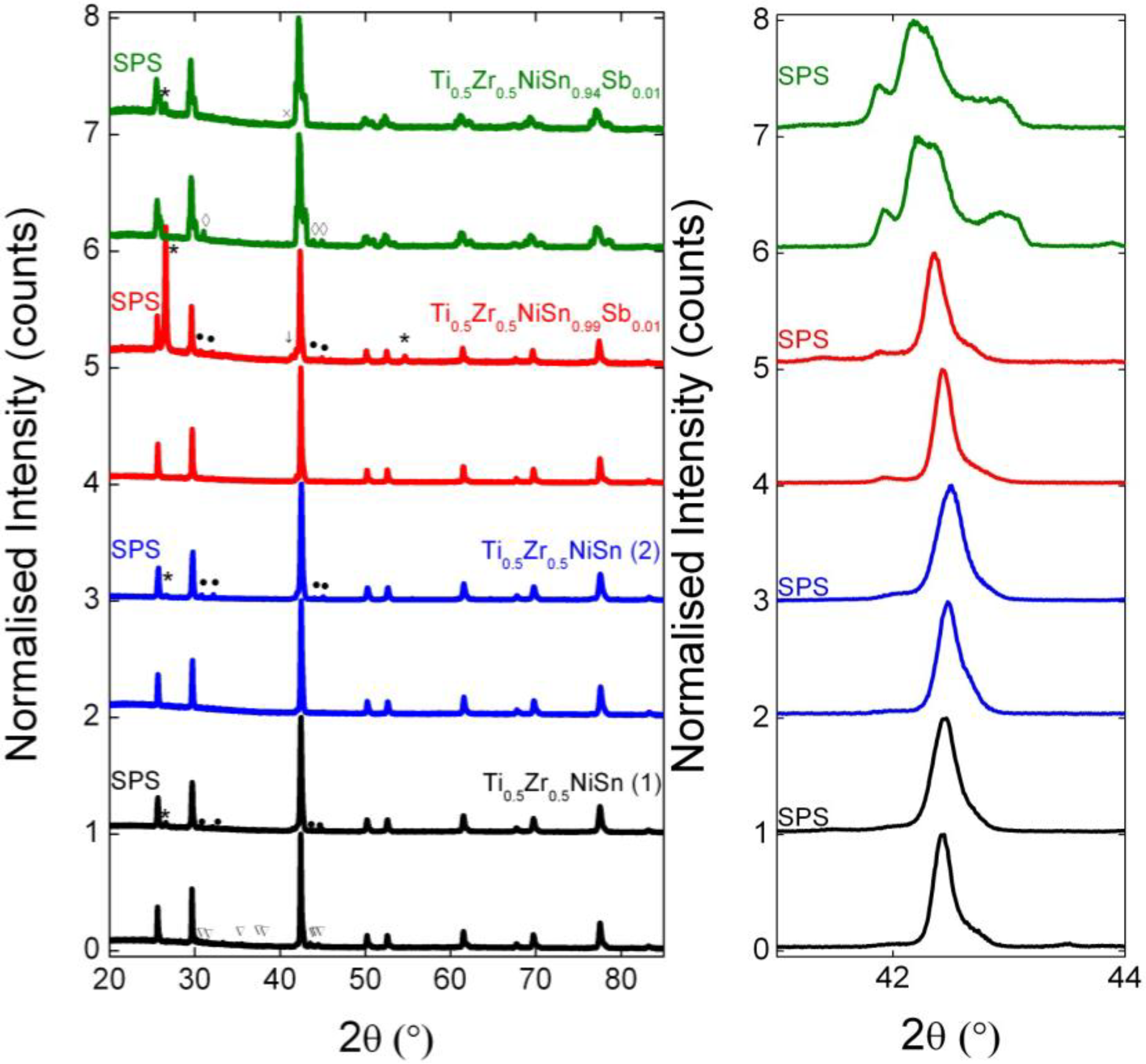
| Composition | a (Å) | xi | Δxi | wt% | xavg | χ2 |
|---|---|---|---|---|---|---|
| Ti0.5Zr0.5NiSn(1) pre-SPS | 5.9915(2) | 0.35(1) | 0.10(1) | 8.5(1) | 0.52(1) | 2.4 |
| 6.0158(2) | 0.48(1) | – | 26.8(5) | |||
| 6.0296(1) | 0.56(1) | 0.13(1) | 64.6(5) | |||
| 6.0965(8) | 0.94(1) | 0.13(1) | 0.1(1) | |||
| Ti0.5Zr0.5NiSn(1) post-SPS | 5.9980(2) | 0.38(1) | 0.13(1) | 7.7(2) | 0.54(1) | 2.2 |
| 6.0206(1) | 0.51(1) | 0.13(1) | 41(1) | |||
| 6.0337(1) | 0.58(1) | 0.14(1) | 51(1) | |||
| 6.0972(4) | 0.94(1) | 0.16(1) | 1.0(1) | |||
| Ti0.5Zr0.5NiSn(2) pre-SPS | 5.9995(2) | 0.39(1) | 0.09(1) | 10.8(2) | 0.52(1) | 2.3 |
| 6.0148(2) | 0.48(1) | 0.09(1) | 19.1(5) | |||
| 6.0278(1) | 0.55(1) | 0.12(1) | 69.8(1) | |||
| 6.100(1) | 0.96(1) | 0.04(1) | 0.4(2) | |||
| Ti0.5Zr0.5NiSn(2) post-SPS | 5.9990(2) | 0.39(1) | 0.12(1) | 8.9(2) | 0.55(1) | 3.5 |
| 6.0170(1) | 0.49(1) | 0.07(1) | 16.3(3) | |||
| 6.0324(1) | 0.58(1) | 0.18(1) | 73.5(3) | |||
| 6.0972(4) | 0.94(1) | 0.10(1) | 1.2(1) | |||
| Ti0.5Zr0.5NiSn0.99Sb0.01 pre-SPS | 5.9929(2) | 0.35(1) | 0.23(1) | 12.9(2) | 0.54(1) | 2.1 |
| 6.0211(1) | 0.51(1) | 0.09(1) | 28.2(5) | |||
| 6.0329(1) | 0.58(1) | 0.09(1) | 57.3(5) | |||
| 6.0995(2) | 0.95(1) | 0.05(1) | 1.6(1) | |||
| Ti0.5Zr0.5NiSn0.99Sb0.01 post-SPS | 5.9947(3) | 0.36(1) | 0.17(1) | 7.9(2) | 0.57(1) | 1.6 |
| 6.0230(3) | 0.52(1) | 0.17(1) | 31(1) | |||
| 6.0358(1) | 0.59(1) | 0.13(1) | 56(1) | |||
| 6.0953(6) | 0.93(1) | 0.23(1) | 5.2(2) | |||
| Ti0.5Zr0.5NiSn0.94Sb0.01 pre-SPS | 5.9573(2) | 0.15(1) | 0.26(1) | 14.9(3) | 0.56(1) | 2.8 |
| 5.9834(5) | 0.30(1) | 0.25(1) | 6.8(2) | |||
| 6.0346(2) | 0.59(1) | 0.21(1) | 41.6(6) | |||
| 6.0600(1) | 0.73(1) | 0.20(1) | 33.3(7) | |||
| 6.0991(1) | 0.95(1) | 0.03(1) | 3.7(1) | |||
| Ti0.5Zr0.5NiSn0.94Sb0.01 post-SPS | 5.9624(3) | 0.18(1) | 0.29(1) | 15.2(3) | 0.58(1) | 2.0 |
| 5.9947(4) | 0.36(1) | 0.18(1) | 5.3(2) | |||
| 6.0351(2) | 0.59(1) | 0.26(1) | 37.8(9) | |||
| 6.0588(2) | 0.72(1) | 0.24(1) | 36.4(1) | |||
| 6.0982(2) | 0.95(1) | 0.06(1) | 5.4(2) |

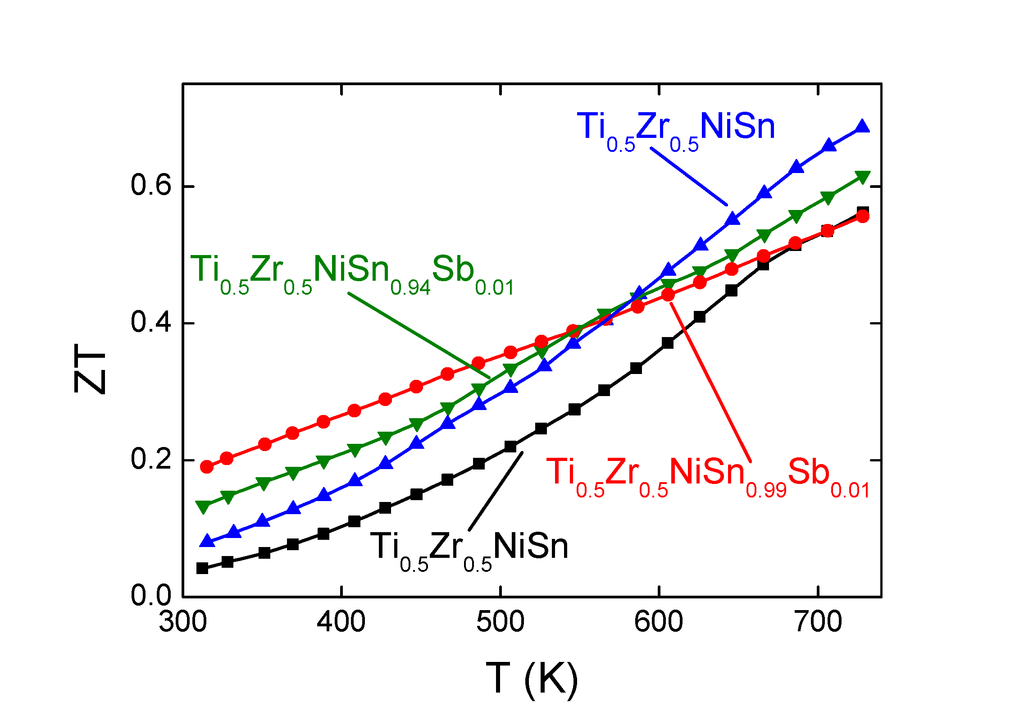
2.2. Thermoelectric Properties
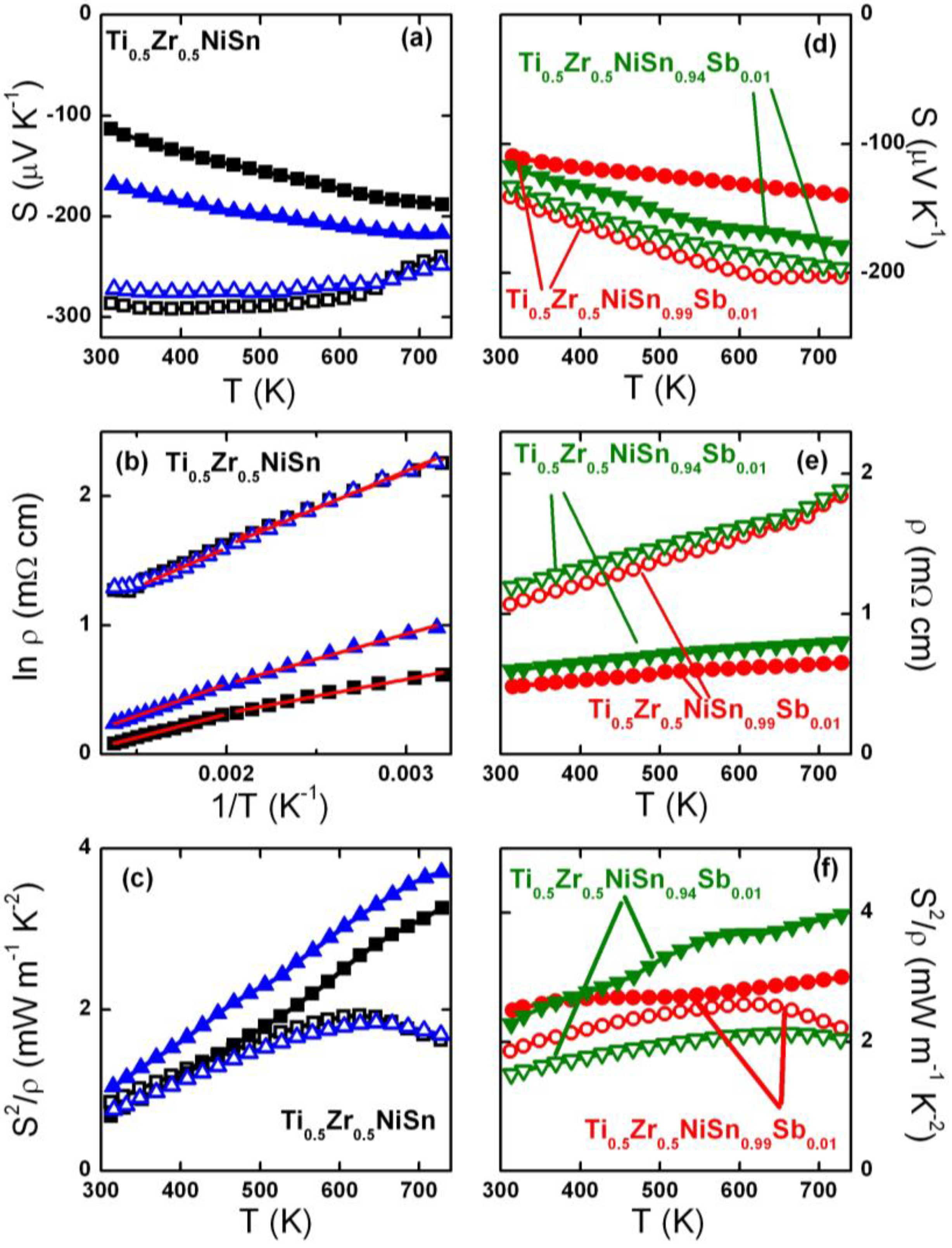
| Sample | T range | Ea (eV) | ρ0 (mΩ cm) | |
|---|---|---|---|---|
| 1 | Pre-SPS | 300–500 K | 0.046(2) | 1.8(1) |
| 500–650 K | 0.055(2) | 1.48(7) | ||
| Post-SPS | 300–500 K | 0.023(1) | 0.81(3) | |
| 500–730 K | 0.032(1) | 0.66(1) | ||
| 2 | Pre-SPS | 300–500 K | 0.051(2) | 1.58(5) |
| 500–650 K | 0.054(5) | 1.48(7) | ||
| Post-SPS | 300–500 K | 0.034(2) | 0.79(2) | |
| 500–730 K | 0.044(1) | 0.64(1) | ||
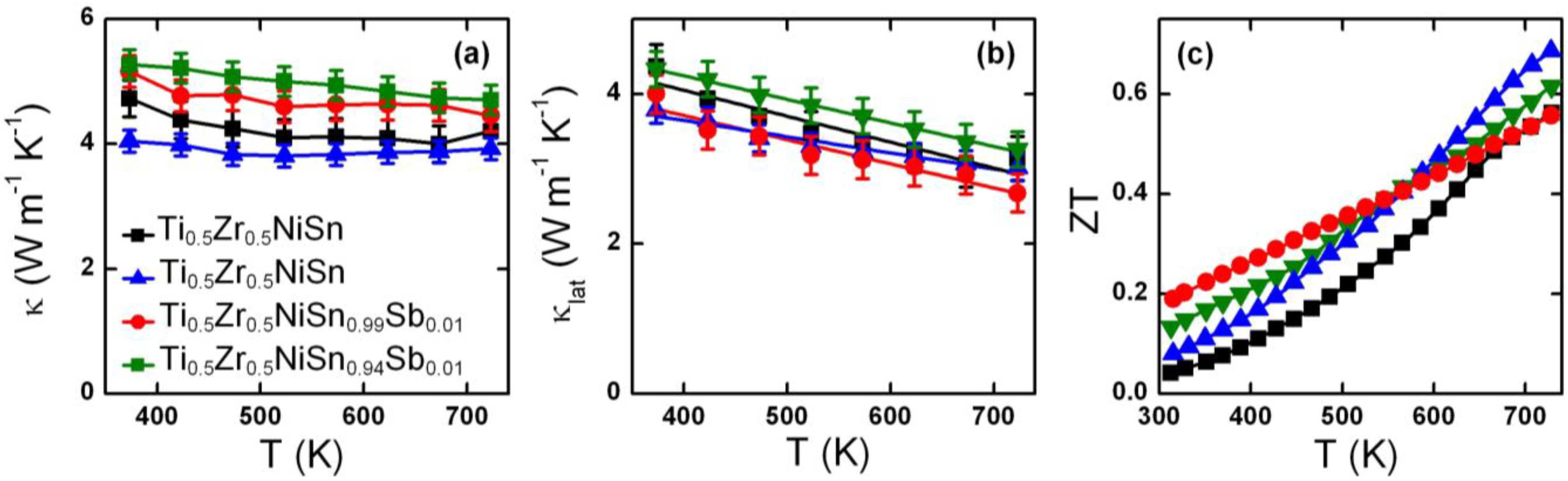
3. Discussion
4. Materials and Methods
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xie, W.; Weidenkaff, A.; Tang, X.; Zhang, Q.; Poon, J.; Tritt, T. Recent advances in nanostructured thermoelectric half-heusler compounds. Nanomaterials 2012, 2, 379–412. [Google Scholar]
- Chen, S.; Ren, Z.F. Recent progress of half-heusler for moderate temperature thermoelectric applications. Mater. Today 2013, 16, 387–395. [Google Scholar] [CrossRef]
- Bos, J.W.G.; Downie, R.A. Half-heusler thermoelectrics: A complex class of materials. J. Phys. Condens. Matter 2014, 26, 433201. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.W.; Kimura, Y.; Mishima, Y. High temperature thermoelectric properties of TiNiSn-based half-heusler compounds. Intermetallics 2007, 15, 349–356. [Google Scholar] [CrossRef]
- Sakurada, S.; Shutoh, N. Effect of Ti substitution on the thermoelectric properties of (Zr,Hf)NiSn half-Heusler compounds. Appl. Phys. Lett. 2005, 86, 082105:1–082105:3. [Google Scholar] [CrossRef]
- Culp, S.R.; Poon, S.J.; Hickman, N.; Tritt, T.M.; Blumm, J. Effect of substitutions on the thermoelectric figure of merit of half-heusler phases at 800 °C. Appl. Phys. Lett. 2006, 88, 042106:1–0421063:3. [Google Scholar] [CrossRef]
- Shen, Q.; Chen, L.; Goto, T.; Hirai, T.; Yang, J.; Meisner, G.P.; Uher, C. Effects of partial substitution of Ni by Pd on the thermoelectric properties of ZrNiSn-based half-Heusler compounds. Appl. Phys. Lett. 2001, 79, 4165–4167. [Google Scholar] [CrossRef]
- Appel, O.; Schwall, M.; Mogilyansky, D.; Kohne, M.; Balke, B.; Gelbstein, Y. Effects of microstructural evolution on the thermoelectric properties of spark-plasma-sintered Ti0.3Zr0.35Hf0.35NiSn half-Heusler compounds. J. Electron. Mater. 2013, 42, 1340–1345. [Google Scholar] [CrossRef]
- Gałązka, K.; Populoh, S.; Xie, W.; Yoon, S.; Saucke, G.; Hulliger, J.; Weidenkaff, A. Improved thermoelectric performance of (Zr0.3Hf0.7)NiSn half-Heusler compounds by Ta substitution. J. Appl. Phys. 2014, 115, 183704:1–183704:8. [Google Scholar] [CrossRef]
- Populoh, S.; Aguirre, M.H.; Brunko, O.C.; Galazka, K.; Lu, Y.; Weidenkaff, A. High figure of merit in (Ti,Zr,Hf)NiSn half-Heusler alloys. Scr. Mater. 2012, 66, 1073–1076. [Google Scholar] [CrossRef]
- Schwall, M.; Balke, B. Phase separation as a key to a thermoelectric high efficiency. Phys. Chem. Chem. Phys. 2013, 15, 1868–1872. [Google Scholar] [CrossRef] [PubMed]
- Muta, H.; Yamaguchi, T.; Kurosaki, K.; Yamanaka, S. Thermoelectric properties of ZrNiSn based half-heusler compounds. In Proceedings of the 24th International Conference on Thermoelectrics, 2005, Clemson, SC, USA, 19–23 June 2005; IEEE: New York, NY, USA, 2005; pp. 351–354. [Google Scholar]
- Katayama, T.; Kim, S.; Kimura, Y.; Mishima, Y. The effects of quaternary additions on thermoelectric properties of TiNiSn-based half-Heusler alloys. J. Electron. Mater. 2003, 32, 1160–1165. [Google Scholar] [CrossRef]
- Kimura, Y.; Ueno, H.; Mishima, Y. Thermoelectric properties of directionally solidified half-Heusler (Ma0.5Mb0.5)NiSn (Ma, Mb = Hf, Zr, Ti) alloys. J. Electron. Mater. 2009, 38, 934–939. [Google Scholar]
- Downie, R.A.; MacLaren, D.A.; Smith, R.I.; Bos, J.W.G. Enhanced thermoelectric performance in TiNiSn-based half-Heuslers. Chem. Commun. 2013, 49, 4184–4186. [Google Scholar] [CrossRef]
- Downie, R.A.; MacLaren, D.A.; Bos, J.W.G. Thermoelectric performance of multiphase XNiSn (X = Ti, Zr, Hf) half-Heusler alloys. J. Mater. Chem. A 2014, 2, 6107–6114. [Google Scholar] [CrossRef]
- Zou, M.; Li, J.-F.; Du, B.; Liu, D.; Kita, T. Fabrication and thermoelectric properties of fine-grained TiNiSn compounds. J. Solid State Chem. 2009, 182, 3138–3142. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Skove, M.J.; Russell, M.; Tritt, T.M.; Xia, Y.; Ponnambalam, V.; Poon, S.J.; Thadhani, N. Effect of boundary scattering on the thermal conductivity of TiNiSn-based half-Heusler alloys. Phys. Rev. B 2008, 77, 184203:1–184203:8. [Google Scholar]
- Bhattacharya, S.; Tritt, T.M.; Xia, Y.; Ponnambalam, V.; Poon, S.J.; Thadhani, N. Grain structure effects on the lattice thermal conductivity of Ti-based half-Heusler alloys. Appl. Phys. Lett. 2002, 81, 43–45. [Google Scholar] [CrossRef]
- Joshi, G.; Dahal, T.; Chen, S.; Wang, H.; Shiomi, J.; Chen, G.; Ren, Z. Enhancement of thermoelectric figure-of-merit at low temperatures by titanium substitution for hafnium in n-type half-Heuslers Hf0.75-xTixZr0.25NiSn0.99Sb0.01. Nano Energy 2013, 2, 82–87. [Google Scholar] [CrossRef]
- Kurosaki, K.; Maekawa, T.; Muta, H.; Yamanaka, S. Effect of spark plasma sintering temperature on thermoelectric properties of (Ti,Zr,Hf)NiSn half-Heusler compounds. J. Alloy. Compd. 2005, 397, 296–299. [Google Scholar] [CrossRef]
- Uher, C.; Yang, J.; Hu, S.; Morelli, D.T.; Meisner, G.P. Transport properties of pure and doped MNiSn (M = Zr, Hf). Phys. Rev. B 1999, 59, 8615–8621. [Google Scholar] [CrossRef]
- Cook, B.A.; Meisner, G.P.; Yang, J.; Uher, C. High temperature thermoelectric properties of MNiSn (M=Zr, Hf). In Proceedings of the Eighteenth International Conference on Thermoelectrics, Baltimore, MD, USA, 29 August–2 September 1999; pp. 64–67.
- Simonson, J.W.; Poon, S.J. Electronic structure of transition metal-doped XNiSn and XCoSb (X = Hf, Zr) phases in the vicinity of the band gap. J. Phys. Condens. Matter 2008, 20, 255220:1–255220:7. [Google Scholar] [CrossRef]
- Simonson, J.W.; Wu, D.; Xie, W.J.; Tritt, T.M.; Poon, S.J. Introduction of resonant states and enhancement of thermoelectric properties in half-heusler alloys. Phys. Rev. B 2011, 83, 235211:1–235211:9. [Google Scholar] [CrossRef]
- Muta, H.; Kanemitsu, T.; Kurosaki, K.; Yamanaka, S. High-temperature thermoelectric properties of Nb-doped MNiSn (M = Ti, Zr) half-Heusler compounds. J. Alloy. Compd. 2009, 469, 50–55. [Google Scholar] [CrossRef]
- Ponnambalam, V.; Pope, A.L.; Xia, Y.; Bhattacharya, S.; Poon, S.J.; Tritt, T.M. Effect of substitution on the transport properties of the half-heusler alloy ZrNiSn. In Proceedings of the Eighteenth International Conference on Thermoelectrics, Baltimore, MD, USA, 29 August–2 September 1999; pp. 340–343.
- Miyamoto, K.; Kimura, A.; Sakamoto, K.; Ye, M.; Cui, Y.; Shimada, K.; Namatame, H.; Taniguchi, M.; Fujimori, S.I.; Saitoh, Y.; et al. In-gap electronic states responsible for the excellent thermoelectric properties of Ni-based half-heusler alloys. Appl. Phys. Express 2008, 1, 081901:1–081901:3. [Google Scholar] [CrossRef]
- Ouardi, S.; Fecher, G.H.; Felser, C.; Blum, C.G.F.; Bombor, D.; Hess, C.; Wurmehl, S.; Buchner, B.; Ikenaga, E. Transport and thermal properties of single-and polycrystalline NiZr0.5Hf0.5Sn. Appl. Phys. Lett. 2011, 99, 152112:1–152112:3. [Google Scholar]
- Ouardi, S.; Fecher, G.H.; Balke, B.; Kozina, X.; Stryganyuk, G.; Felser, C.; Lowitzer, S.; Kodderitzsch, D.; Ebert, H.; Ikenaga, E. Electronic transport properties of electron- and hole-doped semiconducting C1b heusler compounds: NiTi1-xMxSn (M=Sc, V). Phys. Rev. B 2010, 82, 085108:1–085108:9. [Google Scholar] [CrossRef]
- Douglas, J.E.; Birkel, C.S.; Verma, N.; Miller, V.M.; Miao, M.S.; Stucky, G.D.; Pollock, T.M.; Seshadri, R. Phase stability and property evolution of biphasic Ti-Ni-Sn alloys for use in thermoelectric applications. J. Appl. Phys. 2014, 115, 043720:1–043720:11. [Google Scholar] [CrossRef]
- Do, D.T.; Mahanti, S.D.; Pulikkoti, J.J. Electronic structure of Zr-Ni-Sn systems: Role of clustering and nanostructures in half-heusler and heusler limits. J. Phys. Condens. Matter 2014, in press. [Google Scholar]
- Muta, H.; Kanemitsu, T.; Kurosaki, K.; Yamanaka, S. Effect of carrier doping on the thermal conductivity of MNiSn based half-heusler alloy. In Proceedings of the 25th International Conference on Thermoelectrics, Vienna, Austria, 6–10 August 2006; IEEE: New York, NY, USA, 2006; pp. 120–123. [Google Scholar]
- Larson, A.C.; Von Dreele, R.B. General Structure Analysis System (GSAS); Los Alamos National Laboratory Report LAUR 86-748; The Regents of the University of California: Los Alamos, NM, USA, 2000. [Google Scholar]
- Toby, B.H. Expgui, a graphical user interface for gsas. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Downie, R.A.; Popuri, S.R.; Ning, H.; Reece, M.J.; Bos, J.-W.G. Effect of Spark Plasma Sintering on the Structure and Properties of Ti1−xZrxNiSn Half-Heusler Alloys. Materials 2014, 7, 7093-7104. https://doi.org/10.3390/ma7107093
Downie RA, Popuri SR, Ning H, Reece MJ, Bos J-WG. Effect of Spark Plasma Sintering on the Structure and Properties of Ti1−xZrxNiSn Half-Heusler Alloys. Materials. 2014; 7(10):7093-7104. https://doi.org/10.3390/ma7107093
Chicago/Turabian StyleDownie, Ruth A., Srinivas R. Popuri, Huanpo Ning, Mike J. Reece, and Jan-Willem G. Bos. 2014. "Effect of Spark Plasma Sintering on the Structure and Properties of Ti1−xZrxNiSn Half-Heusler Alloys" Materials 7, no. 10: 7093-7104. https://doi.org/10.3390/ma7107093