Estimating the Local Radius of Convergence for Picard Iteration

Abstract

In this paper, we propose an algorithm to estimate the radius of convergence for the Picard iteration in the setting of a real Hilbert space. Numerical experiments show that the proposed algorithm provides convergence balls close to or even identical to the best ones. As the algorithm does not require to evaluate the norm of derivatives, the computing effort is relatively low.

1. Introduction

The well known Ostrowski theorem [1] gives a sufficient condition (the spectral radius of the Jacobian of the iteration mapping in the fixed point to be less than 1) for the local convergence of Picard iteration. “However, no estimate for the size of an attraction ball is known” [2] (2009). The problem of estimating the local radius of convergence for different iterative methods was considered by numerous authors and several results were obtained particularly for Newton method and its variants. Nevertheless “... effective, computable estimates for convergence radii are rarely available” [3] (1975). A similar remark was made in a more recent paper [4] (2015): “The location of starting approximations, from which the iterative methods converge to a solution of the equation, is a difficult problem to solve”. It is worth noticing that the shape of the attraction basins is an unpredictable and sophisticated set, especially for high order methods, and therefore finding a good ball of convergence for these methods is indeed a difficult task. Among the oldest known results on this topic we could mention those given by Vertgeim, Rall, Rheinboldt, Traub and Wozniakowski, Deuflhard and Potra, Smale [3,5,6,7,8,9]. Relatively recent results were communicated by Argyros [10,11,12], Ferreira [13], Hernandez-Veron and Romero [4], Ren [14], Wang [15].

Deuflhard and Potra [5] proposed the following estimation for Newton method. Let $F:D\subset X\to Y$ be a nonlinear mapping, where $X,Y$ are Banach spaces. Suppose that F is Fr$\acute{e}$chet differentiable on D, that $F^{\prime }\left(x\right)$ is invertible for each $x\in D$, and that

$$\parallel F^{\prime }{\left(x\right)}^{-1}(F^{\prime }(x+s(y-x))-F^{\prime }\left(x\right)){(y-x)\parallel \le s\omega \parallel y-x\parallel }^2,$$

for all $x,y\in D,s\in [0,1]$. Under these conditions the equation $F\left(x\right)=0$ has a solution $y^{*}\in D$. Let $y^0\in D$ such that

$$\overline{B}(y^{*},\parallel y^0-y^{*}\parallel )=\{x:\parallel x-y^{*}\parallel \le \parallel y^0-y^{*}\parallel \}\subset D$$

and $y^0\in B(y^{*},2/\omega )$. Then the Newton method remains in $B(y^{*},\parallel y^0-y^{*}\parallel )$ and converges to $y^{*}$.

In [2] the authors propose a simple and elegant formula to estimate the radius of convergence for Picaed iteration and the algorithm presumptively gives a sharp value. More precisely, let $G:D\subset {\mathcal{R}}^m\to D$ be a nonlinear mapping and $x^{*}$ a fixed point of G. Suppose that G is differentiable on some ball centred in $x^{*}$, $B_{r_1}=\{x:\parallel x-x^{*}\parallel \le r_1\}$, and the derivative of G satisfies

$$\begin{array}{c}\parallel G^{\prime }\left(x^{*}\right)\parallel \le q<1,\hfill \\ \parallel G^{\prime }\left(x\right)-G^{\prime }{\left(y\right)\parallel \le k\parallel x-y\parallel }^p,\forall x\in B_{r_1}.\hfill \end{array}$$

Define

$$r_2={\left(\frac{(1+p)(1-q)}{k}\right)}^{\frac{1}{p}},$$

then $r=\min \{r_1,r_2\}$ is an estimation of local convergence radius.

Hernandez and Romero [4] gave the following algorithm for a third-order multi-point method for solving nonlinear equations $F\left(x\right)=0$ in Banach spaces [16]. Suppose that p is a solution of the equation, there exists $F^{\prime }{\left(p\right)}^{-1}$, $\parallel F^{\prime }{\left(p\right)}^{-1}\parallel \le \beta$ and $F^{\prime }$ is k-Lipschitz continuous on some $B_{r_0}=\{x:\parallel x-p\parallel \le r_0\}$. Let $\tilde{r}=\min \{r_0,r\}$, where $r={\zeta }_0/\left[(1+{\zeta }_0)\beta k\right]$ and ${\zeta }_0$ is the positive real root of a certain algebraic equation of degree three. Then $\tilde{r}$ is a local convergence radius. A particular method of this class, which will be investigated in the present study, obtained for a particular value of a numerical parameter of the general class, is the following one point method

$$x_{n+1}=x_n-F^{\prime }{\left(x_n\right)}^{-1}[F\left(x_n\right)+F(x_n-F^{\prime }{\left(x_n\right)}^{-1}F\left(x_n\right))].$$

(1)

In fact this is a modified Newton method in which the derivative is re-evaluated periodically after two steps. Note that, in this particular case, the equation giving the value of ${\zeta }_0$, is $x^3+4x^2-8=0$. We will call (1) the One point Ezquerro-Hernandez method.

Remark 1.

The common way to state that an algorithm (formula) gives the best radius of convergence is to show that for a particular function, there exists a point on the border of the convergence ball for which the conditions of convergence are not satisfied or the considered iteration fails to converge. Several authors who propose an algorithm (formula) and claim that the proposed radius is the best possible, proceed in this way. It would be more satisfactory if the proposed algorithm would be tested for some class of mappings or at least for some test mappings.

Finding a good value for the local convergence radius is rather a difficult task and to find the best one is far more difficult. We propose an algorithm to estimate the radius of convergence for the Picard iteration. Numerical experiments show that the proposed algorithm provides convergence balls close to or even identical to the best ones. It is analogous (but in some details different) with the algorithm for Mann iteration proposed in [17].

From the computational point of view, most algorithms involve the evaluation of H$\ddot{o}$lder (Lipschitz) constant k of the derivative of the iteration mapping, or of the equation mapping. This evaluation entails solving a constraint optimization problem and the optimum must be global on some ball. Usually, solving this problem is not an easy task, whatever norm of the linear mapping is used. However, using a rough value for k diminishes to some extent the convergence radius estimation. The computational effort of the proposed algorithm, using the vector norm and scalar product, is presumptively lower.

The paper is organized as follows. Some preliminaries are presented in Section 2. Two theorems are proved in Section 3 concerning the local convergence of Picard iteration. The algorithm is described in Section 4. A part of a large number of numerical experiments performed by the author showing that the proposed algorithm gives radii close to the best possible values is presented in Section 5. The computer programs for the main steps of the proposed algorithm are given in Appendix A.

2. Preliminaries

Let $\mathcal{H}$ be a real Hilbert space with inner product $\langle ·,·\rangle$ and norm $\parallel ·\parallel$ and let C be an open subset of $\mathcal{H}$.

We recall the following two basic concepts which are essential for our development: demicontractivity and quasi-expansivity.

A mapping $T:C\to \mathcal{H}$ is said to be demicontractive if the set of fixed points of T is nonempty, $Fix\left(T\right)\ne \varnothing$, and

$${\parallel T\left(x\right)-p\parallel }^2\le {\parallel x-p\parallel }^2+L{\parallel x-T\left(x\right)\parallel }^2,\forall (x,p)\in \mathcal{C}\times Fix\left(T\right)$$

(2)

where $L>0$. This condition is equivalent to either of the following two:

$$\langle x-T\left(x\right),x-p\rangle \ge {\lambda \parallel x-T\left(x\right)\parallel }^2,\forall (x,p)\in \mathcal{C}\times Fix\left(T\right),$$

(3)

$$\parallel T\left(x\right)-p\parallel \le \parallel x-p\parallel +\sqrt{L}\parallel T\left(x\right)-x\parallel ,\forall (x,p)\in \mathcal{C}\times Fix\left(T\right),$$

(4)

where $\lambda =(1-L)/2$. Note that (3) is often more suitable in Hilbert spaces, allowing easier handling of the scalar products and norms. The condition (4) was considered in [18] to prove T-stability of the Picard iteration for this class of mappings. Note that the set of fixed points of a demicontractive mapping is closed and convex [19].

We say that the mapping T is quasi-expansive if

$$\parallel x-p\parallel \le \beta \parallel x-T\left(x\right)\parallel ,\forall x\in C,$$

(5)

where $\beta >0$. If $\beta <1$ then $\parallel x-p\parallel \le \frac{\beta }{1-\beta }\parallel T\left(x\right)-p\parallel$ which justifies the terminology. It is also obvious that the set of fixed points of a mapping T which satisfies (5) consists of a unique element p in C.

Condition (5) is similar to the following condition:

$$\parallel x-T\left(x\right)\parallel \ge \alpha \underset{p\in Fix\left(T\right)}{\inf }\parallel x-p\parallel ,\forall x\in C,$$

where $0<\alpha <1$, which is considered in [20,21] as an additional condition to prove strong convergence of the Mann iteration for nonexpansive (quasi-nonexpansive) mappings in Banach spaces.

3. Local Convergence

The following theorem is the basis of our approach in estimating local radius of convergence. Its proof is similar to the proof of Theorem 1 [22], except in some details. We present the detailed proof here for completeness.

Theorem 1.

Let $T:C\to \mathcal{H}$ be a (nonlinear) mapping with nonempty set of fixed points, where C is an open set of a real Hilbert space $\mathcal{H}$. Let $p_0$ be a fixed point and let $r_0$ be such that $B_{r_0}\subset C$. We shall suppose that $Fix\left(T\right)\subset B_{r_0}$ (if $Fix\left(T\right)$ is bounded and $C=\mathcal{H}$, then this condition is satisfied for any $p_0\in Fix\left(T\right)$ and suitable $r_0$). Suppose further that

(i) 

$I-T$ is demiclosed at zero on C,

(ii) 

T is demicontractive with $\lambda >0.5$ on $B_{r_0}$,

then the sequence $\left\{x_n\right\}$ given by Picard iteration, $x_{n+1}=T\left(x_n\right),x_0\in B_{r_0}$ remains in $B_{r_0}$ and converges weakly to some fixed point of T. If, in addition,

(iii) 

T is quasi-expansive on $B_{r_0}$,

then $p_0$ is the unique fixed point of T in $B_{r_0}$ and the sequence $\left\{x_n\right\}$ converges strongly to $p_0$.

Proof. 

Let p be a fixed point of T. If $x_n\in B_{r_0}$ then, using (ii), we have

$$\begin{array}{cc}\parallel x_{n+1}{-p\parallel }^2\hfill & =\parallel (x_n-p)-(x_n-T\left(x_n\right)){\parallel }^2\hfill \\ & =\parallel x_n{-p\parallel }^2-2\langle x_n-T\left(x_n\right),x_n-p\rangle +{\parallel x_n-T\left(x_n\right)\parallel }^2\hfill \\ & \le \parallel x_n{-p\parallel }^2-(2\lambda -1){\parallel x_n-T\left(x_n\right)\parallel }^2.\hfill \end{array}$$

Therefore, for any $p\in B_{r_0}$, including $p_0$, $\parallel x_{n+1}-p\parallel \le \parallel x_n-p\parallel$ and $x_{n+1}\in B_{r_0}$, i.e., $\left\{x_n\right\}\subset B_{r_0}$. Moreover, $\parallel x_n-p\parallel \to {\varrho }_p$, so that

$$\parallel x_n-T\left(x_n\right){\parallel }^2\le \frac{1}{2\lambda -1}\left(\parallel x_n{-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2\right)\to 0.$$

As $B_{r_0}$ is weakly compact and $\left\{x_n\right\}$ is bounded, there exists a subsequence $\left\{x_{n_j}\right\}$ which converges weakly to q. Then $x_{n_j}-T\left(x_{n_j}\right)\to 0$ and (i) implies $q\in Fix\left(T\right)$. Suppose now that there exist two subsequences, say $\left\{u_k\right\}$ and $\left\{v_k\right\}$, which converge weakly to u and v respectively. As above, $u,v\in Fix\left(T\right)$ and $\parallel x_n-u\parallel \to {\varrho }_u$, $\parallel x_n-v\parallel \to {\varrho }_v$. Therefore

$$\begin{array}{c}\parallel u_k-u\parallel \to {\varrho }_u,\parallel v_k-u\parallel \to {\varrho }_u,\hfill \\ \parallel u_k-v\parallel \to {\varrho }_v,\parallel v_k-v\parallel \to {\varrho }_v.\hfill \end{array}$$

Let $e_k$ defined by

$$e_k=\parallel u_k{-u\parallel }^2-\parallel v_k{-u\parallel }^2-\parallel u_k{-v\parallel }^2+{\parallel v_k-v\parallel }^2.$$

We have $e_k\to 0$ as $n\to \infty$. On the other hand, $\frac{1}{2}{e}_k=-\langle u_k-v_k,u-v\rangle \to -{\parallel u-v\parallel }^2$ which entails $u=v$. Therefore $x_n\rightharpoonup q$.

Finally, from (iii) it results that $p_0$ is the unique fixed point of T in $B_{r_0}$ and

$$\parallel x_n-p_0\parallel \le \beta \parallel n_n-T\left(x_n\right)\parallel \to 0.$$

so that $x_n\to p_0$. ☐

A demicontractive mapping is weak contractive, and a quasi-expansive mapping is weak expansive. The next theorem shows that the demicontractivity and the quasi-expansivity are not contradictory, there exists a relatively large class of mappings which are both demicontractive and quasi-expansive.

Theorem 2.

Let $T:C\to C$ be a (nonlinear) mapping, where C is an open convex subset of $\mathcal{H}$. Suppose that $Fix\left(T\right)\ne \varnothing$, that T is differentiable on C and $\parallel T^{\prime }\left(x\right)\parallel \le \eta <\sqrt{5}-2,\forall x\in C$. Then T is both demicontractive and quasi-expansive on C.

Proof. 

(I) T is quasi-expansive on C (therefore $Fix\left(T\right)$ consists of a unique element).

Let p be a fixed point of T. Using mean value theorem, for any $x\in C$, we have

$$x-T\left(x\right)=(x-p)-(T\left(x\right)-T\left(p\right))=(x-p)-\left({\int }_0^1{T}^{\prime }(p+t(x-p))dt\right)(x-p).$$

Using the notation $D_{x,p}={\int }_0^1{T}^{\prime }(p+t(x-p))dt$, we have $x-T\left(x\right)=(I-D_{x,p})(x-p)$ and $\parallel D_{x,p}\parallel \le \eta$. From Banach lemma it results that there exists ${(I-D_{x,p})}^{-1}$ and $\parallel {(I-D_{x,p})}^{-1}\parallel \le 1/(1-\eta )$. Therefore

$$\parallel x-p\parallel =\parallel {(I-D_{x,p})}^{-1}(x-T\left(x\right))\parallel \le \frac{1}{1-\eta }\parallel x-T\left(x\right)\parallel ,$$

that is T is quasi-expansive with $\beta =1/(1-\eta )$.

(II) T is demicontractive on C with $\lambda >0.5$.

Due to the condition $0<\eta <\sqrt{5}-2$, we have $0.5<(1-\eta )/{(1+\eta )}^2<1$. Let λ be such that $0.5<\lambda <(1-\eta )/{(1+\eta )}^2$. Consider the quadratic polynomial

$$P(t,\lambda )=\lambda t^2+(2\lambda +1)t-1+\lambda .$$

The largest zero of P is

$$t_m=\frac{-2\lambda -1+\sqrt{8\lambda +1}}{2\lambda },$$

and $\parallel D_{x,p}\parallel <\eta <t_m$. As $P(0,\lambda )=-1+\lambda <0$ and $P(t_m,\lambda )=0$, we have $P(\parallel D_{x,p}\parallel ,\lambda )<0$, which entails $1-\parallel D_{x,p}\parallel >\lambda (1+\parallel D_{x,p}{\parallel )}^2$. For any $y,\parallel y\parallel =1$ we have

$$\begin{array}{cc}\langle (I-D_{x,p})y,y\rangle \hfill & =1-\langle D_{x,p}y,y\rangle \ge 1-\parallel D_{x,p}\parallel \hfill \\ & >\lambda (1+\parallel D_{x,p}{\parallel )}^2\ge \lambda \parallel I-D_{x,p}{\parallel }^2\ge \lambda {\parallel (I-D_{x,p})y\parallel }^2.\hfill \end{array}$$

Taking $y=(x-p)/\parallel x-p\parallel$ and $(I-D_{x,p})(x-p)=x-T\left(x\right)$, we obtain the condition of demicontracivity. ☐

4. The Algorithm

In finite dimensional spaces the condition of quasi-expansivity is superfluous, since the first two conditions of Theorem 1 are sufficient for the convergence of the Picard iteration. Therefore, in finite dimensional spaces, supposing that the condition (i) of Theorem 1 is fulfilled, we can develop the following algorithm to estimate the local radius of convergence:

Find the largest value for $r_0$ such that

$$m=\underset{x\in B_{r_0}}{\min }\frac{\langle x-T\left(x\right),x-p\rangle }{{\parallel x-T\left(x\right)\parallel }^2},$$

(6)

and $m>0.5$.

This procedure involves the following main processing:

• Apply a line search algorithm (for example of the type half-step algorithm) on the positive real axis to find the largest value for $r_0$;
• At every step of 1 solve the constraint optimization problem (6) and verify the condition $m>0.5$.

The main processing of this algorithm is the solution of the constraint optimization problem (6). Therefore we need to use a global constrained optimization method which, generally, has a considerable computational effort. In our experiences we used a population-based metaheuristic method in combination with a local search method.

The algorithm involves an outer iteration (for line search procedure) and an inner iteration (for solving the constrained optimization problem). In N-dimensional spaces, every step of the inner iteration involves $2N$ evaluations of some functions of N variables each (the components of T), for the computation of $\langle x-T\left(x\right),x-p\rangle$ and ${\parallel x-T\left(x\right)\parallel }^2$.

Remark 2.

Most of the algorithms for estimation the radius of convergence involve the computation of the optimal Hölder/Lipschitz constant of the derivative of T. This implies $N^2$ evaluations of some functions in N variable each (the components of the derivative of T). Therefore a step of inner iteration involves a polynomial complexity of order 2 combined with the complexity of computing the components of T. The proposed algorithm involves $2N$ evaluations of components of T, and, presumptively has a lower complexity. However this estimation has only a relative worth, because the main influence on the computational effort is exerted by the global constrained optimization method, which, as it is well known, is a very expensive computation. A good implementation of these algorithms have some positive impact on the computational process.

5. Numerical Experiments

This section is devoted to numerical experiments in order to evaluate the performance of the proposed algorithm. The obtained radii are compared (numerically or graphically) with the maximum radii of convergence. In our experiments the maximum radius was computed by directly checking the convergence of the iteration process starting from all points of a given net of points. The attraction basin (hence the maximum convergence radius) computed in this way has only relative precision. Nevertheless, this method provides significant information about the attraction basins, and the performance of the algorithm from this point of view can be accurately evaluated.

Several numerical experiments in one and several dimensions were performed to validate this method. It is worthwhile to underline that the values obtained by the proposed algorithm are, to some extent, larger than those given by other methods, and, in some cases, our procedure gives local radii of convergence very close to the maximum ones.

5.1. Experiment 1

We have computed the local radius of convergence with the proposed algorithm for One point Ezquerro-Hernandez method and for a number of real functions. In the most these examples the estimated radii are close to (or even coincide with) the maximum radii. For example, in the case of the function $f\left(x\right)=x^5-2x^2+x$ and $p=1$ the estimate and the best radius (computed with 15 decimal digits) are identical, $r=0.080959069788847$.

5.2. Experiment 2

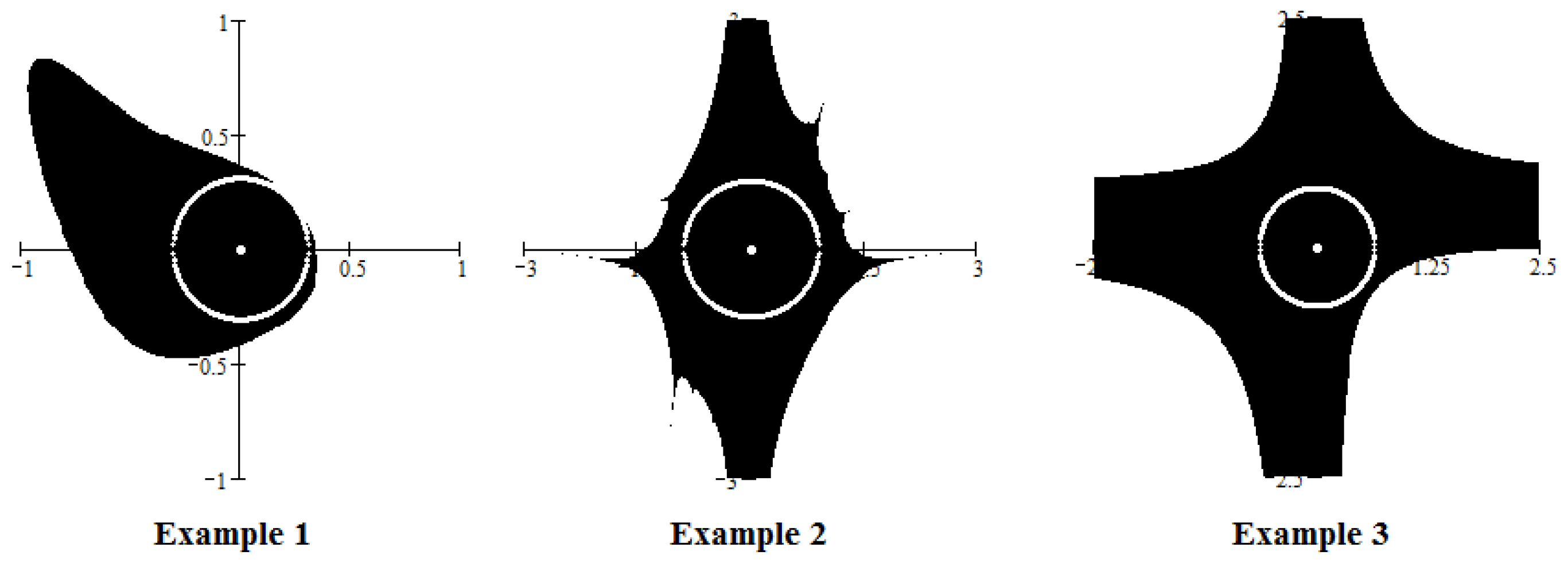
We applied the proposed algorithm to estimate the local radius of convergence for Picard iteration and for a number of mappings in several variables. For the following three test mappings (we will refer to them as Examples 1–3):

$$F_1\left(x\right)=\left(\begin{array}{c}{x}_2^2+0.8x_1-cos\left(x_1\right)+1\\ x_1^3+0.8x_2\end{array}\right),$$

$$F_2\left(x\right)=\left(\begin{array}{c}0.3sin\left(x_1\right)+x_1{x}_2\\ x_1^3-0.5x_2\end{array}\right),F_3\left(x\right)=\left(\begin{array}{c}0.7x_1-x_1{x}_2+0.2x_2\\ x_1{x}_2+0.3x_2\end{array}\right),$$

the results are given in Figure 1.

The black areas represent the domain of convergence corresponding to the fixed point $p={(0,0)}^T$ (for all three examples) and the white circles the local convergence balls. It can be seen that the estimates are satisfactorily close to the best possible ones.

5.3. Experiment 3

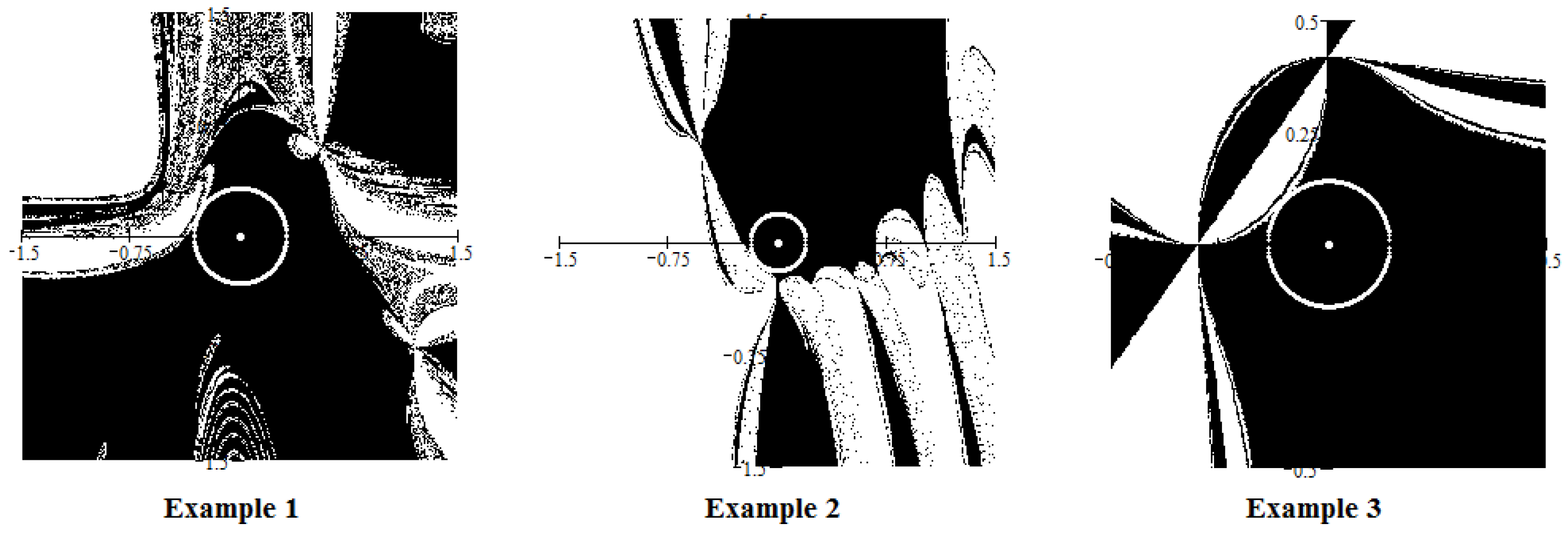
The iteration (1) can be considered as a Picard iteration, $x_{n+1}=T\left(x_n\right)$, where

$$T\left(x\right)=x-F^{\prime }{\left(x\right)}^{-1}[F\left(x\right)+F(x-F^{\prime }{\left(x\right)}^{-1}F\left(x\right))].$$

(7)

Therefore we can apply our algorithm to estimate the local radius of convergence for this method. The results are given in Figure 2.

It can be seen that in this special case the estimates are close (very close) to the best possible radius.

5.4. Experiment 4

In this experiment we estimate numerically the radii of convergence with the proposed algorithm for Picard, Newton and One point Ezquerro-Hernandez methods and for the test mappings. For comparison, we also estimate them by using several other algorithms. In the tables below, we present the results by using the algorithms proposed by Catinas, Deuflhard-Potra and Hernandez-Romero (these algorithms are specifically for considered methods). The last row of each table contains the maximum radii of convergence.

Table 1. Local radii of convergence for Picard method.

Method	Example 1	Example 2	Example 3
Catinas algorithm	0.200000	0.430017	0.376876
Proposed algorithm	0.307939	0.896639	0.645209
Maximum radius	0.311608	1.240665	0.806039

contains the results obtained by Catinas and proposed algoritms for the Picard iteration.

The Catinas algorithm requires us to estimate the H$\ddot{o}$lder (Lipschitz) constant of the derivative of the iteration mapping (7). Even for mappings in two dimensions (which is the case of our test mappings) the computing effort is very high. Therefore, the values for Catinas algorithm in

Table 2. Local radii of convergence for One point Esquerro-Hernandez method.

Method	Example 1	Example 2	Example 3
Catinas algorithm	≈0.194442	≈0.114921	≈0.081090
Hernandez-Romero algorithm	0.221114	0.146160	0.111906
Proposed algorithm	0.319185	0.191426	0.136057
Maximum radius	0.319217	0.197430	0.137130

are only approximative (we use the sign ≈ to indicate these values). This experiment confirm the results of Experiment 3, the proposed algorithm gives radii very close to the maximim radii for One point Ezquerro-Hernandez method.

Table 3. Local radii of convergence for Newton method.

Method	Example 1	Example 2	Example 3
Deuflhard-Potra algorithm	0.346083	0.200051	0.162746
Proposed algorithm	0.363135	0.236905	0.163737
Maximum radius	0.446068	0.254446	0.244121

contains the results obtained by Deuflhard-Potra and proposed algoritms for the Newton method.

The Deuflhard-Potra algorithm gives satisfactory good estimates for Newton method. In the same time this algorithm does not require the evaluation of H$\ddot{o}$lder (Lipschitz) constant of the derivative of the equation mapping and therefore the computing effort is relatively low. Note that in our experiment the parameter s of the algorithm was chosen $s=0.9$, which seems to be most adequate (the algorithm is not very sensitive on this parameter).

Table 2 contains the results obtained by Catinas, Hernandez-Romero and proposed algoritms for the One point Ezquerro-Hernandez method.

6. Conclusions

The proposed algorithm provides radii of convergence close (or very close) to the best possible ones and in some cases (like One point Ezquerro-Hernandez method for one dimension) it seems that the estimates coincide with the maximum radii. As this remarkable characteristic of the proposed algorithm is highlighted in our study only by numerical experiments, it would be a challenge to find the cases in which the two radii are identical.