A Monarch Butterfly Optimization for the Dynamic Vehicle Routing Problem
Abstract
:1. Introduction
2. Dynamic Vehicle Routing Problem (DVRP)
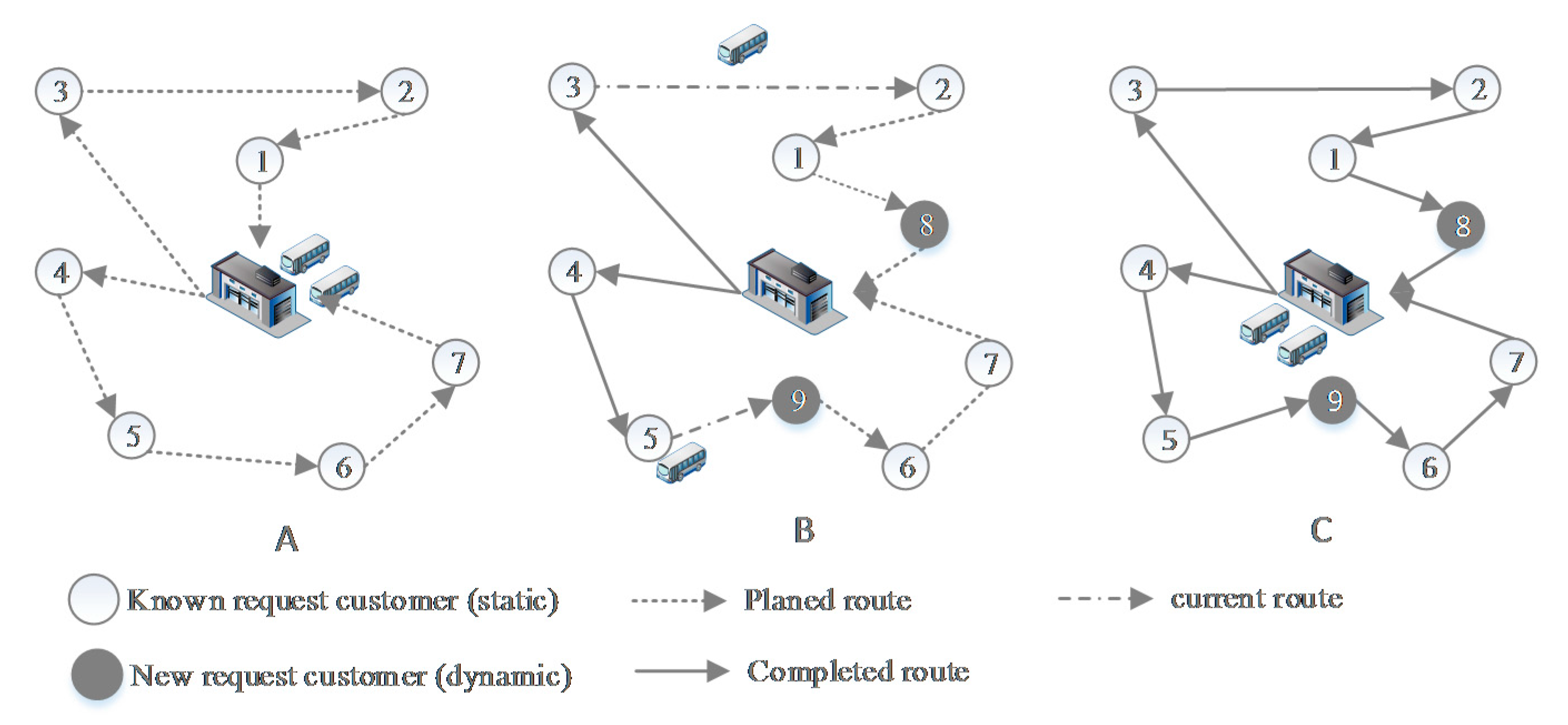
2.1. Problem Description
2.2. Related Work
3. The Proposed Algorithm for DVRP
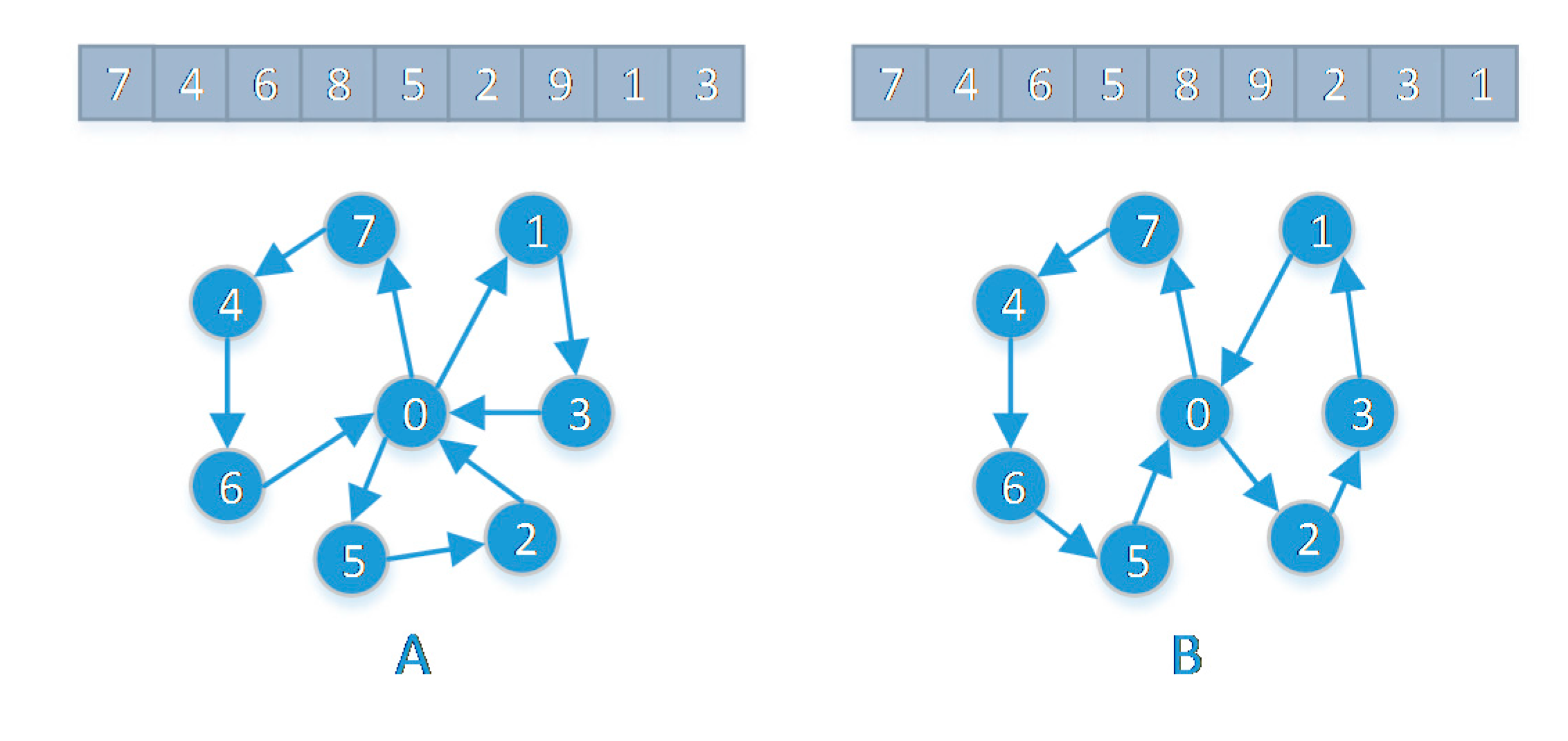
3.1. Solution Representation
3.2. Initial Population
3.3. Monarch Butterfly Optimization (MBO)
3.3.1. Migration Operator
3.3.2. Butterfly Adjusting Operator
3.4. Greedy Acceptance
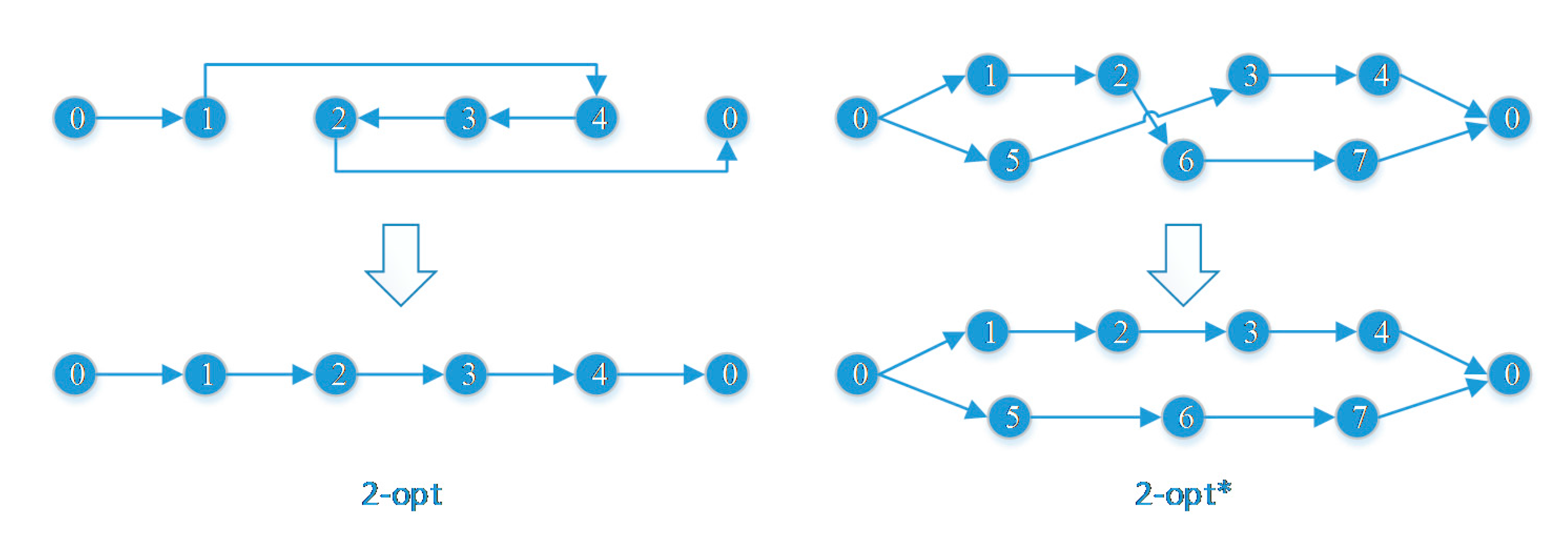
3.5. Later Perturbation
3.6. Algorithm Structure
| Algorithm 1 MBODVRP |
|
4. Experimental Results
4.1. Benchmarks Description
4.2. Comparison with the Literature for DVRP
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Instance: C50 | Best: 570.61 | Time: 42.44 s |
| 1:0-38-9-49-10-39-30-34-21-50-16-11-0 2:0-47-18-13-25-14-0 3:0-12-5-46-0 4:0-37-33-45-15-44-42-19-40-41-4-17-0 5:0-32-2-29-35-36-20-3-28-31-22-1-0 6:0-27-48-8-26-7-43-24-23-6-0 | ||
| Instance: c75 | Best: 897.16 | Time: 83.29 s |
| 1:0-68-2-62-22-28-30-45-0 2:0-63-43-42-64-41-56-23-1-73-0 3:0-51-24-49-16-33-6-17-0 4:0-26-58-72-39-32-40-12-0 5:0-11-66-65-38-10-0 6:0-52-27-13-57-15-20-37-5-29-0 7:0-3-44-50-18-55-25-31-9-0 8:0-8-54-19-59-14-53-35-0 9:0-74-61-69-71-60-70-36-47-21-48-0 10:0-67-7-46-34-4-0 11:0-75-0 | ||
| Instance: c100 | Best: 915.27 | time: 80.80 s |
| 1:0-12-80-68-29-24-54-55-25-67-39-4-21-40-0 2:0-69-31-88-62-7-48-47-36-46-45-8-82-18-52-0 3:0-1-70-10-90-63-11-19-49-64-32-66-20-30-0 4:0-13-87-57-2-41-22-23-56-75-74-72-73-0 5:0-94-95-97-92-37-98-100-91-85-93-61-83-89-0 6:0-76-77-3-79-78-34-35-65-71-9-51-81-33-50-0 7:0-60-5-84-17-16-86-38-44-14-43-15-42-0 8:0-59-99-96-6-0 9:0-53-58-26-28-27-0 | ||
| Instance: c100b | Best: 819.60 | Time: 102.30 s |
| 1:0-75-1-2-4-6-9-11-8-7-3-5-0 2:0-13-17-18-19-15-16-14-12-10-0 3:0-20-22-24-25-27-29-30-28-26-23-21-0 4:0-32-33-31-35-37-38-39-36-34-0 5:0-81-78-76-71-70-73-77-79-80-72-61-64-68-69-0 6:0-43-42-41-40-44-45-46-48-51-50-52-49-47-0 7:0-57-59-60-58-56-53-54-55-0 8:0-66-62-74-63-65-67-0 9:0-98-96-95-94-92-93-97-100-99-0 10:0-91-89-88-85-84-82-83-86-87-90-0 | ||
| Instance: c120 | Best: 1070.18 | Time: 129.27 s |
| 1:0-17-16-19-25-22-24-27-33-30-31-34-36-29-35-32-28-26-23-20-21-81-0 2:0-37-38-39-42-41-44-46-47-49-50-51-48-45-43-40-0 3:0-52-54-57-59-65-61-62-64-66-63-60-56-58-55-53-107-0 4:0-8-12-13-14-15-11-10-9-7-6-5-4-3-1-2-88-0 5:0-67-69-70-71-74-72-75-78-80-79-77-68-76-73-103-0 6:0-82-119-0 7:0-92-91-90-109-108-118-114-18-83-113-117-84-112-85-89-87-86-111-0 8:0-95-96-93-94-97-115-110-98-116-100-99-104-101-102-106-105-120-0 | ||
| Instance: c150 | Best: 1118.03 | Time: 274.47 s |
| 1:0-122-51-120-9-103-66-71-65-136-35-135-34-78-129-0 2:0-137-2-115-145-41-22-133-74-75-23-56-72-73-21-40-0 3:0-26-149-110-4-139-39-67-25-55-130-54-109-0 4:0-53-105-58-13-94-6-147-112-0 5:0-16-141-86-113-17-84-5-118-60-0 6:0-95-117-97-92-59-98-85-61-93-99-104-96-0 7:0-111-1-30-70-101-69-27-0 8:0-127-31-88-148-10-108-126-63-90-32-131-128-20-132-0 9:0-106-7-47-36-143-49-64-11-107-19-123-62-0 10:0-28-138-12-80-150-134-24-29-121-68-116-0 11:0-37-100-91-119-44-140-38-14-142-42-43-15-57-144-87-0 12:0-146-52-82-48-124-46-45-125-8-114-83-18-89-0 13:0-50-102-33-81-79-3-77-76-0 | ||
| Instance: c199 | Best: 1394.74 | Time: 486.88 s |
| 1:0-146-167-127-190-31-162-1-69-132-27-0 2:0-77-3-158-129-79-185-81-33-157-102-176-0 3:0-195-179-4-155-25-55-165-130-54-134-24-163-177-109-0 4:0-18-83-84-17-113-86-16-61-173-5-118-60-0 5:0-88-148-189-10-159-62-182-194-106-153-0 6:0-114-8-82-48-124-46-174-45-125-199-166-0 7:0-51-120-164-34-78-169-29-121-68-150-80-0 8:0-52-123-19-107-175-11-64-49-143-36-47-168-7-0 9:0-105-26-149-198-72-73-21-180-40-58-152-0 10:0-13-117-97-92-151-37-98-91-85-93-59-104-99-96-6-0 11:0-100-193-191-141-44-140-38-119-192-14-142-43-15-0 12:0-101-70-108-126-63-181-90-32-131-160-128-20-30-122-0 13:0-110-139-187-39-170-67-23-186-56-75-197-0 14:0-28-111-76-196-116-184-12-154-138-0 15:0-188-66-71-65-136-35-135-161-103-9-50-0 16:0-144-172-42-57-145-41-22-133-74-171-115-178-2-53-0 17:0-89-147-183-94-95-87-137-112-156-0 | ||
| Instance: f71 | Best: 271.43 | Time: 51.75 s |
| 1:0-14-11-18-35-0 2:0-1-15-19-2-13-17-16-12-71-6-10-5-3-8-4-7-9-0 3:0-60-61-58-59-63-62-64-65-66-67-69-37-38-40-68-39-57-56-34-0 4:0-49-51-70-50-47-48-52-45-53-46-43-44-42-27-28-22-21-30-0 5:0-20-29-23-26-24-25-41-55-54-32-31-33-36-0 | ||
| Instance: f134 | Best: 11759.06 | Time: 210.58 s |
| 1:0-73-74-134-76-77-64-78-63-79-67-70-69-68-80-33-133-0 2:0-72-47-75-1-48-32-34-49-62-61-60-59-31-30-28-26-22-24-23-0 3:0-120-109-108-107-106-114-115-0 4:0-19-65-130-119-117-131-116-132-81-17-66-0 5:0-71-112-125-111-110-122-123-124-126-127-121-128-129-113-18-118-46-0 6:0-58-57-105-97-96-38-95-37-35-36-99-98-100-101-104-102-53-103-56-55-54-52-51-50-0 7:0-82-20-83-85-84-86-87-89-90-16-13-15-88-14-11-12-10-9-8-7-6-5-4-2-42-41-3-40-44-43-39-45-94-93-29-92-27-25-21-91-0 | ||
| Instance: tai75a | Best: 1748.71 | Time: 81.75 s |
| 1:0-54-60-50-46-36-55-31-68-59-45-30-61-65-0 2:0-69-47-43-49-32-34-41-40-42-29-37-33-0 3:0-17-8-5-4-16-0 4:0-25-19-21-27-18-24-12-13-0 5:0-39-48-35-38-44-0 6:0-20-23-15-26-0 7:0-53-62-56-63-64-57-58-0 8:0-6-11-2-3-10-9-7-1-0 9:0-28-22-14-51-67-66-0 10:0-71-73-72-70-52-0 11:0-75-74-0 | ||
| Instance: tai75b | Best: 1371.90 | Time: 97.39 s |
| 1:0-43-50-48-0 2:0-2-0 3:0-51-44-37-49-54-42-39-0 4:0-71-40-23-16-19-3-0 5:0-24-28-35-31-17-34-26-18-47-46-41-0 6:0-45-32-27-29-20-25-21-22-30-33-38-52-14-0 7:0-10-12-5-75-72-15-9-4-0 8:0-69-55-56-61-58-57-60-62-68-70-36-0 9:0-53-65-64-67-66-59-63-73-0 10:0-7-13-6-11-1-8-74-0 | ||
| Instance: tai75c | Best: 1464.37 | Time: 86.22 s |
| 1:0-58-61-3-64-53-54-1-2-51-57-0 2:0-5-4-65-7-0 3:0-75-48-50-40-33-37-42-39-41-52-0 4:0-47-45-18-17-25-28-12-20-0 5:0-6-8-9-62-24-10-0 6:0-68-66-67-71-69-70-13-26-15-16-19-21-23-14-27-22-55-0 7:0-29-31-32-36-60-0 8:0-30-0 9:0-44-43-35-34-46-49-38-63-56-0 10:0-73-74-72-59-11-0 | ||
| Instance: tai75d | Best: 1419.00 | Time: 83.36s |
| 1:0-72-74-73-11-6-3-5-2-0 2:0-37-34-30-32-38-36-33-26-39-29-25-0 3:0-71-75-70-17-12-24-14-15-18-13-16-0 4:0-58-48-41-45-59-51-43-42-54-0-57-0 5:0-55-56-50-28-31-27-35-0 6:0-47-46-53-44-49-52-40-0 7:0-60-64-69-65-68-66-0 8:0-67-62-63-61-4-10-9-1-8-7-0 9:0-20-19-22-23-21-0 | ||
| Instance: tai100a | Best: 2185.49 | Time: 113.82 s |
| 1:0-19-22-23-21-36-34-20-0 2:0-77-86-78-84-79-83-92-82-88-91-0 3:0-1-13-12-9-5-11-4-10-18-6-17-3-7-0 4:0-98-0 5:0-58-59-40-45-44-39-41-48-50-42-47-52-0 6:0-62-29-27-32-33-31-37-28-55-0 7:0-99-16-8-43-49-51-46-100-0 8:0-35-26-38-30-73-68-74-24-25-65-0 9:0-76-89-87-94-96-97-95-0 10:0-81-80-93-85-90-15-14-2-0 11:0-56-61-63-57-64-0 12:0-67-75-66-69-71-72-70-0 13:0-53-60-54-0 | ||
| Instance: tai100b | Best: 2057.80 | Time: 111.99 s |
| 1:0-8-1-7-9-10-3-2-11-6-4-5-0 2:0-84-86-82-83-87-85-88-51-67-66-26-0 3:0-69-60-33-31-29-40-41-34-42-68-45-30-61-0 4:0-65-50-36-46-55-43-44-57-64-54-0 5:0-53-56-58-63-77-52-62-0 6:0-81-80-79-78-70-72-73-71-0 7:0-23-15-74-75-76-25-0 8:0-94-90-96-99-95-89-92-97-0 9:0-24-100-19-21-27-0 10:0-18-93-91-98-12-0 11:0-35-39-49-48-32-37-38-47-59-0 12:0-20-13-16-17-14-22-28-0 | ||
| Instance: tai100c | Best: 1463.42 | Time: 136.82 s |
| 1:0-10-12-5-32-27-25-29-20-21-22-30-33-37-42-0 2:0-90-85-50-43-44-96-0 3:0-87-97-88-98-48-0 4:0-13-91-92-89-93-86-94-95-51-39-52-40-14-0 5:0-2-4-9-0 6:0-15-72-75-99-76-77-0 7:0-49-54-78-82-81-84-79-80-83-65-66-67-64-53-0 8:0-18-38-46-41-100-71-0 9:0-69-55-56-61-58-57-60-62-63-59-73-0 10:0-3-47-16-19-23-31-35-28-17-24-34-26-45-0 11:0-74-8-11-1-36-68-70-6-7-0 | ||
| Instance: tai100d | Best: 1704.35 | Time: 123.25 s |
| 1:0-98-95-7-0 2:0-55-10-22-27-14-23-21-25-17-28-12-20-18-52-47-61-0 3:0-57-2-1-54-53-64-3-62-9-8-6-51-0 4:0-59-97-94-75-0-60-36-50-48-0 5:0-68-66-67-71-69-88-92-90-87-26-89-19-16-15-93-91-13-70-0 6:0-24-0 7:0-96-30-29-100-80-77-0 8:0-65-56-63-39-34-46-35-43-42-37-33-40-32-31-99-0 9:0-78-76-73-74-81-72-11-0 10:0-5-4-0 11:0-79-0 12:0-58-45-41-82-86-84-49-85-83-44-38-0 | ||
| Instance: tai150a | Best: 3560.28 | Time: 367.48 s |
| 1:0-108-112-101-107-0 2:0-19-22-29-27-32-33-31-24-37-28-0 3:0-145-141-148-143-85-90-93-80-79-84-78-86-77-81-138-0 4:0-2-13-18-10-4-11-12-5-9-16-8-43-49-51-0 5:0-91-88-83-82-92-87-89-76-0 6:0-97-96-94-95-0 7:0-113-106-104-100-102-109-105-98-99-110-0 8:0-47-42-46-48-50-41-39-44-45-40-52-59-0 9:0-136-135-119-129-117-123-118-115-114-125-120-30-38-25-0 10:0-126-121-128-124-116-0 11:0-53-137-130-131-134-132-133-26-35-0 12:0-70-73-68-74-127-122-65-0 13:0-7-15-3-6-17-14-1-111-103-0 14:0-146-150-140-139-149-142-144-147-0 15:0-23-20-34-36-21-0 16:0-62-56-61-63-55-57-64-0-60-54-0 17:0-72-71-69-66-75-67-58-0 | ||
| Instance: tai150b | Best: 2966.19 | Time: 401.60 s |
| 1:0-5-4-6-11-2-3-10-9-7-1-8-0 2:0-13-123-12-128-129-137-121-133-139-135-134-24-132-138-0 3:0-39-44-36-46-33-61-69-148-0 4:0-127-120-136-16-125-126-14-144-0 5:0-142-26-145-0 6:0-74-76-75-110-114-0 7:0-53-54-50-60-55-64-57-63-58-56-52-62-0 8:0-98-94-90-89-95-99-96-102-106-20-0 9:0-81-77-80-79-78-70-0 10:0-116-113-109-112-115-118-111-119-117-71-73-72-0 11:0-30-45-31-29-42-40-41-34-32-37-48-49-35-43-38-47-68-59-0 12:0-101-91-93-0 13:0-28-22-131-17-86-82-87-85-88-83-84-51-67-66-65-150-0 14:0-25-19-21-27-130-100-122-18-0 15:0-105-92-97-103-107-104-108-124-0 16:0-140-143-147-149-146-141-15-23-0 | ||
| Instance: tai150c | Best: 2528.04 | Time: 353.91s |
| 1:0-11-1-70-68-8-0 2:0-9-15-106-104-109-100-107-0 3:0-71-12-5-77-76-72-75-69-73-74-10-0 4:0-138-140-26-24-34-17-28-35-31-23-16-19-141-142-0 5:0-27-20-29-25-18-0 6:0-32-33-30-21-22-81-84-79-80-83-82-78-54-49-37-42-0 7:0-91-87-97-98-88-53-90-85-93-0 8:0-41-96-43-50-48-95-0-6-92-89-86-94-36-0 9:0-4-2-0 10:0-14-3-46-45-47-38-44-51-39-52-40-13-7-0 11:0-55-56-61-58-57-60-62-63-59-0 12:0-116-125-118-124-120-123-121-122-119-0 13:0-110-111-115-113-112-114-117-99-102-101-105-108-103-0 14:0-130-132-134-128-129-127-133-135-131-126-136-139-143-137-0 15:0-149-145-146-148-147-150-144-64-67-66-65-0 | ||
| Instance: tai150d | Best: 2980.44 | Time: 292.68 s |
| 1:0-11-5-1-55-54-53-64-58-65-56-63-61-52-62-3-9-8-6-2-0 2:0-126-129-127-122-0 3:0-41-83-85-131-130-132-133-128-124-84-123-125-86-82-0 4:0-24-13-93-109-110-89-87-90-92-88-91-70-69-71-67-66-68-0 5:0-97-99-31-32-30-0-95-96-94-98-80-77-0 6:0-107-103-106-105-108-104-29-100-101-102-0 7:0-18-20-12-17-25-21-19-111-116-115-118-26-16-23-0 8:0-15-114-119-117-112-120-121-113-0 9:0-135-134-137-136-79-0 10:0-141-138-139-0-140-142-144-147-150-0 11:0-59-60-4-51-57-7-0 12:0-149-146-145-148-143-0 13:0-75-72-81-74-73-76-78-0 14:0-47-45-38-44-39-49-46-34-35-43-42-37-33-40-50-0 15:0-10-22-27-14-28-36-48-0 | ||
References
- Ismail, Z. Solving the vehicle routing problem with stochastic demands via hybrid genetic algorithm-tabu search. J. Math. Stat. 2008, 4, 161. [Google Scholar] [CrossRef]
- Oliveira, S.; de Souza, S.R.; Silva, M.A.L. A solution of dynamic vehicle routing problem with time window via ant colony system metaheuristic. In Proceedings of the 10th Brazilian Symposium on Neural Networks, (SBRN ‘08), Salvador, Brazil, 26–30 October 2008; pp. 21–26. [Google Scholar]
- Belfiore, P.C.; Yoshizaki, H.T.Y. Scatter search for a real-life heterogeneous fleet vehicle routing problem with time windows and split deliveries in brazil. Eur. J. Oper. Res. 2009, 199, 750–758. [Google Scholar] [CrossRef]
- Chen, Z.L.; Xu, H. Dynamic column generation for dynamic vehicle routing with time windows. Transp. Sci. 2006, 40, 74–88. [Google Scholar] [CrossRef]
- De Armas, J.; Melián-Batista, B.; Moreno-Pérez, J.A. Restricted Dynamic Heterogeneous Fleet Vehicle Routing Problem with Time Windows. In Advances in Computational Intelligence, Part II, Proceedings of the 12th International Work-Conference on Artificial Neural Networks (IWANN 2013), Puerto de la Cruz, Tenerife, Spain, 12–14 June 2013; Rojas, I., Joya, G., Cabestany, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 36–45. [Google Scholar]
- Wang, G.G.; Zhao, X.; Deb, S. A novel monarch butterfly optimization with greedy strategy and self-adaptive. In Proceedings of the 2015 Second International Conference on Soft Computing and Machine Intelligence (ISCMI), Hong Kong, China, 23–24 November 2015; pp. 45–50. [Google Scholar]
- Ghetas, M.; Yong, C.H.; Sumari, P. Harmony-based monarch butterfly optimization algorithm. In Proceedings of the 2015 IEEE International Conference on Control System, Computing and Engineering (ICCSCE), George Town, Malaysia, 27–29 November 2015; pp. 156–161. [Google Scholar]
- Feng, Y.; Yang, J.; Wu, C.; Lu, M.; Zhao, X.J. Solving 0–1 knapsack problems by chaotic monarch butterfly optimization algorithm with gaussian mutation. Memet. Comput. 2016, 1–16. [Google Scholar] [CrossRef]
- Wang, G.G.; Hao, G.S.; Cheng, S.; Qin, Q. A discrete monarch butterfly optimization for chinese TSP problem. In Advances in Swarm Intelligence, Part I; Proceedings of the 7th International Conference (ICSI 2016), Bali, Indonesia, 25–30 June 2016; Tan, Y., Shi, Y., Niu, B., Eds.; Springer: Cham, Switzerland, 2016; pp. 165–173. [Google Scholar]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2015, 1–20. Available online: https://link.springer.com/article/10.1007/s00521-015-1923-y (accessed on 19 May 2015).
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kilby, P.; Prosser, P.; Shaw, P. Dynamic VRPS: A Study of Scenarios; Technical Report APES-06-1998; University of Strathclyde: Glasgow, UK, 1998. [Google Scholar]
- Montemanni, R.; Gambardella, L.M.; Rizzoli, A.E.; Donati, A.V. Ant colony system for a dynamic vehicle routing problem. J. Comb. Optim. 2005, 10, 327–343. [Google Scholar] [CrossRef]
- Khouadjia, M.R.; Sarasola, B.; Alba, E.; Jourdan, L.; Talbi, E.-G. A comparative study between dynamic adapted PSO and VNS for the vehicle routing problem with dynamic requests. Appl. Soft Comput. 2012, 12, 1426–1439. [Google Scholar] [CrossRef]
- Yang, D.; He, X.; Song, L.; Huang, H.; Du, H. A hybrid large neighborhood search for dynamic vehicle routing problem with time deadline. In Combinatorial Optimization and Applications, Proceedings of the 9th International Conference (COCOA 2015), Houston, TX, USA, 18–20 December 2015; Lu, Z., Kim, D., Wu, W., Li, W., Du, D.-Z., Eds.; Springer: Cham, Switzerland, 2015; pp. 307–318. [Google Scholar]
- Pillac, V.; Gendreau, M.; Guéret, C.; Medaglia, A.L. A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 2013, 225, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Bekta¸S, T.; Repoussis, P.P.; Tarantilis, C.D. Dynamic vehicle routing problems. In Vehicle Routing: Problems, Methods, and Applications, 2nd ed.; Toth, P., Vigo, D., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014; pp. 299–347. [Google Scholar]
- Psaraftis, H.N.; Wen, M.; Kontovas, C.A. Dynamic vehicle routing problems: Three decades and counting. Networks 2016, 67, 3–31. [Google Scholar] [CrossRef] [Green Version]
- Elhassania, M.; Jaouad, B.; Ahmed, E.A. Solving the dynamic vehicle routing problem using genetic algorithms. In Proceedings of the 2nd IEEE International Conference on Logistics Operations Management, Rabat, Morocco, 5–7 June 2014; pp. 62–69. [Google Scholar]
- Euchi, J.; Yassine, A.; Chabchoub, H. The dynamic vehicle routing problem: Solution with hybrid metaheuristic approach. Swarm Evol. Comput. 2015, 21, 41–53. [Google Scholar] [CrossRef]
- Mańdziuk, J.; Żychowski, A. A memetic approach to vehicle routing problem with dynamic requests. Appl. Soft Comput. 2016, 48, 522–534. [Google Scholar] [CrossRef]
- Gendreau, M.; Guertin, F.; Potvin, J.-Y.; Taillard, E. Parallel tabu search for real-time vehicle routing and dispatching. Transp. Sci. 1999, 33, 381–390. [Google Scholar] [CrossRef]
- Bent, R.W.; Van Hentenryck, P. Scenario-based planning for partially dynamic vehicle routing with stochastic customers. Oper. Res. 2004, 52, 977–987. [Google Scholar] [CrossRef]
- Taillard, É. Parallel iterative search methods for vehicle routing problems. Networks 1993, 23, 661–673. [Google Scholar] [CrossRef]
- Christofides, N.; Beasley, J.E. The period routing problem. Networks 1984, 14, 237–256. [Google Scholar] [CrossRef]
- Fisher, M. Vehicle routing. In Handbooks in Operations Research and Management Science; Ball, M., Magnanti, T., Monma, C., Nemhauser, G., Eds.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 8, pp. 1–33. [Google Scholar]
- Hanshar, F.T.; Ombuki-Berman, B.M. Dynamic vehicle routing using genetic algorithms. Appl. Intell. 2007, 27, 89–99. [Google Scholar] [CrossRef]
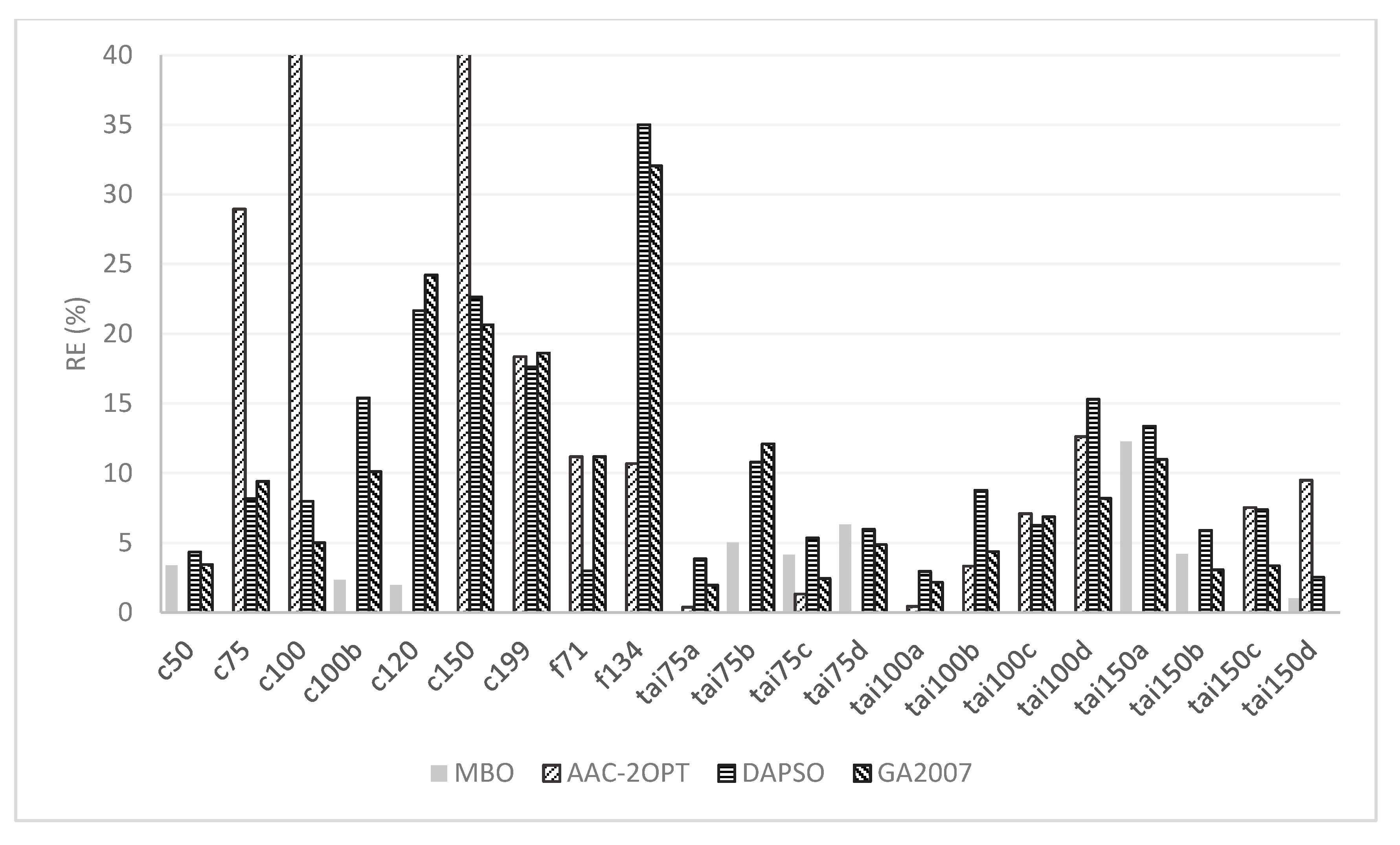
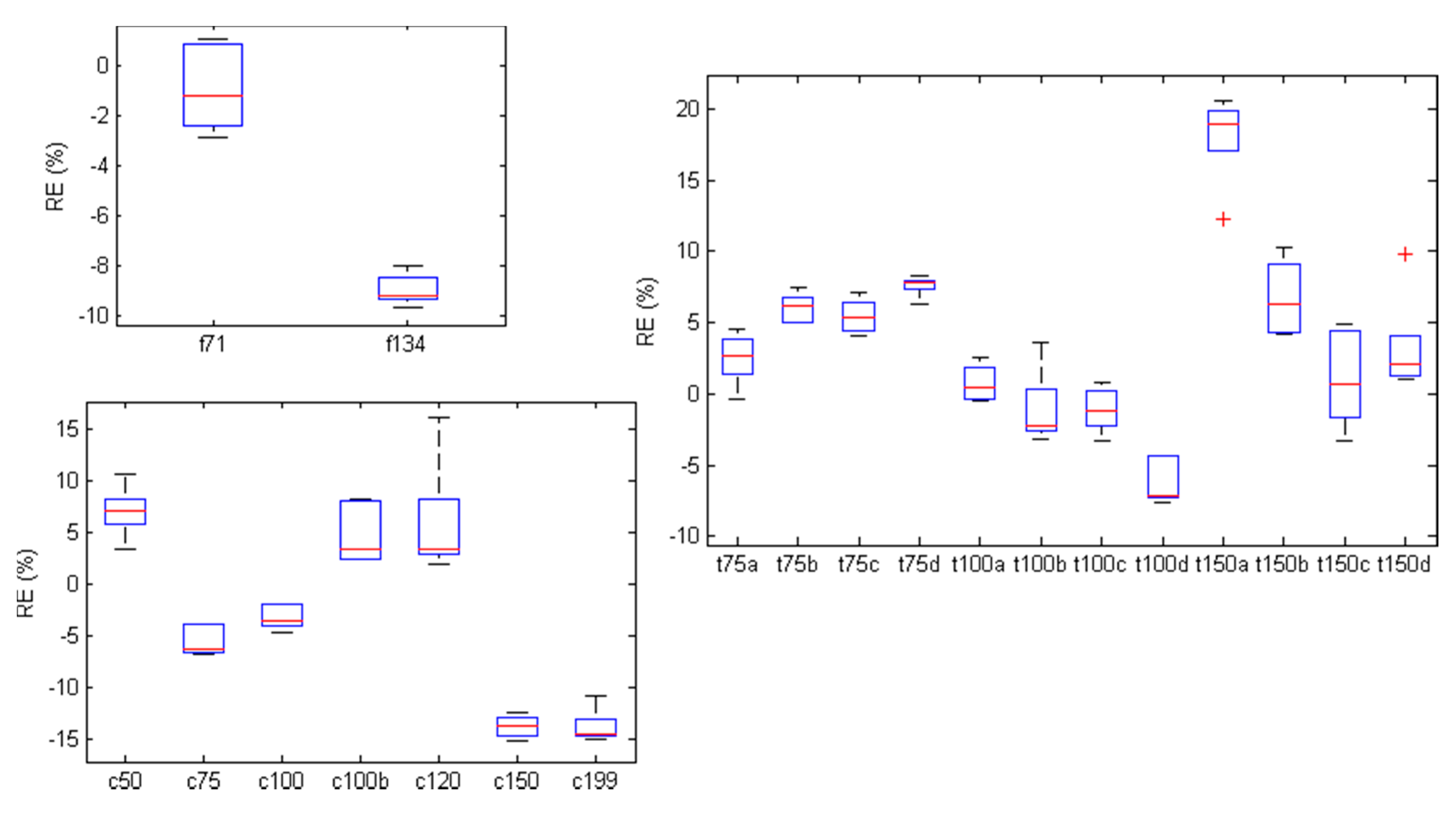
| MBO | BKS | Algorithm | RE (%) | TMBO (s) | |
|---|---|---|---|---|---|
| c50 | 570.61 | 551.95 | AAC-2OPT | 3.38 | 42.44 |
| c75 | 897.16 | 962.79 | GA | −6.82 | 83.01 |
| c100 | 915.27 | 961.10 | GA2007 | −4.77 | 80.80 |
| c100b | 819.60 | 800.93 | AAC-2OPT | 2.33 | 101.77 |
| c120 | 1070.18 | 1049.47 | AAC-2OPT | 1.97 | 122.56 |
| c150 | 1118.03 | 1318.22 | TS | −15.19 | 250.99 |
| c199 | 1394.74 | 1640.40 | DAPSO | −14.98 | 470.15 |
| f71 | 271.43 | 279.52 | DAPSO | −2.89 | 51.53 |
| f134 | 11759.06 | 13015.56 | AAC-2OPT | −9.77 | 205.78 |
| tai75a | 1748.71 | 1755.33 | AAC-2OPT | −0.38 | 81.75 |
| tai75b | 1371.90 | 1306.47 | AAC-2OPT | 5.01 | 90.42 |
| tai75c | 1464.37 | 1406.27 | TS | 4.13 | 77.41 |
| tai75d | 1419.00 | 1334.67 | AAC-2OPT | 6.32 | 83.13 |
| tai100a | 2185.49 | 2194.93 | AAC-2OPT | −0.43 | 113.82 |
| tai100b | 2057.80 | 2126.09 | AAC-2OPT | −3.21 | 108.28 |
| tai100c | 1463.42 | 1490.58 | VNS | −1.82 | 131.28 |
| tai100d | 1704.35 | 1834.60 | GA2007 | −7.10 | 119.77 |
| tai150a | 3560.28 | 2999.27 | AAC-2OPT | 18.70 | 336.75 |
| tai150b | 2966.19 | 2846.28 | AAC-2OPT | 4.21 | 333.55 |
| tai150c | 2528.04 | 2612.68 | GA2007 | −3.24 | 353.91 |
| tai150d | 2980.44 | 2950.61 | GA2007 | 1.01 | 292.68 |
| Average | 2107.91 | 2163.70 | −1.12 | 168.18 |
| MBO | BKS | Algorithm | RE (%) | TMBO (s) | |
|---|---|---|---|---|---|
| c50 | 590.73 | 570.89 | AAC-2OPT | 3.48 | 44.20 |
| c75 | 909.56 | 1013.45 | TS 2007 | −10.25 | 84.50 |
| c100 | 930.38 | 987.59 | GA 2007 | −5.79 | 82.43 |
| c100b | 839.93 | 841.44 | AAC-2OPT | −0.18 | 103.90 |
| c120 | 1112.58 | 1153.29 | AAC-2OPT | −3.53 | 126.08 |
| c150 | 1135.85 | 1386.93 | GA 2007 | −18.10 | 262.19 |
| c199 | 1414.40 | 1758.51 | AAC-2OPT | −19.57 | 492.80 |
| f71 | 277.00 | 306.33 | TS 2007 | −9.57 | 52.48 |
| f134 | 11853.29 | 15528.81 | AAC-2OPT | −23.87 | 215.09 |
| tai75a | 1799.15 | 1782.91 | AAC-2OPT | 0.91 | 83.63 |
| tai75b | 1385.45 | 1452.26 | AAC-2OPT | −4.60 | 93.61 |
| tai75c | 1483.41 | 1441.91 | AAC-2OPT | 2.88 | 81.09 |
| tai75d | 1435.62 | 1422.27 | AAC-2OPT | 0.94 | 86.42 |
| tai100a | 2212.08 | 2232.71 | AAC-2OPT | −0.92 | 116.53 |
| tai100b | 2105.15 | 2182.61 | AAC-2OPT | −3.55 | 111.98 |
| tai100c | 1474.32 | 1541.25 | GA 2014 | −4.04 | 137.05 |
| tai100d | 1722.88 | 1912.43 | AAC-2OPT | −10.78 | 123.70 |
| tai150a | 3539.61 | 3185.727 | AAC-2OPT | 8.78 | 375.45 |
| tai150b | 3038.38 | 2880.57 | AAC-2OPT | 5.48 | 365.32 |
| tai150c | 2641.62 | 2743.55 | AAC-2OPT | −3.72 | 377.15 |
| tai150d | 3047.30 | 3045.16 | GA 2007 | 0.07 | 322.49 |
| Average | 2140.41 | 2350.98 | −9.38 | 178.01 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Chen, R.; Gao, J. A Monarch Butterfly Optimization for the Dynamic Vehicle Routing Problem. Algorithms 2017, 10, 107. https://doi.org/10.3390/a10030107
Chen S, Chen R, Gao J. A Monarch Butterfly Optimization for the Dynamic Vehicle Routing Problem. Algorithms. 2017; 10(3):107. https://doi.org/10.3390/a10030107
Chicago/Turabian StyleChen, Shifeng, Rong Chen, and Jian Gao. 2017. "A Monarch Butterfly Optimization for the Dynamic Vehicle Routing Problem" Algorithms 10, no. 3: 107. https://doi.org/10.3390/a10030107





