An Optimization Algorithm Inspired by the Phase Transition Phenomenon for Global Optimization Problems with Continuous Variables

Abstract

In this paper, we propose a novel nature-inspired meta-heuristic algorithm for continuous global optimization, named the phase transition-based optimization algorithm (PTBO). It mimics three completely different kinds of motion characteristics of elements in three different phases, which are the unstable phase, the meta-stable phase, and the stable phase. Three corresponding operators, which are the stochastic operator of the unstable phase, the shrinkage operator in the meta-stable phase, and the vibration operator of the stable phase, are designed in the proposed algorithm. In PTBO, the three different phases of elements dynamically execute different search tasks according to their phase in each generation. It makes it such that PTBO not only has a wide range of exploration capabilities, but also has the ability to quickly exploit them. Numerical experiments are carried out on twenty-eight functions of the CEC 2013 benchmark suite. The simulation results demonstrate its better performance compared with that of other state-of-the-art optimization algorithms.

1. Introduction

Nature-inspired optimization algorithms have become of increasing interest to many researchers in optimization fields in recent years [1]. After half a century of development, nature-inspired optimization algorithms have formed a great family. It not only has a wide range of contact with biological, physical, and other basic science, but also involves many fields such as artificial intelligence, artificial life, and computer science.

Due to the differences in natural phenomena, these optimization algorithms can be roughly divided into three types. These are algorithms based on biological evolution, algorithms based on swarm behavior, and algorithms based on physical phenomena. Typical biological evolutionary algorithms are Evolutionary Strategies (ES) [2], Evolutionary Programming (EP) [3], the Genetic Algorithm (GA) [4,5,6], Genetic Programming (GP) [7], Differential Evolution (DE) [8], the Backtracking Search Algorithm (BSA) [9], Biogeography-Based Optimization (BBO) [10,11], and the Differential Search Algorithm (DSA) [12].

In the last decade, swarm intelligence, as a branch of intelligent computation models, has been gradually rising [13]. Swarm intelligence algorithms mainly simulate biological habits or behavior, including foraging behavior, search behavior and migratory behavior, brooding behavior, and mating behavior. Inspired by these phenomena, researchers have designed many intelligent algorithms, such as Ant Colony Optimization (ACO) [14], Particle Swarm Optimization (PSO) [15], Bacterial Foraging (BFA) [16], Artificial Bee Colony (ABC) [17,18,19], Group Search Optimization (GSO) [20], Cuckoo Search (CS) [21,22], Seeker Optimization (SOA) [23], the Bat Algorithm (BA) [24], Bird Mating Optimization (BMO) [25], Brain Storm Optimization [26,27] and the Grey Wolf Optimizer (GWO) [28].

In recent years, in addition to the above two kinds of algorithms, intelligent algorithms simulating physical phenomenon have also attracted a great deal of researchers’ attention, such as the Gravitational Search Algorithm (GSA) [29], the Harmony Search Algorithm (HSA) [30], the Water Cycle Algorithm (WCA) [31], the Intelligent Water Drops Algorithm (IWDA) [32], Water Wave Optimization (WWO) [33], and States of Matter Search (SMS) [34]. The classical optimization algorithm about a physical phenomenon is simulated annealing, which is based on the annealing process of metal [35,36].

Though these meta-heuristic algorithms that have many advantages over traditional algorithms, especially in NP hard problems, have been proposed to tackle many challenging complex optimization problems in science and industry, there is no single approach that is optimal for all optimization problems [37]. In other words, an approach may be suitable for solving these problems, but it is not suitable for solving those problems. This is especially true as global optimization problems have become more and more complex, from simple uni-modal functions to hybrid rotated shifted multimodal functions [38]. Hence, more innovative and effective optimization algorithms are always needed.

A natural phenomenon provides a rich source of inspiration to researchers to develop a diverse range of optimization algorithms with different degrees of usefulness and practicability. In this paper, a new meta-heuristic optimization algorithm inspired by the phase transition phenomenon of elements in a natural system for continuous global optimization is proposed, which is termed phase transition-based optimization (PTBO). From a statistical mechanics point of view, a phase transition is a non-trivial macroscopic form of collective behavior in a system composed of a number of elements that follow simple microscopic laws [39]. Phase transitions play an important role in the probabilistic analysis of combinatorial optimization problems, and are successfully applied in Random Graph, Satisfiability, and Traveling Salesman Problems [40]. However, there are few algorithms with the mechanism of phase transition for solving continuous global optimization problems in the literature.

Phase transition is ubiquitous in nature or in social life. For example, at atmospheric pressure, water boils at a critical temperature of 100 °C. When the temperature is lower than 100 °C, water is a liquid, while above 100 °C, it is a gas. Besides this, there are also a lot of examples of phase transition. Everybody knows that magnets attract nails made out of iron. However, the attraction force disappears when the temperature of the nail is raised above 770 °C. When the temperature is above 770 °C, the nail enters a paramagnetic phase. Moreover, it is well-known that mercury is a good conductor for its weak resistance. Nevertheless, the electrical resistance of mercury falls abruptly down to zero when the temperature passes through 4.2 K (kelvin temperature). From a macroscopical view, a phase transition is the transformation of a system from one phase to another one, depending on the values of control parameters, such as temperature, pressure, and other outside interference.

From the above examples, we can see that each system or matter has different phases and related critical points for those phases. We can also observe that all phase transitions have a common law, and we may think that phase transition is the competitive result of two kinds of tendencies: stable order and unstable disorder. In complex system theory, phase transition is related to the self-organized process by which a system transforms from disorder to order. From this point of view, phase transition implicates a search process of optimization. The thermal motion of an element is a source of disorder [41]. The interaction of elements is the cause of order.

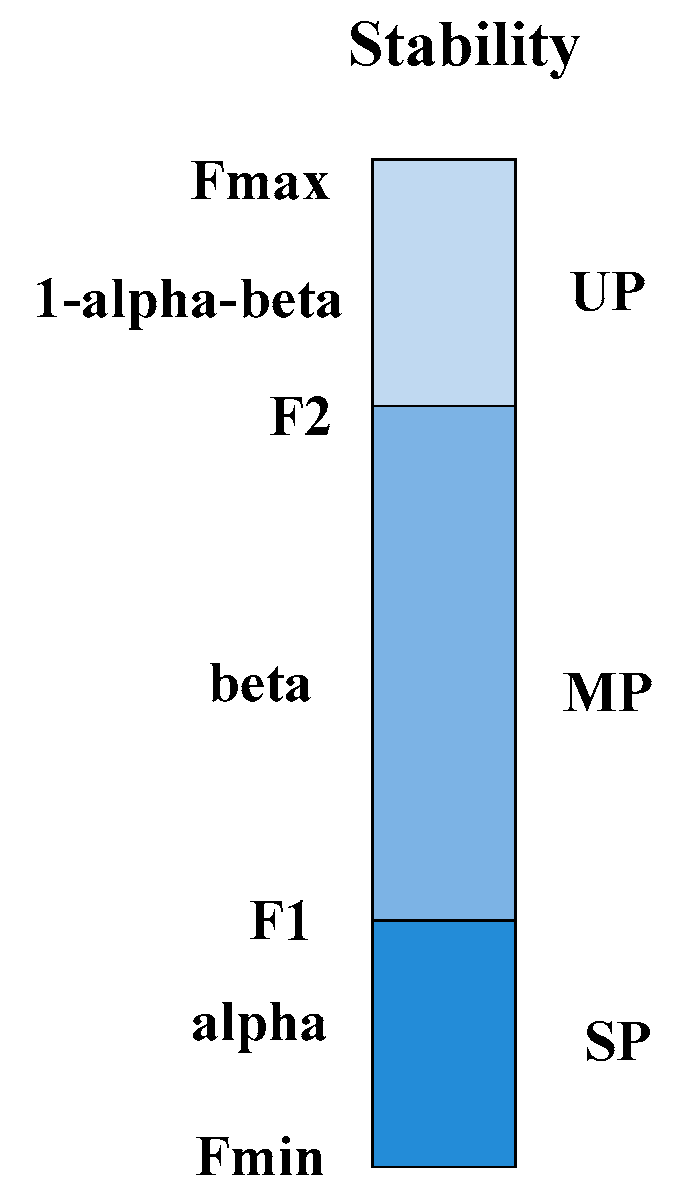
In the proposed PTBO algorithm, the degree of order or disorder is described by stability. We used the value of an objective function to depict the level of stability. For the sake of generality, we extract three kinds of phases in the process of transition from disorder to order, i.e., an unstable phase, a meta-stable phase [42] and a stable phase. From a microscopic viewpoint, the diverse motion characteristics of elements in different phases provide us with novel inspiration to develop a new meta-heuristic algorithm for solving complex continuous optimization problems.

This paper is organized as follows. In Section 2, we briefly introduce the prerequisite preparation for the phase transition-based optimization algorithm. In Section 3, the phase transition-based optimization algorithm and its operators are described. An analysis of PTBO and a comparative study are presented in Section 4. In Section 5, the experimental results with those of other state-of-the-art algorithms are demonstrated. Finally, Section 6 draws conclusions.

2. Prerequisite Preparation

2.1. Fundamental Concepts

Nature itself is a large complex system. In a natural system, the motion of elements transforming from an unstable phase (disorder) to a stable phase (order) is an eternal natural law. In this paper, we uniformly call a molecule in water, an atom in iron, an electron in mercury, etc., an element. The phase of an element in a system may be divided into an unstable phase, a meta-stable phase, and a stable phase. Figure 1 shows three possible positions of elements in a system.

From Figure 1, we can observe that an element is most unstable in the position of point A, and we intuitively call it an unstable phase. On the contrary, in the position of point C, the element is most stable, and we name it a stable phase. The position of point B, between point A and point C, is the transition phase, and we term it a meta-stable phase. The definitions of the three phases are as follows.

Definition 1.

Unstable Phase (UP). The element is in a phase of complete disorder, and moves freely towards an arbitrary direction. In the case of this phase, the element has a large range of motion, and has the ability of global divergence.

Definition 2.

Meta-stable Phase (MP). The element is in a phase between disorder and order, and moves according to a certain law, such as towards the lowest point. In the case of this phase, the element has a moderate activity, and possesses the ability of local shrinkage.

Definition 3.

Stable Phase (SP). The element is in a very regular phase of orderly motion. In the case of this phase, the element has a very small range of activity and has the ability of fine tuning.

According to the above definitions, we can give a more detailed description and examples about the characteristics of the three phases. These motion characteristics in three phases provide us with rich potential to develop the proposed PTBO algorithm. The following

Table 1. The motional characteristics of elements in the three phases.

Phase	Main Property	Motion Tendency	Example
UP	disorder, moving towards an arbitrary direction	stochastic motion	gaseous molecule such as water, atom, or electron in normal temperature
MP	between disorder and order, moving according to a certain law	shrinkage motion	liquid molecule such as water or rapid freezing alloy crystal
SP	order, moving in a very regular mode	vibration motion	solid molecule such as water or an atom of paramagnetic phase in a nail

summarizes the motional characteristics of the unstable phase, the meta-stable phase, and the stable phase.

2.2. The Determination of Critical Interval about Three Phases

As mentioned before, we use stability, which is depicted by the fitness value of an objective function, to describe the degree of order or disorder of an element. In our proposed algorithm, the higher the fitness value of an element is, the worse the stability is. The question of how to divide the critical intervals of the unstable phase, the meta-stable phase, and the stable phase is a primary problem that must be addressed before the proposed algorithm is designed.

For simplicity, we use $F_{\max }$ to denote a maximum fitness value, and we say this element is in the most unstable phase. On the contrary, $F_{\min }$ denotes a minimum fitness value. Then, we set up that the stable phase accounts for $alpha$, and the proportion of the meta-stable phase is $beta$. So, the proportion of the unstable phase is $1-alpha-beta$. The ratio of three critical intervals is shown in Figure 2.

Although $F_{\max }$ and $F_{\min }$ are dynamically changed in each generation, which means the iteration process of phase transition, the basic relationship between the phase of the elements and the critical intervals is shown in

Table 2. The relationship between the intervals and the three phases.

Phase	Interval
UP	[Fmax, F2]
MP	(F2, F1)
SP	[F1, Fmin]

.

3. Phase Transition-Based Optimization Algorithm

3.1. Basic Idea of the PTBO Algorithm

In this work, the motion of elements from an unstable phase to another relative stable phase in PTBO is as natural selection in GA. Many of these iterations from an unstable phase to another relative stable phase can eventually make an element reach absolute stability. The diverse motional characteristics of elements in the three phases are the core of the PTBO algorithm to simulate this phase transition process of elements. In the PTBO algorithm, three corresponding operators are designed. An appropriate combination of the three operators makes an effective search for the global minimum in the solution space.

3.2. The Correspondence of PTBO and the Phase Transition Process

Based on the basic law of elements transitioning from an unstable phase (disorder) to a stable phase (order), the correspondence of PTBO and phase transition can be summarized in

Table 3. The correspondence of phase transition-based optimization (PTBO) algorithm and phase transition.

PTBO Algorithm	Phase Transition Process
Individual	Element
Population size	The number of elements
Fitness function	Stability degree of an element
Global optimal solution	The lowest stability degree of an element
Stochastic operator	The stochastic motion of an element in UP
Shrinkage operator	The shrinkage motion of an element in a MP
Vibration operator	The vibration and fine tuning of an element in SP

.

3.3. The Overall Design of the PTBO Algorithm

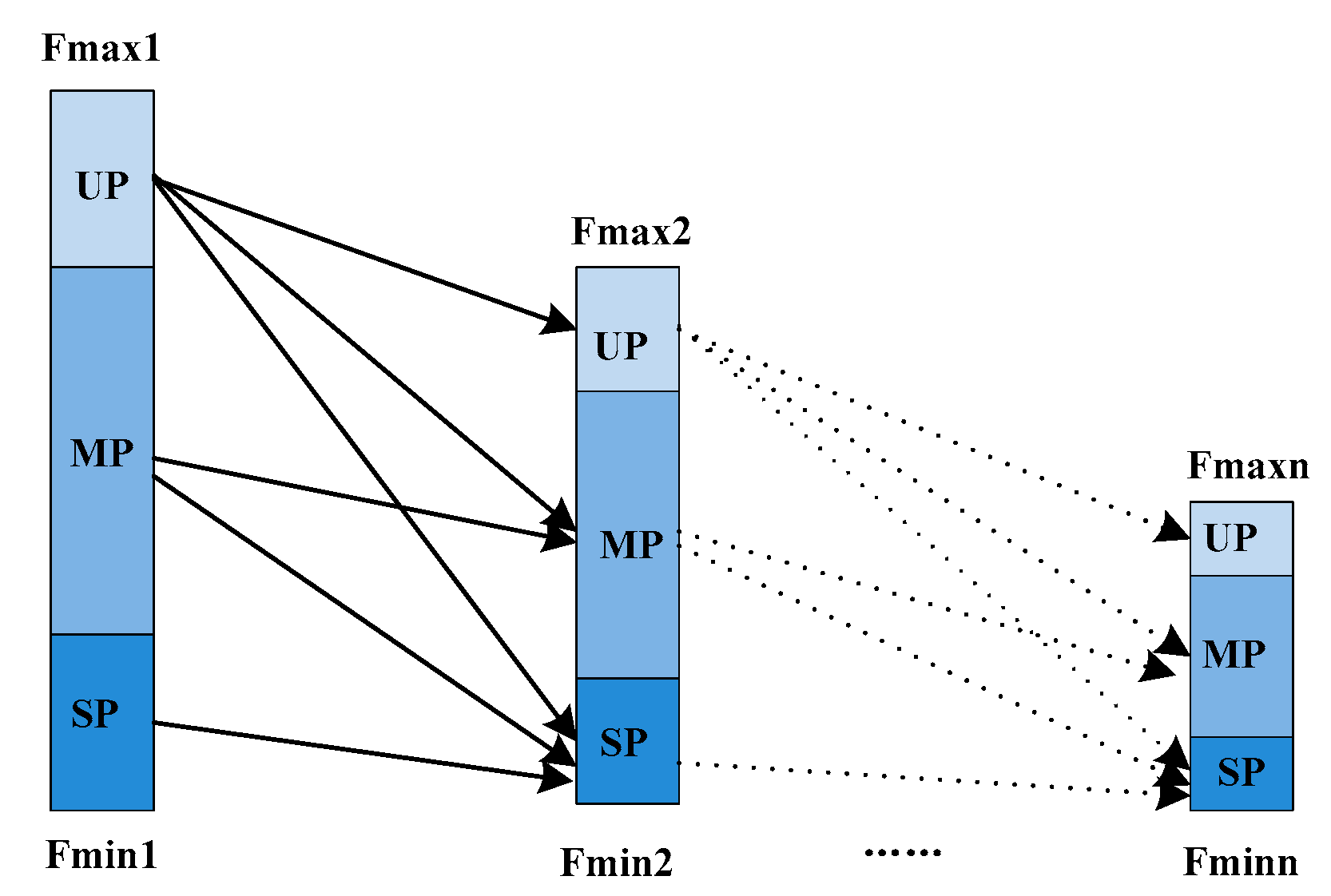
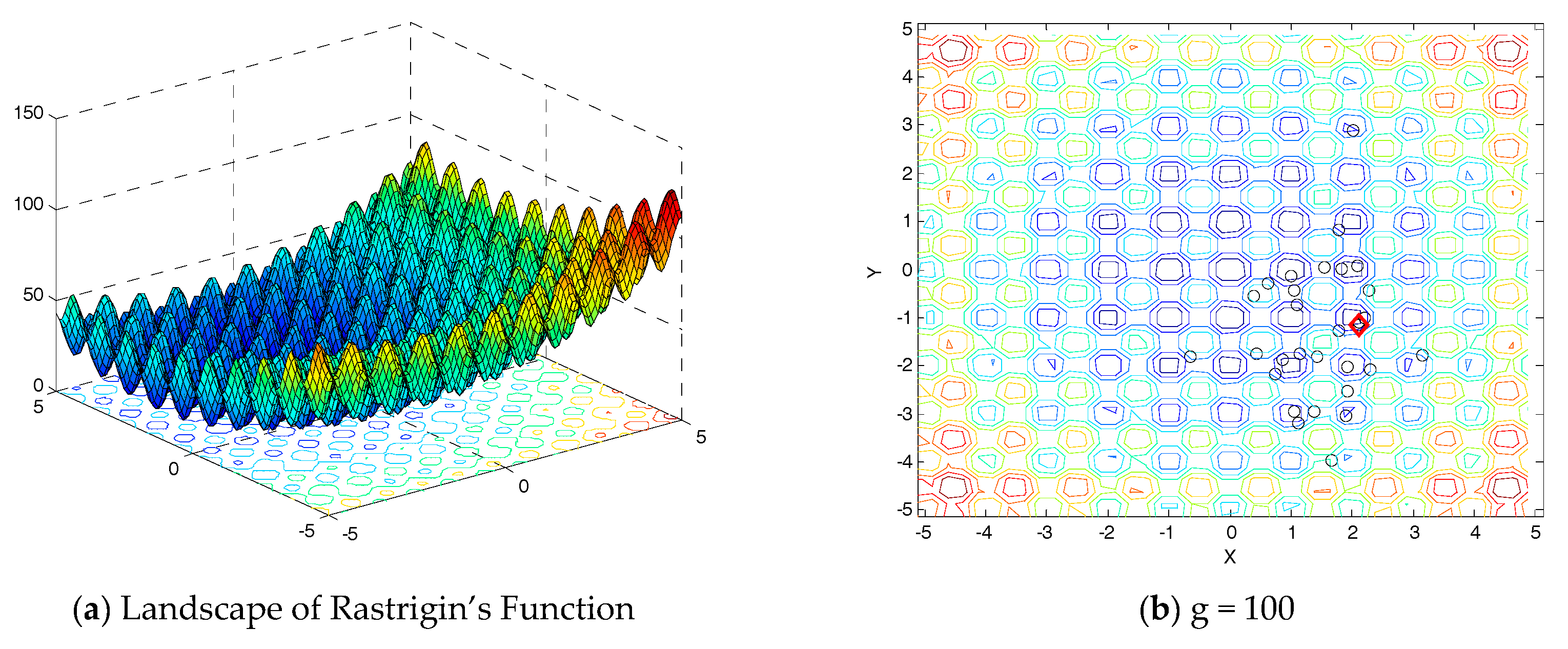
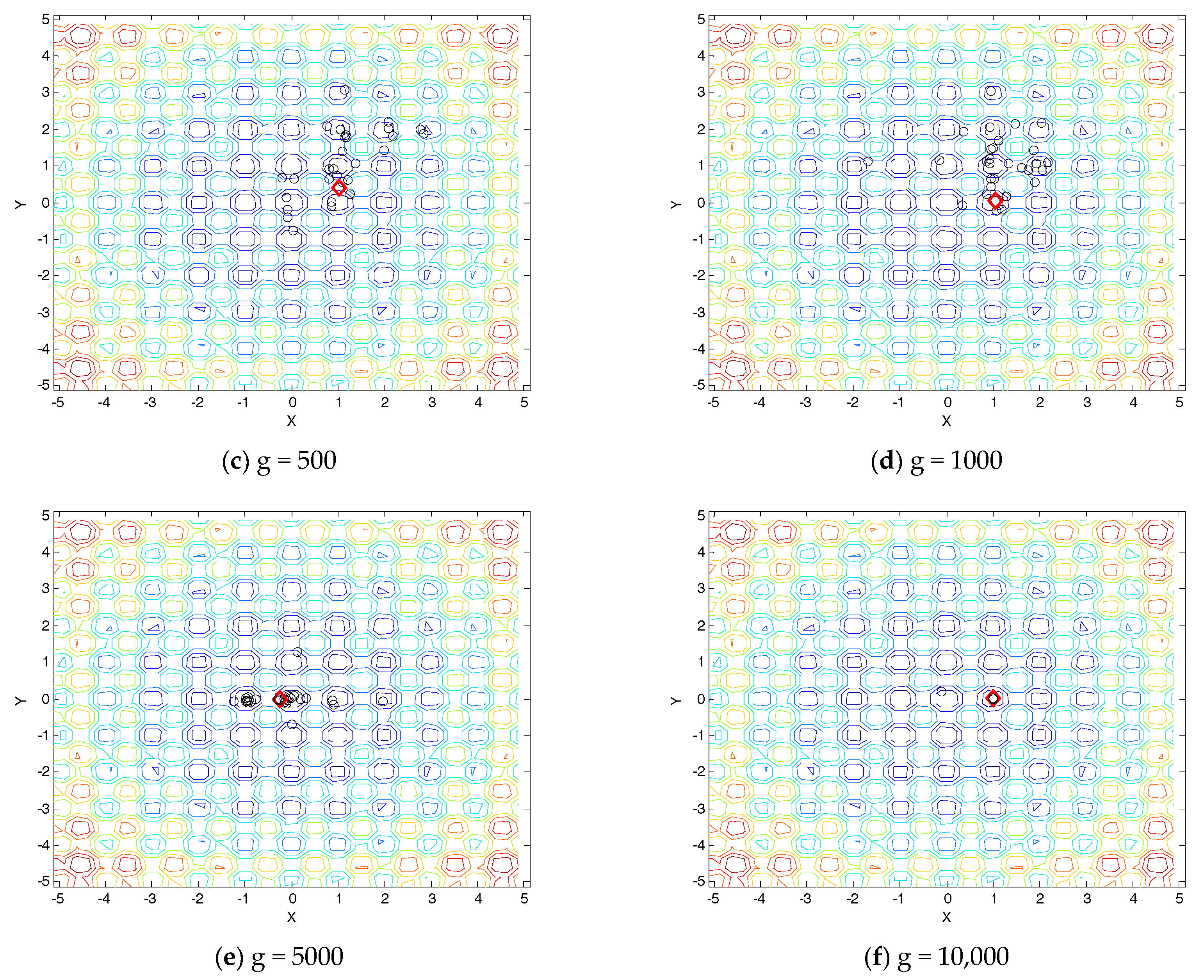
The simplified cyclic diagram of the phase transition process in our PTBO algorithm is shown in Figure 3. It is a complete cyclic process of phase transition from an unstable phase to a stable phase. Firstly, in the first generation, we calculate the maximum and minimum fitness value for each element, respectively, and divide the critical intervals of the unstable phase, the meta-stable phase, and the stable phase according to the rules in Table 2. Secondly, the element will perform the relevant search according to its own phase. If the result of the new degree of stability is better than that of the original phase, the motion will be reserved. Otherwise, we will abandon this operation. That is to say, if the original phase of an element is UP, the movement direction may be towards UP, MP, and SP. However, if the original phase of an element is MP, the movement direction may be towards MP and SP. Of course, if the original phase of an element is SP, the movement direction is towards only SP. Finally, after much iteration, elements will eventually obtain an absolute stability.

Broadly speaking, we may think of PTBO as an algorithmic framework. We simply define the general operations of the whole algorithm about the motion of elements in the phase transition. In a word, PTBO is flexible for skilled users to customize it according to a specific scene of phase transition.

According to the above complete cyclic process of the phase transition, the whole operating process of PTBO can be summarized as three procedures: population initialization, iterations of three operators, and individual selection. The three operators in the iterations include the stochastic operator, the shrinkage operator, and the vibration operator.

3.3.1. Population Initialization

PTBO is also a population-based meta-heuristic algorithm. Like other evolutionary algorithms (EAs), PTBO starts with an initialization of a population, which contains a population size (the size is $N$) of element individuals. The current generation evolves into the next generation through the three operators described as below (see Section 3.3.2). That is to say, the population continually evolves along with the proceeding generation until the termination condition is met. Here, we initialize the j-th dimensional component of the i-th individual as

$$X_{ij}=X_{xj\min }+rand*(X_{j\max }-X_{j\min })$$

(1)

where $rand$ is an uniformly distributed random number between 0 and 1, $X_{j\max }$ and $X_{j\min }$ are the upper boundary and lower boundary of j-th dimension of each individual, respectively.

3.3.2. Iterations of the Three Operators

Now we simply give some certain implementation details about the three operators in the three different phases.

(1) Stochastic operator

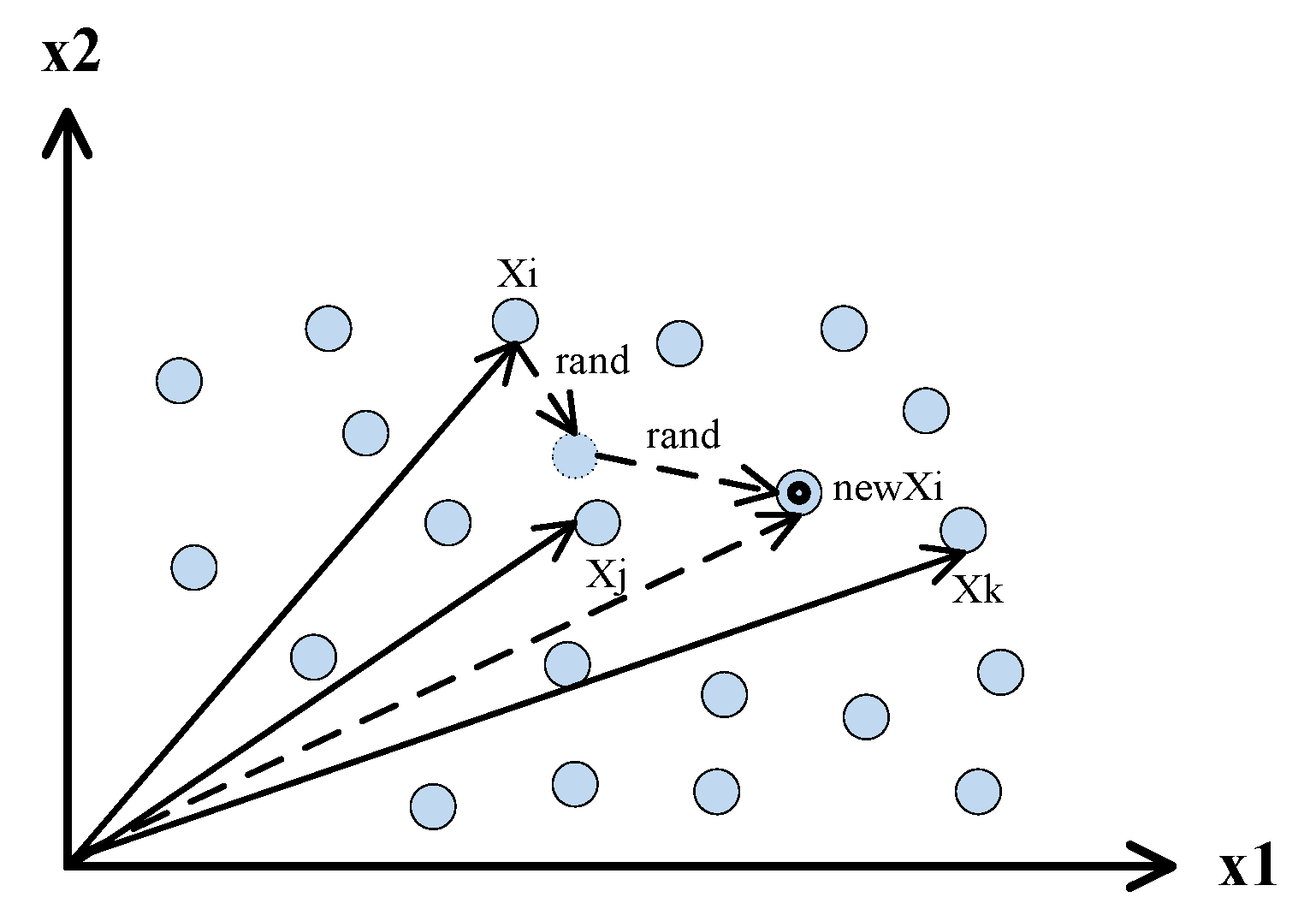
Stochastic diffusion is a common operation in which elements randomly move and pass one another in an unstable phase. Although the movement of elements is chaotic, it actually obeys a certain law from a statistical point of view. We can use the mean free path [43], which is a distance between an element and two other elements in two successive collisions, to represent the stochastic motion characteristic of elements in an unstable phase. Figure 4 simply shows the process of the free walking path of elements.

The free walking path of elements is the distance traveled by an element and other individuals through two collisions. Therefore, the stochastic operator of elements may be implemented as follows:

$$new{X}_i=X_i+ran{d}_1*(X_j-X_i)+ran{d}_2*(X_k-X_i)$$

(2)

where $new{X}_i$ is the new position of $X_i$ after the stochastic motion, $ran{d}_1$ and $ran{d}_2$ are two random vectors, where each element is a random number in the range (0, 1), and the indices j and k are mutually exclusive integers randomly chosen from the range between 1 and N that is also different from the indices i.

(2) Shrinkage operator

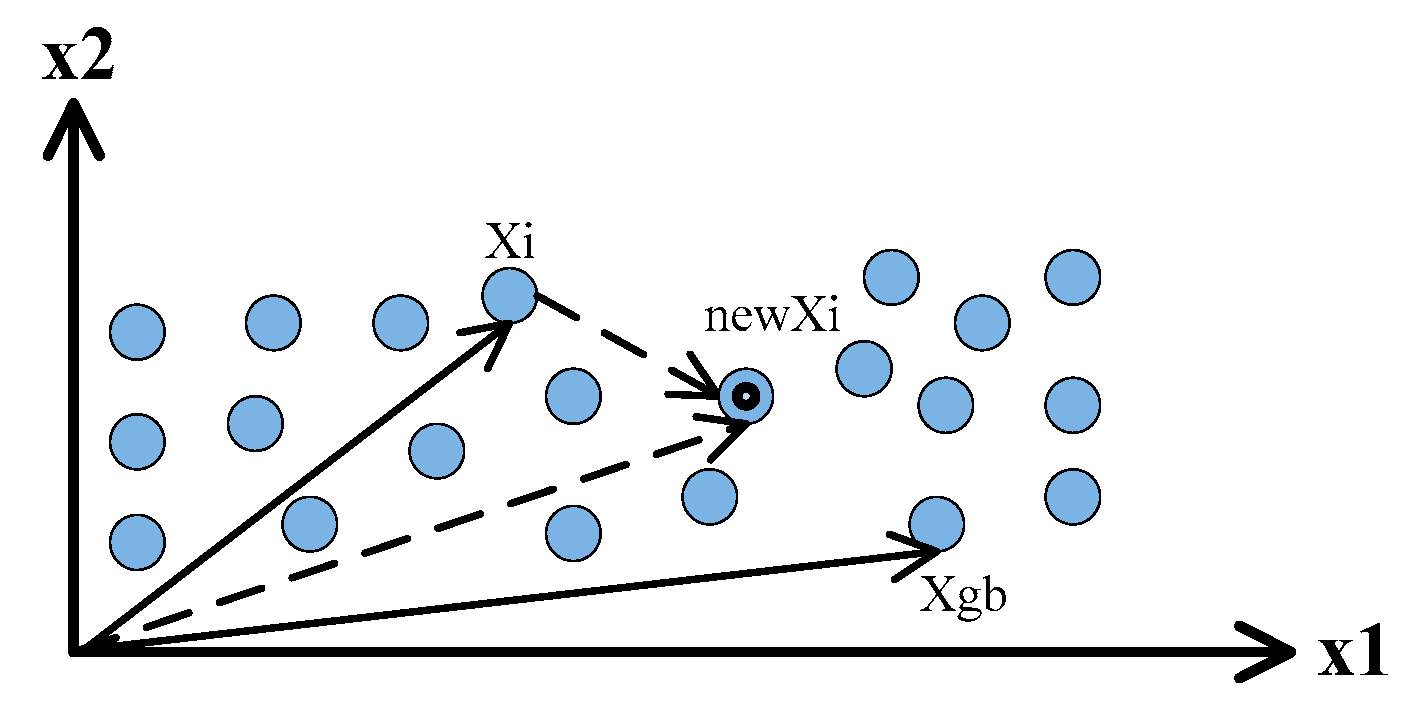
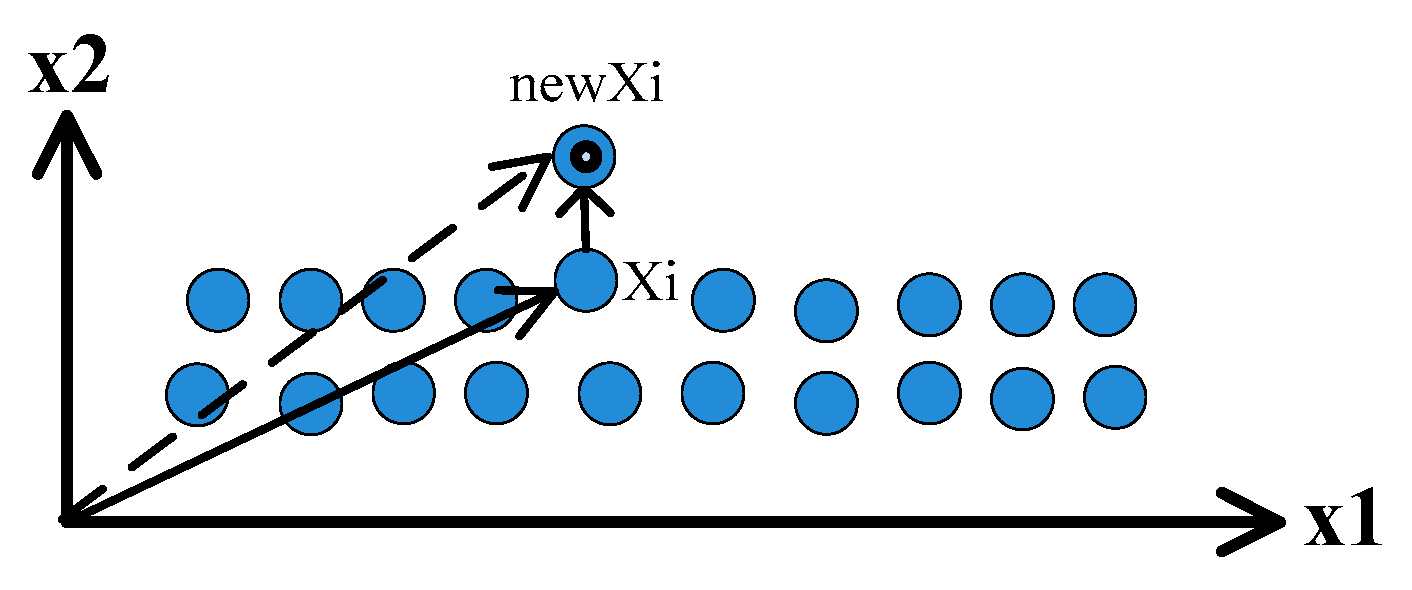
In a meta-stable phase, an element will be inclined to move closer to the optimal one. From a statistical standpoint, the geometric center is a very important digital characteristic and represents the shrinkage trend of elements in a certain degree. Figure 5 briefly gives the shrinkage trend of elements towards the optimal point.

Hence, the gradual shrinkage to the central position is the best motion to elements in a meta-stable phase. So, the shrinkage operator of elements may be implemented as follows:

$$new{X}_i=new{X}_i+(X_{gb}-X_i)*N(0,1)$$

(3)

where $new{X}_i$ is the new position of $X_i$ after the shrinkage operation, $X_{gb}$ is the best individual in the population, and $N(0,1)$ is a normal random number with mean 0 and standard deviation 1. The Normal distribution is an important family of continuous probability distributions applied in many fields.

(3) Vibration operator

Elements in a stable phase will be apt to only vibrate about their equilibrium positions. Figure 6 briefly shows the vibration of elements.

Hence, the vibration operator of elements may be implemented as follows:

$$new{X}_i=new{X}_i+(2*rand-1)*stepSize$$

(4)

where $new{X}_i$ is the new position of $X_i$ after the vibration operation, $rand$ is a uniformly distributed random number in the range (0, 1), and $stepSize$ is the control parameter which regulates the amplitude of jitter with a process of evolutionary generation. With the evolution of the phase transition, the amplitude of vibration will gradually become smaller. $stepSize$ is described as follows:

$$stepSize=\exp (1-G/(G-g+1))$$

(5)

where the $G$ and $g$ denote the maximum number of iterations and current number of iteration respectively, and $\exp ()$ stands for the exponential function.

3.3.3. Individual Selection

In the PTBO algorithm, like other EAs, one-to-one greedy selection is employed by comparing a parent individual and its new generated corresponding offspring. In addition, this greedy selection strategy may raise diversity compared with other strategies, such as tournament selection and rank-based selection. The selection operation at the k-th generation is described as follows:

$$X_i^{k+1}=\{\begin{array}{l}{X}_i^k\mathrm{if}f\left(new{X}_i^k\right)>f\left(X_i^k\right)\\ new{X}_i^k\mathrm{if}f\left(new{X}_i^k\right)<=f\left(X_i^k\right)\end{array}$$

(6)

where $f\left(X\right)$ is the objective function value of each individual.

3.4. Flowchart and Implementation Steps of PTBO

As described above, the main flowchart of the PTBO algorithm is given in Figure 7.

The implementation steps of PTBO are summarized as follows:

Step 1. Initialization: set up algorithm parameters N, D, alpha and beta, randomly generate initial population of elements, and set $g=0$;

Step 2. Evaluation and partition interval: calculate the fitness values of all individuals and obtain the $F_{\max }$ and $F_{\min }$, and divide the critical interval of UP, MP and SP according to Table 2;

Step 3. Stochastic operator: using Formula (2) to create $new{X}_i$;

Step 4. Shrinkage operator: using Formula (3) to update $new{X}_i$;

Step 5. Vibration operator: using Formula (4) and (5) to update $new{X}_i$;

Step 6. Individual selection: accept $new{X}_i$ if $f(new{X}_i)$ is better than $f(X_i)$;

Step 7. Termination judgment: if termination condition is satisfied, stop the algorithm; otherwise, $g=g+1$, go to Step 3.

4. The Analysis of PTBO and a Comparative Study

4.1. The Analysis of Time Complexity

For PTBO, the main operations include the operation of population initialization and the stochastic operator, shrinkage operator, and vibration operator. The time complexity of each operation in a single iteration can be computed as follows:

1

Population initialization operation: $O(N*D)$.

2

Stochastic operator: $O(N*D)$.

3

Shrinkage operator: $O(N*D)$.

4

Vibration operator: $O(N*D)$.

Therefore, the total worst time complexity of PTBO in one iteration is $3*O(N*D)+O(N)$. According to the operational rules of the symbol O, the worst time complexity of one iteration for PTBO can be simplified as $O(N*D)$. It is worth noting that PTBO has the similar time complexity to some popular meta-heuristic algorithms such as PSO ($O(N*D)$).

4.2. The Dynamic Implementation Analysis of PTBO

In this section, the step-wise procedure for the implementation of PTBO for optimization is presented. For the demonstration of the process, Rastrigin’s function [44] is herein considered as an example. Rastrigin’s function is a classic test function in optimization theory in which the point of global minimum is surrounded by a large number of local minima. To converge to the global minimum without being stuck at one of these local minima, however, is extremely difficult. Some numerical solvers need to take a long time to converge to it. Three-dimensional contour plot for Rastrigin’s function is shown in Figure 8a. Rastrigin’s function is described as follows:

$$F(x)={\displaystyle \sum _{i=1}^D(x_i^2-10\cos (2\pi x_i)+10)}$$

(7)

In this experiment, we use 30 individuals to solve the above minimization problem, and the population distribution at various generations in an evolutionary process is shown in Figure 8b–f, with D = 2, alpha = 0.1 and beta = 0.8. In Figure 8b–f, the labels of red diamond represent the optimal point.

From Figure 8b–f, we can observe that the population distribution information can significantly vary at various generations during the run time. PTBO can effectively adapt to a time-varying search space or landscapes.

4.3. The Differences between PTBO and Other Algorithms

4.3.1. The Differences between PTBO and PSO

Like PSO (Particle Swarm Optimization), PTBO is also introduced to deal with unconstrained global optimization problems with continuous variables. In the representational form of implementation, we can certainly think that PTBO is also based on a particle system in the same way as PSO. However, according to the overall design of the PTBO algorithm, there are some differences between PTBO and the classical PSO.

Firstly, in heuristic thought, PSO is inspired by biological behavior or habits for simulating animal swarm behavior, such as fish schooling and bird flocking, while PTBO is inspired by the phase transition phenomenon of elements in nature. Secondly, in PSO, the direction of a particle is calculated by two best positions, $pbest$ and $gbest$. However, the motion direction of an element in PTBO is arbitrarily derived from the other two elements that are different from each other. It may enhance the diversity of the population and ensure the avoidance of premature convergence. Thirdly, in the design of the operators, each particle in PSO contains a velocity item. Nevertheless, in PTBO the concept of velocity does not exist. Besides, PSO uses the position information of $pbest$ and $gbest$ to record the updating of velocity or position. However, PTBO uses only the position information about $gbest$ and the $pbest$ position of elements is not considered.

4.3.2. The Differences between PTBO and SMS

SMS (States of Matter Search) is a nature-inspired optimization algorithm based on the simulation of the states of matter phenomenon [35]. Specifically, SMS is devised by considering each state of matter at one different exploration–exploitation ratio by dividing the whole search process into three stages, i.e., gas, liquid, and solid.

Although the sources of inspiration for PBTO and SMS are similar, which are taken from a physical phenomenon about the states of matter, the evolution processes of PTBO and SMS are completely different. The evolution process of SMS is as follows. At first, all individuals in the population perform exploration in the mode of the gas state. Then, after 50% of the iterations, the search mode is changed into the liquid state for 40% of the iterations, i.e., the search between exploration and exploitation. Finally, the evolutionary process enters the stage of exploitation (liquid state) for 10% of the iterations. However, in PTBO, the three phases are coexistent in the entire search process. In other words, the three different phases of individuals execute dynamically different search tasks according to their phase in each generation. Hence, the implementation about the balance of exploration and exploitation between PTBO and SMS is completely different. Besides, the operators of PTBO and SMS are also completely different. In summary, it can be said that there are fundamental differences between PTBO and SMS.

5. Experimental Results

5.1. Benchmark Functions

In order to verify the effectiveness and robustness of the proposed PTBO algorithm, PTBO is applied in experimental simulation studies for finding the global minimum of the entire 28 test functions of the CEC 2013 special session [44]. The CEC 2013’s test suite, which has been improved on the basis of CEC 2005 [38], covers various types of function optimization, and is summarized in

Table 4. Benchmark functions tested by PTBO (CEC2013).

Type	Function ID	Functions Name
Uni-modal Functions	F01	Sphere Function
	F02	Rotated High Conditioned Elliptic Function
	F03	Rotated Bent Cigar Function
	F04	Rotated Discus Function
	F05	Different Powers Function
Multimodal Functions	F06	Rotated Rosenbrock’s Function
	F07	Rotated Schaffers F7 Function
	F08	Rotated Ackley’s Function
	F09	Rotated Weierstrass Function
	F10	Rotated Griewank’s Function
	F11	Rastrigin’s Function
	F12	Rotated Rastrigin’s Function
	F13	Non-Continuous Rotated Rastrigin’s Function
	F14	Schwefel’s Function
	F15	Rotated Schwefel’s Function
	F16	Rotated Katsuura Function
	F17	Lunacek Bi_Rastrigin Function
	F18	Rotated Lunacek Bi_Rastrigin Function
	F19	Expanded Griewank’s plus Rosenbrock’s Function
	F20	Expanded Scaffer’s F6 Function
Composition Functions	F21	Composition Function 1 (n = 5, Rotated)
	F22	Composition Function 2 (n = 3, Unrotated)
	F23	Composition Function 3 (n = 3, Rotated)
	F24	Composition Function 4 (n = 3, Rotated)
	F25	Composition Function 5 (n = 3, Rotated)
	F26	Composition Function 6 (n = 5, Rotated)
	F27	Composition Function 7 (n = 5, Rotated)
	F28	Composition Function 8 (n = 5, Rotated)

.

The search range of all functions is between −100 and 100 in every dimension. These problems are shifted or rotated to increase their complexity, and are treated as black-box problems. The explicit equations of the problems are not allowed to be used. The test suite of Table 4 consists of five uni-modal functions (F01 to F05), 15 multimodal functions (F06 to F20) and eight composition functions (F21 to F28).

5.2. Parameters Determination of the Interval Ratio of PTBO

In our PTBO algorithm, there are two parameters, the alpha and the beta, that need to be allocated to determine the critical intervals about the three phases. In a natural system, we can observe that the elements in the middle meta-stable phase account for the majority, and the elements in the unstable and stable phases occupy only a small proportion. This phenomenon is consistent with the two-eight law (or the 1/5th rule) [2]. For the case of simplicity, we give a value of 0.8 to beta, which is the proportion of the elements in the meta-stable phase. So, the elements in the unstable and stable phases account for 0.2 in total. The specific interval ratio settings of the three phases are shown in

Table 5. Different interval ratio settings of the three phases.

Ratio Method	No.	Stable Phase	Meta-Stable Phase	Unstable Phase
Fixed ratio	Prop1	0.05	0.8	0.15
	Prop2	0.1	0.8	0.1
	Prop3	0.15	0.8	0.05
Random ratio	Prop4	0.2 * rand	0.8	0.2 * (1 − rand)

.

In order to determine which interval ratio is the most suitable for the PTBO algorithm, we conducted some compared experiments with 50 independent runs according to Table 5. The compared results of different interval ratios are listed in

Table 6. Compared results of different interval ratios.

Func.	Prop1	Prop2	Prop3	Prop4	Func.	Prop1	Prop2	Prop3	Prop4
F01	6.16 × 10−27	6.13 × 10−27	3.82 × 10−28	4.31 × 10−28	F15	4.45 × 103	4.57 × 103	4.27 × 103	4.23 × 103
	2.08 × 10−26	3.70 × 10−26	6.04 × 10−28	5.96 × 10−28		5.99 × 102	6.55 × 102	7.24 × 102	7.64 × 102
F02	7.90 × 105	8.73 × 105	1.02 × 106	8.63 × 105	F16	4.10 × 10−1	4.71 × 10−1	4.11 × 10−1	3.94 × 10−1
	2.89 × 105	3.25 × 105	3.66 × 105	6.60 × 105		2.01 × 10−1	2.59 × 10−1	2.07 × 10−1	1.96 × 10−1
F03	1.95 × 108	1.12 × 108	8.01 × 107	3.84 × 107	F17	7.58 × 101	7.13 × 101	6.68 × 101	6.72 × 101
	2.91 × 108	1.49 × 108	1.22 × 108	5.22 × 107		1.45 × 101	1.25 × 101	9.94	1.63 × 101
F04	8.08 × 103	9.03 × 103	1.30 × 104	8.26 × 103	F18	7.96 × 101	7.57 × 101	6.99 × 101	6.66 × 101
	2.59 × 103	2.35 × 103	3.43 × 103	3.71 × 103		1.47 × 101	1.15 × 101	1.14 × 101	1.23 × 101
F05	1.36 × 10−14	3.00 × 10−15	6.38 × 10−22	2.64 × 10−15	F19	5.05 × 102	5.05 × 102	5.04 × 102	5.04 × 102
	2.19 × 10−14	4.32 × 10−15	1.18 × 10−21	4.44 × 10−15		1.61	1.45	1.06	8.36 × 10−1
F06	2.32 × 101	3.09 × 101	2.74 × 101	2.53 × 101	F20	1.21 × 101	1.19 × 101	1.26 × 101	1.15 × 101
	2.57 × 101	2.88 × 101	2.58 × 101	2.67 × 101		1.68	2.01	2.07	2.12
F07	5.30 × 101	5.01 × 101	4.13 × 101	3.04 × 101	F21	3.01 × 102	3.30 × 102	3.22 × 102	2.97 × 102
	2.31 × 101	1.90 × 101	1.93 × 101	1.73 × 101		7.76 × 101	8.86 × 101	7.19 × 101	8.01 × 101
F08	2.09 × 101	2.09 × 101	2.09 × 101	2.09 × 101	F22	1.01 × 103	8.03 × 102	9.74 × 102	8.61 × 102
	6.18 × 10−2	6.57 × 10−2	6.50 × 10−2	6.50 × 10−2		4.92 × 102	2.79 × 102	4.68 × 102	3.11 × 102
F09	2.49 × 101	2.39 × 101	2.43 × 101	1.90 × 101	F23	5.25 × 103	5.16 × 103	5.07 × 103	4.15 × 103
	5.33	5.24	5.54	5.26		8.49 × 102	6.32 × 102	7.01 × 102	1.40 × 103
F10	3.50 × 10−1	3.39 × 10−1	3.43 × 10−1	3.27 × 10−1	F24	2.42 × 102	2.35 × 102	2.33 × 102	2.33 × 102
	2.03 × 10−1	1.85 × 10−1	1.73 × 10−1	1.77 × 10−1		8.21	8.66	8.46	1.04 × 101
F11	4.85 × 101	4.05 × 101	3.89 × 101	3.92 × 101	F25	2.81 × 102	2.79 × 102	2.78 × 102	2.74 × 102
	1.60 × 101	1.38 × 101	1.12 × 101	1.21 × 101		1.34 × 101	1.46 × 101	1.32 × 101	1.02 × 101
F12	1.40 × 102	1.28 × 102	1.21 × 102	6.32 × 101	F26	2.53 × 102	2.77 × 102	2.48 × 102	2.51 × 102
	2.82 × 101	3.41 × 101	3.72 × 101	2.51 × 101		6.85 × 101	6.93 × 101	6.71 × 101	6.57 × 101
F13	1.61 × 102	1.53 × 102	1.47 × 102	1.18 × 102	F27	7.50 × 102	7.41 × 102	7.23 × 102	6.38 × 102
	3.13 × 101	2.76 × 101	2.67 × 101	3.07 × 101		9.33 × 101	1.21 × 102	1.34 × 102	1.16 × 102
F14	9.52 × 102	8.63 × 102	9.35 × 102	9.47 × 102	F28	3.93 × 102	3.46 × 102	3.51 × 102	2.96 × 102
	3.28 × 102	3.31 × 102	3.49 × 102	2.81 × 102		4.61 × 102	2.74 × 102	3.92 × 102	2.83 × 101

Bold text is the best result obtained by different interval ratios.

. In Table 6, the mean values are listed in the first line, and the standard deviations are displayed in the second line. We can intuitively observe that the ratio of prop4 has the best accuracy results compared with the other three ratios. Hence, in the subsequent experiments, we choose the value of beta to be 0.8, and the proportion of the unstable and stable phases is a random ratio of 0.2 in total.

5.3. Experimental Platform and Algorithms’ Parameter Settings

For a fair comparison, all of the experiments are conducted on the same machine with an Intel 3.4 GHz central processing unit (CPU) and 4GB memory. The operating system is Windows 7 with MATLAB 8.0.0.783(R2012b).

On the test functions, we compare PTBO with classic PSO, DE, and six other recent popular meta-heuristic algorithms, which are BA, CS, BSO, WWO, WCA, and SMS. The first three algorithms belong to the second category, i.e., swarm intelligence, and the remaining three algorithms belong to the third category, i.e., intelligent algorithms simulating physical phenomena. The parameters adopted for the PTBO algorithm and the compared algorithms are given in

Table 7. The parameter settings of the compared algorithms.

No.	Algorithm	Parameter Setting
1	PSO	$\omega \in [0.9,0.4],c1=c2=2,V_{\max }=0.2*range$
2	DE	$F=0.5,CR=0.9$
3	BA	$A=0.25,r=0.5$
4	CS	$pa=0.25,stepsize=0.05$
5	BSD	$m=5,p\_replace=0.2,p\_one=0.8,p\_one\_center=0.4,p\_two\_center=0.5,k=20$
6	WWO	$hMax=12,alpha=1.0026,betaMax=0.25,betaMin=0.001$
7	WCA	$Nsr=4,d\max =1e-16$
8	SMS	Gas state:$\rho \in [0.8,1],\beta =0.8,\alpha =0.8,H=0.9$
		Liquid state:$\rho \in [0.3,0.6],\beta =0.4,\alpha =0.2,H=0.2$
		Solid state:$\rho \in [0,0.1],\beta =0.1,\alpha =0,H=0$
9	PTBO	alpha is random ratio, beta = 0.8

PSO: particle swarm optimization; DE: Differential Evolution; BA: Bat Algorithm; CS: Cuckoo Search; BSO: Brain Storm Optimization; WWO: Water Wave Optimization; WCA: Water Cycle Algorithm; SMS: States of Matter Search.

.

5.4. The Compared Experimental Results

Each of the experiments was repeated for 50 independent runs with different random seeds, and the average function values of the best solutions were recorded.

5.4.1. Comparisons on Solution Accuracy

The accuracy results of the uni-modal, multimodal, and composition functions are given in

Table 8. The results of solution accuracy for the uni-modal functions.

Func.	PTBO	PSO	DE	BA	CS	BSO	WWO	WCA	SMS
F01	4.31 × 10−28	3.56 × 103 ǂ	2.65 × 103 ǂ	1.05 × 10−3 ǂ	4.46 × 103 ǂ	3.71 × 10−3 ǂ	2.62 × 10−28 ξ	1.58 × 10−28 ξ	4.63 × 104 ǂ
	5.96 × 10−28	2.65 × 103	8.98 × 10−1	1.29 × 10−4	3.10 × 102	5.71 × 10−3	1.30 × 10−28	1.45 × 10−28	4.24 × 103
F02	8.63 × 105	1.12 × 107 ǂ	1.56 × 107 ξ	4.82 × 104 ξ	4.21 × 107 ǂ	1.17 × 106 ǂ	1.20 × 106 ǂ	7.53 × 105 ξ	4.91 × 108 ǂ
	6.60 × 105	1.56 × 107	2.05 × 105	1.81 × 104	4.04 × 106	3.35 × 105	7.19 × 105	7.54 × 105	8.49 × 107
F03	3.84 × 107	4.98 × 1010 ǂ	4.72 × 1010 ǂ	8.96 × 108 ǂ	1.72 × 1010 ǂ	1.66 × 108 ǂ	3.98 × 108 ǂ	2.94 × 109 ǂ	1.00 × 1010 ǂ
	5.22 × 107	4.72 × 1010	3.57 × 107	3.48 × 108	2.11 × 109	2.22 × 108	6.71 × 108	4.30 × 109	0.00
F04	8.26 × 103	5.64 × 103 ξ	8.41 × 103 ǂ	2.42 × 104 ǂ	6.05 × 104 ǂ	5.44 × 103 ξ	5.57 × 104 ǂ	6.55 × 101 ξ	8.14 × 104 ǂ
	3.71 × 103	8.41 × 103	1.27 × 103	3.91 × 102	6.61 × 102	2.22 × 103	1.05 × 104	2.07 × 102	9.79 × 103
F05	2.64 × 10−15	1.58 × 103 ǂ	1.25 × 103 ǂ	1.37 × 10−2 ǂ	1.09 × 103 ǂ	4.12 × 10−2 ǂ	5.53 × 10−2 ǂ	2.95 × 10−12 ǂ	1.38 × 104 ǂ
	4.44 × 10−15	1.25 × 103	1.84 × 101	2.08 × 10−3	6.70 × 101	1.74 × 10−2	2.90 × 10−1	7.89 × 10−12	2.66 × 103
ǂ/ξ/~		4/1/0	4/1/0	4/1/0	5/0/0	4/1/0	4/1/0	2/3/0	5/0/0

“ǂ”, “ξ”, and “~” denote that the performance of PTBO is better than, worse than, and similar to that of the corresponding algorithm, respectively. Bold text is the best result obtained by the compared algorithms.

,

Table 9. The results of solution accuracy for the multimodal functions.

Function	PTBO	PSO	DE	BA	CS	BSO	WWO	WCA	SMS
F06	2.53 × 101	2.51 × 102 ǂ	3.20 × 101 ǂ	1.36 ξ	4.99 × 102 ǂ	4.30 × 101 ǂ	5.51 × 101 ǂ	3.27 × 101 ǂ	6.18 × 103 ǂ
	2.67 × 101	2.11 × 102	2.51 × 101	6.61	5.70 × 101	2.84 × 101	2.76 × 101	2.67 × 101	9.16 × 102
F07	3.04 × 101	1.19 × 102 ǂ	2.44 × 101 ξ	2.59 × 108 ǂ	2.51 × 108 ǂ	1.59 × 102 ǂ	8.91 × 101 ǂ	1.90 × 102 ǂ	5.50 × 103 ǂ
	1.73 × 101	4.67 × 101	1.43 × 101	4.83 × 107	2.44 × 107	1.11 × 102	3.02 × 101	4.00 × 101	3.85 × 103
F08	2.09 × 101	2.09 × 101 ~	2.09 × 101 ~	2.10 × 101 ~	2.11 × 101 ~	2.09 × 101 ~	2.09 × 101 ~	2.09 × 101 ~	2.09 × 101 ~
	6.50 × 10−2	5.71 × 10−2	4.33 × 10−2	6.52 × 10−2	6.15 × 10−2	7.40 × 10−2	5.56 × 10−2	5.56 × 10−2	5.31 × 10−2
F09	1.90 × 101	2.18 × 101 ~	1.86 × 101 ξ	5.77 × 101 ǂ	5.73 × 101 ǂ	3.42 × 101 ǂ	2.76 × 101 ǂ	3.40 × 101 ǂ	4.00 × 101 ǂ
	5.26	2.73	4.40	3.29	1.16	3.72	4.29	3.01	1.48
F10	3.27 × 10−1	7.01 × 102 ǂ	6.65 × 10−1 ~	1.14 ǂ	9.05 × 102 ǂ	9.62 × 10−1 ~	1.41 × 10−1 ξ	3.17 × 10−1 ~	5.60 × 103 ǂ
	1.77 × 10−1	4.13 × 102	1.21	6.95 × 10−1	4.90 × 101	2.16 × 10−1	7.49 × 10−2	2.00 × 10−1	6.76 × 102
F11	3.92 × 101	1.05 × 102 ǂ	2.27 × 101 ξ	9.90 × 102 ǂ	9.90 × 102 ǂ	6.03 × 102 ǂ	1.22 × 102 ǂ	1.05 × 102 ǂ	7.65 × 102 ǂ
	1.21 × 101	5.68 × 101	7.87	2.71 × 101	2.24 × 101	1.03 × 102	3.80 × 101	4.84 × 101	6.72 × 101
F12	6.32 × 101	1.07 × 102 ǂ	4.14 × 101 ξ	9.50 × 102 ǂ	9.52 × 102 ǂ	5.97 × 102 ǂ	1.36 × 102 ǂ	3.38 × 102 ǂ	7.63 × 102 ǂ
	2.51 × 101	3.62 × 101	1.21 × 101	1.28 × 101	1.34 × 101	1.04 × 102	3.51 × 101	9.25 × 101	5.78 × 101
F13	1.18 × 102	2.80 × 102 ǂ	2.09 × 102 ǂ	1.12 × 103 ǂ	1.12 × 103 ǂ	6.51 × 102 ǂ	2.07 × 102 ǂ	3.46 × 102 ǂ	7.68 × 102 ǂ
	3.07 × 101	3.13 × 101	3.63 × 101	4.65 × 101	3.75 × 101	7.86 × 101	5.72 × 101	6.77 × 101	5.35 × 101
F14	9.47 × 102	2.00 × 103 ǂ	1.46 × 103 ǂ	5.72 × 103 ǂ	5.90 × 103 ǂ	4.42 × 103 ǂ	3.23 × 103 ǂ	2.37 × 103 ǂ	7.72 × 103 ǂ
	2.81 × 102	6.45 × 102	4.71 × 102	4.38 × 102	4.38 × 102	7.77 × 102	6.47 × 102	7.83 × 102	3.88 × 102
F15	4.23 × 103	4.02 × 103 ξ	7.21 × 103 ǂ	5.02 × 103 ǂ	4.99 × 103 ǂ	4.33 × 103 ~	5.16 × 103 ǂ	4.72 × 103 ǂ	7.59 × 103 ǂ
	7.64 × 102	6.52 × 102	3.53 × 102	2.58 × 102	2.57 × 102	6.67 × 102	1.72 × 103	6.74 × 102	2.60 × 102
F16	3.94 × 10−1	1.94 ǂ~	2.49 ǂ	1.98 ǂ	1.89 ǂ	3.13 × 10−1 ξ	2.00 ǂ	1.63 ǂ	2.59 ǂ
	1.96 × 10−1	4.89 × 10−1	3.29 × 10−1	9.87 × 10−1	8.45 × 10−1	1.16 × 10−1	8.11 × 10−1	4.95 × 10−1	3.08 × 10−1
F17	6.72 × 101	8.45 × 101 ǂ	6.39 × 101 ξ	8.29 × 102 ǂ	8.42 × 102 ǂ	6.10 × 102 ǂ	1.43 × 102 ǂ	2.39 × 102 ǂ	1.51 × 103 ǂ
	1.63 × 101	3.92 × 101	9.90	1.12 × 101	1.41 × 101	1.03 × 102	3.67 × 101	1.09 × 102	1.02 × 102
F18	6.66 × 101	1.26 × 102 ǂ	2.92 × 102 ǂ	8.26 × 102 ǂ	8.33 × 102 ǂ	5.13 × 102 ǂ	1.42 × 102 ǂ	4.66 × 102 ǂ	1.53 × 103 ǂ
	1.23 × 101	4.99 × 101	1.86 × 101	1.17 × 101	1.02 × 101	9.43 × 101	3.31 × 101	1.43 × 102	8.20 × 101
F19	5.04 × 102	2.16 × 103 ǂ	5.65 × 102 ǂ	3.37 × 103 ǂ	1.55 × 103 ǂ	5.12 × 102 ~	5.16 × 102 ~	5.14 × 102 ~	5.90 × 105 ǂ
	8.36 × 10−1	3.38 × 103	2.84	1.85 × 102	7.16 × 101	2.41	1.71	5.60	2.78 × 105
F20	1.15 × 101	1.24 × 101 ǂ	1.28 × 101 ǂ	1.50 × 101 ǂ	1.50 × 101 ǂ	1.45 × 101 ǂ	1.29 × 101 ǂ	1.50 × 101 ǂ	1.50 × 101 ǂ
	2.12	8.98 × 10−1	5.20 × 10−1	0.00	0.00	9.18 × 10−2	1.00	0.00	5.71 × 10−2
ǂ/ξ/~		12/1/2	8/5/2	13/1/1	14/0/1	10/1/4	12/1/2	10/3/2	14/0/1

“ǂ”, “ξ”, and “~” denote that the performance of PTBO is better than, worse than, and similar to that of the corresponding algorithm, respectively. Bold text is the best result obtained by the compared algorithms.

and

Table 10. The results of solution accuracy for the composition functions.

Function	PTBO	PSO	DE	BA	CS	BSO	WWO	WCA	SMS
F21	2.97 × 102	4.91 × 102 ǂ	4.20 × 102 ǂ	3.01 × 102 ~	1.50 × 103 ǂ	3.48 × 102 ǂ	3.25 × 102 ~	3.51 × 102 ~	3.64 × 103 ǂ
	8.01 × 101	2.21 × 102	8.52 × 101	2.68 × 10−2	8.81 × 101	8.87 × 101	8.01 × 101	8.51 × 101	2.17 × 102
F22	8.61 × 102	2.17 × 103 ǂ	1.33 × 103 ǂ	8.52 × 103 ǂ	8.52 × 103 ǂ	5.62 × 103 ǂ	4.09 × 103 ǂ	4.01 × 103 ǂ	8.39 × 103 ǂ
	3.11 × 102	6.53 × 102	3.94 × 102	1.76 × 102	1.93 × 102	8.61 × 102	7.54 × 102	1.23 × 103	3.46 × 102
F23	4.15 × 103	4.16 × 103 ~	6.61 × 103 ǂ	7.55 × 103 ǂ	7.74 × 103 ǂ	5.67 × 103 ǂ	5.40 × 103 ~	6.64 × 103 ǂ	8.25 × 103 ǂ
	1.40 × 103	8.98 × 102	9.13 × 102	5.35 × 102	3.99 × 102	6.67 × 102	1.33 × 103	6.71 × 102	2.72 × 102
F24	2.33 × 102	2.84 × 102 ǂ	2.95 × 102 ǂ	7.03 × 102 ǂ	7.28 × 102 ǂ	3.34 × 102 ǂ	2.63 × 102 ǂ	3.08 × 102 ǂ	3.58 × 102 ǂ
	1.04 × 101	1.23 × 101	1.05 × 101	9.88 × 101	1.43 × 101	1.89 × 101	1.44 × 101	3.54 × 101	1.05 × 101
F25	2.74 × 102	3.03 × 102 ~	2.66 × 102 ξ	4.48 × 102 ǂ	4.45 × 102 ǂ	3.56 × 102 ǂ	3.04 × 102 ~	3.17 × 102 ~	3.73 × 102 ǂ
	1.02 × 101	9.32	7.55	2.23 × 101	4.24	1.76 × 101	1.47 × 101	1.11 × 101	8.47
F26	2.51 × 102	3.23 × 102 ǂ	2.70 × 102 ǂ	5.52 × 102 ǂ	5.15 × 102 ǂ	2.38 × 102 ξ	2.00 × 102 ξ	3.51 × 102 ~	2.62 × 102 ǂ
	6.57 × 101	6.95 × 101	7.11 × 101	3.00 × 101	3.47 × 101	7.46 × 101	3.74 × 10−2	7.68 × 101	1.61 × 101
F27	6.38 × 102	9.62 × 102 ǂ	7.14 × 102 ~	3.30 × 103 ǂ	2.83 × 103 ǂ	1.36 × 103 ǂ	9.90 × 102 ǂ	1.22 × 103 ǂ	1.50 × 103 ǂ
	1.16 × 102	7.94 × 101	7.45 × 101	2.89 × 102	8.94 × 101	9.72 × 101	1.20 × 102	8.93 × 101	4.49 × 101
F28	2.96 × 102	2.11 × 103 ǂ	3.00 × 102 ~	7.53 × 103 ǂ	8.82 × 103 ǂ	4.95 × 103 ǂ	5.36 × 102 ǂ	2.03 × 103 ǂ	5.34 × 103 ǂ
	2.83 × 101	5.50 × 102	1.09 × 10−1	4.46 × 102	2.61 × 102	7.15 × 102	5.90 × 102	1.69 × 103	4.17 × 102
ǂ/ξ/~		6/0/2	5/1/2	7/0/1	8/0/0	7/0/1	4/1/3	5/0/3	8/0/0

“ǂ”, “ξ”, and “~” denote that the performance of PTBO is better than, worse than, and similar to that of the corresponding algorithm, respectively. Bold text is the best result obtained by the compared algorithms.

, respectively. The accuracy results are in terms of the mean optimum solution and the standard deviation of the solutions obtained by each algorithm over 300,000 function evaluation times (FES) or 10,000 maximum generations. In all experiments, the dimensions of all problems are 30. The best results among the algorithms are shown in bold. In each row of the three tables, the mean values are listed in the first line, and the standard deviations are displayed in the second line. A two-tailed t-test [45] is performed with a 0.05 significance level to evaluate whether the median fitness values of two sets of obtained results are statistically different from each other. In the below three tables, if PTBO significantly outperforms another algorithm, a ‘ǂ’ is labeled in the back of the corresponding result obtained by this algorithm. Corresponding to ‘ξ’, ‘ξ’ denotes that PTBO is worse than other algorithms, and ‘~’ denotes that there is no significance between PTBO and the compared algorithm. At the last row of each table, a summary of the total number of ‘ǂ’, ‘ξ’, and ‘~’ is calculated.

(1) The accuracy results of uni-modal functions

The results of the uni-modal functions are shown in Table 8 in terms of the mean optimum solution and the standard deviation of the solutions.

In Table 8, among the five functions, PTBO has yielded the best results on two of them (F03 and F05). Although PTBO is worse than WCA, which obtains the best results on F01, F02, and F04, we observe from the statistical results that the performance of PTBO in uni-modal functions is significantly better than PSO, DE, BA, CS, BSO, WWO, and SMS.

(2) The accuracy results of multimodal functions

From Table 9, it can be observed that the mean value and the standard deviation value of PSO displays the best results for the function F15. DE obtains the best results on F07, F09, and F12, and BA has the best result for the function F06. BSO has the best result for the function F16. WCA obtains the best results on F8 and F10. CS, WWO, and SMS do not obtain any best result except for the function F8. With regard to the function F8, there is no big difference about all eight algorithms. The PTBO algorithm performs well for the functions F11, F13, F14, F17, F18, and F20, and according to the data of the last row in Table 9, it can be concluded that the PTBO algorithm has good performance in solution accuracy for multimodal benchmark functions.

(3) The accuracy results of composition functions

It can be seen from Table 10 that DE acquires the best results on F25, and WWO obtains the best results on F26. However, PTBO obtains the best results on F21, F22, F23, F24, F27, and F28. In general, PTBO shows the best overall performance from the statistical results according to the data of the last row in Table 10.

(4) The total results of solution accuracy of the 28 functions

A summary of the total number of ‘ǂ’, ‘ξ’, and ‘~’ about the solution accuracy of 28 functions is given in

Table 11. The total results of solution accuracy for the 28 functions.

PTBO vs.	PSO	DE	BA	CS	BSO	WWO	WCA	SMS
F01–05	4/1/0	4/1/0	4/1/0	5/0/0	4/1/0	4/1/0	2/3/0	5/0/0
F06–20	12/1/2	8/5/2	13/1/1	14/0/1	10/1/4	12/1/2	10/3/2	14/0/1
F21–28	6/0/2	5/1/2	7/0/1	8/0/0	7/0/1	4/1/3	5/0/3	8/0/0
ǂ/ξ/~	22/2/4	17/7/4	24/4/2	27/0/1	21/2/5	20/3/5	17/6/5	27/0/1

. From Table 11, it can be observed that PTBO has the best performance of the nine algorithms.

5.4.2. The Comparison Results of Convergence Speed

Due to page limitation, Figure 9 presents the convergence graphs of parts of the 28 test functions in terms of the mean fitness values achieved by each of the nine algorithms for 50 runs. From Figure 9, it can be observed that PTBO converges towards the optimal values faster than the other algorithms in most cases, i.e., F1, F6, F12, F18, F21, F27, and F28.

5.4.3. The Comparison Results of Wilcoxon Signed-Rank Test

To further statistically compare PTBO with the other eight algorithms, a Wilcoxon signed-rank test [45] has been carried out to show the differences between PTBO and the other algorithms. The p-values on every function by a two-tailed test with a significance level of 0.05 between PTBO and other algorithms are given in

Table 12. Wilcoxon signed-rank test of 28 functions.

PTBO vs.	R+	R−	p-Value
PSO	305	73	2.69 × 10−4
DE	215	163	3.16 × 10−1
BA	325	53	1.19 × 10−4
CS	368	10	3.79 × 10−6
BSO	340	38	1.57 × 10−4
WWO	359	19	2.52 × 10−5
WCA	320	58	1.20 × 10−3
SMS	360	18	2.96 × 10−5

Bold text is the best result obtained by the compared algorithms.

.

From the results of the signed-rank test in Table 12, we can observe that our PTBO algorithm has a significant advantage over seven other algorithms in p-value, which are PSO, BA, CS, BSO, WWO, WCA, and SMS. Although PTBO has no significant advantage over DE, PTBO significantly outperforms DE in R⁺ value. R⁺ is the sum of ranks for the functions on which the first algorithm outperformed the second [46], and the differences are ranked according to their absolute values. So, according to the statistical results, it can be concluded that PTBO generally offered better performance than other algorithms for all 28 functions.

The above comparisons between PTBO and other nature-based meta-heuristic algorithms may offer a possible explanation for why PTBO could obtain better results on some optimization problems and that it is possible for PTBO to deal with more complex problems better.

5.4.4. The Comparison Results of Time Complexity

The total comparisons of mean time complexity of the 28 functions about the nine algorithms are given in Figure 10. From Figure 10, we can observe that PTBO is ranked sixth, and is only better than BSO and WWO. However, we can find that the mean CPU time of PTBO is slightly worse than PSO and DE, and it also confirms the analysis in Section 4.1.

6. Conclusions

In this work, a new meta-heuristic optimization algorithm simulating the phase transition of elements in a natural system, named PTBO, has been described. Although the proposed PTBO algorithm is an algorithm with some similarities to the SMS and PSO algorithms, the main concepts are slightly different. It is very simple and very flexible when compared to the existing nature-inspired algorithms. It is also very robust, at least for the test problems considered in this work. From the numerical simulation results and comparisons, it is concluded that PTBO can be used for solving uni-modal and multimodal numerical optimization problems, and is similarly effective and efficient compared with other optimization algorithms. It is worth noting that PTBO performs slightly worse than PSO and DE in time complexity. In the future, further research contents include (1) developing a more effective division method for the three phases, (2) combining the PTBO algorithm with other evolution algorithms, and (3) applying PTBO to real-world optimization problems, such as the reliability–redundancy allocation problem and structural engineering design optimization problems.