3. Computational Experiments
In this section, we present comparisons of our
MCDA with Croux and Ruiz-Gazen’s robust PCA [
5] and Brooks
et al.’s
PCA [
17]. Since both Croux and Ruiz-Gazen’s and Brooks
et al.’s PCA methods are also widely used for the data with outliers, comparisons of our
MCDA with their methods are imperative.
The following eight types of distributions were used for the computational experiments:
n-Dimensional () Gaussian without and with additional artificial outliers;
n-Dimensional () Student t (degree of freedom = 1) without and with additional artificial outliers;
Four superimposed n-dimensional () Gaussians without and with additional artificial outliers;
Four superimposed n-dimensional () Student t (degree of freedom = 1) without and with additional artificial outliers.
All computational results were generated using MATLAB codes in [
18] and
MATLAB R2012a [
19] on a 2.50 GHz PC with 4 GB memory. Samples from Gaussian and Student
t distributions were generated using the
MATLAB mvnrnd and mvtrnd modules, respectively, with the covariance/correlation matrix
where
and
n is the size of the covariance/correlation matrix. In our experiment, the computational time for each sample was restricted to 3600 s.
For the one-major-direction situation, the ratio of the length of the longest major direction to that of other major directions (which are equal for the covariance/correlation matrix
) is set to be a constant
C for all
n. To accomplish this, we set the ratio of the maximum eigenvalue (
) to the minimal eigenvalue (
) to be
,
i.e.,
. Hence,
in the covariance/correlation matrix
. In our experiment, we chose
, which requires that
. Therefore, for the one-major-direction situation, the major direction is
and the ratio of the length of the longest major direction to that of other major directions is 10. In
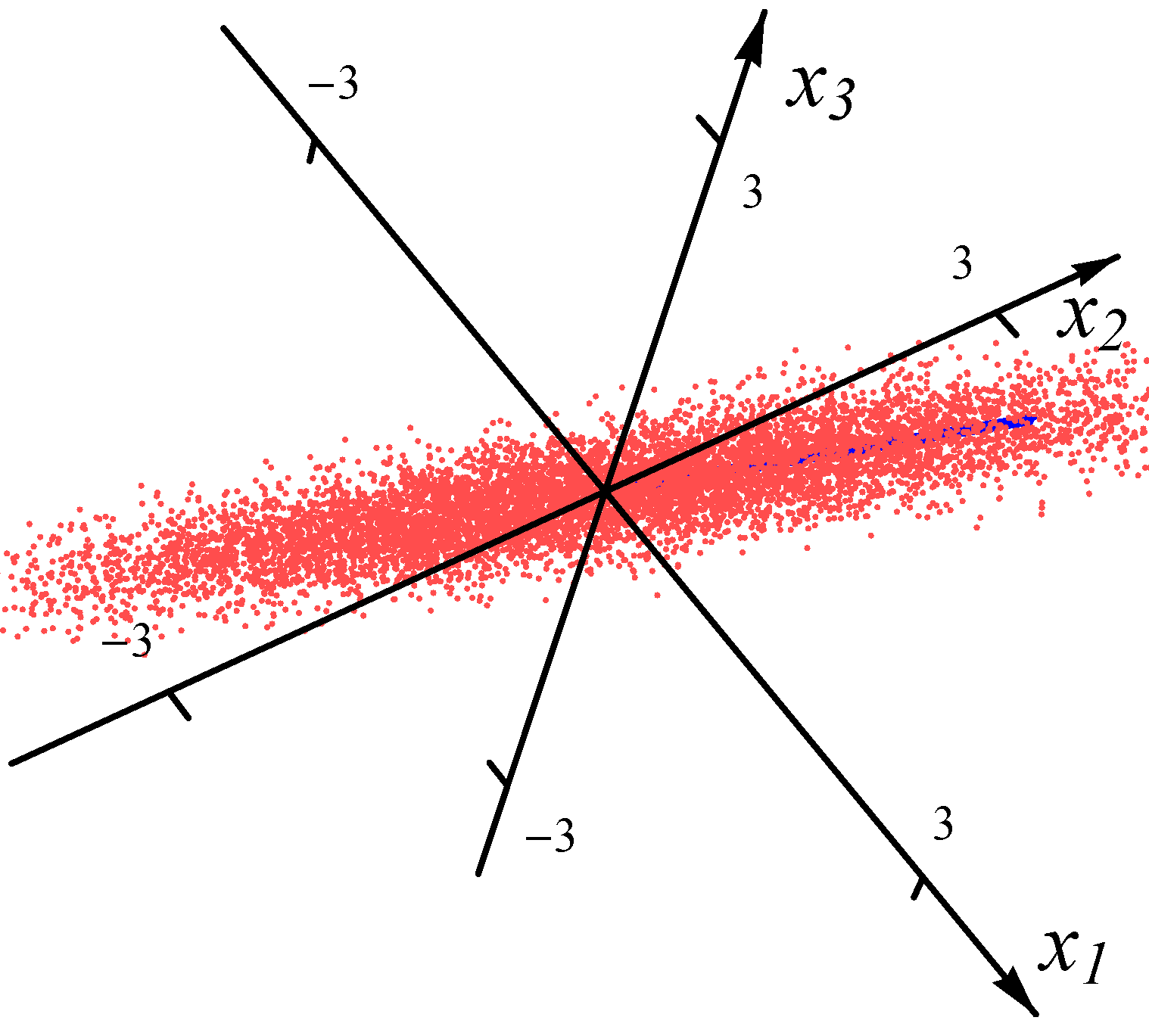
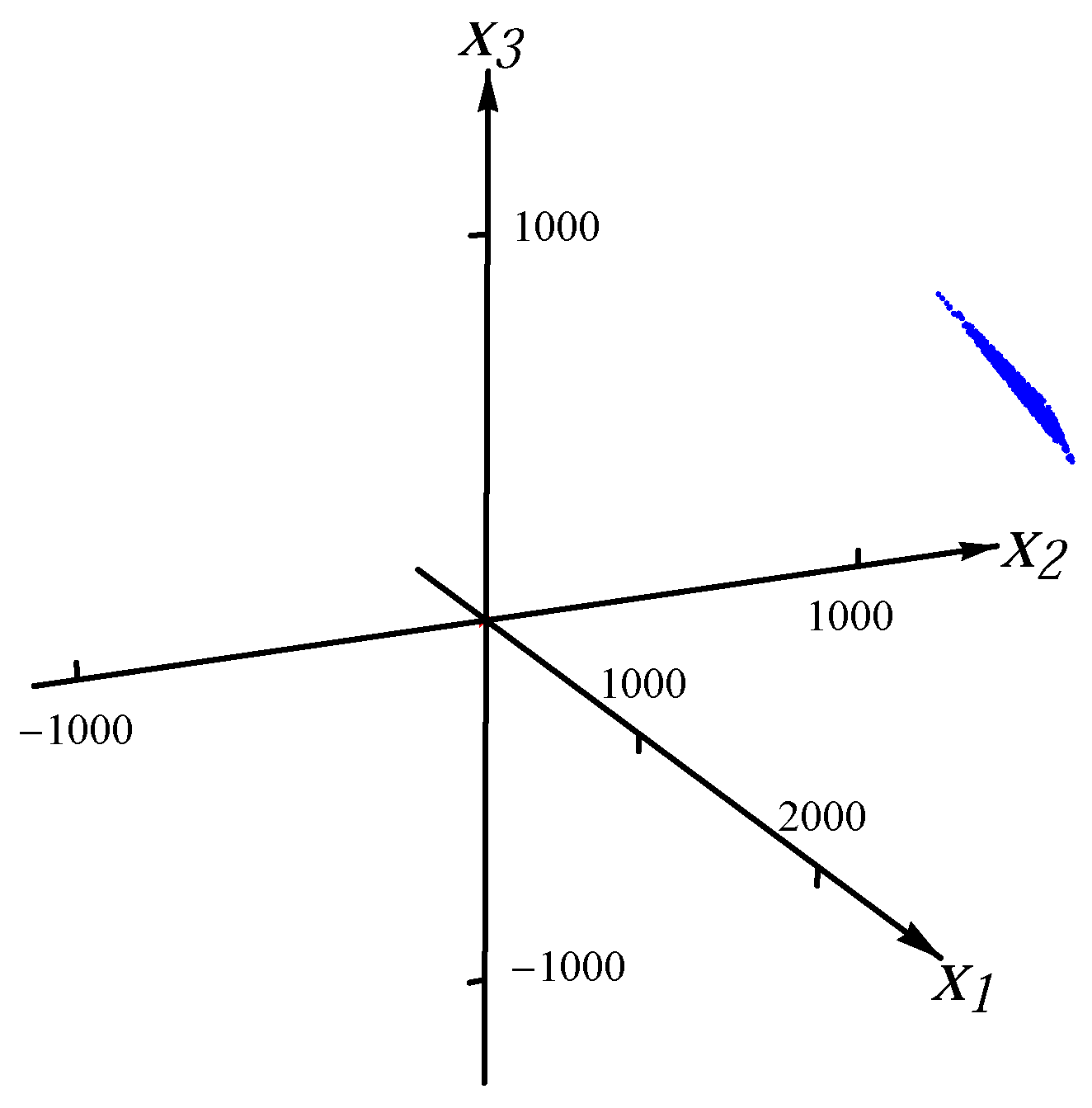
Figure 1 and
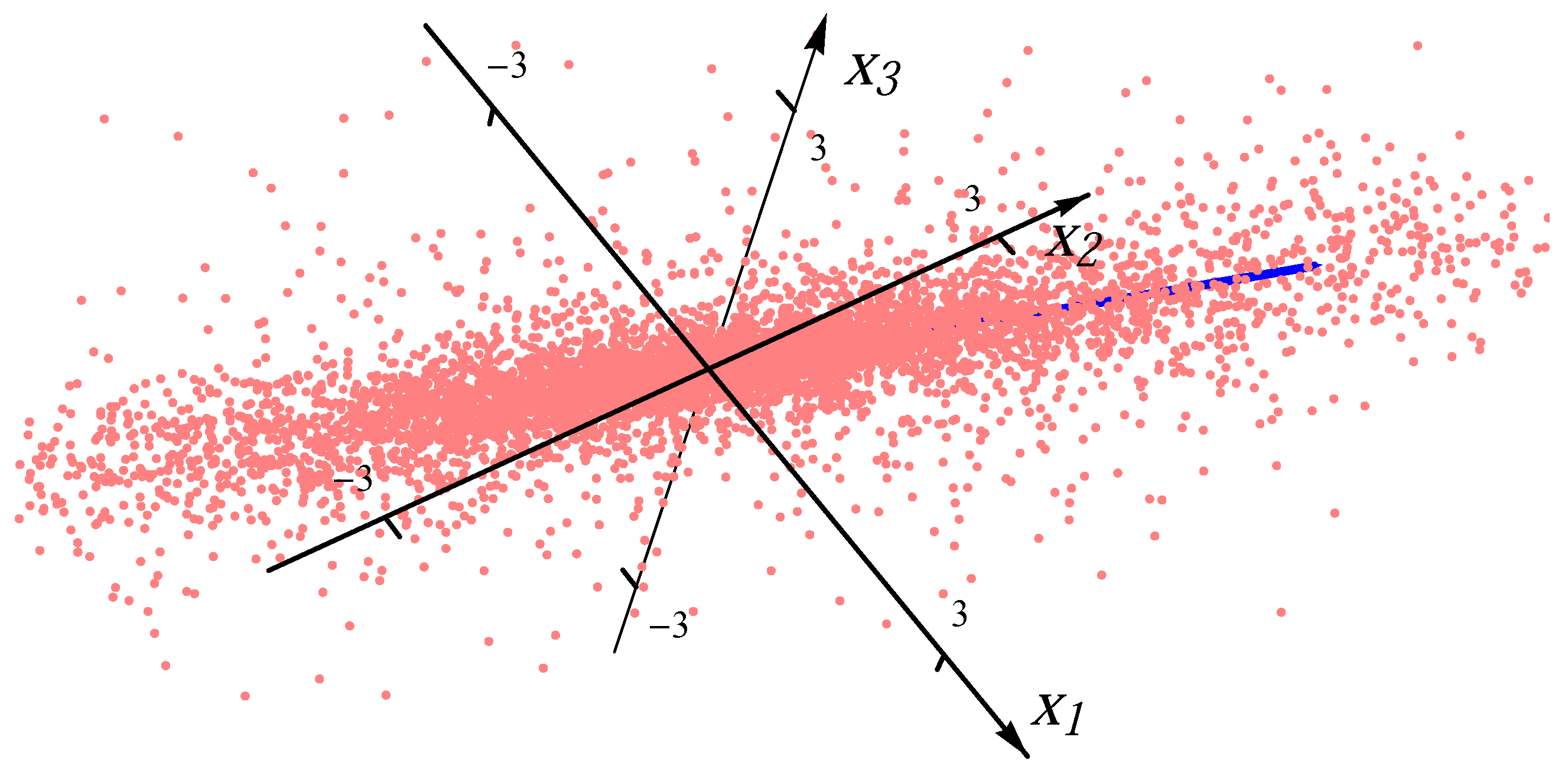
Figure 2, we present the examples of the datasets with 8000 data points (red dots) for one Gaussian distribution and one Student
t distribution, respectively. In order to exhibit the major component clearly, the plot range in
Figure 2 is the same as the one in
Figure 1. There are many points outside the plot range of
Figure 2. The directions and magnitudes of median radii in the major directions are indicated by blue bars emanating from the origin.
Figure 1.
Sample from one Gaussian distribution.
Figure 1.
Sample from one Gaussian distribution.
Figure 2.
Sample from one Student t distribution.
Figure 2.
Sample from one Student t distribution.
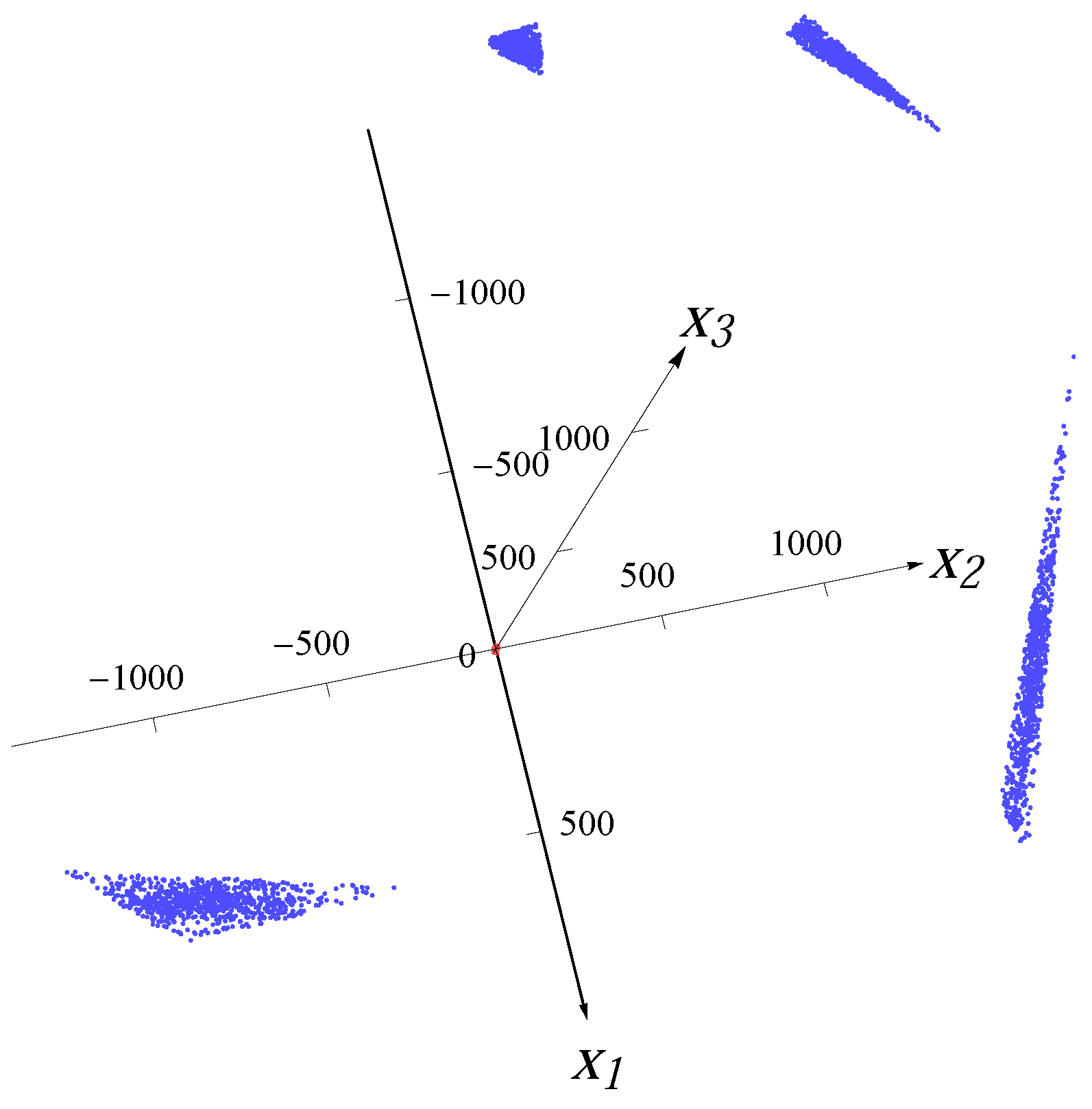
For the four-major-directions situation, we overlaid four distributions rotated to the directions
,
,
and
. The samples for each major direction are first generated with correlation/covariance matrix
, and then rotated in
-norm to other major directions after multiplying by a factor (to make the lengths of the “spokes” different from each other). For example, for the 3D four-major-directions distribution created by overlaying four Gaussians, the median radii of the four major directions are 2.643, 3.964, 1.586 and 7.928.
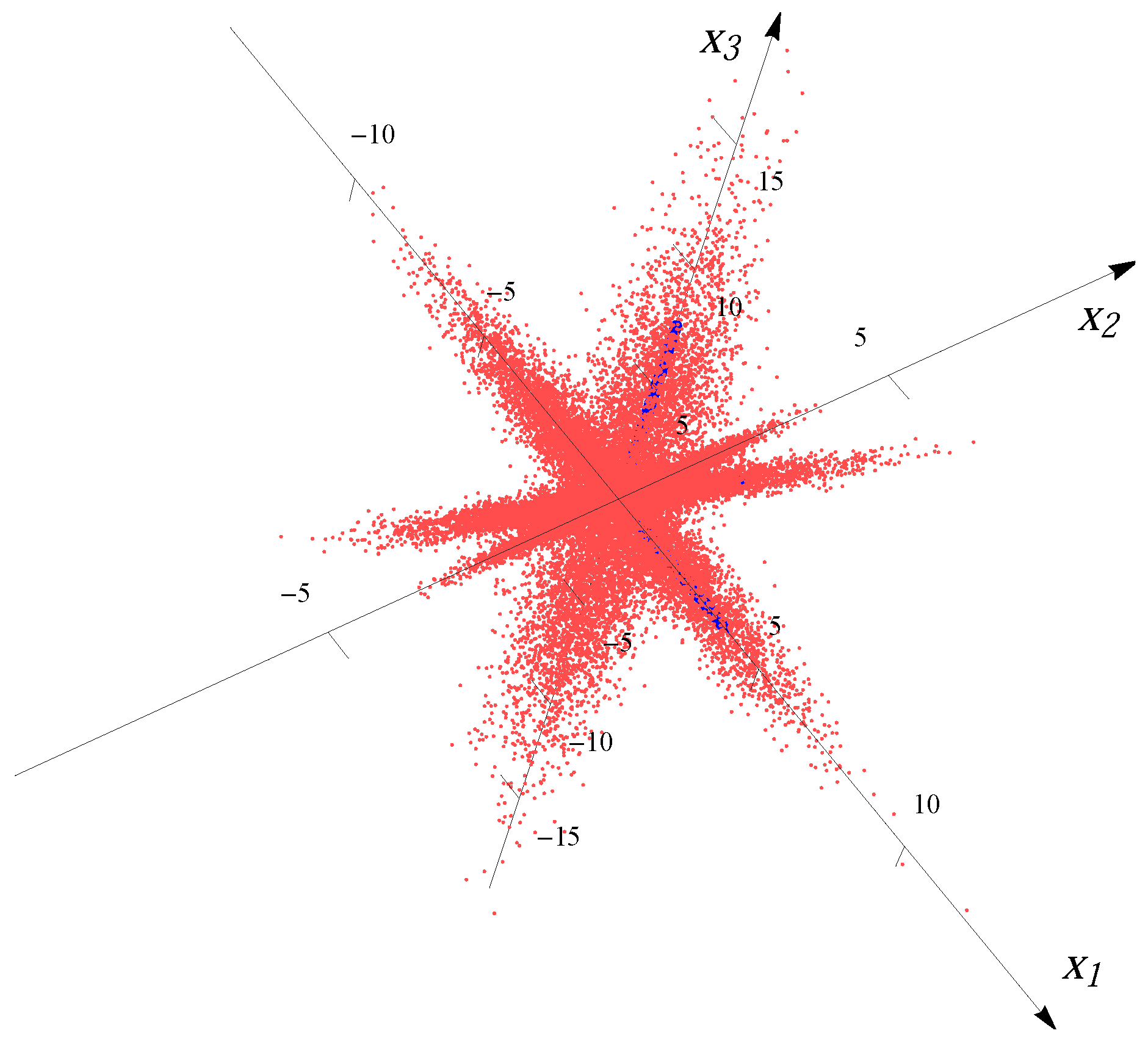
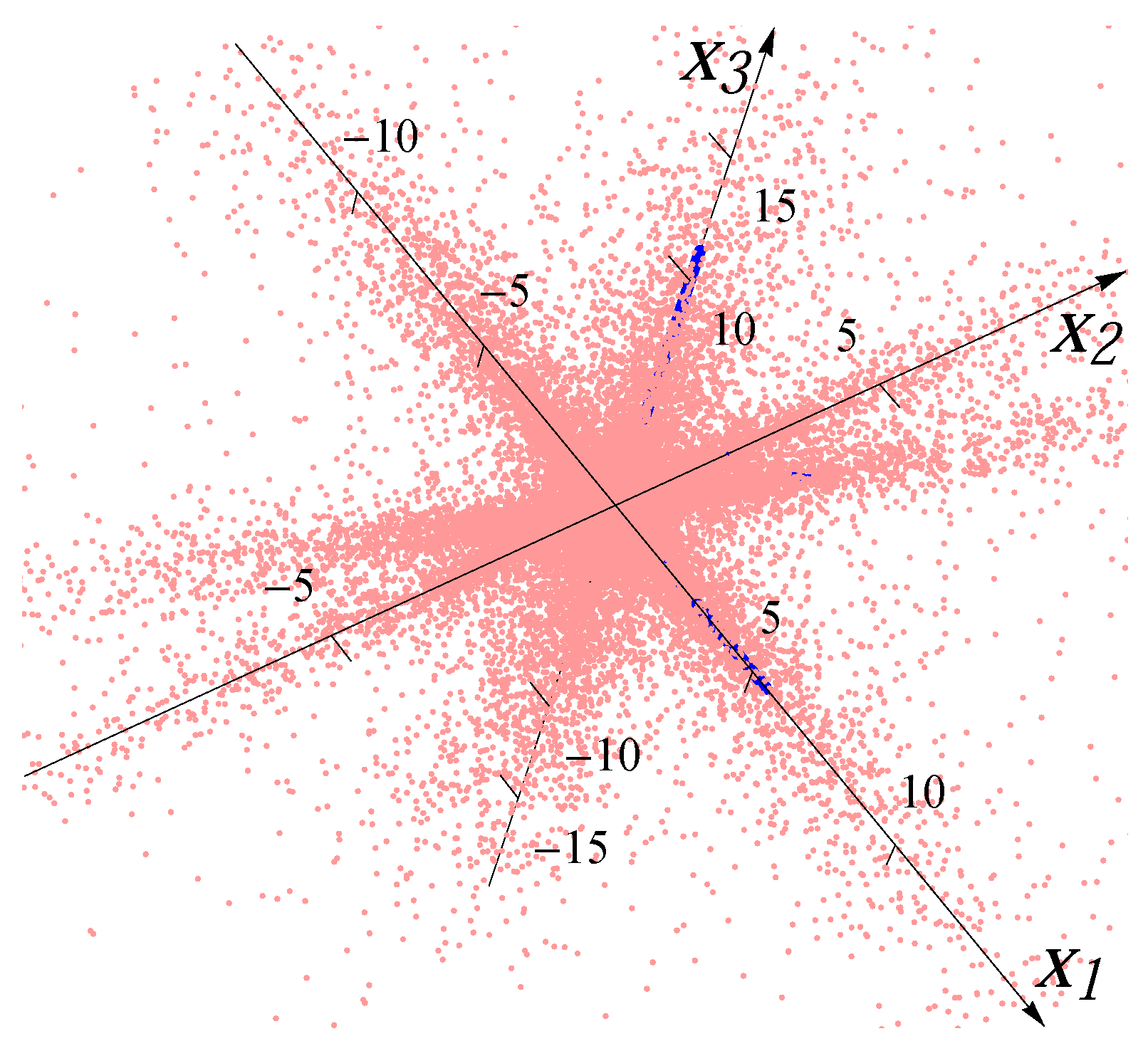
Figure 3 and
Figure 4 show the examples of the datasets with 32,000 data points (red dots) for four superimposed Gaussian distributions and four Student
t distributions, respectively. The blue bars indicate the major directions and the magnitudes of median radii in the major directions.
Figure 3.
Sample from four overlaid Gaussian distributions.
Figure 3.
Sample from four overlaid Gaussian distributions.
Figure 4.
Sample from four overlaid Student t distributions.
Figure 4.
Sample from four overlaid Student t distributions.
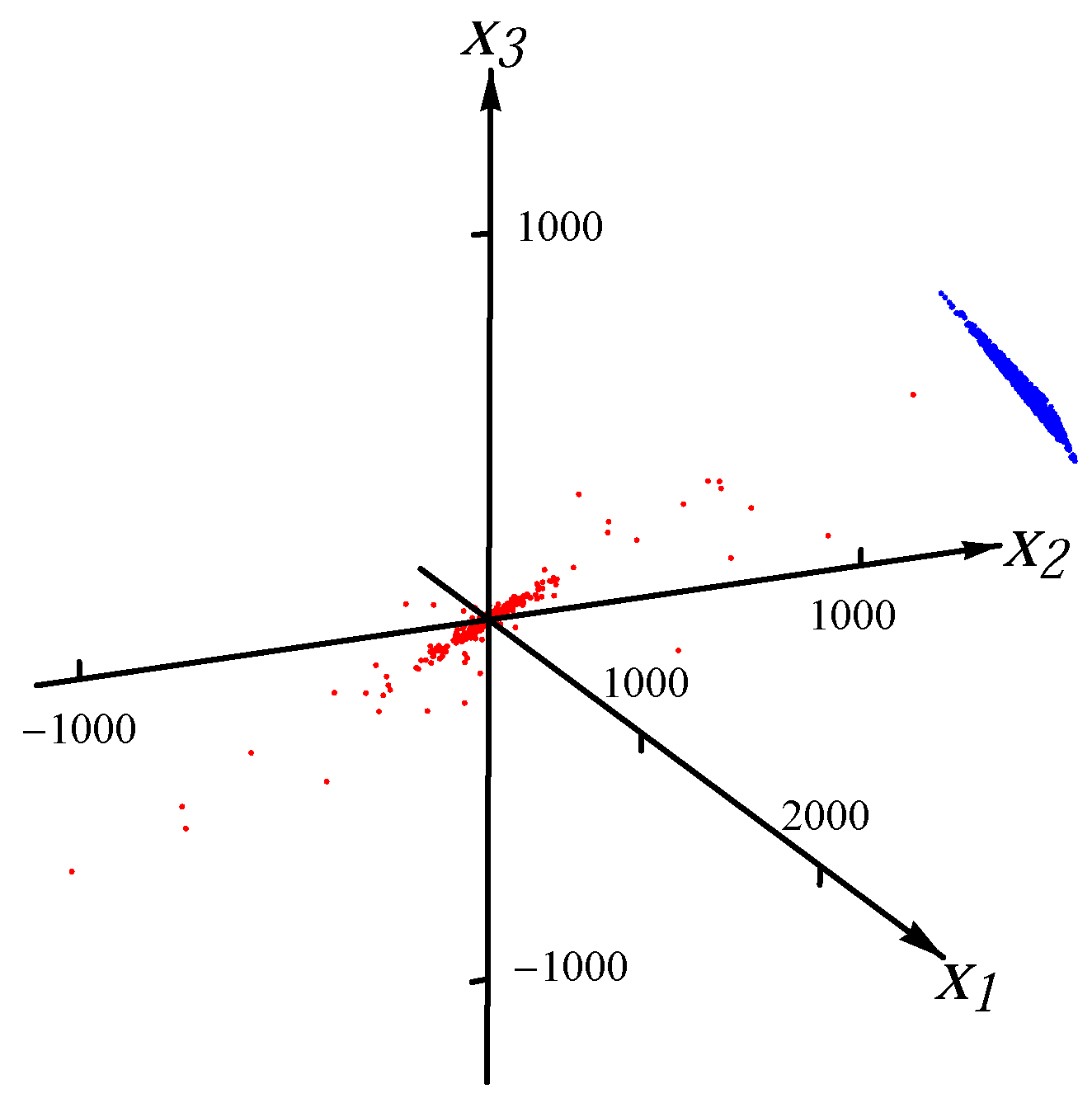
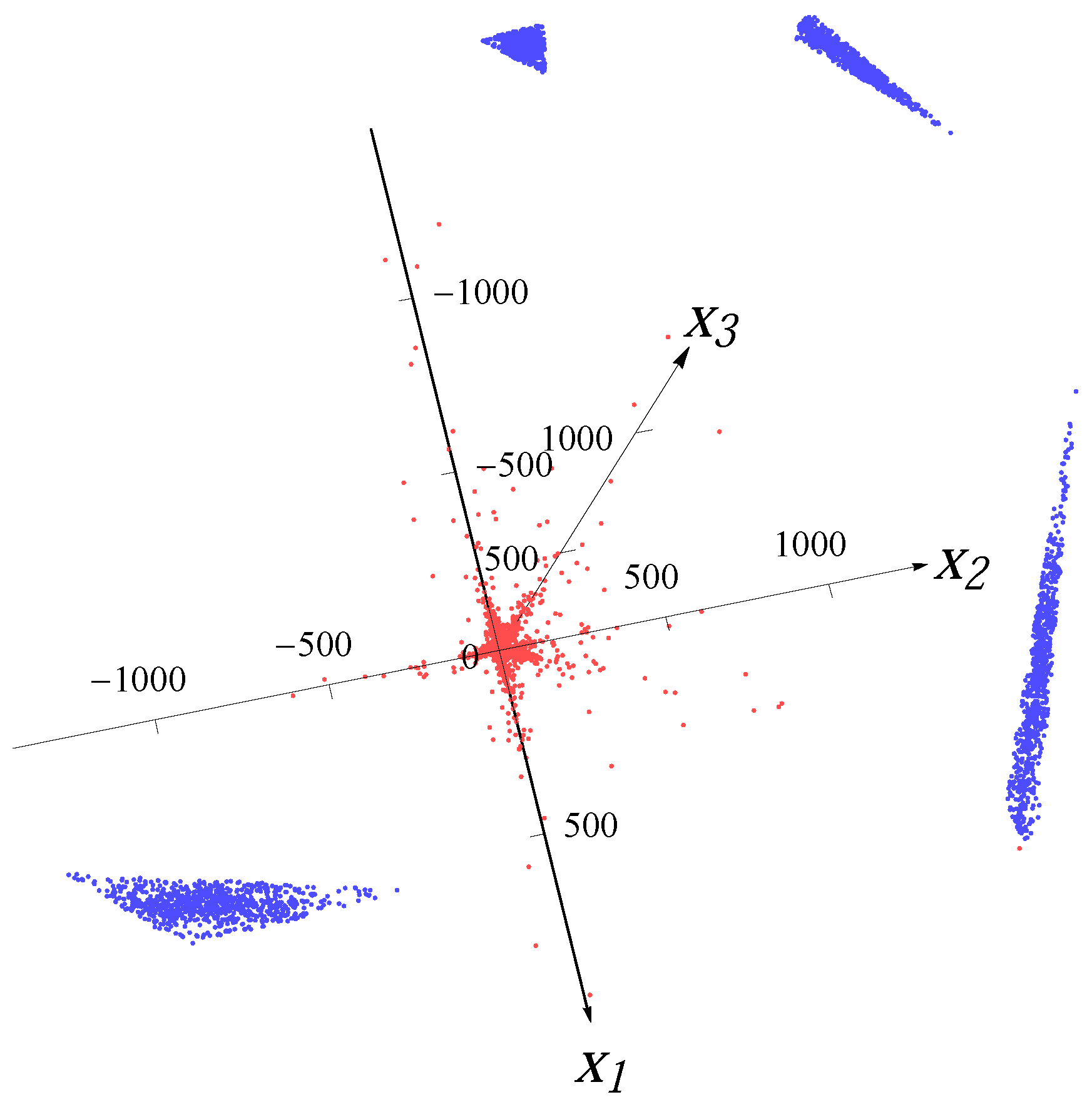
The artificial outliers are generated from a uniform distribution on a simplex. The
n vertices of the simplex are randomly chosen from the intersection of the ball
with the hyperplane
. For each distribution in the data, the angle between the normal of the hyperplane
and the major direction of the distribution is 45
. In
Figure 5,
Figure 6,
Figure 7 and
Figure 8, we present examples with 10% artificial outliers (depicted by blue dots) for one Gaussian distribution, one Student
t distribution, four superimposed Gaussian distributions and four superimposed Student
t distributions (points from distributions depicted by red dots), respectively.
Figure 5.
Sample from one Gaussian distribution with 10% artificial outliers.
Figure 5.
Sample from one Gaussian distribution with 10% artificial outliers.
Figure 6.
Sample from one Student t distribution with 10% artificial outliers.
Figure 6.
Sample from one Student t distribution with 10% artificial outliers.
Figure 7.
Sample from four Gaussian distributions with 10% artificial outliers.
Figure 7.
Sample from four Gaussian distributions with 10% artificial outliers.
Figure 8.
Sample from four Student t distributions with 10% artificial outliers.
Figure 8.
Sample from four Student t distributions with 10% artificial outliers.
For each type of data, we carried out 100 computational experiments, each time with a new sample from the statistical distribution(s), including the uniform distributions that generated the outliers. The neighbors required in Steps 4 and 6 of the proposed
MCDA were calculated by the
k-nearest-neighbors (kNN) method [
20]. Other methods for identifying neighbors may also be used.
To measure the accuracy of the results, we calculated the average over 100 computational experiments of the absolute error of each major direction and the average of the relative error of the median radius in that direction vs. the theoretical values of the direction of maximum spread and the median radius in that direction of the distribution. The theoretical value of major direction for the one-major-direction case is and the theoretical values of major directions for the four-major-directions case are , , , , respectively. The theoretical value of median radius for each major direction is calculated as the value of such that by numerical integration, where is the conditional probability density function of radius r along the major direction θ.
In
Table 1,
Table 2,
Table 3 and
Table 4, we present computational results for the sets of 8000 points with local neighborhood of size
(2% of total points) for the one-major-direction situation. We compared our method with the methods that appeared in the literature [
5,
17]. Specifically, the
MATLAB version of
pcaPP [
21] package of the
R language for statistical computing [
22] was used to implement the robust PCA proposed by Croux and Ruiz-Gazen in [
5]. Brooks
et al.’s
PCA [
17] was implemented by using
MATLAB and
IBM ILOG CPLEX 12.5 [
23]. The computational results for those two PCA methods are also summarized in
Table 1,
Table 2,
Table 3 and
Table 4.
Table 5 shows the average computational time for each method when
. For higher dimensions, the average computational time of
MCDA is shorter than the other two PCA methods. In
Table 6,
Table 7,
Table 8 and
Table 9, we present the computational results for 32,000 points with local neighborhood of size
, 160 and 80 (
i.e., 2%, 1% and 0.5% of total points, respectively) for the four-major-directions situation.
Table 1.
The results of MCDA and Robust PCAs on one Gaussian distribution.
Table 1.
The results of MCDA and Robust PCAs on one Gaussian distribution.
| n | MCDA | Croux + Ruiz-Gazen | Brooks et al. |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0112 | 0.0314 | 0.0289 | 0.0681 | 0.0556 | 0.0675 |
| 8 | 0.0233 | 0.2498 | 0.0399 | 0.2177 | 0.0118 | 0.1586 |
| 10 | 0.0277 | 0.3129 | 0.0308 | 0.2683 | 0.0090 | 0.2256 |
| 30 | 0.0315 | 0.5772 | 0.0112 | 0.5308 | 0.0052 | 0.5099 |
| 50 | 0.0363 | 0.6539 | 0.0136 | 0.6269 | – | – |
Table 2.
The results of MCDA and Robust PCAs on one Student t distribution.
Table 2.
The results of MCDA and Robust PCAs on one Student t distribution.
| n | MCDA | Croux + Ruiz-Gazen | Brooks et al. |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0276 | 0.0921 | 0.0346 | 0.1224 | 0.0557 | 0.1310 |
| 8 | 0.0423 | 0.2035 | 0.0483 | 0.2113 | 0.0118 | 0.1800 |
| 10 | 0.0441 | 0.2717 | 0.0455 | 0.2625 | 0.0090 | 0.2352 |
| 30 | 0.0446 | 0.5367 | 0.0113 | 0.5163 | 0.0053 | 0.4869 |
| 50 | 0.0448 | 0.6350 | 0.0140 | 0.6100 | – | – |
Table 3.
The results of MCDA and Robust PCAs for one Gaussian distribution with 10% artificial outliers.
Table 3.
The results of MCDA and Robust PCAs for one Gaussian distribution with 10% artificial outliers.
| n | MCDA | Croux + Ruiz-Gazen | Brooks et al. |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0119 | 0.0373 | 0.0318 | 0.0759 | 0.0560 | 0.0654 |
| 8 | 0.0236 | 0.2512 | 0.0499 | 0.2292 | 0.0211 | 0.1588 |
| 10 | 0.0279 | 0.3134 | 0.0549 | 0.2781 | 0.0170 | 0.2289 |
| 30 | 0.0322 | 0.5785 | 0.0990 | 0.5376 | 0.0072 | 0.5077 |
| 50 | 0.0375 | 0.6601 | 0.1393 | 0.6308 | – | – |
Table 4.
The results of MCDA and Robust PCAs for one Student t distribution with 10% artificial outliers.
Table 4.
The results of MCDA and Robust PCAs for one Student t distribution with 10% artificial outliers.
| n | MCDA | Croux + Ruiz-Gazen | Brooks et al. |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0276 | 0.0969 | 0.0366 | 0.1140 | 0.0554 | 0.1515 |
| 8 | 0.0424 | 0.2038 | 0.0556 | 0.2054 | 0.0214 | 0.1714 |
| 10 | 0.0441 | 0.2725 | 0.0616 | 0.2775 | 0.0170 | 0.2314 |
| 30 | 0.0467 | 0.5376 | 0.1009 | 0.5238 | 0.0072 | 0.4833 |
| 50 | 0.0449 | 0.6351 | 0.1390 | 0.6142 | – | – |
Table 6.
The results of MCDA on four superimposed Gaussian distributions.
Table 6.
The results of MCDA on four superimposed Gaussian distributions.
| n | knn = 640 (2%) | knn = 320 (1%) | knn = 160 (0.5%) |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0124 | 0.0499 | 0.0089 | 0.0374 | 0.0121 | 0.0428 |
| 10 | 0.0226 | 0.0904 | 0.0294 | 0.0666 | 0.0364 | 0.0805 |
| 50 | 0.0269 | 0.5323 | 0.0352 | 0.4931 | 0.0448 | 0.4518 |
Table 7.
The results of MCDA on four superimposed Student t distributions.
Table 7.
The results of MCDA on four superimposed Student t distributions.
| n | knn = 640 (2%) | knn = 320 (1%) | knn = 160 (0.5%) |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0120 | 0.0552 | 0.0155 | 0.0794 | 0.0211 | 0.1420 |
| 10 | 0.0225 | 0.3225 | 0.0318 | 0.2458 | 0.0437 | 0.1777 |
| 50 | 0.0250 | 0.6220 | 0.0335 | 0.5814 | 0.0430 | 0.5355 |
Table 8.
The results of MCDA on four superimposed Gaussian distributions with 10% artificial outliers.
Table 8.
The results of MCDA on four superimposed Gaussian distributions with 10% artificial outliers.
| n | knn = 640 (2%) | knn = 320 (1%) | knn = 160 (0.5%) |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0152 | 0.0396 | 0.0099 | 0.0406 | 0.0171 | 0.0493 |
| 10 | 0.0271 | 0.2614 | 0.0208 | 0.3044 | 0.0173 | 0.3615 |
| 50 | 0.0379 | 0.6275 | 0.0308 | 0.6566 | 0.0261 | 0.6920 |
Table 9.
The results of MCDA on four superimposed Student t distributions with 10% artificial outliers.
Table 9.
The results of MCDA on four superimposed Student t distributions with 10% artificial outliers.
| n | knn = 640 (2%) | knn = 320 (1%) | knn = 160 (0.5%) |
|---|
| | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length | av. abs_err of angle | av. rel_err ra. of length |
|---|
| 3 | 0.0279 | 0.1639 | 0.0184 | 0.0941 | 0.0173 | 0.0501 |
| 10 | 0.0452 | 0.1671 | 0.0336 | 0.2570 | 0.0238 | 0.3308 |
| 50 | 0.0499 | 0.5333 | 0.0388 | 0.5851 | 0.0293 | 0.6198 |
Remark 3. In Table 1, Table 2, Table 3 and Table 4, the radius information for the robust PCA methods [5,17] was generated by Step 6 of the algorithm described in this paper with the major directions returned by their own. Some results are not available because the computational time exceeded the limit of 3600 s. Remark 4. In Table 6, Table 7, Table 8 and Table 9, no results for either Croux and Ruiz-Gazen’s robust PCA or Brooks et al.
’s PCA are presented, because these two methods provide only one major direction for the superimposed distributions and do not yield any meaningful information about the individual major direction. The results in
Table 1 and
Table 2 indicate that, when there is only one major direction in the data,
MCDA obtains comparable results to Croux and Ruiz-Gazen’s robust PCA in accuracy. Although Brooks
et al.’s
PCA outperforms the proposed
MCDA, it requires much longer computational time as shown in
Table 5. The results in
Table 3 and
Table 4 indicate that
MCDA outperforms Croux and Ruiz-Gazen’s robust PCA in all cases, especially when the dimension is larger than 30. Brooks
et al.’s
PCA obtained similar results as
MCDA but consumed much more CPU time as shown in
Table 5. It is noticeable that the accuracy of the proposed method decreases as the dimension increases. The reason is that for a given data size, the number of points falling into a fixed neighbor of the major direction decreases and the two-level median estimation deteriorates as the dimension grows higher. In contrast, the accuracy of the robust PCAs increases as the dimension increases because both robust PCAs used project-pursuit method, whose performance degrades when the underlying dimension decreases [
17].
The results in
Table 6,
Table 7,
Table 8 and
Table 9 indicate that our method can obtain good accuracy by using a small neighbor size (up to 2% of the size of given data) for the four-major-directions case. It is worth to point out that the four major directions are not orthogonal to each other, and the proposed
MCDA is very robust by noting that the accuracy of
MCDA for data with the artificial outliers is as good as the one of
MCDA without outliers. Although the distributions designed in the experiment are symmetrically around some center, the proposed algorithm can also deal with the data from asymmetric distributions.
The computational results show that, for the types of data considered here, MCDA has the marked advantage in accuracy and efficiency when comparing with robust PCAs. Moreover, MCDA can deal with cases of multiple components for which standard and robust PCAs perform less well or even poorly.