2.2. Explanation of the System
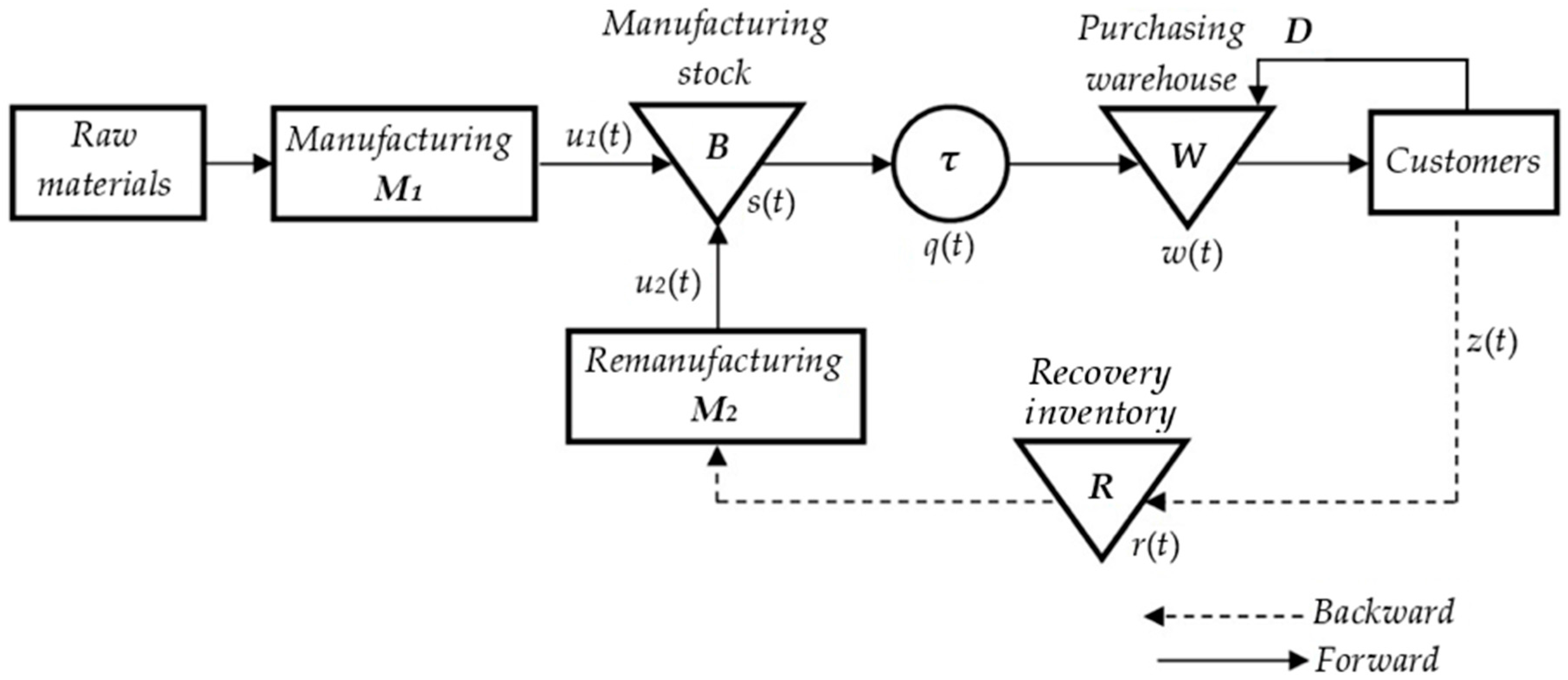
The studied closed-loop supply chain system (see
Figure 1) consists of two parallel machines (denoted
M1 and
M2, for manufacturing and remanufacturing, respectively), which are subject to random repairs and failures. Both machines are assumed to produce the same type of product. Machine
M1 produces from raw materials and machine
M2 produces from used products that were returned (end-of-life products). Indeed, in this closed-loop supply chain system, the production activity is considered in forward and reverse directions. Remanufactured products are of the same quality as the products that are made from raw materials. Therefore, both types of products (manufactured and remanufactured) can be distributed like new. At every time
t, customers demand a constant quantity of products
D, which is satisfied from the purchasing warehouse
W. Machines
M1 and
M2 are filling up the manufacturing stock
B that supplies the purchasing warehouse
W with a transport vehicle. Thus, products outgoing from
B are transported to the warehouse, and take a transportation time
τ to arrive to
W. Indeed, when the products leave
S at time
t, they will arrive at time
t + τ. The vehicle has a maximum capacity
V and transports a quantity of products
q(
t) at time
t between
B and
W. The maximum capacity of purchasing warehouse W is defined by variable
X. Another inventory
R is available for stock keeping of the returned used end-of-life products, before their remanufacturing process. It is assumed that inventory
R has an infinite capacity. As mentioned in the introduction, to study more realistic situations, we calculate
z(
t) at every time period, with taking into account the lost sales that have occurred.
Let [0,
T] be the finite horizon discretized into
K periods
Δt (see
Figure 2). Indeed,
Δt is the time period length that represents simulation time step, thus the total simulation time
T =
K·Δt. Occurrence of the events in system (machine failure, stock empty, etc.) is defined by the instant time
t є [0,
T].
Possible system events at every time t are: machine M1 failure, machine M1 repair, machine M2 failure, machine M2 repair, manufacturing stock full, manufacturing stock full empty, purchasing warehouse full, purchasing warehouse empty, lost sales, products transport, return of used products, recovery inventory full, recovery inventory empty, manufacturing of products and remanufacturing of used products.
We suppose that machine M1 will never starve. M1 is either up or down.
Machine
M1 state at time
t is represented by:
The machine
M2 state at time
t is represented by:
Time to repair and time between failures are exponentially distributed. In the case that machine M1 is up, production rate u1(t) can be between 0 and its maximum U1, i.e., 0 u1(t) U1. In the case that machine M1 is down, u1(t) = 0. Machine M2 is in the same case, where u2(t) is its production rate and U2 is its maximum production rate. The failure/repair process is an independent random process.
We consider the following assumptions:
- (1)
In order to simplify the calculations, we assume Δt = 1.
- (2)
When the demand is not satisfied, loss occurs which results into lost sales costs (l(t)).
- (3)
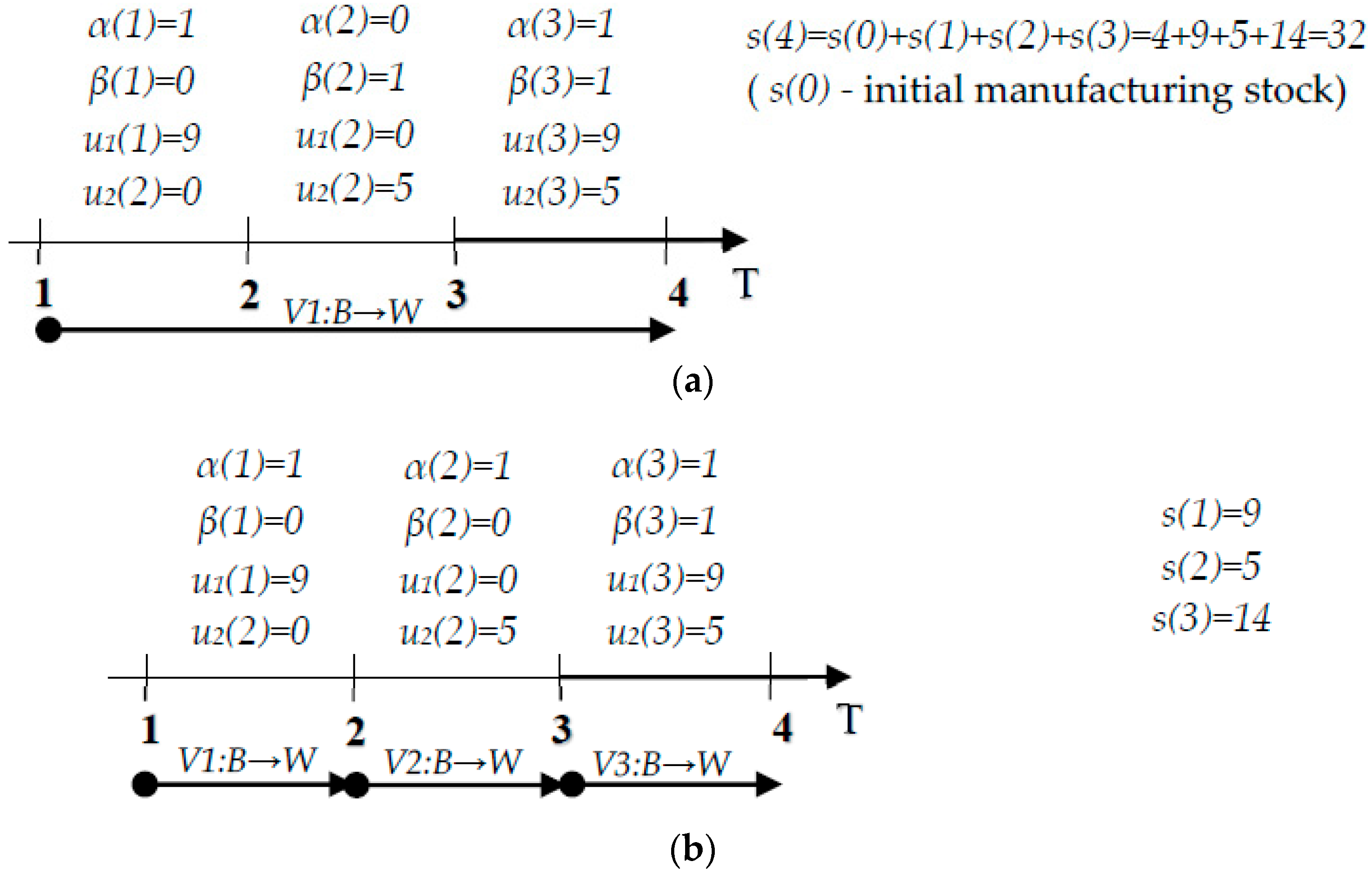
To consider transportation time, we assume that τ > 0, known and constant. Indeed, τ is multiple of Δt with τ = m·Δt = m (Δt = 1) and m = {1, 2, 3, …, T}. We assume also that the time for changing and discharging the vehicle is included in the transportation time τ.
- (4)
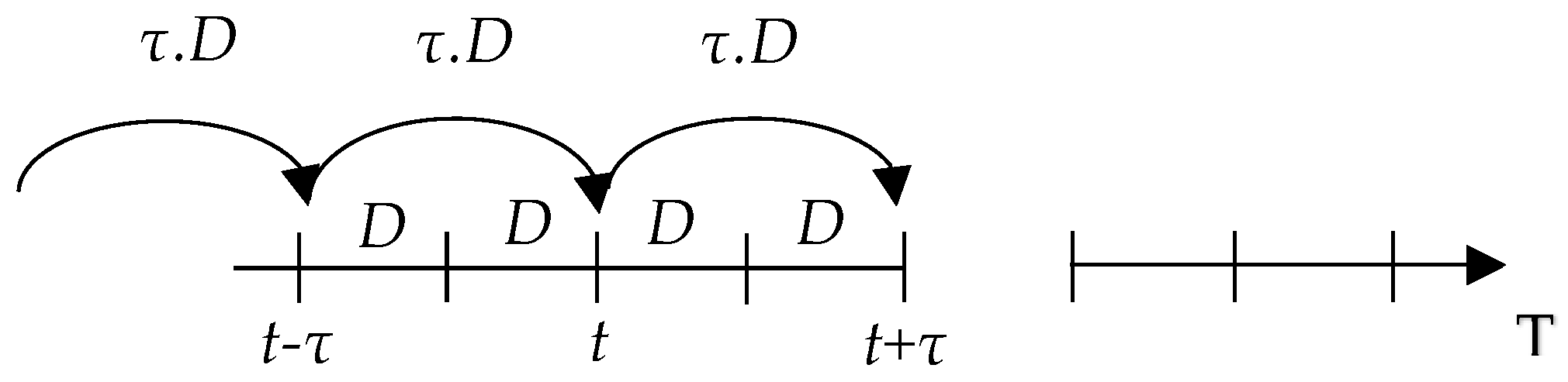
We assume the case where transport is ensured by two vehicles, vehicle 1 and vehicle 2. When vehicle 1 reaches
W, vehicle 2 departs from
B and when vehicle 1 comes back to
B, vehicle 2 reaches
W and vice versa. This assumption allows having one trip from
B to
W for every
τ period and the objective is to reduce the number of trips (see
Figure 3: an example when
m = 2 we have
τ = 2
·Δt = 2). This assumption is the usual case of companies that ensure manufacturing and transport of products.
- (5)
Companies are working to keep a good level service by satisfying customers’ demands. Thus, in inventory management, to avoid having too much lost sales (unsatisfied demand), we must avoid having both manufacturing stock B and purchasing warehouse W is always empty. Thus, we made the following assumptions:
- (5.1)
Maximum production rate U satisfies the demand (i.e., U ≥ D). This assumption avoids having manufacturing stock B always empty.
- (5.2)
Purchasing of the warehouse capacity
W should be equal or higher than the sum of demands during the transportation time (i.e.,
X ≥ τ·D). Indeed, the fact that
W satisfies the customers demand
D at each period and is fulfilled every period equals to the transport time
τ = m·Δt. The level of
W should be equal or higher than the sum of demands during
τ (
w(
t) ≥
m·D) to satisfy the demands. Thus, if capacity
X < τ·D, we always have lost sales. Let us look at the following example (see
Figure 4).
If we assume that m = 2 (i.e., τ = 2·Δt = 2) and D = 10 products/period, at the purchasing warehouse, the capacity should be X ≥ τ·D = 2 × 10 = 20.
- (5.3)
The vehicle capacity should also be equal or higher than the sum of the demands during the transportation time (i.e., V ≥ τ·D). Indeed, the vehicle supplies the purchasing warehouse W. If V < τ·D, the level of W will never reach τ·D, and then we always have lost sales.
- (6)
Maximum production rate U2 is higher than the return amount, (i.e., U2 > z). This assumption avoids having the remanufacturing inventory R always full.
- (7)
Remanufactured products have the same quality and price as the brand new ones.
- (8)
We suppose that we have enough parts in the warehouse to satisfy the demand in a given time period t = 0, i.e., w(0) ≥ D.
2.3. Mathematical Model
As mentioned in our introduction, we use a discrete flow model to formulate the problem. Assumptions in this model are the same as those presented in the beginning of
Section 2.
As mentioned above, the studied time horizon is discretized in equal periods. We should also emphasize the fact that, in our model, demand
D is always satisfied at the beginning of each period, which means that we use the purchasing warehouse level of the previous period
w(
t −
∆t). Thus, the value of satisfied demand at time
t could be found with following equation:
The Purchasing warehouse
W, which satisfies customers’ demand, is replenished with products coming from the manufacturing stock and being transported by the vehicle. Thus, the purchasing warehouse level at time
t (
w(
t)) is the sum of the amount of products in this warehouse remaining from the previous period (
t −
∆t), and of the amount of products that left manufacturing stock at time (
t −
τ), minus the amount of products that were sold in the current period:
The transportation time τ can obviously take values greater than 1. Thus, we need to note that, if (t − τ) < 0, then g(t − τ) = 0.
However, if (t − τ) = 0, we are obliged to set boundaries for g(0), assuming that the transportation from the manufacturing stock (B) to the purchasing warehouse (W) has the frequency of τ, thus and , so .
The purchasing warehouse level, after the transportation and the satisfaction of the demands during period
τ, is given by:
Remark 1. We introduced this equation because it is needed for further calculations.
Outgoing products from manufacturing stock
B at time
t need time
τ to be transported to the purchasing warehouse
W. The amount of products outgoing from manufacturing stock
S at time
t (
g(
t)) depends on the purchasing warehouse level at time
t + τ and its total capacity, manufacturing stock level at time
t −
∆t , vehicle capacity and the demand:
With n = {1, 2, 3, …, [T/τ]}, where [T/τ] is the integer part of T/τ and is the number of transportations during the finite time horizon [0,T]. Thus, g(t) = 0 when and means that the products outgoing from B at each period τ (see Assumption 3).
The Products from machines
M1 and
M2 replenish the manufacturing stock
S which supplies the purchasing warehouse.
Therefore, the manufacturing stock level at time
t consists of the level of this stock remained from the previous period, plus the quantity of products that was produced during the previous period, minus the amount of products outgoing from manufacturing stock
S at time
t:
The amount of unsatisfied demand (lost sales) at time
t and is calculated by subtracting the amount of products that were sold at time
t from the customers’ demand:
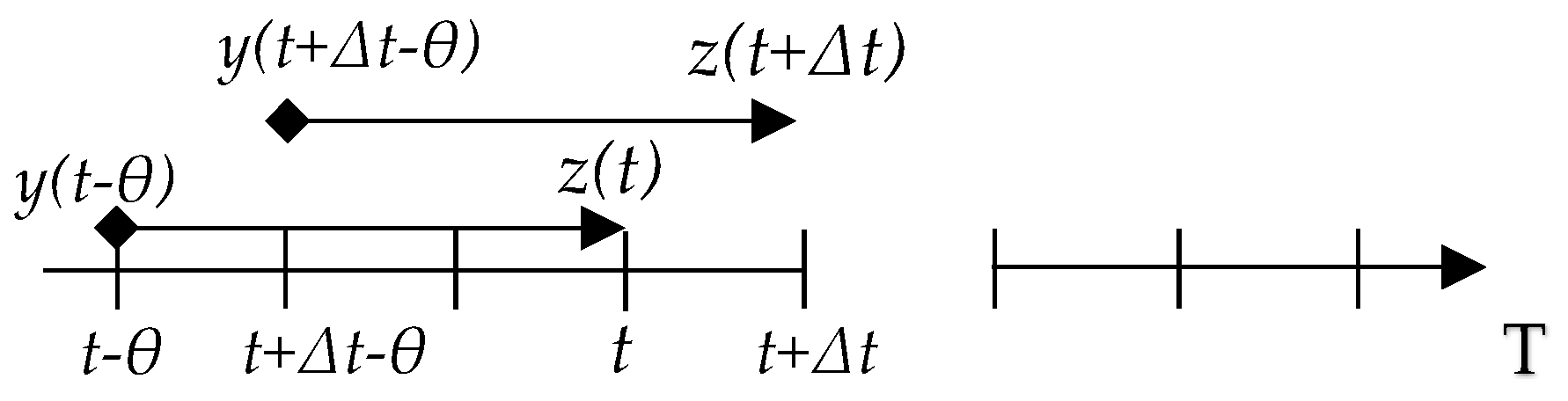
The number of returned used end-of-life products at time
t (see
Figure 5) is proportional to the quantity of sold products at time
t −
θ (when the products were sold to the customer). We denote by
p (0 <
p < 1) the percentage of products which are returned for remanufacturing relatively to sales. As it was mentioned above,
θ stands for the products’ service time. Obviously, in case if (
t −
θ) < 0, there are no returns.
In the following figure, we illustrate the products’ sales and returns (e.g., θ = 3).
The returned products inventory
R, which supplies the machine
M2, is replenished by the returned products
z(
t). Thus, the returned products inventory level at time
t consists of the level of this inventory that remained from the previous period, plus the amount of the products that were returned in the current period, minus the amount of products that were used by the remanufacturing machine
M2 on the previous period:
We consider that the parts are transported in a vehicle. The amount of products that entered the vehicle at time t is the amount of parts being transported during the time . That is to say, the shipment enters the vehicle at time (n·τ) and the next shipment enters another vehicle at time (n + 1)·τ.
The number of products being transported at time
t is described as follows:
As described above, n = {1, 2, 3, …, [T/τ]}, where [T/τ] is the integer part of T/τ and is the number of transportations during the finite time horizon [0, T].
For machines productions rates, we use the hedging point policy [
28], which ensures that the amount of products does not exceed the manufacturing stock capacity.
In order to determine the production rates for
M1 and
M2 while both machines are working we need to introduce a partitioning policy. Therefore, we assume that:
and
We are now going to explain the production control of both machines, according to machines states and inventories cases. This policy controls machines production, with preserving coordination between manufacturing, remanufacturing, inventorying and return of end-of-life products.
Transforming the previous equations, we can determine the production rates of
M1 and
M2 separately:
Cost function at time
t, which consists of inventory costs (manufacturing stock, returned products inventory, purchasing warehouse), transportation cost, lost sales costs, manufacturing/remanufacturing costs and return of used products cost:
The total cost function (the objective function) and is given by:
where
T is the total simulation time.