Nonnegative Matrix Factorization With Data-Guided Constraints For Hyperspectral Unmixing
Abstract
:1. Introduction
2. Preliminaries
2.1. NMF
2.2. NMF with Sparseness Constraints
2.2.1. -NMF
2.2.2. -NMF
3. Proposed NMF with Data-Guided Constraints for Hyperspectral Unmixing
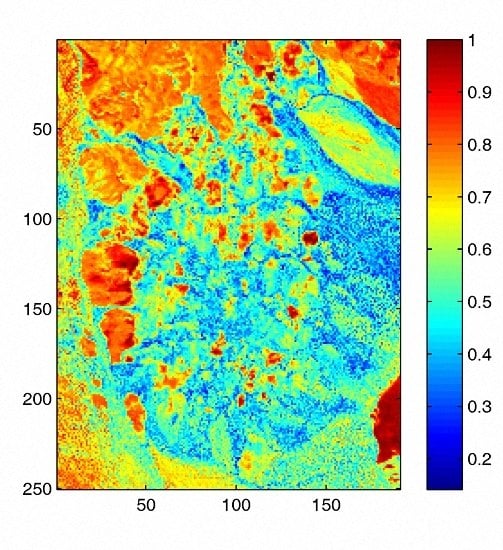
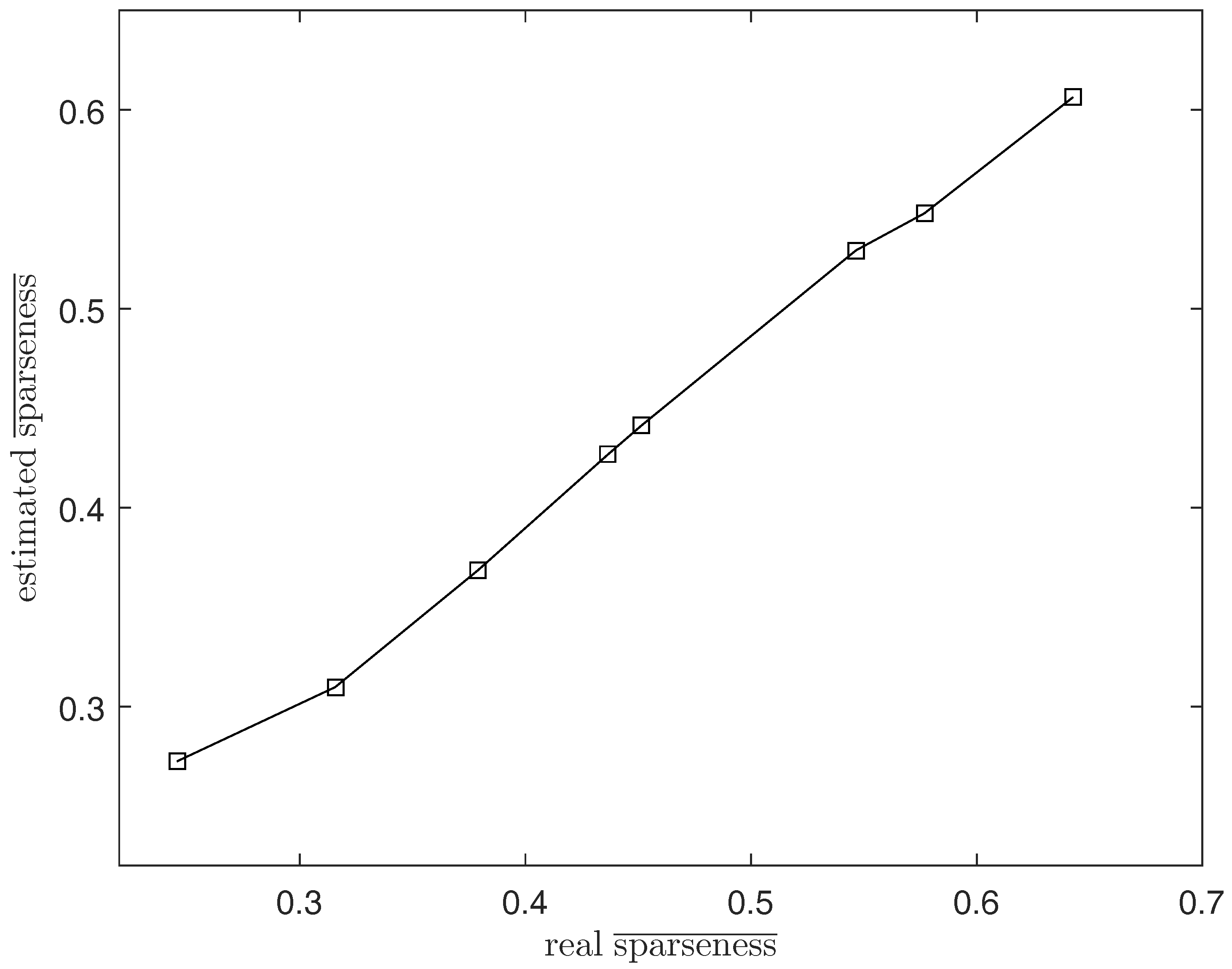
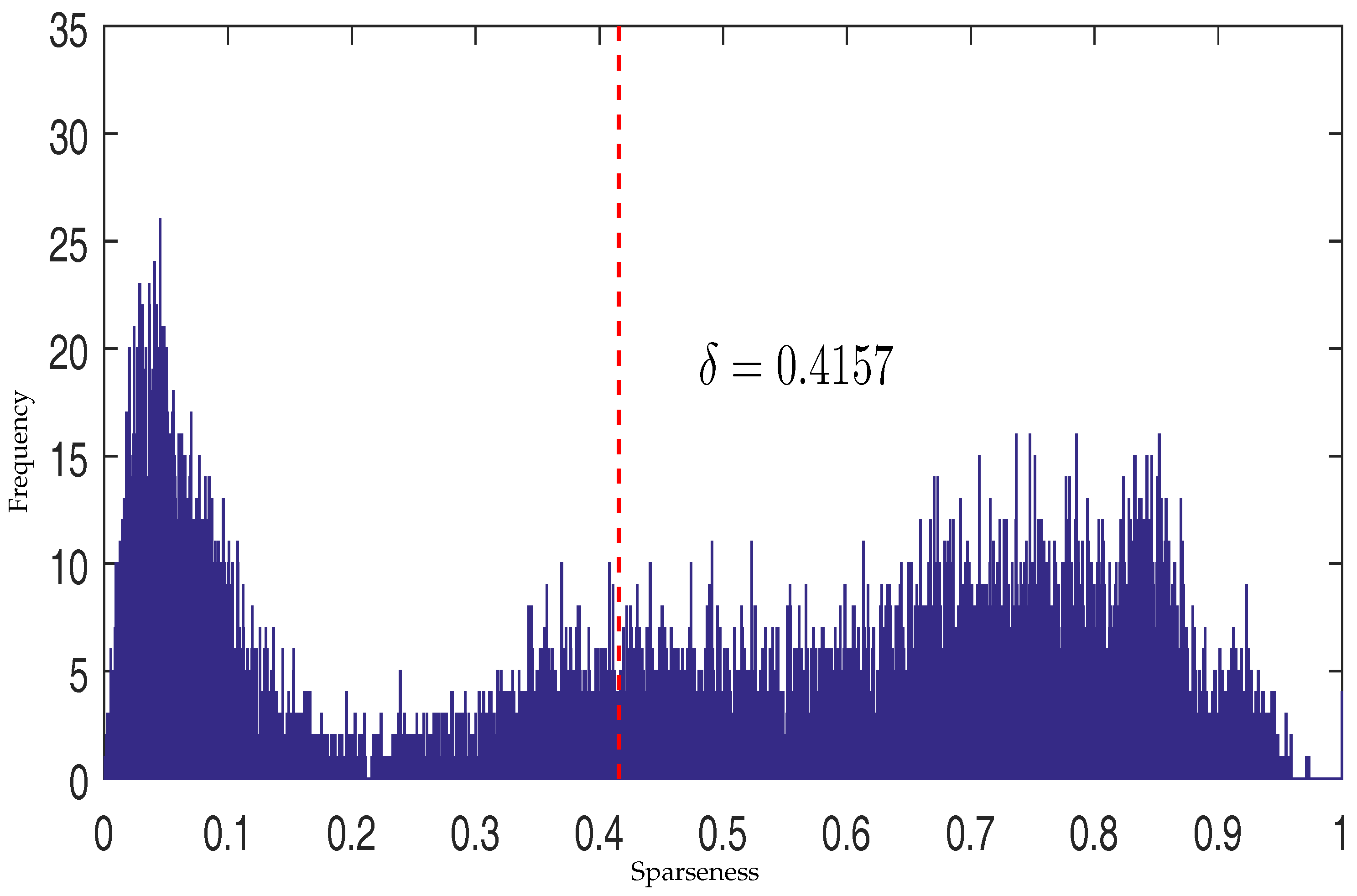
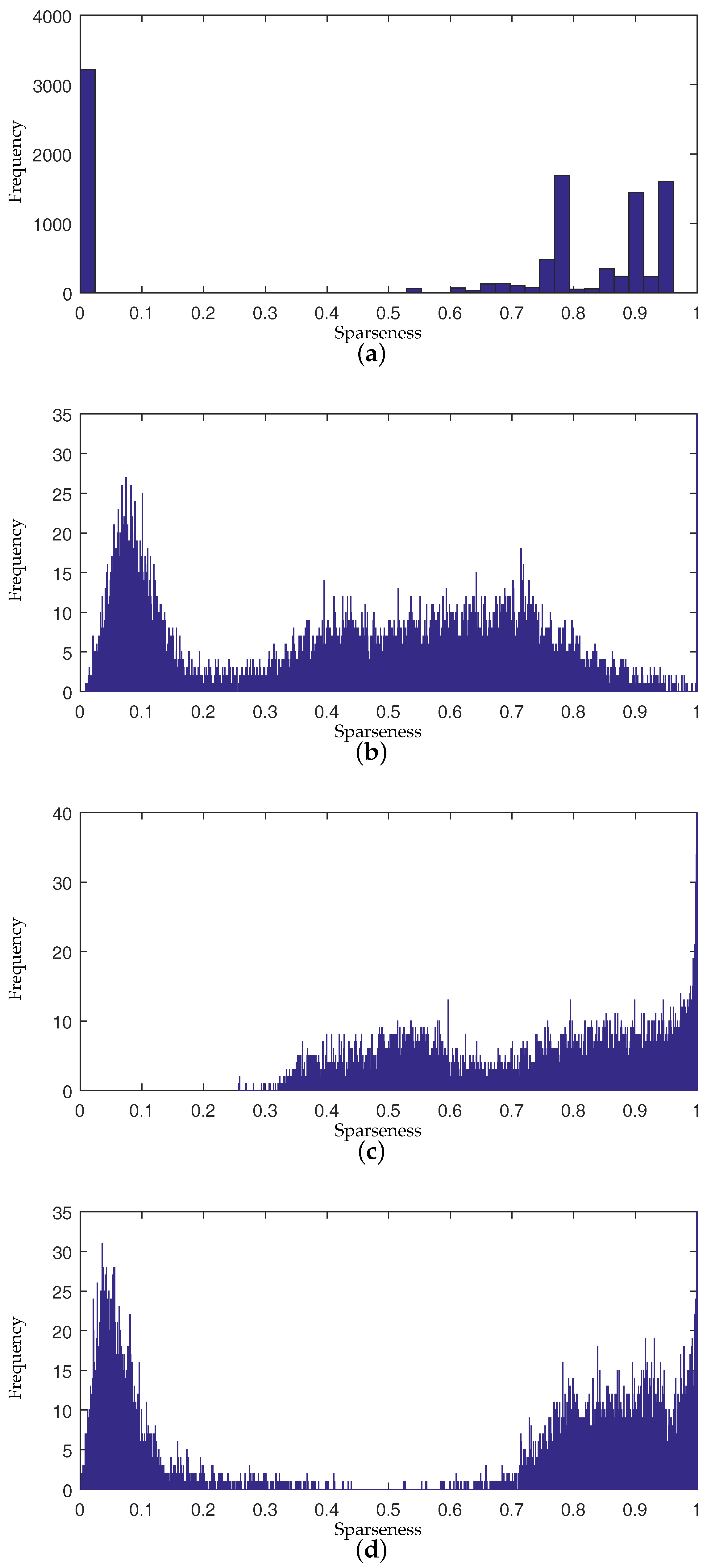
3.1. Sparsity Analysis
3.2. DGC-NMF Algorithm
| Algorithm 1 DGC-NMF algorithm |
| Input: Hyperspectral data ; the number of endmembers P. |
Initialization: Initialize endmember matrix and abundance matrix by SGA-FCLS.
|
4. Experimental Results and Analysis
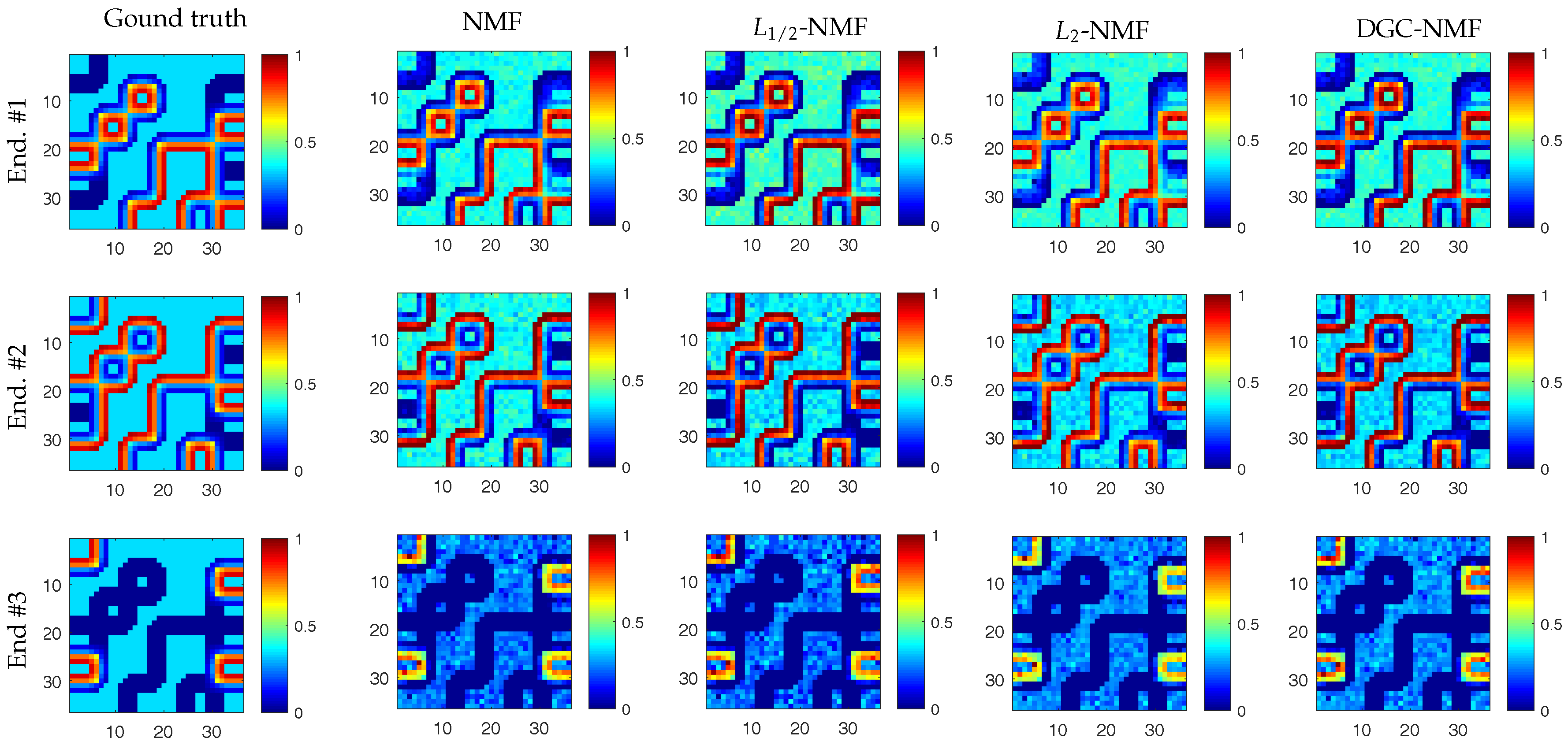
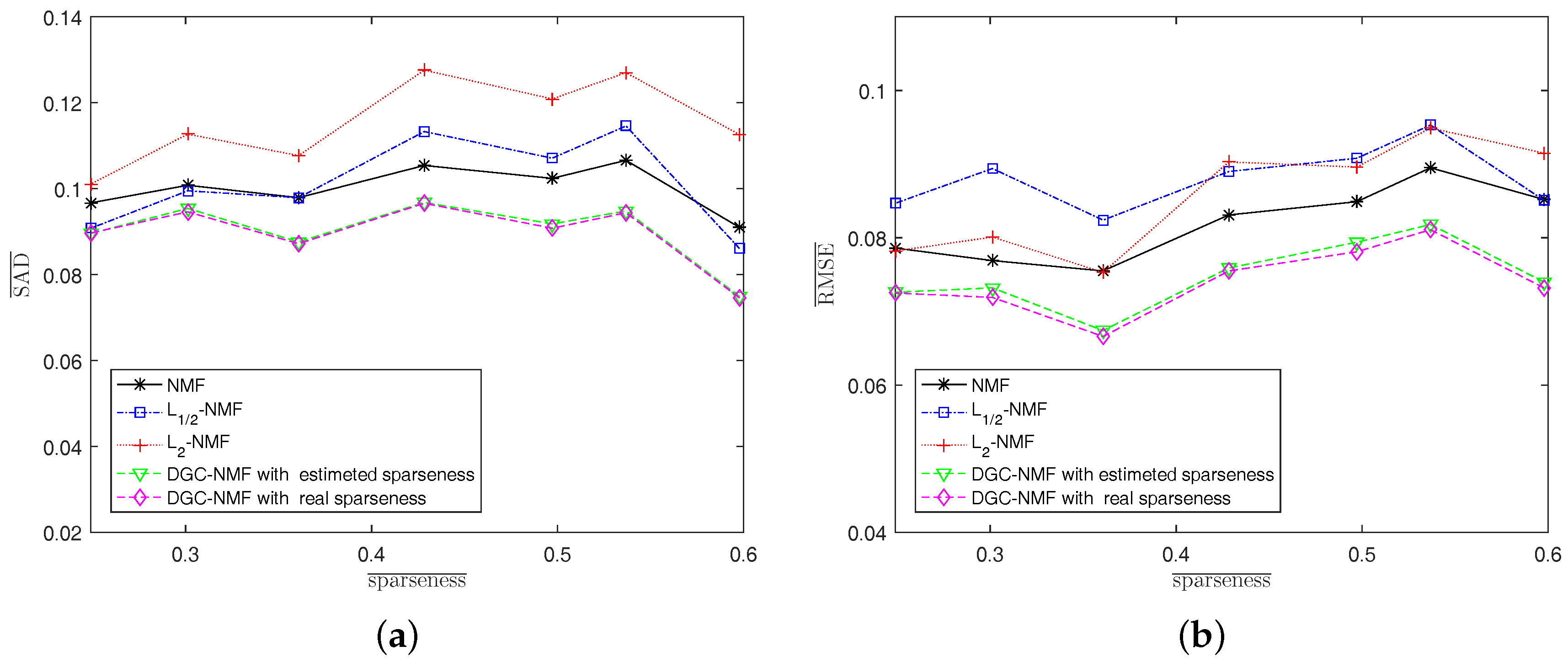
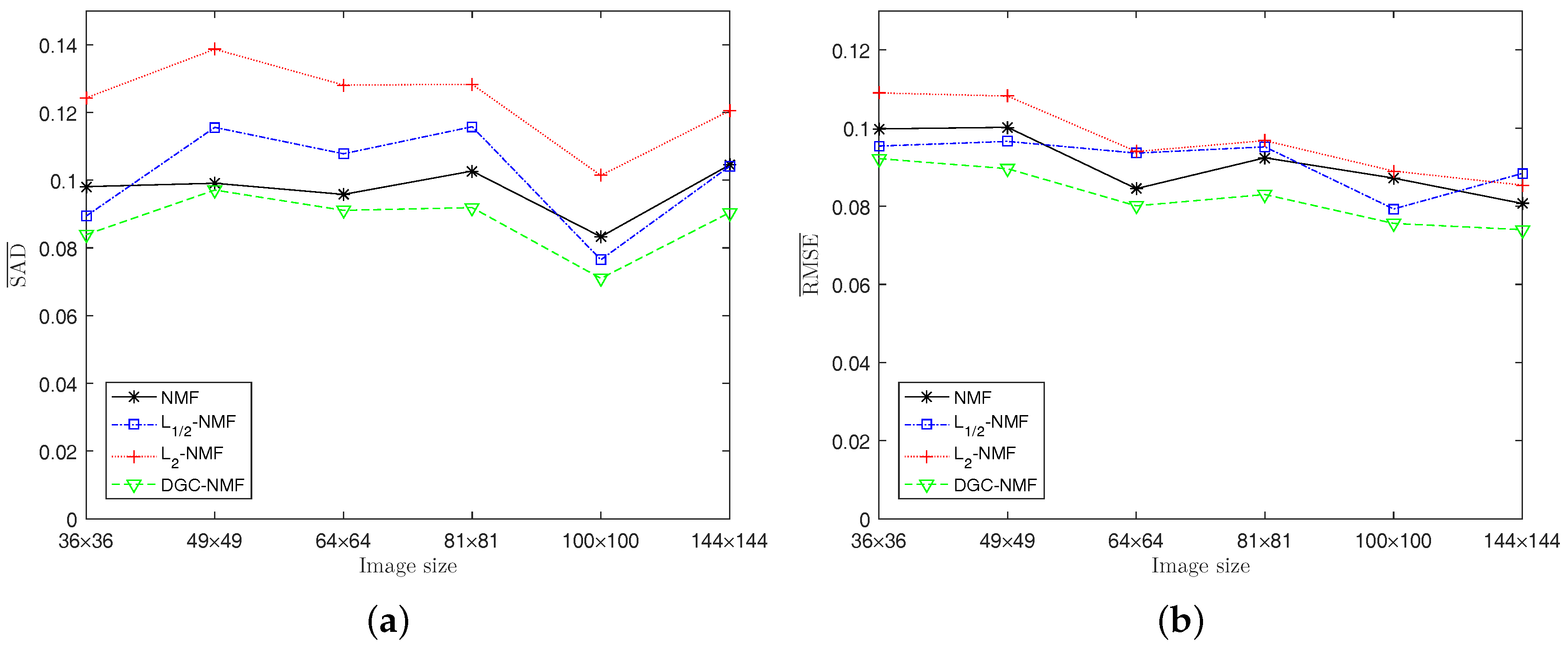
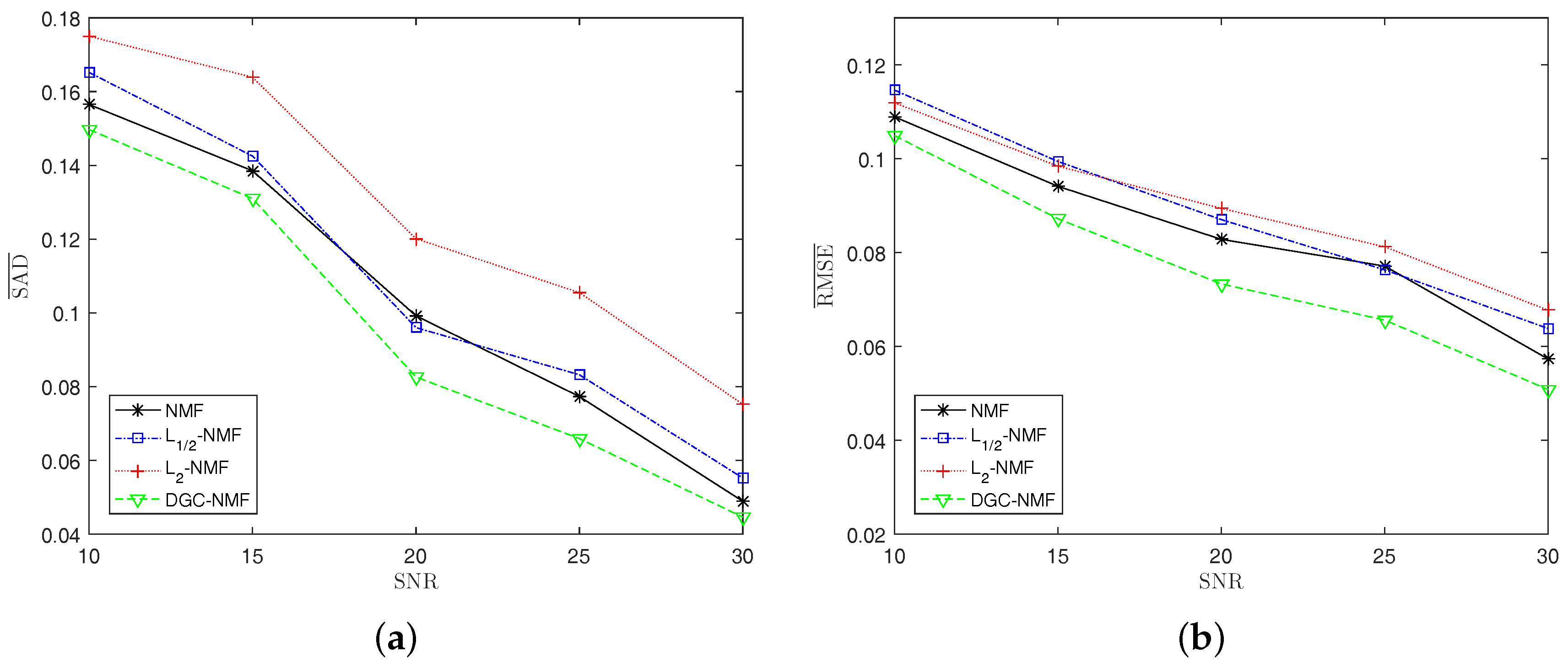
4.1. Experiments on Synthetic Data
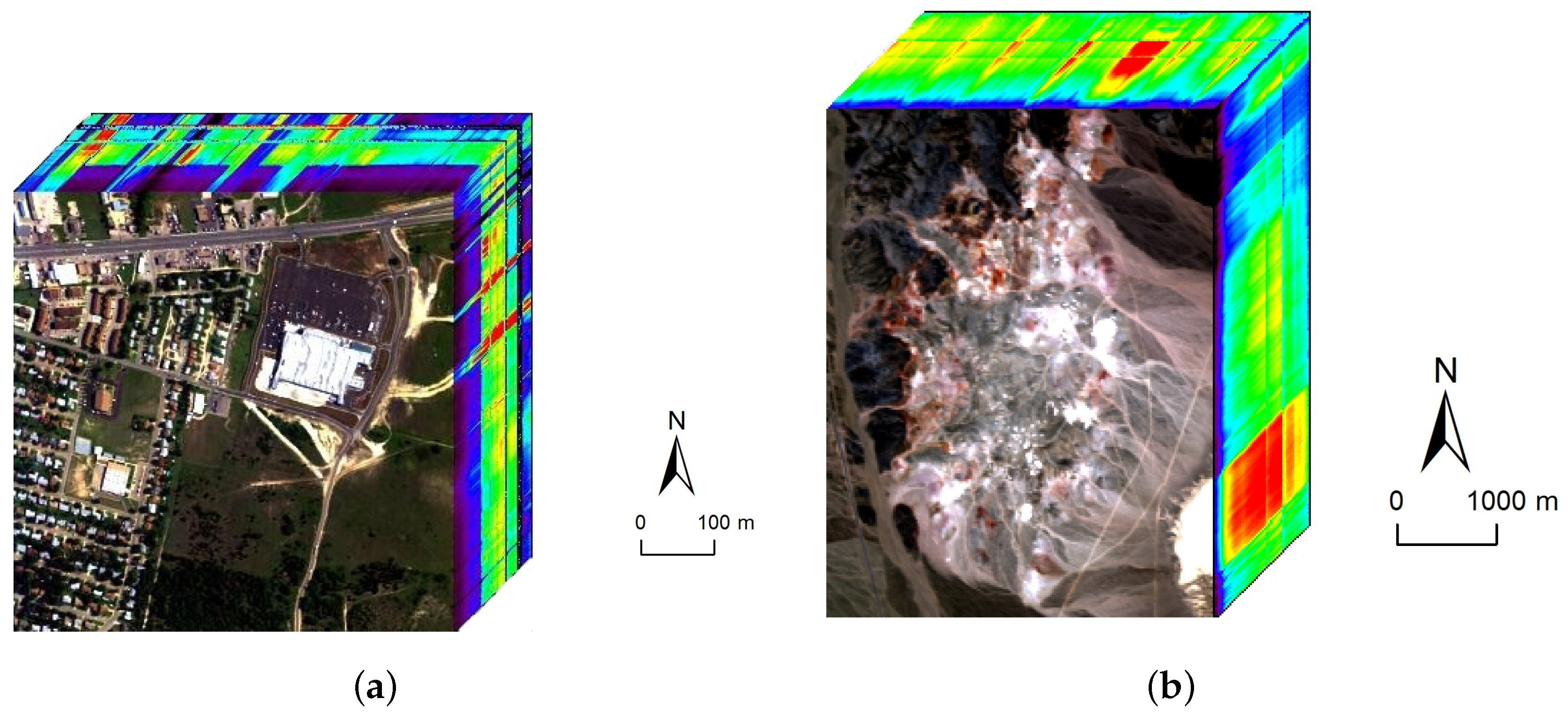
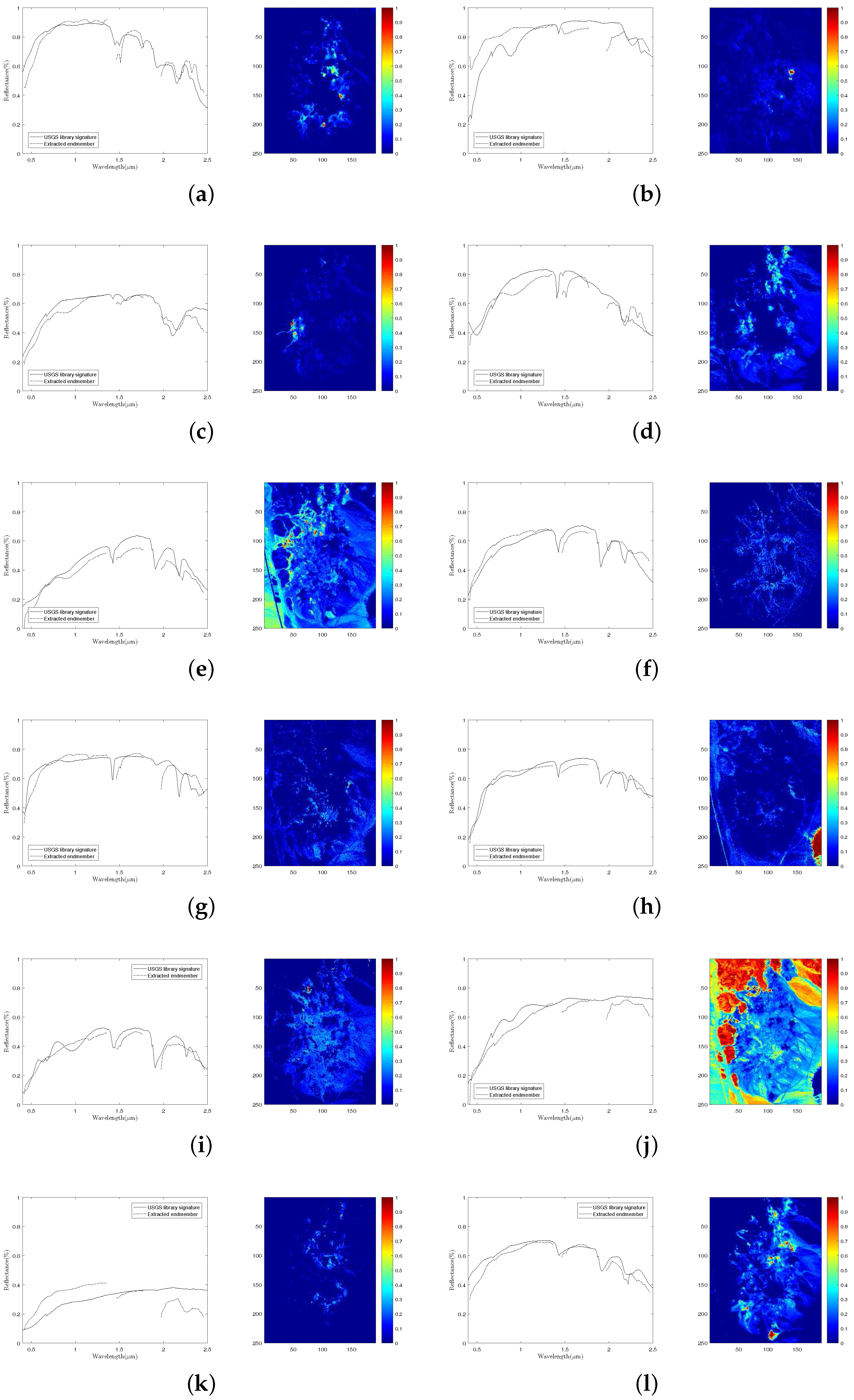
4.2. Experiments on Real Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Altmann, Y.; Dobigeon, N.; Tourneret, J.Y. Unsupervised post-nonlinear unmixing of hyperspectral images using a Hamiltonian Monte Carlo algorithm. IEEE Trans. Image Process. 2014, 23, 2663–2675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Pan, C.; Xiang, S.; Zhu, F. Robust hyperspectral unmixing with correntropy-based metric. IEEE Trans. Image Process. 2015, 24, 4027–4040. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Chen, M.; Tourneret, J.Y.; Godsill, S. Unsupervised nonlinear spectral unmixing based on a multilinear mixing model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4534–4544. [Google Scholar] [CrossRef]
- Qian, Y.; Xiong, F.; Zeng, S.; Zhou, J.; Tang, Y.Y. Matrix-vector nonnegative tensor factorization for blind unmixing of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1776–1792. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y.; Chang, C.I. Semi-supervised linear spectral unmixing using a hierarchical Bayesian model for hyperspectral imagery. IEEE Trans. Signal Process. 2008, 56, 2684–2695. [Google Scholar] [CrossRef] [Green Version]
- Altmann, Y.; Halimi, A.; Dobigeon, N.; Tourneret, J.Y. Supervised nonlinear spectral unmixing using a postnonlinear mixing model for hyperspectral imagery. IEEE Trans. Image Process. 2012, 21, 3017–3025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boardman, J.W. Geometric mixture analysis of imaging spectrometry data. In Proceedings of the 14th Annual International Geoscience and Remote Sensing Symposium: Surface and Atmospheric Remote Sensing: Technologies, Data Analysis and Interpretation, Pasadena, CA, USA, 8–12 August 1994; Volume 4, pp. 2369–2371. [Google Scholar]
- Winter, M.E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 18–23 July 1999; pp. 266–275. [Google Scholar]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Chang, C.I.; Wu, C.C.; Liu, W.; Ouyang, Y.C. A new growing method for simplex-based endmember extraction algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2804–2819. [Google Scholar] [CrossRef]
- Chang, C.I.; Wen, C.H.; Wu, C.C. Relationship exploration among PPI, ATGP and VCA via theoretical analysis. Int. J. Comput. Sci. Eng. 2013, 8, 361–367. [Google Scholar] [CrossRef]
- Li, H.; Chang, C.I. Linear spectral unmixing using least squares error, orthogonal projection and simplex volume for hyperspectral Images. In Proceedings of the 7th Workshop Hyperspectral Image & Signal Processing: Evolution Remote Sensing (WHISPERS), Tokyo, Japan, 2–5 June 2015; pp. 2–5. [Google Scholar]
- Chang, C.I.; Chen, S.Y.; Li, H.C.; Chen, H.M.; Wen, C.H. Comparative study and analysis among ATGP, VCA, and SGA for finding endmembers in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4280–4306. [Google Scholar] [CrossRef]
- Dobigeon, N.; Tourneret, J.Y. Spectral unmixing of hyperspectral images using a hierarchical Bayesian model. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 16–20 April 2007; Volume 3. [Google Scholar]
- Dobigeon, N.; Moussaoui, S.; Coulon, M.; Tourneret, J.Y.; Hero, A.O. Joint Bayesian endmember extraction and linear unmixing for hyperspectral imagery. IEEE Trans. Signal Process. 2009, 57, 4355–4368. [Google Scholar] [CrossRef] [Green Version]
- Themelis, K.E.; Rontogiannis, A.A.; Koutroumbas, K.D. A novel hierarchical Bayesian approach for sparse semisupervised hyperspectral unmixing. IEEE Trans. Signal Process. 2012, 60, 585–599. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001; pp. 556–562. [Google Scholar]
- Zhu, F.; Wang, Y.; Xiang, S.; Fan, B.; Pan, C. Structured sparse method for hyperspectral unmixing. ISPRS J. Photogramm. Remote Sens. 2014, 88, 101–118. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [PubMed]
- Wang, N.; Du, B.; Zhang, L. An endmember dissimilarity constrained non-negative matrix factorization method for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 554–569. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Huck, A.; Guillaume, M. Robust hyperspectral data unmixing with spatial and spectral regularized NMF. In Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, Iceland, 14–16 June 2010; pp. 1–4. [Google Scholar]
- Tong, L.; Zhou, J.; Qian, Y.; Bai, X.; Gao, Y. Nonnegative-matrix-factorization-based hyperspectral unmixing with partially known endmembers. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6531–6544. [Google Scholar] [CrossRef]
- Lu, X.; Wu, H.; Yuan, Y.; Yan, P.; Li, X. Manifold regularized sparse NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2815–2826. [Google Scholar] [CrossRef]
- Liu, X.; Xia, W.; Wang, B.; Zhang, L. An approach based on constrained nonnegative matrix factorization to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 757–772. [Google Scholar] [CrossRef]
- Yuan, Y.; Fu, M.; Lu, X. Substance dependence constrained sparse NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2975–2986. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Wang, Y.; Chang, X.; Liang, Y. L1/2 regularization. Sci. China Inf. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. L1/2 Sparsity constrained nonnegative matrix factorization for hyperspectral unmixing. In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications (DICTA), Sydney, Australia, 1–3 December 2010; pp. 447–453. [Google Scholar]
- Pauca, V.P.; Piper, J.; Plemmons, R.J. Nonnegative matrix factorization for spectral data analysis. Linear Algebra Appl. 2006, 416, 29–47. [Google Scholar] [CrossRef]
- Jia, S.; Qian, Y. Constrained nonnegative matrix factorization for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2009, 47, 161–173. [Google Scholar] [CrossRef]
- Wu, C.; Shen, C. Spectral unmixing using sparse and smooth nonnegative matrix factorization. In Proceedings of the International Conference on Geoinformatics, Kaifeng, China, 20–22 June 2013; pp. 1–5. [Google Scholar]
- Zhu, F.; Wang, Y.; Fan, B.; Xiang, S.; Meng, G.; Pan, C. Spectral unmixing via data-guided sparsity. IEEE Trans. Image Process. 2014, 23, 5412–5427. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Wang, Y.; Fan, B.; Meng, G.; Pan, C. Effective spectral unmixing via robust representation and learning-based sparsity. arXiv, 2014; arXiv:1409.0685. [Google Scholar]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. Hyperspectral unmixing via L1/2 sparsity-constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4282–4297. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Hoyer, P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 1–38. [Google Scholar]
- Saul, L.; Pereira, F. Aggregate and mixed-order Markov models for statistical language processing. arXiv, 1997; arXiv:cmp-lg/9706007. [Google Scholar]
- Berry, M.W.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Gallagher, A.J.; King, T.V.; Calvin, W.M. The US Geological Survey, Digital Spectral Library, Version 1 (0.2 to 3.0 um); Technical report; Geological Survey (US): Reston, VA, USA, 1993.
- Dunteman, G.H. Principal Components Analysis; Sage Publications, Inc.: Thousand Oaks, CA, USA, 1989. [Google Scholar]
- Zhu, F. Hyperspectral Unmixing Datasets & Ground Truths. Available online: http://www.escience.cn/people/feiyunZHU/Dataset_GT.html (accessed on 5 June 2017).
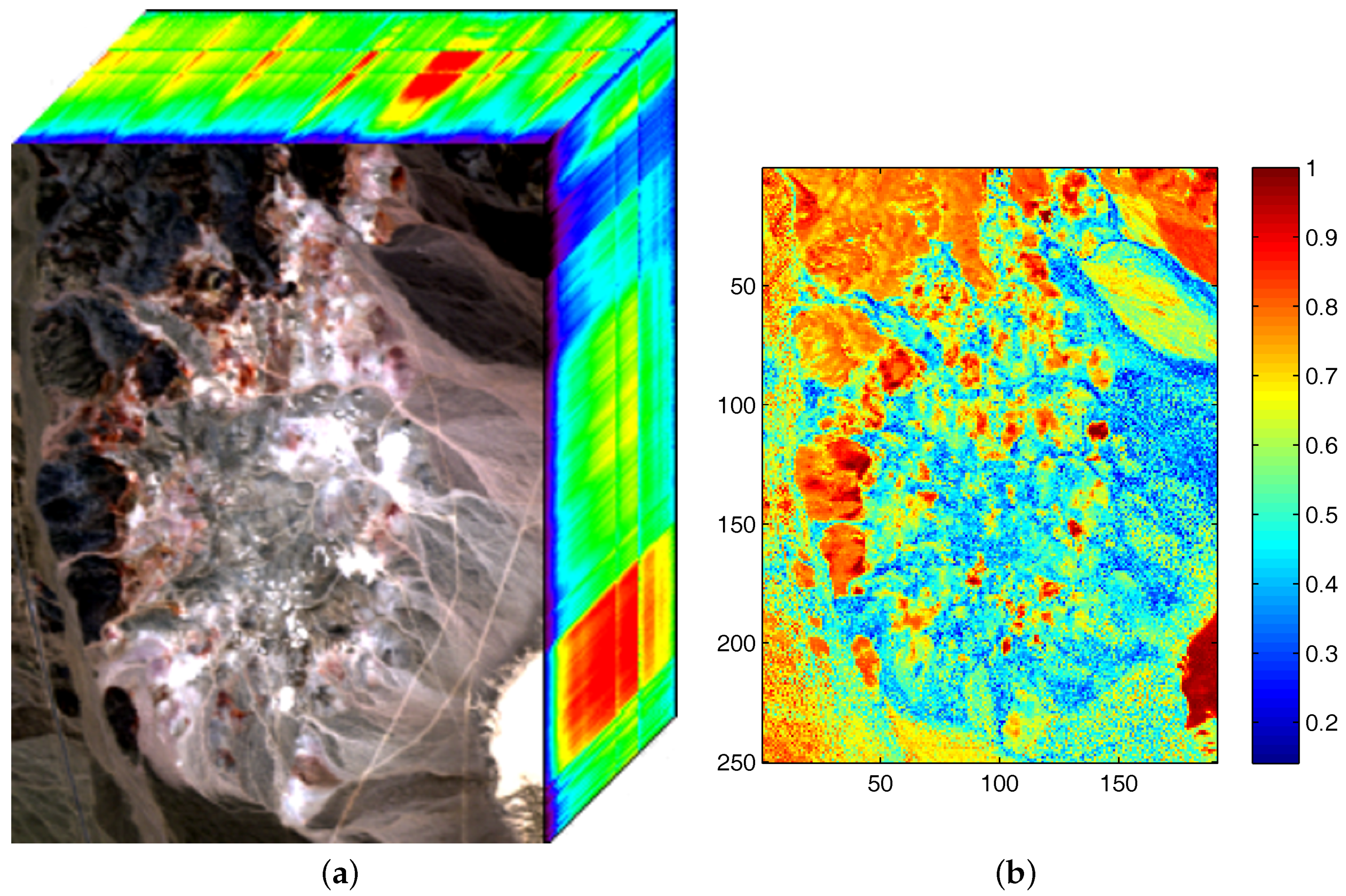





| NMF | L2-NMF | L1/2-NMF | DGC-NMF |
|---|---|---|---|
| 7.61 s | 7.68 s | 8.66 s | 18.80 s |
| Endmember | Spectral Angle Distance (10−2) | |||||
|---|---|---|---|---|---|---|
| VCA-FCLS | SGA-FCLS | NMF | L2-NMF | L1/2-NMF | DGC-NMF | |
| Asphalt | 21.04 ± 3.64 | 13.16 | 32.33 | 23.04 | 96.14 | 20.82 |
| Grass | 36.95 ± 0.28 | 109.21 | 124.92 | 81.87 | 36.06 | 51.53 |
| Trees | 28.38 ± 7.78 | 7.43 | 10.19 | 15.93 | 12.70 | 10.07 |
| Roofs | 77.01 ± 0.07 | 21.74 | 39.54 | 138.98 | 38.94 | 6.20 |
| Mean | 40.84 ± 2.87 | 37.89 | 51.75 | 64.96 | 45.96 | 22.16 |
| Endmember | Root Mean Square Error (10−2) | |||||
|---|---|---|---|---|---|---|
| VCA-FCLS | SGA-FCLS | NMF | L2-NMF | L1/2-NMF | DGC-NMF | |
| Asphalt | 42.42 ± 12.41 | 30.63 | 23.68 | 32.23 | 41.79 | 20.72 |
| Grass | 47.46 ± 1.23 | 47.19 | 39.00 | 48.24 | 50.00 | 36.57 |
| Trees | 26.92 ± 11.79 | 26.96 | 23.05 | 19.36 | 27.66 | 21.23 |
| Roofs | 18.33 ± 2.00 | 19.40 | 20.30 | 24.18 | 8.84 | 15.08 |
| Mean | 33.78 ± 6.86 | 31.05 | 26.51 | 31.00 | 32.07 | 23.40 |
| Endmember | Spectral Angle Distance (10−2) | |||||
|---|---|---|---|---|---|---|
| VCA-FCLS | SGA-FCLS | NMF | L2-NMF | L1/2-NMF | DGC-NMF | |
| Alunite | 17.85 ± 9.39 | 11.05 | 10.03 | 10.18 | 16.01 | 9.91 |
| Andradite | 8.21 ± 2.29 | 8.44 | 13.12 | 7.65 | 12.48 | 12.17 |
| Buddingtonite | 9.82 ± 2.33 | 11.27 | 6.71 | 9.10 | 8.24 | 8.97 |
| Dumortierite | 13.36 ± 3.56 | 13.65 | 13.19 | 10.37 | 6.84 | 10.71 |
| Kaolinite #1 | 7.68 ± 0.18 | 17.90 | 7.33 | 10.88 | 6.88 | 6.40 |
| Kaolinite #2 | 9.82 ± 2.35 | 7.00 | 8.87 | 9.50 | 8.37 | 14.02 |
| Muscovite | 16.51 ± 7.09 | 8.72 | 10.05 | 10.47 | 20.31 | 10.42 |
| Montmorillonite | 11.07 ± 4.63 | 6.81 | 6.42 | 8.76 | 5.89 | 5.88 |
| Nontronite | 7.48 ± 0.15 | 13.39 | 12.53 | 10.52 | 10.90 | 8.69 |
| Pyrope | 9.30 ± 3.25 | 14.69 | 25.36 | 15.67 | 6.24 | 6.12 |
| Sphene | 10.30 ± 5.48 | 23.64 | 5.58 | 65.07 | 28.27 | 24.23 |
| Chalcedony | 12.31 ± 5.22 | 11.66 | 13.20 | 12.62 | 12.28 | 12.41 |
| Mean | 11.14 ± 3.83 | 12.35 | 11.03 | 15.07 | 11.89 | 10.83 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Li, X.; Zhao, L. Nonnegative Matrix Factorization With Data-Guided Constraints For Hyperspectral Unmixing. Remote Sens. 2017, 9, 1074. https://doi.org/10.3390/rs9101074
Huang R, Li X, Zhao L. Nonnegative Matrix Factorization With Data-Guided Constraints For Hyperspectral Unmixing. Remote Sensing. 2017; 9(10):1074. https://doi.org/10.3390/rs9101074
Chicago/Turabian StyleHuang, Risheng, Xiaorun Li, and Liaoying Zhao. 2017. "Nonnegative Matrix Factorization With Data-Guided Constraints For Hyperspectral Unmixing" Remote Sensing 9, no. 10: 1074. https://doi.org/10.3390/rs9101074