Multivariate Spatial Data Fusion for Very Large Remote Sensing Datasets
Abstract
:1. Introduction
2. Remote Sensing Data Sources for Atmospheric CO2
3. Multivariate Spatial Data Fusion
3.1. Data Model and Properties
3.2. Multivariate Spatial Data Fusion (MSDF)
3.3. Constructing the Spatial Basis Function
3.4. EM Algorithm for Parameter Estimation
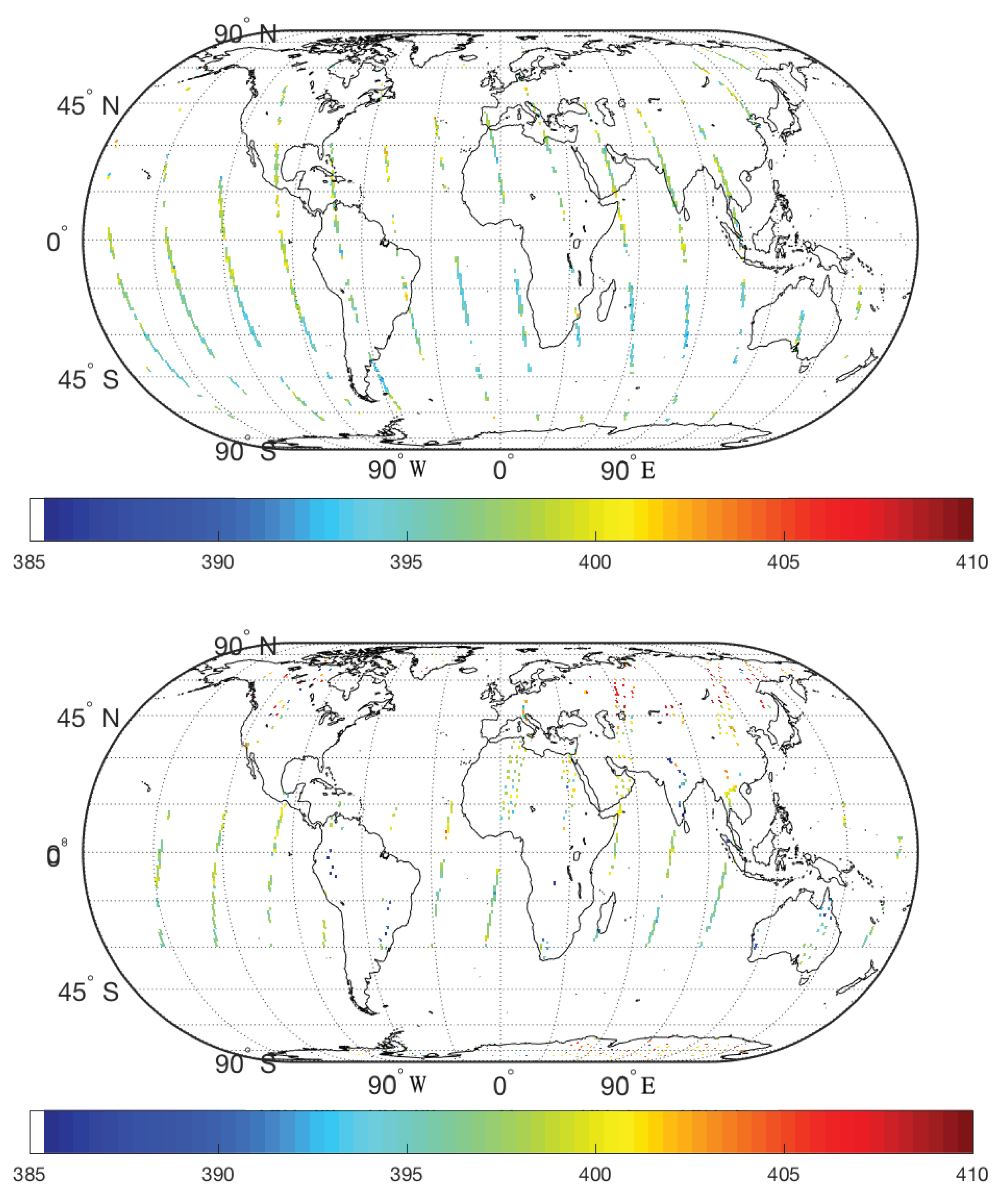
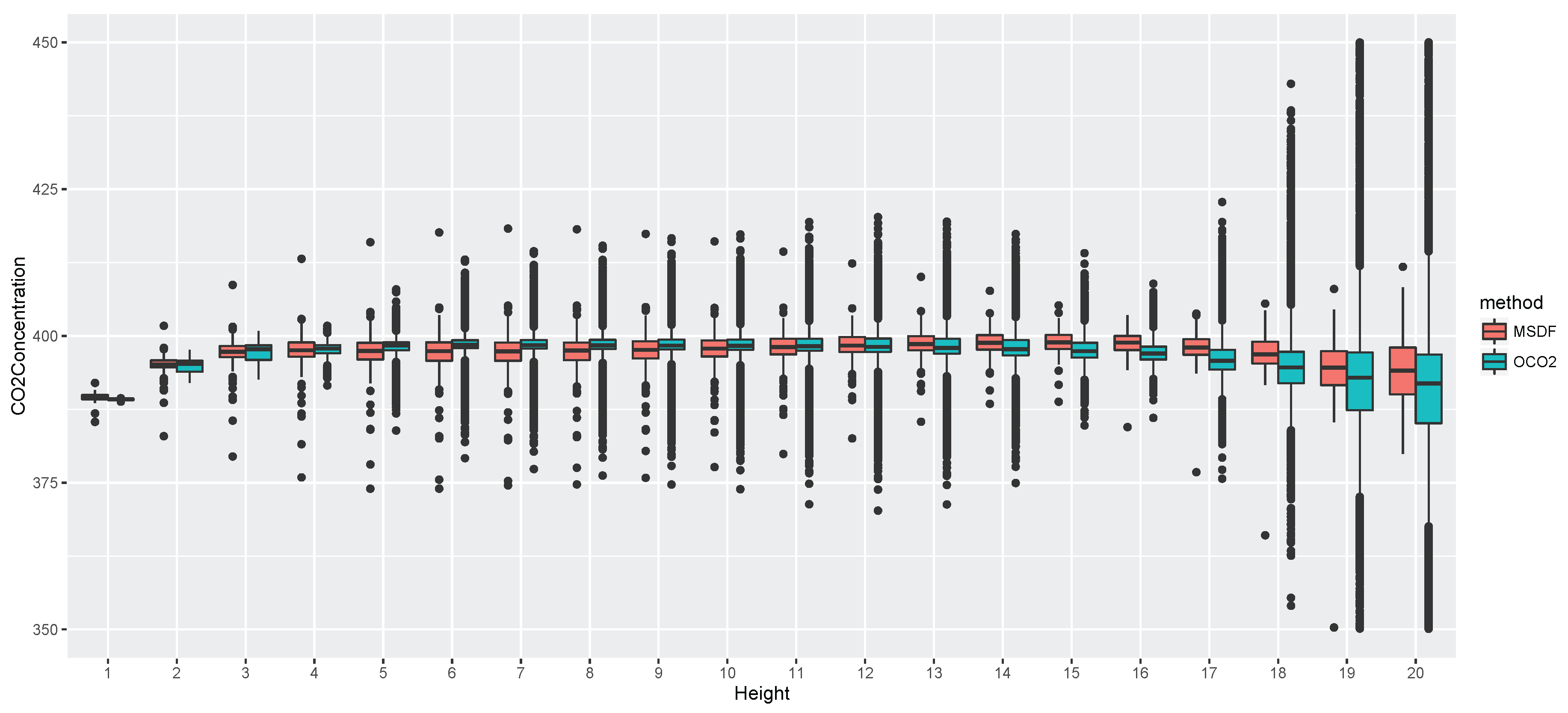
4. Application to CO2 Data from ACOS and OCO-2
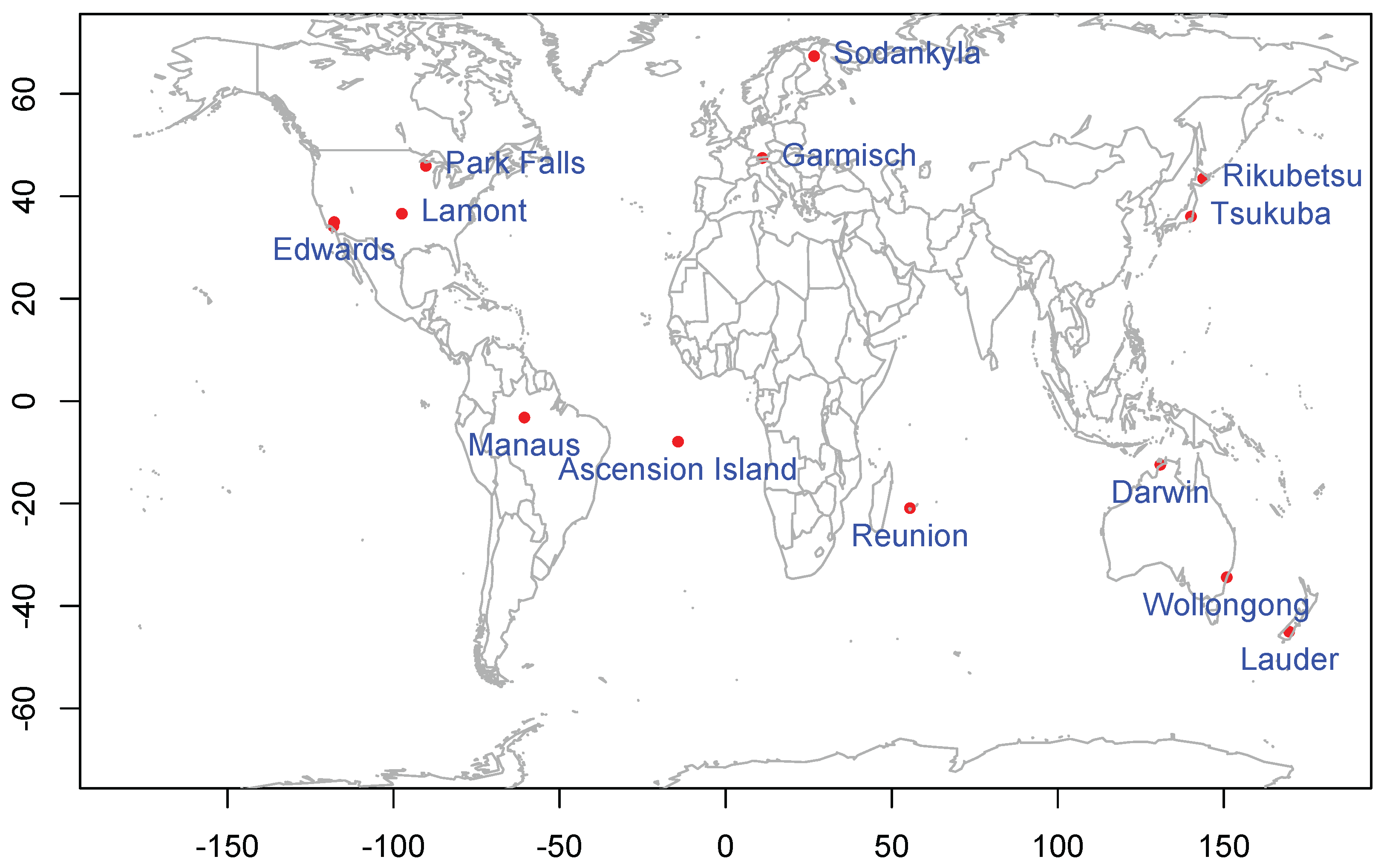
4.1. Overview of ACOS, OCO-2, and TCCON Data
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; van der Linden, P.J.; Dai, X.; Maskell, K.; Johnson, C.A. Climate Change 2001: The Scientific Basis; Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: River Edge, NJ, USA, 2000. [Google Scholar]
- Crisp, D.; Boesch, H.; Brown, L.; Castano, R.; Christi, M.; Conner, B.; Frankenberg, C.; McDuffie, J.; Miller, C.; Natraj, V.; et al. OCO (Orbiting Carbon Observatory): Level 2 Full Physics Retrieval Algorithm Theoretical Basis; Jet Propulsion Laboratory, NASA: Pasadena, CA, USA, 2010. [Google Scholar]
- Nguyen, H.; Cressie, N.; Braverman, A. Spatial statistical data fusion for remote sensing applications. J. Am. Stat. Assoc. 2012, 107, 1004–1018. [Google Scholar] [CrossRef]
- Nguyen, H.; Katzfuss, M.; Cressie, N.; Braverman, A. Spatio-Temporal Data Fusion for Very Large Remote Sensing Datasets. Technometrics 2014, 56, 174–185. [Google Scholar] [CrossRef]
- Kulawik, S.S.; O’Dell, C.; Payne, V.H.; Kuai, L.; Worden, H.M.; Biraud, S.C.; Sweeney, C.; Stephens, B.; Iraci, L.T.; Yates, E.L.; Tanaka, T. Lower-tropospheric CO2 from near-infrared ACOS-GOSAT observations. Atmos. Chem. Phys. Discuss. 2016, 2016, 1–55. [Google Scholar] [CrossRef]
- Cressie, N.; Johannesson, G. Fixed rank kriging for very large spatial data sets. J. R. Stat. Soc. Ser. B 2008, 70, 209–226. [Google Scholar] [CrossRef]
- Hamazaki, T.; Kaneko, Y.; Kuze, A.; Kondo, K. Fourier transform spectrometer for Greenhouse Gases Observing Satellite (GOSAT). In Proceedings of the International Society for Optical Engineering (SPIE) Symposium, Remote Sensing of the Atmosphere, Ocean, Environment, and Space, Honoluu, HI, USA, 8–12 November 2004.
- Morino, I.; Uchino, O.; Inoue, M.; Yoshida, Y.; Yokota, T.; Wennberg, P.O.; Toon, G.C.; Wunch, D.; Roehl, C.M.; Notholt, J.; et al. Preliminary validation of column-averaged volume mixing ratios of carbon dioxide and methane retrieved from GOSAT short-wavelength infrared spectra. Atmos. Meas. Tech. 2011, 4, 1061–1076. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Connor, B.; Bösch, H.; O’Brien, D.; Frankenberg, C.; Castano, R.; Christi, M.; Eldering, D.; Fisher, B.; Gunson, M.; et al. The ACOS CO2 retrieval algorithm Part 1: Description and validation against synthetic observations. Atmos. Meas. Tech. 2012, 5, 99–121. [Google Scholar] [CrossRef]
- Cressie, N. Change of support and the modifiable areal unit problem. Geogr. Syst. 1996, 3, 159–180. [Google Scholar]
- Berliner, L.; Wikle, C.; Milliff, R. Multiresolution Wavelet Analyses in Hierarchical Bayesian Turbulence Models. In Bayesian Inference in Wavelet-Based Models; Miller, P., Vidakovic, B., Eds.; Springer Lecture Notes in Statistics, No. 141; Springer: New York, NY, USA, 1999. [Google Scholar]
- Wikle, C.K.; Milliff, R.F.; Nychka, D.; Berliner, L.M. Spatio-Temporal hierarchical Bayesian modeling: Tropical ocean surface winds. J. Am. Stat. Assoc. 2001, 96, 382–397. [Google Scholar] [CrossRef]
- Nychka, D.; Wikle, C.K.; Royle, J. Multiresolution models for nonstationary spatial covariance functions. Stat. Model. 2002, 2, 315–331. [Google Scholar] [CrossRef]
- Hooten, M.B.; Larsen, D.R.; Wikle, C.K. Predicting the spatial distribution of ground flora on large domains using a hierarchical Bayesian model. Landsc. Ecol. 2003, 18, 487–502. [Google Scholar] [CrossRef]
- Royle, J.; Wikle, C. Efficient Statistical Mapping of Avian Count Data. Ecol. Environ. Stat. 2005, 12, 225–243. [Google Scholar] [CrossRef]
- Banerjee, S.; Gelfand, A.E.; Finley, A.O.; Sang, H. Gaussian prediction process models for large spatial data sets. J. R. Stat. Soc. Ser. B 2008, 70, 825–848. [Google Scholar] [CrossRef] [PubMed]
- Calder, C. A Bayesian dynamic process convolution approach to modelling the point distribution of PM2.5 and PM10. Envirometrics 2008, 19, 39–48. [Google Scholar] [CrossRef]
- Stein, M.L.; Jun, M. Nonstationary covariance models for global data. Ann. Appl. Stat. 2008, 2, 1271–1289. [Google Scholar]
- Cressie, N.; Shi, T.; Kang, E.L. Fixed Rank Filtering for Spatio-Temporal Data. J. Comput. Graph. Stat. 2010, 19, 724–745. [Google Scholar] [CrossRef]
- Lindgren, F.; Rue, H.; Lindstrom, J. An explicit link between Guassian fields and Gaussian Markov random fields: The stochastic partial different equation approach. J. R. Stat. Soc. Ser. B 2011, 73, 423–498. [Google Scholar] [CrossRef]
- Henderson, H.; Searle, S. On deriving the inverse of a sum of matrices. SIAM Rev. 1981, 23, 53–60. [Google Scholar] [CrossRef]
- Katzfuss, M.; Cressie, N. Spatio-temporal smoothing and EM estimation for massive remote-sensing data sets. J. Time Ser. Anal. 2011, 32, 430–446. [Google Scholar] [CrossRef]
- Carr, D.; Kahn, R.; Sahr, K.; Olsen, T. ISEA discrete global grids. Stat. Comput. Stat. Graph. 1998, 8, 31–39. [Google Scholar]
- Bartels, R.H.; Beatty, J.C.; Barsky, B.A. Hermite and Cubic Spline Interpolation; Morgan Kaufmann: San Francisco, CA, USA, 1998. [Google Scholar]
- Karion, A.; Sweeney, C.; Tans, P.; Newberger, T. AirCore: An Innovative Atmospheric Sampling System. J. Atmos. Ocean. Technol. 2010, 27. [Google Scholar] [CrossRef]
- Osterman, G.; Eldering, A.; Avis, C.; O’Dell, C.; Martinez, E.; Crisp, D.; Frankenberg, C.; Fisher, B. ACOS Level 2 Standard Product Data User’s Guide v3.5. Revision Date: Revision D, 6 March 2016. Available online: http://disc.sci.gsfc.nasa.gov/OCO-2/documentation/gosat-acos/gosat-acosdoc/ACOS_v3.5_DataUsersGuide.pdf (accessed on 15 May 2016).
- Osterman, G.; Eldering, A.; Avis, C.; Chafin, B.; O’Dell, C.; Frankenberg, C.; Fisher, B.; Mandrake, L.; Wunch, D.; Granat, R.; et al. OCO2 Data Product User’s Guide, Operational L1 and L2 Data Versions 7 and 7R. Revision Date: Version G, 30 June 2016. Available online: http://disc.sci.gsfc.nasa.gov/OCO-2/documentation/oco-2-v7/OCO2_DUG.V7.pdf (accessed on 23 May 2016).
- ACOS Data Access. Goddard Earth Sciences Data and Information Services Center. Available online: http://disc.sci.gsfc.nasa.gov/acdisc/documentation/ACOS.shtml (accessed on 23 May 2016).
- OCO-2 Data Access. Goddard Earth Sciences Data and Information Services Center. Available online: http://disc.sci.gsfc.nasa.gov/OCO-2 (accessed on 23 May 2016).
- Wunch, D.; Toon, G.; Blavier, J.; Washenfelder, R.; Notholt, J.; Connor, B.; Griffith, D.; Sherlock, V.; Wennberg, P. The Total Carbon Column Observing Network. Philos. Trans. R. Soc. A 2011, 369, 2087–2112. [Google Scholar] [CrossRef] [PubMed]
- Crisp, D.; Fisher, B.M.; O’Dell, C.; Frankenberg, C.; Basilio, R.; Boesch, H.; Brown, L.R.; Castano, R.; Connor, B.; Deutscher, N.M.; et al. The ACOS CO2 retrieval algorithm—Part II: Global XCO2 data characterization. Atmos. Meas. Tech. 2012, 5, 687–707. [Google Scholar] [CrossRef]
- Washenfelder, R.A.; Toon, G.C.; Blavier, J.F.; Yang, Z.; Allen, N.T.; Wennberg, P.O.; Vay, S.A.; Matross, D.M.; Daube, B.C. Carbon dioxide column abundances at the Wisconsin Tall Tower site. J. Geophys. Res. Atmos. 2006, 111, D22305. [Google Scholar] [CrossRef]
- Deutscher, N.M.; Griffith, D.W.T.; Bryant, G.W.; Wennberg, P.O.; Toon, G.C.; Washenfelder, R.A.; Keppel-Aleks, G.; Wunch, D.; Yavin, Y.; Allen, N.T.; et al. Total column CO2 measurements at Darwin, Australia-site description and calibration against in situ aircraft profiles. Atmos. Meas. Tech. 2010, 3, 947–958. [Google Scholar] [CrossRef]
- Messerschmidt, J.; Geibel, M.C.; Blumenstock, T.; Chen, H.; Deutscher, N.M.; Engel, A.; Feist, D.G.; Gerbig, C.; Gisi, M.; Hase, F.; et al. Calibration of TCCON column-averaged CO2: The first aircraft campaign over European TCCON sites. Atmos. Chem. Phys. 2011, 11, 10765–10777. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Wennberg, P.O.; Wofsy, S.C.; Stephens, B.B.; Fischer, M.L.; Uchino, O.; Abshire, J.B.; Bernath, P.; Biraud, S.C.; et al. Calibration of the Total Carbon Column Observing Network using aircraft profile data. Atmos. Meas. Tech. 2010, 3, 1351–1362. [Google Scholar] [CrossRef] [Green Version]
- TCCON Data Access. TCCON Data Archive. Available online: http://tccon.ornl.gov/ (accessed on 23 May 2016).
- Connor, B.; Boesch, H.; McDuffie, J.; Taylor, T.; Fu, D.; Frankenberg, C.; O’Dell, C.; Payne, V.; Gunson, M.; Pollock, R.; et al. Quantification of Uncertainties in OCO-2 Measurements of XCO2: Simulations and Linear Error Analysis. Atmos. Meas. Tech. Discuss. 2016, 9, 5227–5238. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; O’Dell, C.; Mandrake, L.; Viatte, C.; Griffith, D.W.; et al. Comparisons of the Orbiting Carbon Observatory-2 (OCO-2) XCO2 measurements with TCCON. Atmos. Meas. Tech. Discuss. 2016, 2016. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Toon, G.C.; Connor, B.J.; Fisher, B.; Osterman, G.B.; Frankenberg, C.; Mandrake, L.; O’Dell, C.; Ahonen, P.; et al. A method for evaluating bias in global measurements of CO2 total columns from space. Atmos. Chem. Phys. 2011, 11, 12317–12337. [Google Scholar] [CrossRef]
- Gruber, N.; Gloor, M.; Fletcher, S.E.M.; Dutkiewicz, S.; Follows, M.; Doney, S.C.; Gerber, M.; Jacobson, A.R.; Lindsay, K.; Menemenlis, D.; et al. Oceanic sources, sinks, and transport of atmospheric CO2. Glob. Biochem. Cycles 2009, 23. [Google Scholar] [CrossRef]
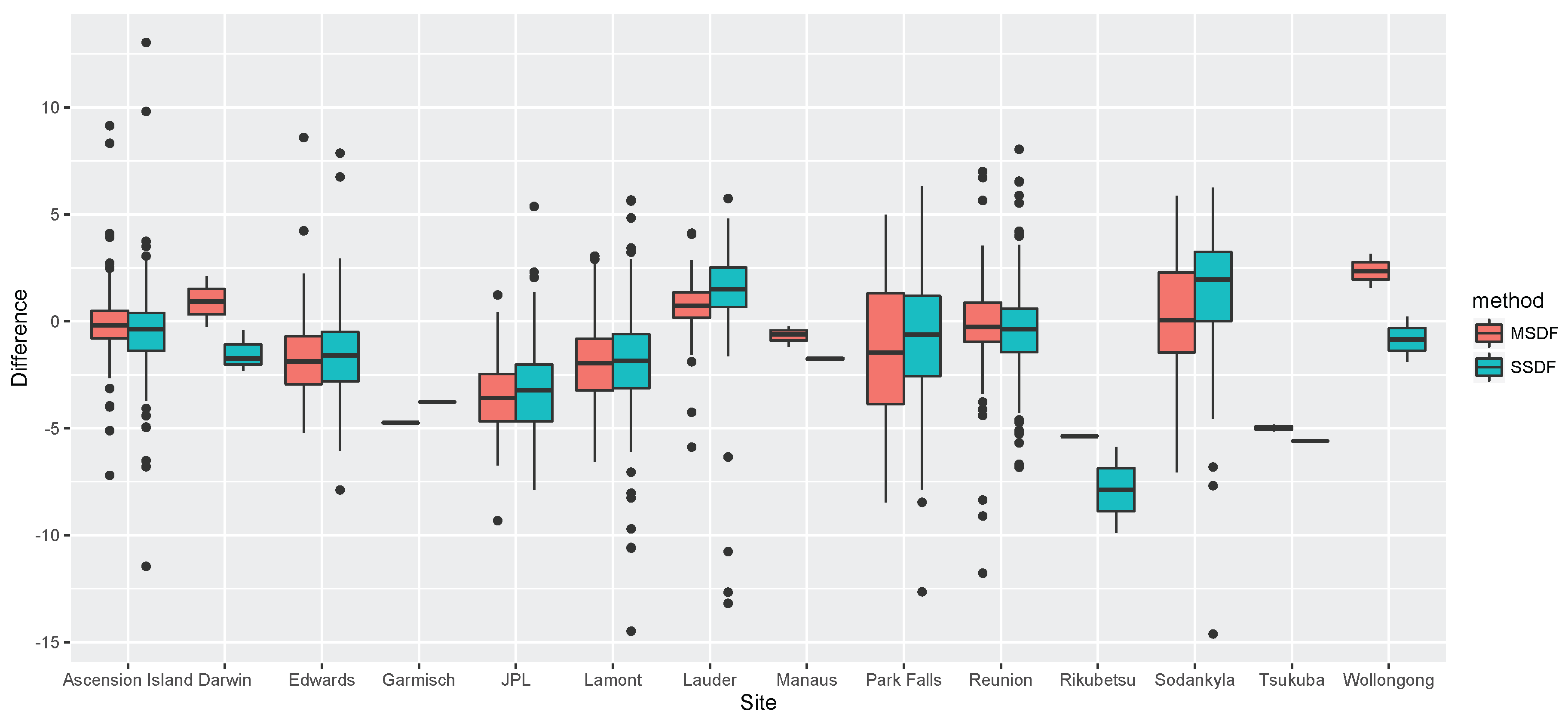
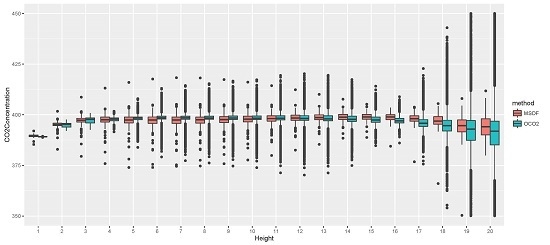
| SCC | SSDF | MSDF | |
|---|---|---|---|
| MSE | 7.8416 | 7.0498 | 6.8741 |
| Mean | 1.4936 | 1.3098 | 1.3582 |
| Variance | 5.6108 | 5.3342 | 5.0294 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.; Cressie, N.; Braverman, A. Multivariate Spatial Data Fusion for Very Large Remote Sensing Datasets. Remote Sens. 2017, 9, 142. https://doi.org/10.3390/rs9020142
Nguyen H, Cressie N, Braverman A. Multivariate Spatial Data Fusion for Very Large Remote Sensing Datasets. Remote Sensing. 2017; 9(2):142. https://doi.org/10.3390/rs9020142
Chicago/Turabian StyleNguyen, Hai, Noel Cressie, and Amy Braverman. 2017. "Multivariate Spatial Data Fusion for Very Large Remote Sensing Datasets" Remote Sensing 9, no. 2: 142. https://doi.org/10.3390/rs9020142