1. Introduction
For numerical models verifications, observational data are essential. A network of meteorological observation stations is placed around the world to observe weather and provide data for this purpose; however, this network is still insufficient. Therefore, sounding, radar technology and satellite systems have been added since the past century to overcome the lack of information on all meteorological variables by giving improved spatial (horizontal and vertical) coverage of the meteorological state.
For the particular case of precipitation, the Tropical Rainfall Measuring Mission (TRMM) products gave scientists the opportunity to verify their numerical models simulations from a satellite perspective. However, the satellite responsible for gathering the precipitation information was shut down, and consequently, a new version of these products has been created: the Global Precipitation Measurement (GPM; [
1]). The GPM satellite constellation is now generating the new precipitation product called IMERG (Integrated Multi-satellitE Retrievals for GPM). The IMERG product possesses higher temporal and spatial resolutions (30 min and ~11 km) compared with those of TRMM products (3 h and ~25 km).
The availability of this precipitation product brought the opportunity for these models verification at higher resolutions. However, the main problem with all new satellite precipitation products is the lack of evaluation and that they are not thoroughly tested for all regions. For example, Wang et al. [
2] briefly analyzed the IMERG product and found an overall agreement with the previous TRMM data set. Huffman et al. [
1] mentioned that monthly and daily precipitation gauges were used to improve, at least in some regions, the biases that characterize the IMERG precipitation estimates. However, concerns regarding the quality of this data set at higher temporal resolutions still remain due to the relative novelty of the IMERG precipitation product. Other studies have been made worldwide that help improve our understanding of the IMERG precipitation product [
3,
4,
5,
6]. Sharifi et al. [
3] assessed the GPM
–IMERG final run against gauge data over four small regions in Iran, with diverse topography and climate conditions. They also compared IMERG with the ERA-Interim product from the European Centre for Medium Range Weather Forecasts (ECMWF) and TRMM data and found that IMERG performed better for heavy, daily precipitation. Ma et al. [
4] also compared IMERG with TRMM and gauge data at a three-hourly scale over the Tibetan Plateau and found that IMERG performed better for light and solid precipitation at higher elevations than TRMM. Rios Gaona et al. [
5] compared IMERG against gauge-adjusted radar rainfall data at different time scales over the relatively flat terrains of the Netherlands. An overall underestimation of the IMERG data and higher correlations with increasing time scales were found. Also, Guo et al. [
7] provided a quantitative study of error characteristics of the IMERG over China. Here, it was found that this satellite product overestimates light rainfall events over arid areas. All this research focused its analysis on particular areas of interest. However, there is no study, to our current knowledge, that evaluates the IMERG precipitation dataset over the Mexican region.
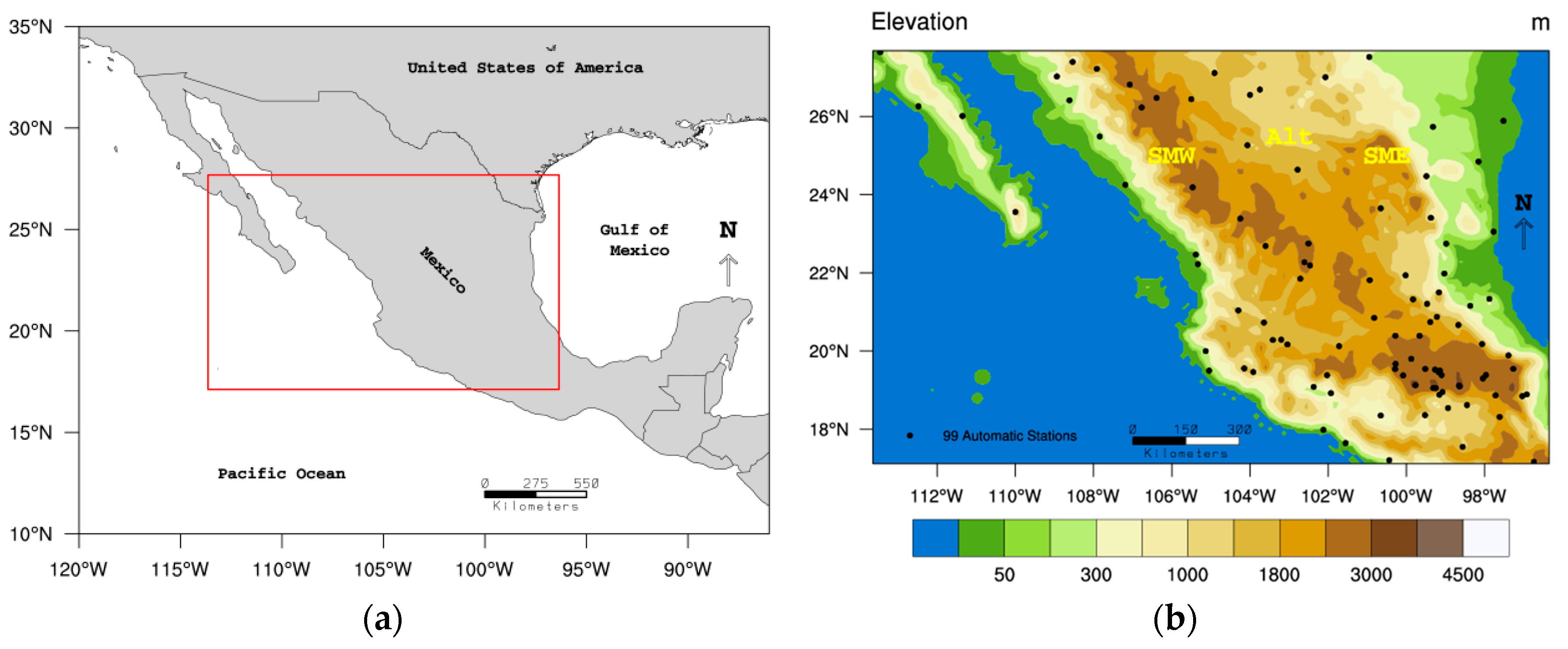
Mexico is a developing country which relies on a sparse rain-gauge network to provide the rainfall data needed to manage their water resources. Although these water resources are not scarce, they are not equally distributed throughout the region. In addition, Mexico figures as one of the twelve countries with the greatest biodiversity worldwide [
8]. Therefore, the estimation and proper management of water resources is of great importance to the country. Also, in remote areas, such as mountains, deserts and oceans, where rain gauges are unable to be installed and radar systems are not available; the satellite-derived rainfall may be the only tool to provide precipitation information with relatively high spatial and temporal resolutions [
3].
Therefore, the present study aims to evaluate the IMERG precipitation dataset over the Mexico region by analyzing different time scales of precipitation, such as hourly, daily and seasonal cumulative precipitation. The automatic meteorological network located within this region has been used as the reference since it provides rain gauges at time scales smaller than the analysis scales. This investigation, which is to our knowledge, the first to evaluate the IMERG precipitation data over Mexico, will contribute to a better understanding of the IMERG dataset and it will also open the doors to future studies with hydrological applications over the region.
This article is organized as follows:
Section 2 will describe the data, methods and the area of study. In
Section 3 results will be presented through three sub-sections that analyze the IMERG data with different time scales of the precipitation. To complement the evaluation study, IMERG is analyzed as a function of the elevation given the location of the automatic meteorological stations. The discussion and conclusions are presented in
Section 4 and
Section 5 respectively.
4. Discussion
From results found in this research, it can be said that the IMERG generally captures the trends of the average precipitation observed for all time scales analyzed (hourly, daily and seasonal). However, for the daily precipitation cycle, a 2-h lag in terms of the peak time was observed. Tang et al. [
24] found a similar result but with a more severe lag between 2 and 5 h for six sub-regions of China. These lags have been associated to the use of geo-infrared satellites in the estimation of the precipitation [
25].
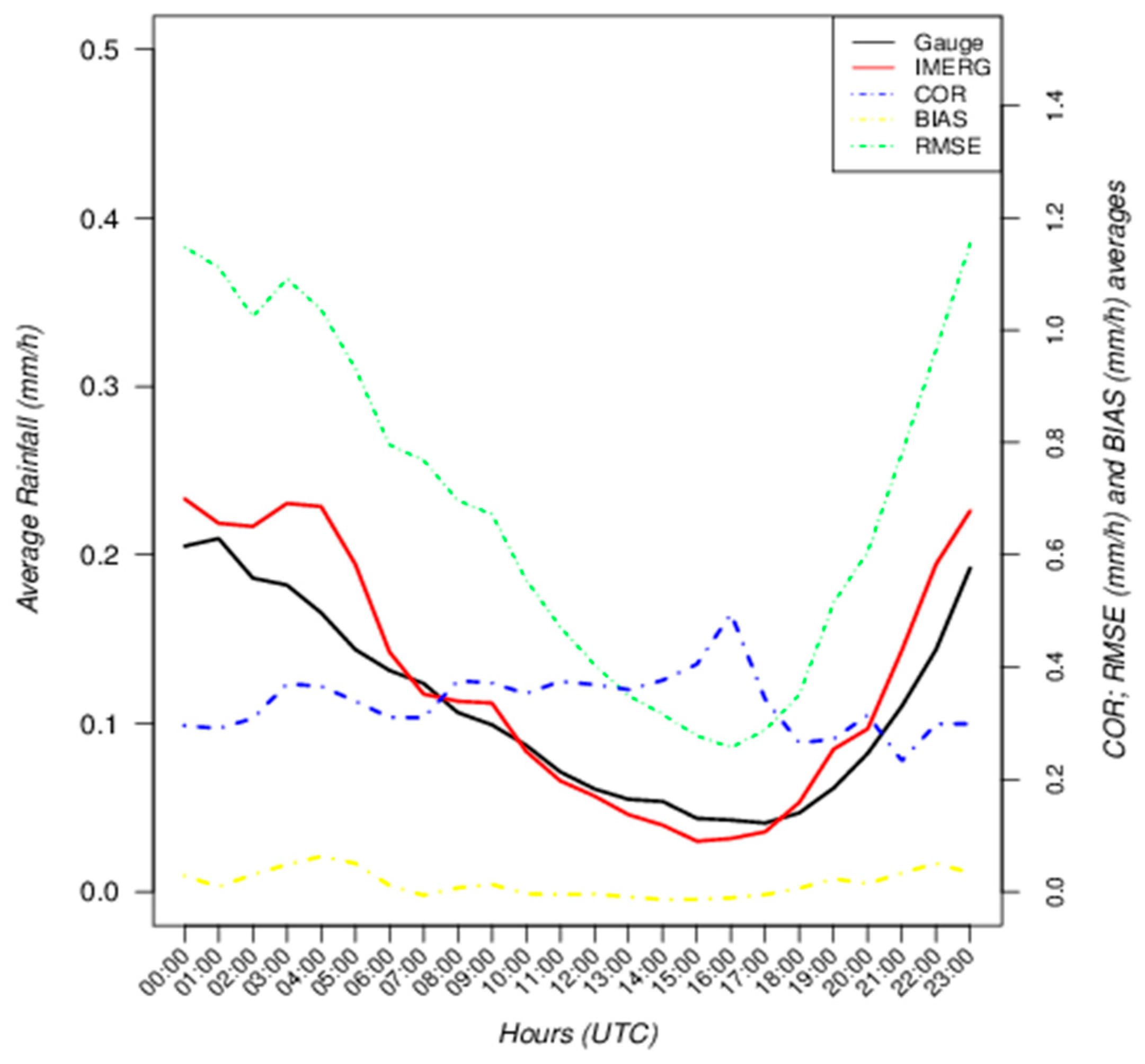
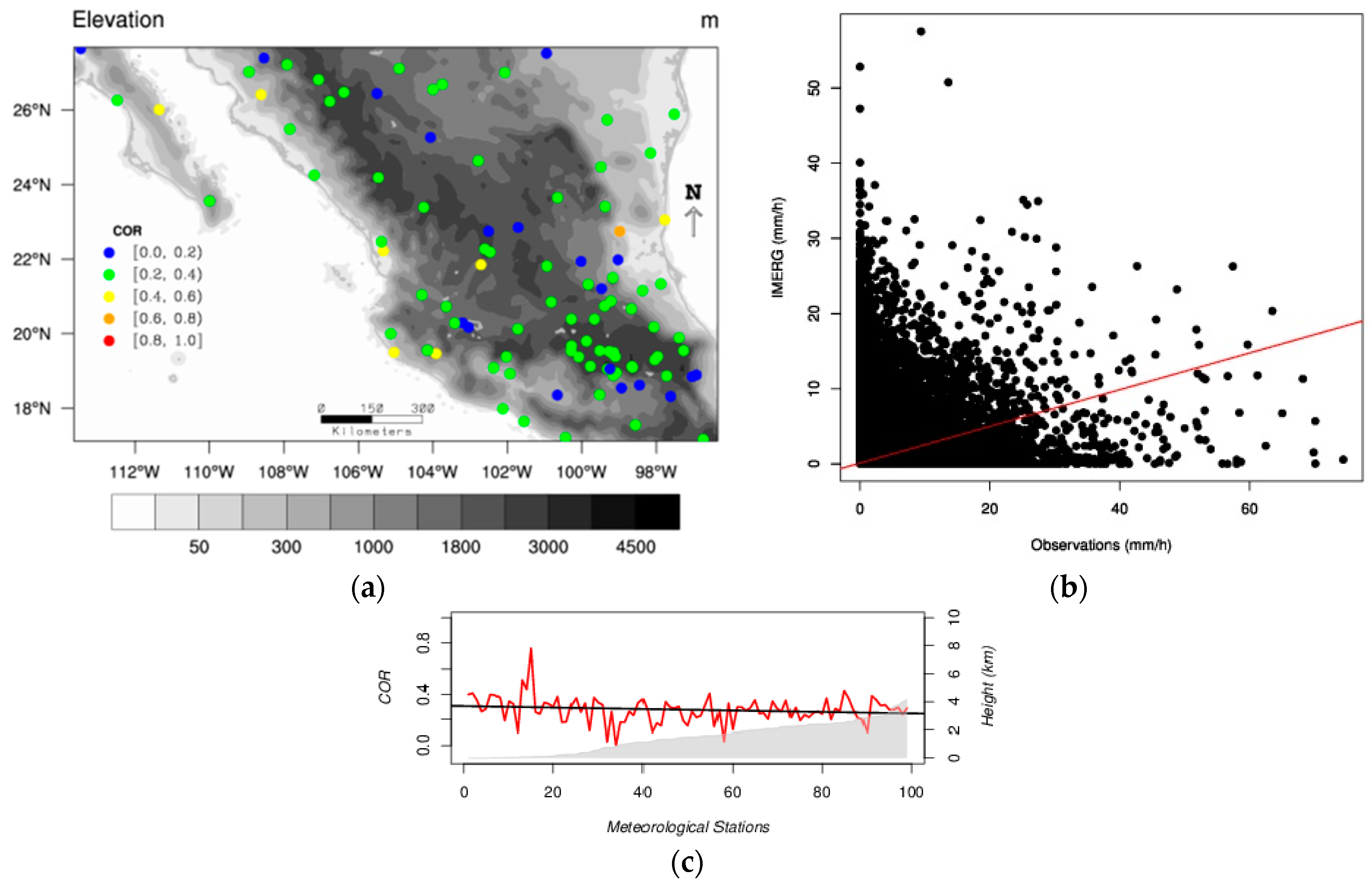
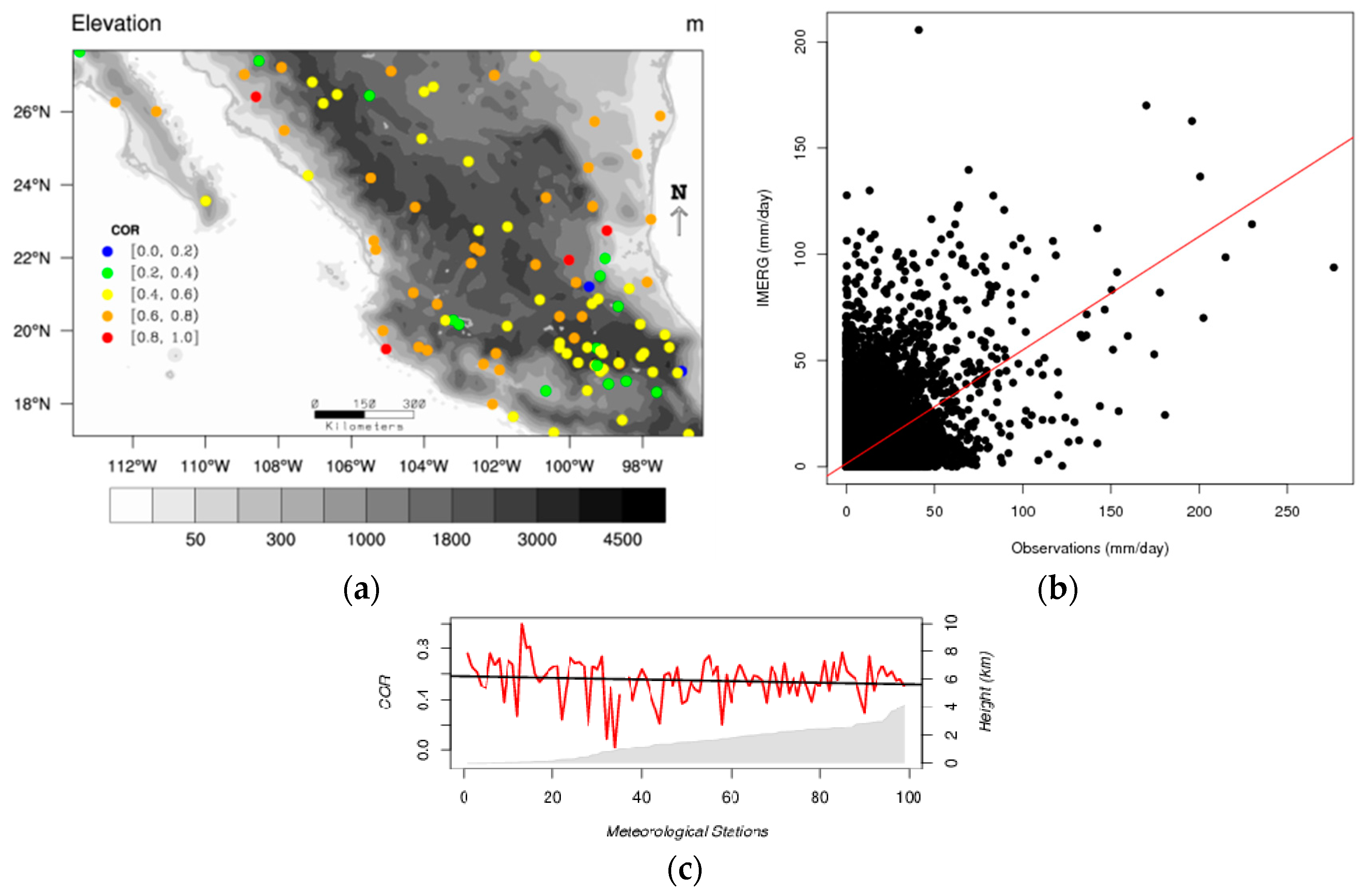
Hourly correlation values of approximately 0.35 (see
Figure 2) have been reported previously [
4]. It can also be expected that these values get higher as the temporal scale increases [
6]. Therefore, correlation results found for the daily (
Figure 6) and seasonal (
Table 4) analysis are in agreement with the later.
Statistical biases suggest that IMERG tends to overestimate average gauge data for small amounts of precipitation. The study of biases in the satellite-based precipitation products is challenging. Among the many studies that have been conducted, the results vary depending on the study region and the precipitation time scale. For example, Sharifi et al. [
3] found that IMERG generally underestimated rain gauges, but their analysis only included cases with observed precipitation. Ma et al. [
4] found overall positive biases over the Tibetan Plateau region using a three-hourly time scale. In addition, it was also observed that the probability for the IMERG to overestimate gauge data decreases with the meteorological station altitude for the hourly and daily precipitation data. Bharti and Singh [
20] found that the TRMM precipitation product overestimated rainfall on elevation ranges less than 3000 m but severely underestimated precipitation over higher elevations in the Himalayan region. The relation existing between all satellite precipitation products and the orography is undeniable [
4,
20,
26]. However, in this study this relationship becomes more evident for the daily than for the hourly precipitation.
The differences in biases between regions might be due to the randomly selected number of gauges used for bias correction in satellite products and/or due to the spatial resolution of the satellite-based precipitation estimates [
3]. Another source for error in precipitation biases among regions is the types of typical clouds that differ from one area to the other. It has been said [
27] that the precipitation produced by shallow orographic systems can be underestimated by microwave radiometer algorithms. Also, the presence of dense, cold cirrus clouds often leads to overestimation of rainfall [
28]. Therefore, the variability and complexity of the Mexican orography is enough for the IMERG precipitation product to be conditioned by all error sources previously mentioned. On both shores of the country, there are low elevation stations with moist advection coming from the oceans. Inwards of the country, close to the coasts, the presence of high mountainous systems and high plains in the center of the country can be observed in
Figure 1b. Therefore, the humidity is forced to rise due to orography, and deep cumulonimbus clouds are formed mainly in summer time, windward of the mountain systems spreading large areas of dense cirrus. This regional situation might easily lead to overestimation of precipitation. Also, one source of precipitation over the high plains in Mexico is from the shallow cumulus clouds that most often form during the dry season. However, during summertime, large convective systems may form during night-time hours leading to the overestimation of precipitation by IMERG.
On the other hand, the analysis of the extreme precipitation events showed a different behavior of the IMERG precipitation estimates. Both hourly and daily cumulative precipitations from IMERG underestimate rain gauge extreme events by more than 60 and 40% of the mean rain gauges respectively. It may seem contradictory that the probability for IMERG to overestimate the hourly precipitation (see
Figure 2) increases during night-time hours when there is more probability for precipitation to occur. However, this result is representative of the mean values of the hourly precipitation for which the mode of the precipitation (0 mm) plays an important role. It could also be related with the bilinear interpolation method applied to the IMERG gridded data in order to obtain point values comparable to rain gauges. The extreme events analysis in this study took into consideration the 98th to 99.99th percentiles of the hourly and daily precipitation distributions. The hourly analysis confirms that 98% of the rain gauge data used in this study registered precipitation amounts below 1.2 mm/h and that a large portion of these data may consist of no-precipitation (0 mm/h) cases. Precipitation above the value of 1.2 mm/h are more likely to be underestimated by IMERG. The latter is in agreement with Sharifi et al. [
3]. Daily analysis precipitation above 27 mm/day were found to be underestimated by IMERG. However,
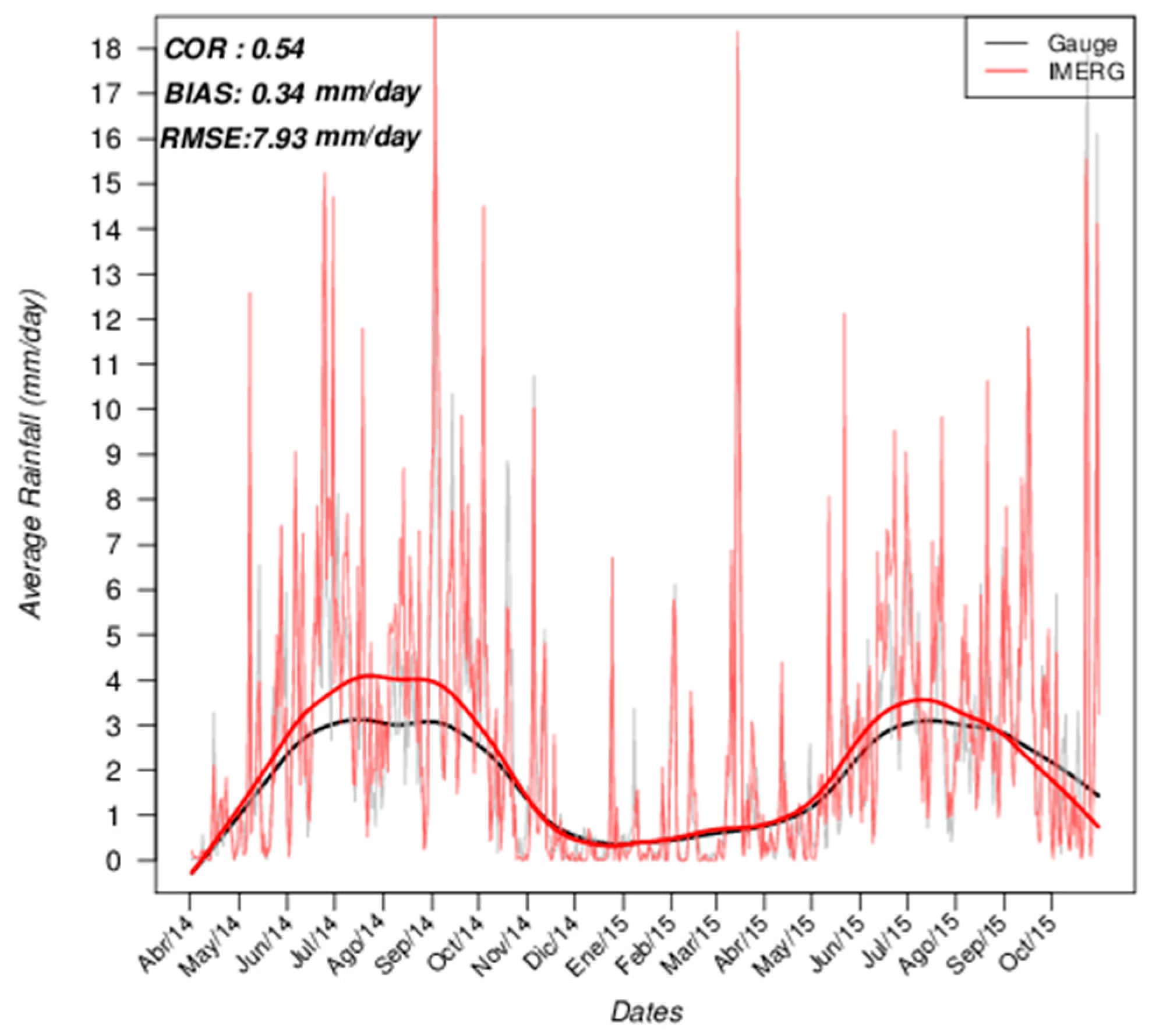
Figure 8b suggests that this underestimation could still be produced for precipitation intensities below this threshold.
In addition, the daily analysis of precipitation intensities and the elevation shows no relation (
Figure 7). IMERG shows no significant deviation when daily precipitations are lower than 10 mm/day; the same as in Ma et al. [
4]. However, when precipitations are higher or extreme, deviations of IMERG can be over 15 mm/day per station regardless of its altitude. In
Figure 6, it can be noted that IMERG deviates during particular days when precipitation might be considered extreme or intense.
RMSE values in
Figure 2,
Table 2,
Table 3 and
Table 4 also confirm that the larger the amounts of precipitation, the larger the deviations. Gaona et al. [
5] consistently stated that IMERG overestimates rainfall intensities higher than 9 mm/day and attributed it to the fact that extreme rainfall events evolve rapidly, reducing the probability of the direct detection of such events given the approximate 3-h sampling of the whole GPM satellite constellation.
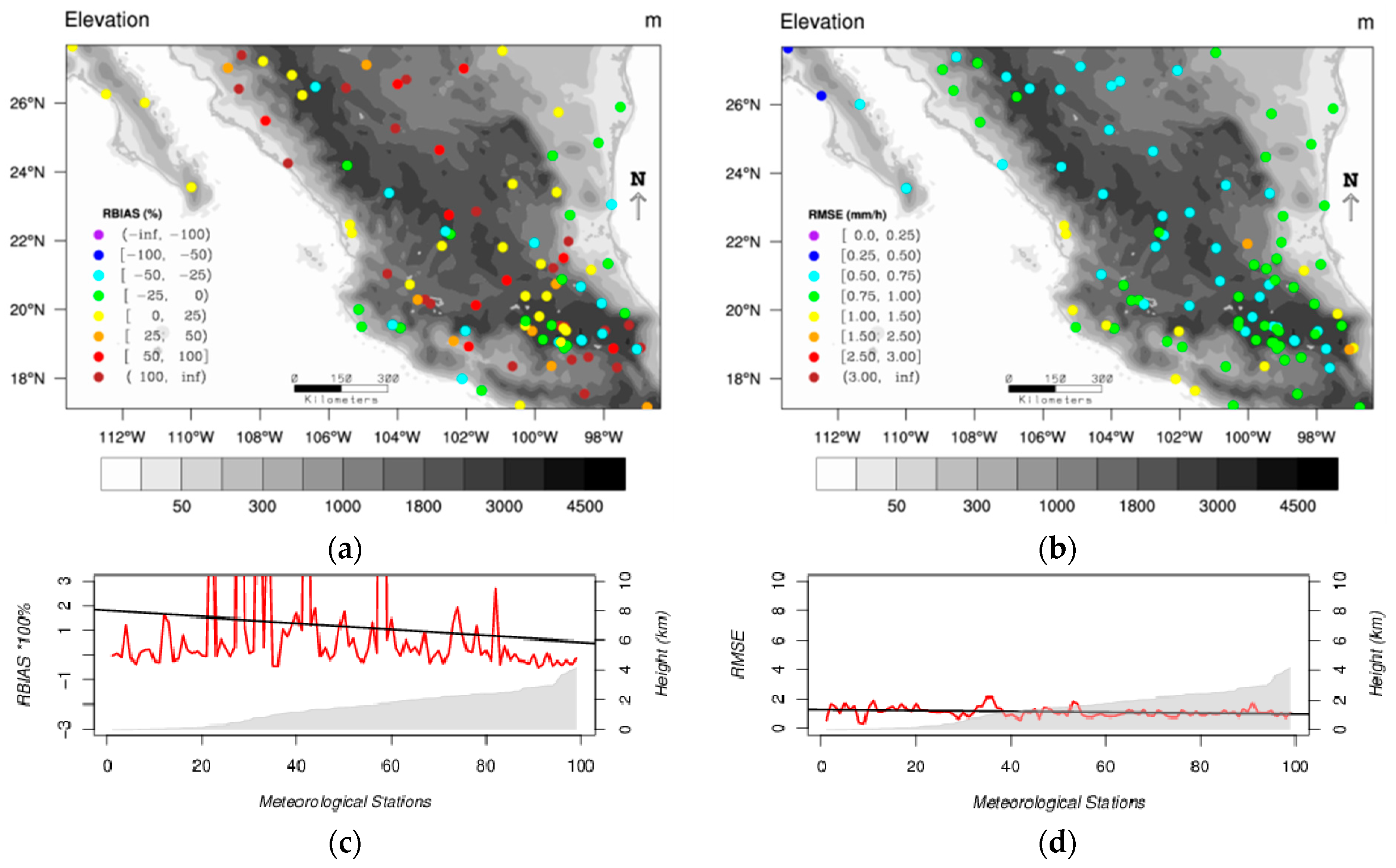
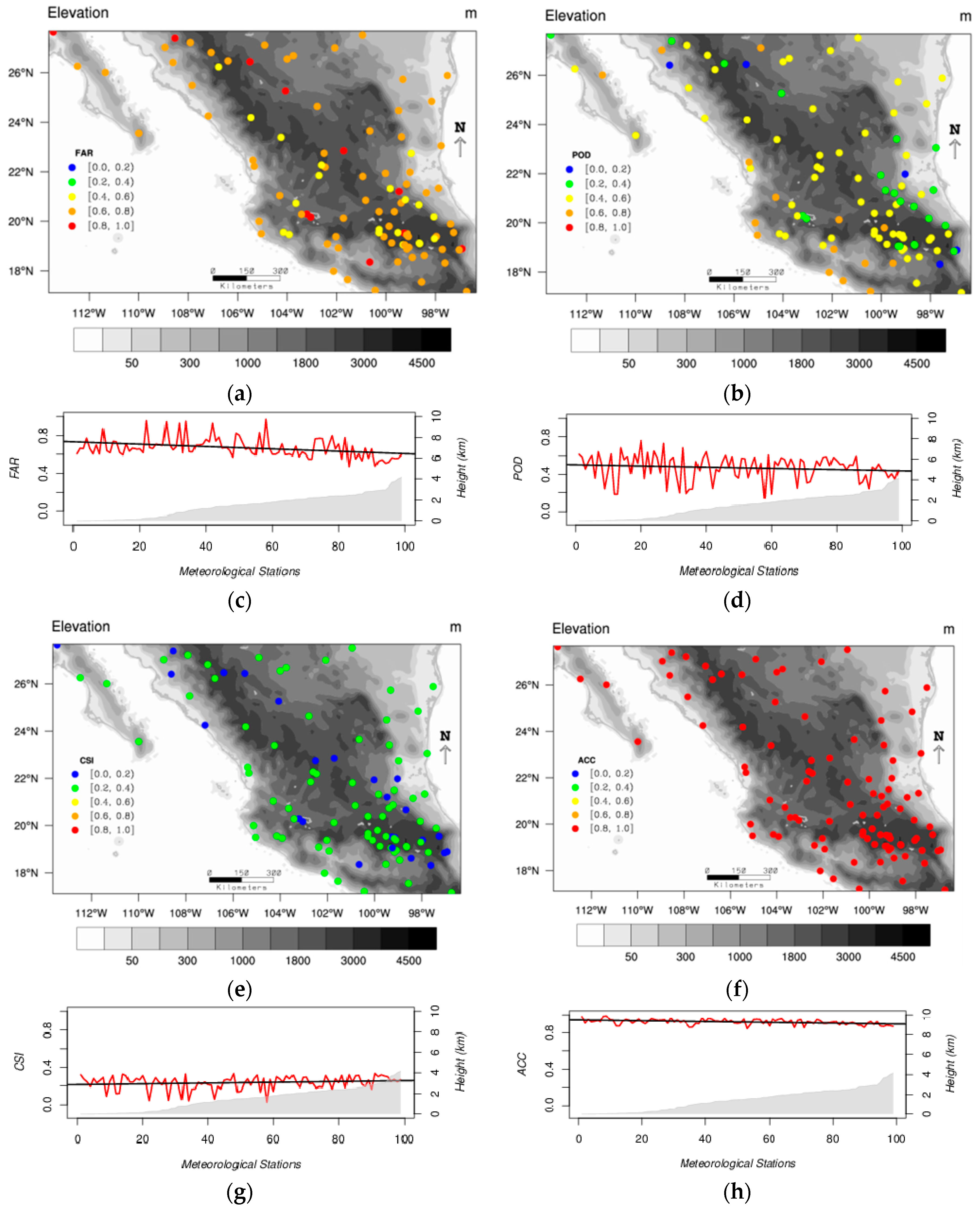
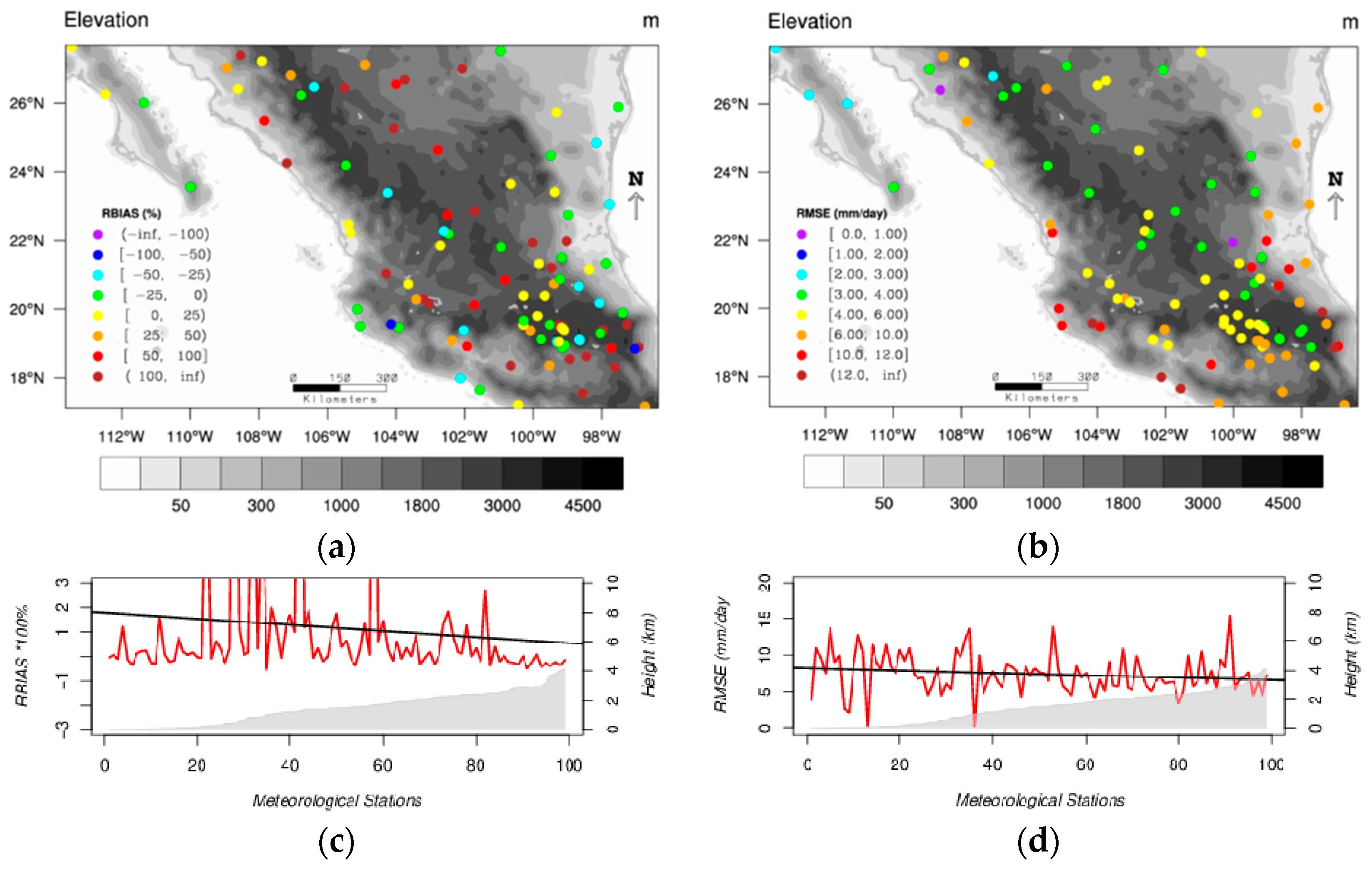
Furthermore, the accuracy of the IMERG estimates also improves with the time scale. Spatial values of
RBIAS (
Figure 4a and
Figure 9a) and
RMSE (
Figure 4b and
Figure 9b) are also better for the daily analysis but the trend for IMERG to overestimate mean values is maintained. Also, the
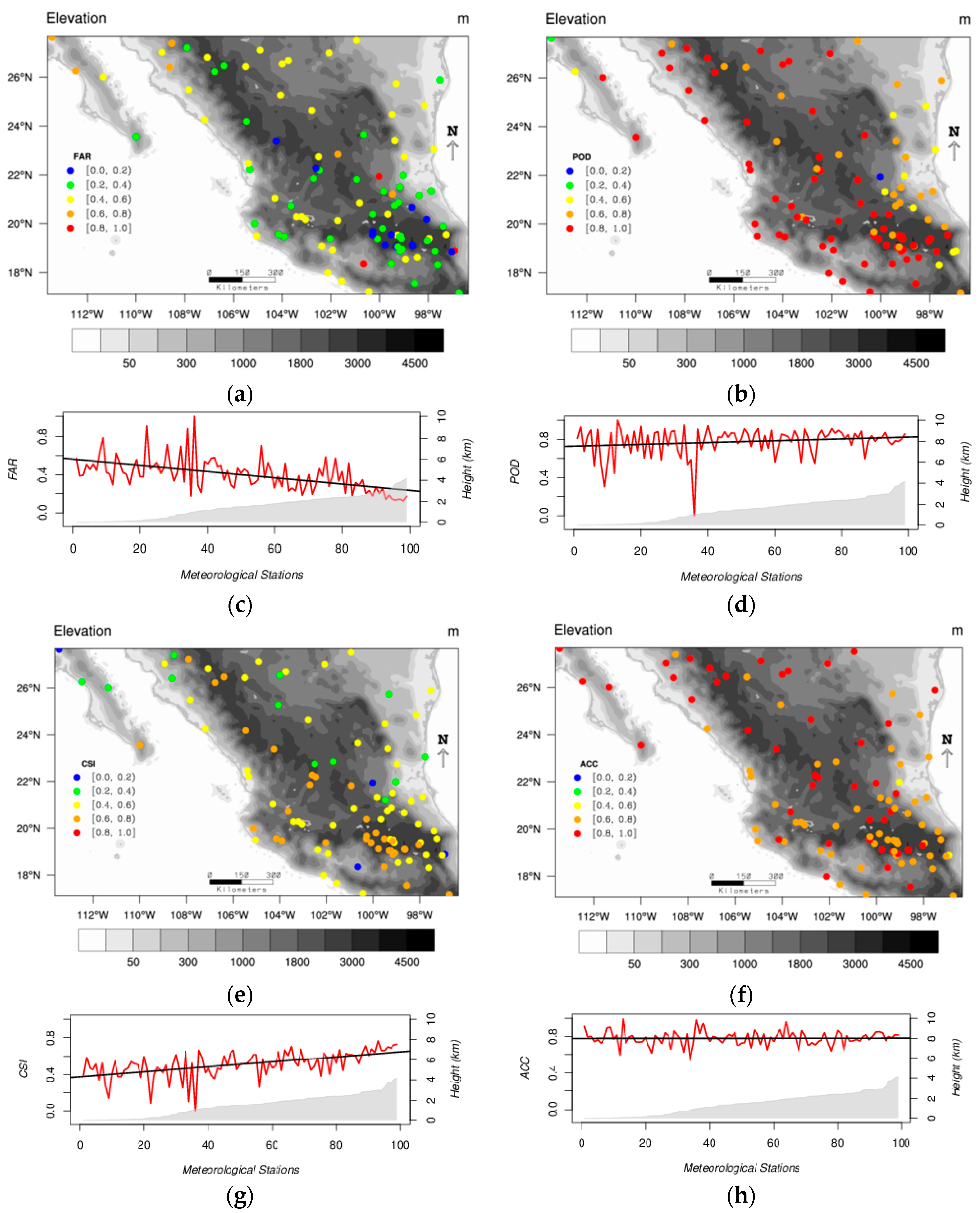
POD and
CSI values are closer to 1 for the daily precipitation than for the hourly precipitation. However, the
ACC is better for the hourly than for the daily precipitation. This happens because
ACC is sensible to the amount of no-precipitation events which decreases with the time scale. In addition, results found here show that the
FAR decreases with increasing altitude while the
POD and the
CSI increase with increasing altitude (
Figure 5 and
Figure 9). The mean values of these categorical and the other continuous statistics are consistent with earlier studies [
3,
4].
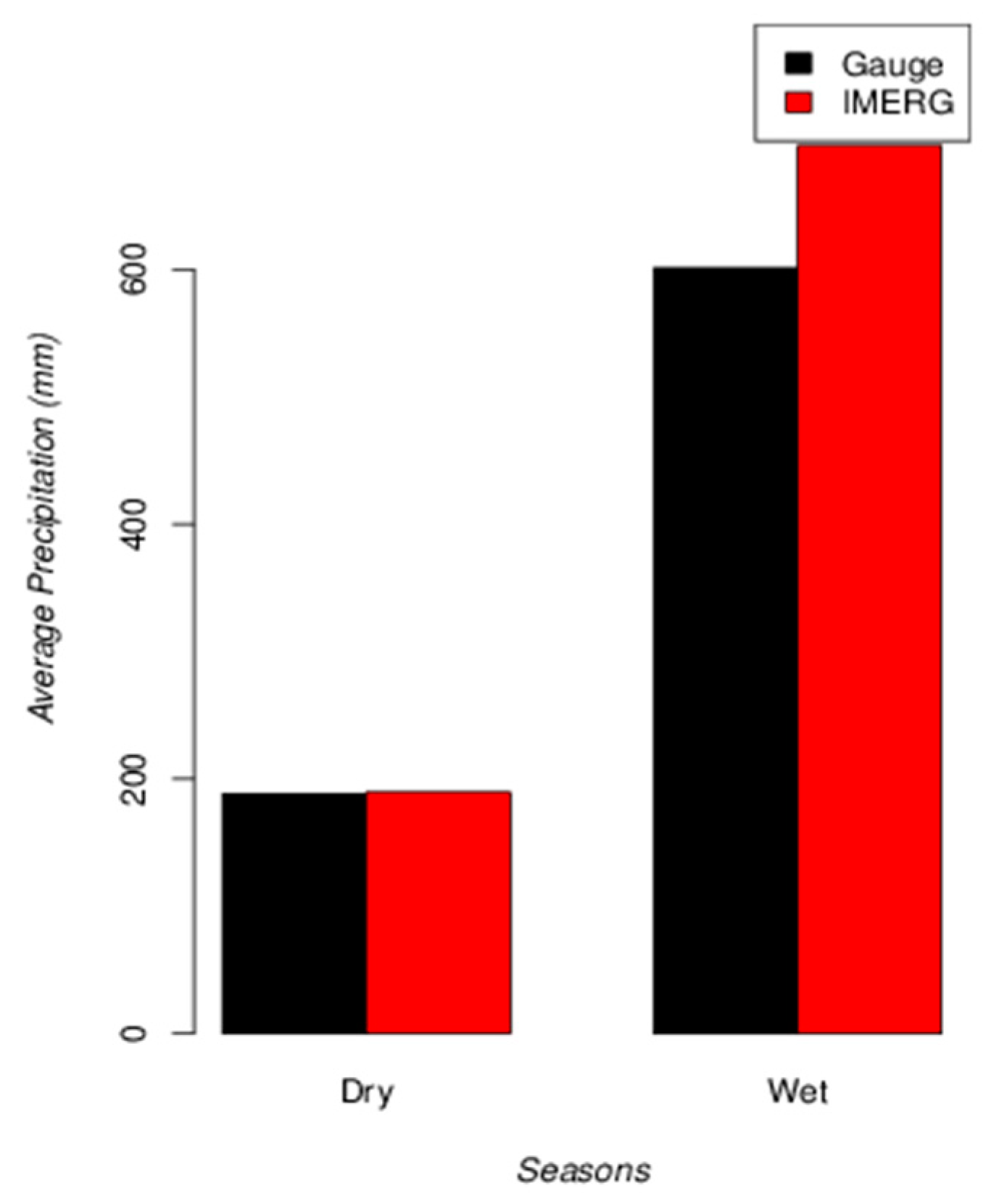
Finally, the seasonal analysis showed good results, particularly for the dry season. For the wet season, positive deviations of IMERG may be expected.
5. Conclusions
In this research, the IMERG precipitation data have been evaluated over a Mexican region during the period between 1 April 2014 and 31 October 2015. This assessment has been made for different time scales (hourly, daily and seasonal) using precipitation gauges, as the reference data, from 99 automatic meteorological stations. The main conclusions of the study are summarized below:
The IMERG hourly precipitation product is able to reproduce the diurnal cycle. A small agreement was found with respect to hourly rain gauges with an average COR of about 0.35. IMERG tends to overestimate mean hourly values with relatively large deviations. For extreme values of hourly precipitation, its performance is quite poor with a COR of 0.18 and a trend to underestimate rain gauges by 61%.
IMERG shows better performance at the daily time scale resolution, with a COR of 0.54. An overall bias of 0.34 mm/day over mean daily rain gauges was found. For extreme precipitation events the COR (0.36) also improved with respect to the hourly analysis and a trend to underestimate daily rain gauges by 46% was observed. In addition, the deviations of IMERG are minima for precipitation intensities below 10 mm/day and they increase for precipitation rates over this value.
The seasonal analysis showed good results, particularly for the dry season with a COR of 0.69 and a positive bias of 1.11 mm. For the wet season a COR of 0.51 and positive bias of 96.36 mm was found. For this season, very large deviations of IMERG may be expected.
In terms of categorical statistics, the FAR, POD and CSI values were found to improve from hourly to daily time scales. The FAR decreased from 0.7 to 0.4 approximately; the POD values increased from 0.5 to 0.8 in average and CSI values increased from 0.2 to 0.6. These statistics were also found to improve with topography. However, in this study this relationship becomes more evident for the daily than for the hourly precipitation. While FAR values decreased with elevation, POD and CSI values behaved the other way around.
According to this research, the IMERG hourly precipitation product should be used with caution over Mexico. Users should be aware of its poor performance, especially during heavy rainfall events. The daily and seasonal IMERG precipitation estimates are more reliable. Our findings differ from the suggestions of Tan et al. [
6] that IMERG would perform poorer over mountainous areas. This study found that IMERG tends to improve precipitation detection and to decrease magnitude errors over the higher terrain elevations of Mexico. This result could be highly influenced by a non-homogeneous distribution of gauges along the elevation ranges. In order to support our finding, it is advised to include all (daily and synoptic) rain gauges available in the country, which were disregarded in this study due to their relatively low time resolution. However insufficient and sparse these rain gauges are over the region, IMERG is not quite yet an accurate substitute for real observations.
This research is, to our knowledge, the first study to evaluate IMERG precipitation data over Mexico and provides a reference for IMERG users on its performance. Consequently, it opens a window for future works regarding spatial verification of modeled precipitation and hydrological applications over the region. The results presented in this article are of great value to Mexico where the current precipitation data sources are still insufficient. Also, this study complements previous research and helps in improving our understanding of the IMERG database.