A Machine Learning Method for Co-Registration and Individual Tree Matching of Forest Inventory and Airborne Laser Scanning Data
Abstract
:1. Introduction
1.1. Positional Accuracy of Forest Inventory Data
1.2. Co-Registration and Individual Tree Matching
1.2.1. Automated Co-Registration of Field Survey Plots
1.2.2. Automated Individual Tree Matching
1.2.3. Related Methods for Co-Registration and Tree Matching
1.2.4. Research Gap
1.3. Objective
2. Data and Materials
2.1. Inventory Data
2.2. ALS Data
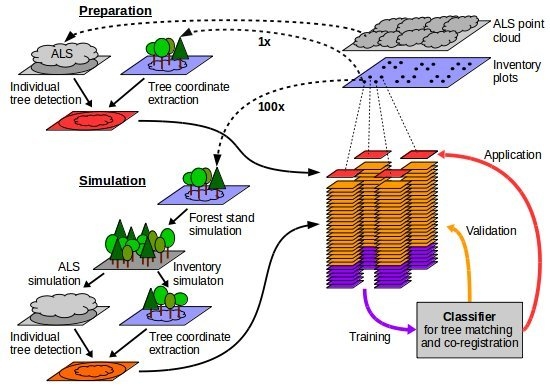
3. Methods
3.1. Definitions
3.2. Digital Terrain Model (DTM) Generation
3.3. Individual Tree Detection
3.4. Simulation
3.4.1. Forest Stand Simulation
3.4.2. Synthetic Inventory Data
3.4.3. Synthetic Tree Detections
3.5. Simulation Quality Assessment
3.6. Classification-Based Tree Matching and Co-Registration
- Classification-based estimation of the matching probability for each potential tree pair.
- Co-registration of the survey trees based on the estimated matching probabilities.
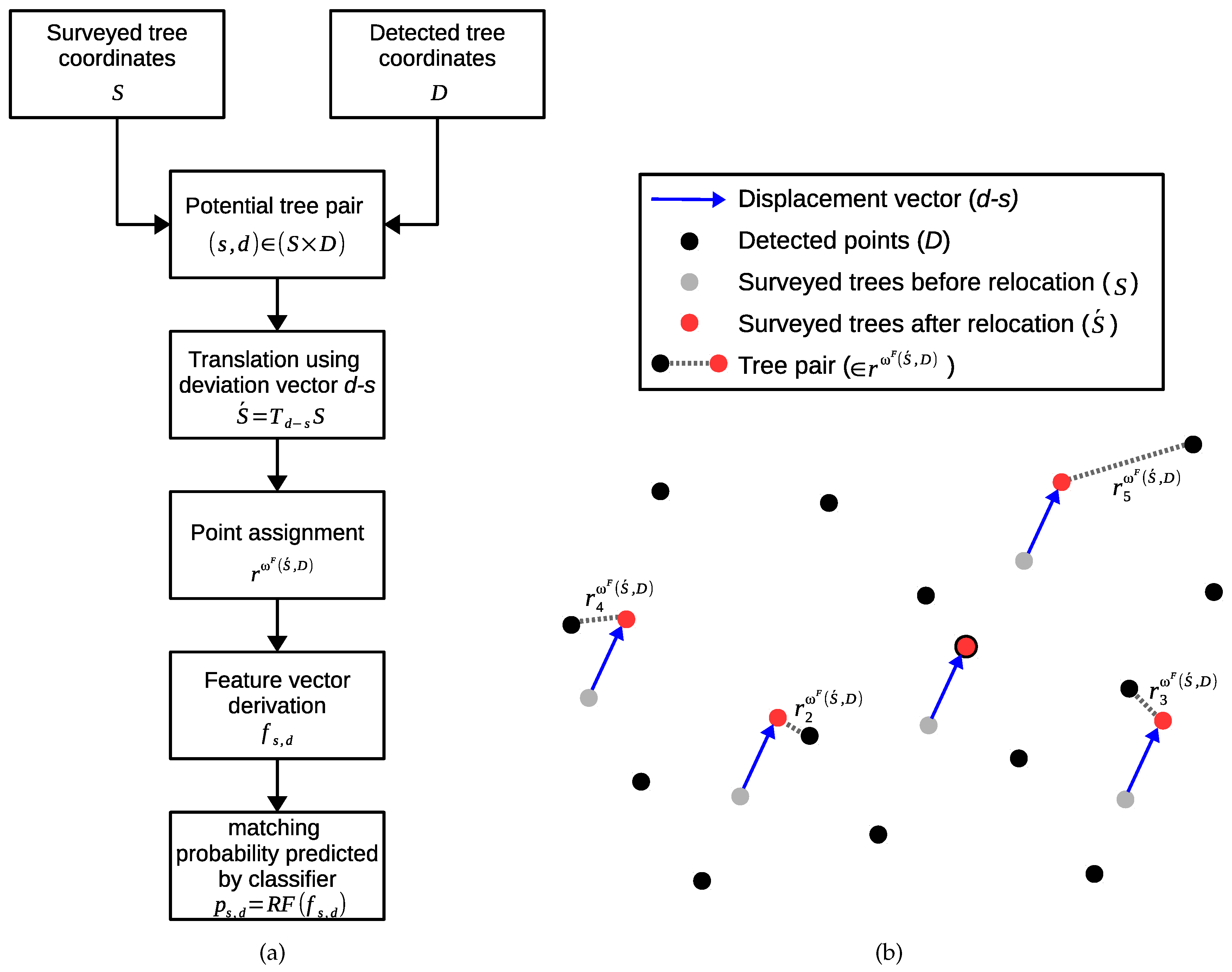
3.6.1. Point Assignment Process
3.6.2. Distance-Based Tree Assignment
3.6.3. Classification-Based Tree Matching
3.6.4. Co-Registration Method
3.7. Application
3.8. Methods for Accuracy Assessment
3.9. Methods for the Evaluation of Feature Importance and Effects
4. Results and Discussion
4.1. Quality of the Synthetic Datasets
4.2. Accuracy Assessment
4.3. Feature Importance and Effects
4.4. Effect of the Data Characteristics on the Co-Registration Results
4.5. Method Performance
4.6. Limitations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ALS | Airborne Laser Scanning |
| BWI | German National Forest Inventory |
| CHM | Canopy Height Model |
| DBH | Diameter at Breast Height |
| DTM | Digital Terrain Model |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| NND | Nearest-Neighbor Distance |
| RMSE | Root Mean Squared Error |
| RANSAC | RANdom SAmple Consensus |
| WMS | Web Map Service |
References
- Cao, L.; Coops, N.C.; Innes, J.L.; Dai, J.; Ruan, H.; She, G. Tree species classification in subtropical forests using small-footprint full-waveform LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 39–51. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation—Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A Benchmark of Lidar-Based Single Tree Detection Methods Using Heterogeneous Forest Data from the Alpine Space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
- Dorigo, W.; Hollaus, M.; Wagner, W.; Schadauer, K. An application-oriented automated approach for co-registration of forest inventory and airborne laser scanning data. Int. J. Remote Sens. 2010, 31, 1133–1153. [Google Scholar] [CrossRef]
- Baltsavias, E.P. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Frazer, G.; Magnussen, S.; Wulder, M.; Niemann, K. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; Alho, P. Advances in Forest Inventory Using Airborne Laser Scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
- Koenig, K.; Höfle, B. Full-Waveform Airborne Laser Scanning in Vegetation Studies—A Review of Point Cloud and Waveform Features for Tree Species Classification. Forests 2016, 7, 198. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkanen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2011, 85, 27–40. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating tree detection and segmentation routines on very high resolution UAV LiDAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Hoppus, M.; Lister, A. The status of accurately locating forest inventory and analysis plots using the Global Positioning System. In Proceedings of the Seventh Annual Forest Inventory and Analysis Symposium, Portland, ME, USA, 3–6 October 2007. [Google Scholar]
- Wing, M.G.; Eklund, A.; John, S.; Richard, K. Horizontal measurement performance of five mapping-grade global positioning system receiver configurations in several forested settings. West. J. Appl. For. 2008, 23, 166–171. [Google Scholar]
- Andersen, H.E.; Clarkin, T.; Winterberger, K.; Strunk, J. An accuracy assessment of positions obtained using survey-and recreational-grade global positioning system receivers across a range of forest conditions within the Tanana Valley of interior Alaska. West. J. Appl. For. 2009, 24, 128–136. [Google Scholar]
- Valbuena, R.; Mauro, F.; Rodriguez-Solano, R.; Manzanera, J. Accuracy and precision of GPS receivers under forest canopies in a mountainous environment. Span. J. Agric. Res. 2010, 8, 1047–1057. [Google Scholar] [CrossRef]
- Monnet, J.M.; Mermin, É. Cross-correlation of diameter measures for the co-registration of forest inventory plots with airborne laser scanning data. Forests 2014, 5, 2307–2326. [Google Scholar] [CrossRef]
- Luoma, V.; Saarinen, N.; Wulder, M.; White, J.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Assessing Precision in Conventional Field Measurements of Individual Tree Attributes. Forests 2017, 8, 38. [Google Scholar] [CrossRef]
- Hollaus, M.; Wagner, W.; Maier, B.; Schadauer, K. Airborne laser scanning of forest stem volume in a mountainous environment. Sensors 2007, 7, 1559–1577. [Google Scholar] [CrossRef]
- Olofsson, K.; Lindberg, E.; Holmgren, J. A method for linking field-surveyed and aerial-detected single trees using cross correlation of position images and the optimization of weighted tree list graphs. In Proceedings of the SilviLaser 2008—8th International Conference on LiDAR Applications in Forest Assessment and Inventory, Edinburgh, UK, 17–19 September 2008. [Google Scholar]
- Mongus, D.; Žalik, B. An efficient approach to 3D single tree-crown delineation in LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Sattler, T.; Leibe, B.; Kobbelt, L. Fast image-based localization using direct 2d-to-3d matching. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Bienert, A.; Pech, K.; Maas, H.G. Verfahren zur Registrierung von Laserscannerdaten in Waldbeständen— Methods for registration laser scanner point clouds in forest stands. Schweiz. Z. Forstwes. 2011, 162, 178–185. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE 1991, 14, 239–256. [Google Scholar] [CrossRef]
- Rangarajan, A.; Chui, H.; Bookstein, F.L. The softassign procrustes matching algorithm. In Information Processing in Medical Imaging; Duncan, J., Gindi, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; pp. 29–42. [Google Scholar]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed]
- Golyanik, V.; Ali, S.A.; Stricker, D. Gravitational Approach for Point Set Registration. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Castellani, U.; Cristani, M.; Fantoni, S.; Murino, V. Sparse points matching by combining 3D mesh saliency with statistical descriptors. Comput. Graph. Forum 2008, 27, 643–652. [Google Scholar] [CrossRef]
- Donoser, M.; Schmalstieg, D. Discriminative feature-to-point matching in image-based localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Bitterlich, W. The Relascope Idea. Relative Measurements in Forestry; Commonwealth Agricultural Bureaux: Farnham Royal, UK, 1984. [Google Scholar]
- Kublin, E. Einheitliche Beschreibung der Schaftform—Methoden und Programme -BDATPro. A Uniform Description of Stem Profiles—Methods and Programs -BDATPro. Forstwiss. Cent. 2003, 122, 183–200. [Google Scholar] [CrossRef]
- Kublin, E.; Breidenbach, J.; Kändler, G. A flexible stem taper and volume prediction method based on mixed-effects B-spline regression. Eur. J. For. Res. 2013, 132, 983–997. [Google Scholar] [CrossRef]
- Copernicus. Available online: http://image.discomap.eea.europa.eu/arcgis/services/GioLandPublic/HRL_Forest_Cover_Type_2012/MapServer/WMSServer?request=GetCapabilities&service=WMS (accessed on 12 April 2017).
- Langley, R.B. Dilution of precision. GPS World 1999, 10, 52–59. [Google Scholar]
- RIEGL. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/10_DataSheet_Q560_20-09-2010_01.pdf (accessed on 27 September 2016).
- Hansen, J.; Nagel, J. Waldwachstumskundliche Softwaresysteme auf Basis von TreeGrOSS-Anwendung und Theoretische Grundlagen; Niedersächsische Staats-und Universitätsbibliothek: Göttingen, Germany, 2014. [Google Scholar]
- Nagel, J. Waldwachstumssimulation mit dem Java Software Paket TreeGross—Neuerungen, Erweiterungsmöglichkeiten und Qualitätsmanagement. In Proceedings of the 20th annual DVFFA Conference, Freiburg, Germany, 22–24 September 2016. [Google Scholar]
- Bundesministerium für Ernährung, Landwirtschaft und Verbraucherschutz. Aufnahmeanweisung für die Dritte Bundeswaldinventur (BWI3): (2011–2012); BMELV: Bonn, Germany, 2011; Volume 2.
- Pretzsch, H. Modellierung des Waldwachstums; Parey: Berlin, Germany, 2001. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Scikit Learn. Available online: http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html (accessed on 11 November 2016).

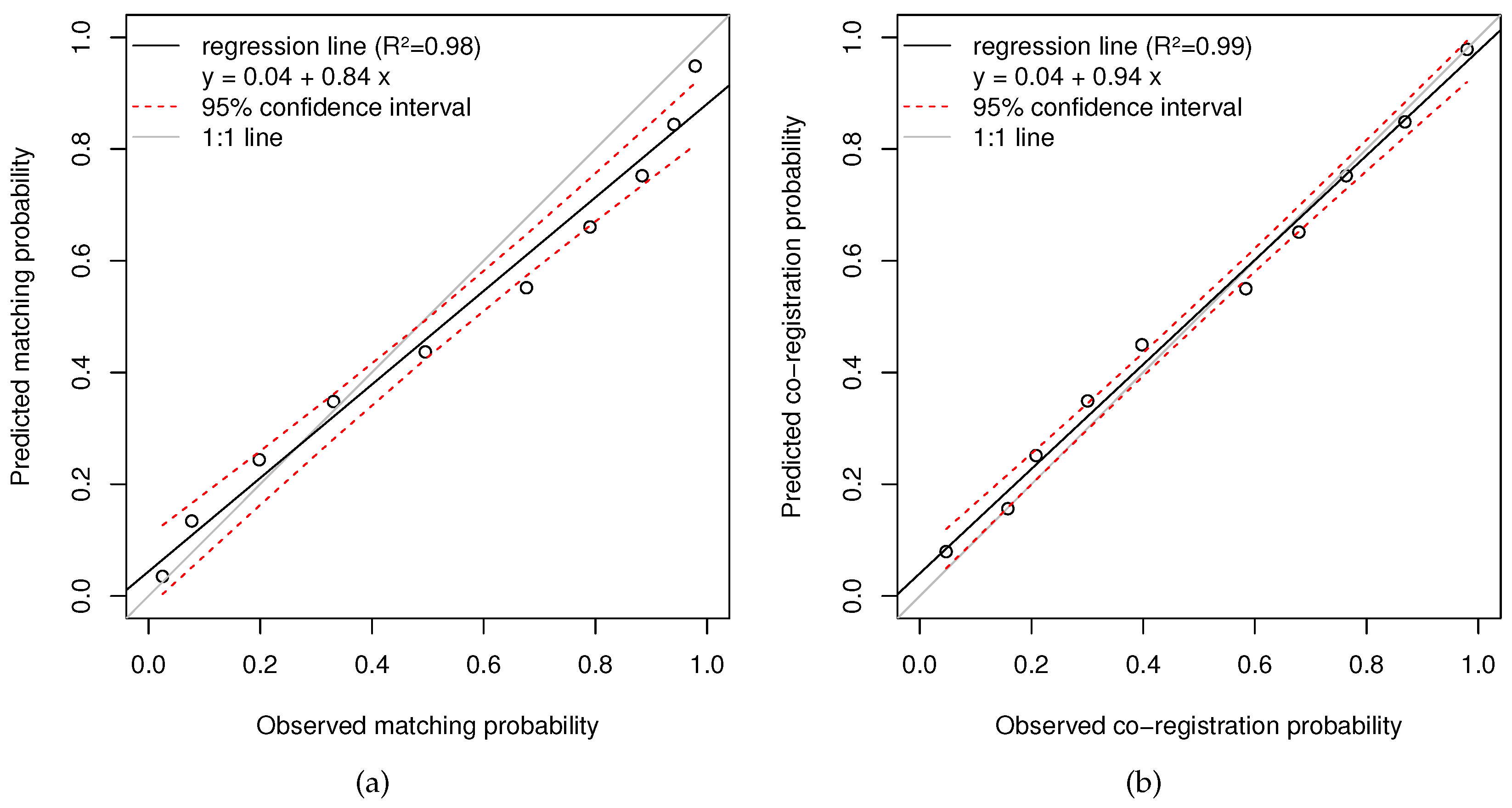
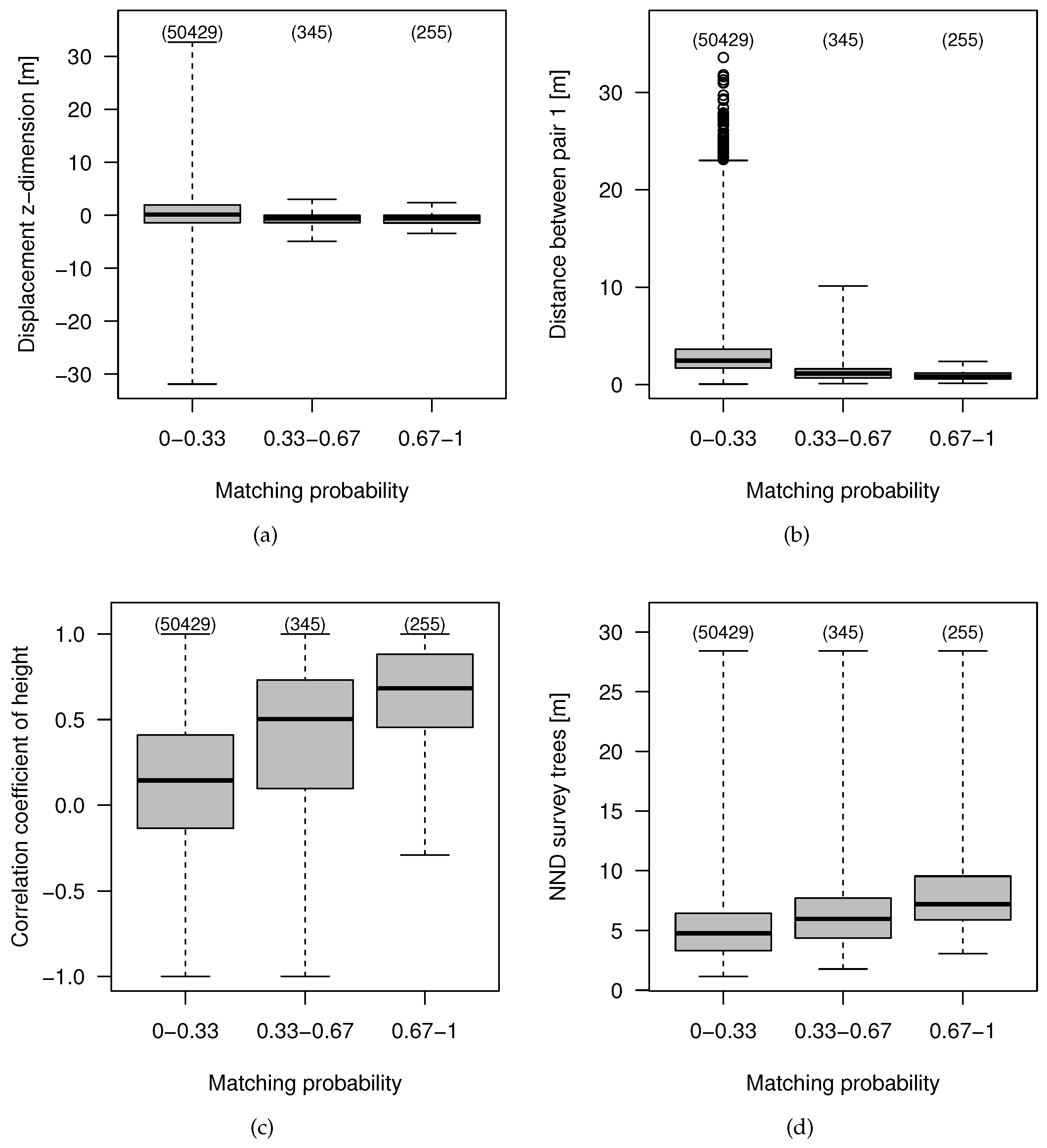
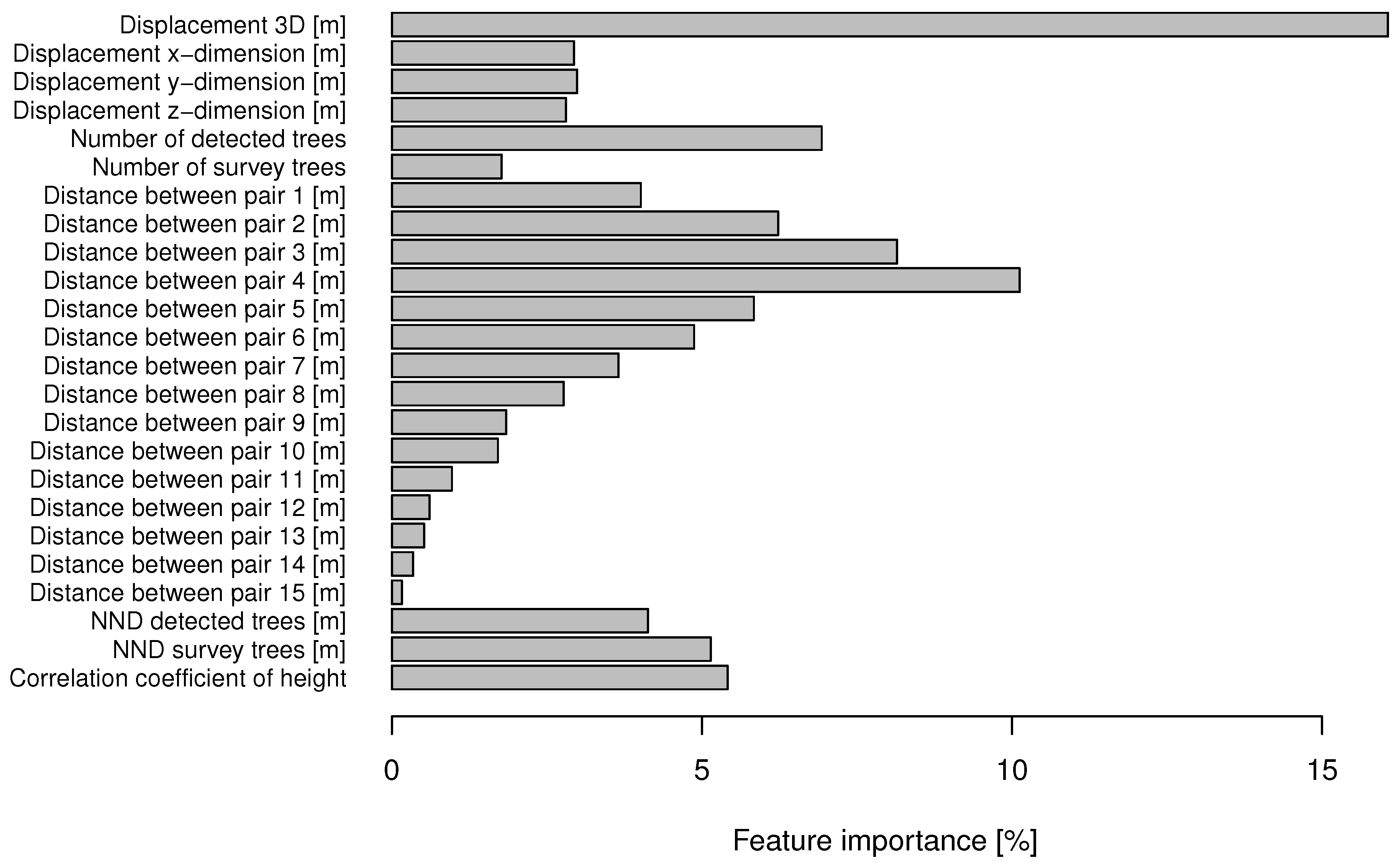
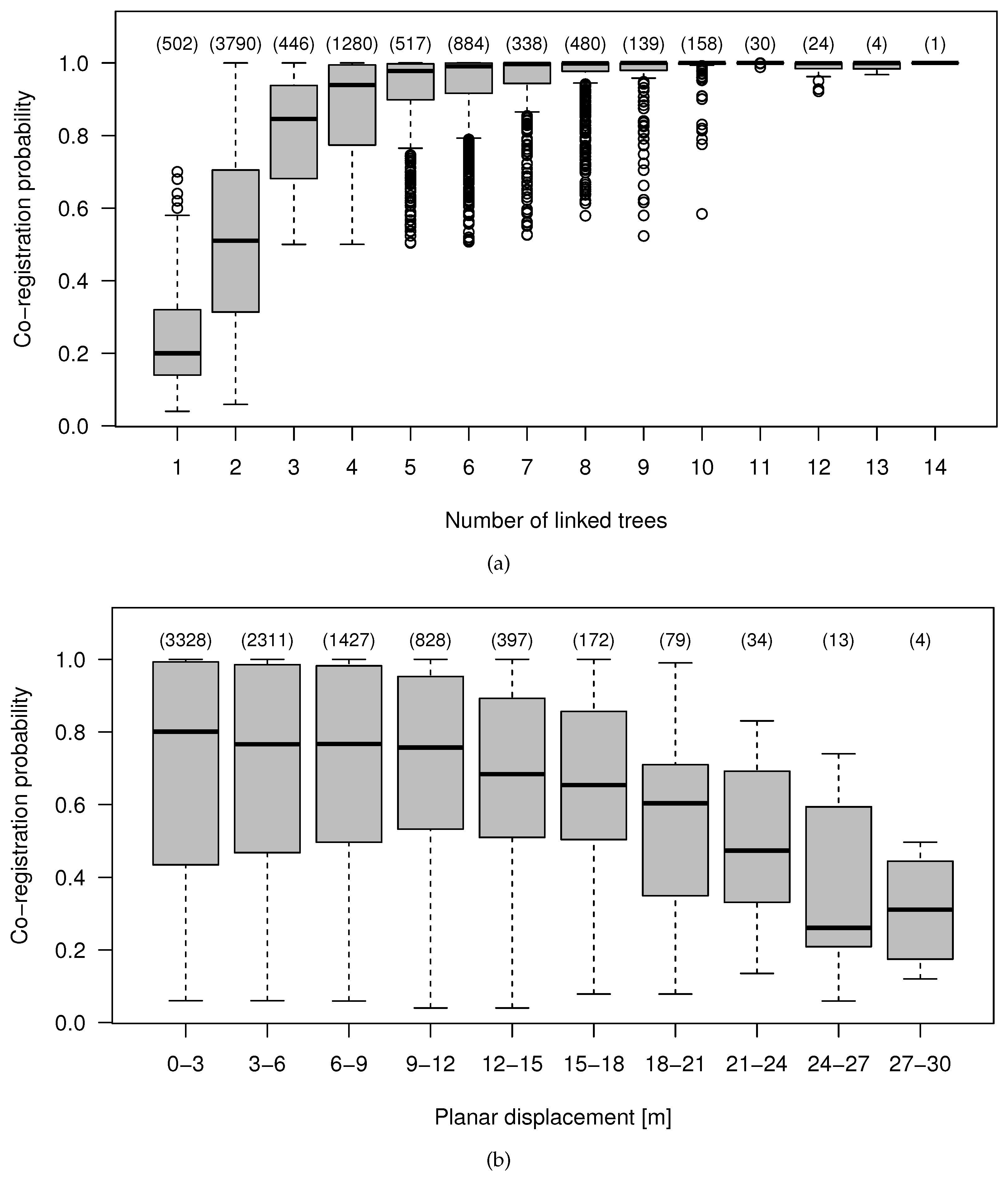

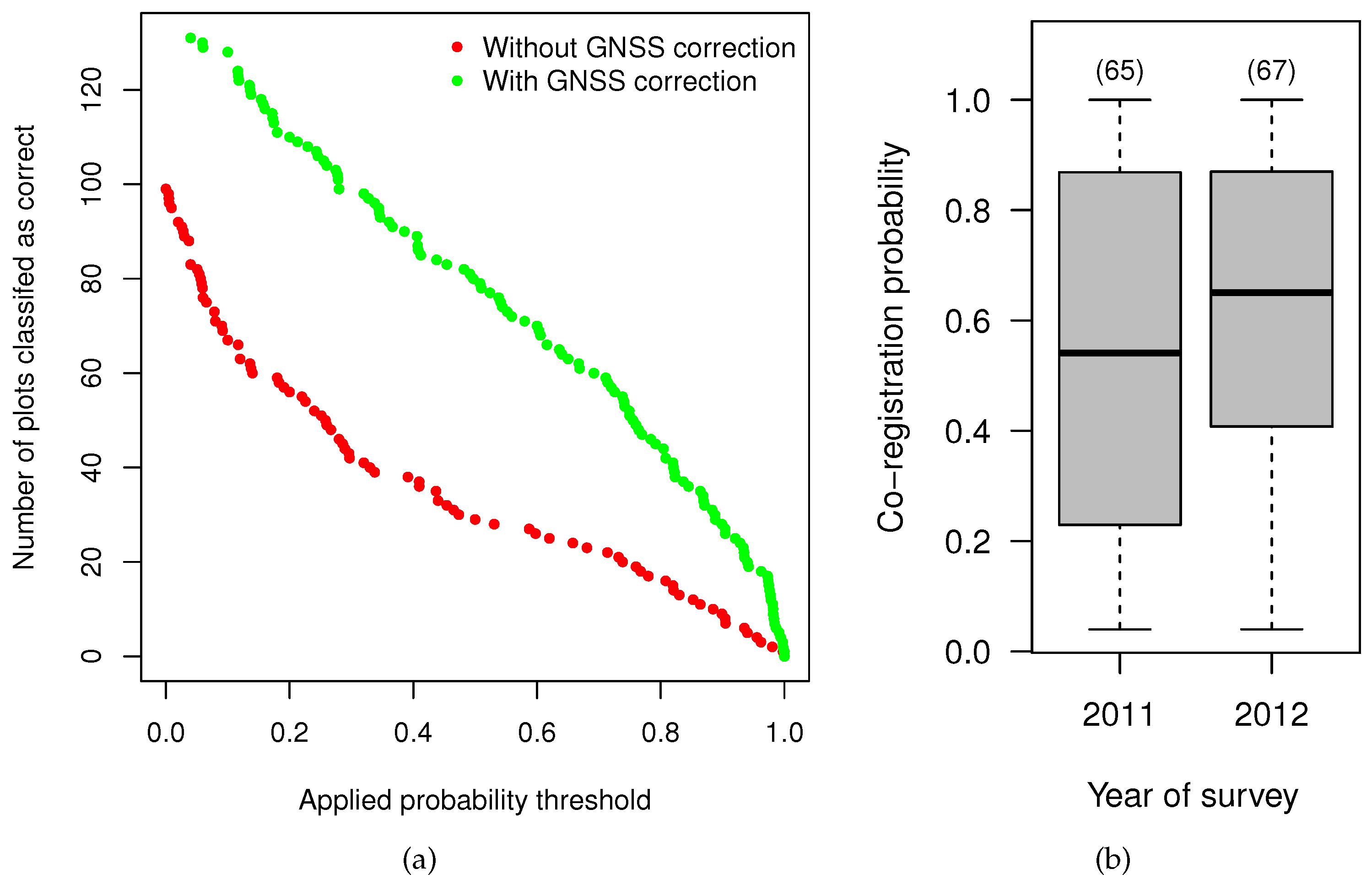
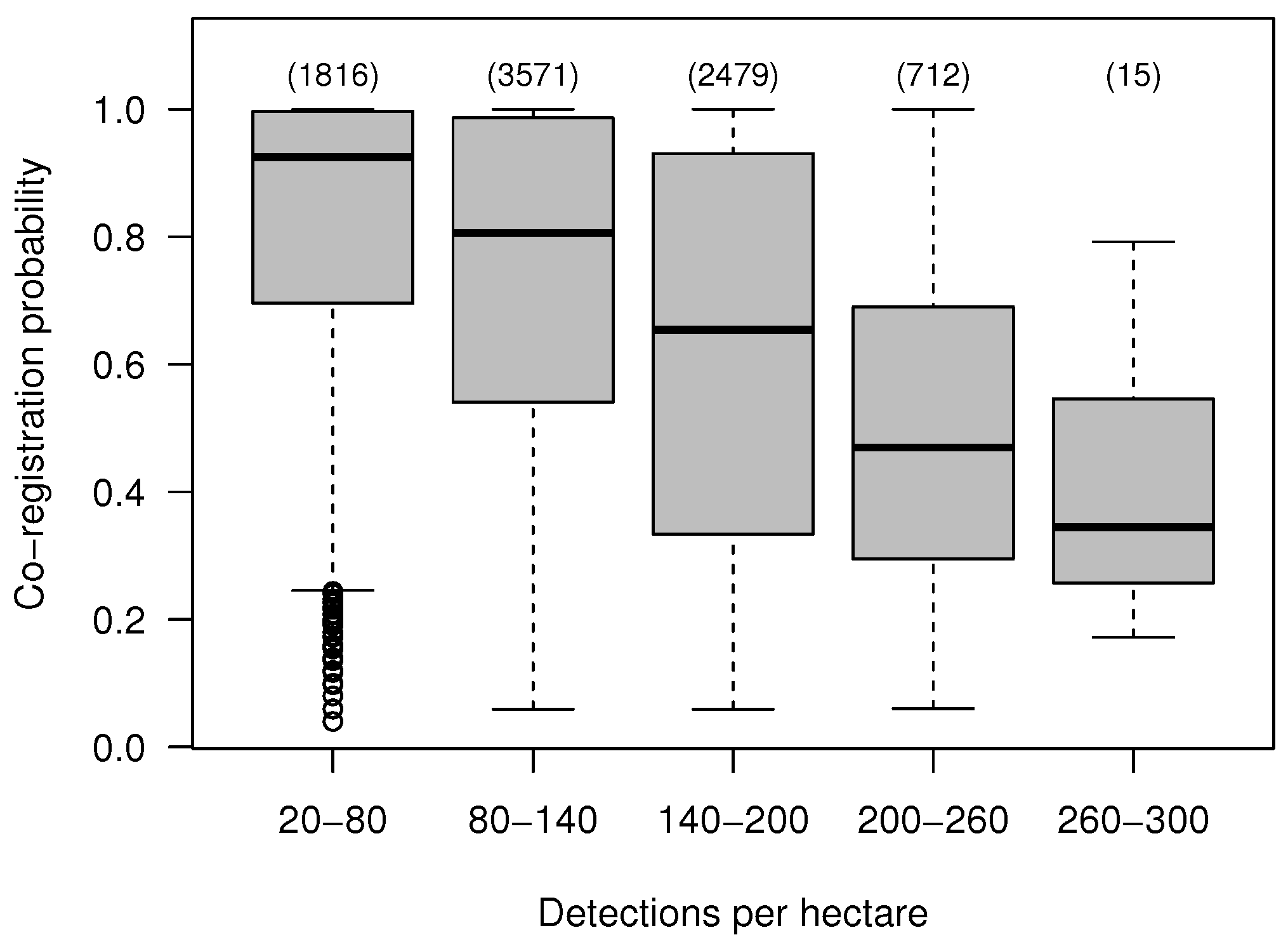
| Attribute | Minimum | 1th Quartile | Median | Mean | 3th Quartile | Maximum |
|---|---|---|---|---|---|---|
| DBH (cm) | 7.0 | 23.8 | 36.2 | 36.73 | 47.9 | 112.5 |
| Tree height (m) | 5.2 | 19.8 | 24.8 | 24.65 | 29.9 | 50.6 |
| Stems per hectare | 48 | 202 | 412 | 742.4 | 839 | 6014 |
| Number of recorded trees per plot | 2 | 5 | 7 | 7.6 | 10 | 16 |
| Maximum radius (m) | 0.3 | 3.0 | 5.25 | 5.9 | 8.1 | 20.8 |
| Limiting circle radius (m) | 2.6 | 8.9 | 12.6 | 12.4 | 15.7 | 28.1 |
| HDOP | 0.8 | 1.1 | 1.2 | 1.32 | 1.5 | 3.2 |
| Species | c | b |
|---|---|---|
| Quercus petraea (sessile oak) | 0.50 | 0.50 |
| Fagus silvatica (European beech) | 0.40 | 0.33 |
| Abies alba (European fir) | 0.50 | 0.50 |
| Alnus glutinosa (European alder) | 0.56 | 0.50 |
| Picea abies (Norway spruce) | 0.66 | 1.00 |
| Pseudotsuga menziesii (Douglas fir) | 0.66 | 1.00 |
| Pinus silvestris (Scots pine) | 0.64 | 0.50 |
| Larix decidua (European larch) | 0.80 | 0.45 |
| Attribute | Overall | On Plot Level | ||||
|---|---|---|---|---|---|---|
| Characteristic Values (Minimum, Mean, Maximum) | Two Sample Wilcoxon Test | F-Test | Pearson’s Correlation Coefficient | RMSE | Paired Wilcoxon Test | |
| Amount of Surveyed Trees | ; ; ; ; | (p = 0.66) | (p = 0.47) | 0.98 | 0.69 | (p = 0.00) |
| Amount of Detected Trees | ; ; ; ; | (p = 0.50) | (p = 0.00) | 0.64 | 15.00 | (p = 0.74) |
| Amount of Detected Trees per Survey Tree | ; ; ; ; | (p = 0.69) | (p = 0.91) | 0.83 | 3.30 | (p = 0.33) |
| Mean NND for Surveyed Trees (m) | ; ; ; ; | (p = 0.00) | (p = 0.01) | 0.81 | 1.90 | (p = 0.00) |
| Mean NND for Detected Trees (m) | ; ; ; ; | (p = 0.00) | (p = 0.00) | 0.58 | 1.36 | (p = 0.00) |
| Actual Class | Totals | Users’s Accuracy | |||
|---|---|---|---|---|---|
| Not Matching | Matching | ||||
| Predicted Class | Not Matching | 12,747 | 1663 | 14,410 | 88.5% |
| Matching | 683 | 7662 | 8345 | 91.8% | |
| Totals | 13,430 | 9325 | 22,755 | ||
| Producer’s accuracy | 94.9% | 82.2% | |||
| Actual Class | Totals | Users’s Accuracy | |||
|---|---|---|---|---|---|
| Co-Registration Failed | Co-Registration Successful | ||||
| Predicted Class | Co-Registration failed | 1731 | 595 | 2326 | 74.4% |
| Co-Registration successful | 890 | 5377 | 6267 | 85.8% | |
| Totals | 2621 | 5972 | 8593 | ||
| Producer’s accuracy | 66.0% | 90.0% | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamprecht, S.; Hill, A.; Stoffels, J.; Udelhoven, T. A Machine Learning Method for Co-Registration and Individual Tree Matching of Forest Inventory and Airborne Laser Scanning Data. Remote Sens. 2017, 9, 505. https://doi.org/10.3390/rs9050505
Lamprecht S, Hill A, Stoffels J, Udelhoven T. A Machine Learning Method for Co-Registration and Individual Tree Matching of Forest Inventory and Airborne Laser Scanning Data. Remote Sensing. 2017; 9(5):505. https://doi.org/10.3390/rs9050505
Chicago/Turabian StyleLamprecht, Sebastian, Andreas Hill, Johannes Stoffels, and Thomas Udelhoven. 2017. "A Machine Learning Method for Co-Registration and Individual Tree Matching of Forest Inventory and Airborne Laser Scanning Data" Remote Sensing 9, no. 5: 505. https://doi.org/10.3390/rs9050505