Circular Regression Applied to GNSS-R Phase Altimetry
Abstract
:1. Introduction
2. GNSS-R Altimetry Using Phase Measurement
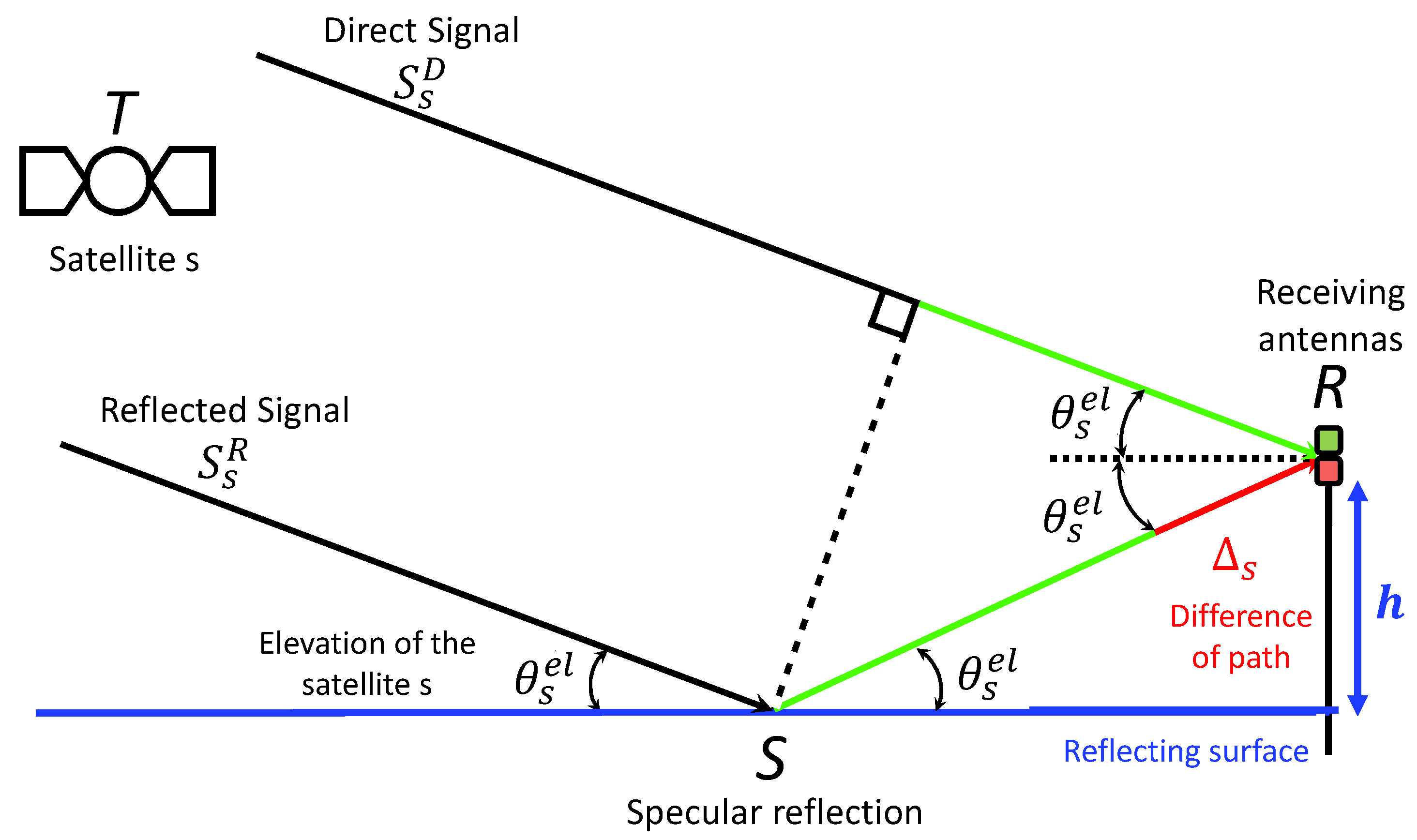
2.1. Height Retrieval Using GNSS Phase Signals
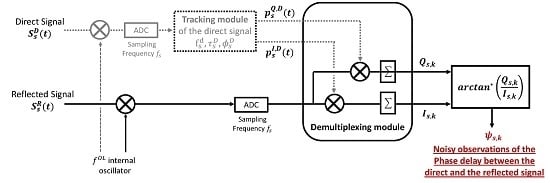
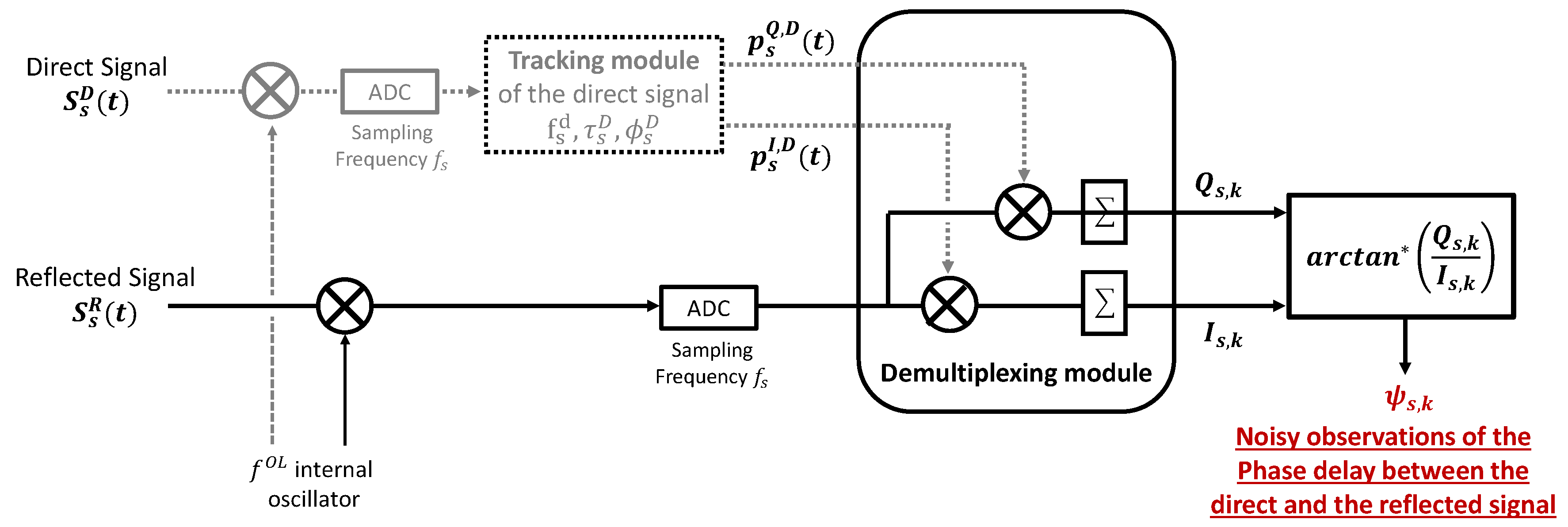
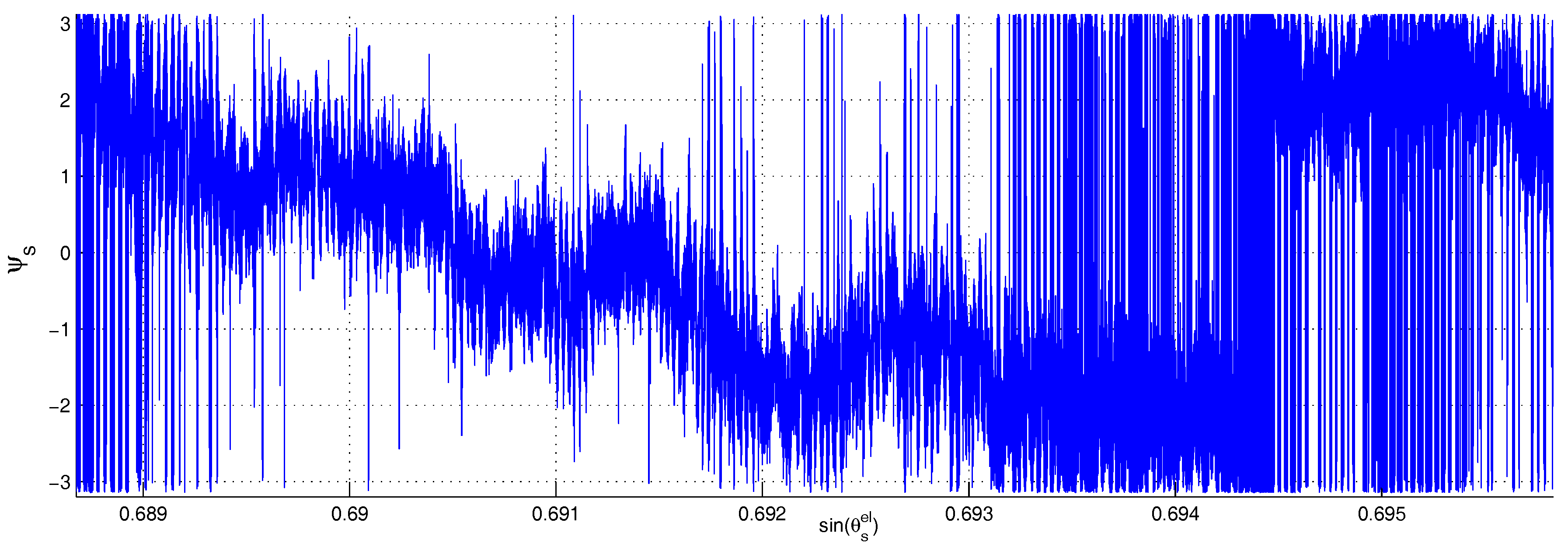
2.2. Phase Observation
3. Linear-Circular Regression Applied to GNSS-R Altimetry
3.1. Circular Model
3.2. Log-Likelihood Estimator
3.3. Initialization and Assessment
4. Experimentation
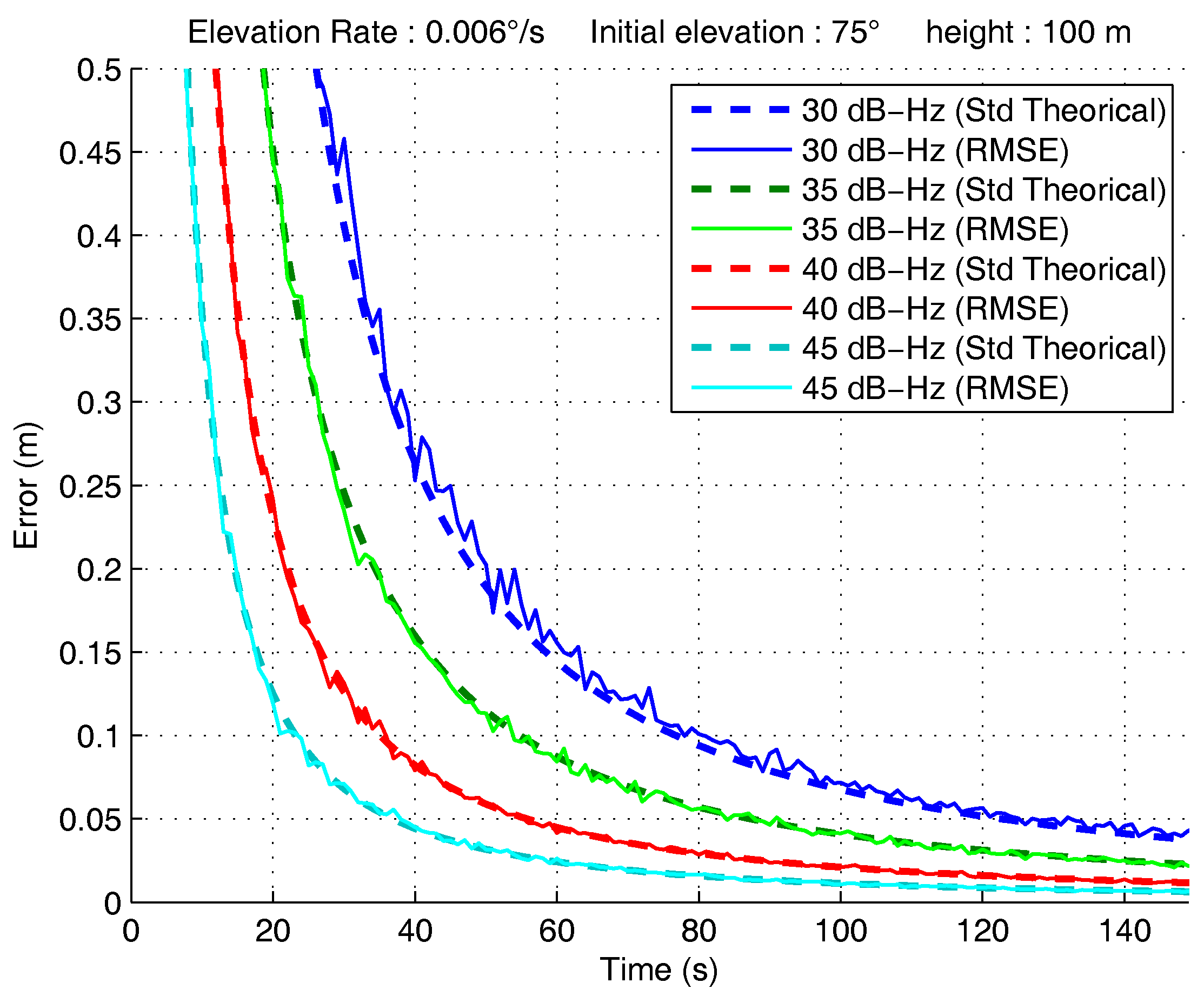
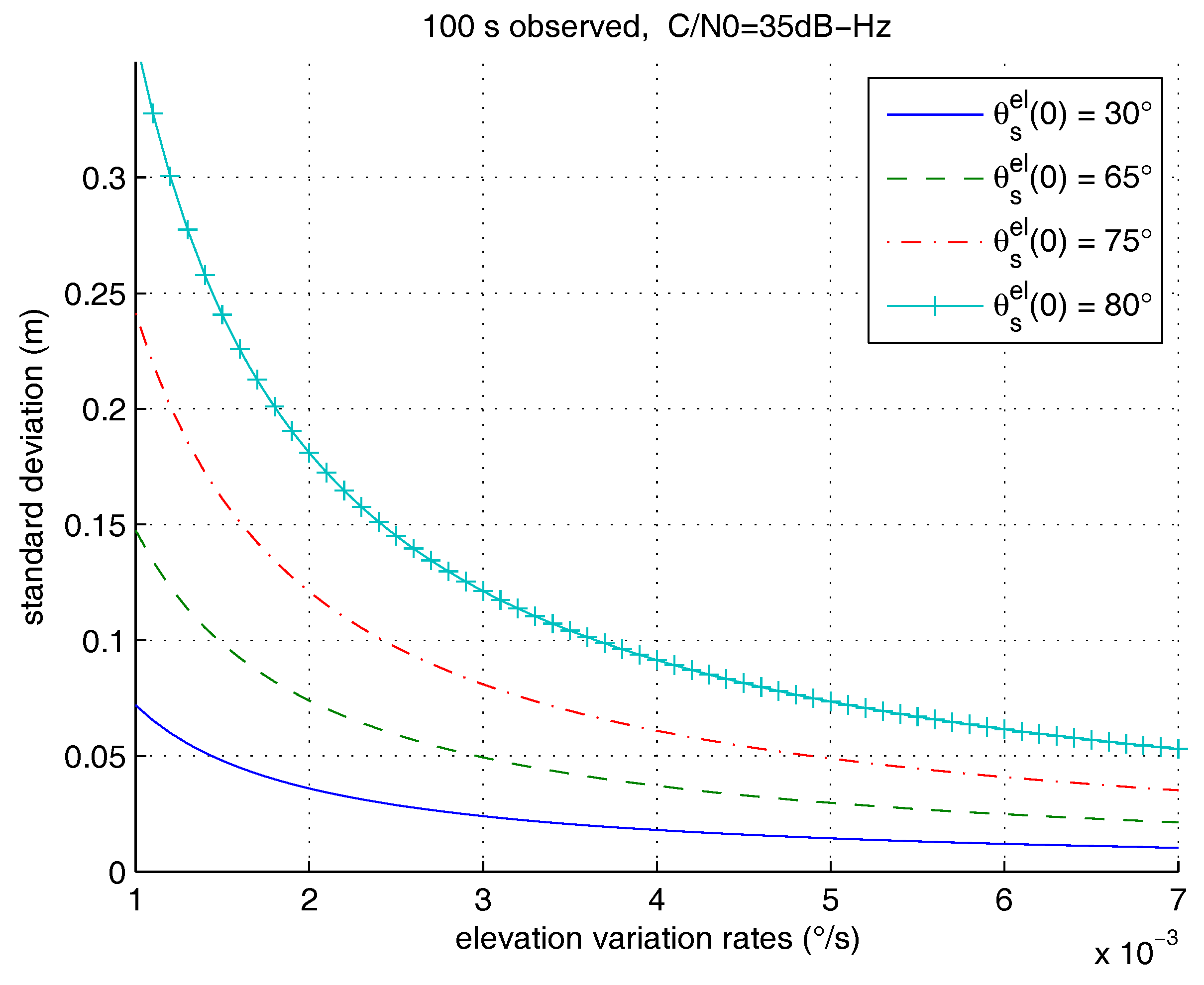
4.1. Assessment with Synthetic Data
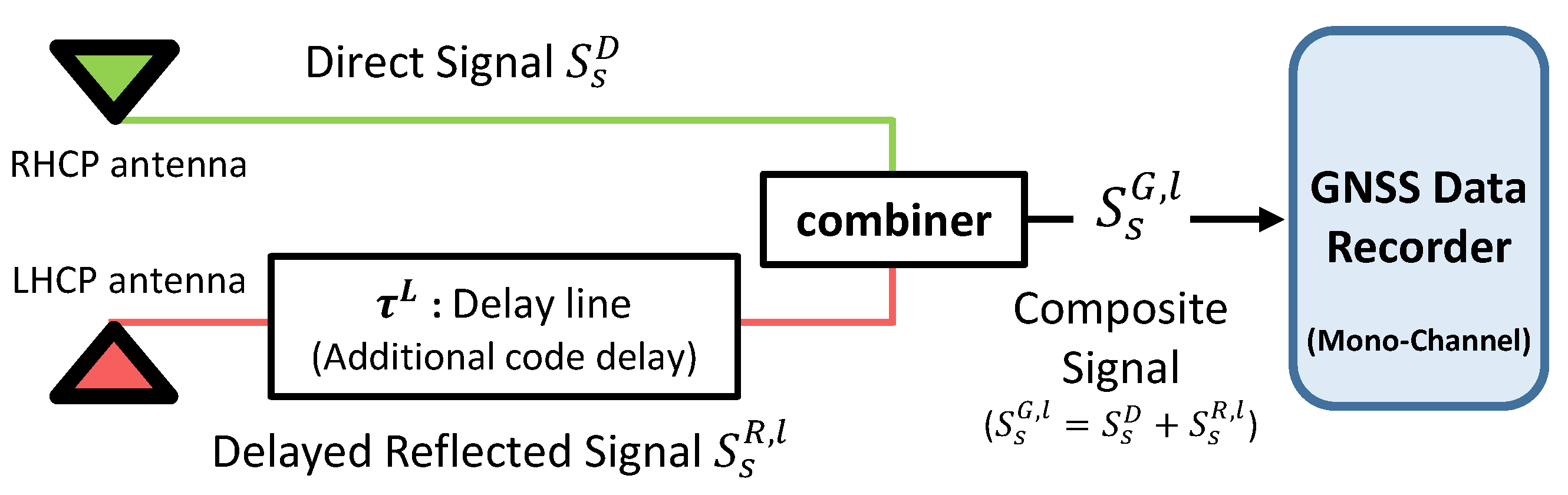
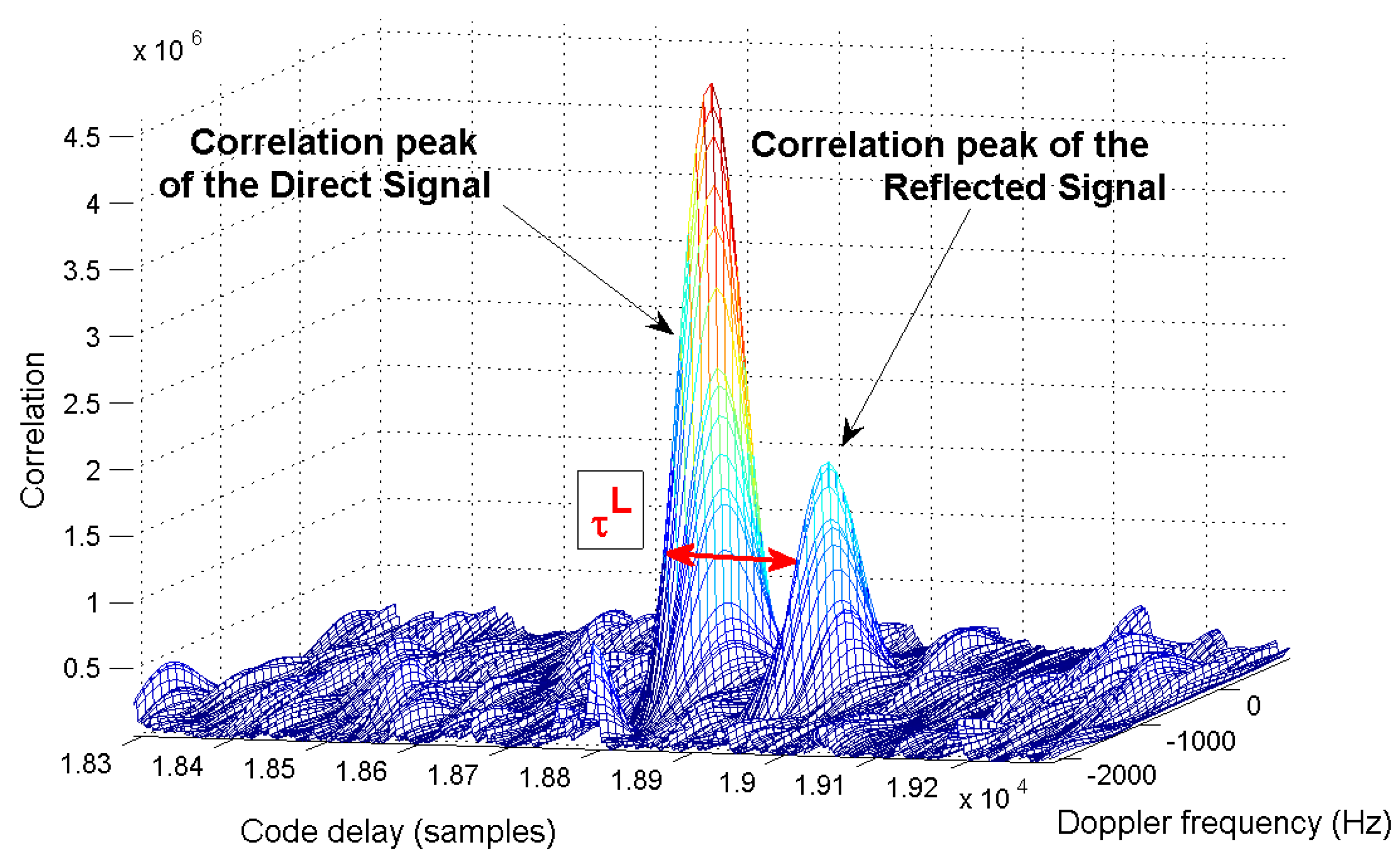
4.2. Experimental Setup
4.3. Assessment with Real Data
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Garrison, J.; Komjathy, A.; Zavorotny, V.; Katzberg, S. Wind speed measurement using forward scattered GPS signals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 50–65. [Google Scholar] [CrossRef]
- Masters, D.; Zavorotny, V.; Katzberg, S.; Emery, W. GPS signal scattering from land for moisture content determination. In Proceedings of the 2000 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 24–28 July 2000; Volume 7, pp. 3090–3092. [Google Scholar]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Ramos-Perez, I.; Valencia, E.; Park, H.; Vall-Llossera, M. Water level monitoring using the interference pattern GNSS-R technique. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 2334–2337. [Google Scholar]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Ribot, M.A.; Kucwaj, J.C.; Botteron, C.; Reboul, S.; Stienne, G.; Leclère, J.; Choquel, J.B.; Farine, P.A.; Benjelloun, M. Normalized GNSS interference pattern technique for altimetry. Sensors 2014, 14, 10234–10257. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Arroyo, A.; Camps, A.; Park, H.; Pascual, D.; Onrubia, R.; Martin, F. Retrieval of Significant Wave Height and Mean Sea Surface Level Using the GNSS-R Interference Pattern Technique: Results From a Three-Month Field Campaign. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3198–3209. [Google Scholar] [CrossRef]
- Martin-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS concept: An experimental demonstration of sea surface altimetry using GPS reflected signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Lowe, S.T.; Zuffada, C.; Chao, Y. 2-cm GPS altimetry over Crater Lake. Geophys. Res. Lett 2001, 28, 4343–4346. [Google Scholar] [CrossRef]
- Lowe, S.T.; Zuffada, C.; Chao, Y.; Kroger, P.; Young, L.E.; LaBrecque, J.L. 5-cm-Precision aircraft ocean altimetry using GPS reflections. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Cardellach, E.; Fabra, F.; Nogués-Correig, O.; Oliveras, S.; Ribó, S.; Rius, A. GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets. Radio Sci. 2011, 46, RS0C04. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Camps, A.; Ramos-Perez, I.; Rius, A. Experimental evaluation of GNSS-reflectometry altimetric precision using the P (Y) and C/A signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1493–1500. [Google Scholar] [CrossRef]
- Kucwaj, J.C.; Stienne, G.; Reboul, S.; Choquel, J.B.; Benjelloun, M. Accurate Pseudorange Estimation by Means of Code and Phase Delay Integration: Application to GNSS-R Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4854–4864. [Google Scholar] [CrossRef]
- Fabra, F.; Cardellach, E.; Rius, A.; Ribó, S.; Oliveras, S.; Nogués-Correig, O.; Rivas, M.B.; Semmling, M.; Addio, S.D. Phase altimetry with dual polarization GNSS-R over sea ice. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2112–2121. [Google Scholar] [CrossRef]
- Hobiger, T.; Haas, R.; Lofgren, J. Software-Defined Radio Direct Correlation GNSS Reflectometry by Means of GLONASS. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4834–4842. [Google Scholar] [CrossRef]
- Wang, G. Millimeter-accuracy GPS landslide monitoring using Precise Point Positioning with Single Receiver Phase Ambiguity (PPP-SRPA) resolution: A case study in Puerto Rico. J. Geod. Sci. 2013, 3, 22–31. [Google Scholar] [CrossRef]
- Semmling, M.; Beyerle, G.; Stosius, R.; Dick, G.; Wickert, J.; Fabra, F.; Cardellach, E.; Ribó, S.; Rius, A.; Helm, A.; et al. Detection of Arctic Ocean tides using interferometric GNSS-R signals. Geophys. Res. Lett. 2011, 38, L04103. [Google Scholar] [CrossRef]
- Kucwaj, J.C.; Stienne, G.; Reboul, S.; Choquel, J.B.; Benjelloun, M. A model-based angle unwrapper: Application to the GNSS-R Interference Pattern Technique. In Proceedings of the 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 2095–2100. [Google Scholar]
- Semmling, A.; Wickert, J.; Schön, S.; Stosius, R.; Markgraf, M.; Gerber, T.; Ge, M.; Beyerle, G. A Zeppelin experiment to study airborne altimetry using specular global navigation satellite system reflections. Radio Sci. 2013, 48, 427–440. [Google Scholar] [CrossRef]
- Kucwaj, J.C.; Stienne, G.; Reboul, S.; Choquel, J.B.; Benjelloun, M. High rate interference pattern technique applied to real time altimetry. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5631–5634. [Google Scholar]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef]
- Lestarquit, L.; Peyrezabes, M.; Darrozes, J.; Motte, E.; Roussel, N.; Wautelet, G.; Frappart, F.; Ramillien, G.; Biancale, R.; Zribi, M. Reflectometry with an open-source software GNSS Receiver: Use case with carrier phase altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4843–4853. [Google Scholar] [CrossRef]
- Semmling, A.M.; Leister, V.; Saynisch, J.; Zus, F.; Heise, S.; Wickert, J. A phase-altimetric simulator: Studying the sensitivity of Earth-reflected GNSS signals to ocean topography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6791–6802. [Google Scholar] [CrossRef]
- Borre, K.; Akos, D.M.; Bertelsen, N.; Rinder, P.; Jensen, S.H. A Software-Defined GPS and Galileo Receiver: A Single-Frequency Approach; Springer Science & Business Media: Boston, MA, USA, 2007. [Google Scholar]
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Cai, J.; Grafarend, E.W.; Hu, C. The statistical property of the GNSS carrier phase observations and its effects on the hypothesis testing of the related estimators. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 331–338. [Google Scholar]
- Ghosh, K.; Jammalamadaka, S.R.; Vasudaven, M. Change-point problems for the von Mises distribution. J. Appl. Stat. 1999, 26, 423–434. [Google Scholar] [CrossRef]
- Sengupta, A.; Kumar Laha, A. A Bayesian analysis of the change-point problem for directional data. J. Appl. Stat. 2008, 35, 693–700. [Google Scholar] [CrossRef]
- Jammalamadaka, S.R.; Sengupta, A. Topics in Circular Statistics; World Scientific: Singapore, 2001; Volume 5. [Google Scholar]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley & Sons: Chichester, UK, 2009; Volume 494. [Google Scholar]
- Fisher, N.I. Statistical Analysis of Circular Data; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Nikolaidis, N.; Pitas, I. Nonlinear processing and analysis of angular signals. IEEE Trans. Signal Proc. 1998, 46, 3181–3194. [Google Scholar] [CrossRef]
- Stienne, G.; Reboul, S.; Azmani, M.; Choquel, J.B.; Benjelloun, M. A multi-temporal multi-sensor circular fusion filter. Inf. Fusion 2014, 18, 86–100. [Google Scholar] [CrossRef]
- Stienne, G.; Reboul, S.; Azmani, M.; Choquel, J.B.; Benjelloun, M. GNSS dataless signal tracking with a delay semi-open loop and a phase open loop. Signal Proc. 2013, 93, 1192–1209. [Google Scholar]
- Marković, I.; Ćesić, J.; Petrović, I. Von Mises Mixture PHD Filter. IEEE Signal Proc. Lett. 2015, 22, 2229–2233. [Google Scholar] [CrossRef]
- Kurz, G.; Gilitschenski, I.; Julier, S.; Hanebeck, U.D. Recursive Bingham filter for directional estimation involving 180 degree symmetry. J. Adv. Inf. Fusion 2014, 9, 90–105. [Google Scholar]
- Routtenberg, T.; Tabrikian, J. Bayesian parameter estimation using periodic cost functions. IEEE Trans. Signal Proc. 2012, 60, 1229–1240. [Google Scholar] [CrossRef]
- Kurz, G.; Gilitschenski, I.; Hanebeck, U.D. Recursive Bayesian Filtering in Circular State Spaces. arXiv, 2015; arXiv:1501.05151. [Google Scholar]
- Hussin, A.G. Hypothesis Testing of Parameters for Ordinary Linear Circular Regression. Pak. J. Stat. Oper. Res. 2006, 2, 185–188. [Google Scholar] [CrossRef]
- Rius, A.; Nogués-Correig, O.; Ribó, S.; Cardellach, E.; Oliveras, S.; Valencia, E.; Park, H.; Tarongí, J.M.; Camps, A.; van der Marel, H.; et al. Altimetry with GNSS-R interferometry: First proof of concept experiment. GPS Solut. 2012, 16, 231–241. [Google Scholar] [CrossRef]


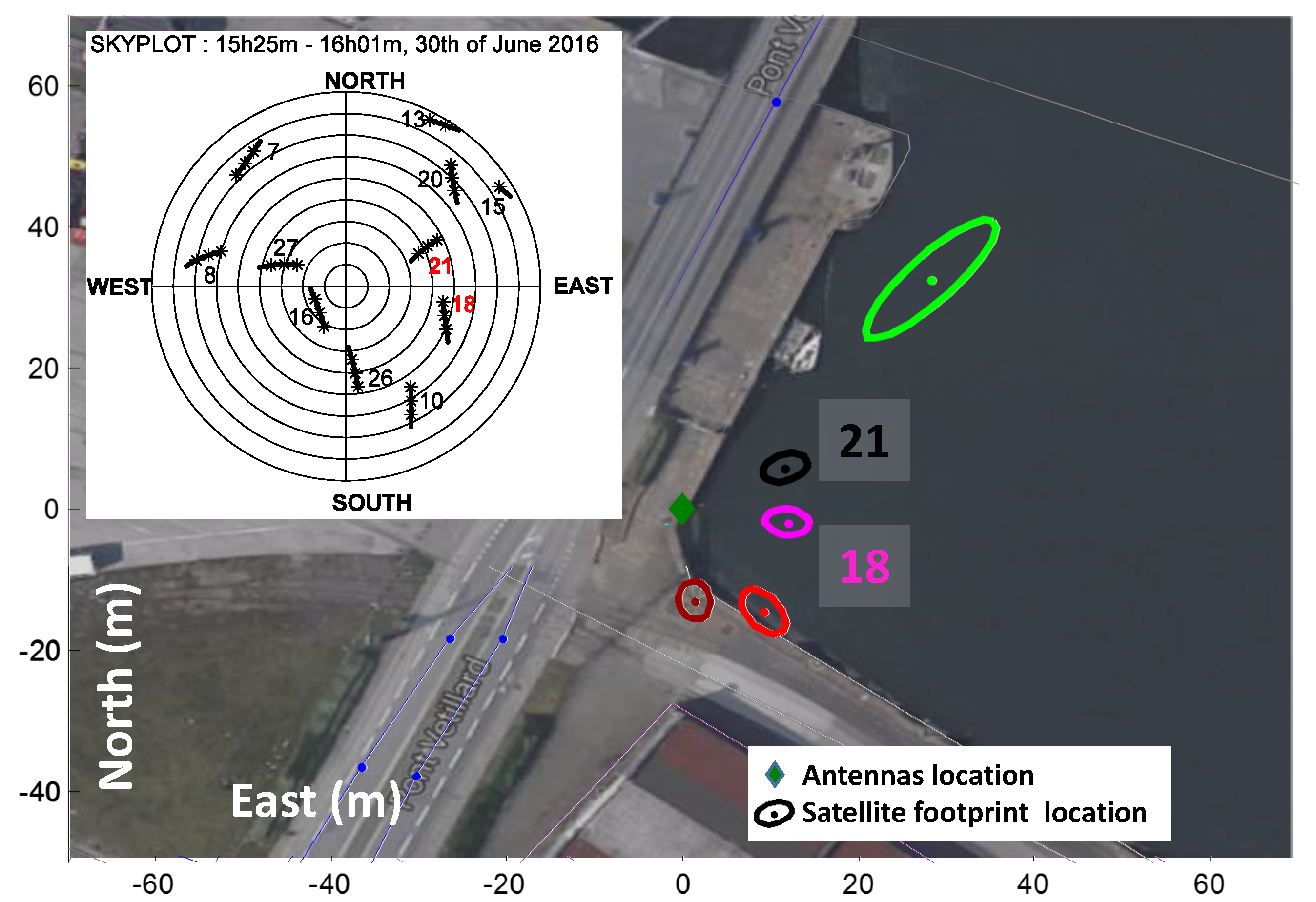
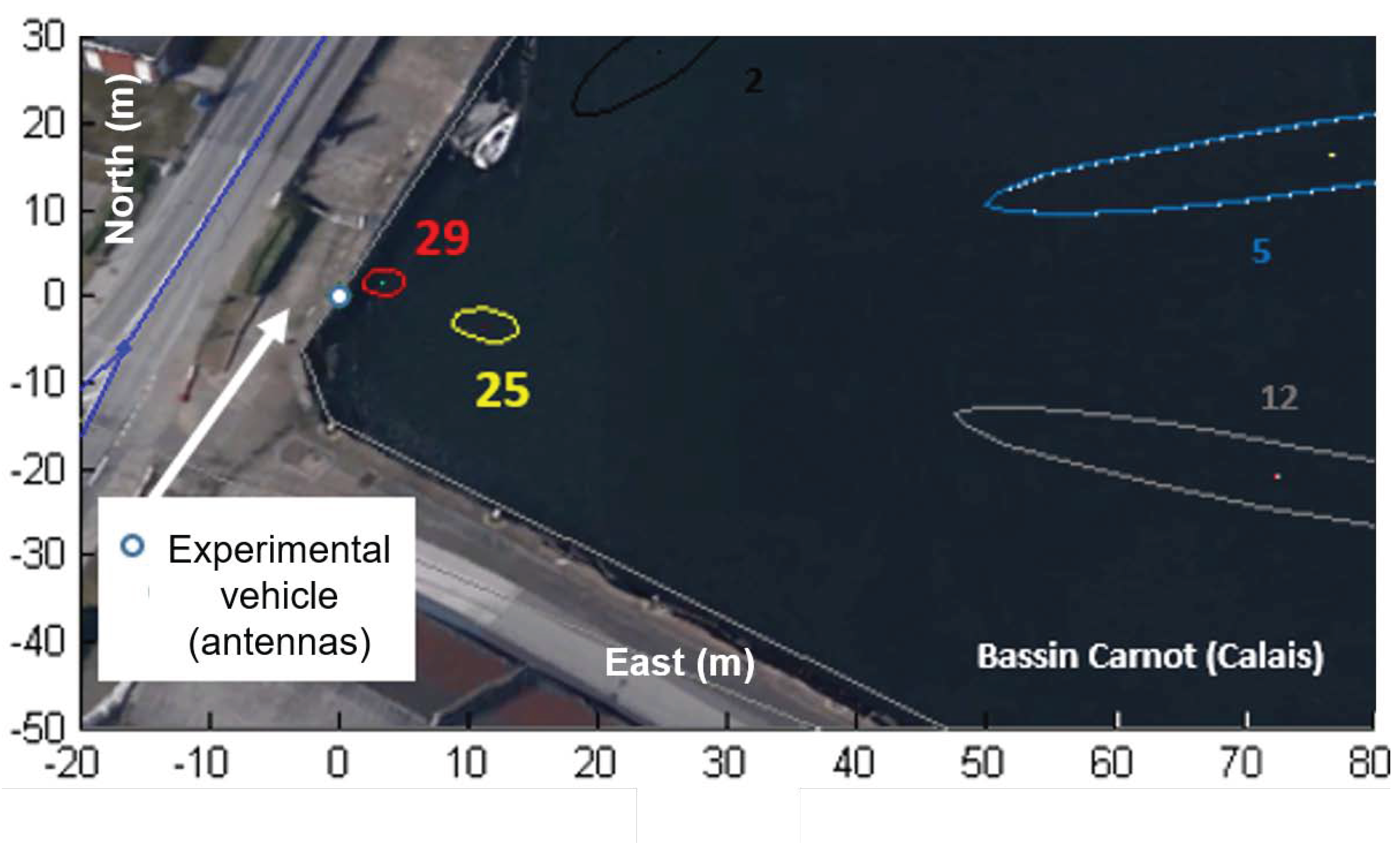
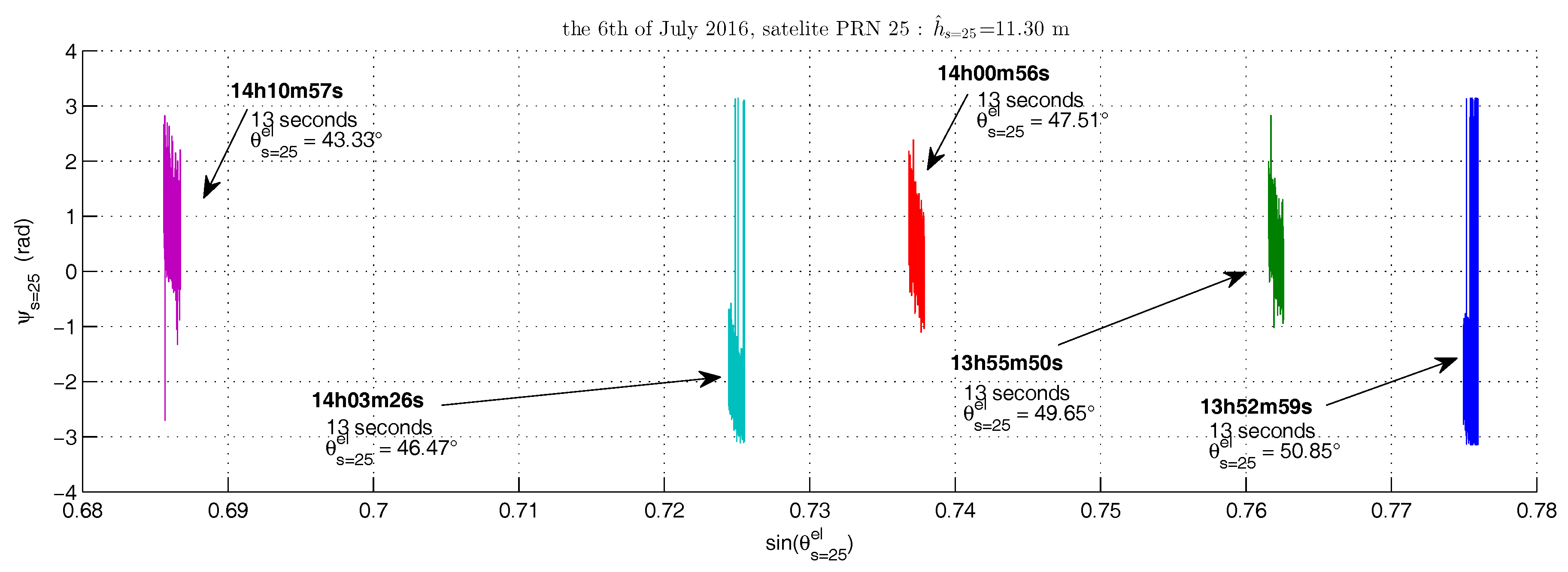
| (dB-Hz) | 30 | 35 | 40 | 45 |
| 1.35 | 2.96 | 9.34 | 30.82 |
| 15 h 25 min | |||||
| Satellite PRN | Interferometric Signal C/ (dB-Hz) | Elevation | |||
| min. () | max. () | mean () | rate (/s) | ||
| 18 | 36.5 | 36.44 | 39.21 | 37.85 | 0.0046 |
| 21 | 34 | 53.73 | 57.56 | 55.65 | −0.0064 |
| 15 h 38 min | |||||
| Satellite PRN | Interferometric Signal / (dB-Hz) | Elevation | |||
| min. () | max. () | mean () | rate (/s) | ||
| 18 | 37 | 39.99 | 42.23 | 41.15 | 0.0037 |
| 21 | 34.1 | 48.55 | 52.51 | 50.53 | −0.0066 |
| 15 h 51 min | |||||
| Satellite PRN | Interferometric Signal / (dB-Hz) | Elevation | |||
| min. () | max. () | mean () | rate (/s) | ||
| 18 | 35 | 42.80 | 44.38 | 43.63 | 0.0026 |
| 21 | 32.3 | 43.39 | 47.38 | 45.38 | −0.0066 |
| Satellite PRN | 15 h 25 min | 15 h 38 min | 15 h 51 min |
|---|---|---|---|
| m | m | m | |
| Estimated Height (m) | Estimated Height (m) | Estimated Height (m) | |
| 18 | 12.68 | 12.87 | 13.02 |
| 21 | 12.65 | 12.49 | 12.36 |
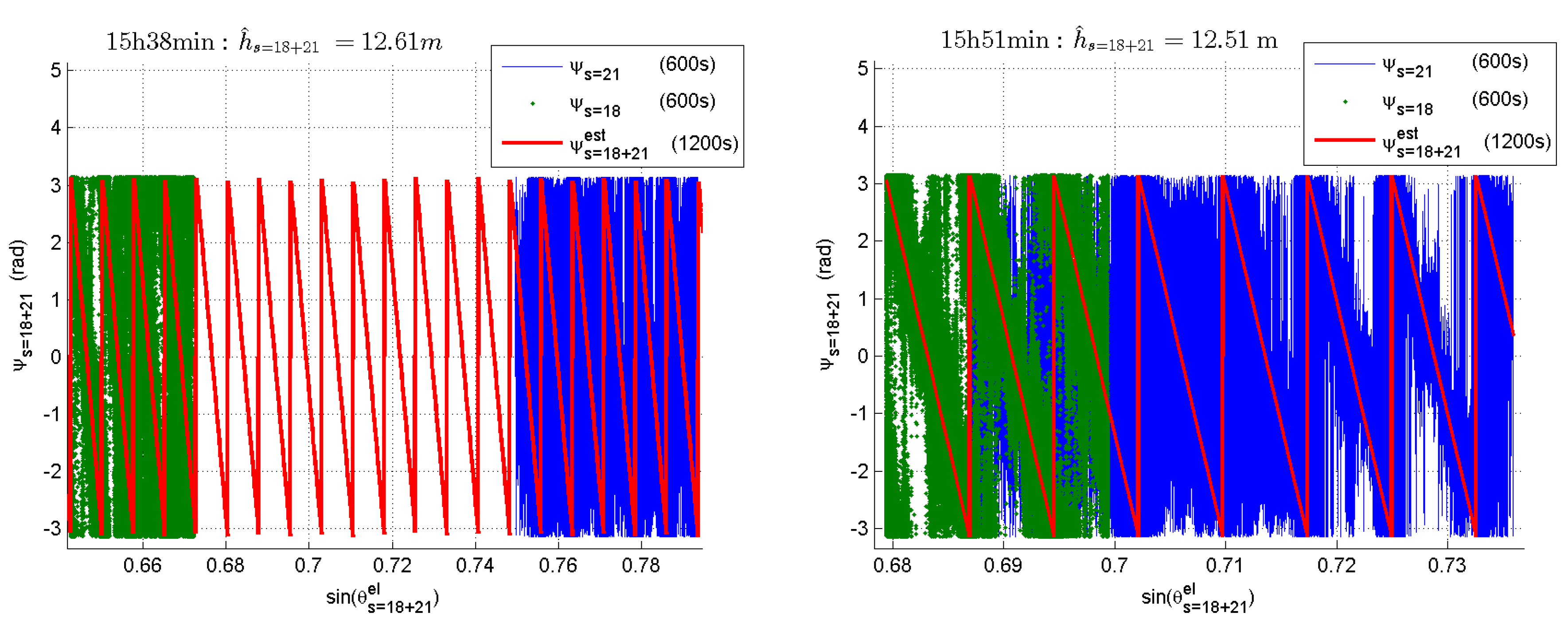
| 18 + 21 | 12.61 * | 12.61 * | 12.51 * |
| 18 + 21 | 12.60 ** | ||
| Sat.: 18 + 21 | 15 s | 30 s | 50 s | 100 s | 150 s | 300 s | 600 s |
|---|---|---|---|---|---|---|---|
| 15 h 25 min | 8.80 | 12.63 | 12.62 | 12.62 | 12.61 | 12.62 | 12.61 |
| 15 h 38 min | 7.54 | 12.62 | 12.61 | 12.61 | 12.62 | 12.62 | 12.61 |
| 15 h 51 min | 16.01 | 12.56 | 12.53 | 12.54 | 12.55 | 12.55 | 12.51 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kucwaj, J.-C.; Reboul, S.; Stienne, G.; Choquel, J.-B.; Benjelloun, M. Circular Regression Applied to GNSS-R Phase Altimetry. Remote Sens. 2017, 9, 651. https://doi.org/10.3390/rs9070651
Kucwaj J-C, Reboul S, Stienne G, Choquel J-B, Benjelloun M. Circular Regression Applied to GNSS-R Phase Altimetry. Remote Sensing. 2017; 9(7):651. https://doi.org/10.3390/rs9070651
Chicago/Turabian StyleKucwaj, Jean-Christophe, Serge Reboul, Georges Stienne, Jean-Bernard Choquel, and Mohammed Benjelloun. 2017. "Circular Regression Applied to GNSS-R Phase Altimetry" Remote Sensing 9, no. 7: 651. https://doi.org/10.3390/rs9070651