An Improved Spectrum Model for Sea Surface Radar Backscattering at L-Band
Abstract
:1. Introduction
2. Modeling
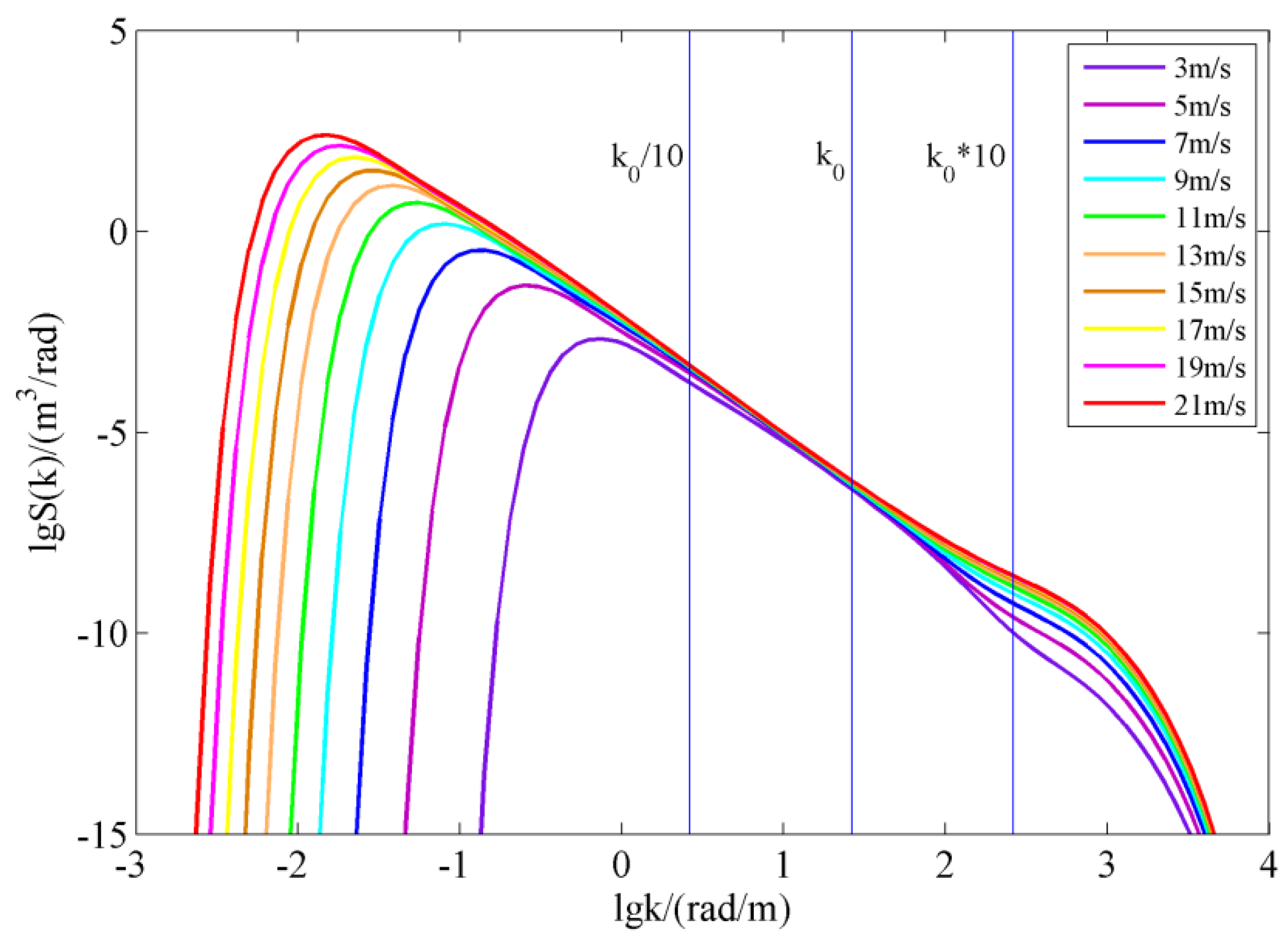
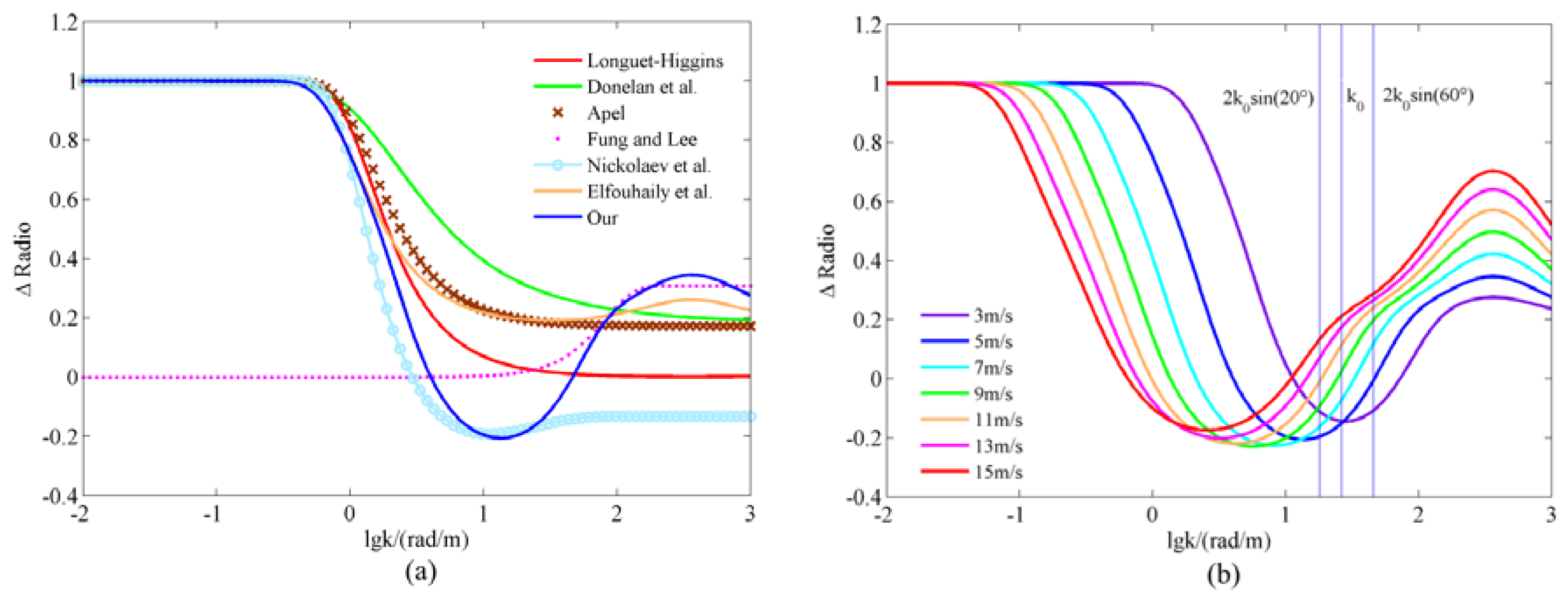
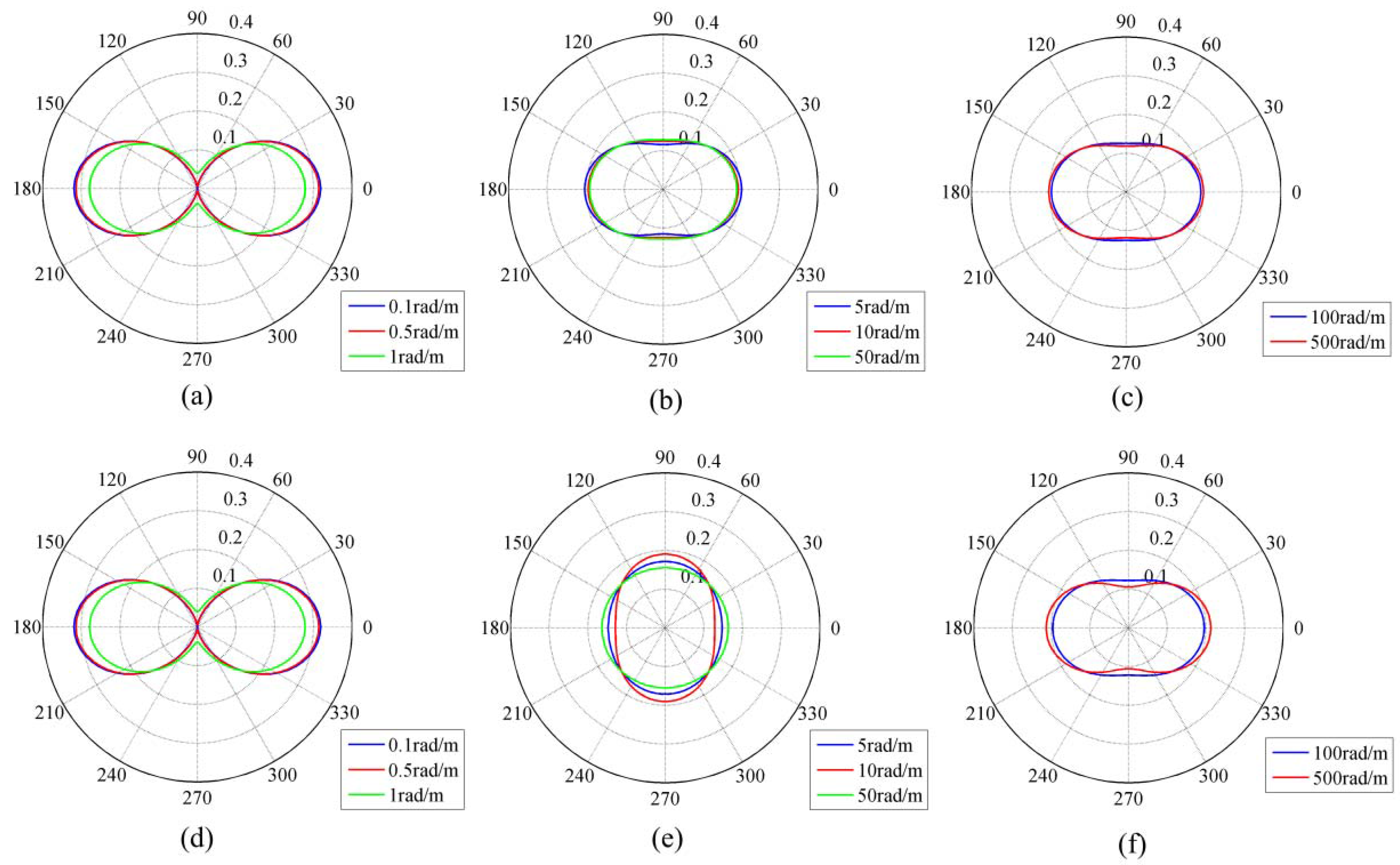
2.1. An Improved Directional Spectrum
2.2. Scattering Model
3. Validation and Discussion
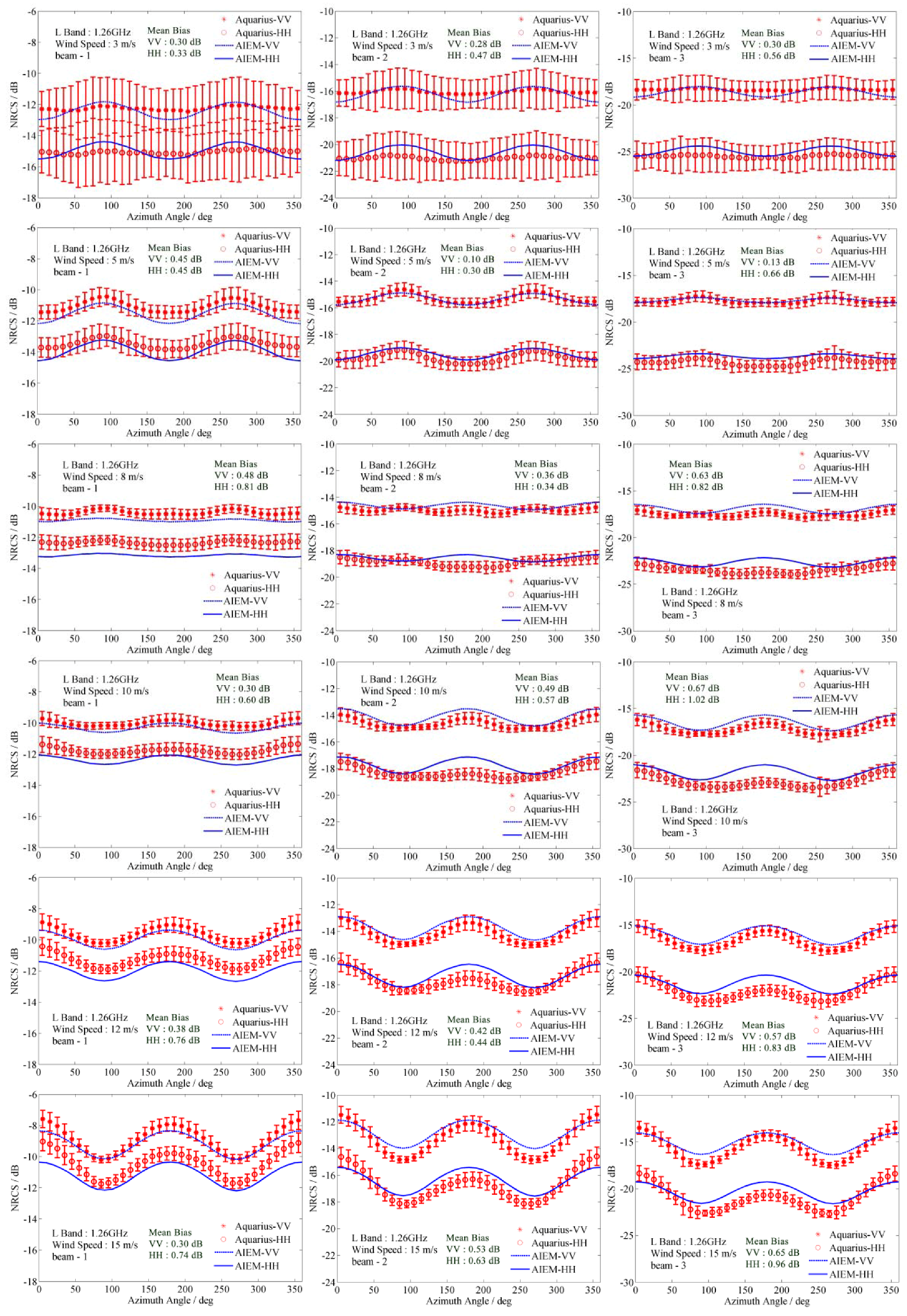
3.1. Data Description
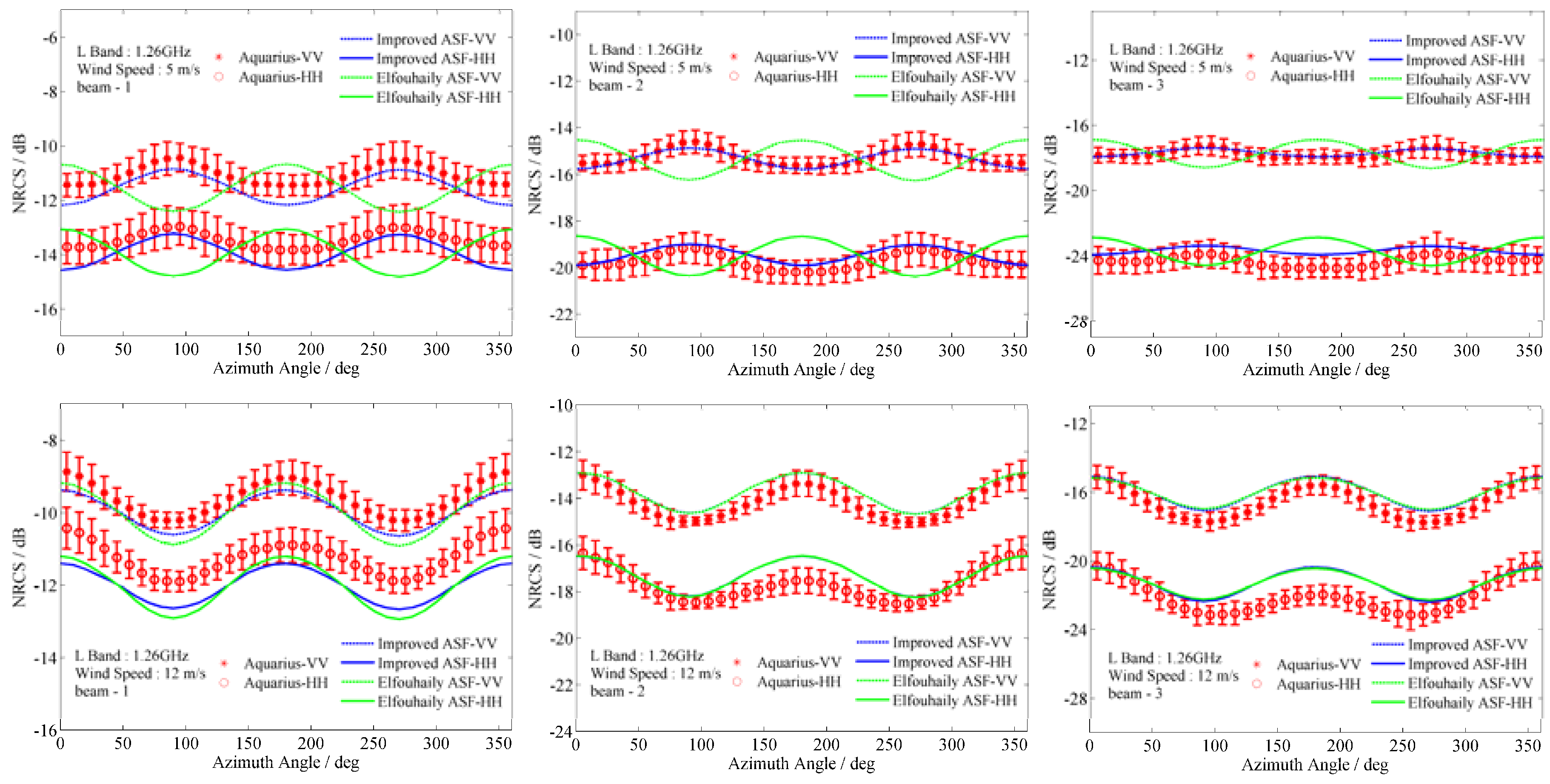
3.2. Results and Discussion
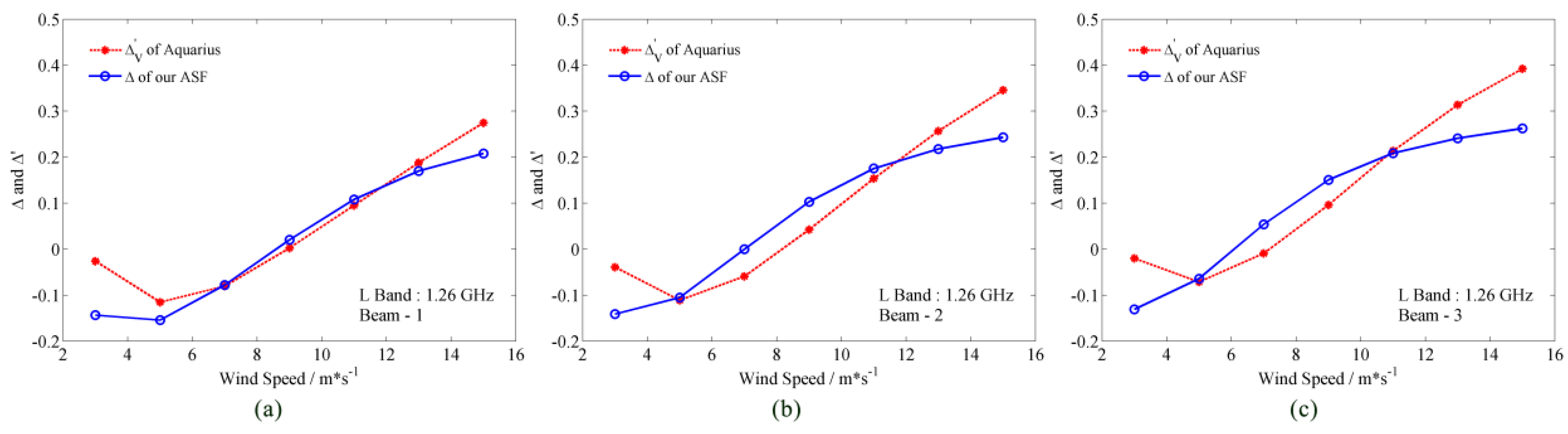
3.3. Numerical Analysis of Scattering Directionality
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yueh, S.H.; Chaubell, J. Sea surface salinity and wind retrieval using combined passive and active L-band microwave observations. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1022–1032. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J.; Ricciardulli, L. The emission and scattering of L-band microwave radiation from rough ocean surfaces and wind speed measurements from the Aquarius sensor. J. Geophys. Res.-Oceans 2014, 119, 6499–6522. [Google Scholar] [CrossRef]
- Yueh, S.H.; Tang, W.Q.; Fore, A.G.; Neumann, G.; Hayashi, A.; Freedman, A.; Chaubell, J.; Lagerloef, G.S.E. L-band passive and active microwave geophysical model functions of ocean surface winds and applications to Aquarius retrieval. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4619–4632. [Google Scholar] [CrossRef]
- Ma, W.T.; Yang, X.F.; Yu, Y.; Liu, G.H.; Li, Z.W.; Jing, C. Impact of rain-induced sea surface roughness variations on salinity retrieval from the Aquarius/SAC-D satellite. Acta Oceanol. Sin. 2015, 34, 89–96. [Google Scholar] [CrossRef]
- Yueh, S.H.; Dinardo, S.J.; Fore, A.G.; Li, F.K. Passive and active L-band microwave observations and modeling of ocean surface winds. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3087–3100. [Google Scholar] [CrossRef]
- Isoguchi, O.; Shimada, M. An L-band ocean geophysical model function derived from PALSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1925–1936. [Google Scholar] [CrossRef]
- Lagerloef, G.; Colomb, F.R.; Le Vine, D.; Wentz, F.; Yueh, S.; Ruf, C.; Lilly, J.; Gunn, J.; Chao, Y.; de Charon, A.; et al. The Aquarius/SAC-D mission: Designed to meet the salinity remote-sensing challenge. Oceanography 2008, 21, 68–81. [Google Scholar] [CrossRef]
- Spencer, M.; Wheeler, K.; White, C.; West, R.; Piepmeier, J.; Hudson, D.; Medeiros, J. The soil moisture active passive (SMAP) mission L-band radar/radiometer instrument. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3240–3243. [Google Scholar]
- Bruce, N.C.; Dainty, J.C. Multiple-scattering from random rough surfaces using the kirchhoff approximation. J. Mod. Opt. 1991, 38, 579–590. [Google Scholar] [CrossRef]
- Sotocrespo, J.M.; Nietovesperinas, M.; Friberg, A.T. Scattering from slightly rough random surfaces—A detailed study on the validity of the small perturbation method. J. Opt. Soc. Am. A 1990, 7, 1185–1201. [Google Scholar] [CrossRef]
- Khenchaf, A.; Daout, F.; Saillard, J. The two-scale model for random rough surface scattering. In Proceedings of the Oceans ‘96 MTS/IEEE Conference Proceedings, Prospects for the 21st Century, Fort Lauderdale, FL, USA, 23–26 September 1996; Volumes 1–3, pp. 887–891. [Google Scholar]
- Voronovich, A. Small-slope approximation for electromagnetic-wave scattering at a rough interface of dielectric half-spaces. Wave Random Media 1994, 4, 337–367. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.Q.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Fung, A.K.; Tjuatja, S. Backscattering and emission signatures of randomly rough surfaces based on IEM. In Proceedings of the 1993 International Geoscience Remote Sensing Symposium (IGARSS ’93), Better Understanding of Earth Environment, Tokyo, Japan, 18–21 August 1993; pp. 1006–1008. [Google Scholar]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.C.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Shi, J.C. A model-based inversion of rough soil surface parameters from radar measurements. J. Electromagn. Wave 2001, 15, 173–200. [Google Scholar] [CrossRef]
- Chen, K.S.; Fung, A.K.; Amar, F. An empirical bispectrum model for sea-surface scattering. IEEE Trans. Geosci. Remote Sens. 1993, 31, 830–835. [Google Scholar] [CrossRef]
- Chen, K.S.; Fung, A.K.; Weissman, D.E. A backscattering model for ocean surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 811–817. [Google Scholar] [CrossRef]
- Fung, A.K.; Zuffada, C.; Hsieh, C.Y. Incoherent bistatic scattering from the sea surface at L-band. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1006–1012. [Google Scholar] [CrossRef]
- Xu, F.; Li, X.F.; Wang, P.; Yang, J.S.; Pichel, W.G.; Jin, Y.Q. A backscattering model of rainfall over rough sea surface for synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3042–3054. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res.-Oceans 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Fung, A.K.; Lee, K.K. A semi-empirical sea-spectrum model for scattering coefficient estimation. IEEE J. Ocean. Eng. 1982, 7, 166–176. [Google Scholar] [CrossRef]
- Apel, J.R. An improved model of the ocean surface-wave vector spectrum and its effects on radar backscatter. J. Geophys. Res.-Oceans 1994, 99, 16269–16291. [Google Scholar] [CrossRef]
- Durden, S.L.; Vesecky, J.F. A physical radar cross-section model for a wind-driven sea with swell. IEEE J. Ocean. Eng. 1985, 10, 445–451. [Google Scholar] [CrossRef]
- Donelan, M.A.; Pierson, W.J. Radar scattering and equilibrium ranges in wind-generated waves with application to scatterometry. J. Geophys. Res.-Oceans 1987, 92, 4971–5029. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross section of the sea surface, 2. Radar modulation transfer function. J. Geophys. Res.-Oceans 2003, 108. [Google Scholar] [CrossRef]
- Hwang, P.A. A note on the ocean surface roughness spectrum. J. Atmos. Ocean. Technol. 2011, 28, 436–443. [Google Scholar] [CrossRef]
- Yurovskaya, M.V.; Dulov, V.A.; Chapron, B.; Kudryavtsev, V.N. Directional short wind wave spectra derived from the sea surface photography. J. Geophys. Res.-Oceans 2013, 118, 4380–4394. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Makin, V.K.; Chapron, B. Coupled sea surface-atmosphere model—2. Spectrum of short wind waves. J. Geophys. Res.-Oceans 1999, 104, 7625–7639. [Google Scholar] [CrossRef]
- Bringer, A.; Chapron, B.; Mouche, A.; Guerin, C.A. Revisiting the short-wave spectrum of the sea surface in the light of the weighted curvature approximation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 679–689. [Google Scholar] [CrossRef]
- Benetazzo, A. Measurements of short water waves using stereo matched image sequences. Coast. Eng. 2006, 53, 1013–1032. [Google Scholar] [CrossRef]
- Bechle, A.J.; Wu, C.H. Virtual wave gauges based upon stereo imaging for measuring surface wave characteristics. Coast. Eng. 2011, 58, 305–316. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The effect of nonlinearities on statistical distribution in the theory of sea waves. J. Fluid Mech. 1963, 17, 459–480. [Google Scholar] [CrossRef]
- Mitsuyasu, H.; Tasai, F.; Suhara, T.; Mizuno, S.; Ohkusu, M.; Honda, T.; Rikiishi, K. Observations of directional spectrum of ocean waves using a cloverleaf buoy. J. Phys. Oceanogr. 1975, 5, 750–760. [Google Scholar] [CrossRef]
- Nickolaev, N.I.; Yordanov, O.I.; Michalev, M.A. Non-gaussian effects in the 2-scale model for rough-surface scattering. J. Geophys. Res.-Oceans 1992, 97, 15617–15624. [Google Scholar] [CrossRef]
- Shemdin, O.H.; Tran, H.M.; Wu, S.C. Directional measurement of short ocean waves with stereophotography. J. Geophys. Res.-Oceans 1988, 93, 13891–13901. [Google Scholar] [CrossRef]
- Banner, M.L.; Jones, I.S.F.; Trinder, J.C. Wavenumber Spectra of Short Gravity-Waves. J. Fluid Mech. 1989, 198, 321–344. [Google Scholar] [CrossRef]
- Hara, T.; Bock, E.J.; Lyzenga, D. In-situ measurements of capillary-gravity wave spectra using a scanning laser slope gauge and microwave radars. J. Geophys. Res.-Oceans 1994, 99, 12593–12602. [Google Scholar] [CrossRef]
- Donelan, M.A.; Hamilton, J.; Hui, W.H. Directional spectra of wind-generated waves. Philos. Trans. R. Soc. A 1985, 315, 509–562. [Google Scholar] [CrossRef]
- Fung, A.K.; Chen, K.S. An update on the iem surface backscattering model. IEEE Geosci. Remote Sens. Lett. 2004, 1, 75–77. [Google Scholar] [CrossRef]
- Fung, A.K.; Chen, K.S. Microwave Scattering and Emission for Users; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Marrazzo, M.; Sabia, R.; Migliaccio, M. IEM sea surface scattering and the generalized p-power spectrum. In Proceedings of the 2003 IEEE International Geoscience Remote Sensing Symposium (IGARSS ’03), Toulouse, France, 21–25 July 2003; pp. 136–138. [Google Scholar]
- Du, Y.L.; Ma, W.T.; Yang, X.F.; Liu, G.H.; Yu, Y.; Li, Z.W. A rapid atmospheric correction model for l-band microwave radiometer under the cloudless condition. Acta Phys. Sin.-Chin. Ed. 2015, 64. [Google Scholar] [CrossRef]
- Klein, L.A.; Swift, C.T. Improved model for dielectric-constant of sea-water at microwave-frequencies. IEEE Trans. Antennas Propag. 1977, 25, 104–111. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; de Haan, S. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res.-Oceans 2007, 112. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B. Global C-band envisat, radarsat-2 and sentinel-1 SAR measurements in copolarization and cross-polarization. J. Geophys. Res.-Oceans 2015, 120, 7195–7207. [Google Scholar] [CrossRef]
- Mouche, A.A.; Chapron, B.; Reul, N. A simplified asymptotic theory for ocean surface electromagnetic wave scattering. Wave Random Complex 2007, 17, 321–341. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Yang, X.; Chen, K.-S.; Ma, W.; Li, Z. An Improved Spectrum Model for Sea Surface Radar Backscattering at L-Band. Remote Sens. 2017, 9, 776. https://doi.org/10.3390/rs9080776
Du Y, Yang X, Chen K-S, Ma W, Li Z. An Improved Spectrum Model for Sea Surface Radar Backscattering at L-Band. Remote Sensing. 2017; 9(8):776. https://doi.org/10.3390/rs9080776
Chicago/Turabian StyleDu, Yanlei, Xiaofeng Yang, Kun-Shan Chen, Wentao Ma, and Ziwei Li. 2017. "An Improved Spectrum Model for Sea Surface Radar Backscattering at L-Band" Remote Sensing 9, no. 8: 776. https://doi.org/10.3390/rs9080776