Dynamic Electroosmotic Flows of Power-Law Fluids in Rectangular Microchannels
Abstract
:1. Introduction
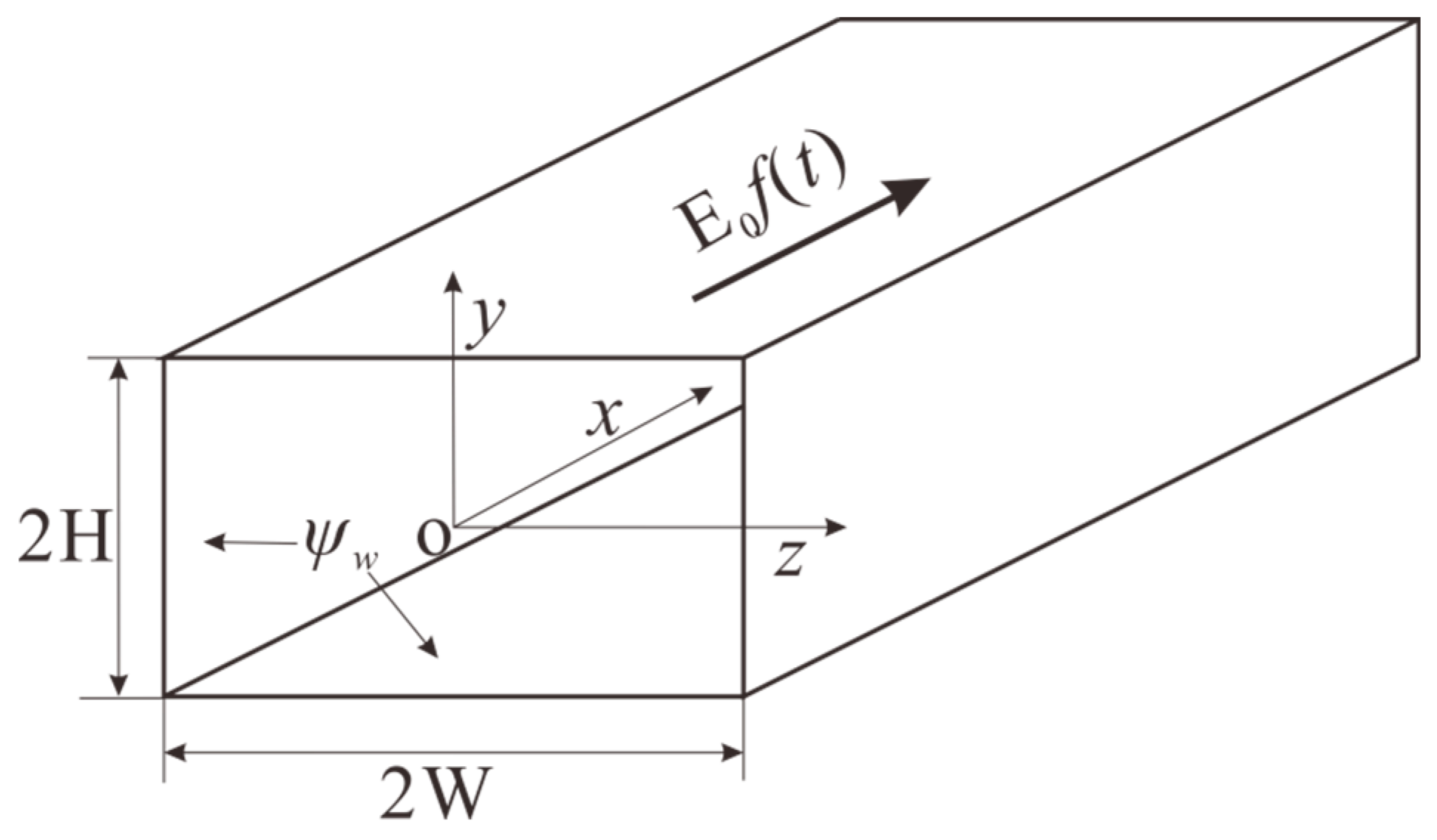
2. Problem Formulation
2.1. Electric Field in the EDL
2.2. Electroosmotic Flow of Power-Law Fluids
3. Numerical Method and Model Validation
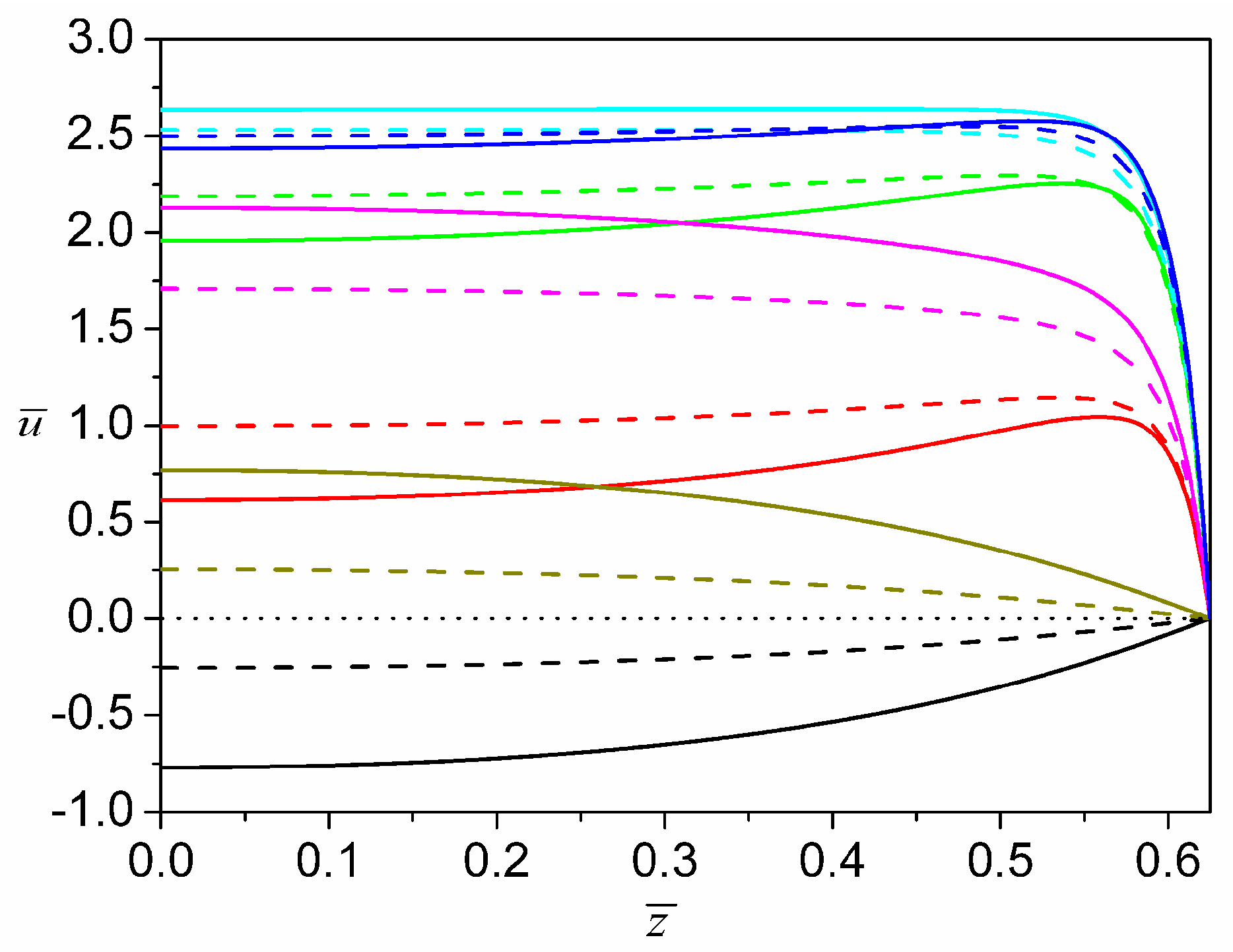
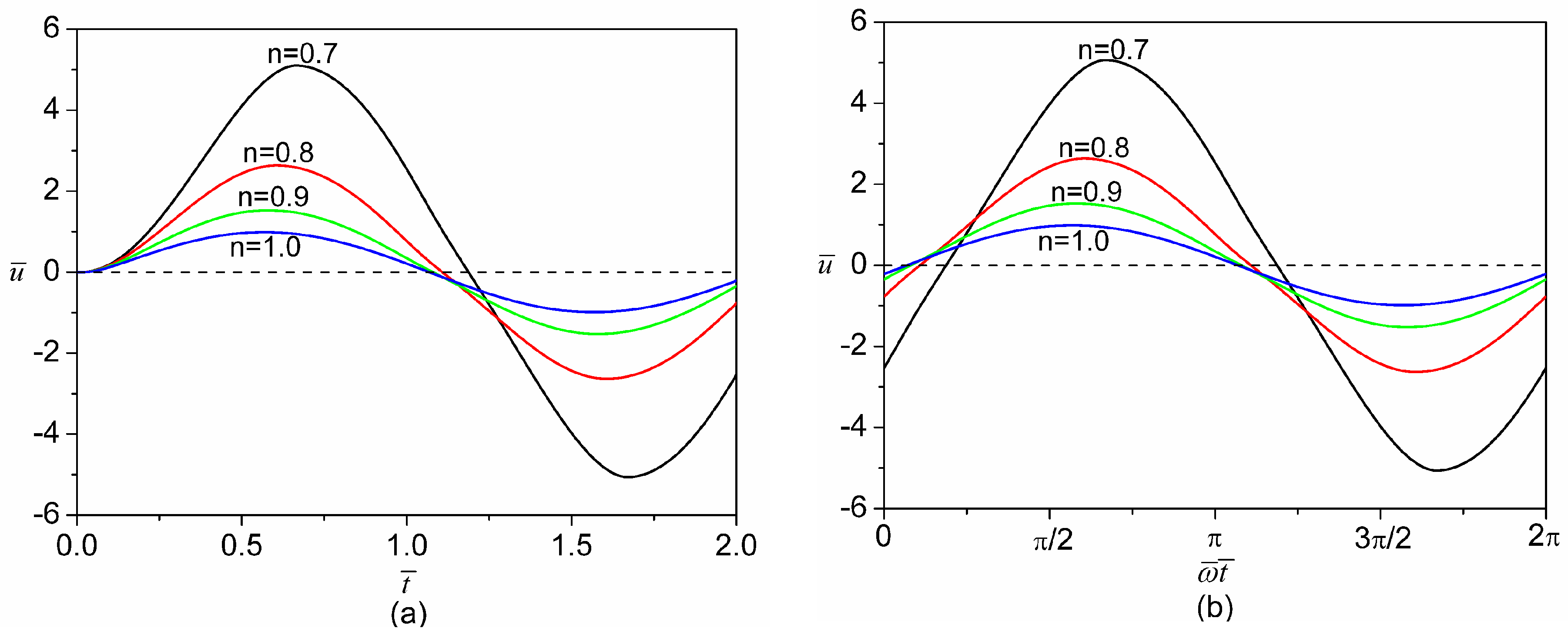
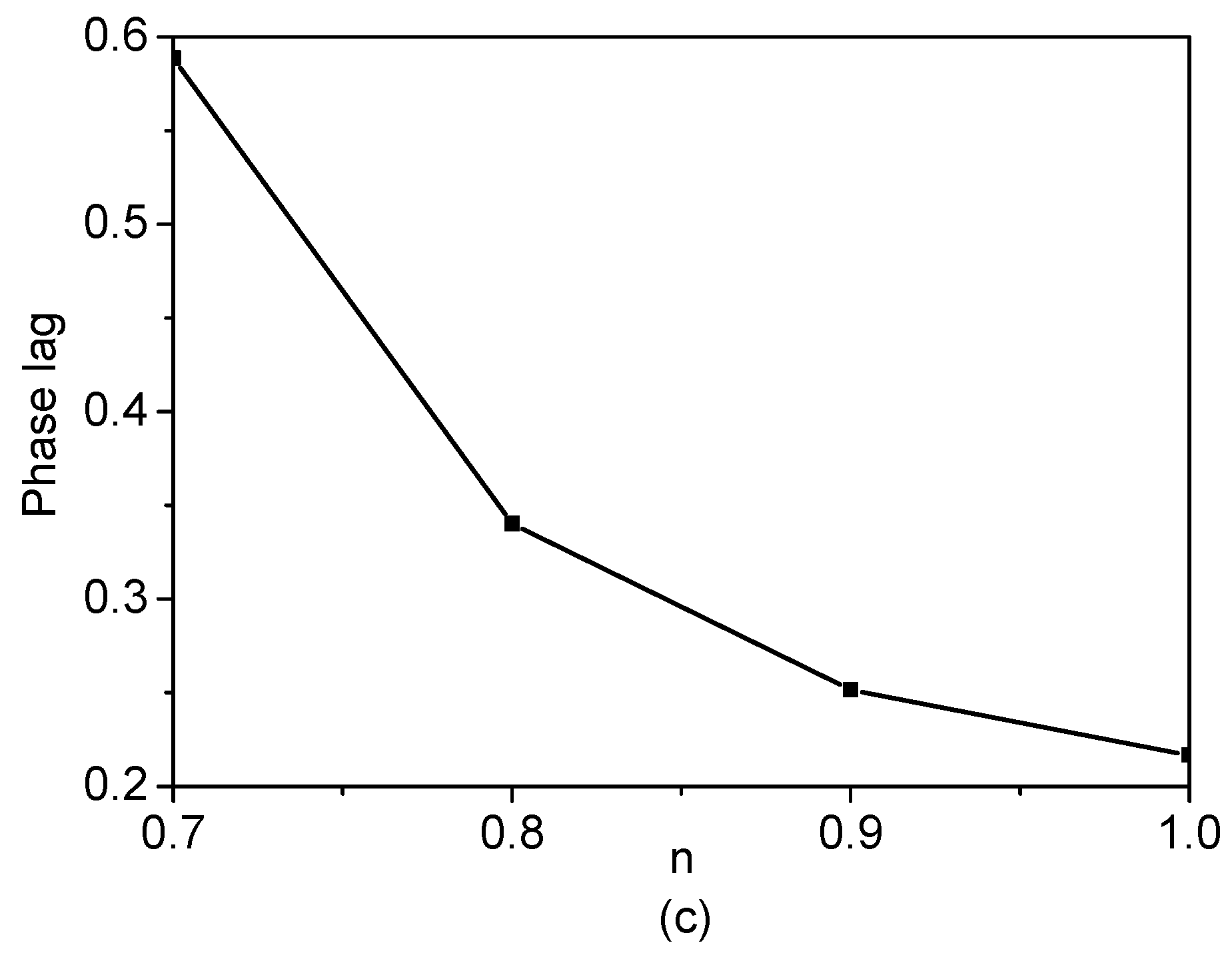
4. Results and Discussion
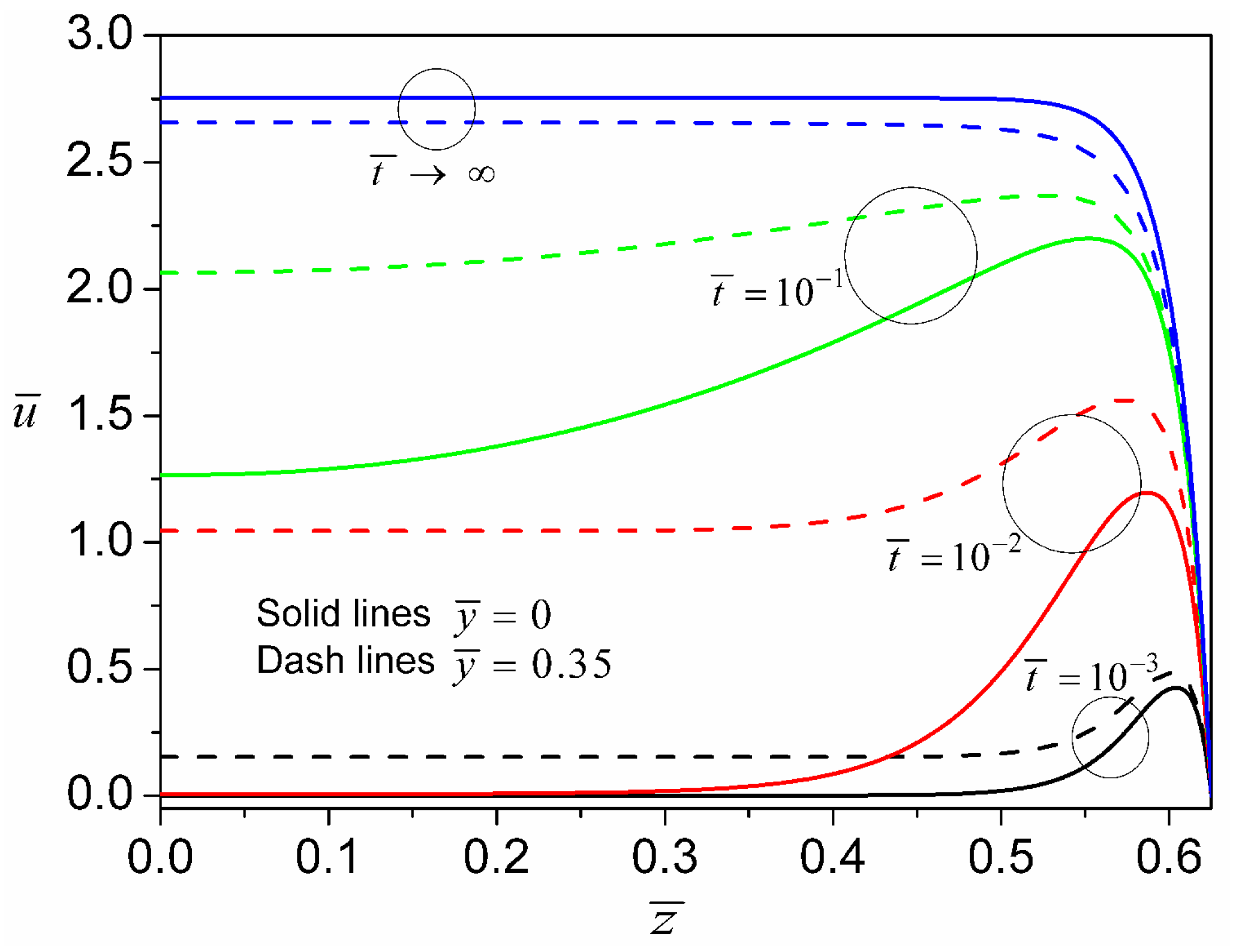
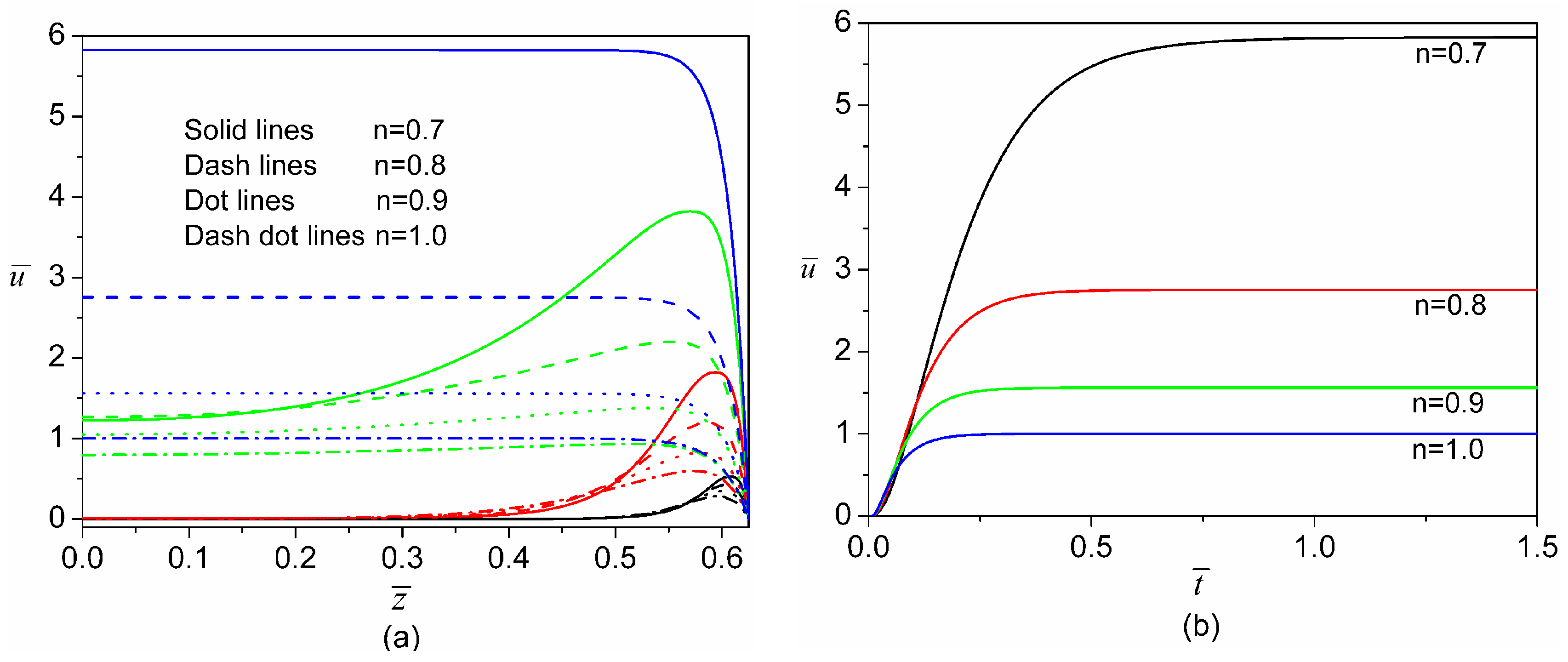
4.1. Transient Electroosmotic Flows of Power-Law Fluids under DC Electric Fields
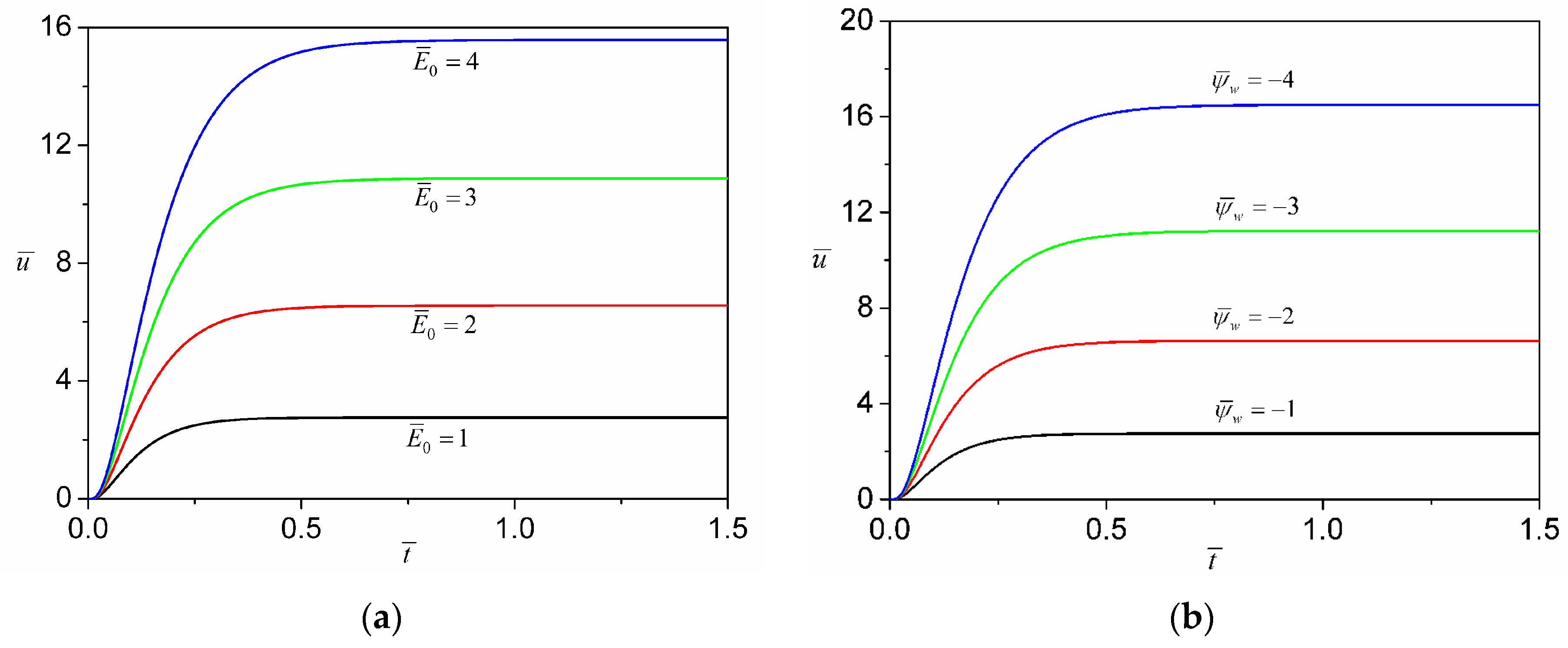
4.2. Transient Electroosmotic Flows of Power-Law Fluids under AC Electric Fields
4.3. Enhancement of Electroosmotic Flows of Power-Law Fluids by AC/DC Combined Electric Fields
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Harrison, D.J.; Fluri, K.; Seiler, K.; Fan, Z.; Effenhauser, C.S.; Manz, A. Micromachining a miniaturized capillary electrophoresis-based chemical analysis system on a chip. Science 1993, 261, 895–897. [Google Scholar] [CrossRef] [PubMed]
- Bousse, L.; Cohen, C.; Nikiforov, T.; Chow, A.; Kopf-Sill, A.R.; Dubrow, R.; Parce, J.W. Electrokinetically controlled microfluidic analysis systems. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 155–181. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Manz, A.; Effenhauser, C.S.; Burggraf, N.; Harrison, D.J.; Seiler, K.; Fluri, K. Electroosmotic pumping and electrophoretic separations for miniaturized chemical analysis systems. J. Micromech. Microeng. 1994, 4, 257–265. [Google Scholar] [CrossRef]
- Yossifon, G.; Frankel, I.; Miloh, T. Macro-scale description of transient electro-kinetic phenomena over polarizable dielectric solids. J. Fluid Mech. 2009, 620, 241–262. [Google Scholar] [CrossRef]
- Fan, Z.H.; Harrison, D.J. Micromachining of capillary electrophoresis injectors and separators on glass chips and evaluation of flow at capillary intersections. Anal. Chem. 1994, 66, 177–184. [Google Scholar] [CrossRef]
- Jacobson, S.C.; Culbertson, C.T.; Daler, J.E.; Ramsey, J.M. Microchip structures for submillisecond electrophoresis. Anal. Chem. 1998, 70, 3476–3480. [Google Scholar] [CrossRef]
- Jacobson, S.C.; Hergenröder, R.; Koutny, L.B.; Ramsey, J.M. High-Speed Separations on a Microchip. Anal. Chem. 1994, 66, 1114–1118. [Google Scholar] [CrossRef]
- Söderman, O.; Jönsson, B. Electro-osmosis: Velocity profiles in different geometries with both temporal and spatial resolution. J. Chem. Phys. 1996, 105, 10300–10311. [Google Scholar] [CrossRef]
- Ajdari, A. Pumping liquids using asymmetric electrode arrays. Phys. Rev. E 2000, 61, R45–R48. [Google Scholar] [CrossRef]
- González, A.; Ramos, A.; Green, N.G.; Castellanos, A.; Morgan, H. Fluid flow induced by nonuniform AC electric fields in electrolytes on microelectrodes. II. A linear double-layer analysis. Phys. Rev. E 2000, 61, 4019–4028. [Google Scholar] [CrossRef]
- Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. AC electric-field-induced fluid flow in microelectrodes. J. Colloid Interface Sci. 1999, 217, 420–422. [Google Scholar] [CrossRef] [PubMed]
- Hanna, W.T.; Osterle, J.F. Transient electro-osmosis in capillary tubes. J. Chem. Phys. 1968, 49, 4062–4068. [Google Scholar] [CrossRef]
- Ivory, C.F. Transient electroosmosis: The momentum transfer coefficient. J. Colloid Interface Sci. 1983, 96, 296–298. [Google Scholar] [CrossRef]
- Keh, H.J.; Tseng, H.C. Transient electrokinetic flow in fine capillaries. J. Colloid Interface Sci. 2001, 242, 450–459. [Google Scholar] [CrossRef]
- Kang, Y.; Yang, C.; Huang, X. Dynamic aspects of electroosmotic flow in a cylindrical microcapillary. Int. J. Eng. Sci. 2002, 40, 2203–2221. [Google Scholar] [CrossRef]
- Yang, C.; Ng, C.B.; Chan, V. Transient analysis of electroosmotic flow in a slit microchannel. J. Colloid Interface Sci. 2002, 248, 524–527. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Kwok, D.Y. Time-dependent laminar electrokinetic slip flow in infinitely extended rectangular microchannels. J. Chem. Phys. 2003, 118, 354–363. [Google Scholar] [CrossRef]
- Campisi, M.; Accoto, D.; Dario, P. AC electroosmosis in rectangular microchannels. J. Chem. Phys. 2005, 123, 204724. [Google Scholar] [CrossRef] [PubMed]
- Mishchuk, N.A.; González-Caballero, F. Nonstationary electroosmotic flow in open cylindrical capillaries. Electrophoresis 2006, 27, 650–660. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Yang, C.; Nguyen, N.T.; Huang, X. Diagnosis of transient electrokinetic flow in microfluidic channels. Phys. Fluids 2007, 19, 017114. [Google Scholar] [CrossRef]
- Sundstrom, D.W.; Kaufman, A. Pulsating Flow of Polymer Solutions. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 320–325. [Google Scholar] [CrossRef]
- Phan-Thien, N. On pulsating flow of polymeric fluids. J. Non-Newton. Fluid Mech. 1978, 4, 167–176. [Google Scholar] [CrossRef]
- Mazumdar, J.N. Biofluid Mechanics; World Scientific: Singapore, 1992. [Google Scholar]
- Tu, C.; Deville, M. Pulsatile flow of non-Newtonian fluids through arterial stenoses. J. Biomech. 1996, 29, 899–908. [Google Scholar] [CrossRef]
- Buchanan, J.R.; Kleinstreuer, C.; Comer, J.K. Rheological effects on pulsatile hemodynamics in a stenosed tube. Comput. Fluids 2000, 29, 695–724. [Google Scholar] [CrossRef]
- Zimmerman, W.; Rees, J.; Craven, T. Rheometry of non-Newtonian electrokinetic flow in a microchannel T-junction. Microfluid. Nanofluid. 2006, 2, 481–492. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Zhao, C.; Zholkovskij, E.; Masliyah, J.H.; Yang, C. Analysis of electroosmotic flow of power-law fluids in a slit microchannel. J. Colloid Interface Sci. 2008, 326, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Park, H.M.; Lee, W.M. Effect of viscoelasticity on the flow pattern and the volumetric flow rate in electroosmotic flows through a microchannel. Lab Chip 2008, 8, 1163–1170. [Google Scholar] [CrossRef] [PubMed]
- Berli, C.L.A. Output pressure and efficiency of electrokinetic pumping of non-Newtonian fluids. Microfluid. Nanofluid. 2009, 8, 197–207. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Analysis of Power-Law Fluid Flow in a Microchannel with Electrokinetic Effects. Int. J. Emerg. Multidiscip. Fluid Sci. 2009, 1, 37–52. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Nonlinear Smoluchowski velocity for electroosmosis of Power-law fluids over a surface with arbitrary zeta potentials. Electrophoresis 2010, 31, 973–979. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Yang, C. An exact solution for electroosmosis of non-Newtonian fluids in microchannels. J. Non-Newton. Fluid Mech. 2011, 166, 1076–1079. [Google Scholar] [CrossRef]
- Zhao, C. Electro-osmotic mobility of non-Newtonian fluids. Biomicrofluidics 2011, 5, 014110. [Google Scholar] [CrossRef] [PubMed]
- Vakili, M.A.; Sadeghi, A.; Saidi, M.H.; Mozafari, A.A. Electrokinetically driven fluidic transport of power-law fluids in rectangular microchannels. Colloids Surf. A 2012, 414, 440–456. [Google Scholar] [CrossRef]
- Chen, S.; He, X.; Bertola, V.; Wang, M. Electro-osmosis of non-Newtonian fluids in porous media using lattice Poisson-Boltzmann method. J. Colloid Interface Sci. 2014, 436, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Jian, Y.; Su, J.; Chang, L.; Liu, Q.; He, G. Transient electroosmotic flow of general Maxwell fluids through a slit microchannel. Z. Angew. Math. Phys. 2014, 65, 435–447. [Google Scholar] [CrossRef]
- Bandopadhyay, A.; Ghosh, U.; Chakraborty, S. Time periodic electroosmosis of linear viscoelastic liquids over patterned charged surfaces in microfluidic channels. J. Non-Newton. Fluid Mech. 2013, 202, 1–11. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, S.; Wei, S. Transient electro-osmotic flow of Oldroyd-B fluids in a straight pipe of circular cross section. J. Non-Newton. Fluid Mech. 2013, 201, 135–139. [Google Scholar] [CrossRef]
- Liu, Q.-S.; Jian, Y.-J.; Chang, L.; Yang, L.-G. Alternating current (AC) electroosmotic flow of generalized Maxwell fluids through a circular microtube. Int. J. Phys. Sci. 2012, 7, 5935–5941. [Google Scholar]
- Bao, L.-P.; Jian, Y.-J.; Chang, L.; Su, J.; Zhang, H.-Y.; Liu, Q.-S. Time Periodic Electroosmotic Flow of the Generalized Maxwell Fluids in a Semicircular Microchannel. Commun. Theor. Phys. 2013, 59, 615–622. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Exact solutions for electro-osmotic flow of viscoelastic fluids in rectangular micro-channels. Appl. Math. Comput. 2009, 211, 502–509. [Google Scholar] [CrossRef]
- Deng, S.Y.; Jian, Y.J.; Bi, Y.H.; Chang, L.; Wang, H.J.; Liu, Q.S. Unsteady electroosmotic flow of power-law fluid in a rectangular microchannel. Mech. Res. Commun. 2012, 39, 9–14. [Google Scholar] [CrossRef]
- Li, D. Electrokinetics in Microfluidics; Elsevier Academic Press: London, UK, 2004. [Google Scholar]
- Chang, C.C.; Wang, C.Y. Starting electroosmotic flow in an annulus and in a rectangular channel. Electrophoresis 2008, 29, 2970–2979. [Google Scholar] [CrossRef] [PubMed]
- Marcos Yang, C.; Wong, T.N.; Ooi, K.T. Dynamic aspects of electroosmotic flow in rectangular microchannels. Int. J. Eng. Sci. 2004, 42, 1459–1481. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Dudek, J. Pulsating flow of a plastic fluid. Nature 1982, 296, 843–844. [Google Scholar] [CrossRef]

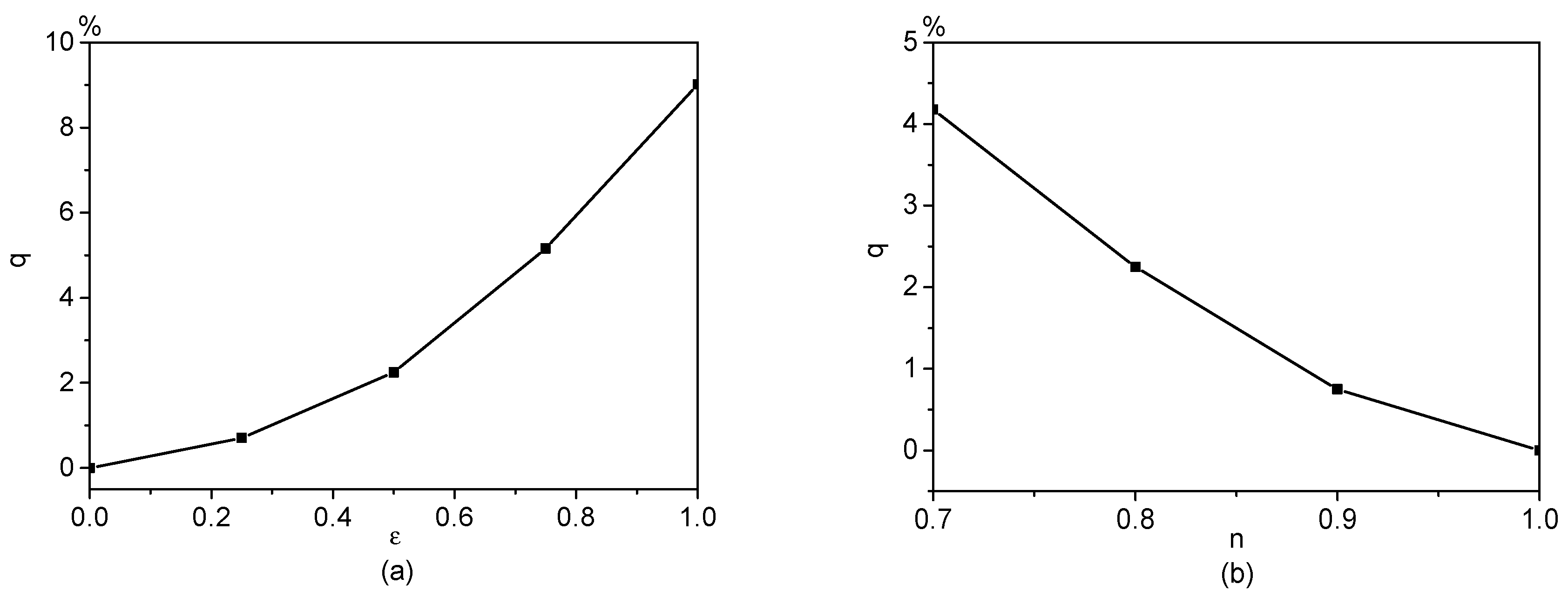
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Zhang, W.; Yang, C. Dynamic Electroosmotic Flows of Power-Law Fluids in Rectangular Microchannels. Micromachines 2017, 8, 34. https://doi.org/10.3390/mi8020034
Zhao C, Zhang W, Yang C. Dynamic Electroosmotic Flows of Power-Law Fluids in Rectangular Microchannels. Micromachines. 2017; 8(2):34. https://doi.org/10.3390/mi8020034
Chicago/Turabian StyleZhao, Cunlu, Wenyao Zhang, and Chun Yang. 2017. "Dynamic Electroosmotic Flows of Power-Law Fluids in Rectangular Microchannels" Micromachines 8, no. 2: 34. https://doi.org/10.3390/mi8020034




