Optimal Control-Based Inverse Determination of Electrode Distribution for Electroosmotic Micromixer
Abstract
:1. Introduction
2. Methodology
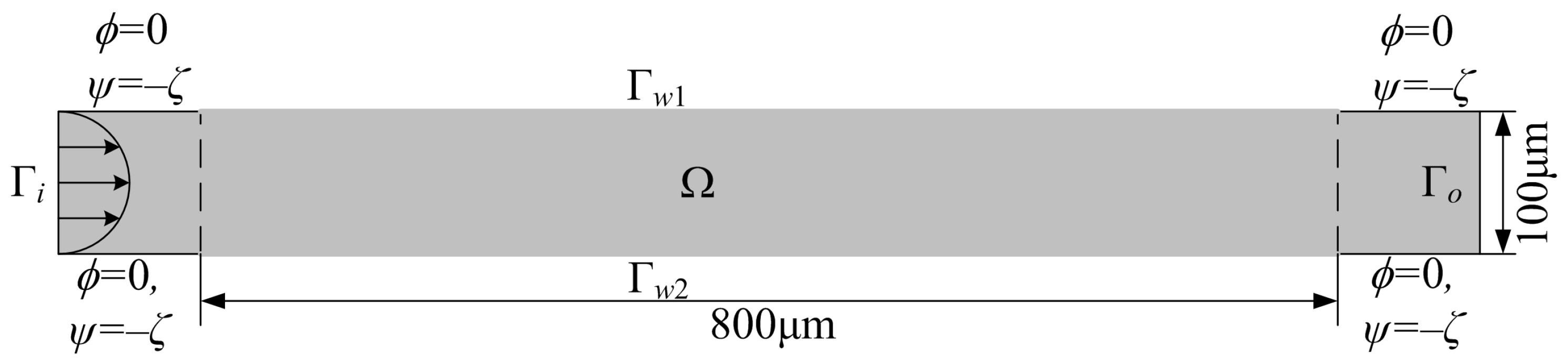
2.1. Modeling
2.2. Analyzing and Solving
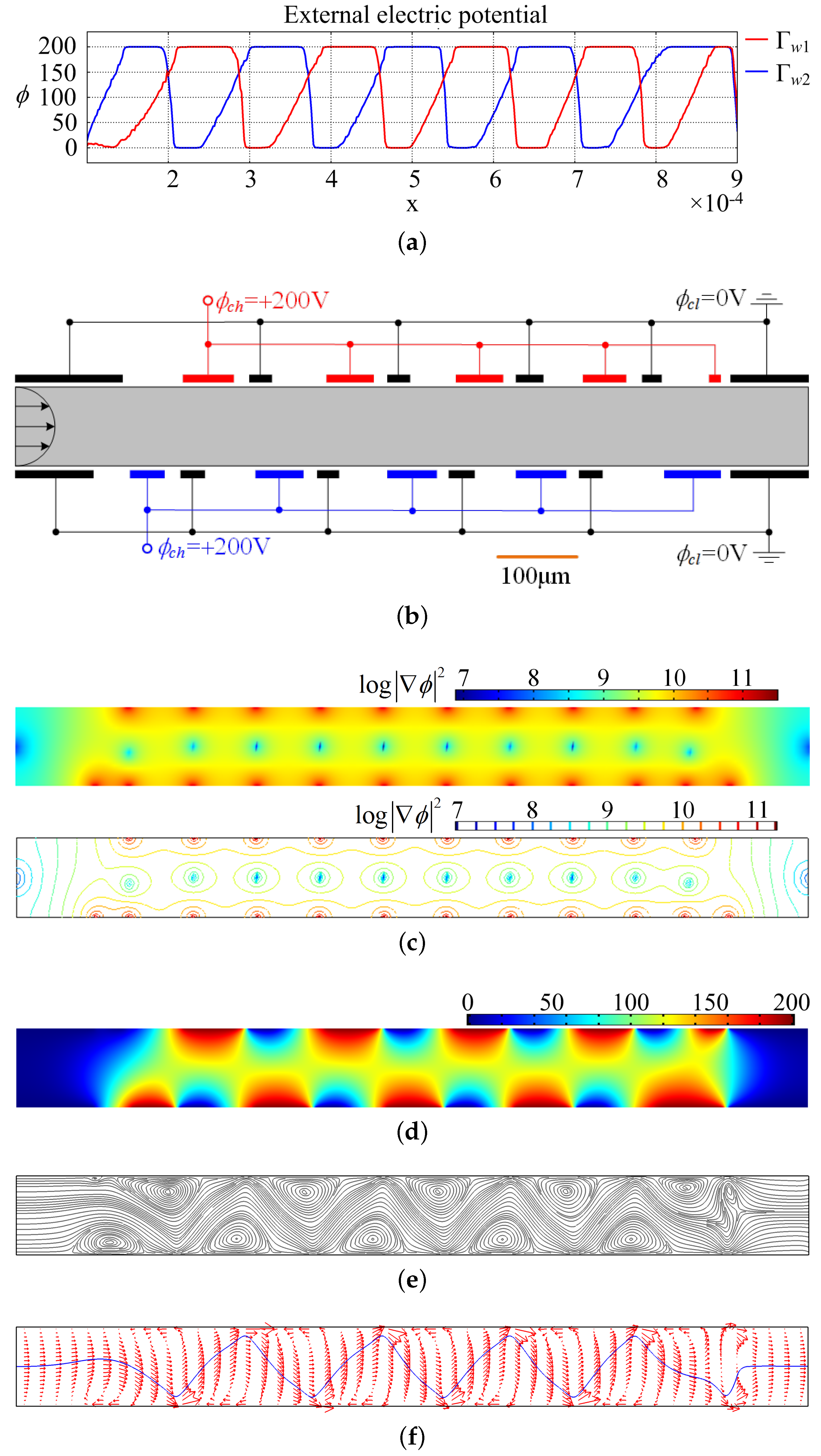
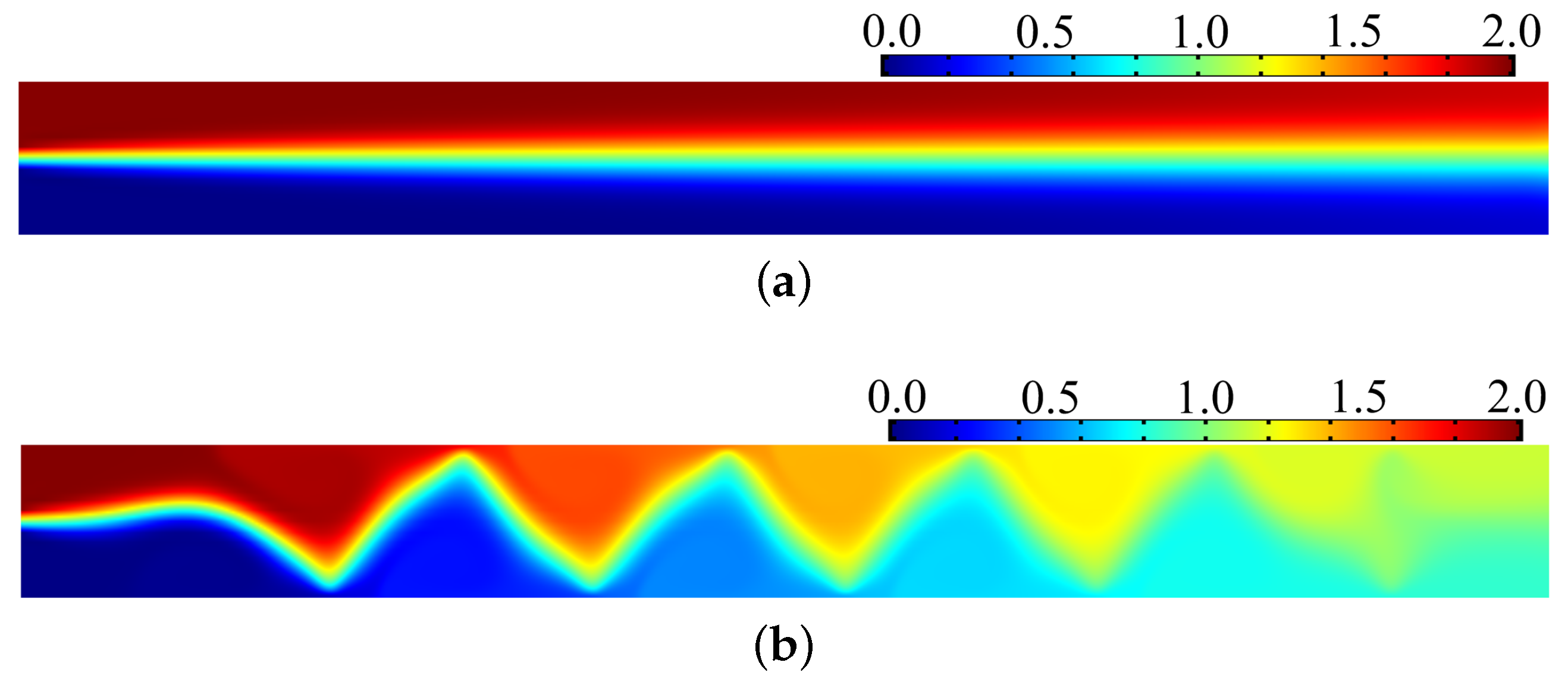
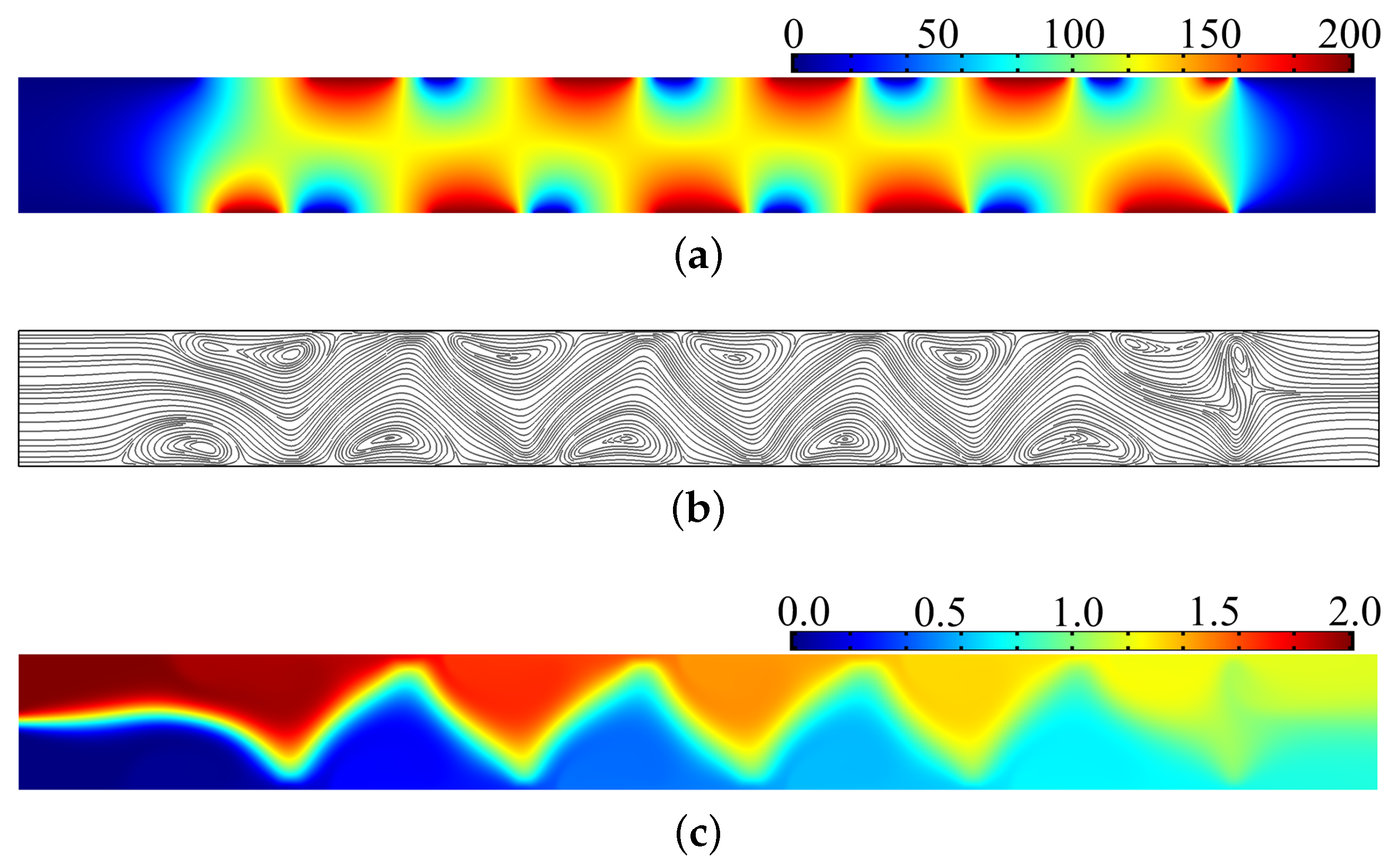
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dittrich, P.S.; Manz, A. Lab-on-a-chip: Microfluidics in drug discovery. Nat. Rev. Drug Discov. 2006, 5, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Manz, A.; Eijkel, J.C.T. Miniaturization and chip technology. What can we expect? Pure Appl. Chem. 2001, 73, 1555–1561. [Google Scholar] [CrossRef]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics on the nanoliter scale. Rev. Mod. Phys. 2005, 77. [Google Scholar] [CrossRef]
- OuYang, L.; Wang, C.; Du, F.; Zheng, T.; Liang, H. Paper electrochromatographic separations of multi-component metal complexes on a microfluidic paper-based device with a simplified photolithography. RSC Adv. 2014, 4, 1093–1101. [Google Scholar] [CrossRef]
- Jeong, G.S.; Chung, S.; Kim, C.B.; Lee, S.H. Applications of micromixing technology. Analyst 2010, 135, 460–473. [Google Scholar] [CrossRef] [PubMed]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezić, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Li, D. Encyclopedia of Microfluidics and Nanofluidics; Springer: Berlin, Germany, 2007. [Google Scholar]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Deng, Y.; Liu, Z.; Zhang, P.; Liu, Y.; Gao, Q.; Wu, Y. A flexible layout design method for passive micromixers. Biomed. Microdevices 2012, 14, 929–945. [Google Scholar] [CrossRef] [PubMed]
- Ammam, M. Electrophoretic deposition under modulated electric fields: A review. RSC Adv. 2012, 2, 7633–7646. [Google Scholar] [CrossRef]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles and Applications; Academic: New York, NY, USA, 1981. [Google Scholar]
- Qian, S.; Ye, A. Electrokinetic Particle Transport in Micro/Nano-fluidics: Direct Numerical Simulation Analysis; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Wang, X.; Cheng, C.; Wang, S.; Liu, S. Electroosmotic pumps and their applications in microfluidic systems. Microfluid Nanofluid 2009, 6, 145–162. [Google Scholar] [CrossRef] [PubMed]
- Johnson, T.J.; Ross, D.; Locascio, L.E. Rapid microfluidic mixing. Anal. Chem. 2002, 74, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Yang, R.J. Electrokinetic Mixing in Microfluidic Systems. Microfluid Nanofluid 2007, 3, 501–525. [Google Scholar] [CrossRef]
- Oddy, M.H.; Santiago, J.G.; Mikkelsen, J.C. Electrokinetic instability micromixing. Anal. Chem. 2001, 73, 5822–5832. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Storey, B.D.; Oddy, M.H.; Chen, C.H.; Santiago, J.G. Instability of electrokinetic microchannel flows with conductivity gradients. Phys. Fluids 2004, 16, 1922–1935. [Google Scholar] [CrossRef]
- Chen, C.H.; Lin, H.; Lele, S.K.; Santiago, J.G. Convective and absolute electrokinetic instability with conductivity gradients. J. Fluid Mech. 2005, 524, 263–303. [Google Scholar] [CrossRef]
- Shin, S.M.; Kang, I.S.; Cho, Y.K. Mixing enhancement by using electrokinetic instability under time-periodic electric field. J. Micromech. Microeng. 2005, 15, 455–462. [Google Scholar] [CrossRef]
- Qian, S.; Bau, H.H. A chaotic electroosmotic stirrer. Anal. Chem. 2002, 74, 3616–3625. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Yang, R.J. A particle tracking method for analyzing chaotic electroosmotic flow mixing in 3D microchannels with patterned charged surfaces. J. Micromech. Microeng. 2006, 16, 1453–1462. [Google Scholar] [CrossRef]
- Zhang, J.B.; He, G.W.; Liu, F. Electroosmotic flow and mixing in heterogeneous microchannels. Phys. Rev. E 2006, 73. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.Y.; Lam, Y.C.; Yang, C. Mixing enhancement in microfluidic channel with a constriction under periodic electroosmotic flow. Biomicrofluidics 2010, 4. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, J.R. Mixing enhancement in electroosmotic flows via modulation of electric fields. Phys. Fluids 2008, 20. [Google Scholar] [CrossRef]
- Chen, L.; Deng, Y.; Zhou, T.; Pan, H.; Liu, Z. A novel electroosmotic micromixer with asymmetric lateral structures and DC electrode arrays. Micromachines 2017, 8, 105. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, H.; Shi, L.; Liu, Z.; Joo, S.W. An enhanced electroosmotic micromixer with an efficient asymmetric lateral structure. Micromachines 2016, 7, 218. [Google Scholar] [CrossRef]
- Jain, M.; Yeung, A.; Nandakumar, K. Induced charge electro osmotic mixer: Obstacle shape optimization. Biomicrofluidics 2009, 3. [Google Scholar] [CrossRef] [PubMed]
- Yuecel, H.; Benner, P. Adaptive discontinuous Galerkin methods for state constrained optimal control problems governed by convection diffusion equations. Comput. Optim. Appl. 2015, 62, 291–321. [Google Scholar] [CrossRef]
- De Los Reye, J.C.; Yousept, I. Optimal control of electrorheological fluids through the action of electric fields. Comput. Optim. Appl. 2015, 62, 241–270. [Google Scholar] [CrossRef]
- Danckwerts, P. The difinition and measurement of some characteristics of mixtures. Appl. Sci. Res. 1952, 3, 279–296. [Google Scholar] [CrossRef]
- Probstein, R.F. Physicochemical Hydrodynamics: An Introduction; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Patankar, N.A.; Hu, H.H. Numerical simulations of electroosmotic flow. Anal. Chem. 1998, 70, 1870–1881. [Google Scholar] [CrossRef] [PubMed]
- Lazarov, B.; Sigmund, O. Filters in topology optimization based on Helmholtz type differential equations. Int. J. Numer. Methods Eng. 2011, 86, 765–781. [Google Scholar] [CrossRef]
- Guest, J.; Prevost, J.; Belytschko, T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Methods Eng. 2004, 61, 238–254. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Liu, Y.; Wu, Y. Combination of topology optimization and optimal control method. J. Comput. Phys. 2014, 257, 374–399. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes: A new method for structural optimization. Int. J. Numer. Meth. Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Topology optimization of fluid in Stokes flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Hinze, M.; Pinnau, R.; Ulbrich, M.; Ulbrich, S. Optimization with PDE Constraints; Springer: Berlin, Germany, 2009. [Google Scholar]
- Donea, J.; Hureta, A. Finite Element Methods for Flow Problems; Wiley: West Sussex, UK, 2003. [Google Scholar]
- Andreasen, C.S.; Gersborg, A.R.; Sigmund, O. Topology optimization of microfluidic mixers. Int. J. Numer. Methods Fluids 2009, 61, 498–513. [Google Scholar] [CrossRef]



| 1. Give the initial value of the control variable ; |
| 2. Solve the coupled system of Equations (2), (4), (6), and (8) by the finite element method; |
| 3. Solve the weak form adjoint equations (Equations (17)–(19), and (21)); |
| 4. Compute the adjoint derivatives (Equations (20) and (22)) and |
| the corresponding objective and constraint values; |
| 5. Update the control variable by MMA; |
| 6. Check for convergence; if the stopping conditions are not satisfied, go to 2; and |
| 7. Post-processing |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Deng, Y.; Liu, Z.; Zhou, T.; Wu, Y.; Qian, S. Optimal Control-Based Inverse Determination of Electrode Distribution for Electroosmotic Micromixer. Micromachines 2017, 8, 247. https://doi.org/10.3390/mi8080247
Ji Y, Deng Y, Liu Z, Zhou T, Wu Y, Qian S. Optimal Control-Based Inverse Determination of Electrode Distribution for Electroosmotic Micromixer. Micromachines. 2017; 8(8):247. https://doi.org/10.3390/mi8080247
Chicago/Turabian StyleJi, Yuan, Yongbo Deng, Zhenyu Liu, Teng Zhou, Yihui Wu, and Shizhi Qian. 2017. "Optimal Control-Based Inverse Determination of Electrode Distribution for Electroosmotic Micromixer" Micromachines 8, no. 8: 247. https://doi.org/10.3390/mi8080247





