Nonlinear Robust Adaptive Multi-Modal Vibration Control of Bi-Electrode Micro-Switch with Constraints on the Input
Abstract
:1. Introduction
2. Dynamic Modeling and Equations of Motion
2.1. Continuous Modeling
2.2. Discretized Modeling
3. Active Vibration Control of a Nonlinear System
- (i)
- , and are bounded for any .
- (ii)
- for any bounded disturbance and , the following inequality holds for some positive numbers , , andas long as is square integrable and is absolutely integrable. is the vector of estimates of the unknown parameters, which is updated by an adaptation law,
- (iii)
- when the disturbance is zero at all times, and (the regulation control problem), converges to zero asymptotically.
- (a)
- (b)
- is Lipschitz and continuous
- (c)
- (d)
- .
4. Simulations and Discussion
4.1. Safe Region for Applied Voltage
4.2. Safe Region for Applied Voltage
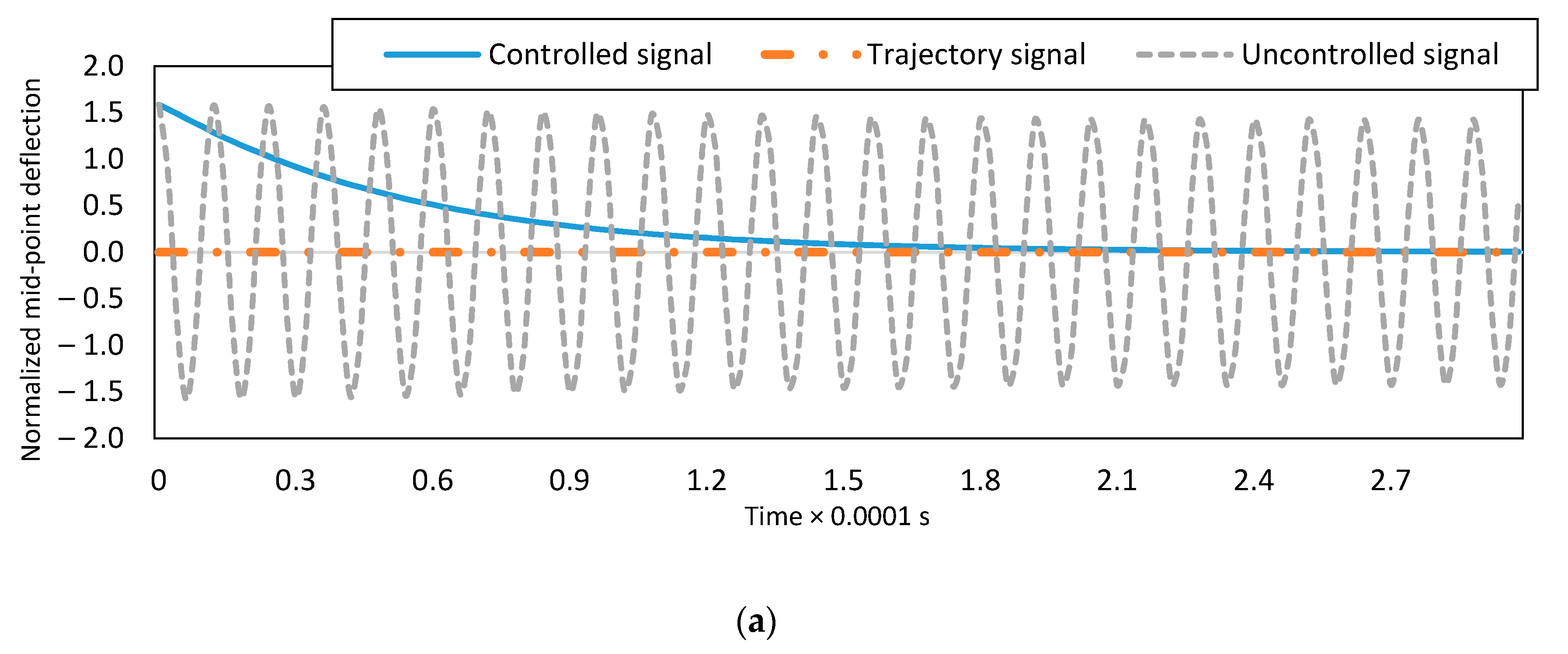
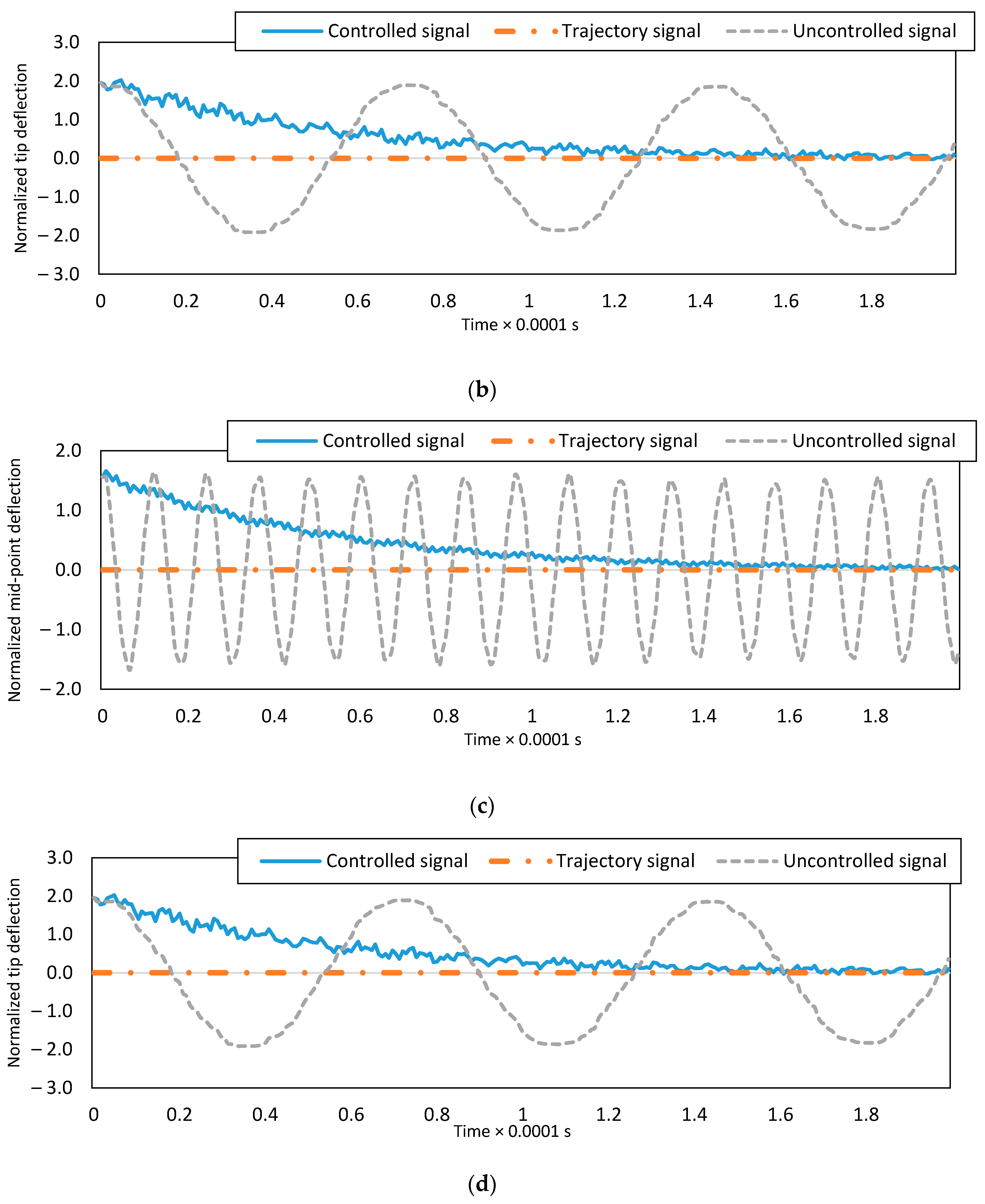
4.3. Multimode Simulation of the Controlled System in Regulation
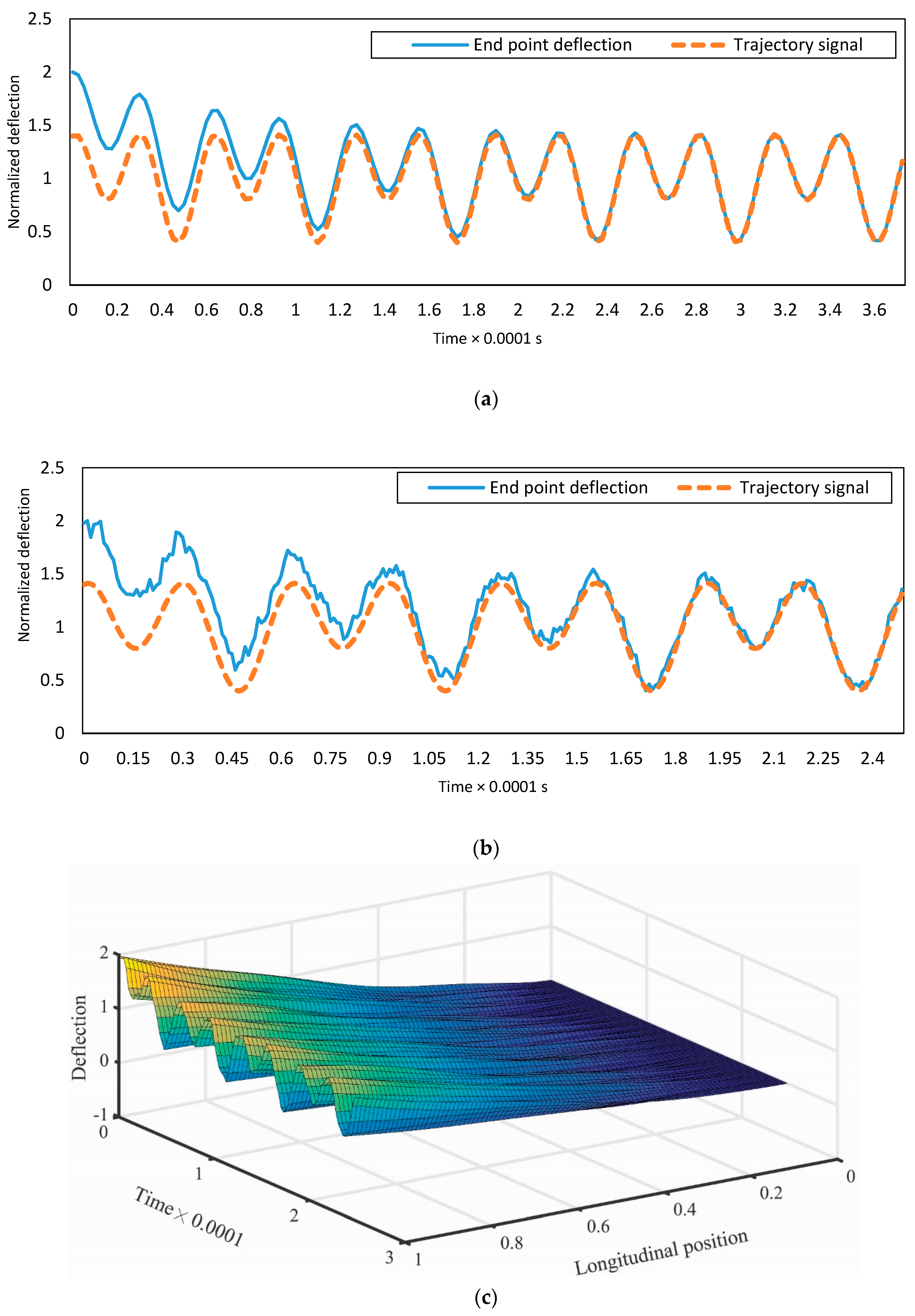
4.4. Tracking the Non-Zero Desired Dynamical Response
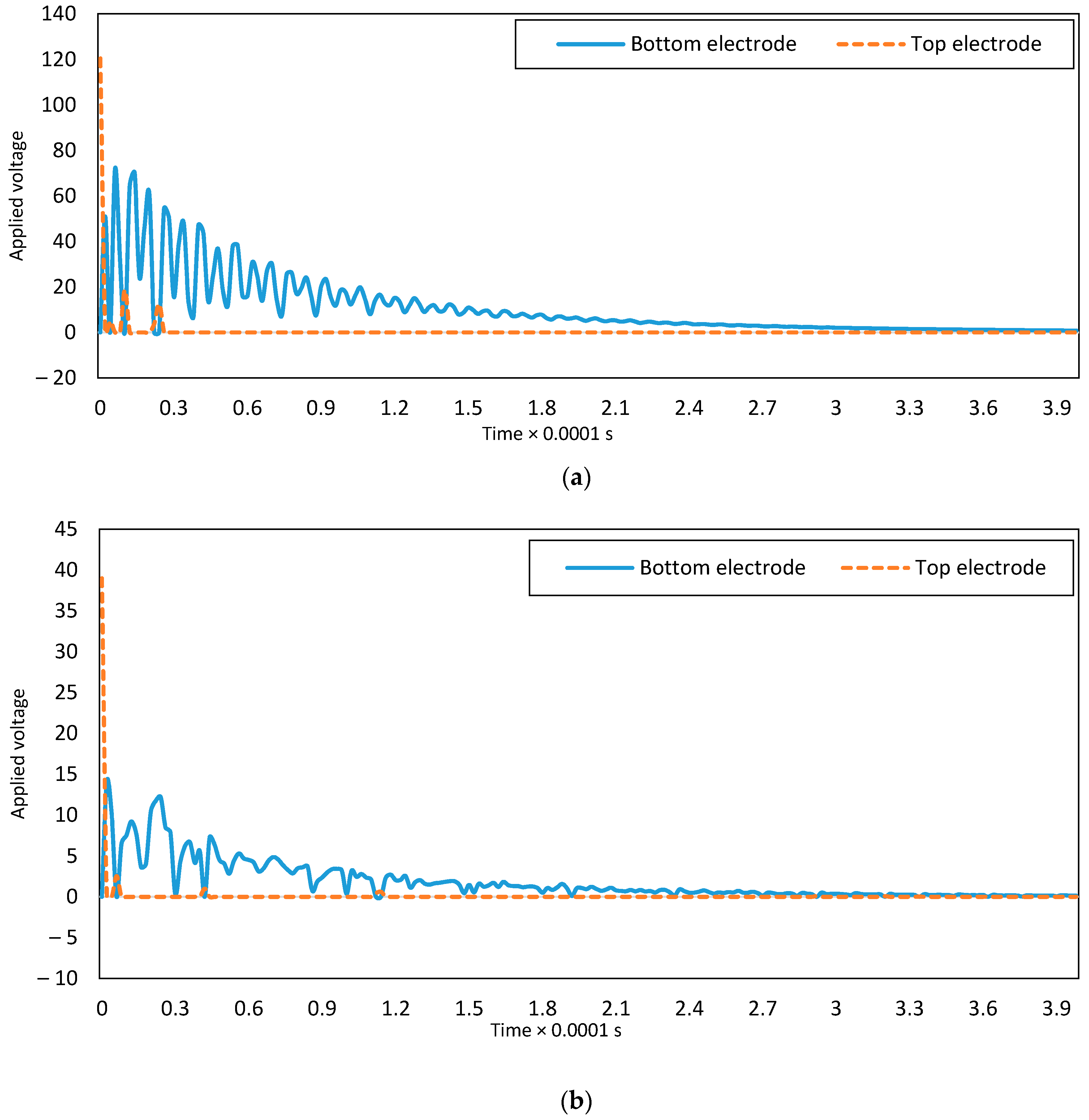
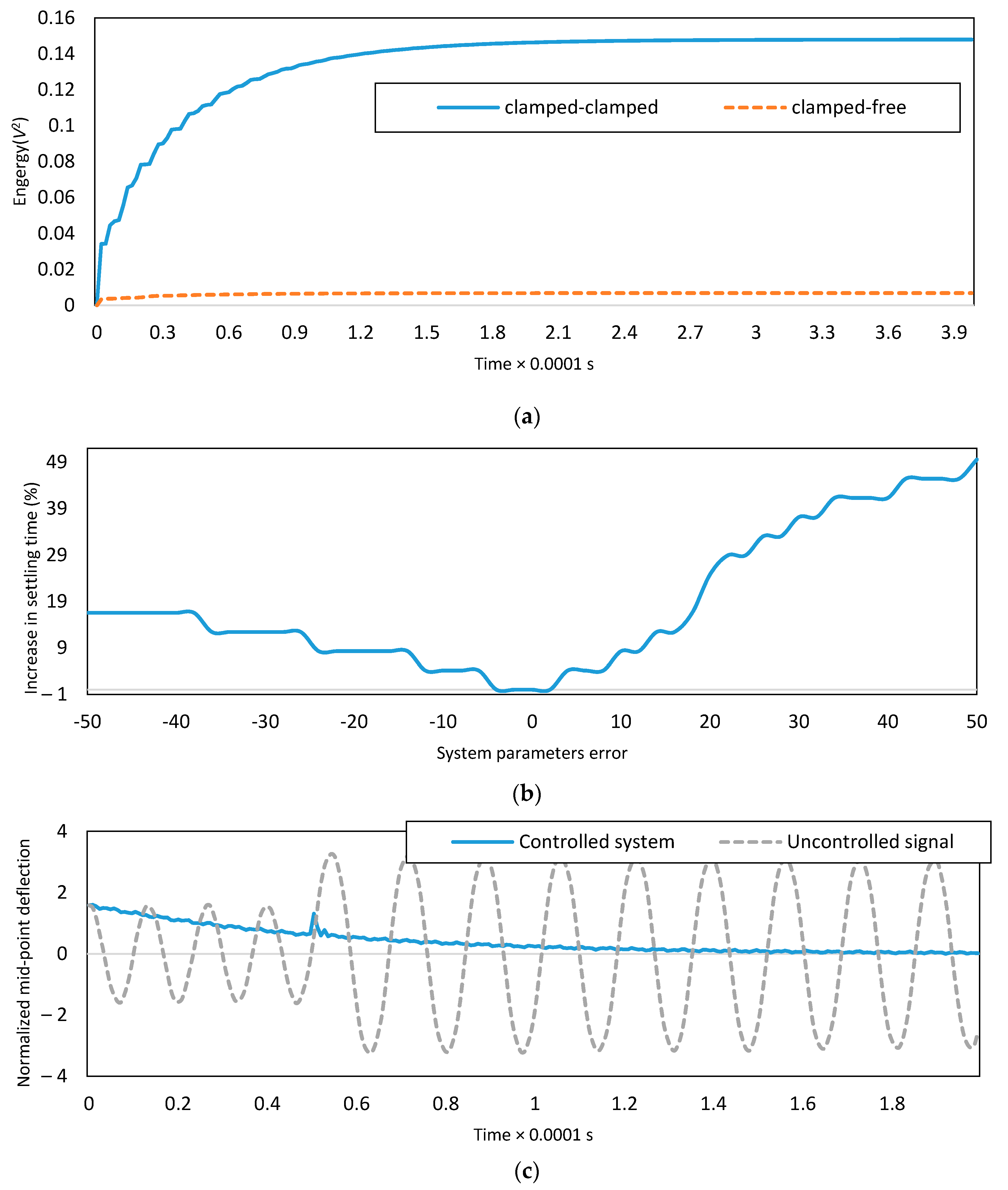
4.5. Energy Consumption
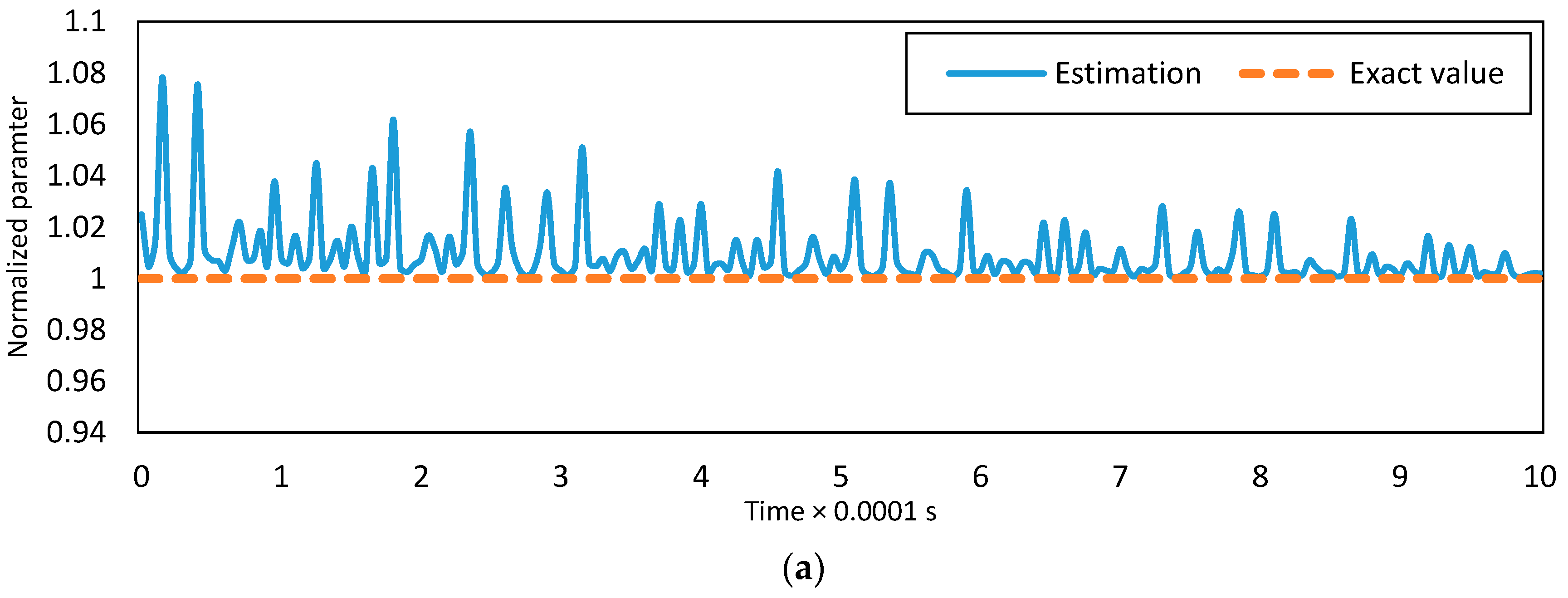
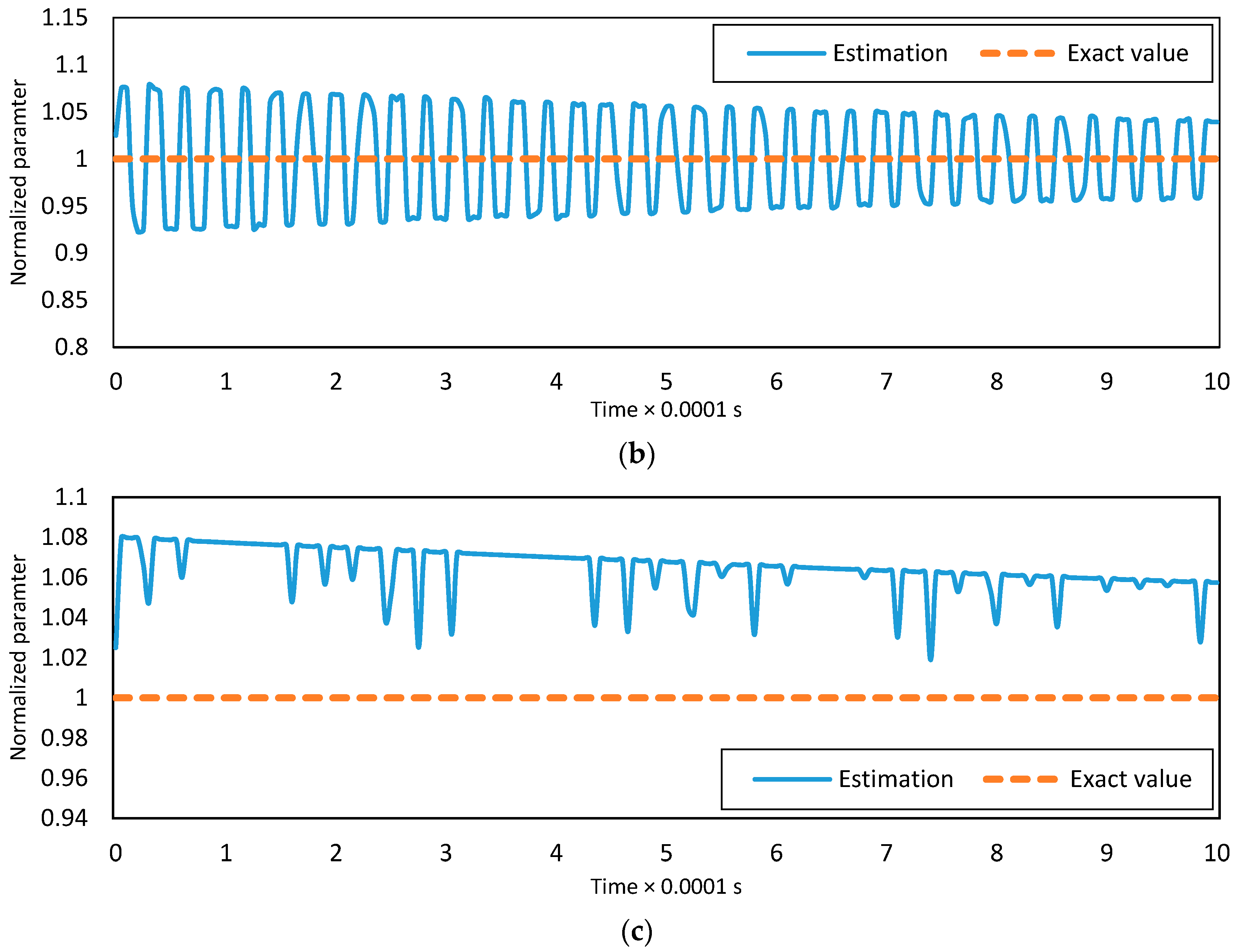
4.6. Effect of Error of Initial Estimates of the Parameters
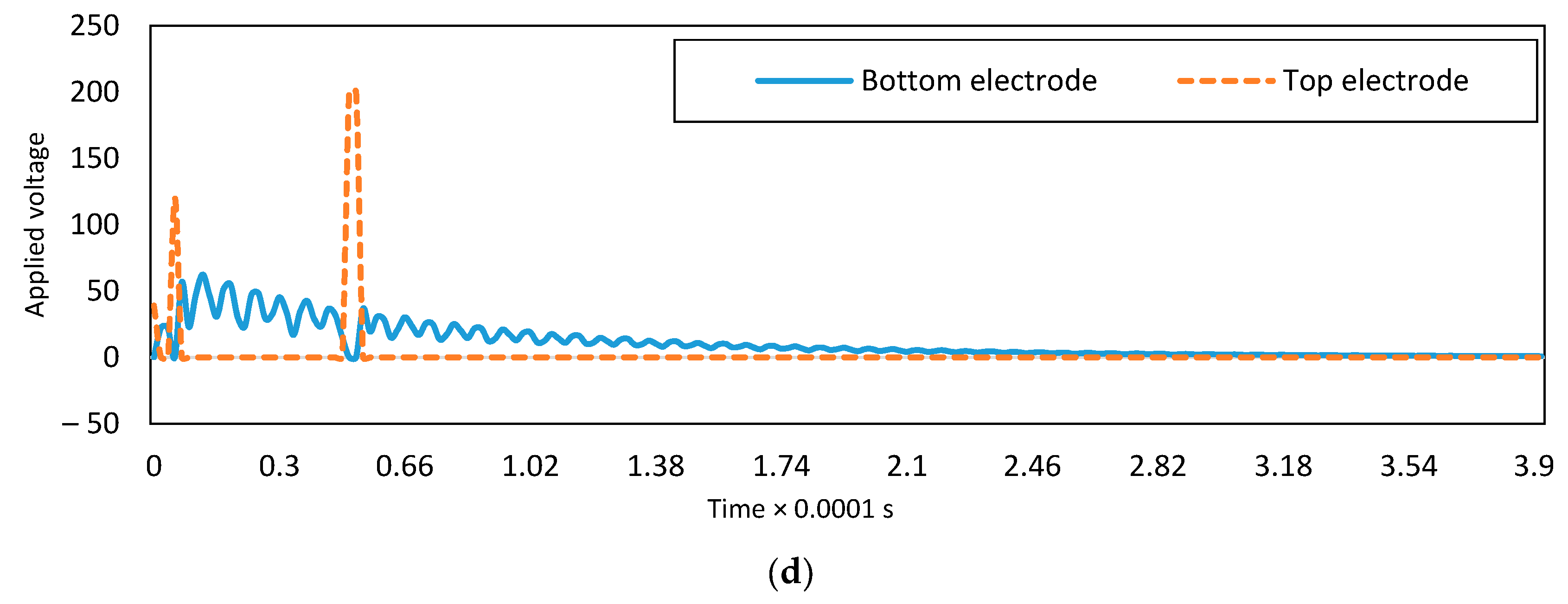
4.7. Effect of Impulse on the System
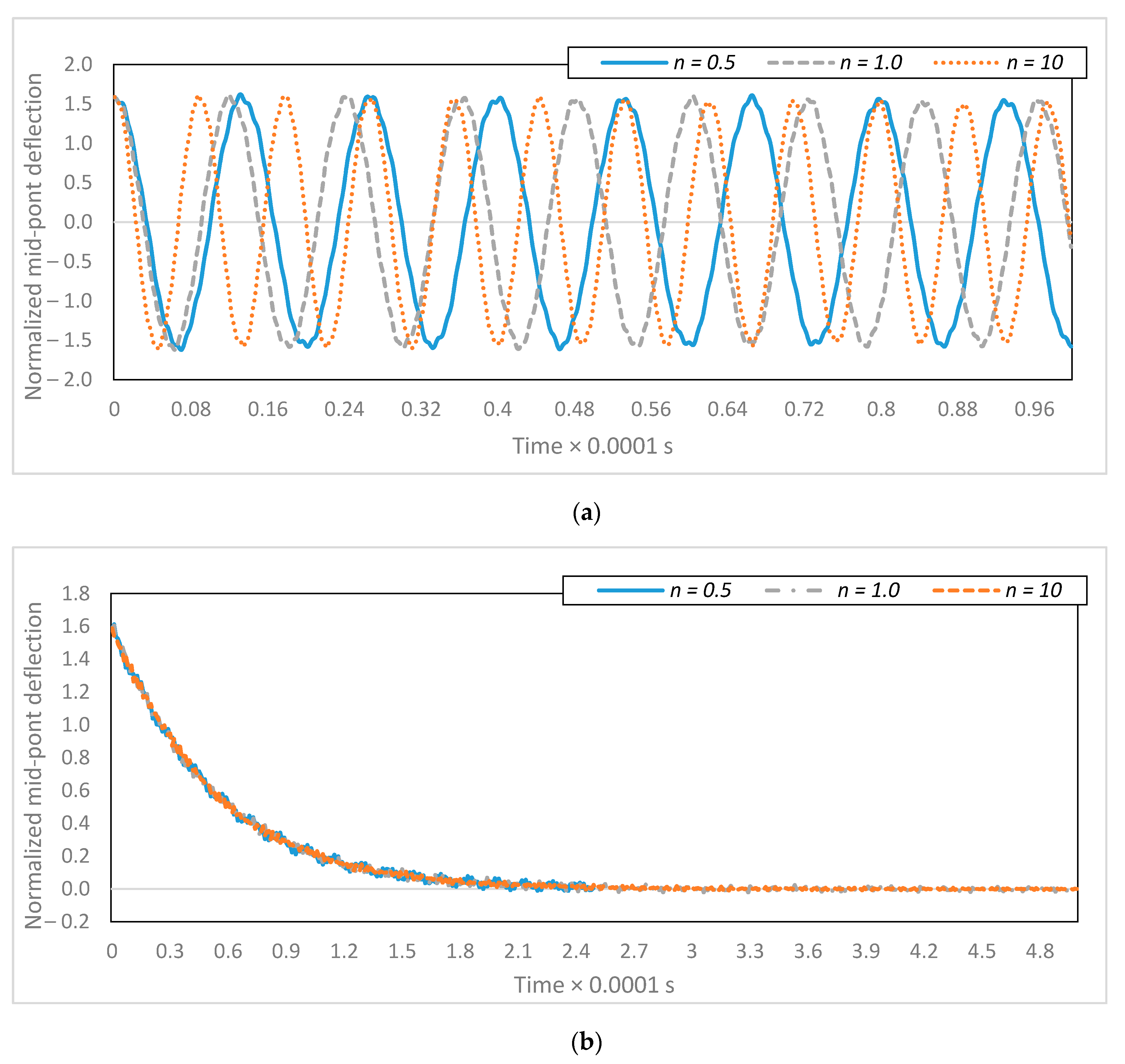
4.8. Effect of Material Volume Fraction
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Spearing, S.M. Materials issues in microelectromechanical systems (MEMS). Acta Mater. 2000, 48, 179–196. [Google Scholar] [CrossRef]
- Maluf, N.; Williams, K. Introduction to Microelectromechanical Systems Engineering; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Aktakka, E.E.; Peterson, R.L.; Najafi, K. High stroke and high deflection bulk-PZT diaphragm and cantilever micro actuators and effect of pre-stress on device performance. J. Microelectromech. Syst. 2014, 23, 438–451. [Google Scholar] [CrossRef]
- Jia, X.L.; Yang, J.; Kitipornchai, S.; Lim, C.W. Resonance frequency response of geometrically nonlinear micro-switches under electrical actuation. J. Sound Vib. 2012, 331, 3397–3411. [Google Scholar] [CrossRef]
- Butt, H.J.; Cappella, B.; Kappl, M. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar] [CrossRef]
- Schliesser, A.; Kippenberg, T.J. Cavity optomechanics with whispering-gallery mode optical micro-resonators. Adv. At. Mol. Opt. Phys. 2010, 58, 207–323. [Google Scholar]
- Rabin, B.; Shiota, I. Functionally Gradient Materials. MRS Bull. 1995, 20, 14–18. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing and Applications; Springer Science & Business Media: Berlin, Germany, 2013; Volume 5. [Google Scholar]
- Chakraborty, A.; Gopalakrishnan, S.; Reddy, J.N. A new beam finite element for the analysis of functionally graded materials. Int. J. Mech. Sci. 2003, 45, 519–539. [Google Scholar] [CrossRef]
- Mohammadi, H.; Mahzoon, M.; Mohammadi, M.; Mohammadi, M. Postbuckling instability of nonlinear nanobeam with geometric imperfection embedded in elastic foundation. Nonlinear Dyn. 2014, 76, 2005–2016. [Google Scholar] [CrossRef]
- Mohammadi, H.; Mahzoon, M. Thermal effects on postbuckling of nonlinear microbeams based on the modified strain gradient theory. Compos. Struct. 2013, 106, 764–776. [Google Scholar] [CrossRef]
- Sankar, B.V. An elasticity solution for functionally graded beams. Compos. Sci. Technol. 2001, 61, 689–696. [Google Scholar] [CrossRef]
- Aydogdu, M.; Taskin, V. Free vibration analysis of functionally graded beams with simply supported edges. Mater. Des. 2007, 28, 1651–1656. [Google Scholar] [CrossRef]
- Witvrouw, A.; Mehta, A. The use of functionally graded poly-SiGe layers for MEMS applications. In Materials Science Forum; Trans. Tech. Publications: Zurich, Switzerland, 2005; pp. 255–260. [Google Scholar]
- Fu, Y.; Du, H.; Zhang, S. Functionally graded TiN/TiNi shape memory alloy films. Mater. Lett. 2003, 57, 2995–2999. [Google Scholar] [CrossRef]
- Rahaeifard, M.; Kahrobaiyan, M.H.; Ahmadian, M.T. Sensitivity analysis of atomic force microscope cantilever made of functionally graded materials. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; American Society of Mechanical Engineers: New York, NY, USA, 2009; pp. 539–544. [Google Scholar]
- Farokhi, H.; Ghayesh, M.H. Electrically actuated MEMS resonators: Effects of fringing field and nonlinear viscoelasticity. Mech. Syst. Signal Process. 2017, 95, 345–362. [Google Scholar] [CrossRef]
- Farokhi, H.; Misra, A.K.; Païdoussis, M.P. A new electrostatic load model for initially curved carbon nanotube resonators: Pull-in characteristics and nonlinear resonant behaviour. Nonlinear Dyn. 2017, 88, 1187–1211. [Google Scholar] [CrossRef]
- De Pietro, G.; Hui, Y.; Giunta, G.; Belouettar, S.; Carrera, E.; Hu, H. Hierarchical one-dimensional finite elements for the thermal stress analysis of three-dimensional functionally graded beams. Compos. Struct. 2016, 153, 514–528. [Google Scholar] [CrossRef]
- Giunta, G.; Koutsawa, Y.; Belouettar, S.; Hu, H. Analysis of nano-plates by atomistic-refined models accounting for surface free energy effect. Acta Mech. 2014, 225, 31–51. [Google Scholar] [CrossRef]
- Fleck, N.A.; Muller, G.M.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Stölken, J.S.; Evans, A.G. A microbend test method for measuring the plasticity length scale. Acta Mater. 1998, 46, 5109–5115. [Google Scholar] [CrossRef]
- Asghari, M.; Ahmadian, M.T.; Kahrobaiyan, M.H.; Rahaeifard, M. On the size-dependent behavior of functionally graded micro-beams. Mater. Des. 2010, 31, 2324–2329. [Google Scholar] [CrossRef]
- Giunta, G.; Koutsawa, Y.; Belouettar, S.; Hu, H. Static, free vibration and stability analysis of three-dimensional nano-beams by atomistic refined models accounting for surface free energy effect. Int. J. Solids Struct. 2013, 50, 1460–1472. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of size-dependent functionally graded microbeams. Int. J. Eng. Sci. 2012, 50, 256–267. [Google Scholar] [CrossRef]
- Mohammadi, H.; Mahzoon, M. Investigating thermal effects in nonlinear buckling analysis of micro beams using modified strain gradient theory. Iran. J. Sci. Tech. Trans. Mech. Eng. 2014, 38, 303–320. [Google Scholar]
- Asghari, M.; Rahaeifard, M.; Kahrobaiyan, M.H.; Ahmadian, M.T. The modified couple stress functionally graded Timoshenko beam formulation. Mater. Des. 2011, 32, 1435–1443. [Google Scholar] [CrossRef]
- Farokhi, H.; Païdoussis, M.P.; Misra, A.K. A new nonlinear model for analyzing the behaviour of carbon nanotube-based resonators. J. Sound Vib. 2016, 378, 56–75. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent performance of microgyroscopes. Int. J. Eng. Sci. 2016, 100, 99–111. [Google Scholar] [CrossRef]
- Giunta, G.; Crisafulli, D.; Belouettar, S.; Carrera, E. Hierarchical theories for the free vibration analysis of functionally graded beams. Compos. Struct. 2011, 94, 68–74. [Google Scholar] [CrossRef]
- Mohammadi-Alasti, B.; Rezazadeh, G.; Borgheei, A.M.; Minaei, S.; Habibifar, R. On the mechanical behavior of a functionally graded micro-beam subjected to a thermal moment and nonlinear electrostatic pressure. Compos. Struct. 2011, 93, 1516–1525. [Google Scholar] [CrossRef]
- Jia, X.L.; Yang, J.; Kitipornchai, S.; Lim, C.W. Pull-in instability and free vibration of electrically actuated poly-SiGe graded micro-beams with a curved ground electrode. Appl. Math. Model. 2012, 36, 1875–1884. [Google Scholar] [CrossRef]
- Jia, X.L.; Ke, L.L.; Feng, C.B.; Yang, J.; Kitipornchai, S. Size effect on the free vibration of geometrically nonlinear functionally graded micro-beams under electrical actuation and temperature change. Compos. Struct. 2015, 133, 1137–1148. [Google Scholar] [CrossRef]
- Jia, X.L.; Yang, J.; Kitipornchai, S. Pull-in instability of geometrically nonlinear micro-switches under electrostatic and Casimir forces. Acta Mech. 2011, 218, 161–174. [Google Scholar] [CrossRef]
- Chen, K.S.; Ou, K.S. Command-shaping techniques for electrostatic MEMS actuation: Analysis and simulation. J. Microelectromech. Syst. 2007, 16, 537–549. [Google Scholar] [CrossRef]
- Alsaleem, F.; Younis, M.I. Integrity analysis of electrically actuated resonators with delayed feedback controller. J. Dyn. Syst. Meas. Control 2011, 133, 031011. [Google Scholar] [CrossRef]
- Fu, Y.; Unnithan, V. Forward modeling of paleo heat flow: A case study of Kristin Field, Mid-Norwegian continental shelf. In Proceedings of the OCEANS 2009-EUROPE, Bremen, Germany, 11–14 May 2009; pp. 1–9. [Google Scholar]
- Batur, C.; Sreeramreddy, T.; Khasawneh, Q. Sliding mode control of a simulated MEMS gyroscope. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 4160–4165. [Google Scholar]
- Vagia, M. A frequency independent approximation and a sliding mode control scheme for a system of a micro-cantilever beam. ISA Trans. 2012, 51, 325–332. [Google Scholar] [CrossRef] [PubMed]
- Sadek, I.; Kucuk, I.; Zeini, E.; Adali, S. Optimal boundary control of dynamics responses of piezo actuating micro-beams. Appl. Math. Model. 2009, 33, 3343–3353. [Google Scholar] [CrossRef]
- Nguyen, Q.C.; Krylov, S. Nonlinear tracking control of vibration amplitude for a parametrically excited microcantilever beam. J. Sound Vib. 2015, 338, 91–104. [Google Scholar] [CrossRef]
- Shivashankar, P.; Kandagal, S.B. Analytical modeling and optimal resistance estimation in vibration control of beams with resistively shunted piezoelectrics. Int. J. Mech. Sci. 2016, 119, 310–319. [Google Scholar] [CrossRef]
- Sun, Y.; Nelson, B.J.; Potasek, D.P.; Enikov, E. A bulk microfabricated multi-axis capacitive cellular force sensor using transverse comb drives. J. Micromech. Microeng. 2002, 12, 832. [Google Scholar] [CrossRef]
- Sun, Y.; Piyabongkarn, D.; Sezen, A.; Nelson, B.J.; Rajamani, R. A high-aspect-ratio two-axis electrostatic microactuator with extended travel range. Sens. Actuators A Phys. 2002, 102, 49–60. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Hussain, S. Large-amplitude dynamical behaviour of microcantilevers. Int. J. Eng. Sci. 2016, 106, 29–41. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A. Dynamics of functionally graded micro-cantilevers. Int. J. Eng. Sci. 2017, 115, 117–130. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Hussain, S. Modal interactions and energy transfers in large-amplitude vibrations of functionally graded microcantilevers. J. Vib. Control 2017. [Google Scholar] [CrossRef]
- Pomet, J.B.; Praly, L. Adaptive nonlinear regulation: Estimation from the Lyapunov equation. IEEE Trans. Autom. Control 1992, 37, 729–740. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1996; Volume 3. [Google Scholar]
- Ibrahim, A.; Jaber, N.; Chandran, A.; Thirupathi, M.; Younis, M. Dynamics of Microbeams under Multi-Frequency Excitations. Micromachines 2017, 8, 32. [Google Scholar] [CrossRef]
- Hu, Y.C.; Chang, C.M.; Huang, S.C. Some design considerations on the electrostatically actuated microstructures. Sens. Actuators A Phys. 2004, 112, 155–161. [Google Scholar] [CrossRef]
- Zhang, W.M.; Yan, H.; Peng, Z.K.; Meng, G. Electrostatic pull-in instability in MEMS/NEMS: A review. Sens. Actuators A Phys. 2014, 214, 187–218. [Google Scholar] [CrossRef]
- Mohammadi, M.; Eghtesad, M.; Mohammadi, H. Stochastic analysis of dynamic characteristics and pull-in instability of FGM micro-switches with uncertain parameters in thermal environments. Int. J. Mech. Mater. Des. 2017. [Google Scholar] [CrossRef]
- Sastry, S.; Bodson, M. Adaptive Control: Stability, Convergence and Robustness; Dover Publications: Mineola, NY, USA, 2011. [Google Scholar]


| Boundary Conditions | |||||
|---|---|---|---|---|---|
| C-C | 4.7300 | 7.8532 | 10.9956 | 14.1371 | 17.2787 |
| C-F | 1.8751 | 4.6941 | 7.8548 | 10.9955 | 14.1372 |
| Material Property | Silicon Nitride (Si3N4) | Nickel (Ni) |
|---|---|---|
| Density () | ||
| Young’s modulus () | ||
| Shear modulus () | ||
| Poisson’s ratio |
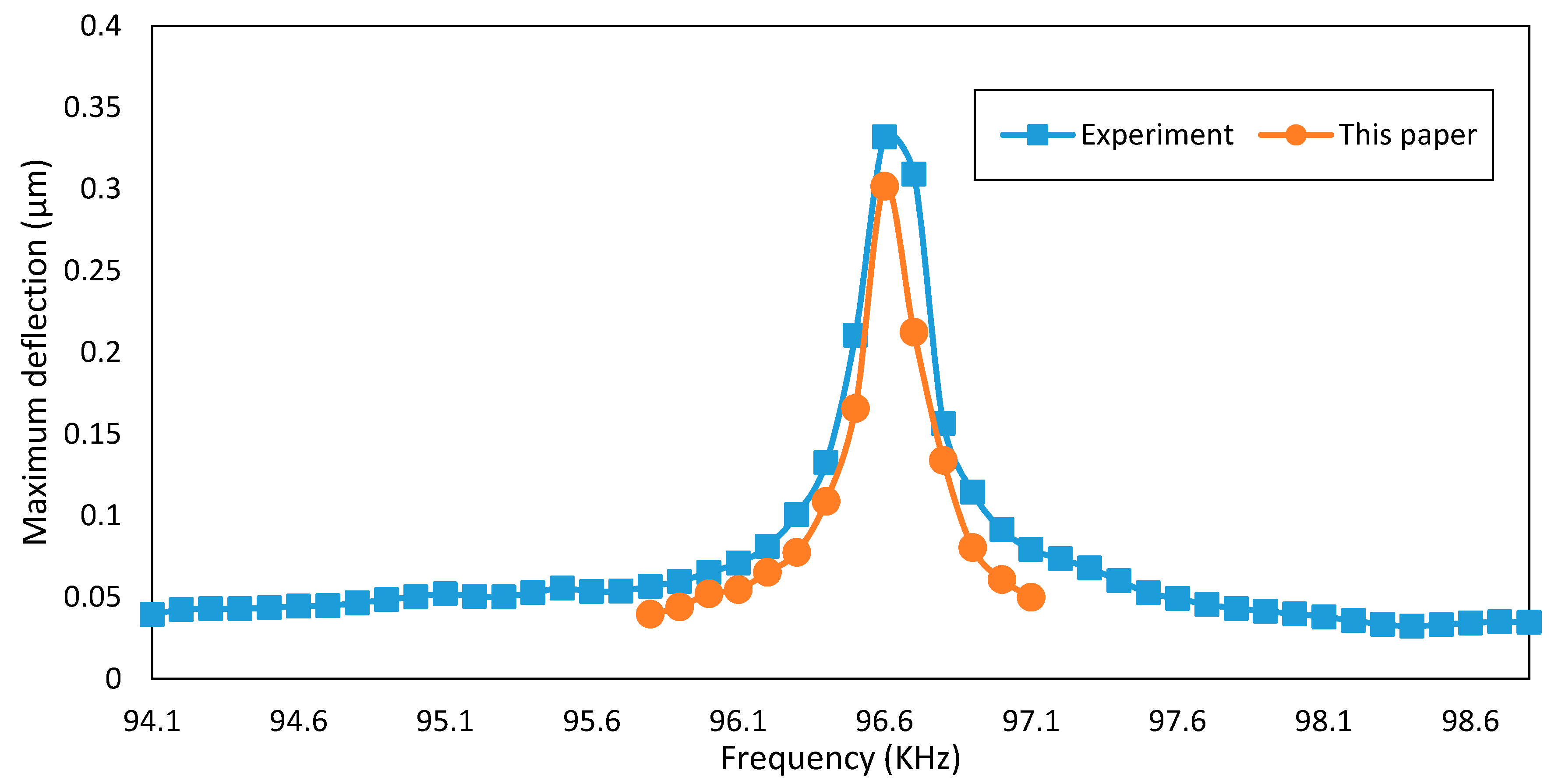
| Applied Voltage | This Paper | Experimental Data | Error (%) |
|---|---|---|---|
| 0 | 92 | 92.415 | 0.451087 |
| 20 | 90.41261 | 91.018 | 0.669583 |
| 40 | 85.21468 | 84.232 | 1.153177 |
| 45 | 81.97923 | 81.437 | 0.661419 |
| 50 | 79.51302 | 78.643 | 1.09419 |
| 55 | 75.30798 | 74.651 | 0.872396 |
| 60 | 71.47106 | 70.06 | 1.974304 |
| 64 | 64.40234 | 62.874 | 2.373112 |
| 67 | 59.20658 | 57.485 | 2.907757 |
| 69 | 52.79904 | 51 | 3.407331 |
| Boundary Conditions | The Top Electrode | The Bottom Electrode | ||||
|---|---|---|---|---|---|---|
| C-C | 261.0 V | 267.8 V | 285.5 V | 160.6 V | 165.5 V | 173 V |
| C-F | 43.0 V | 44.1 V | 49.9 V | 25.3 V | 24.7 V | 26.5 V |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, M.; Eghtesad, M.; Mohammadi, H.; Necsulescu, D. Nonlinear Robust Adaptive Multi-Modal Vibration Control of Bi-Electrode Micro-Switch with Constraints on the Input. Micromachines 2017, 8, 263. https://doi.org/10.3390/mi8090263
Mohammadi M, Eghtesad M, Mohammadi H, Necsulescu D. Nonlinear Robust Adaptive Multi-Modal Vibration Control of Bi-Electrode Micro-Switch with Constraints on the Input. Micromachines. 2017; 8(9):263. https://doi.org/10.3390/mi8090263
Chicago/Turabian StyleMohammadi, Mohsen, Mohammad Eghtesad, Hossein Mohammadi, and Dan Necsulescu. 2017. "Nonlinear Robust Adaptive Multi-Modal Vibration Control of Bi-Electrode Micro-Switch with Constraints on the Input" Micromachines 8, no. 9: 263. https://doi.org/10.3390/mi8090263




