Economic Harmony: An Epistemic Theory of Economic Interactions

Abstract

We propose an epistemic theory of micro-economic interactions, termed Economic Harmony. In the theory, we modify the standard utility, by changing its argument from the player’s actual payoff, to the ratio between the player’s actual payoff and his or her aspired payoff. We show that the aforementioned minor epistemic modification of the concept of utility is quite powerful in generating plausible and successful predictions of experimental results, obtained in the standard ultimatum game, and the sequential common pool resource dilemma (CPR) game. Notably, the cooperation and fairness observed in the studied games are accounted for without adding an other-regarding component in the players’ utility functions. For the standard ultimatum game, the theory predicts a division of φ and 1 − φ, for the proposer and responder, respectively, where φ is the famous Golden Ratio (≈0.618), most known for its aesthetically pleasing properties. We discuss possible extensions of the proposed theory to repeated and evolutionary ultimatum games.

1. Introduction

The game theoretic approach to human and animal interactions relies on the economic rationality assumption, which prescribes that in any interaction, all players are utility maximizers, and that their utilities are non-decreasing functions of their payoffs. For the case of risk-neutral players, the theory prescribes that rational players will strive to maximize their payoffs. Despite being self-consistent and mathematically sound, standard game theory is, in many cases, at odds with experimental and real-life data. Examples of strategic interactions in which the standard game theoretic predictions fail to account for human behavior, include experimental and real-life data on the provision of public goods, the management of common pool resources, bargaining situations, and situations involving trust.

From a philosophical perspective, the assumption of risk neutrality, or even of a homogeneous population with respect to risk behavior, deprives game theory from an important epistemic attribute. The fact that game theory fails to consider the players’ cognitions, motivations, aspirations, and other individual attributes, reduces the analysis of economic interactions to an ontological level, in which the behaviors of players involved in the interaction are thought to be solely determined by the formal game structure. According to the standard approach, the variability of data resulting from individual differences is measurement noise which should be reduced to a minimum. Proponents of such an approach advise experimentalists to strive for lowering the data variability, by putting strict constraints on players’ behavior [1]. Psychologists, on the other hand, view the data variability as the “bread and butter” of their research [2].

A major shortcoming of standard game theory, resulting from ignoring epistemic factors, is manifest in its complete failure to predict the significant levels of cooperation and fairness observed in a variety of non-cooperative and zero-sum games. For example, for the dictator game [3,4], standard game theory prescribes that the player in the role of the dictator should keep the entire amount minus an infinitesimally small portion, and the same prediction holds for the ultimatum game, in which the responder has veto power [4,5]. In experimental studies, we find that dictators behave altruistically, and transfer, on average, about 20%–25% of the entire amount, while in the ultimatum game the amount transferred, on average, is about 40% of the total amount [4,5,6,7]. Non-negligible levels of cooperation are also observed in Public Goods, Common Pool Resource (CPR), and other social dilemma games [8,9,10].

Several modifications of standard game theory have been proposed to account for the cooperation and fairness observed in short-term strategic interactions. Such modifications were usually accomplished by incorporating an other-regarding component in the players’ utility functions. This type of modification includes the theory of Equity, Reciprocity and Competition (or ERC) [11], and Inequality Aversion theory (IA) [12]. ERC posits that along with pecuniary gain, people are motivated by the ratio of their own payoffs to the payoff of others. IA assumes that in addition to the motivation for maximizing own payoffs, individuals are motivated to reduce the difference in payoffs between themselves and others, although with greater distaste for having lower, rather than higher earnings. Another interesting model is the “fairness equilibrium” model [13] in which the rationality assumption is modified by assuming that players make decisions based on their perceptions of others’ intentions. Although such epistemic modifications yield superior predictions to the standard game theoretic predictions, they do not qualify as general models of interactive behavior. For the ultimatum game discussed hereafter, the predictions of ERC and IA are uninformative. ERC predicts that the proposer should offer any amount that is larger than zero and less or equal to 50% of the entire amount, while IA’s prediction is nonspecific, as it requires an estimation of the relative weight of the fairness component in the proposer’s utility function. Moreover, the two theories are strongly refuted by a three-person ultimatum game [14] designed specifically to test their predictions. In this game, Player X offers to split a sum of money $m, allocating (m − (y + z), y, z) for herself, player Y, and player Z, respectively. One of the latter players is chosen at random (with probability p) to accept or reject the offer. If the responder accepts, then the proposed allocation is binding, as in the standard ultimatum game. However, if the responder rejects the offer, then she and X receive zero payoffs, and the non-responder receives a “consolation prize” of $c. The consolation prize was varied across four conditions with ($)c = 0, 1, 3, 12. The probability of designating Y or Z as responder was p = 1/2 and the amount to be allocated in all conditions was m = $15. The findings of [14] contradicted the predictions of both ERC and IA. Frequent rejections were detected, when both theories call for acceptance. In addition, the effect of the consolation prize for the non-responder on the probability of the responders’ acceptance rate was insignificant, and did not increase monotonically with the size of the consolation prize, as both theories predict.

More recently, epistemic game theoretic models were proposed as alternatives to standard game theory, including static models based on Aumann’s interactive epistemology [15,16] and dynamic models of interactive reasoning [17,18]. In the present paper, we propose a new epistemic theory of economic interactions termed Economic Harmony. Instead of looking at cold cognitive variables characterizing human players, we focus on their aspiration levels. As we shall demonstrate hereafter, accounting for the interacting players’ aspiration levels proves successful in generating impressively good predictions of players’ behavior in well-known experimental games.

2. Economic Harmony Theory

The proposed Economic Harmony theory postulates that instead of maximizing utilities, defined as functions of their own payoffs, rational players strive to maximize utilities, which are functions of their actual payoffs relative to their aspired payoffs. Moreover, while game theory looks at points of equilibrium in the game, in which no player can increase his or her utility by unilaterally changing his or her equilibrium strategy, economic harmony theory solves for a point of harmony, at which the intersection of the strategies played by the individuals yields equal utilities for all, or in psychological terms, the point at which the satisfaction levels of all players are equal.

The view that in economic decisions, individuals compare their actual payoffs with their aspired ones, has a long tradition in psychology [19,20,21]. It has been also well studied in the domain of individual decision-making under risk, especially in relation to Security-Potential/Aspiration (CP/A) theory [22,23,24,25]. Several studies have also incorporated individual models of aspirations in predicting behaviors in interactive situations [26,27,28,29,30,31,32]. As examples, study [27] investigated the role of aspiration levels in players’ choices in a repeated prisoner’s dilemma game, and study [30] investigated the role of aspirations in coalition formation. Common to CP/A theory and similar models, is the use of Herbert Simon’s conceptualization of satisficing vs. non-satisficing outcomes [21].

The proposed model resembles the aforementioned individual choice models in assuming that individuals make choices based on their levels of satisfaction from possible outcomes, as well as in assuming that individuals evaluate their actual outcomes by comparing them with their aspired outcomes. However, the new model differs from previous aspiration level models in two significant aspects: (1) it treats interactive situations rather than individual choice ones; (2) the levels of satisfaction are defined as the ratio of the individuals’ actual outcomes to their aspired outcomes, rather than the common definition as the difference between the actual and aspired outcomes. We contend that the ratio scale is more fit for defining outcome satisfaction, than the difference scale. First, the ratio scale is dimensionless and does not depend on the measurement units of the divided goods; second, it is the standard scale in psychophysics, starting with Fechner’s law [33] and Steven’s power law [34,35] to more recent theories of audio and visual perception [36] and signal detection [37]; third, the ratio scale is very common in physics, biology, evolution, and other exact sciences; fourth, all types of statistical measures are applicable to ratio scales, and only with these scales may we properly indulge in logarithmic transformations [34].

Theory Predictions

For deriving predictions based on the proposed theory, consider an economic interaction involving n players. Let ${\mathit{S}}^{\mathit{i}}$ denote the vector of player i’s admissible strategies. ${\mathit{S}}^{\mathit{i}}$ = ${\{s_j^i\}}_{j=1}^{J^i}$, where $s_j^i$ is strategy j of player i (j = 1, 2, .. $J^i$, i = 1, 2, …, n). In Economic Harmony theory, we preserve the rationality principle, while introducing a plausible modification of the players’ utility functions. Specifically, we define the subjective utility of each player i as:

$$u_i(..)=u_i(\frac{r_i}{a_i})$$

(1)

where $r_i$ is player i’s actual payoff, $a_i$ is his or her aspired payoff, and u(..) is a bounded non-decreasing utility function with its argument. For simplicity, we assume that u(0) = 0 and u(1) = 1. Note that in social-psychological terms, the aforementioned definition implies that each player puts an upper limit to his or her greed.

A point of harmony in the interaction is defined as an intersection point of strategies played by the n interacting individuals, at which the utilities of all players, as defined above, are equal.

In formal notation, a point of harmony in the interaction is a vector of outcomes ${\mathit{r}}^{*}$ = $r_1^{*},r_2^{*},r_3^{*},\dots .r_n^{*}$) for which the subjective utilities of all n players’ outcomes satisfy:

$$u_i(\frac{r_i^{*}}{a_i})=u_j\left(\frac{r_j^{*}}{a_j}\right)\mathrm{For}\mathrm{all}i\mathrm{and}j$$

(2)

Assuming linear utilities, Equation (2) becomes:

$$\frac{r_i^{*}}{a_i}=\frac{r_j^{*}}{a_j}\mathrm{For}\mathrm{all}i\mathrm{and}j$$

(3)

Two remarks are in order: First, harmony points are not equilibrium points. In equilibrium, no player can increase his or her utility by changing his or her equilibrium strategy unilaterally. In contrast, if a harmony point is reached, a player may increase his or her utility (and decrease the utilities of other players) by switching to another strategy. For a harmonious solution to emerge and stabilize, it should be supported by an efficient social or institutional mechanism. In the ultimatum and the sequential CPR games, discussed hereafter, the supporting mechanism is a second-party punishment. However, other supporting mechanisms can be effective in sustaining harmony, such as a third-party punishment [38], group punishment [39], punishment by a central authority [40], reciprocity [41], reputation [42] and religious and civic moralizing [43]. Second, as in the case of the Nash equilibrium, players are not expected to “solve” the game and play their harmonious strategies. Rather, it is conjectured that harmonious strategies can emerge through processes of learning and adaptation. In our epistemic theory, adaptation processes are expected to act interdependently on each individual’s decisions and aspirations, according to criteria of success or failure [21,44,45]. In fact, valuable insights into the co-evolution of strategies and aspiration levels have been provided by recent simulation studies of both evolutionary, and reinforcement learning, games, which we shall discuss in the closing section.

In the following sections, we shall demonstrate that despite its evident simplicity, Economic Harmony theory is highly successful in accounting for the cooperation and fairness reported in several experiments on the standard ultimatum, and sequential CPR games.

3. Predicting Behavior in Experimental Games

3.1. Predicting Offers in the Ultimatum Game

In the standard two-person ultimatum game [4,5], one player is designated the role of “proposer”, and the second player is designated the role of “responder”. The proposer receives an amount of monetary units and must decide how much to keep for himself or herself, and how much to transfer to the responder. The responder replies either by accepting the proposed allocation, in which case both players receive their shares, or by rejecting it, in which case the two players receive nothing. Thus, whereas the proposer has complete entitlement to make an offer, the responder can inflict a harsh, although costly, punishment on an unfair proposer.

Game theory predicts that a rational proposer, who believes that the responder is also rational, should offer the smallest amount possible, since the responder, being rational, will accept any positive offer. Experimental findings of numerous ultimatum studies refute this prediction. The modal offer in most experiments is the equal split, and the mean offer is about 40% of the entire amount. In the first ultimatum experimental [5], the mean offer was 41.9%. Numerous studies have repeatedly replicated these results. For example, despite differences in culture, socio-economic background, and type of currency, Kahneman et al. [6] reported a mean offer of 42.1% (for commerce students in an American university), and Suleiman [7] reported a mean offer of 41.8% for Israeli students. A more recent meta-analysis of ultimatum experiments conducted in twenty-six countries with different cultural backgrounds [46] reported a mean offer of 41.5% (S.D. (standard deviation) = 5.7%), and yet another large cross-cultural study conducted in 15 small-scale societies [47] reported a mean offer of 40.5% (S.D. = 8.3). In stark difference with the prediction of game theory, in the above cited studies, and in many other studies, a division of about 60–40 (%), for the proposer and responder, respectively, seems to be robust across countries, cultures, socio-economic levels, monetary stakes, etc.

It is important to note that altruism alone cannot account for the relatively fair divisions observed in ultimatum bargaining. This conclusion is supported by several experiments [7,48,49]. As examples, studies [48] and [49] compared the mean offers made by the allocators in the ultimatum and dictator games. It was hypothesized that if genuine concern for the recipients’ well-being is the major factor behind equitable allocations, then the mean allocation to them should be similar in the two games. Results from the studies cited above refuted the above hypothesis, by showing that the mean allocations to recipients were significantly lower in the dictator game, than in the ultimatum game. For example, in [49], 70% of the dictator games played under a double anonymity condition ended with the first mover demanding the whole ‘cake’.

3.1.1. Economic Harmony Prediction

For simplicity, but without loss of generality, we set the sum to be divided by the proposer to be one monetary unit (1 MU). If he or she demands to keep x MUs (and transfer 1 − x MUs to the responder), then using Equation (3) we can write:

$$\frac{x}{a_p}=\frac{1-x}{a_r}$$

(4)

where $a_p$ and $a_r$ are the aspiration levels of the proposer and the responder, respectively. Solving for x yields:

$$x=\frac{a_p}{a_p+a_r}$$

(5)

And the amount offered to the responder is:

$$x_r=1-x=1-\frac{a_p}{a_p+a_r}=\frac{a_r}{a_p+a_r}$$

(6)

Determining $x$, which guarantees a harmonious allocation, in the sense of equal levels of satisfaction, requires the measurement of the players’ aspiration levels. Probing the players’ aspiration levels by self-reports before, or after, they make their decisions in the game is somewhat problematic due to the notorious interdependence between attitudes and behavior. However, this problem could be eliminated or at least minimized by using suitable experimental designs. A possible design is to utilize the “one–one” ultimatum game treatment played according to the strategy protocol [50]. In this game, proposers are instructed to divide a pie of a given size between themselves and their designated responders. If the amount proposed is equal or larger than the responder’s demand, the two players receive their shares and the game ends; but if the proposer’s offer is less than the responder’s demand, then the proposer is given a second chance to make an offer. Under this treatment, rational proposers and responders are expected to utilize the first round of the game to signal their aspiration levels.

In the absence of empirical data about the players’ aspiration levels, the assumption of rational players, who are motivated to maximize their individual utilities, enables us to make a first-order estimate about their aspiration levels. We conjecture that a self-interested proposer would aspire for the entire sum (i.e., $a_p$ = 1). On the other hand, a rational responder, who believes that the proposer is also rational, cannot aspire that the proposer gives him or her the entire amount or even any amount larger than the amount that the proposer would keep for himself or herself. Embedded in this line of reasoning is the view that in contemplating their aspiration levels, proposers and responders use qualitatively different reference points. Proposers are assumed to adhere to a fixed reference-point, by comparing their demands to the complete sum, which they were given the right to divide. Their highest aspiration would be to keep the entire amount for themselves. The responders are assumed to adhere to a social comparison rule, using the amount demanded by the proposer as their reference-point. Another possibility, which we shall consider hereafter, is that responders might base their aspiration levels on the equality norm, and aspire to receive half of the total amount. Under the “social comparison” assumption, we have $a_r$ = x, while under the “equality norm” assumption we have $a_r$ = $\frac{1}{2}$. For the latter case, substituting $a_p$ = 1 and $a_r$ = $\frac{1}{2}$ in Equation (5) yields:

$$x=\frac{a_p}{a_p+a_r}=\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\mathrm{MU}$$

(7)

And the amount offered to the responder is:

$$x_r=1-x=1-\frac{2}{3}=\frac{1}{3}\mathrm{MU}$$

(8)

Under the social comparison assumption, we have $a_p$ = 1 and $a_r$ = x. Substitution in Equation (5) yields:

$$x=\frac{1}{1+x}$$

(9)

Solving for $x$. we get:

$$x^2+x-1=0$$

(10)

Which yields the positive solution:

$$x=\frac{\sqrt{5}-1}{2}=\mathsf{\phi }\approx 0.618\mathrm{MU}$$

(11)

where φ is the famous Golden Ratio, which plays a key role in many fields of science and aesthetics [51,52]. This ratio is known to be equal to ${\lim }_{\mathrm{n}\to \infty }\left(\frac{f_n}{f_{n+1}}\right)$, where $f_n$ is the nth term of the Fibonacci Series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, .., in which each term is equal to the sum of the two preceding terms, or: $f_n=f_{n-1}+f_{n-2}$. The corresponding portion for the responder is equal to:

$$x_r=1-x=1-\mathsf{\phi }\approx 0.38\mathrm{MU}$$

(12)

3.1.2. Empirical Validation

We tested the prediction in Equation (12) using data from study [46], which reported a Meta-analysis on 75 ultimatum experiments conducted in 26 countries with different cultural backgrounds, and from study [47], which reported results from 15 small-scale societies, including three groups of foragers, six groups of slash-and-burn horticulturalists, four groups of nomadic herders, and two groups of small-scale agriculturalists. The reported mean proportional offers in the two aforementioned studies were 0.395 and 0.405 for studies [46,47], respectively, which are quite close to the Golden Ratio prediction of ≈0.382. A Two one-sided test of equivalence (TOST) [53] validates this conjecture. A rule of thumb in testing for equivalence using TOST, is to set a confidence level of ±10%. For study [46], the analysis yielded significant results for the upper and lower bounds of the equivalence range (upper bound = 42.016, p < 0.0001; lower bound = 34.377, p = 0.0425; overall significance = 0.0425). For study [47], the results were also significant (upper bound = 42.016, p = 0.012; lower bound = 34.377, p = 0.0255; overall significance = 0.0255).

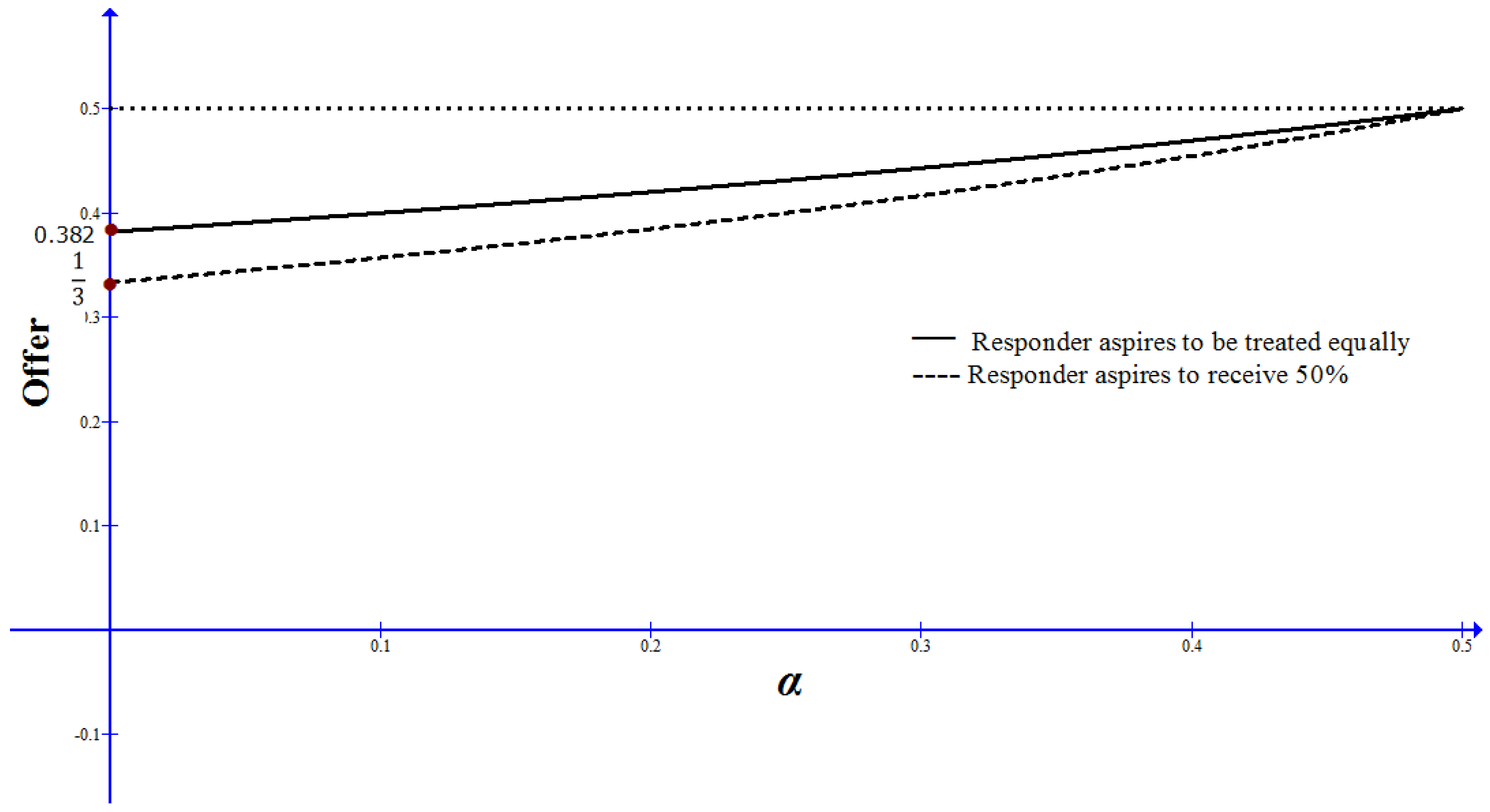
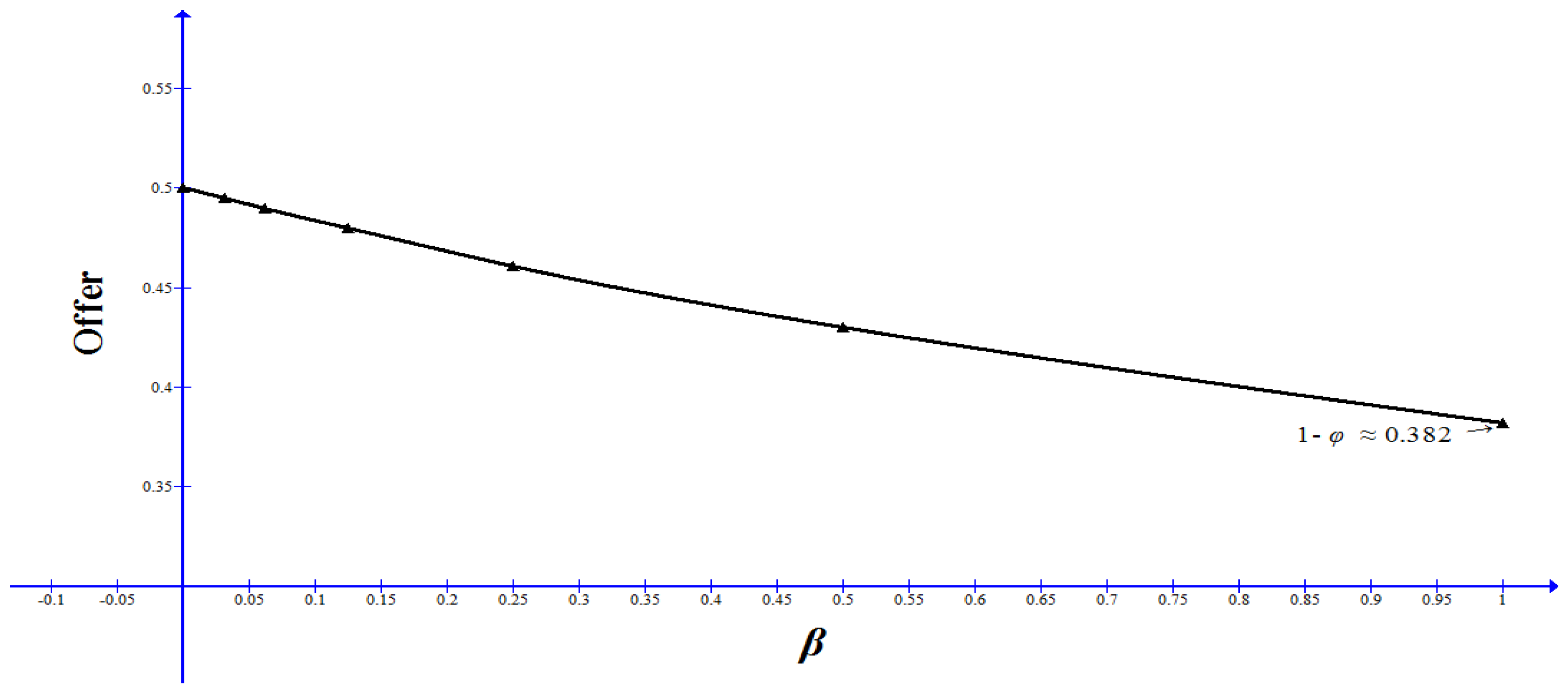
3.1.3. Relaxing the Rationality Assumption

In deriving the “harmony” points, we assumed that a rational proposer would aspire for the entire amount (of 1 MU). We relax this assumption by supposing that proposers might aspire to receive any amount between 1 MU, and 1 − α (0 ≤ α ≤ 0.5), where α is a “security” parameter [22]. Under the assumption that the responder aspires to receive $\frac{1}{2}$, Equation (3) becomes:

$$\frac{x}{1-\mathsf{\alpha }}=\frac{1-x}{0.5}$$

(13)

Solving for $x$ we get:

$$x=\frac{1-\mathsf{\alpha }}{\left(1.5-\mathsf{\alpha }\right)}$$

(14)

And the amount proposed to the responder becomes:

$$x_r=1-x=1-\frac{1-\mathsf{\alpha }}{\left(1.5-\mathsf{\alpha }\right)}=\frac{0.5}{\left(1.5-\mathsf{\alpha }\right)}$$

(15)

On the other hand, assuming that the responder aspires to be treated equally (i.e., $a_r$ = $x$), we have:

$$\frac{x}{1-\mathsf{\alpha }}=\frac{1-x}{x}$$

(16)

Solving for $x$ yields:

$$x^2+\left(1-\mathsf{\alpha }\right)x-\left(1-\mathsf{\alpha }\right)=0$$

(17)

Which solves for:

$$x=\frac{\sqrt{{\left(1-\mathsf{\alpha }\right)}^2+4\left(1-\mathsf{\alpha }\right)}-\left(1-\mathsf{\alpha }\right)}{2}$$

(18)

And the offer to the responder is:

$$\begin{array}{ll}{x}_r=1-\mathrm{x}=& 1-\frac{\sqrt{{\left(1-\mathsf{\alpha }\right)}^2+4\left(1-\mathsf{\alpha }\right)}-\left(1-\mathsf{\alpha }\right)}{2}\\ & =\frac{3+\mathsf{\alpha }+\sqrt{{\left(1-\mathsf{\alpha }\right)}^2+4\left(1-\mathsf{\alpha }\right)}}{2}\end{array}$$

(19)

Figure 1 depicts the predicted offers by Equations (15) and (19) as functions of α in the range α = 0 − 0.5.

If we assume that the proposers might aspire for any amount between 1 and 1 − α with equal probability, the predicted mean offer could be calculated by averaging $x_r$ over the range (0, α). Under the assumption $a_r$ = $\frac{1}{2}$, using Equation (15) we have:

$$x_r=\frac{1}{\mathsf{\alpha }}{{\displaystyle \int }}_0^{\mathsf{\alpha }}\frac{0.5}{\left(1.5-\alpha \right)}\mathrm{d}\mathsf{\alpha }=\frac{1}{2\alpha }\left[\ln \left(3\right)–\ln \left(3-2\alpha \right)\right]$$

(20)

While under the assumption $a_r$ = x, using Equation (19) we get:

$$\begin{array}{l}{x}_r=\frac{1}{\mathsf{\alpha }}{{\displaystyle \int }}_0^{\mathsf{\alpha }}\left(\frac{3+\mathsf{\alpha }+\sqrt{{\left(1-\mathsf{\alpha }\right)}^2+4\left(1-\mathsf{\alpha }\right)}}{2}\right)\mathrm{d}\mathsf{\alpha }\\ =2[3\alpha -\frac{{\alpha }^2}{2}-\frac{1}{2}\left(\frac{\alpha }{2}-\frac{3}{2}\right)\sqrt{{\alpha }^2-6\alpha +5}+2\ln (3-\mathsf{\alpha }\\ -\sqrt{{\alpha }^2-6\alpha +5})\end{array}$$

(21)

As an example, suppose that the proposer aspires to get any amount between 100% and 75% of the entire amount. Under the equality norm assumption, substituting α = 0.25 in Equation (20) yields an offer of $x_r$ ≈ 0.37, which is only slightly higher than the offer of $\frac{1}{3}$, predicted for a completely rational proposer (i.e., for α = 0). Under the social comparison assumption, substituting α = 0.25 in Equation (21) yields an offer of $x_r$ ≈ 0.40, which is also slightly higher than 0.38, the predicted offer for α = 0.

3.1.4. Relaxing the Linearity Assumption

For the proposer and responder with power utility functions $u_p$ = ${(\frac{x}{a_p})}^a$ and $u_r$ = ${(\frac{1-x}{a_r})}^b$, applying the harmony condition in Equation (2) yields:

$${(\frac{x}{a_p})}^a={(\frac{1-x}{a_r})}^b$$

(22)

Setting $a_p$ = $1-{\alpha }_p$ and $a_r$ = $x-{\alpha }_r$ we obtain:

$${(\frac{x}{1-{\alpha }_p})}^a={(\frac{1-x}{x-{\alpha }_r})}^b$$

(23)

For the case of ${\alpha }_p$ = ${\alpha }_r$ = 0 we obtain:

$$\frac{x^{a+b}}{{\left(1-x\right)}^b}=1$$

(24)

Which could be written as:

$$x\left(x^{\beta }+1\right)=1$$

(25)

where β = $\frac{a}{b}$.

Figure 2 depicts the predicted offer, $x_r$ = 1 − x, as a function of β. For practical cases, it is plausible to assume that players are generally risk averse, preferring a sure thing over a gamble of equal expected value, and a gamble with low variance over a riskier one [54]. It is also plausible to conjecture that proposers who face the risk of losing a larger amount (in case or rejecting their offers), will display more risk aversion than responders who would lose a smaller amount in case they decide to reject an unfair offer. We thus may assume that a and b are smaller than 1, and that a < b, implying 0 ≤ β ≤ 1. For β in the range (0.5, 1), numerical integration on $x_r$ as a function of β yields a mean offer of about 0.402, which is only about 0.02 less than the 0.382 predictions obtained under the linearity assumption.

3.2. Predicting Requests in a Sequential CPR Game

The common pool resource dilemma (CPR) game models situations in which a group of people consume a limited shared resource. Under the sequential protocol of play [55] with a step-level rule, individual requests are made in an exogenously determined order, which is common knowledge, such that each player knows his or her position in the sequence and the total requests of the players who proceed him or her in the sequence. If the total request does not exceed the pool size, all players receive their requests. However, if the total request exceeds the pool size, all players receive nothing [56,57,58].

The n-person sequential CPR with a step-level resource has the structure of an n-person ultimatum game, in which by making a sufficiently large request, any player can “veto” the request decisions of the players preceding him or her in the sequence. The sub-game perfect equilibrium of the sequential CPR game prescribes that the first mover should demand almost all the amount available in the common pool, leaving an infinitesimally small portion to the other players. This prediction is strongly refuted by experimental results, showing that first movers do not exploit their advantageous position in the sequence, and that they leave a substantial portion of the resource to the other players. Moreover, these studies reveal a robust position effect: individual requests are inversely related to the players’ positions in the sequence, with the first mover making the highest request and the last mover making the lowest request [58,59,60,61].

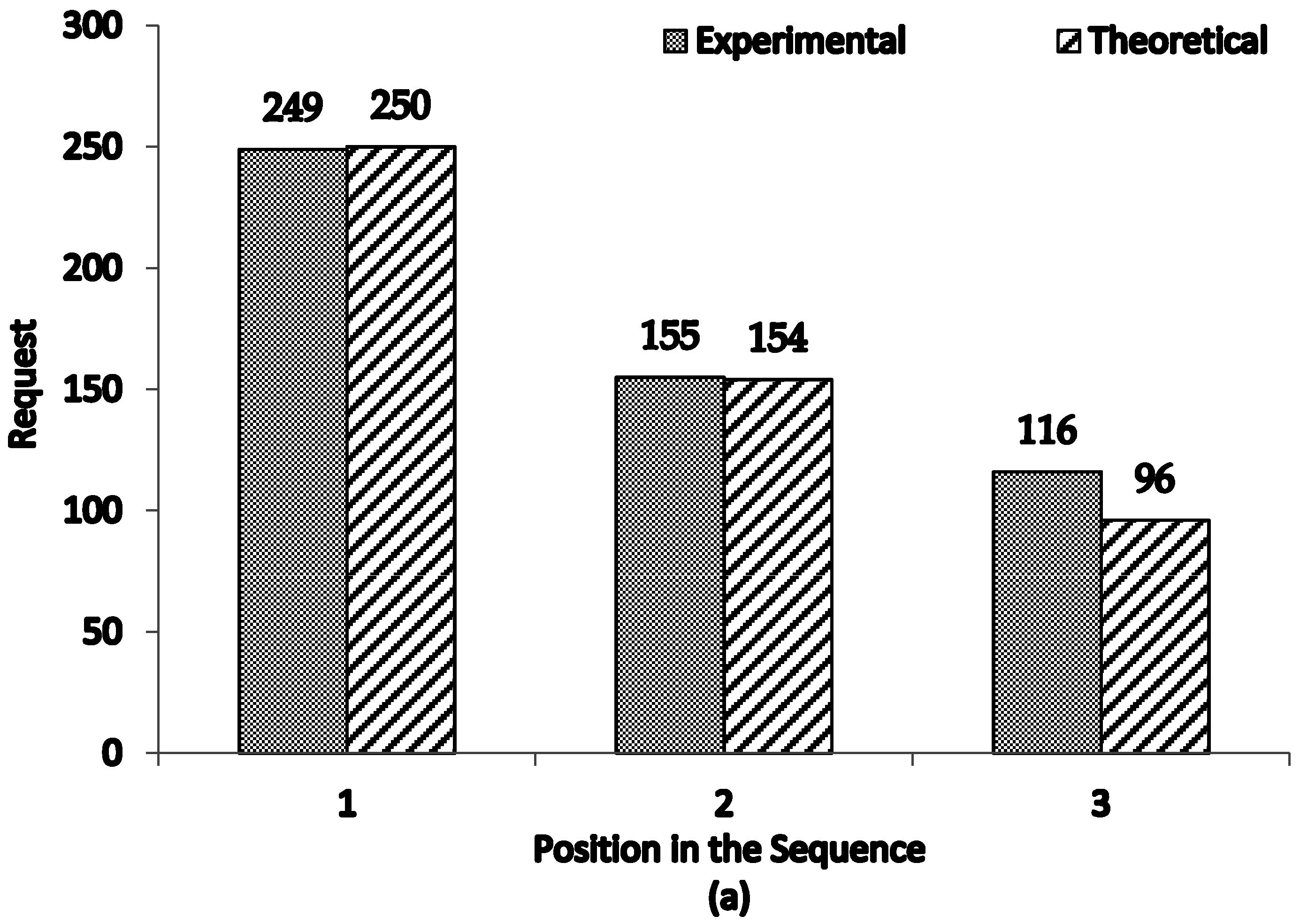
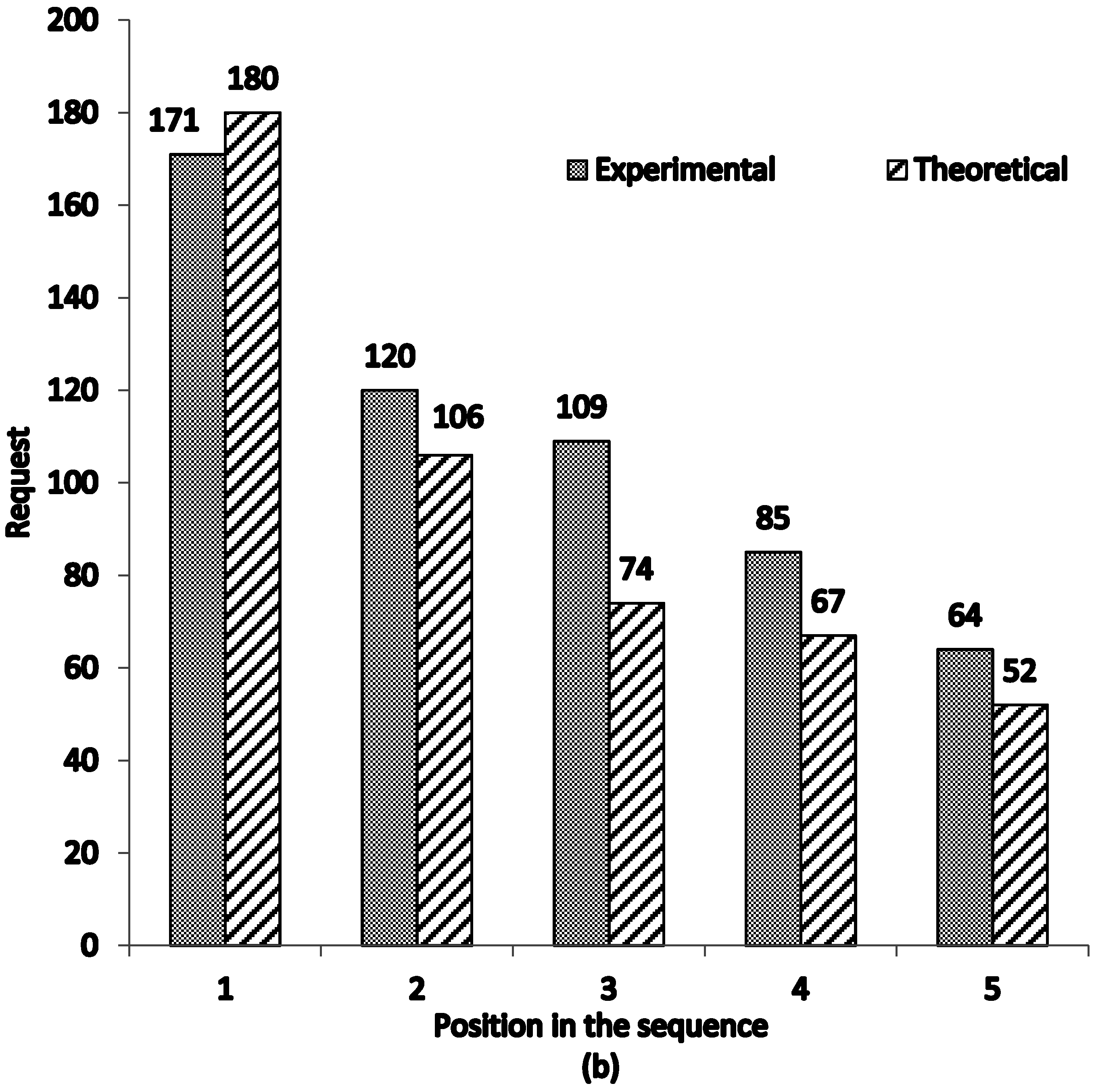
3.2.1. Economic Harmony Prediction

To derive the harmony solution for the sequential CPR game, consider a game with n players. Denote the request of the player occupying position i in the sequence by $r_i$ (i = 1, 2, … n). For two successive players $r_i$ and $r_{i+1},$ the game is reduced to a two-person ultimatum game, in which harmony is achieved when $r_i=$ φ, and $r_{i+1}=$ 1 – φ, where φ is the Golden Ratio (see Section 3.1.1). Thus:

$$\begin{gathered} \frac{r_{i+1}}{r_i}=\frac{1-\mathsf{\phi }}{\mathsf{\phi }}=\frac{1}{\mathsf{\phi }}–1=1+\mathsf{\phi }-1=\mathsf{\phi }\approx 0.618 \\ \left(i=1,2,\dots n-1\right) \end{gathered}$$

(26)

3.2.2. Empirical Validation

We tested the above prediction using data reported in one study using groups of three players and three studies using groups of five players [56,59,60,61]. In all studies, the pool size was 500 points. The resulting predictions (using Equation (26) and a pool size of 500), together with the experimental results, are depicted Figure 3. As shown in the figure, the match between the theoretical prediction, and the experimental results is impressive, particularly for n = 3 (see Figure 3a). For the three, and five players’ games, Kolmogorov–Smirnov tests revealed that the difference between the distributions of the theoretical and observed requests are non-significant (p = 1 and p = 0.975, for the three and five players’ games, respectively).

4. Summary and Concluding Remarks

Previous theories of cooperation and fairness in strategic interactions in the short term have usually attempted to account for the observed cooperation in zero-some and mixed-motive games, by adding an other-regarding component in the players’ utility functions (e.g., [11,12]). In the proposed Economic Harmony theory, we retained the rationality principle, but altered the utility function by defining the players’ utilities as the ratio between their actual payoffs and their aspired payoffs. Instead of looking at points of equilibrium, we looked at the point of harmony in a given interaction, at which the subjective utilities (satisfaction levels) of all players are equal.

For the two games discussed in this article, the Golden Ratio emerged as the point of harmony. Notably, for the two-person ultimatum game, the same result was obtained independently in [62] using the method of infinite continued fractions and the Fibonacci numbers. The derived solution prescribes that a rational proposer should offer a fair division of about (0.618, 0.382) to himself/herself, and the responder, respectively. The emergence of the Golden Ratio as a point of harmony, or homeostasis in economic interactions, adds to its numerous appearances in all fields of sciences [63,64,65,66,67]. It is not unreasonable to conjecture that the Golden Ratio is a point of homeostasis in physical, biological, and socioeconomic systems. Moreover, the fact that the Golden Ratio plays a key role in human aesthetics and beauty [51,68] suggests that humans’ taste for fairness and beauty are neutrally correlated. A recent fMRI (functional magnetic resonance imaging) study [69] lends support to our conjecture, by demonstrating that participants who performed evaluations of facial beauty (beautiful/common), and morality in scenes describing social situations (moral/neutral), exhibited common involvement of the orbitofrontal cortex (OFC), inferior temporal gyrus, and medial superior frontal gyrus.

It is worth emphasizing that in the discussed games, fairness is predicted by the theory, and not presupposed by it, as in ERC and inequality aversion theories. Notwithstanding, the predicted fairness (at the Golden Ratio) was shown to account quite nicely for the levels of fairness observed in many ultimatum and CPR games. We have also shown elsewhere [70] that the theory is successful in predicting the results of several variants of the ultimatum game, including a three-person ultimatum game with uncertainty regarding the identity of the responder [14], a modified ultimatum game with varying veto power [7], and an ultimatum game with one-sided uncertainty about the “pie” size [71]. In addition, the theory was shown to yield good predicting of the players’ decisions in the prisoner’s dilemma game and in the public goods game with punishment (see [72]).

In deriving the analytic solutions for the discussed games’ points of harmony, we relied on rational reasoning to conjecture about the aspiration levels of the interacting players. In reality, it is likely that different individuals might adhere to different rules and anchor their aspiration levels on different reference points. Accounting for such epistemic variability could be undertaken by an empirical assessment of each individual’s aspiration level, given the game structure and the player’s position in the game. When measurement of the individuals’ aspiration levels is unreliable, costly, or difficult to perform, the predictability power of the proposed theory could be enhanced by assuming that the players’ aspiration levels are sampled from a theoretical probability distribution. An example for using an underlying probability distribution of aspiration levels to infer about offers was briefly attended to in Section 3.1.3, in which we assumed that the proposers’ aspiration levels are in the range between 1 (perfect rationality), and 1 − α (a bounded rationality), where α is a uniformly distributed “security” factor.

We view the proposed theory as one step towards a more general theory of rational fairness-economics. An interesting inquiry, which we hope to address in future research, concerns the dynamic aspects of aspirations. By using repeated experimental games or computer simulations, we can test the dynamics of players’ aspirations in strategic games, including the two games treated in the present paper. In particular, we would like to investigate the co-evolution process of aspirations and decisions in repeated and evolutionary games and to test whether the predicted points of harmony for each game will emerge as attractors for the behavioral dynamics. An insightful explanation of the process in which players in such games might update their aspiration levels was provided in [73]. Using analytical solutions and computer simulations, the study demonstrated that when individuals could obtain some information on which offers have been accepted by others in previous encounters, responders in the game learn to maintain high aspiration levels. As explained by the authors of the aforementioned study, responders who lower their aspiration levels (low demands), increase the chance of receiving reduced offers in subsequent encounters. In contrast, by maintaining high aspiration levels (high demands), although costly, they gain a reputation as individuals who insist on a fair offer. The authors summarize their findings by stating that “when reputation is included in the ultimatum game, adaptation favors fairness over reason… information on the co-player fosters the emergence of strategies that are non-rational, but promote economic exchange” [73].

Several other studies on evolutionary ultimatum games [74,75], using various updating rules, reveal that, in general, the dynamics in the investigated ultimatum game were similar to the one reported in [73]. In general, proposers’ demands and responders’ acceptance thresholds converge to a relatively steady-state which is far away from the predicted equilibrium. Remarkably, the mean proposers’ demands converged to levels that were strictly above the equal split, while the mean responders’ demands converged to much lower levels, implying that above-equal demands were accepted. In [74], the rate of proposers’ demands (p) and the rate of responders’ acceptance thresholds (q) were co-evolved with an underlying network typology containing 1500 individuals. The results of many simulations run for two million steps showed that at the beginning of the simulation, p and q underwent a fast decrease from p = q = 0.5 (equal split) to about p = 0.38 and q = 0.19, after which the decrease in both demands was very slow, till the simulations’ termination after 2 million steps. A similar result was reported in [75], using a learning-mutation process. The study found that the mean offer increased if it was smaller than 0.4, and oscillated between 0.4 and 0.5.

Interestingly, convergence to a stable mean offer of about 0.4 is also evident in simulated games played in the intermediate term using reinforcement learning models [76,77]. The findings in [76] show that in many simulations, starting from initial conditions drawn randomly from a uniform distribution over the integers 1–9, the simulated proposers started by demanding 5 out of 9, but increased their demand in the progression of the simulation to 6. Interestingly, the mean proposers’ demands remained in the range between 6 and 7, and did not increase further, since strategies higher than 7 died out in the course of the simulated game. These dynamics are explained by the difference in the speed at which the proposer and the responder update their demands. This explanation is confirmed in [78], which demonstrated that “proposers learn not to make small offers faster than responders learn not to reject them” [78].

The findings described above share several features: (1) the proposers’ mean demands in the relatively steady states reached in all the aforementioned simulation studies are much lower than the predicted (sub-game) equilibrium; (2) the mean demands increase steeply from 0.5 at the initial phase of the game, reaching a ratio of about 0.6 at the final simulation trials; (3) the proposers’ mean acceptance threshold decreases from 0.5, at the initial phase of the game, to low levels of about 0.2–0.3 at the final simulation trials. While the aforementioned common features seem to agree with Economic Harmony predictions, the question of whether the mean demands in these and in similar games converge to the Golden Ratio or to a different nearby point is left to future research.