Theory of Dirac Electrons in Organic Conductors

Abstract

The dynamical property of electrons with the tilted Dirac cone was examined using the tilted Weyl equation. The polarization function exhibits cusps and nonmonotonic structures by varying both the frequency and the momentum. A pair of tilted Dirac cones exhibits a new plasmon for the intermediate magnitude of momentum owing to the combined effects of two tilted cones. Dirac electrons with the zero-gap state (ZGS) in organic conductor α-(BEDT-TTF)₂I₃ are examined by calculating the Berry curvature, which displays the peak structure for a pair of Dirac particles between the conduction band and the valence band. The ZGS is theoretically predicted for 3B1;-(BEDT-TTF)₂NH₄Hg(SCN)₄ under uniaxial pressure. Examining the band structure of the stripe charge ordered state of α-(BEDT-TTF)₂I₃ under pressure, we have found a topological transition from a conventional insulator to a new phase of a pair of Dirac electrons with a finite mass. Further, investigating the zero-energy (N = 0) Landau level under a strong magnetic field, we propose ferromagnetism breaking the SU(2) valley-pseudo-spin symmetry, and the phase fluctuations of the order parameters leading to Kosterlitz-Thouless transition at lower temperatures.

1. Introduction

The organic conductor α-(BEDT-TTF)₂I₃ (BEDT-TTF=bis(ethylene-dithio)tetrathiafulvalene) [1] exhibits a band structure of two-dimensional semimetal or a narrow gap semiconductor as claimed by Mori et al. [2] based on the extended Huckel molecular orbital calculation. Actually, under high pressure, the material undergoes the metal-insulator transition [3], and exhibits the peculiar property that the carrier (hole) density and mobility change by about six orders of magnitude [4]. A similar behavior was found under uniaxial pressure [5], but at rather a lower pressure where the crystal structure under uniaxial strain and ambient pressure, and at room and low temperatures has been determined [6]. Using these transfer integrals between molecules [6], massless Dirac fermion has been found [7,8] in the band calculation. This novel state settles the long-standing problem of anomalous transport phenomena under pressure. In such a massless Dirac fermion, a noticeable property is expected due to the tilted Dirac cone. In the tilted Weyl equation [9,10], the magnitude of the tilt is characterized by the parameter α = v₀/v_c = 0.8 [11], where α = 0 corresponds to the isotropic case. The tilt affects the characteristic temperature dependence of the Hall coefficient [12]. Since the conductor is a layered two-dimensional massless Dirac fermion system [13], the inter-plane magnetoresistance also exhibits noticeable properties, as shown theoretically by the angle dependence of the magnetic field [14]. New phenomena induced by the tilted Dirac cones have been maintained by calculating the transport coefficient under strong magnetic field, i.e., the electric-field-induced lifting of the valley degeneracy [15].

The first discovery of massless Dirac fermion in condensed matter was in graphite [16], where the motions of electrons obey the Weyl equation [17]. Anomalous properties in transport phenomena, e.g., absence of the backward scattering and universal conductivity, have been elucidated theoretically [18] on the bases of this equation, and the experimental evidence was obtained in the context of a single layer in graphite structure, graphene [19]. Compared with graphene, α-(BEDT-TTF)₂I₃ has three unique features: (1) The layered structure with a highly two-dimensional electronic system, which enables us to use powerful experimental methods for bulk material such as NMR [20,21]; (2) the inner degree of freedom which comes from four BEDT-TTF molecule sites participating in the Dirac fermion in a unit cell; (3) the tilt of the Dirac cone, which produces various new electronic properties as described in the present paper.

This paper reviews recent theoretical studies related to the tiled Dirac cone in organic conductors. The outline is as follows. In section 2, dynamical properties such as electron-hole excitation and collective excitation are examined to verify the role of tilting. Although the electronic state has been studied extensively, the dynamical properties associated with the polarization function are not yet clear compared with those in the isotropic case [22]. The dynamical polarization function with the arbitrary wave vector and frequency is calculated analytically by treating a case where the contact point of the Dirac cone is located below the Fermi energy [23]. A noticeable effect of tilted cone is found in the case of two valleys where a new plasmon appears due to the combined effect of the right cone and the left cone [24]. In section 3, Dirac electrons with the zero-gap state (ZGS) in the organic conductor α-(BEDT-TTF)₂I₃ are examined by calculating the Berry curvature. In addition to the peak structure for a pair of Dirac particles between the conduction band and the valence band, the other neighboring bands show another pair of peaks of Dirac electrons with a tendency toward merging [25]. In section 4, the ZGS is theoretically predicted for α-(BEDT-TTF)₂ NH₄Hg(SCN)₄ under uniaxial pressure [26]. The peaks of the Berry curvature are highly anisotropic at the ambient pressure, while those become nearly isotropic at high pressure. In section 5, we re-examine the band structure of the stripe charge ordered state of α-(BEDT-TTF)₂I₃ under pressure using an extended Hubbard model [27]. By increasing pressure, we find a topological transition from a conventional insulator with a single-minimum in the dispersion relation to a new phase with a double-minimum. This transition is characterized by the emergence of a pair of Dirac electrons with a finite mass. In section 6, the possible quantum Hall ferromagnet and Kosterlitz-Thouless transition are investigated for the zero-energy (N = 0) Landau level in α-(BEDT-TTF)₂I₃ under strong magnetic field [28]. Ferromagnetism breaking the SU(2) valley-pseudo-spin symmetry in the N = 0 Landau level is proposed by noting the fact that the scattering processes between valleys becomes non-zero in the case of the tilted Dirac cones. In this case, the phase fluctuations of the order parameters can be described by the XY model leading to a Kosterlitz-Thouless transition at lower temperatures. A summary is given in section 7.

2. Dynamical Polarization Function

We examine the following 2x2 effective Hamiltonian [9] which gives the tilted Weyl equation on the Luttinger-Korn basis at the Dirac point,

(1)

where the matrix is given by

(2)

Here we define ξskR(L) = +(–)v0kx + svc|k|, (s = +,-) and α = v0/vc. From the two contact points corresponding to two valleys of cones, we focus on one, which is given by the state located close to k0. The polarization function per valley is calculated as

(3)

where f(ξ) = 1/(1 + exp[(ξ – μ)/T] with T being the temperature. In terms of the eigen function, F_s(k), of the 2 × 2 matrix Hamiltonian, we obtain

(4)

The polarization function is calculated on the plane of q and ω for respective regions as shown in Figure 1.

Figure 1. Several regions on the q-ω plane for calculating the polarization function (Equation (3)). From [23]. Reproduced with permission from JPSJ.

Figure 1. Several regions on the q-ω plane for calculating the polarization function (Equation (3)). From [23]. Reproduced with permission from JPSJ.

The results consist of six regions. These regions 1A, 2A, 3A, 1B, 2B, and 3B are classified into two regions, A and B, corresponding to the process of intraband and interband excitations, respectively. The regions A and B are separated by a solid line expressed as ω_res = (1 + cosθ_q)v_cq, which is called the resonance frequency. The resonance frequency is obtained owing to the nesting of the excitations with the linear dispersion, and the polarization function diverges with the chirality factor F_s(k). The boundary between 2A and 3A is given by ω₊. The boundary between 2A and 1A (2B and 1B) is given by ω_A. The boundary between 2B and 3B is given by ω_B. 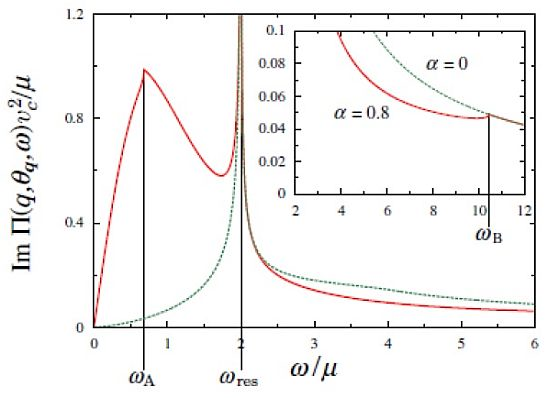In the case of the isotropic Dirac cone (i.e., α = 0), there is a boundary given by ω/μ + v_cq/μ = 2 which separates 1A and 2A (1B and 2B) for the intraband (the interband). In the regions 3A and 1B, the imaginary part vanishes. For the tilted Dirac cone, the boundary between 1A and 2A exhibits a noticeable behavior characterized by the appearance of cusps for the imaginary part as shown in Figure 2.

Figure 2. Normalized imaginary part, Im Π(q,θq,ω) vc2/μ, as a function of ω/μ, for θq = π/2 and α = 0.8. From [23]. Reproduced with permission from JPSJ.

Figure 2. Normalized imaginary part, Im Π(q,θq,ω) vc2/μ, as a function of ω/μ, for θq = π/2 and α = 0.8. From [23]. Reproduced with permission from JPSJ.

Figure 3 shows the normalized imaginary part, Im Π(θq,ω) v_c²/μ, on the plane of v_cq/μ and ω/μ for θ_q = π/2. The color gauge with the gradation represents the magnitude of the imaginary part. The global feature is mainly determined by the property of ω_res. In the case of v_c q/μ >> 1, where the characteristic energy becomes much larger than the interband energy, Im Π(θ_q,ω) of the intraband excitation (ω < ω_res) becomes much smaller than that of the interband excitation (ω > ω_res) in contrast to the case,v_c q/μ = 2. The broad peak in the intraband excitation does not change much for θ_q < π/2, while it is strongly masked for π/2 < θ_q < π due to the rapid decreasing ω_res.

Figure 3. Normalized imaginary part, Im Π(θq,ω) vc2/μ, on the plane of vcq/μ and ω/μ for θq = π/2. From [23]. Reproduced with permission from JPSJ.

Figure 3. Normalized imaginary part, Im Π(θq,ω) vc2/μ, on the plane of vcq/μ and ω/μ for θq = π/2. From [23]. Reproduced with permission from JPSJ.

In Figure 4 the normalized optical conductivity of Reσ(θ_q,ω) is shown as a function of ω/μ with some choices of θ q = 0, π/4 and π/2, with α = 0.8. The dotted line denotes the isotropic case where Re σ is zero for ω < μ and is constant for μ < ω. The conductivity Re σ is zero for ω < 2 μ/(1 + α) and 1 for ω > 2μ /(1 – α), while it takes an intermediate value for 2 μ/(1 + α) < ω < 2μ/(1 – α).

Figure 4. Normalized optical conductivity of Reσ(θ_q,ω) as a function of ω/μ. From [23]. Reproduced with permission from JPSJ.

Figure 4. Normalized optical conductivity of Reσ(θ_q,ω) as a function of ω/μ. From [23]. Reproduced with permission from JPSJ.

The plasma mode is calculated from 1 + v_q ReΠ(q,θ_q,ω_pl(1,2)) = 0 with v_q = 2πe²/ε₀q. Since the plasma frequency ω_pl is located just above the resonance frequency, the solution is expected close to ω_pl1 =ω⁰_pl1 and ω_pl2=ω⁰_pl2, respectively. However, the imaginary part is complicated due to the combined effects of Π ^R(q,θ_q,ω) + Π ^L(q,θ_q,ω). We use the scaled quantities as qv_c/μ and ω/μ with e²/(ε₀v_c) = 1. The plasma frequency corresponds to ω, which gives a peak of ImΠ_RPA(q,θ_q,ω).

In Figure 5(a), Im Π_RPA(q,θ_q,ω) for θ_q = 0 is shown as a function of ω/μwith fixed v_cq/μ = 0.5, 0.75, 1, 1.5, 2, 3, 4, 5 and 6, respectively. The dash-dotted line (ω_pl1(q,θq) denotes the location of ω/μ for the peak of the plasmon, which is appreciable for small v_cq/μ. The dotted line denotes the location of ω for the novel plasmon, i.e., ω_pl2(q,θq), which is found for the intermediate magnitude of v_cq/μ. Such a plasmon, ω_pl2(q,θq) originates from the interplay of two tilted cones. These two plasmons, which are found just above ω_res are obtained as the hybridization of the electron of the right cone and that of the left cone. The appreciable peak of Im Π_RPA(q,θ_q,ω) moves from ω_pl1(q,θq) to ω_pl2(q,θq) with increasing q, i.e., the weight for small q is determined by ω_pl1(q,θq) and that of intermediate q is determined by ω_pl2(q,θq). In Figure 5(b), Im Π_RPA(q,θ_q,ω) is shown for θ_q = π/4. It is found that the weight for ω_pl2(q,θq) is suppressed. This implies that both the dispersion relation and the intensity exhibit appreciable θq dependence. Such an anisotropy of the intensity gives rise to plasmon filtering. The novel plasmon has the following characteristics. The plasma frequency ω_pl2(q,θq) in the case of θq = 0 exists for any q. At θ_q = π/4, ω_pl2(q,θq) does not exist for small q, and is also absent for any q when θ_q = π/2. Furthermore, we find that ω_pl1(q,θq) is proportional to q^1/2 for small q, and that ω_pl2(q,θq)-ω_res is proportional to q for intermediate v_cq/μ.

Figure 5. Im ΠRPA(q,θq,ω) as a function of ω/μwith fixed vcq/μ = 0.5, 0.75, 1, 1.5, 2, 3, 4, 5 and 6, for θq = 0 (a), and θq =π /4 (b). From [24]. Reproduced with permission from JPSJ.

Figure 5. Im ΠRPA(q,θq,ω) as a function of ω/μwith fixed vcq/μ = 0.5, 0.75, 1, 1.5, 2, 3, 4, 5 and 6, for θq = 0 (a), and θq =π /4 (b). From [24]. Reproduced with permission from JPSJ.

Here we examine the filtering of the plasma frequency by tuning the angle θ_q of the external field with frequency ω and q. Figure 6 is an example of Im Π_RPA(q,θ_q,ω) when the external frequency is chosen as ω = ω_pl2(q,0) (solid line), ω_pl2(q,π/8) (dotted line), and ω_pl2(q,π/4) (dashed line) for the fixed v_cq/μ = 5. For ω = ω_pl2(q,0), a pronounced peak with the peak height (about 15) and the width (0.036 π) shows that the plasmon excitation occurs in the narrow region close to θ_q = 0. For the choice of ω = ω_pl2(q,π/8), the peak appears at θ_q = +(–)π/8 where the intensity is reduced less than 1/10 compared with ω = ω_pl2(q,0). The peak is further reduced for ω = ω_pl2(q,π/4). No peak is expected when the frequency is outside of the regime of the plasma frequency. In terms of the dielectric function ε(q,θ_q,ω), the location of the peak is determined by Reε(q,θ_q,ω) = 0 while the height and the width are determined by Im ε(q,θ_q,ω).Thus the peak (or the double peak) structure gives the filtering of plasmon, which depends on θ_q.

Figure 6. θ_q dependence of Im Π_RPA(q,θ_q,ω) for v_cq/μ = 5 with the fixed ω = ω_pl2(q,0) (solid line), ω_pl2(q,π/8) (dotted line), and ω_pl2(q,π/4) (dashed line). From [24]. Reproduced with permission from JPSJ.

Figure 6. θ_q dependence of Im Π_RPA(q,θ_q,ω) for v_cq/μ = 5 with the fixed ω = ω_pl2(q,0) (solid line), ω_pl2(q,π/8) (dotted line), and ω_pl2(q,π/4) (dashed line). From [24]. Reproduced with permission from JPSJ.

3. Berry Curvature of the Dirac Particle of α-(BEDT-TTF)2I3

The contact point in a normal state, i.e., without charge ordering, is determined essentially by the property of the transfer energy, and the effect of interaction is to modify mainly the location of the contact point. Then, by taking account of only the transfer energy, we examine the Hamiltonian for α-(BEDT-TTF)₂I₃ given by

(5)

where α and β(=1, 2, 3,4) are indices for the site of each molecule A(1), A'(2), B(3) and C(4) in the unit cell, and i, j are those for the cell forming a square lattice with N sites. The quantity a denotes the annihilation operator for the electron, and t denotes the transfer energy between the neighboring site. As shown in Figure 7, there are seven transfer energies given by t_b1, …, t_b4 for the direction of the b(-x)-axis and t_a1, …, t_a3 for the direction of the a(y) -axis, respectively.

Figure 7. Crystal structure on a two-dimensional plane with four molecules A(1), A’(2), B(3), and C(4), in the unit cell where the respective bonds represent seven transfer energies tb1, ..., ta3. From [25]. Reproduced with permission from JPSJ.

Figure 7. Crystal structure on a two-dimensional plane with four molecules A(1), A’(2), B(3), and C(4), in the unit cell where the respective bonds represent seven transfer energies tb1, ..., ta3. From [25]. Reproduced with permission from JPSJ.

By introducing site potentials given by I_1σ = −I_2σ= −∆₀, and I_3σ = −I_4σ = 0, the 4 × 4 Hamiltonian on the site basis and with a Fourier transform is given by

(6)

In the above Hamiltonian, k_x is replaced by k_x + π and then the center corresponds to X point. We obtain four bands E_j(k) where E₁ > E₂ > E₃ > E₄. For ∆₀ = 0, the inversion symmetry between A and A' is kept, and E₁ and E₂ touches at Dirac point, k₀, where the ZGS is found for the uniaxial pressure P_a being larger than 3 kbar. For the calculation of the Berry curvature, we consider the case of a finite value of ∆₀, which induces a gap at the Dirac point.

The Berry curvature B_n(k) for each band E_n(k) is calculated as [29]

(7)

where |n > denotes the eigen vector of E_n. Note that B₁(k) is essentially determined by E₁ and E₂, i.e., the effect of E₃ and E₄ is negligibly small within our numerical calculation. We define B_n(k) as the component of B_n(k), which is perpendicular to the k_x − k_y plane. For the small limit of ∆₀, we obtain B₁ = ∝ (∆₀)⁻².

The energy band and Berry phase under uniaxial P_a are calculated using an extrapolation fort (P_a) [8]. Energy bands of E₁(a) and E₂(b) for Pa =6 kbar and ∆₀ = 0.02 eV is shown in Figure 8(a) and (b).

Figure 8. Energy bands of E1(a) and E2(b) for Pa = 6 kbar. From [25]. Reproduced with permission from JPSJ.

Figure 8. Energy bands of E1(a) and E2(b) for Pa = 6 kbar. From [25]. Reproduced with permission from JPSJ.

The Dirac cone exists at +(-)k₀, with k₀= (0.57 π, - 0.3 π), as shown by arrows. A pair of cones is seen close to E₁(k₀) and E₂(k₀) and the cones in the same band are symmetric with respect to the Γ (=(0,0)) point. For E₁(k), the maximum is seen at the Y(=(0,π)) point, while saddle points are seen for the X(=(0,π)), M(=(π,π)), and Γ points. For E₂(k), the minimum is seen at the M point while saddle points are seen for the X, Y, and Γpoints. The accidental degeneracy, which is found at +(–)k₀ for −△₀ ➝ 0 is realized as the minimum of E₁(k) and the maximum of E₂(k).

The corresponding Berry curvature B₁(k) is shown in Figure 9. The peak around –k₀ (+k₀) is positive (negative). They are antisymmetric with respect to the Γ. Since the curvature exhibits a noticeable peak close to +(–)k₀, such a peak may be identified as the Dirac particle instead of calculating the contact point.

Figure 9. Berry curvature B₁(k) (component perpendicular to the k_x–k_y plane). From [25]. Reproduced with permission from JPSJ.

Figure 9. Berry curvature B₁(k) (component perpendicular to the k_x–k_y plane). From [25]. Reproduced with permission from JPSJ.

We examined the Berry curvature for other bands. The Berry curvature of the second band E₂(k) is shown for several choices of P_a in Figure 10. The peak located at +(–)k₀ has a sign opposite to that of E₁(k). Figure 10(d) denotes B₁(k) at Pa = 6 kbar corresponding to Figure 9. In addition to such a peak, another pair of peaks appears close to the Γ point. The latter one is rather extended to a direction slightly declined toward the horizontal axis, suggesting a large anisotropy of the Dirac cone. The anisotropic peak disappears for P_a smaller than 3 kbar while it becomes rather isotropic for large P_a. Such a behavior resembles the emergence of the Dirac particle in the charge ordered state, which has been shown in α-(BEDT-TTF)₂I₃ [27]. The Berry curvature for E₃(k) is obtained similarly where a pair of peaks close to the Γ point also exists with a sign opposite to that of E₂(k). There is another peak close to the M point, which compensates for that of E₄(k). These results show that each neighboring band provides a pair of Dirac particles followed by the Berry curvature with an opposite sign. When a pair of Dirac particles between neighboring two bands is found, one may expect a pair of Dirac particles for the other neighboring bands.

Figure 10. Contour of the Berry curvature, B₁(k), of the second band E₂(k) for Pa = 0(a), 2(b), 4(c), 6(d), 8(e), and 10(f) kbar respectively. Γ = (0,0). The Dirac particle at k₀ with the positive B₁(k) exists in the bright region of k_x > 0 and k_y < 0.

Figure 10. Contour of the Berry curvature, B₁(k), of the second band E₂(k) for Pa = 0(a), 2(b), 4(c), 6(d), 8(e), and 10(f) kbar respectively. Γ = (0,0). The Dirac particle at k₀ with the positive B₁(k) exists in the bright region of k_x > 0 and k_y < 0.

4. Zero-Gap State in α-(BEDT-TTF)2 NH4Hg(SCN)4

In addition to α-(BEDT-TTF)₂I₃, the ZGS, where a contact point of the Dirac cone coincides with the chemical potential, is predicted for α-(BEDT-TTF)₂ NH₄Hg(SCN)₄ under uniaxial pressure, P_c along the stacking axis [26].

There are the electron and hole surfaces owing to band-overlap at ambient pressure. The ZGS emerges under the uniaxial pressure along the stacking axis in the conducting plane, for P_c > 5 kbar. Figure 11 shows the energy dispersions of the conduction and valence band at P_c = 6 kbar, where the transfer energies are calculated by extrapolation using the data at P_c = 0 kbar [30,31] and 1.5 kbar [31] obtained from the X-ray experiment. A pair of the Dirac cones is located at k₀ = (−0.25, 0.51) π. The chemical potential coincides with the contact points since there is no band-overlap. The Dirac cones are rather isotropic compared with those of α-(BEDT-TTF)₂I₃.

The singularity of phase of the wave function, which describes the intrinsic property of the Dirac electron, has been confirmed using the Berry curvature. There is a pair of peaks in the Berry curvature, which corresponds to a pair of Dirac electrons with opposite chirality. The peaks of the Berry curvature are highly anisotropic at ambient pressure, while those become nearly isotropic at P_c = 6 kbar.

In addition, the effective Hamiltonian on the Luttinger-Kohn representation has been investigated. It has been found that the Dirac cone, which exists below the chemical potential, is anisotropic and tilted at ambient pressure. The anisotropy of the Dirac electron at ambient pressure is related to the one-dimension-like valley (ridge) structure between two contact points in the conduction (valence) band. The anisotropy and tilting of the Dirac cone are reduced with increasing pressure.

Figure 11. Energy dispersions of the conductionand valence band at P_c = 6 kbar of α-(BEDT-TTF)₂ NH₄Hg(SCN)₄. From [26]. Reproduced with permission from JPSJ.

Figure 11. Energy dispersions of the conductionand valence band at P_c = 6 kbar of α-(BEDT-TTF)₂ NH₄Hg(SCN)₄. From [26]. Reproduced with permission from JPSJ.

5. Emergence of Dirac Electron Pair in Charge Ordered State of α-(BEDT-TTF)2I3

We re-examined the band structure of the stripe charge ordered state of α-(BEDT-TTF)₂I₃ under pressure using an extended Hubbard model [27]. The model used to describe the two-dimensional electronic system in α-(BEDT-TTF)₂I₃ is shown in Figure 12. The unit cell consists of four BEDT-TTF molecules on sites A, A’, B and C. The sites A, B and C are inequivalent, while A is equivalent to A’ so that inversion symmetry is preserved in the normal state. There are six electrons for the four molecules in a unit cell, i.e., the band is 3/4-filled. On the basis of the HOMO orbitals, the electronic system is described by the extended Hubbard model with several transfer energies, the on-site repulsive interaction U and the anisotropic nearest-neighbor repulsive interaction V_αβ,

(8)

where i, j denote site indices of a given unit cell, and a,b = A, A’, B and C are indices of BEDT-TTF sites in the unit cell. In the first term, the transfer energies as a function of a uniaxial pressure (P_a) along the a-axis are estimated from an extrapolation using the data at P = 0 kbar [2] and P_a = 2 kbar [6]. We use the parameter U = 0.4 eV and the V_ab takes on two different values, V_a = 0.17~0.18 eV along the stacking direction, and V_b= 0.05 eV along the perpendicular direction. With this choice of parameters, we obtain a pressure dependence of the electronic spectrum consistent with experimental results [5]. Throughout the paper, the lattice constant is taken as unity. As in previous work [32], we restrict ourselves to a Hartree mean field theory.

Figure 12. The model describing the electronic system ofα-(BEDT-TTF)₂I₃. The unit cellconsists of four BEDT-TTF molecules A, A’, B and C with seven transfer energies. The nearestneighbor repulsive interactions are given by Vaand Vb [27].

Figure 12. The model describing the electronic system ofα-(BEDT-TTF)₂I₃. The unit cellconsists of four BEDT-TTF molecules A, A’, B and C with seven transfer energies. The nearestneighbor repulsive interactions are given by Vaand Vb [27].

The Pa-Va phase diagram obtained from the self-consistent Hartree approximation is shown in Figure 13 [27]. This figure exhibits three transition lines. Two of them (the continuous and dashed lines) have already been found in previous work [32] and the third one (dotted line) is a novel transition. The schematic band spectrum close to the Fermi surface is also shown in Figure 13. The solid line marks a charge ordering transition resulting from the simultaneous breaking of time reversal and inversion symmetries. It separates the charge ordered metallic state (COM) from the Zero Gap state (ZGS). In the ZGS phase, energy bands are spin degenerate and inversion symmetry is preserved. Coming from this high-pressure ZGS phase and traversing the continuous line, the inversion symmetry is spontaneously broken by the electronic interactions. As a consequence, a gap opens leading to an insulating phase. However the time reversal symmetry is also spontaneously broken by the interactions so that the degeneracy between up and down bands is now lifted. Therefore the simultaneous breaking of time reversal and inversion symmetries results in a semi-metallic phase (COM) with band overlap leading to small electrons and hole pockets of opposite spin orientations. In striking contrast with the continuous line, the dashed line marks a metal-insulator transition from a charge ordered metallic (COM) phase to a charge ordered insulator (CO) without breaking of any symmetry.

In traversing this transition line, the dispersion relations stay similar but their relative positions to the Fermi level vary. In this work, by a more detailed analysis of the COM and CO phases, we find a new topological transition (dotted line in Figure 13) that further splits each of the COM and CO phases into two phases: COM(I,II) and CO(I,II). This transition concerns a modification in the two energy bands close to the Fermi energy. They correspond to a given value of the spin that we choose to denote as “up”. The two other bands (down) are not concerned by this transition. As illustrated in Figure 13, the transition from CO(I) to CO(II) is characterized by a change in the form of the dispersion relation of the valence and conduction bands. In the CO(I) phase, there is a single minimum of charge gap whose position in the k space stays at the M-point. In the CO(II) phase, the single charge gap separates into two points at symmetrical positions from the M-point. There is now a double-well structure in the dispersion relation. This transition corresponds to the emergence of a pair of Dirac points.

Figure 13. The phase diagram on the Pa-Va plane, where U = 0.4 eV, and Vb = 0.05 eV [27].The CO and COM denote insulating and metallic states with charge ordering ,respectively. Phase (I) shows a single minimum, while phase (II) is characterized by a doubleminimum in the up spin band. In the schematic energy spectrum close to the Fermi energy (horizontal line), thered and blue bands correspond to the up and down spin band, respectively.

Figure 13. The phase diagram on the Pa-Va plane, where U = 0.4 eV, and Vb = 0.05 eV [27].The CO and COM denote insulating and metallic states with charge ordering ,respectively. Phase (I) shows a single minimum, while phase (II) is characterized by a doubleminimum in the up spin band. In the schematic energy spectrum close to the Fermi energy (horizontal line), thered and blue bands correspond to the up and down spin band, respectively.

This modification of the band structure is described by an effective low energy Luttinger-Kohn Hamiltonian with nine parameters that can be extracted from a numerical Hartree calculation. From a detailed study of this Hamiltonian and the corresponding energy spectrum, we show that the transition is driven by a single quantity detSM whose sign changes at the transition. SM is the stability matrix, which governs the stability of the M-point [27]. A similar scenario occurs for the COM(I)-COM(II) transition.

The existence of a pair of Dirac points is characterized by a special structure of the Berry curvature. In the CO(II) and COM(II) states, the Berry curvature shows two sharp peaks with opposite signs. On the other hand, in CO(I) and COM(I) phases, the Berry curvature becomes very small owing to cancelation of the positive and negative contributions. The existence of the Dirac point is also verified by integrating the Berry curvature over a region limited by a closed energy contour around a single point [27].

This topological transition could be probed in a magnetic field by the modification of the Landau level structure, therefore by e.g. magnetoresistance experiments.

6. Tilted-Cone-Induced Easy-Plane Pseudo-Spin Ferromagnet and Kosterlitz-Thouless Transition in Massless Dirac Fermions

We have considered the low-energy effective Hamiltonian for N = 0 Landau states in a pair of tilted Dirac cones [28] using the bases of the Wannier functions [33] for the magnetic rectangular lattice, which is constructed by a linear combination of the wave functions of N = 0 Landau states in the Landau gauge. This Wannier functions satisfy orthonormality and are localized around R = (ma, nb) with integers m and n. A unit cell satisfies ab = 2πl² with the magnetic length l = (hc/2π eH)^1/2and has a magnetic flux quantum hc/e. By taking the long-range Coulomb interaction and the Zeeman energy E_Z, the low-energy effective Hamiltonian is given by

(9)

where i, j, k, and l denote the unit cells of the magnetic rectangular lattice at Ri, Rj, Rk, and Rl, respectively, σ denote the spin, τ denote the valley-pseudo-spin which represents the degree of freedom on a pair of Dirac cones, and c_iστ⁺ (c_iστ) is the creation (annihilation) operator on the bases of the Wannier functions. The forward-scattering term of the long-range Coulomb interaction, Vijkl, comes from the long wave length part. This term does not depend on the spin and valley-pseudo-spin, and then it does not break the SU(4) symmetry, neither in the spin subspace nor in that of the pseudo-spin. It has been found that the forward-scattering term is not affected by the tilting. On the other hand, the backscattering term of the long-range Coulomb interaction, Wijkl, which is the inter-valley scattering term exchanging large momentum 2k₀ and breaks the SU(2) symmetry in the subspace of the valley-pseudo-spin, comes from the short wave length part. In the absence of tilting, as e.g., in graphene, the backscattering term vanishes. We found that the tilting is essential to have a non-zero backscattering term. The ratio between the forward and backscattering terms is given by Wijkl/Vijkl~α²α_L/l, where α is the tilting parameter, α_L is the real lattice constant. The backscattering term is proportional to α_L, since the large momentum |2k₀|~π/α_L is exchanged. We note that the lattice constant of α-(BEDT-TTF)2I3, α_L~1 nm, is much larger than that of graphene. Thus it is expected that the backscattering term plays an important role for electron-correlation effects in α-(BEDT-TTF)2I3. The typical value of the ratio Wijkl/Vijkl is approximately 0.07 for α-(BEDT-TTF)2I3 at H = 10 T using the tilting parameter α = 0.8.

In the absence of an explicit symmetry breaking, such as the Zeeman effect or the above-mentioned backscattering term, no particular spin or valley-pseudo-spin channel is selected, and one may even find an entangled spin-pseudo-spin ferromagnetic state at low temperature. The symmetry-breaking terms may, thus, be viewed as ones that choose a particular channel (spin or valley-pseudo-spin) and direction of a pre-existing ferromagnetic state by explicitly breaking the original SU(4) symmetry.

In the spin-polarized state without valley-pseudo-spin polarization (Δ = 0), electrons reside in the spin-up branches of the N = 0 Landau levels as shown on the left hand side of Figure 14, where m is the spin polarization and I is the on-site effective interaction in the magnetic rectangular lattice. In the valley-pseudo-spin ferromagnetic state, where the easy-plane (XY) pseudo-spin polarization lifts the valley-pseudo-spin degeneracy and then the spin polarization is suppressed as shown on the right hand side of Figure 14. Although the mean field approximation gives the first order transition from the spin-polarized state to the valley-pseudo-spin-polarized state with decreasing temperature, the valley splitting of Landau levels owing to the partial valley-pseudo-spin polarization may occur continuously with decreasing temperature owing to the two-dimensional fluctuation. Actually, the valley-splitting has been observed in the interlayer magnetoresistance [34].

Figure 14. Schematic figure of the energy levels in the spin-polarized state (left hand side) and the valley-pseudo-spinferromagnetic state (right hand side). Blue and orange arrows denote the real spins, and μ is the chemical potential. From [28]. Reproduced with permission from JPSJ.

Figure 14. Schematic figure of the energy levels in the spin-polarized state (left hand side) and the valley-pseudo-spinferromagnetic state (right hand side). Blue and orange arrows denote the real spins, and μ is the chemical potential. From [28]. Reproduced with permission from JPSJ.

In the presence of the order parameter with a finite amplitude, phase fluctuation exists with the characteristic length of spatial variation much longer than the fictitious lattice spacing. The effect of this phase fluctuation, which has so far been ignored in the mean-field approximation, is treated on the basis of the Wannier functions and the resulting model is similar to the XY model leading to the Kosterlitz-Thouless transition [28].

7. Summary

In the present review, we have shown the effect of tilting of Dirac cone and the characteristic behavior of the Berry curvature in organic conductors.

The tilting effect is examined by calculating the polarization function of the massless Dirac particle for a finite doping. Using the tilted Weyl equation, the dynamical polarization is calculated to find the anisotropic behavior in optical conductivity and plasma frequency. A new plasma mode appears owing to the combined effect of the two tilted cones, leading to the filtering effect.

We examined the Berry curvature to understand the zero-gap state under the uniaxial pressure. The pronounced peak of the Berry curvature around the Dirac point is obtained by adding a small potential acting on the A and A' sites with opposite signs, which breaks the inversion symmetry. Such a method of calculating the Berry curvature is useful to find the Dirac electron in an organic conductor. In addition to α-(BEDT-TTF)₂I₃, the zero-gap state is theoretically predicted for the organic conductor α-(BEDT-TTF)₂ NH₄Hg(SCN)₄ under uniaxial pressure. The band structure of the stripe charge ordered state of α-(BEDT-TTF)₂I₃ is re-examined using an extended Hubbard model. We found a topological transition from a conventional insulator towards a new phase, which is characterized by the emergence of a pair of Dirac electrons with a finite mass.

Finally, by examining the zero-energy N = 0 Landau level in α-(BEDT-TTF)₂I₃ under strong magnetic field, we found the tilted-cone-induced XY valley-pseudo-spin ferromagnetic state and Kosterlitz-Thouless transition as an effect of tilting.