Optical Effects Accompanying the Dynamical Bragg Diffraction in Linear 1D Photonic Crystals Based on Porous Silicon
Abstract
:1. Introduction
2. Dynamical Bragg Diffraction in Linear 1D PhC: The Main Approach

3. Composition of Multilayer Porous Silicon Based 1D Photonic Crystals
4. Experimental Results
4.1. Temporal Splitting of the Femtosecond Laser Pulses


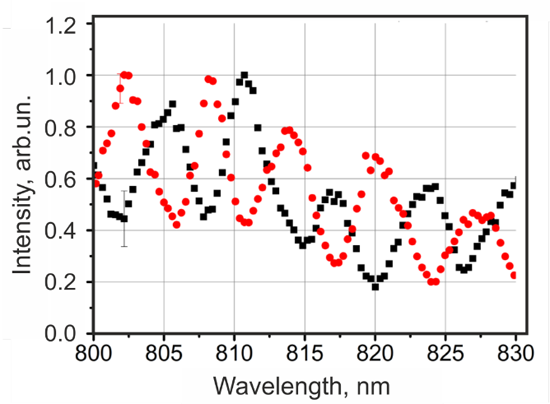
4.2. Dynamical Bragg Diffraction of Chirped Femtosecond Laser Pulses: The Effect of Selective Pulse Compression
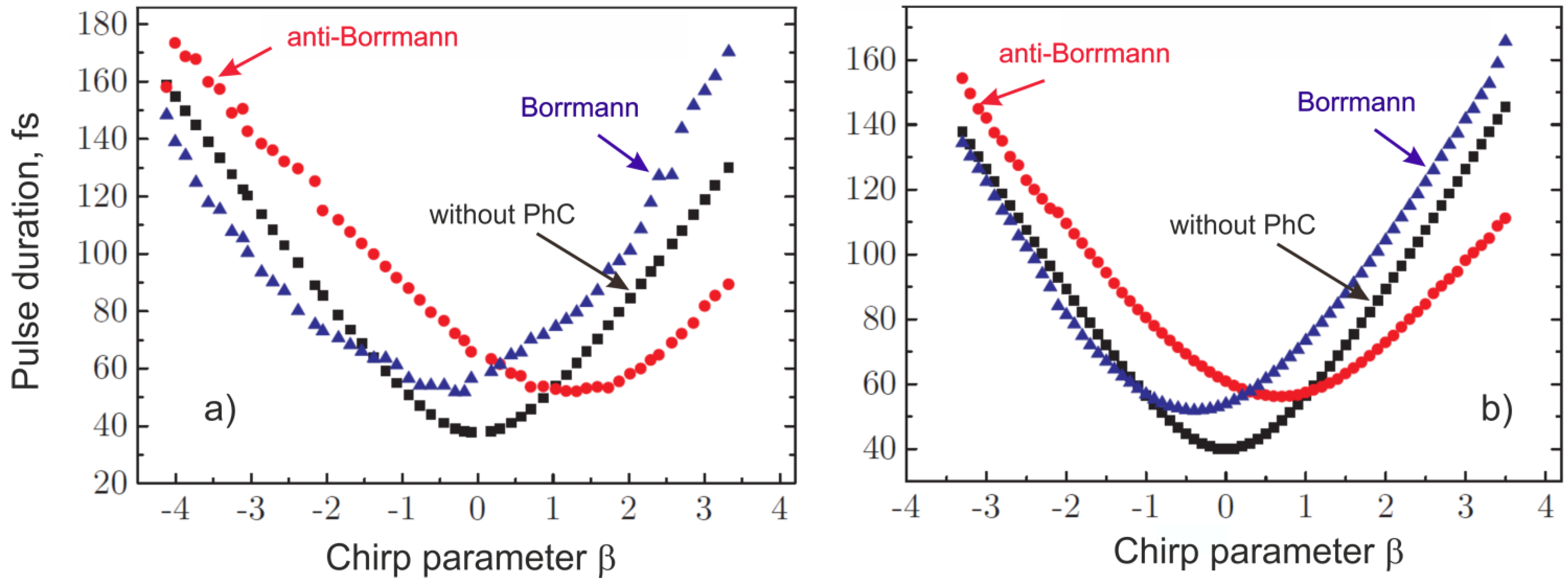
4.3. Pendulum Effect in the Laue Diffraction Scheme in 1D Porous Silicon PhC

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sakoda, K. Optical Properties of Photonic Crystals, 2nd ed.; Springer: Berlin, Germany, 2004. [Google Scholar]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Gersen, H.; Karle, T.J.; Engelen, R.J.; Bogaerts, W.; Korterik, J.P.; van Hulst, N.F.; Krauss, T.F.; Kuipers, L. Real-space observation of ultraslow light in photonic crystal waveguides. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.; Yariv, A.; Hong, C. Electromagnetic propagation in periodic stratified media. I. General theory. J. Opt. Soc. Am. 1977, 67, 423–438. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Chak, P.; Poon, J.K.S.; DeRose, G.A.; Yariv, A.; Scherer, A. Electrically-pumped, broad-area, single-mode photonic crystal lasers. Opt. Express 2007, 15, 5966–5975. [Google Scholar] [CrossRef] [PubMed]
- Scalora, M.; Bloemer, M.J.; Manka, A.S.; Dowling, J.P.; Bowden, C.M.; Viswanathan, R.; Haus, J.W. Pulsed second harmonic generation in nonlinear one-dimensional periodic structures. Phys. Rev. A 1997, 56, 3166–3174. [Google Scholar] [CrossRef]
- Soboleva, I.V.; Murchikova, E.M.; Fedyanin, A.A.; Aktsipetrov, O.A. Second- and third-harmonic generation in birefringent photonic crystals and microcavities based on anisotropic porous silicon. Appl. Phys. Lett. 2007, 87, 241110:1–241110:3. [Google Scholar]
- Inoue, M.; Fujikawa, R.; Baryshev, A.; Khanikaev, A.; Lim, P.B.; Uchida, H.; Aktsipetrov, O.; Fedyanin, A.; Murzina, T.; Granovsky, A. Magnetophotonic crystals. J. Phys. D Appl. Phys. 2006, 39. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic: Waltham, MA, USA, 2003. [Google Scholar]
- Mok, J.T.; de Sterke, C.M.; Eggleton, B.J. Delay-tunable gap-soliton-based slow-light system. Opt. Express 2006, 14, 11987–11996. [Google Scholar] [CrossRef] [PubMed]
- Calvo, M.L.; Cheben, P.; Martínez-Matos, O.; Monte, F.; Rodrigo, J.A. Experimental Detection of the Optical Pendellösung Effect. Phys. Rev. Lett. 2006, 97. [Google Scholar] [CrossRef] [PubMed]
- Savo, S.; di Gennaro, E.; Miletto, C.; Andreone, A.; Dardano, P.; Moretti, L.; Mocella, V. Pendellosung effect in photonic crystals. Opt. Express 2008, 16, 9097–9105. [Google Scholar] [CrossRef] [PubMed]
- Borrmann, G. Über Extinktionsdiagramme der Röntgenstrahlen von Quarz. Phys. Z. 1941, 42, 157–162. (In German) [Google Scholar]
- Bushuev, V.A.; Mantsyzov, B.I.; Skorynin, A.A. Diffraction-induced laser pulse splitting in a linear photonic crystal. Phys. Rev. A 2009, 79. [Google Scholar] [CrossRef]
- Skorynin, A.A.; Bushuev, V.A.; Mantsyzov, B.I. Dynamical Bragg diffraction of optical pulses in photonic crystals in the Laue geometry: Diffraction-induced splitting, selective compression, and focusing of pulses. J. Exp. Theor. Phys. 2012, 115, 56–67. [Google Scholar] [CrossRef]
- Pavesi, L. Porous silicon dielectric multilayers and microcavities. Riv. Nuovo Cimento 1997, 20, 1–76. [Google Scholar] [CrossRef]
- Svyakhovskiy, S.E.; Maydykovsky, A.I.; Murzina, T.V. Mesoporous silicon photonic structures of thousands of periods. J. Appl. Phys. 2012, 112. [Google Scholar] [CrossRef]
- Svyakhovskiy, S.E.; Kompanets, V.O.; Maydykovskiy, A.I.; Murzina, T.V.; Chekalin, S.V.; Skorynin, A.A.; Bushuev, V.A.; Mantsyzov, B.I. Observation of the temporal Bragg-diffraction-induced laser-pulse splitting in a linear photonic crystal. Phys. Rev. A 2012, 86. [Google Scholar] [CrossRef]
- Timoshenko, V.Y.; Osminkina, L.A.; Efimova, A.I.; Golovan, L.A.; Kashkarov, P.K.; Kovalev, D.; Kunzner, N.; Gross, E.; Diener, J.; Koch, F. Anisotropy of optical absorption in birefringent porous silicon. Phys. Rev. B 2003, 67. [Google Scholar] [CrossRef]
- Golovan, L.A.; Melnikov, V.A.; Konorov, S.O.; Fedotov, A.B.; Timoshenko, V.Y.; Zheltikov, A.M.; Kashkarov, P.K.; Ivanov, D.A.; Petrov, G.I.; Yakovlev, V.V. Linear and nonlinear optical anisotropy of amorphous oxidized silicon films induced by a network of pores. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
- Svyakhovskiy, S.E.; Skorynin, A.A.; Bushuev, V.A.; Chekalin, S.V.; Kompanets, V.O.; Maydykovskiy, A.I.; Murzina, T.V.; Novikov, V.B.; Mantsyzov, B.I. Polarization effects in diffraction-induced laser pulse splitting in one-dimensional photonic crystals. JOSA B 2013, 30. [Google Scholar] [CrossRef]
- Svyakhovskiy, S.E.; Maydykovskiy, A.I.; Novikov, V.B.; Kompanets, V.O.; Chekalin, S.V.; Skorynin, A.A.; Bushuev, V.A.; Mantsyzov, B.I.; Murzina, T.V. Selective Compression of Femtosecond Laser Pulses in a Linear Photonic Crystal. In Proceedings of the Frontiers in Optics FTu3A.21, Orlando, FL, USA, 6–10 October 2013.
- Mocella, V. Negative refraction in Photonic Crystals: Thickness dependence and Pendellosung phenomenon. Opt. Express 2005, 13, 1361–1367. [Google Scholar] [CrossRef] [PubMed]
- Mocella, V.; Dardano, P.; Moretti, L.; Rendina, I. A polarizing beam splitter using negative refraction of photonic crystals. Opt. Express 2005, 13, 7699–7707. [Google Scholar] [CrossRef] [PubMed]
- Merzlikin, A.M.; Vinogradov, A.P. Superprism effect in 1D photonic crystal. Opt. Commun. 2006, 259, 700–703. [Google Scholar] [CrossRef]
- Panoiu, N.C.; Bahl, M.; Osgood, R.M. Optically tunable superprism effect in nonlinear photonic crystal. Opt. Lett. 2003, 28, 2503–2505. [Google Scholar] [CrossRef]
- Novikov, V.B.; Svyakhovskiy, S.E.; Skorynin, A.A.; Bushuev, V.A.; Mantsyzov, B.I.; Maydykovskiy, A.I.; Murzina, T.V. Control over the Light Propagation by Means of the Pendellösung Effect in 1D Porous Quartz Photonic Crystal. In Proceedings of the ICONO/LAT 2013, Moscow, Russia, 18–22 June 2013.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maydykovskiy, A.; Novikov, V.; Svyakhovskiy, S.; Murzina, T. Optical Effects Accompanying the Dynamical Bragg Diffraction in Linear 1D Photonic Crystals Based on Porous Silicon. Crystals 2014, 4, 427-438. https://doi.org/10.3390/cryst4040427
Maydykovskiy A, Novikov V, Svyakhovskiy S, Murzina T. Optical Effects Accompanying the Dynamical Bragg Diffraction in Linear 1D Photonic Crystals Based on Porous Silicon. Crystals. 2014; 4(4):427-438. https://doi.org/10.3390/cryst4040427
Chicago/Turabian StyleMaydykovskiy, Anton, Vladimir Novikov, Sergey Svyakhovskiy, and Tatiana Murzina. 2014. "Optical Effects Accompanying the Dynamical Bragg Diffraction in Linear 1D Photonic Crystals Based on Porous Silicon" Crystals 4, no. 4: 427-438. https://doi.org/10.3390/cryst4040427