The Physics of the Hume-Rothery Electron Concentration Rule
Abstract
:1. Introduction
1.1. e/a versus Valence in the Hume-Rothery Electron Concentration Rule
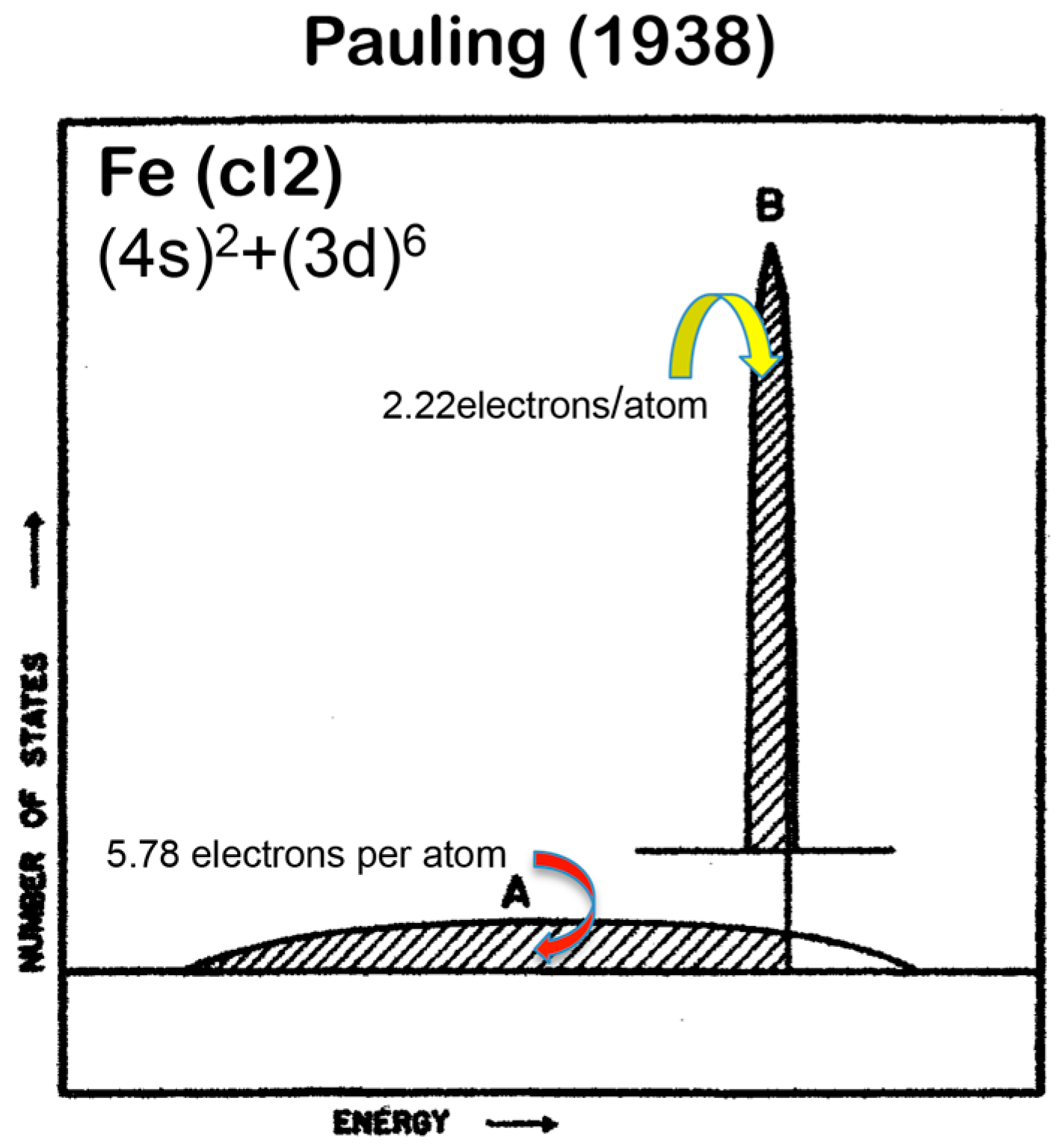
1.2. Historical Survey on the e/a Issue for Transition Metals (TM) and Their Compounds
1.3. e/a-Dependent Hume-Rothery-Type Stabilization Mechanism
1.4. Stoichiometric Compounds versus Chemically Disordered Solid Solutions
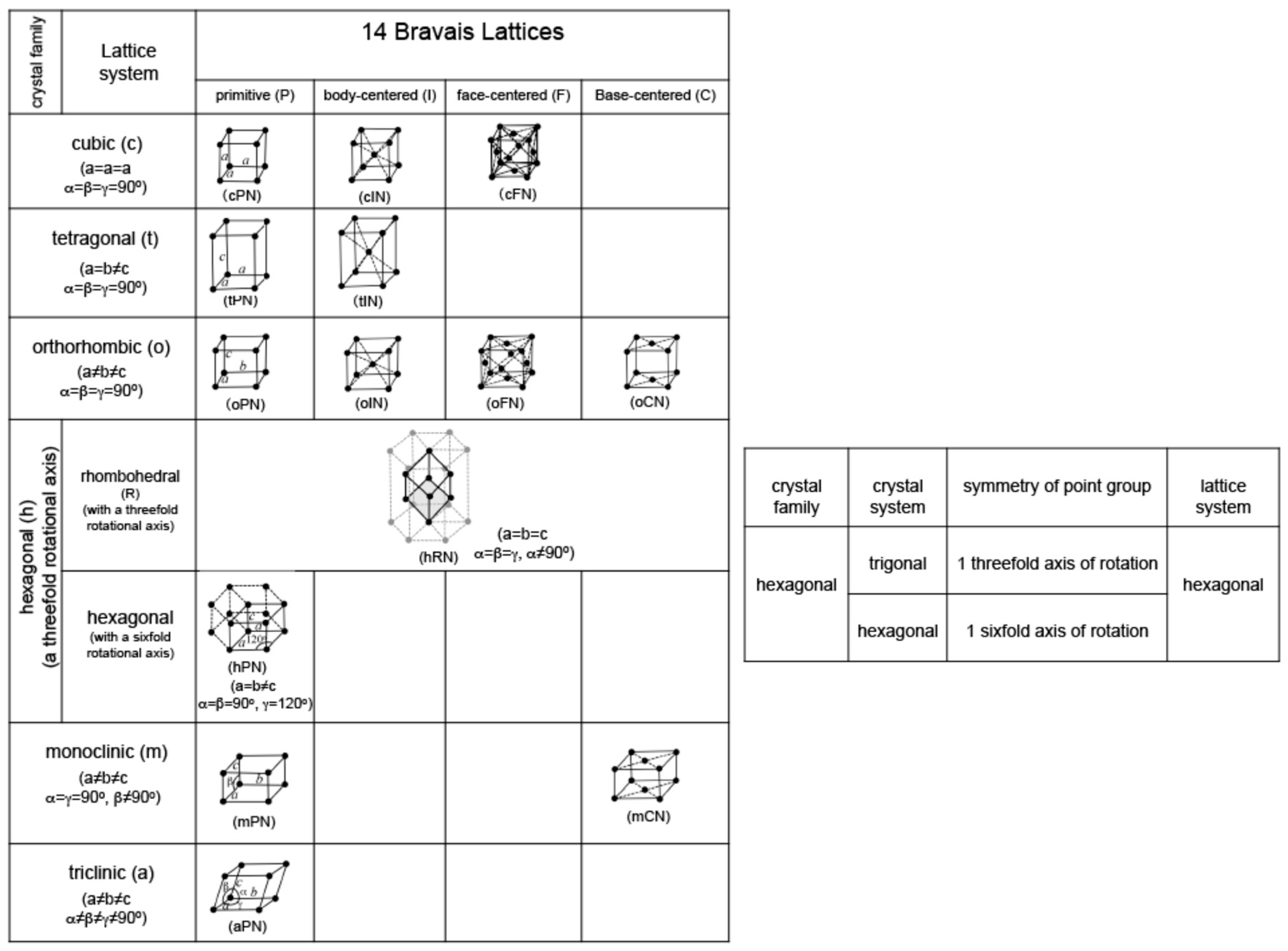
2. The FLAPW-Fourier Theory and Its Application to Elements in the Periodic Table
2.1. WIEN2k-FLAPW Program Package
2.2. Representations of Quantities in Reciprocal Space
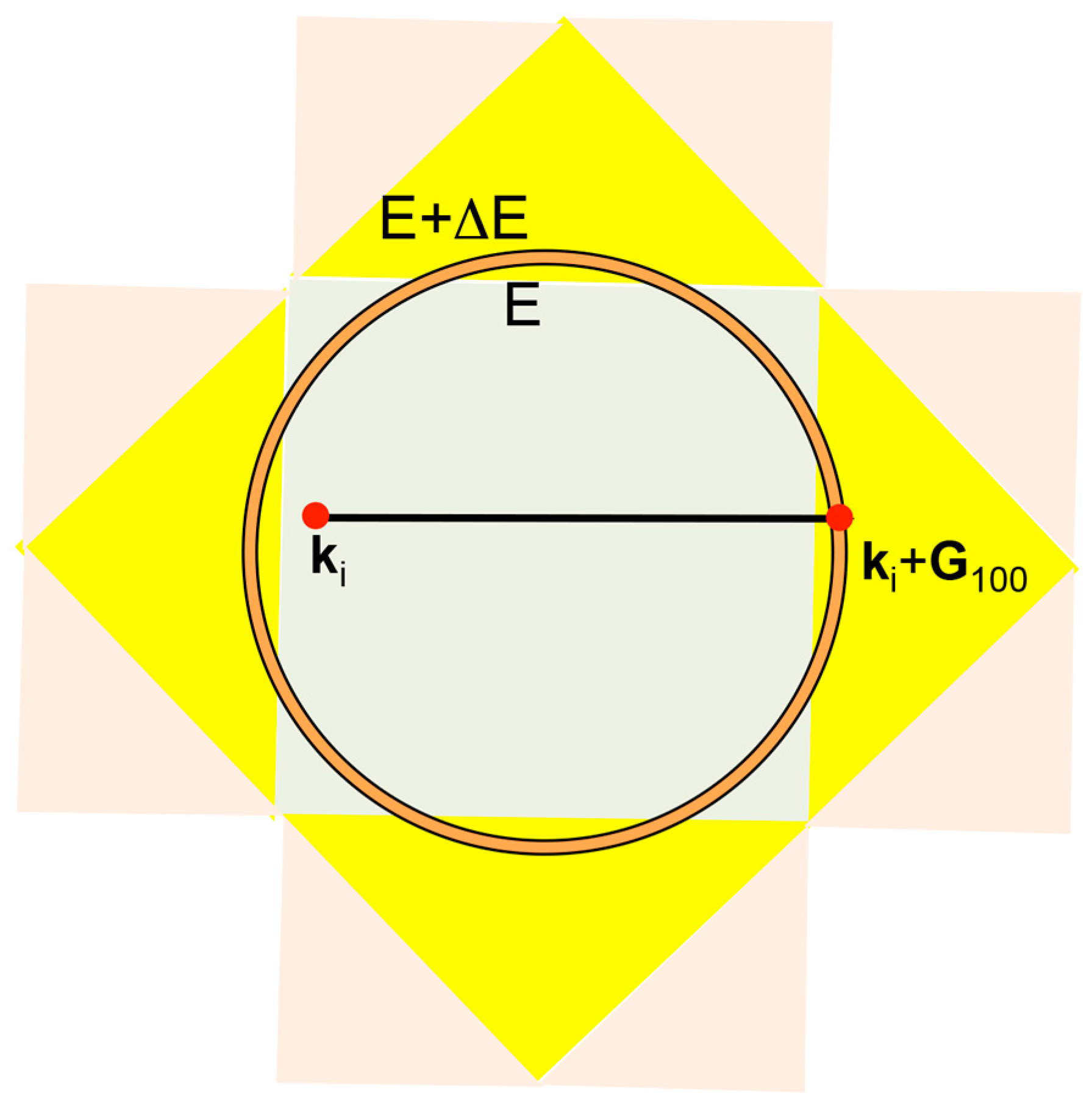
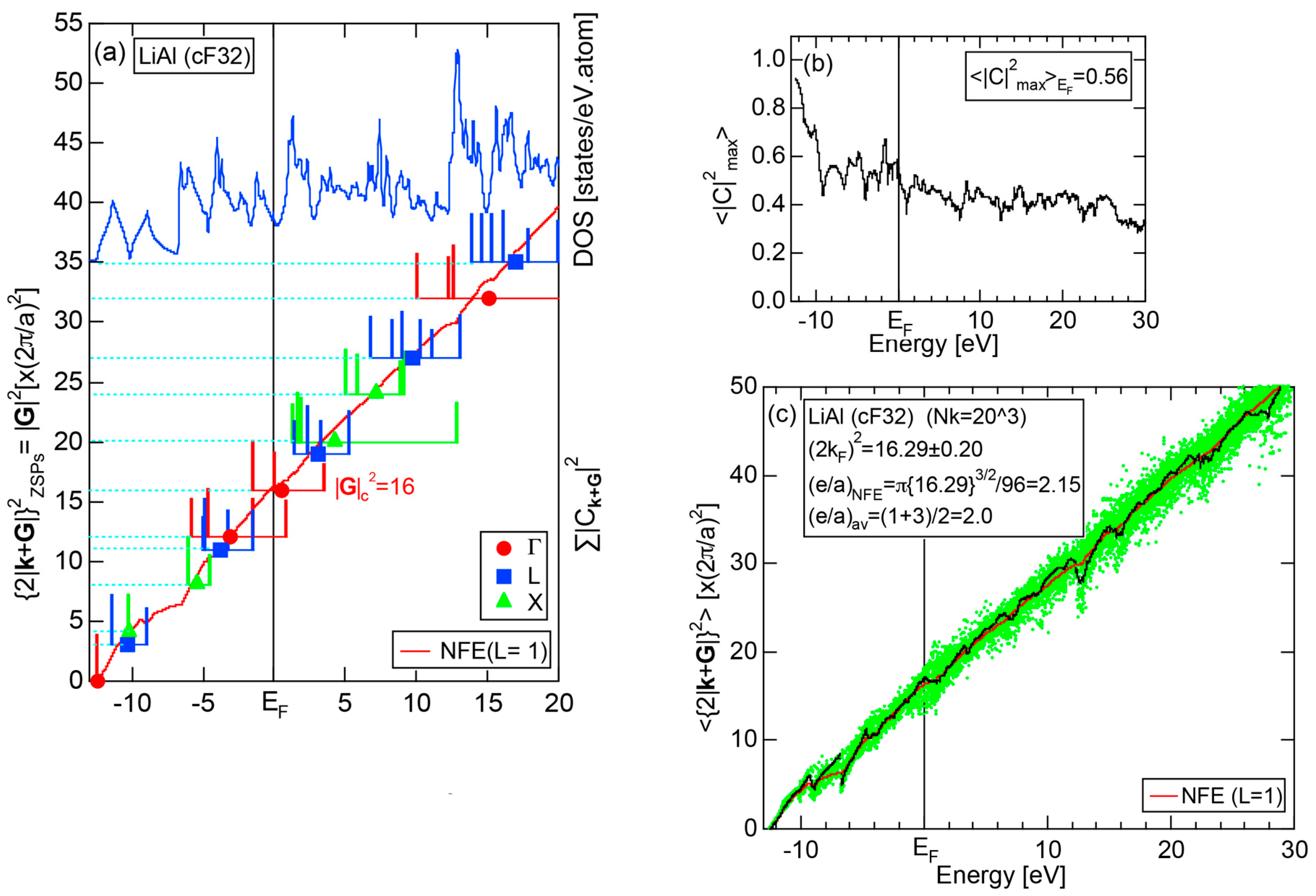
2.3. The FLAPW-Fourier Theory
2.4. FLAPW-Fourier Spectra
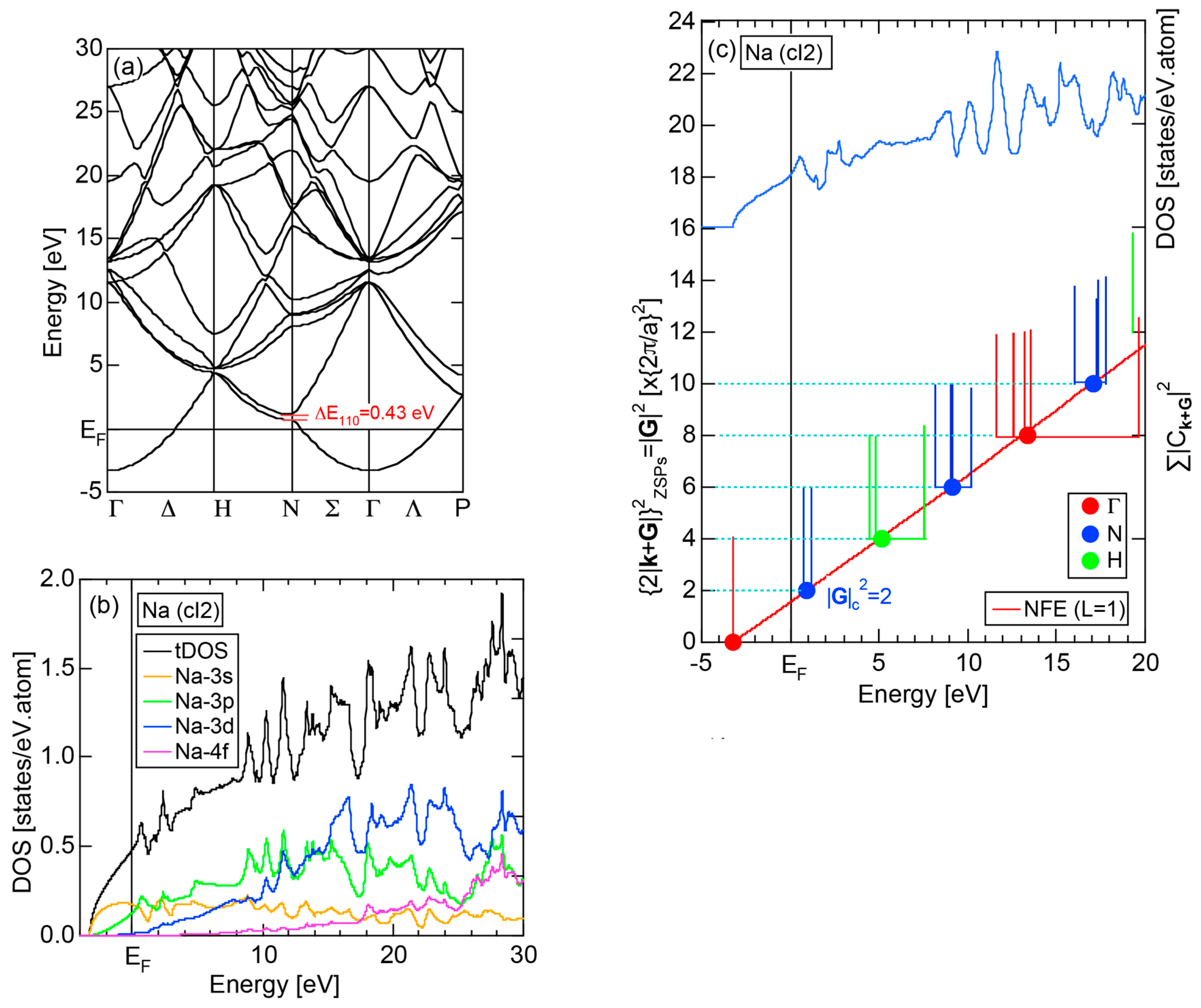
2.4.1. Na (cI2)
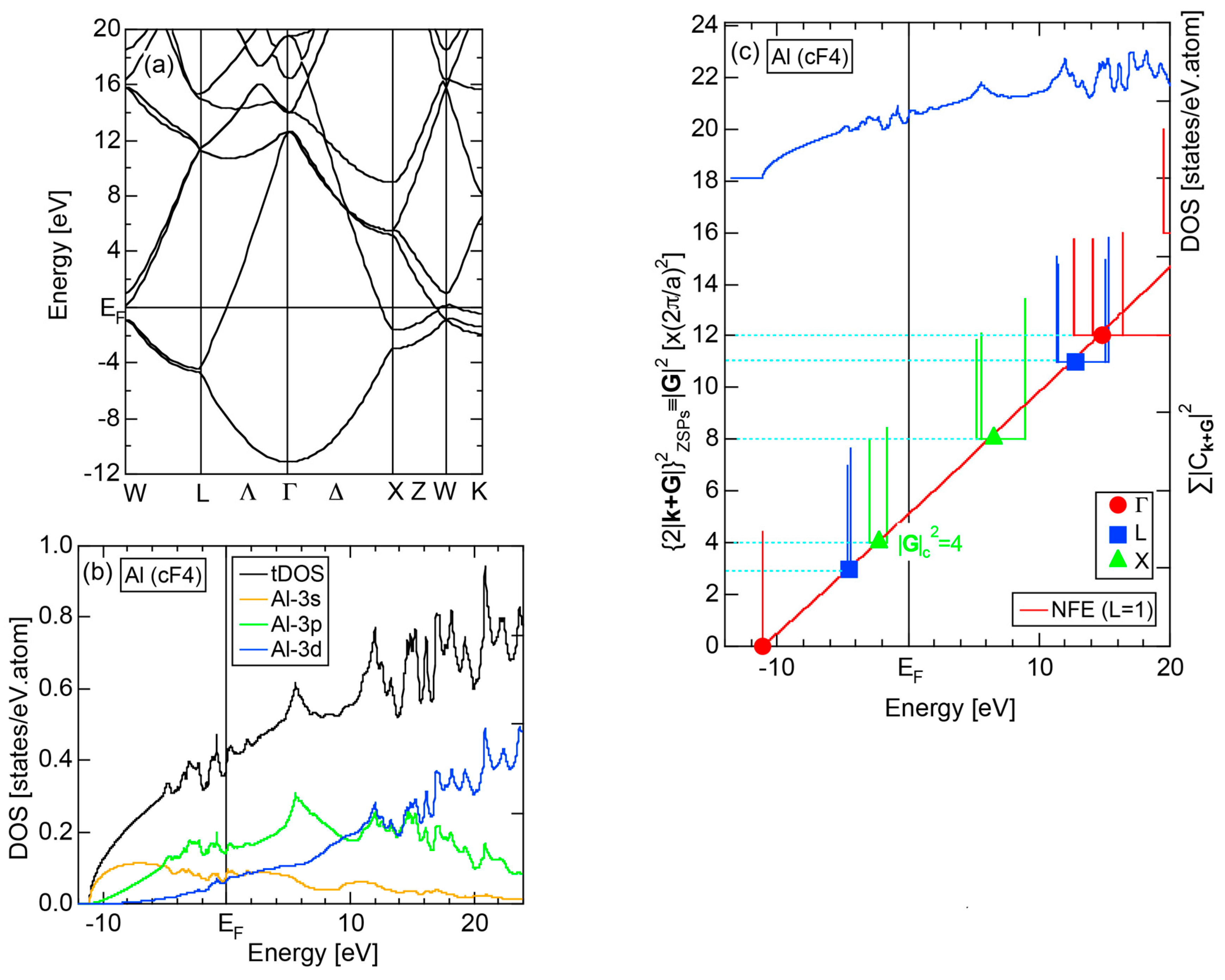
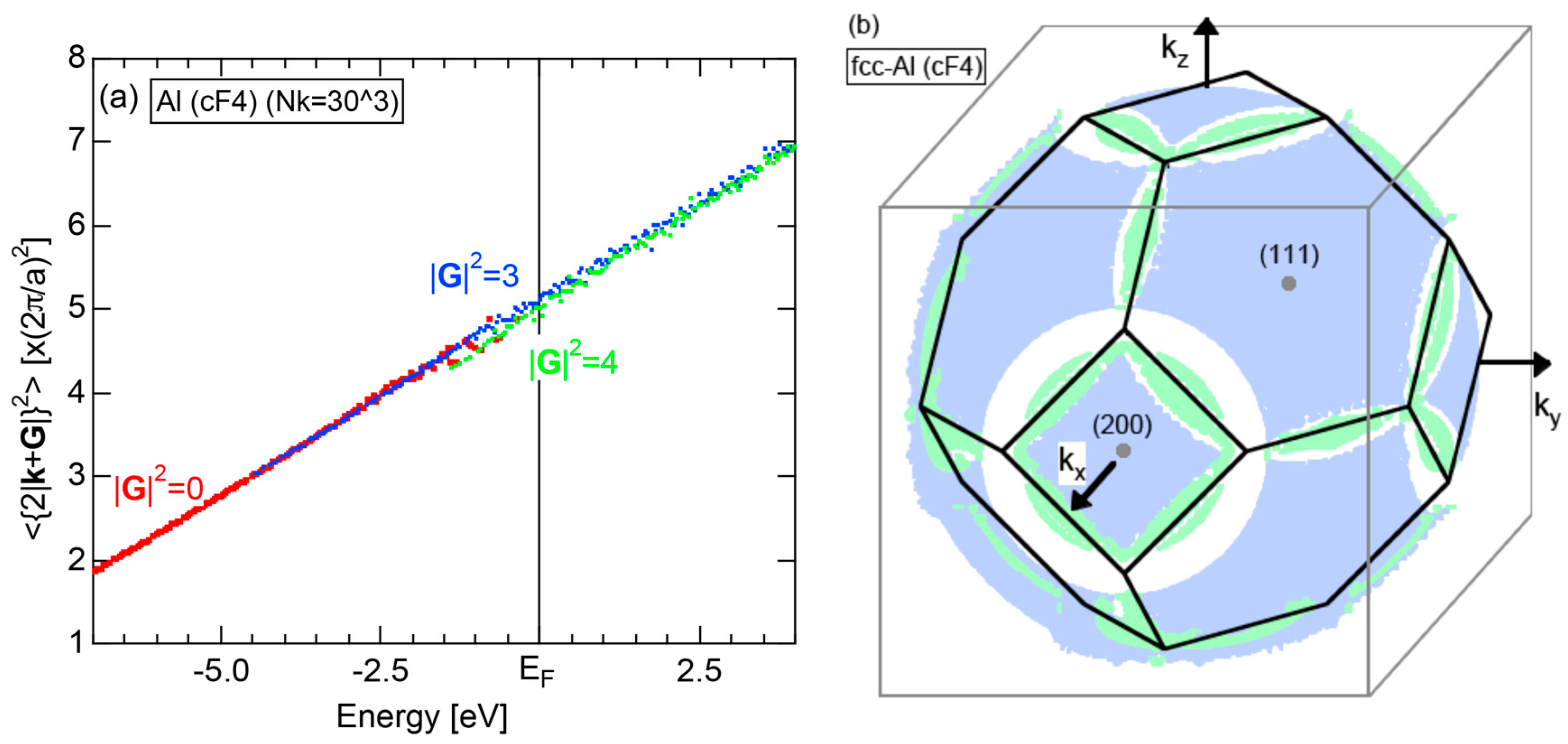
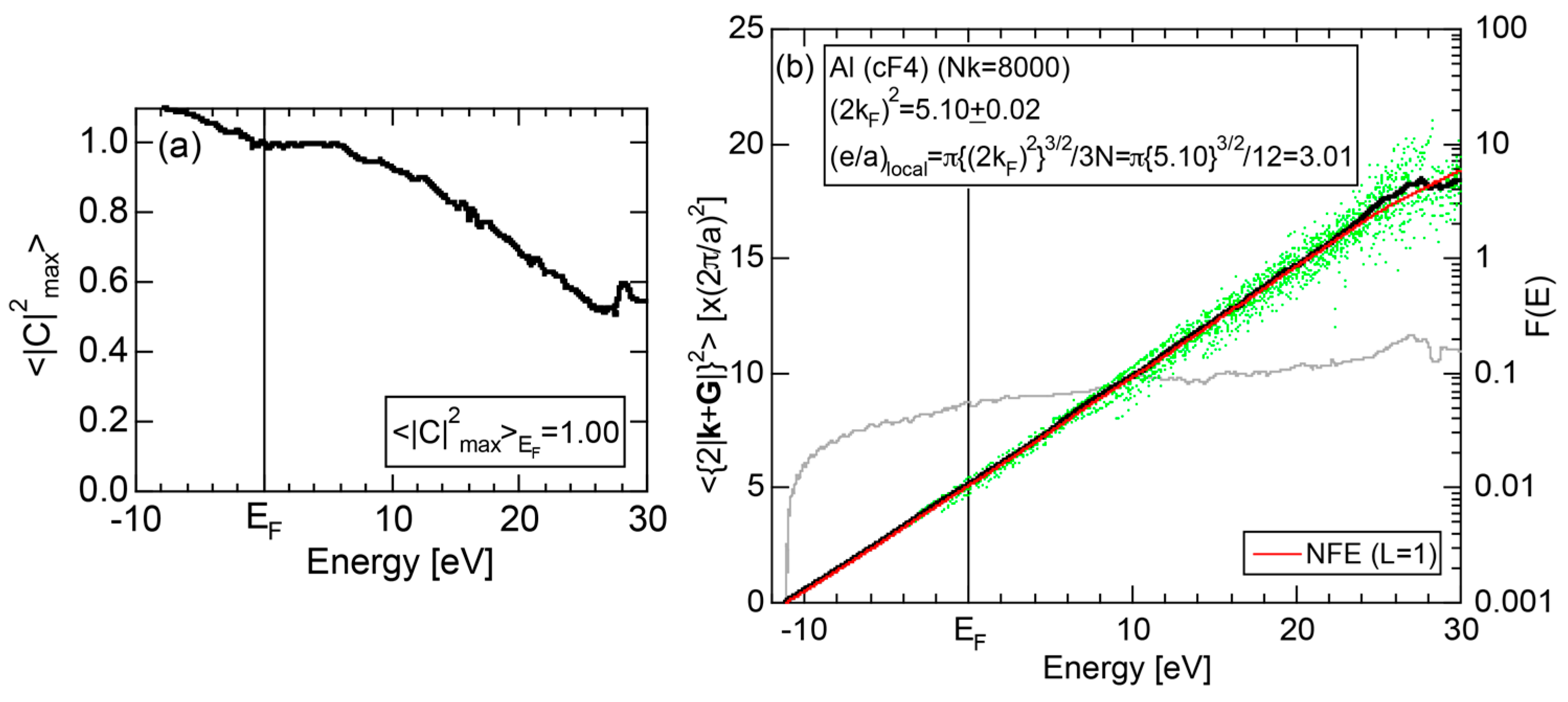
2.4.2. Al (cF4)
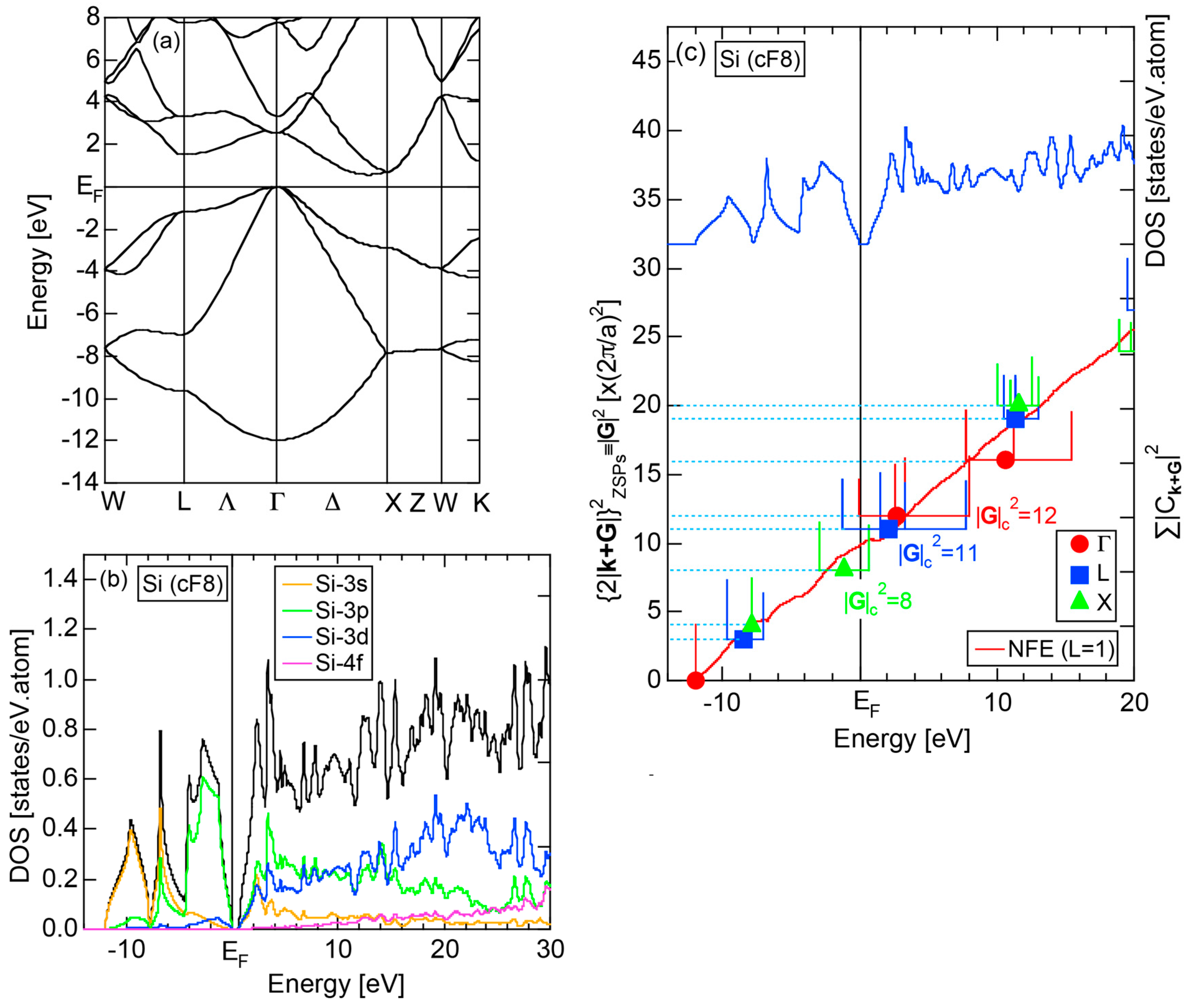
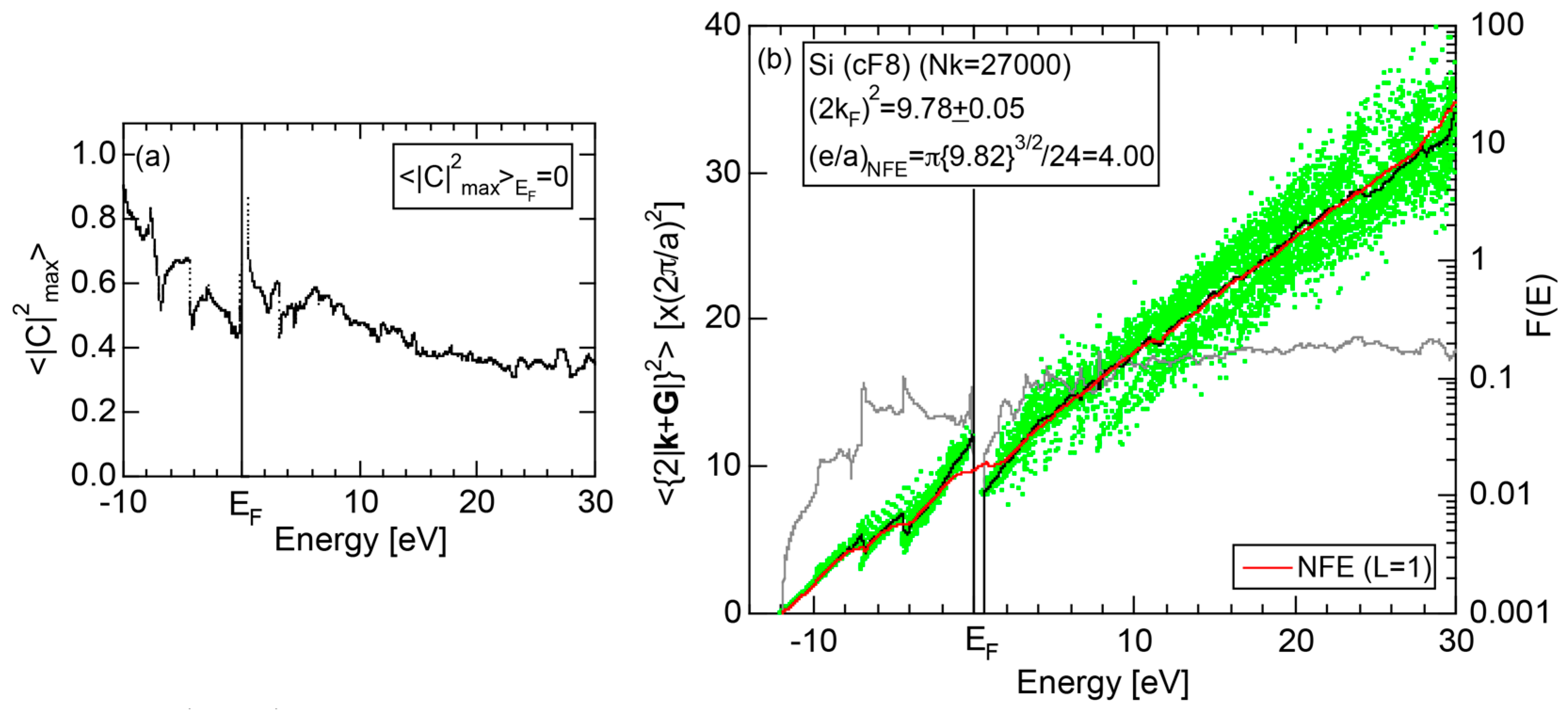
2.4.3. Si (cF8)
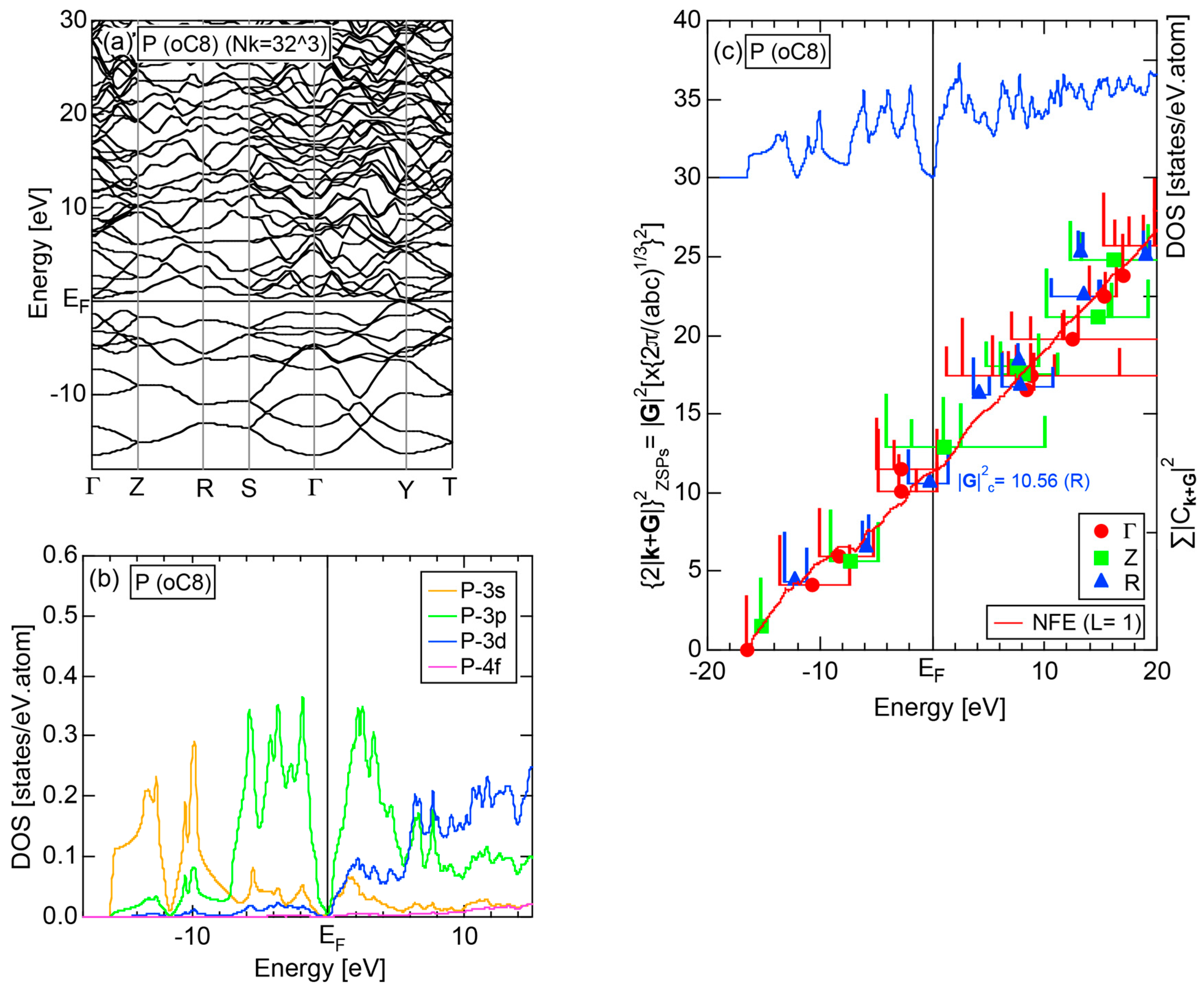
2.4.4. P (oC8)
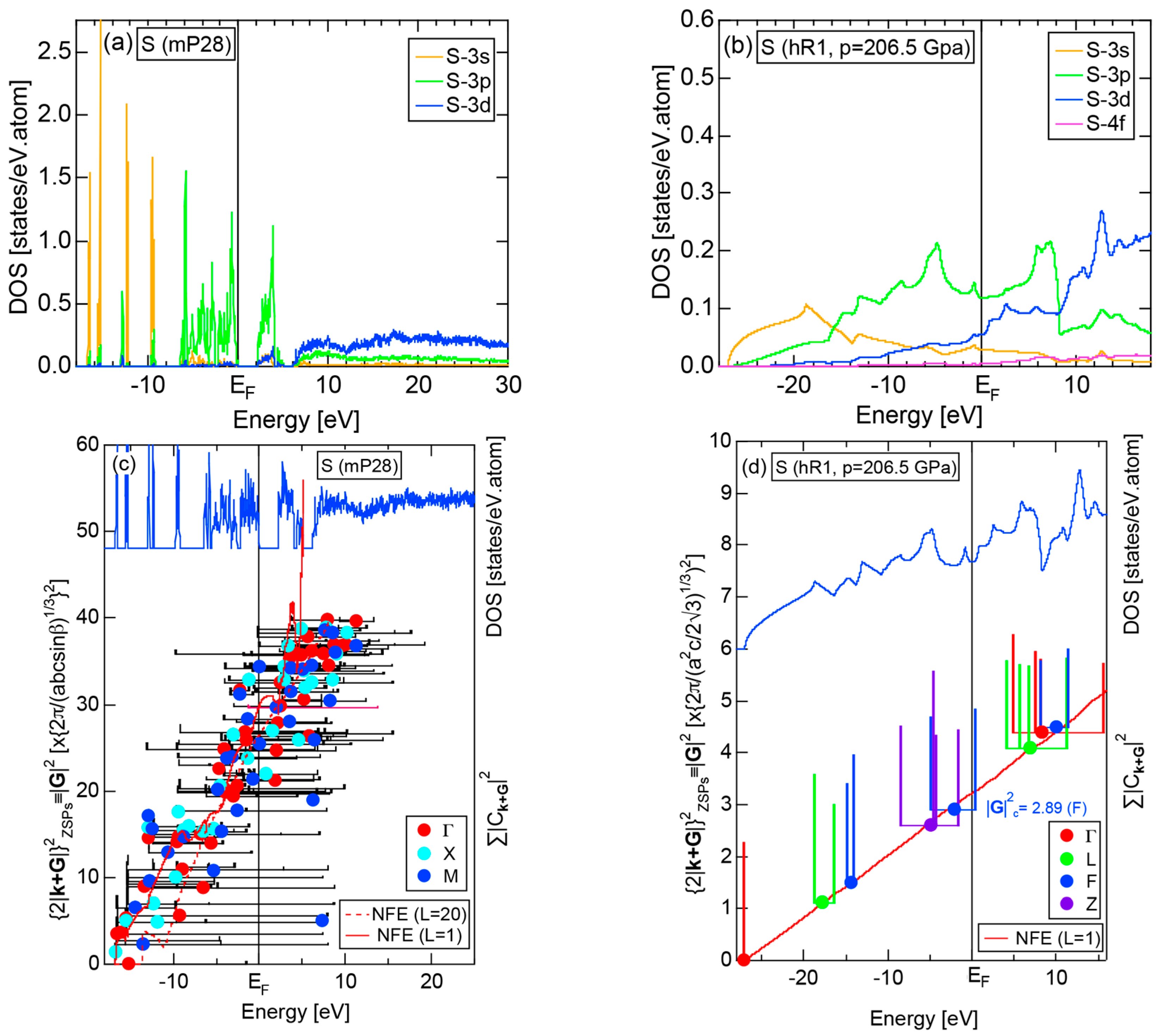
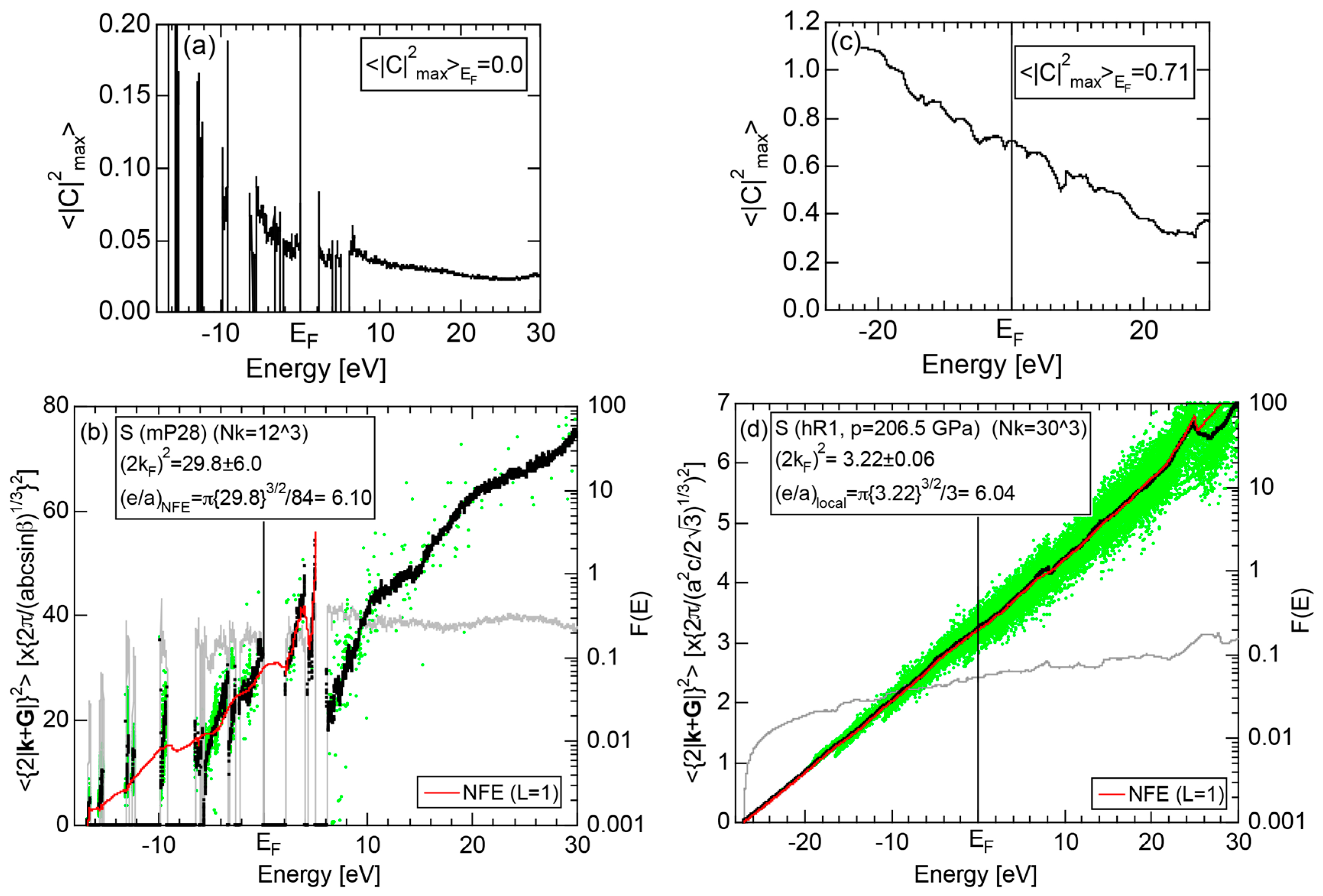
2.4.5. Insulating S (mP28) versus High-Pressure Metallic S (hR1)
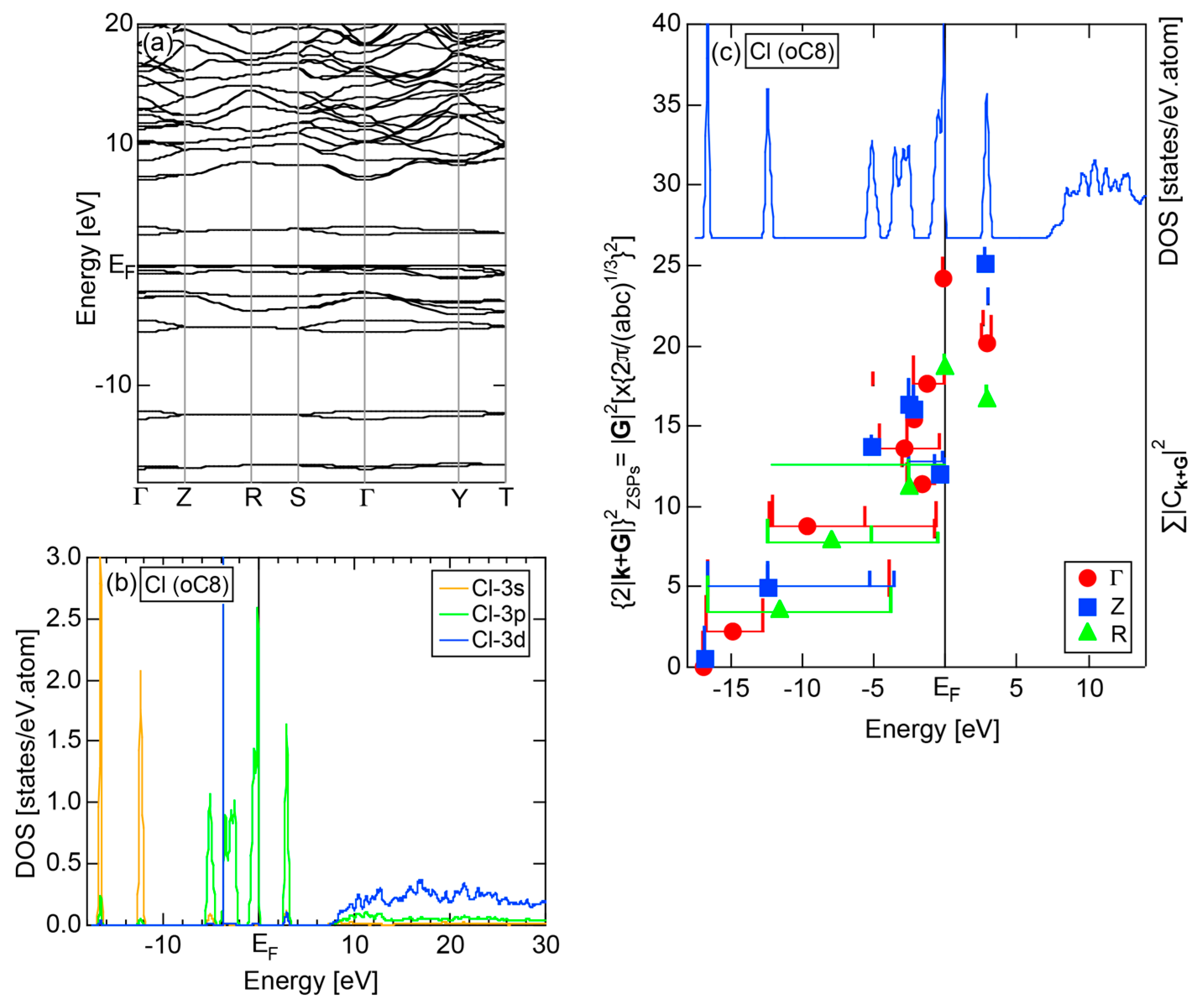
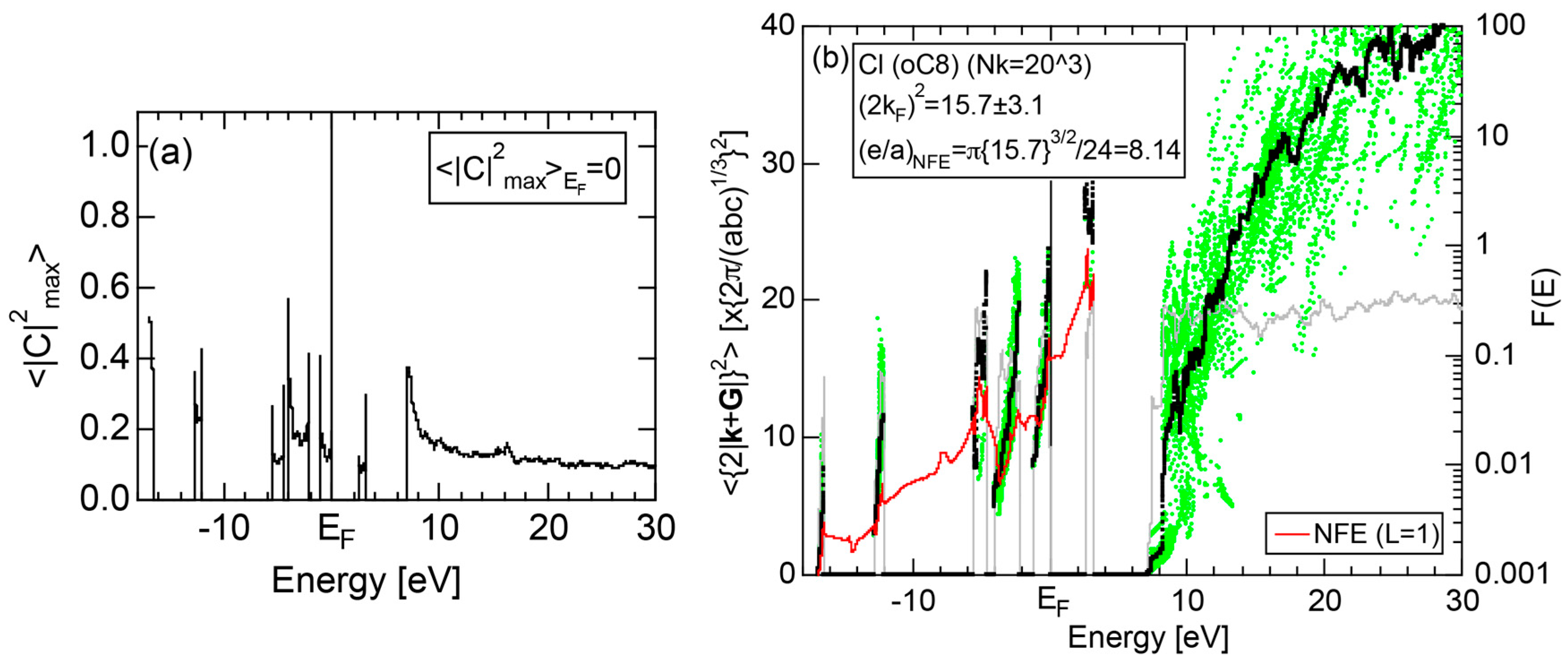
2.4.6. Insulating Solid Cl (oC8)
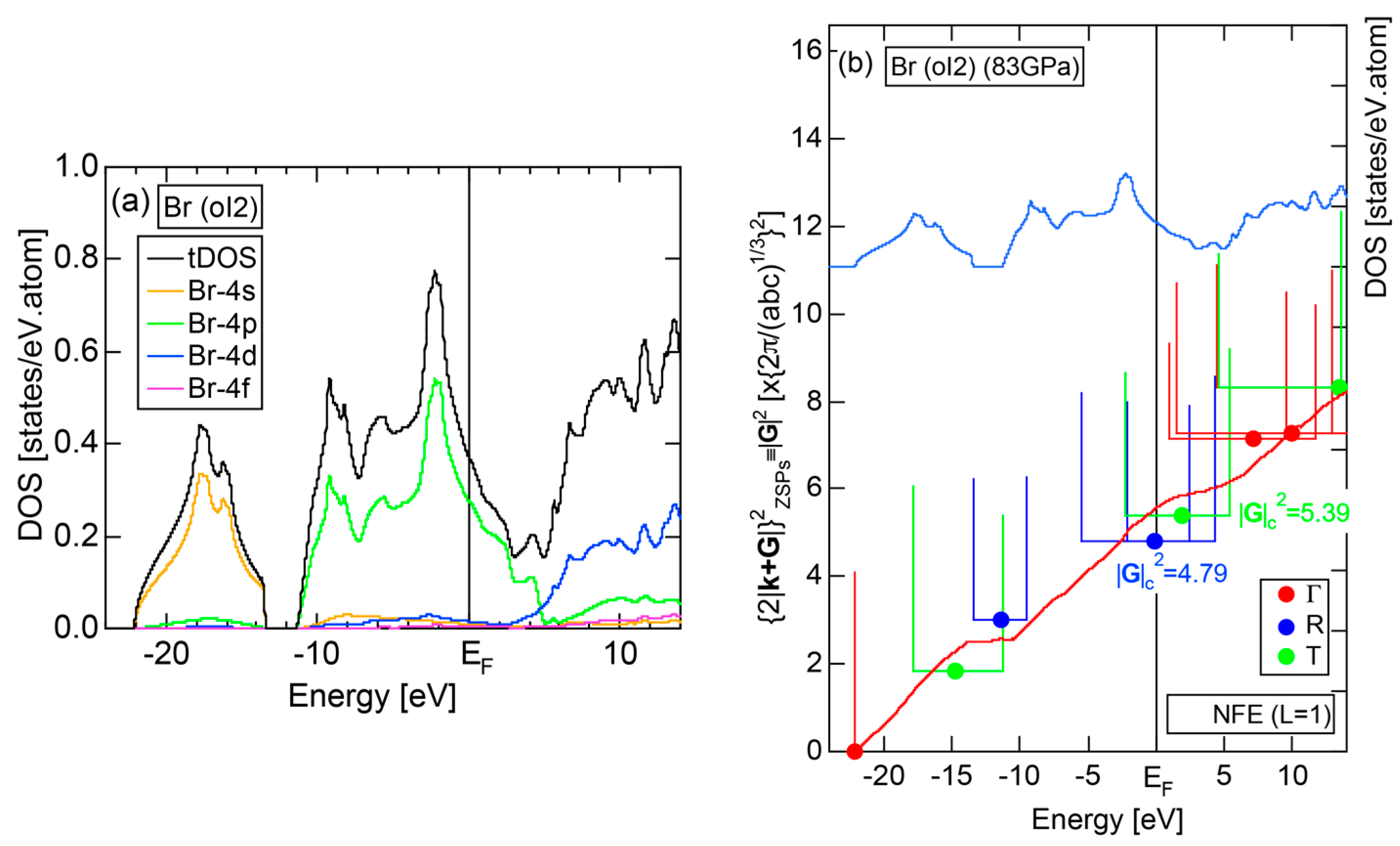
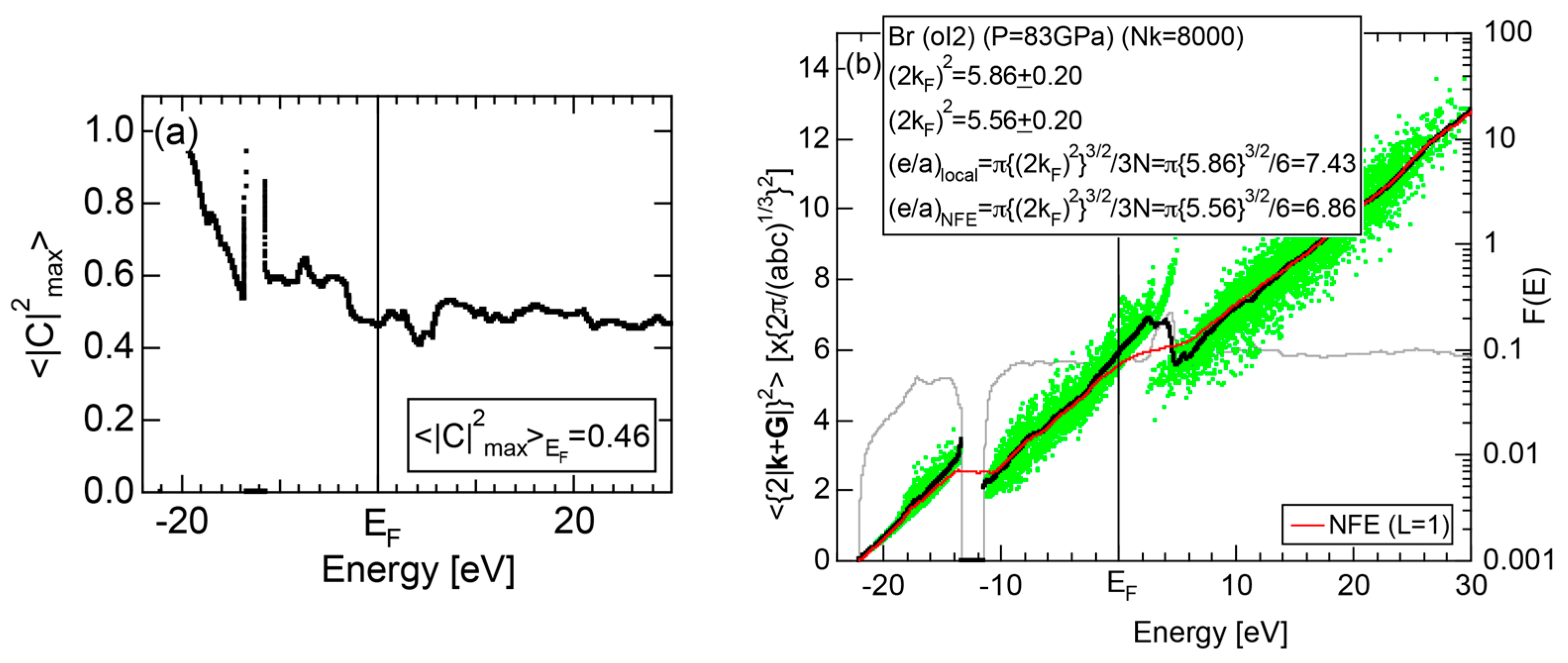
2.4.7. High-Pressure Metallic solid Br (oI2)
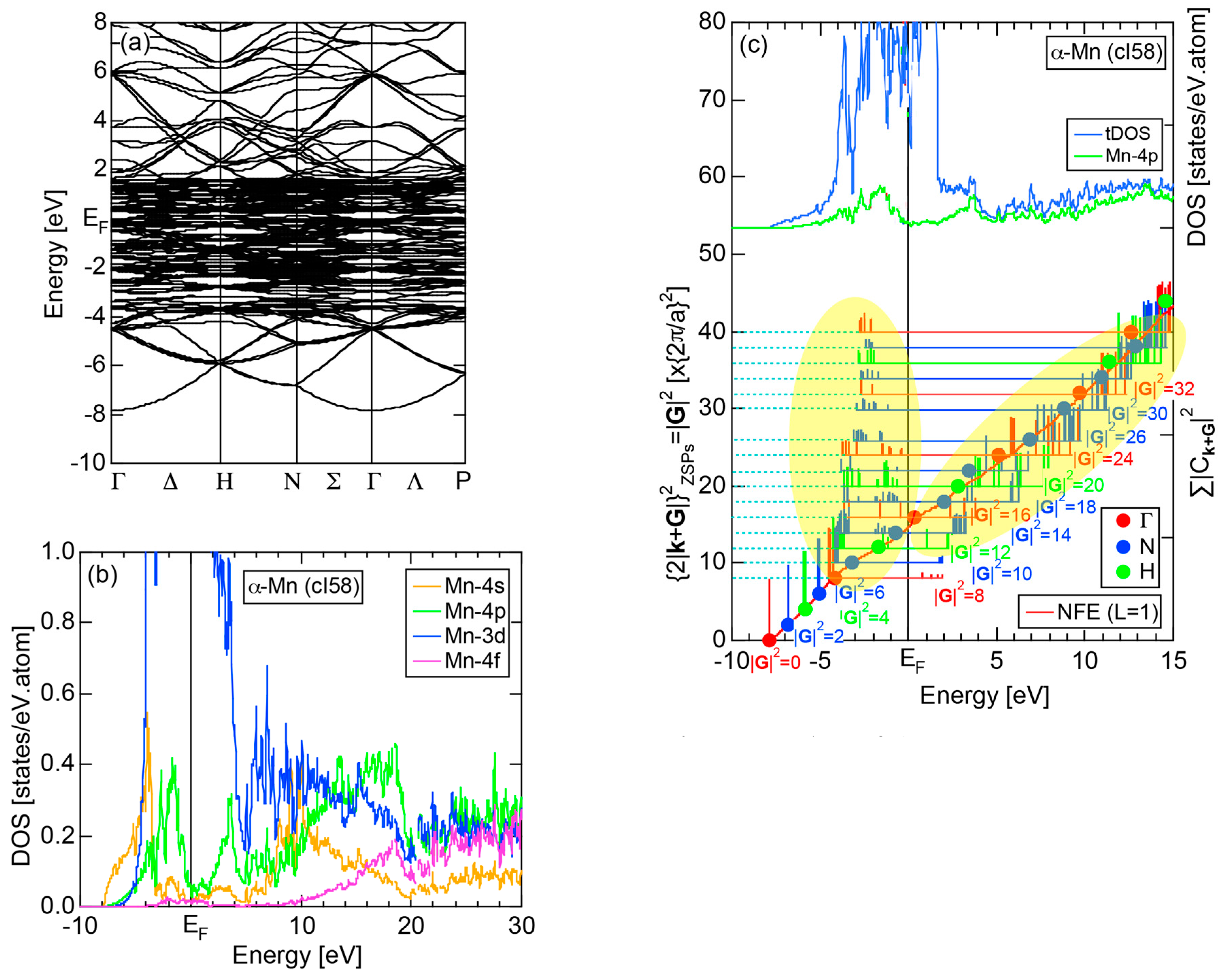
2.4.8. α-Mn (cI58)
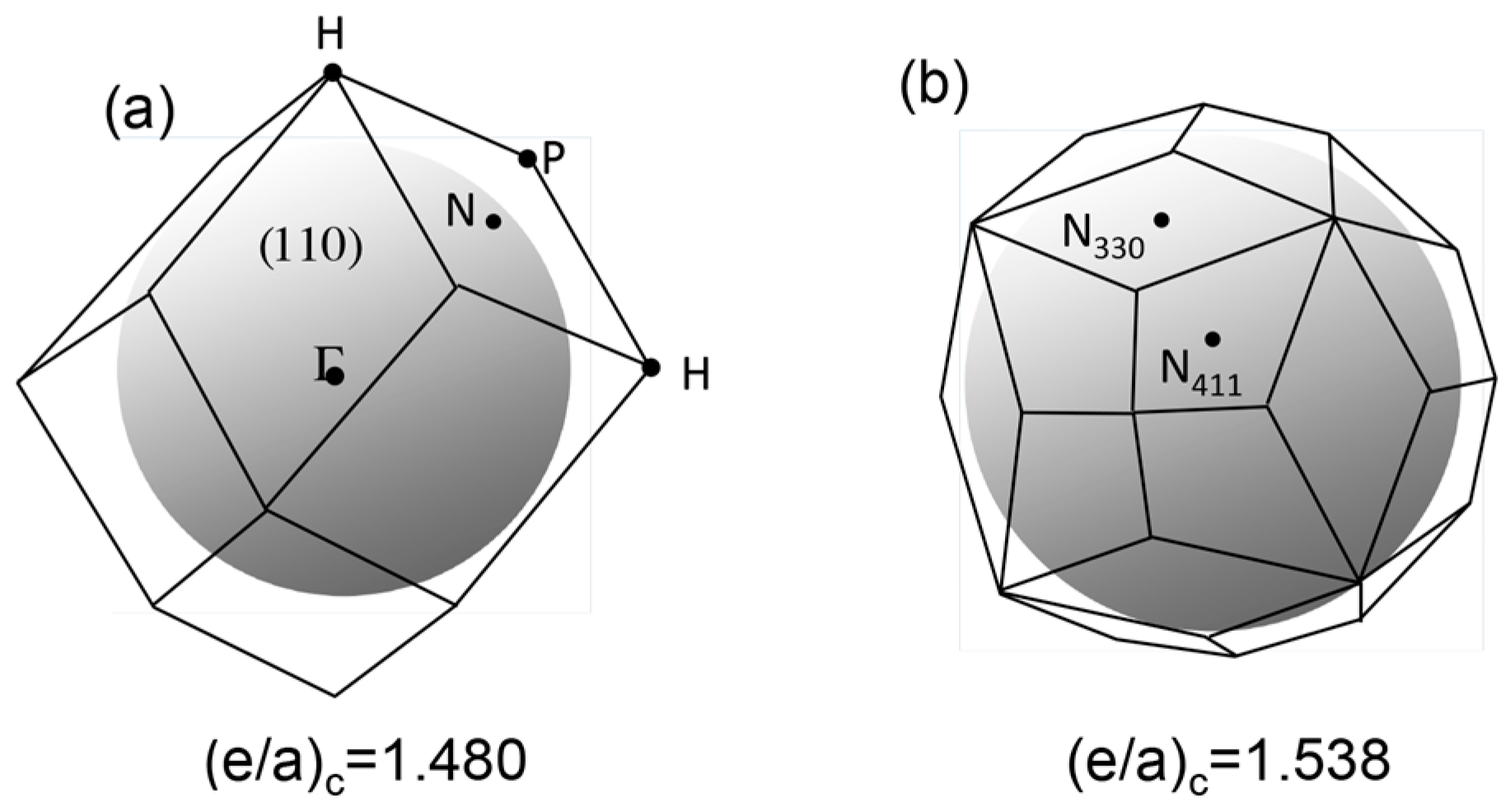
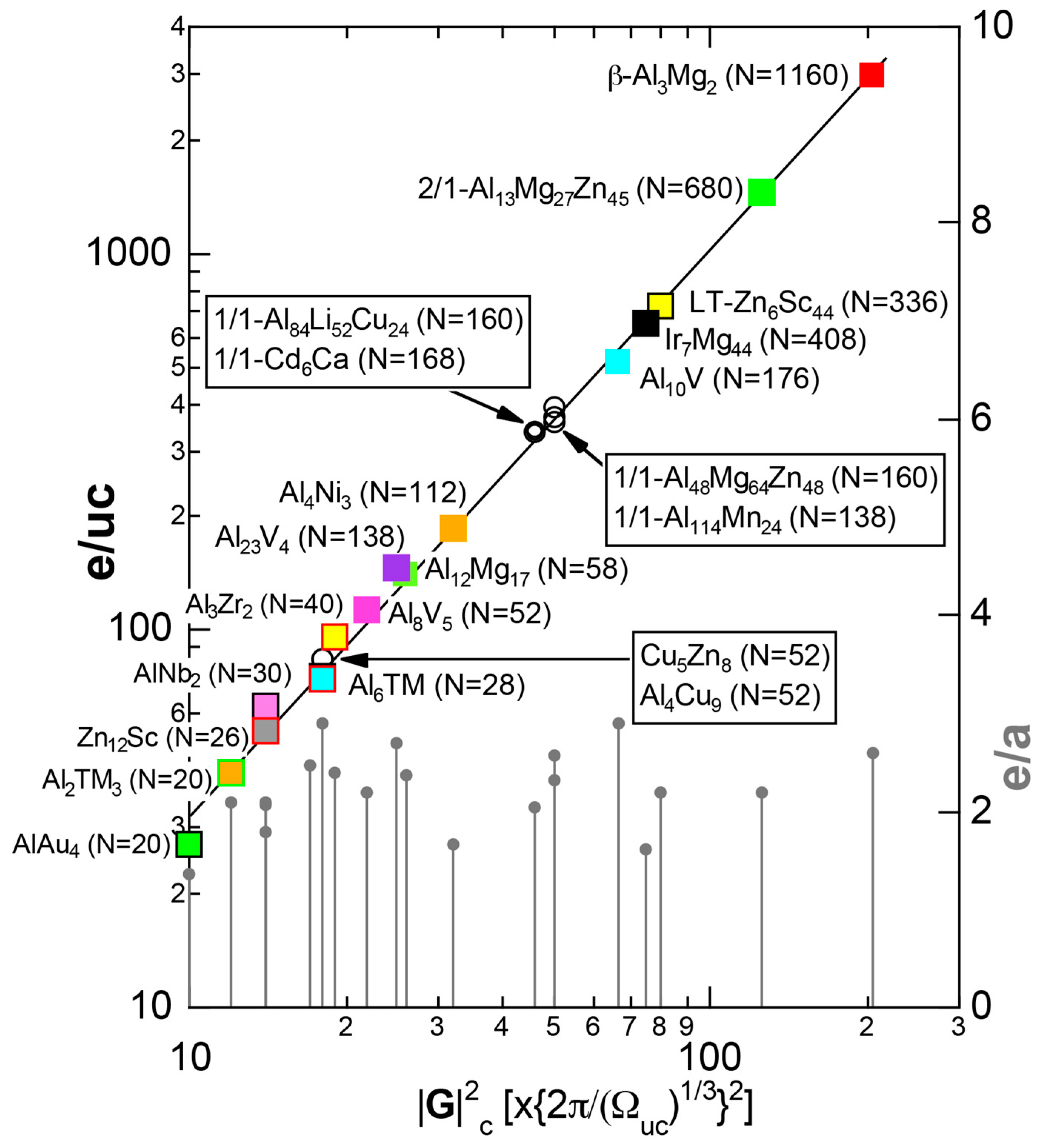
2.5. Hume-Rothery Plot
2.6. Criterion to Judge Itinerancy of Electrons at the Fermi Level
2.7. Why Can the Hume-Rothery Plot Generate Dispersion Relations in the Extended Zone Scheme?
2.8. Determination of and e/a for Representative Elements in the Periodic Table
2.8.1. Na (cI2)
2.8.2. Al (cF4)
2.8.3. Si (cF8)
2.8.4. P (oC8)
2.8.5. Insulating Phase S (mP28) versus High-Pressure Metallic Phase S (hR1)
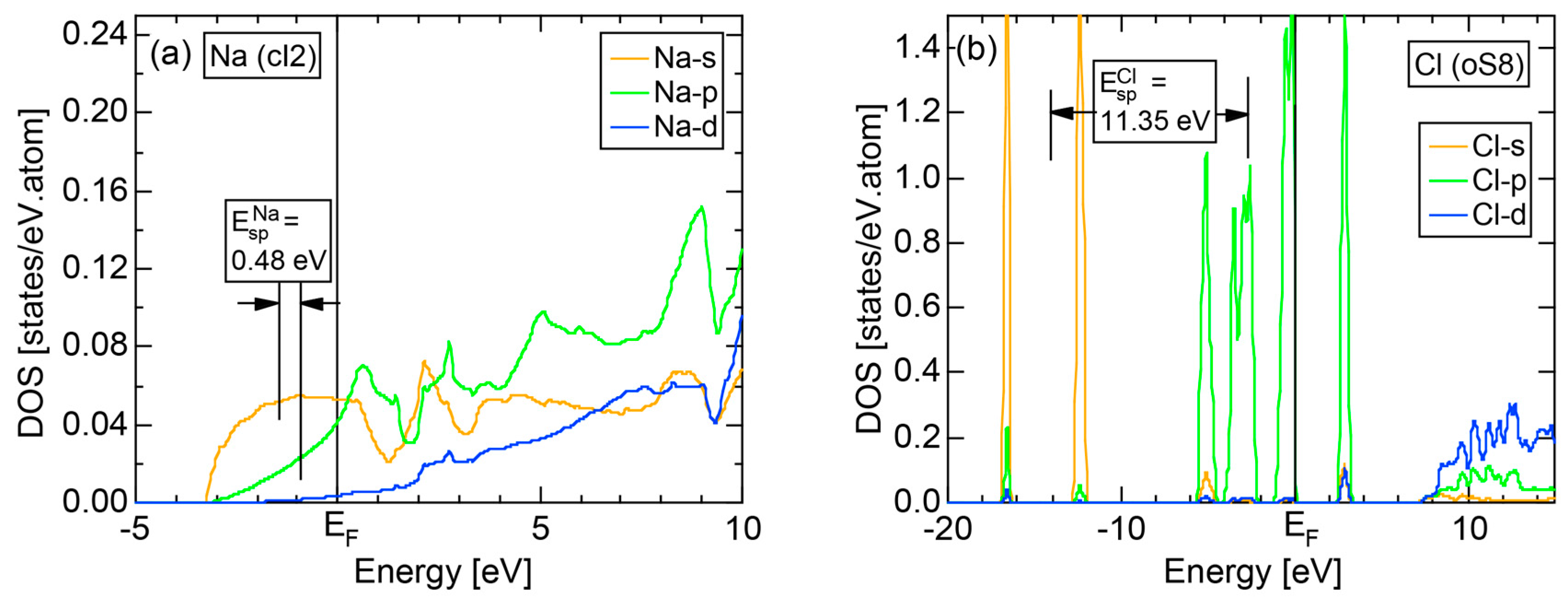
2.8.6. Insulating Solid Cl (oC8)
2.8.7. High-Pressure Metallic Br (oI2)
2.8.8. α-Mn (cI58)
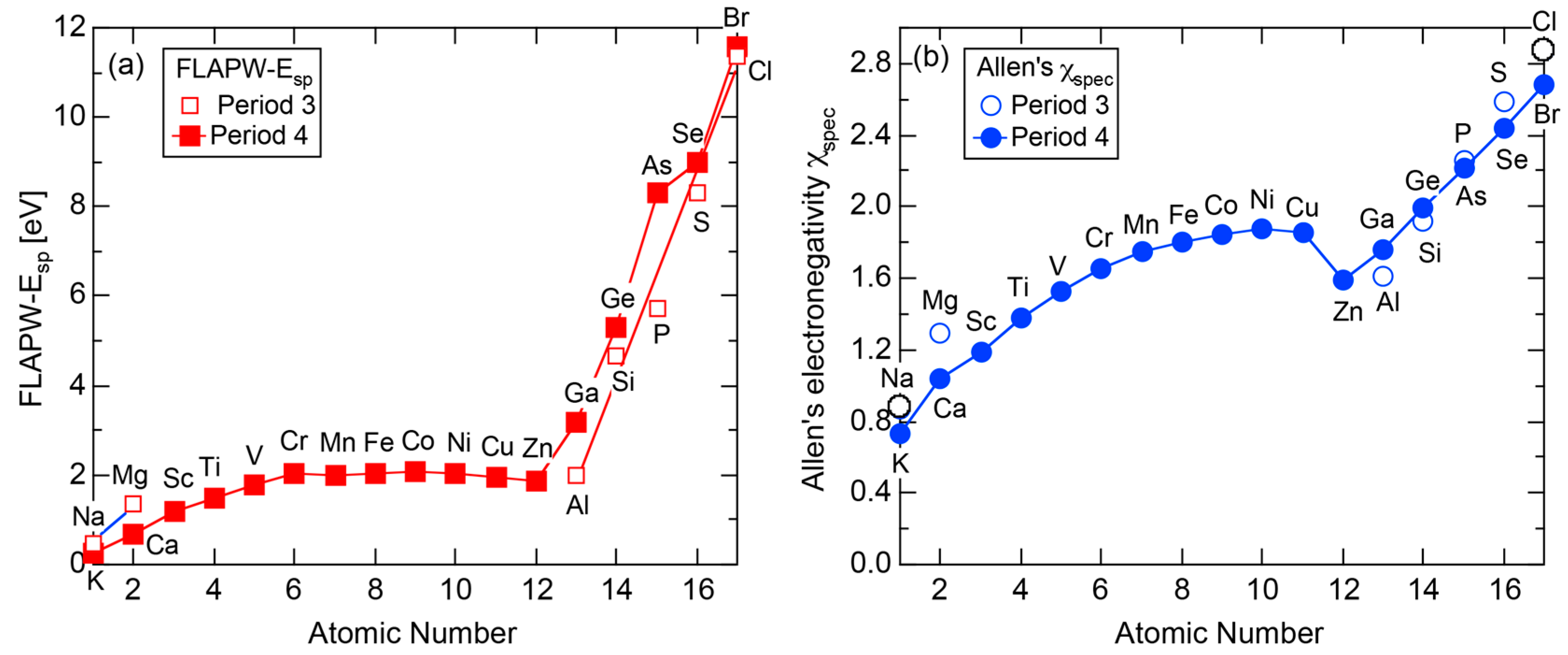
2.9. e/a Determination for 54 Elements in the Periodic Table
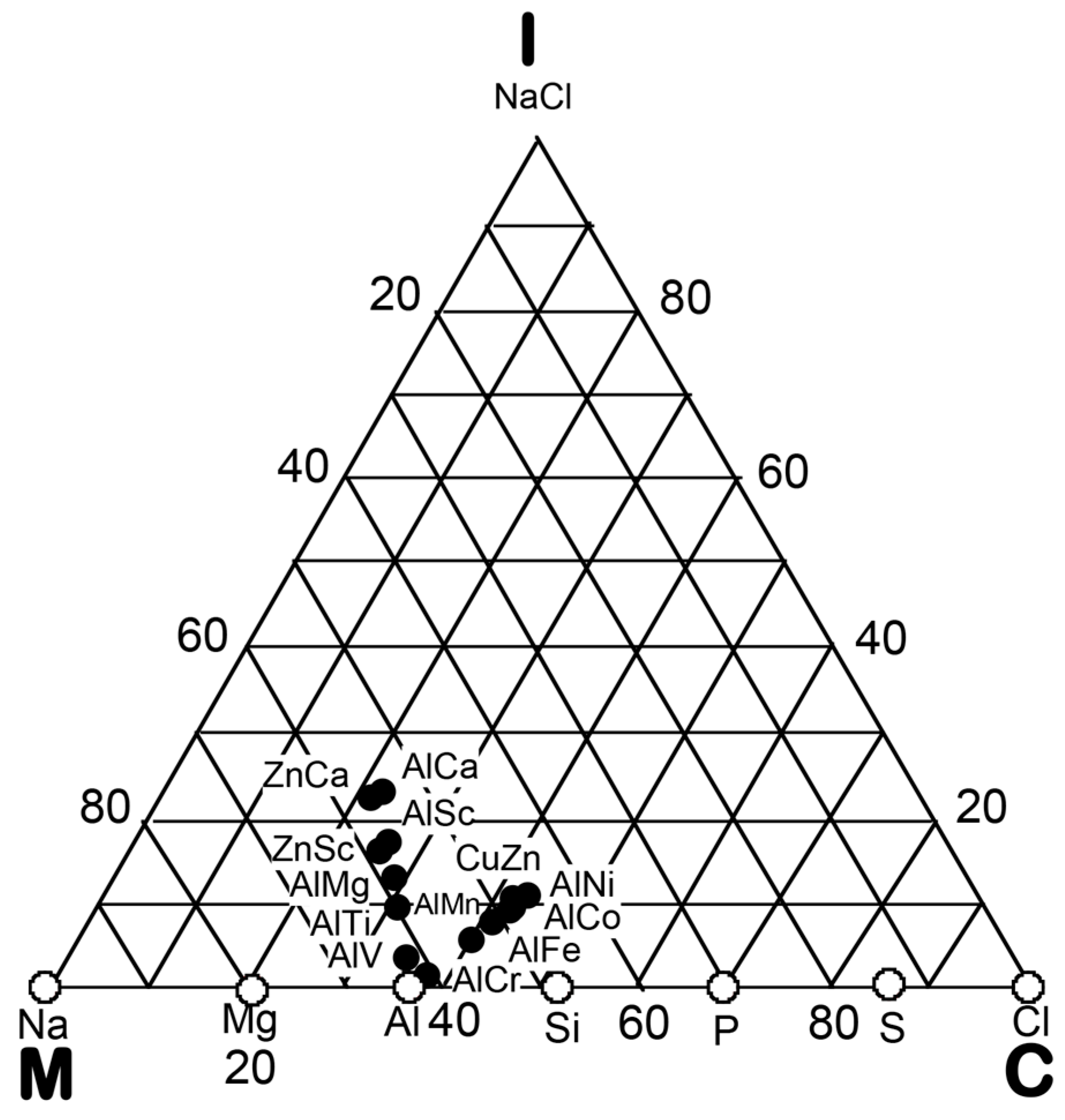
3. Bond-Type Classification of Compounds on Van Arkel-Ketelaar Triangle Map
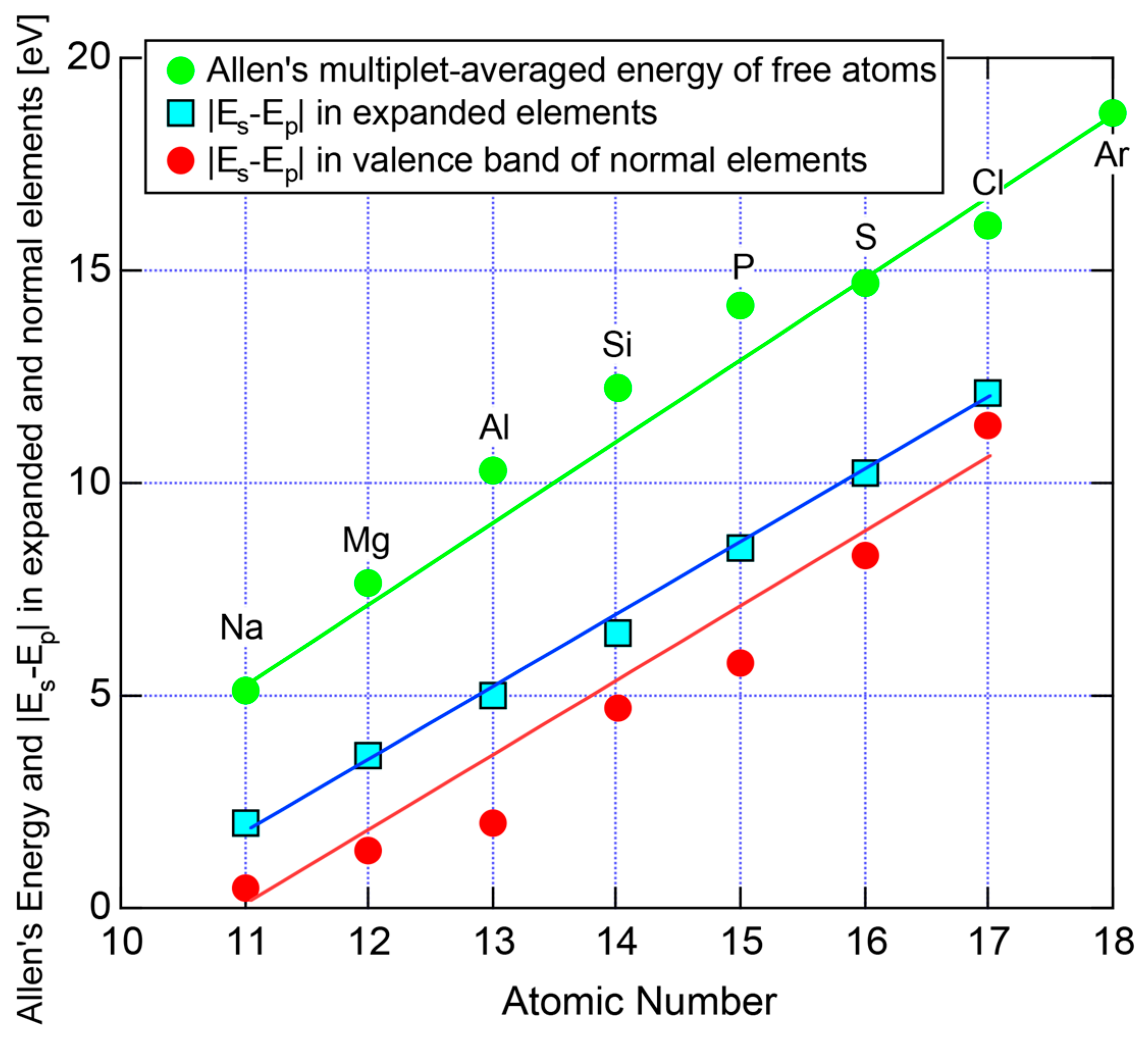
3.1. Scaling of Van Arkel-Ketelaar Triangle in Terms of Allen’s Electronegativity
3.2. The Physics behind the Allen Electronegativity
4. Hume-Rothery Electron Concentration Rule in Al-, Zn- and Cd-Based Alloy Systems
4.1. How to Explore Systems Obeying a New Hume-Rothery Electron Concentration Rule?
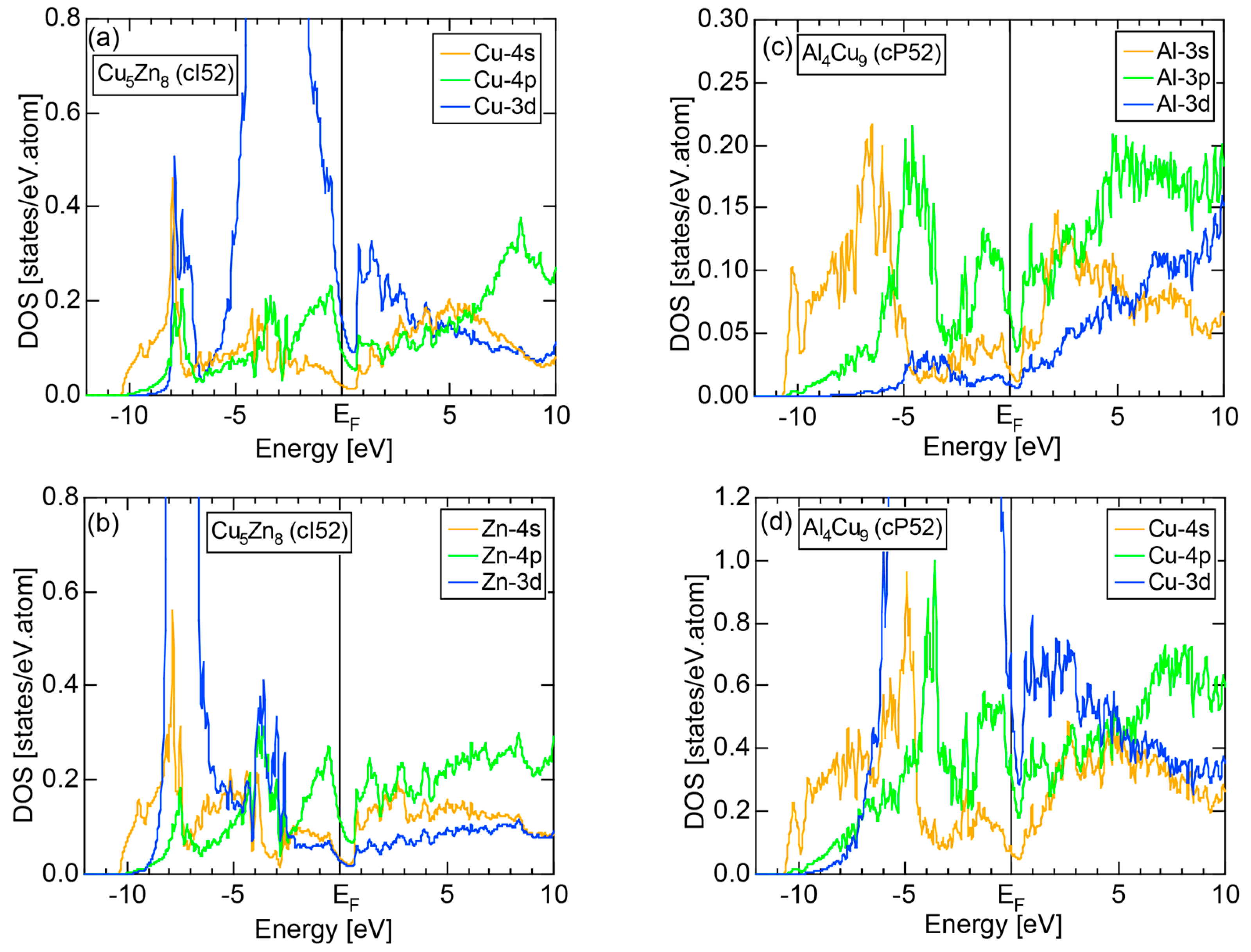
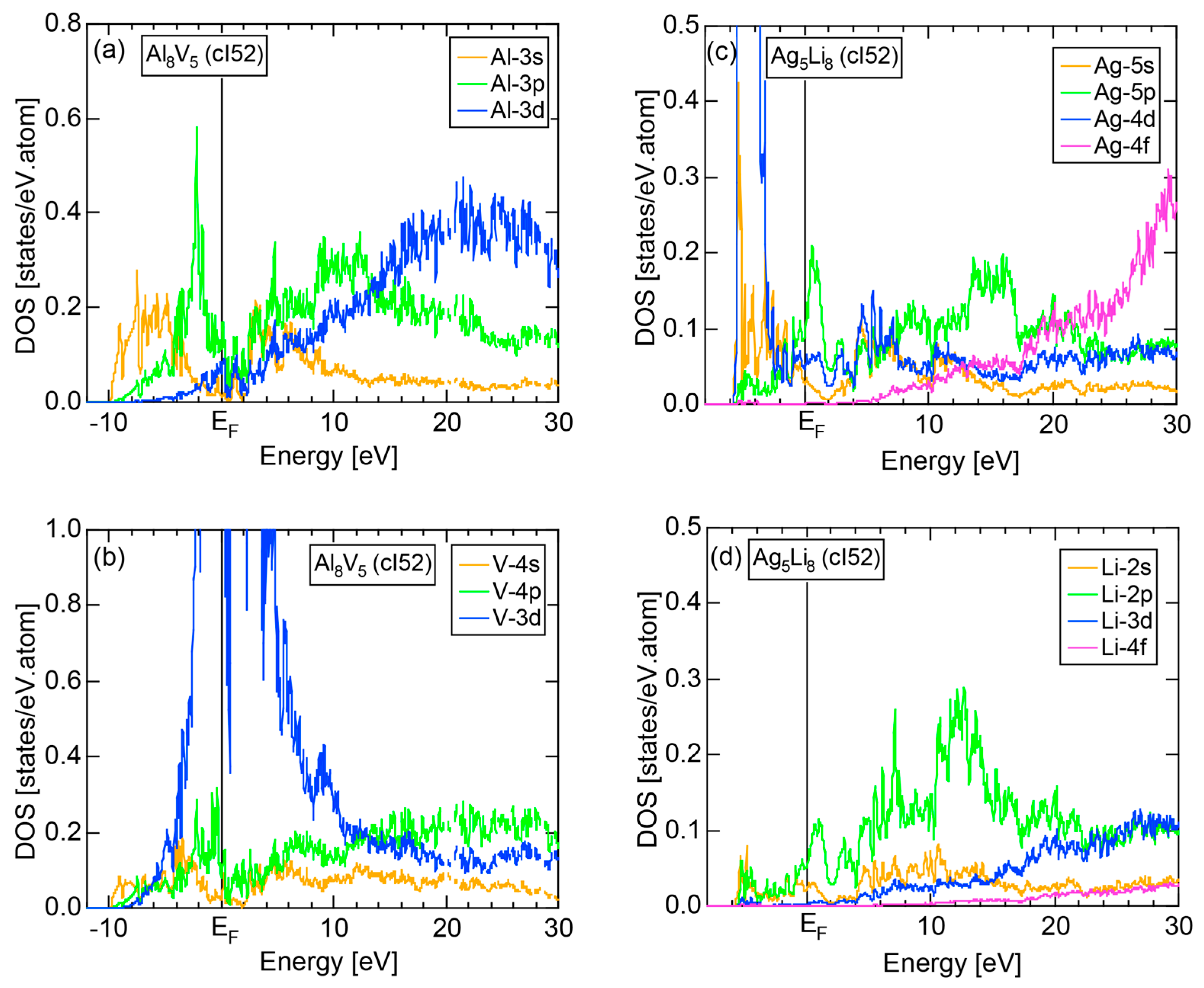
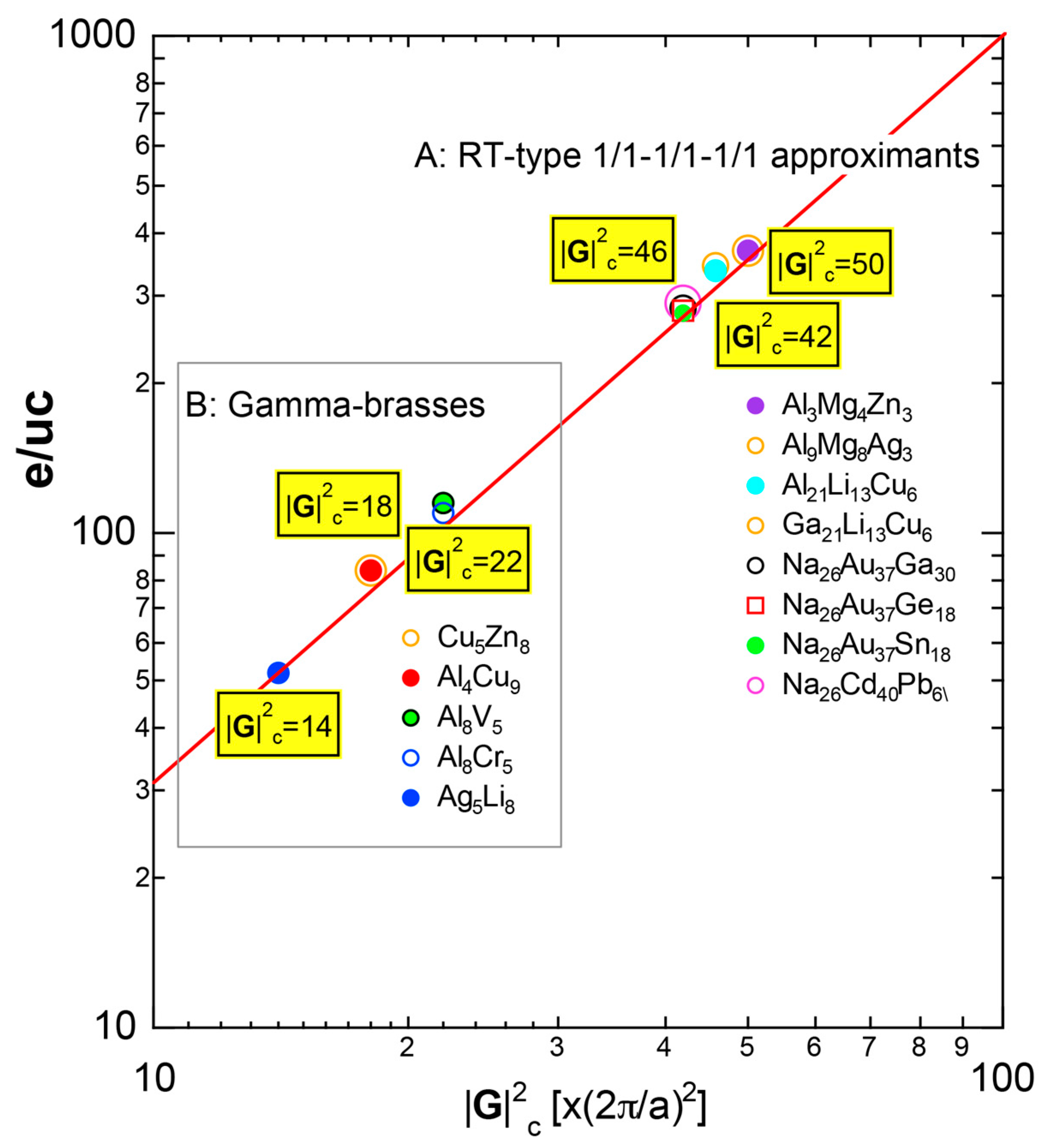
4.2. Gamma-Brasses (cI52 or cP52)
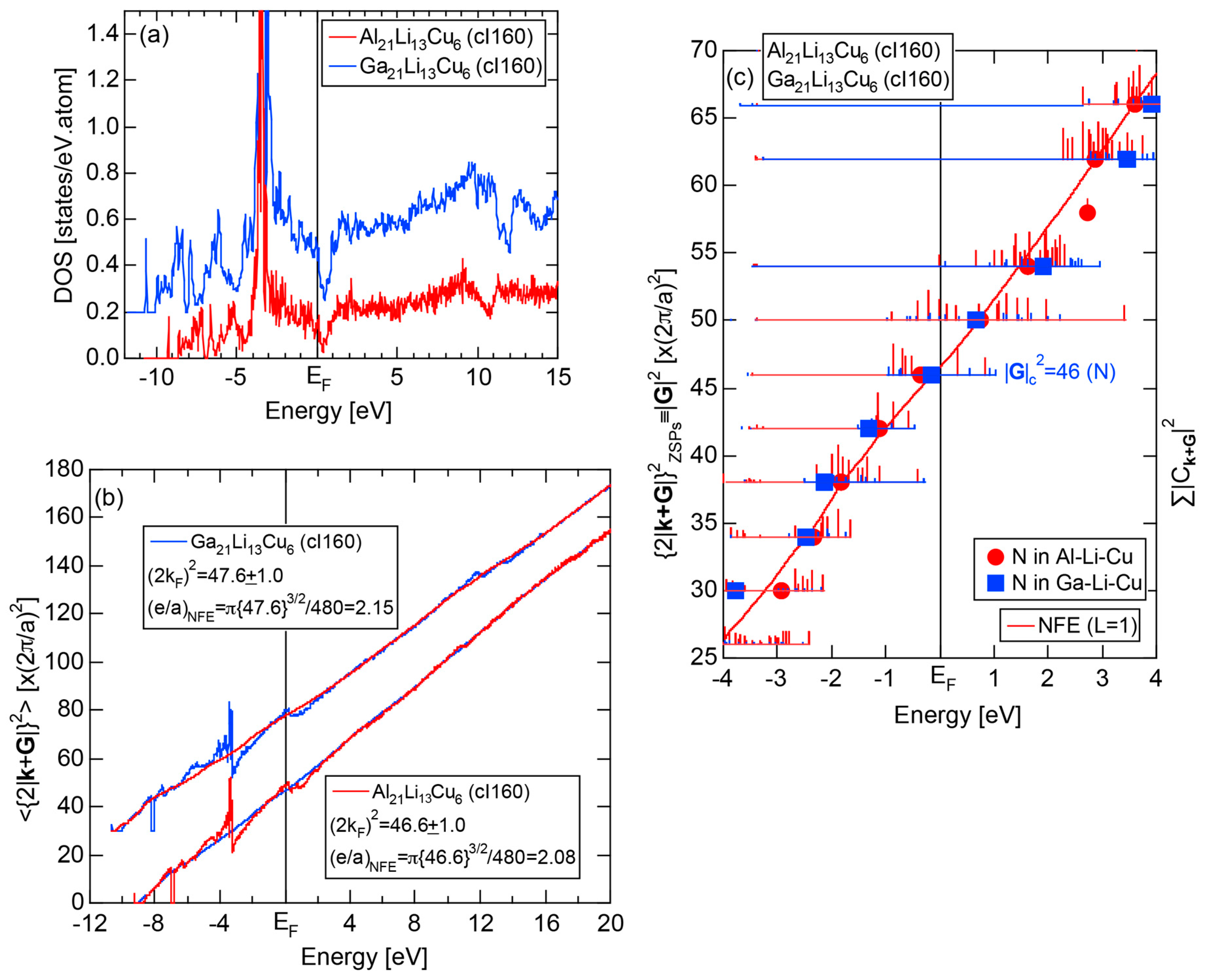
4.3. RT-Type 1/1-1/1-1/1 Approximants (cI160 or cI162)
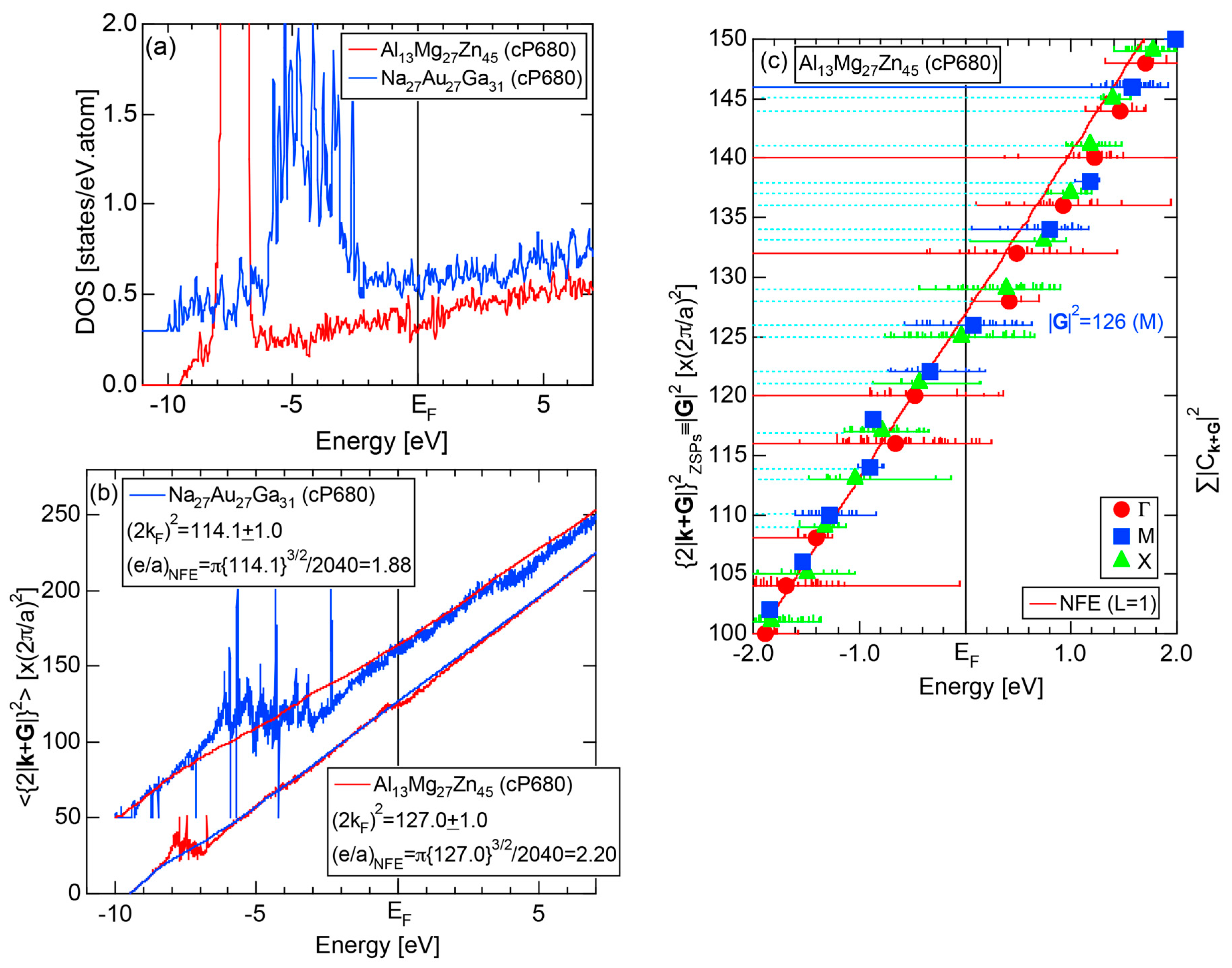
4.4. RT-Type 2/1-2/1-2/1 Approximants (cP680)
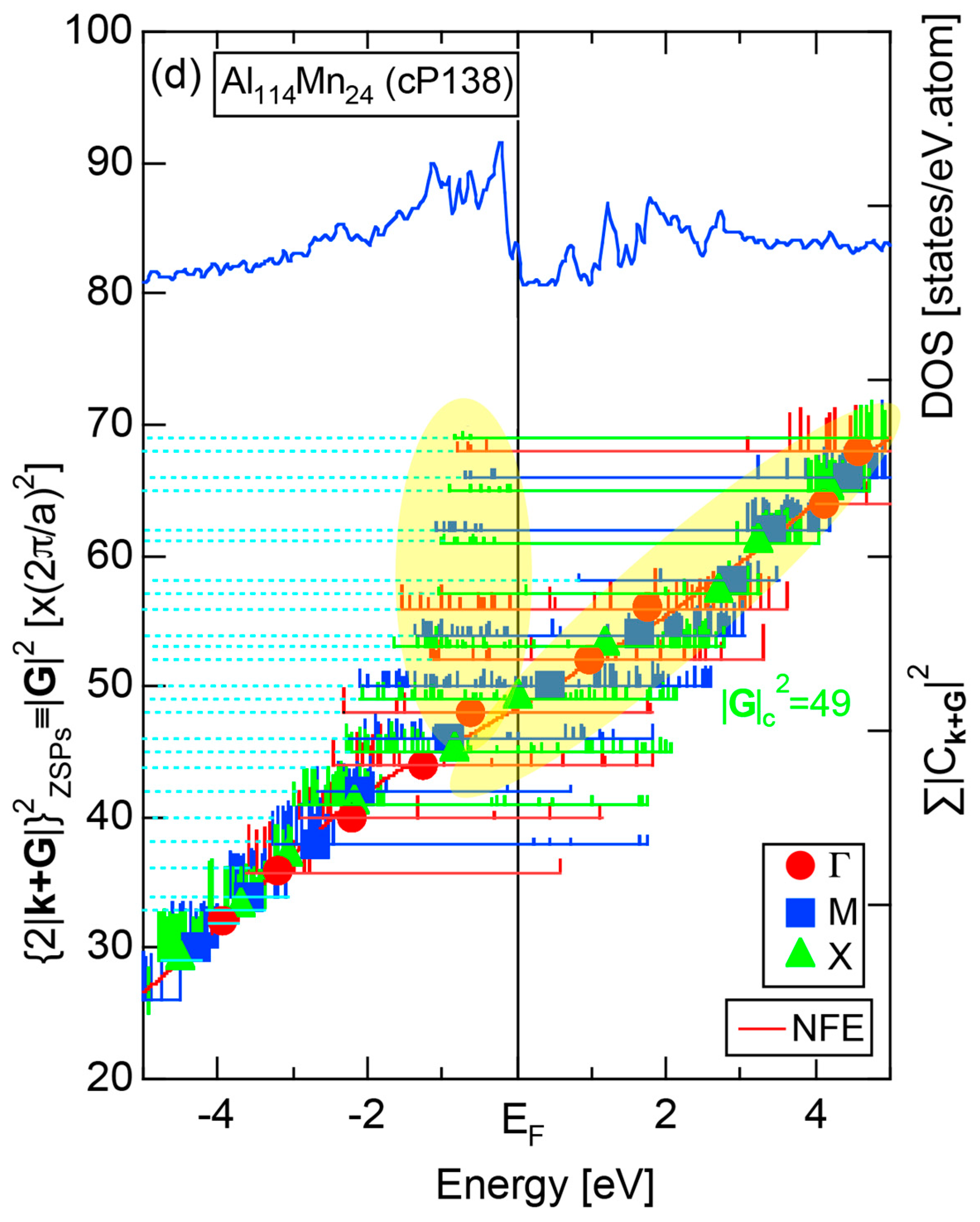
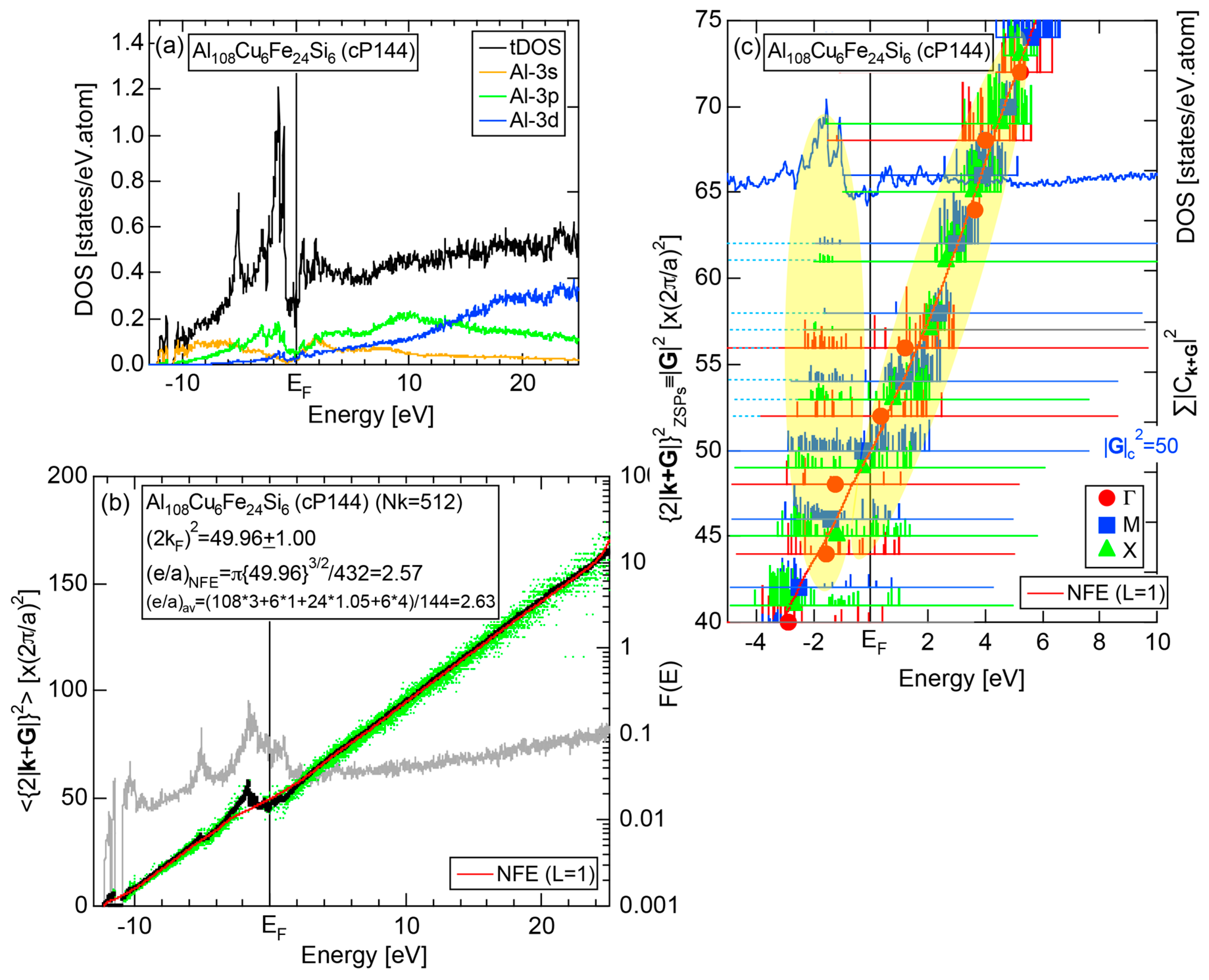
4.5. MI-Type 1/1-1/1-1/1 Approximants (cP138, cP144)
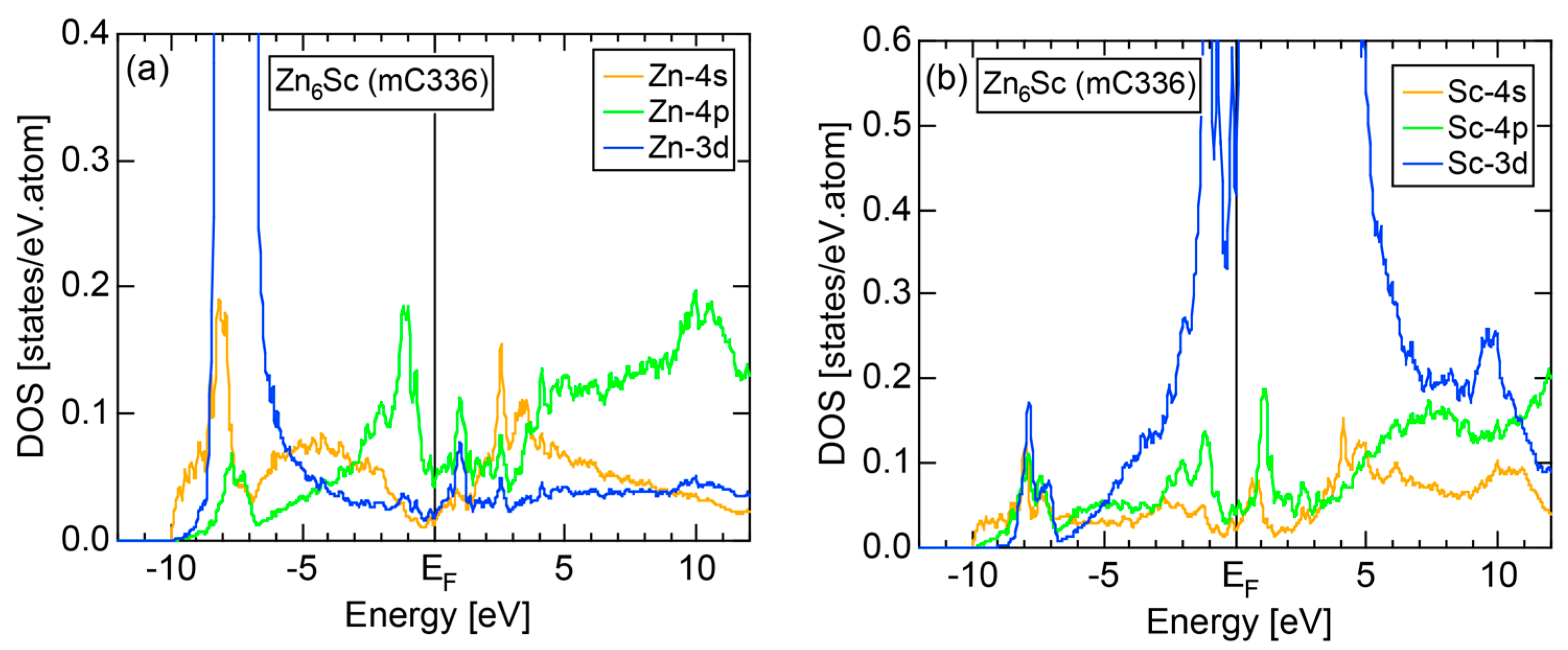
4.6. Tsai-Type 1/1-1/1-1/1 Approximants (cP168, mC336)
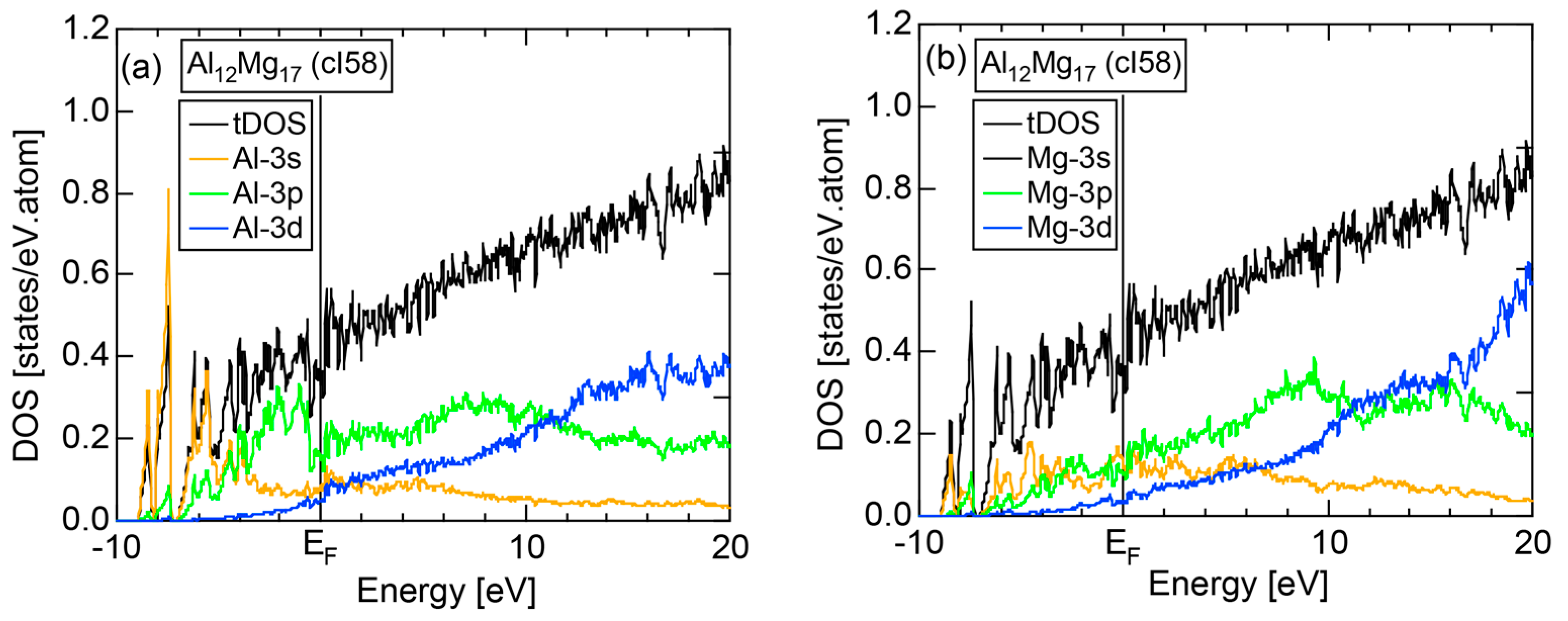
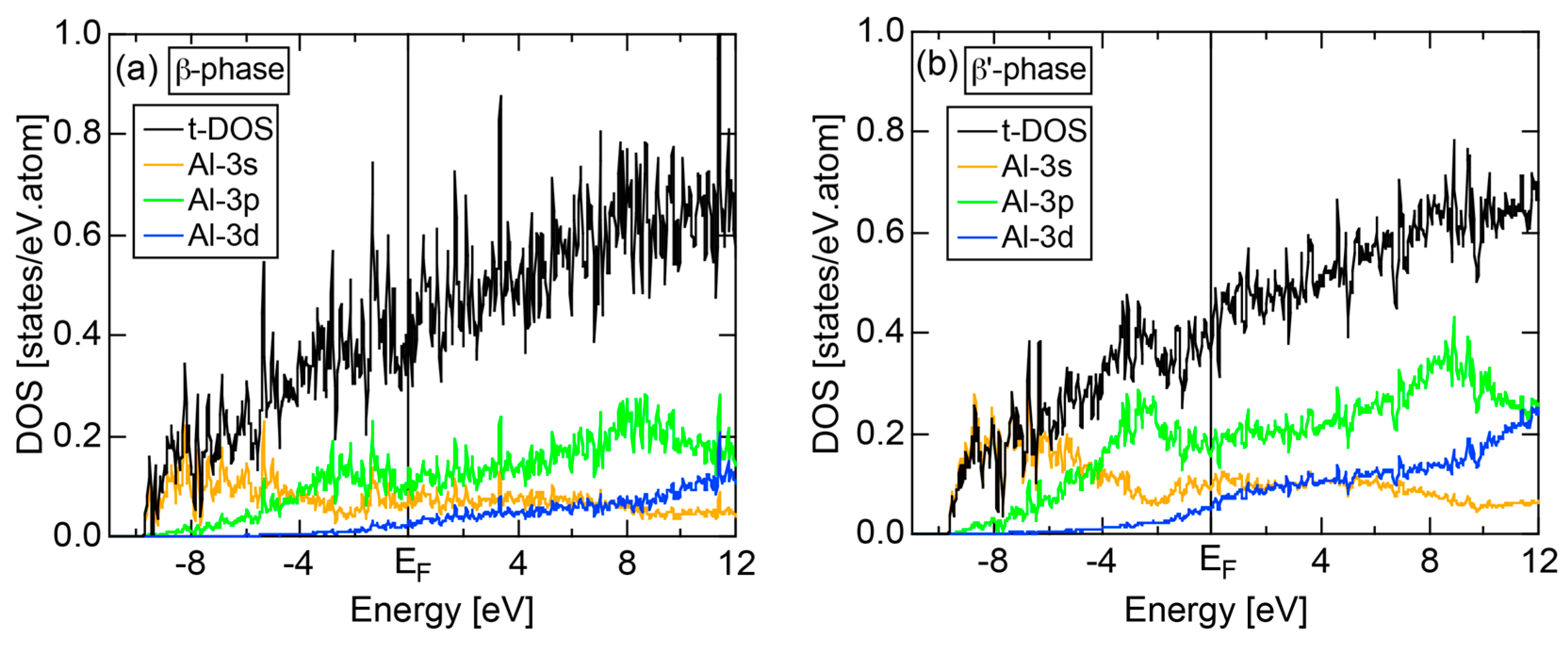
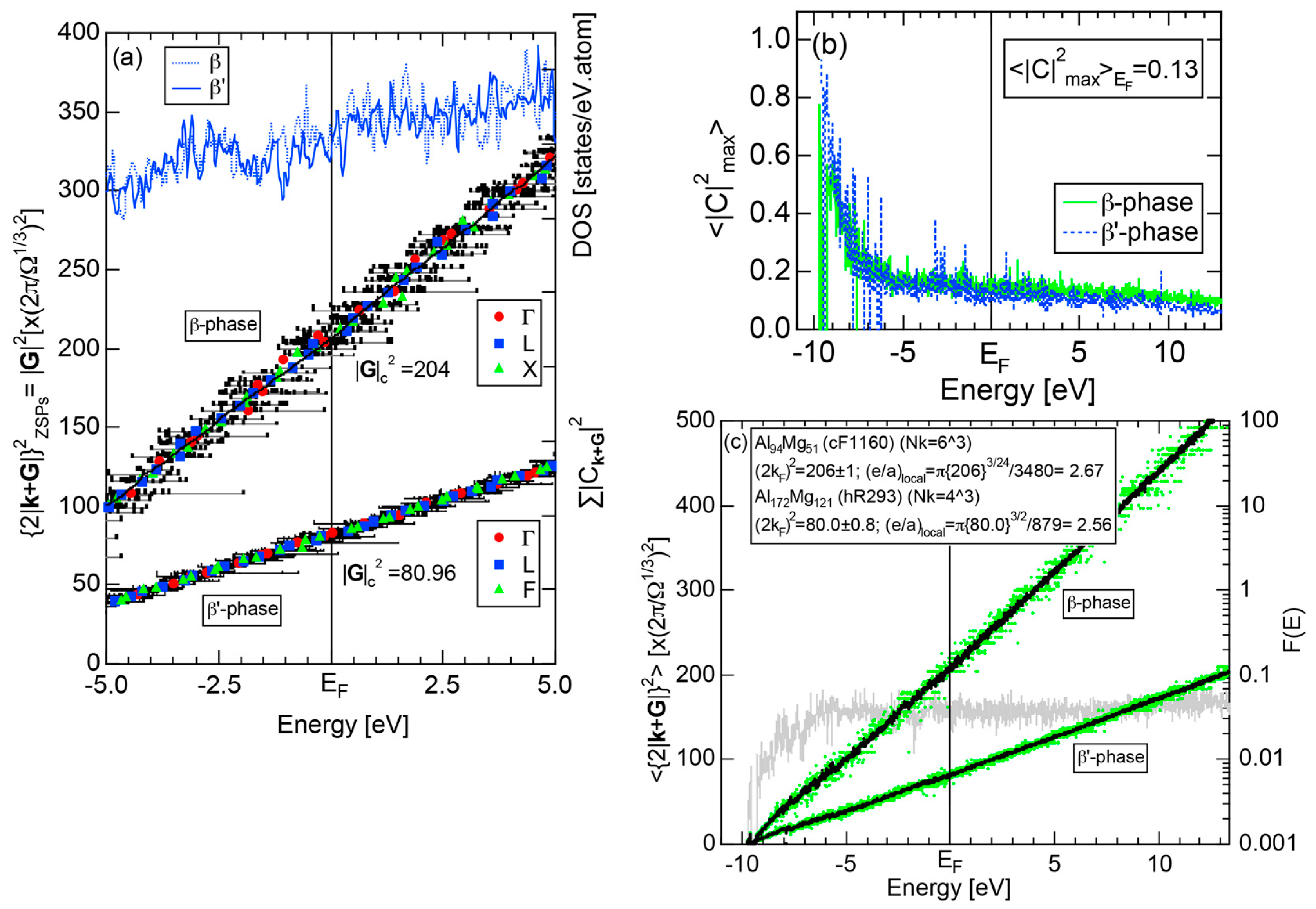
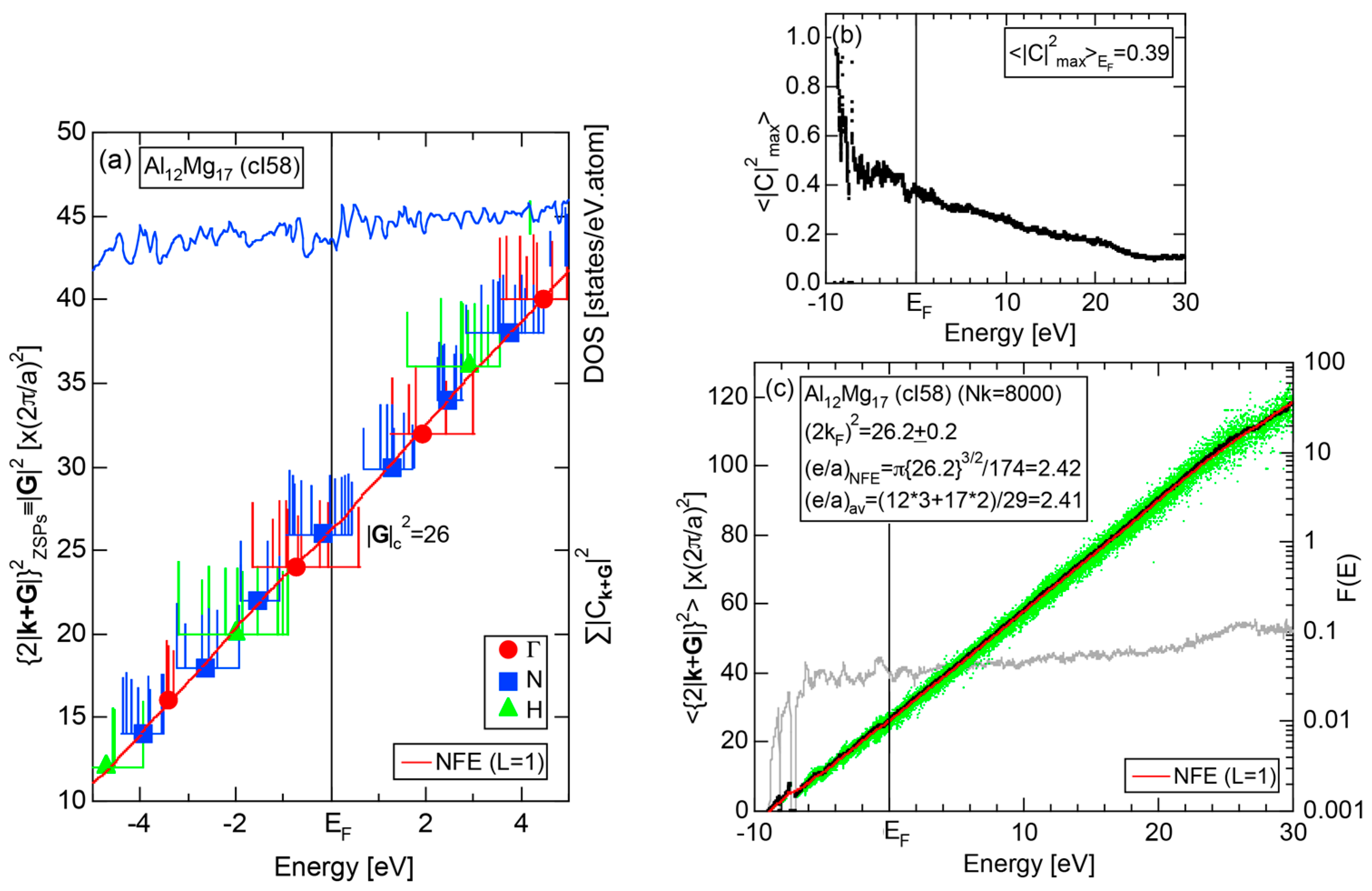
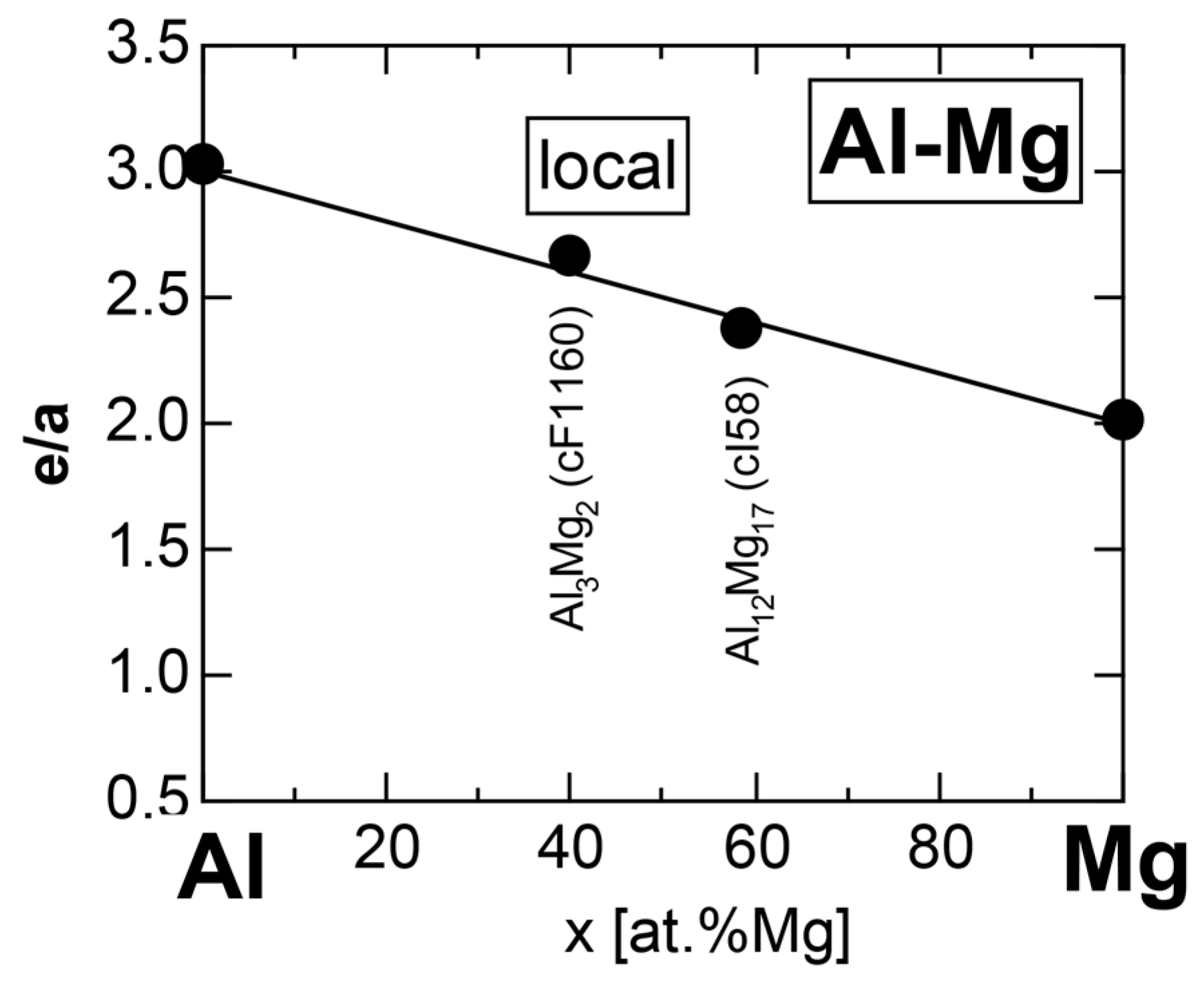
4.7. Samson Compound Al3Mg2 (cF1178) and Al12Mg17 (cI58)
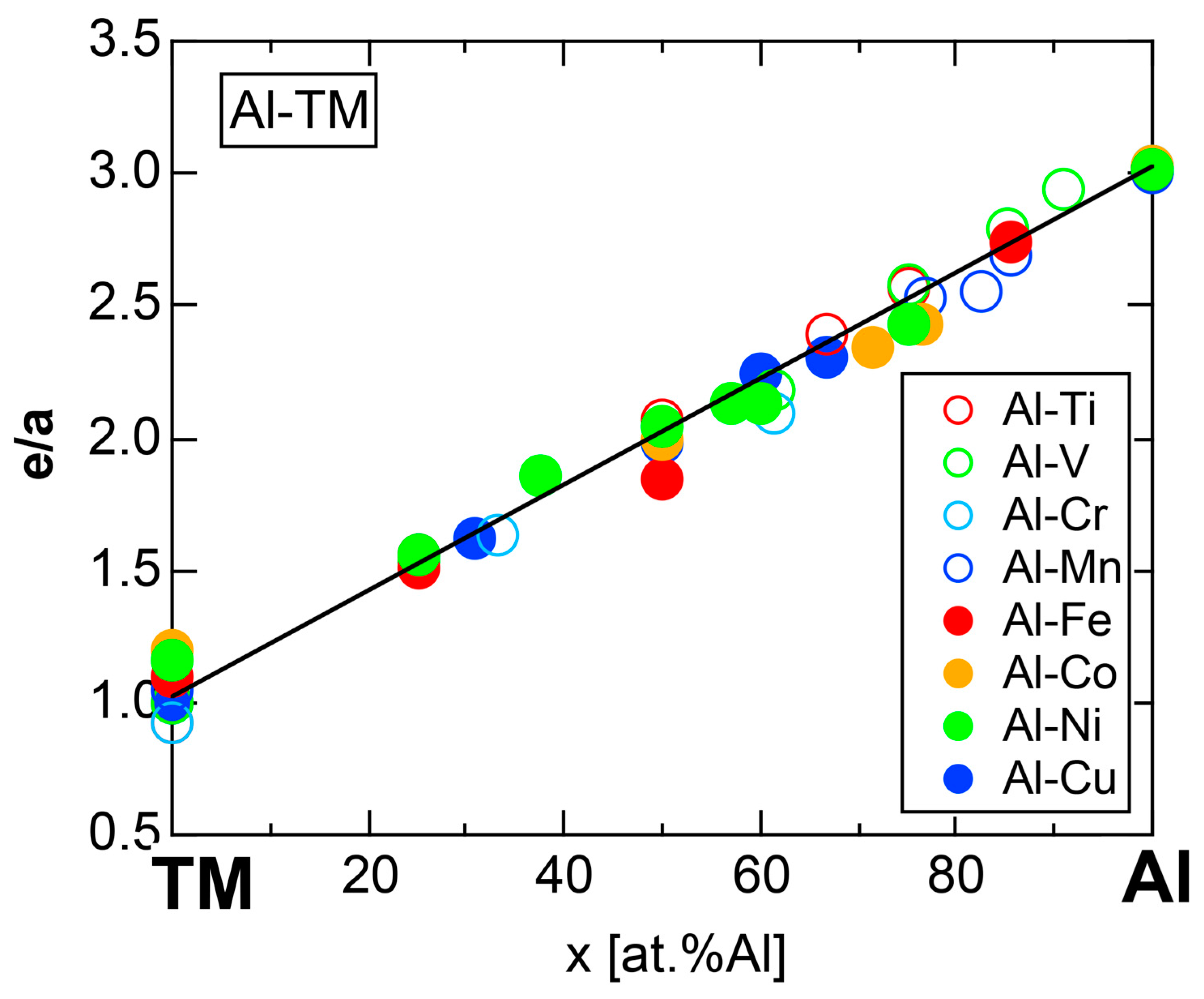
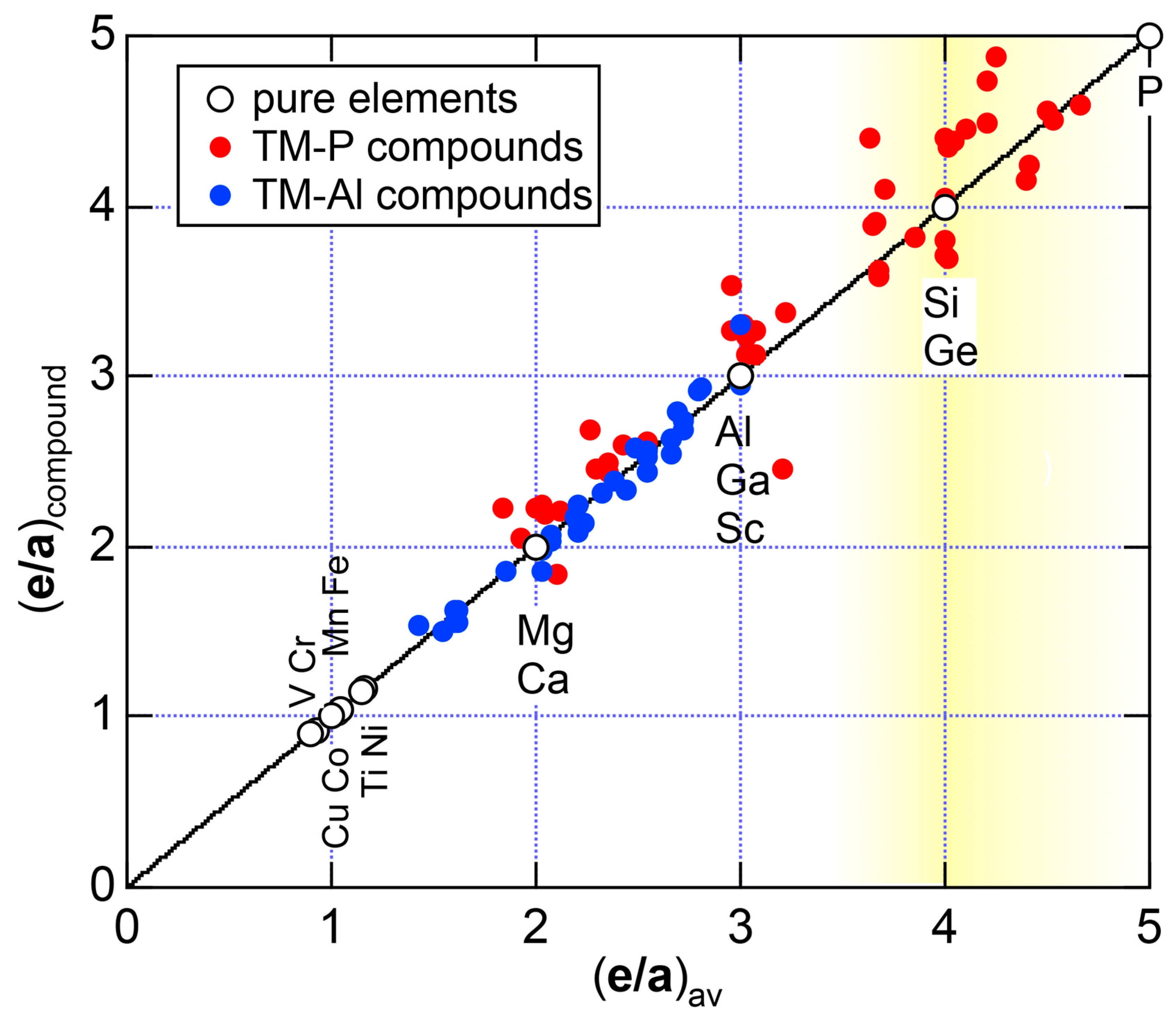
4.8. e/a Determination for TM-Al Binary Compounds
4.9. Interference Condition for Al-, Zn- and Cd-Compounds
5. Hume-Rothery Electron Concentration Rule in Zintl Compounds
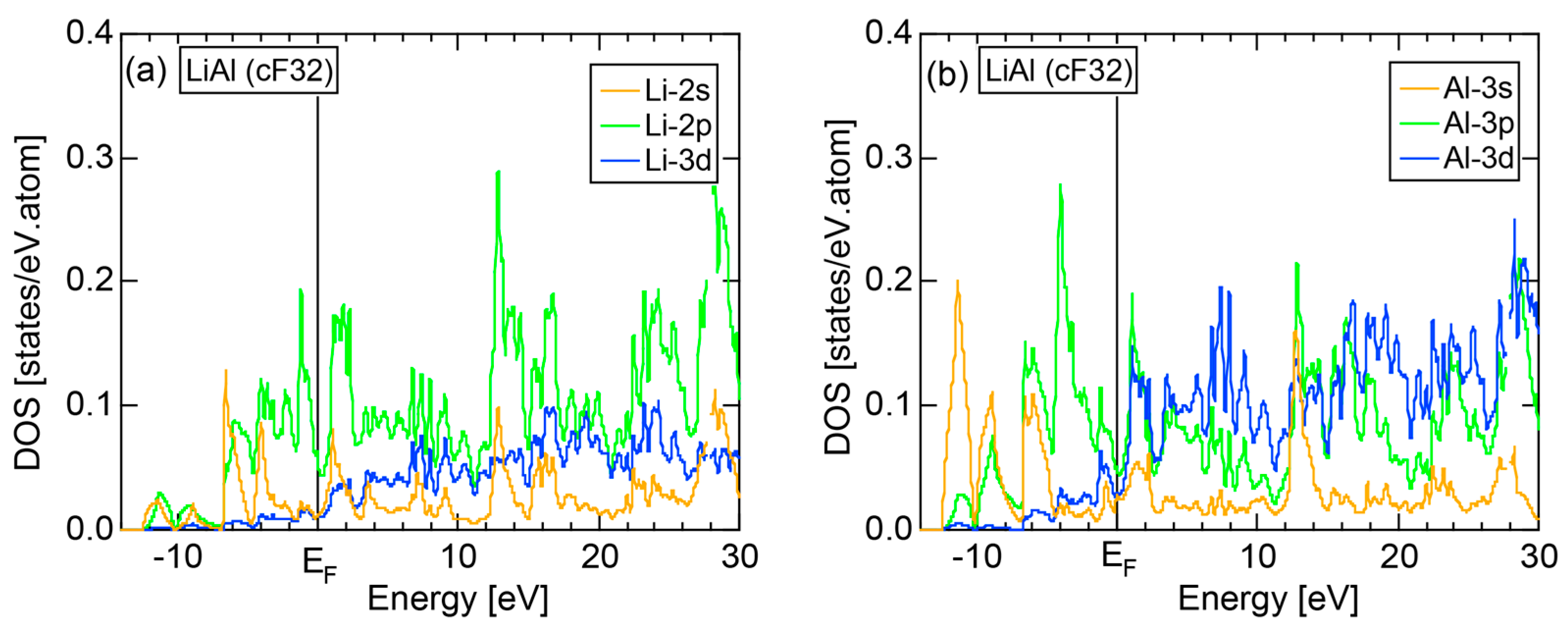
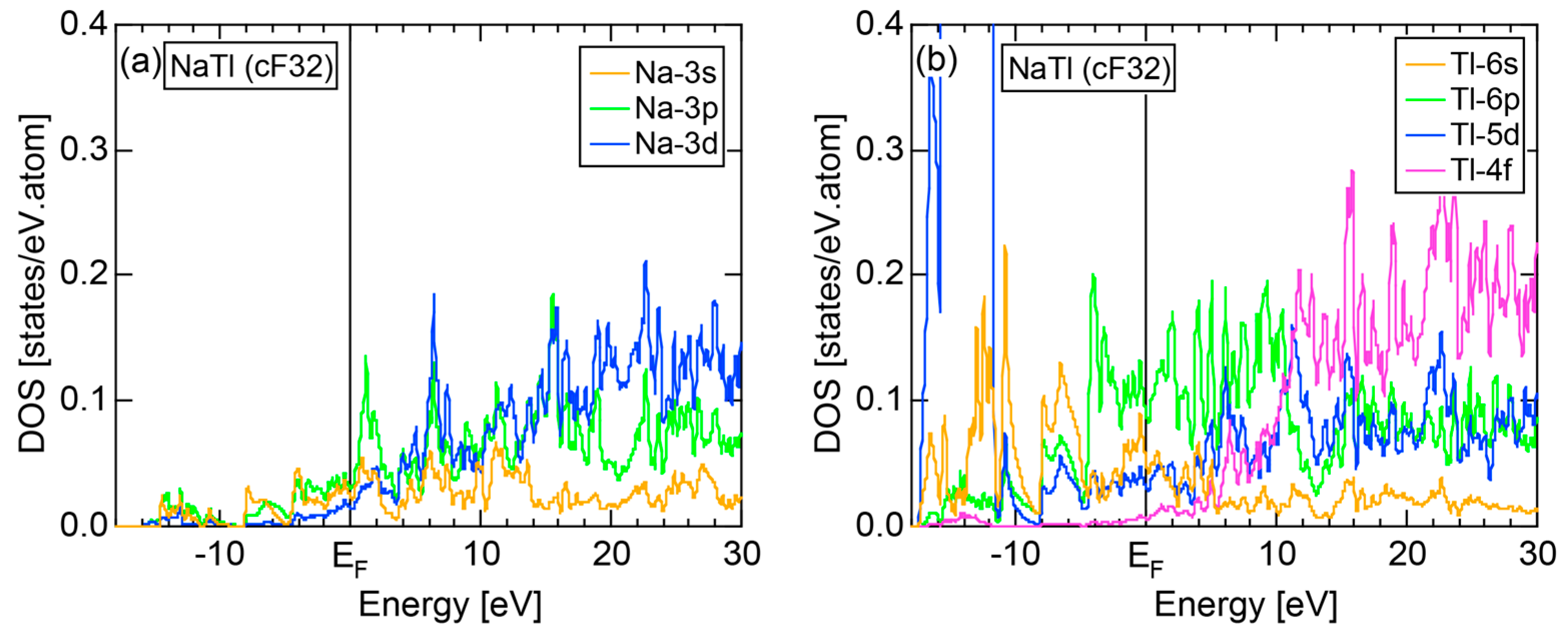
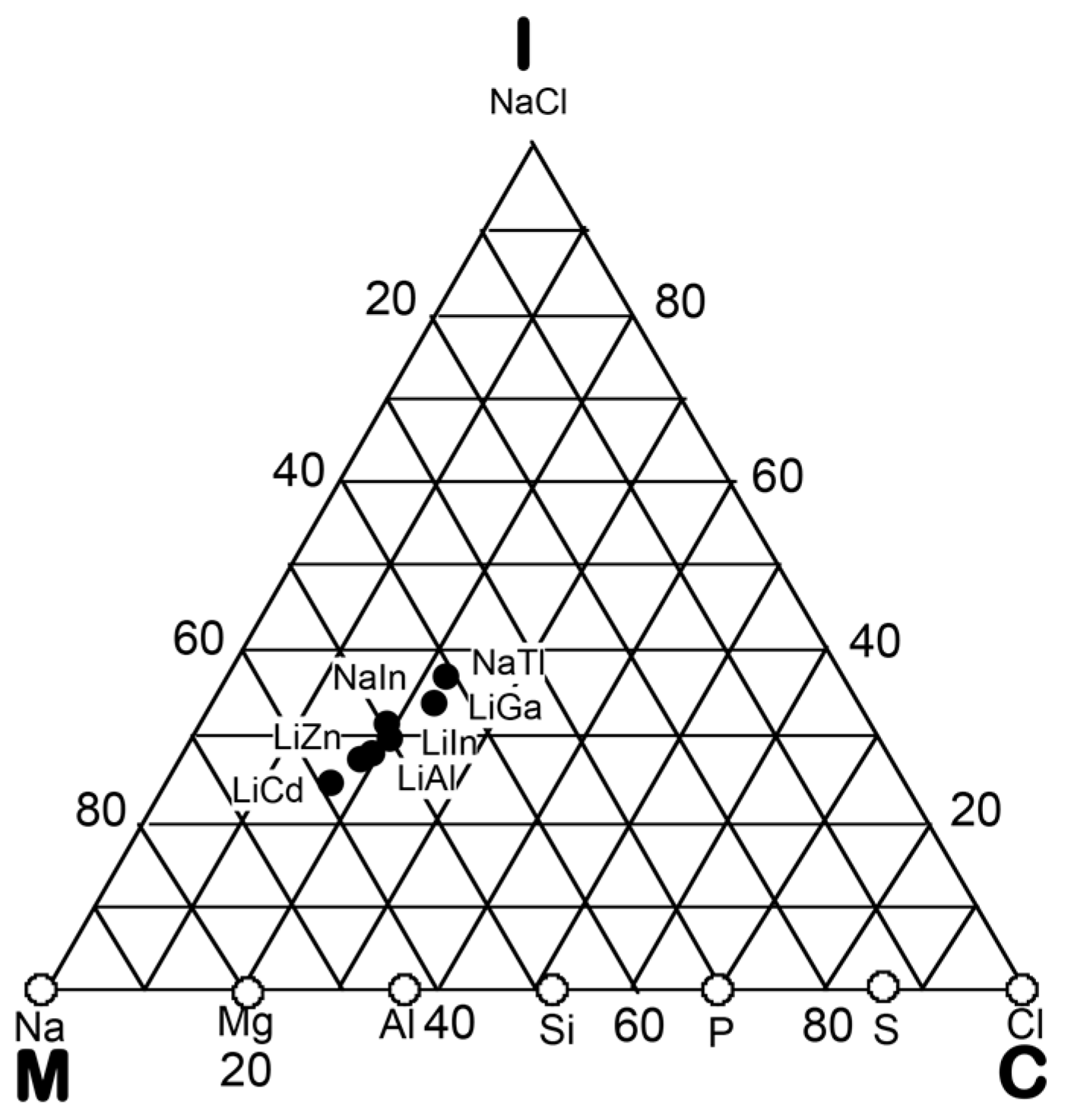
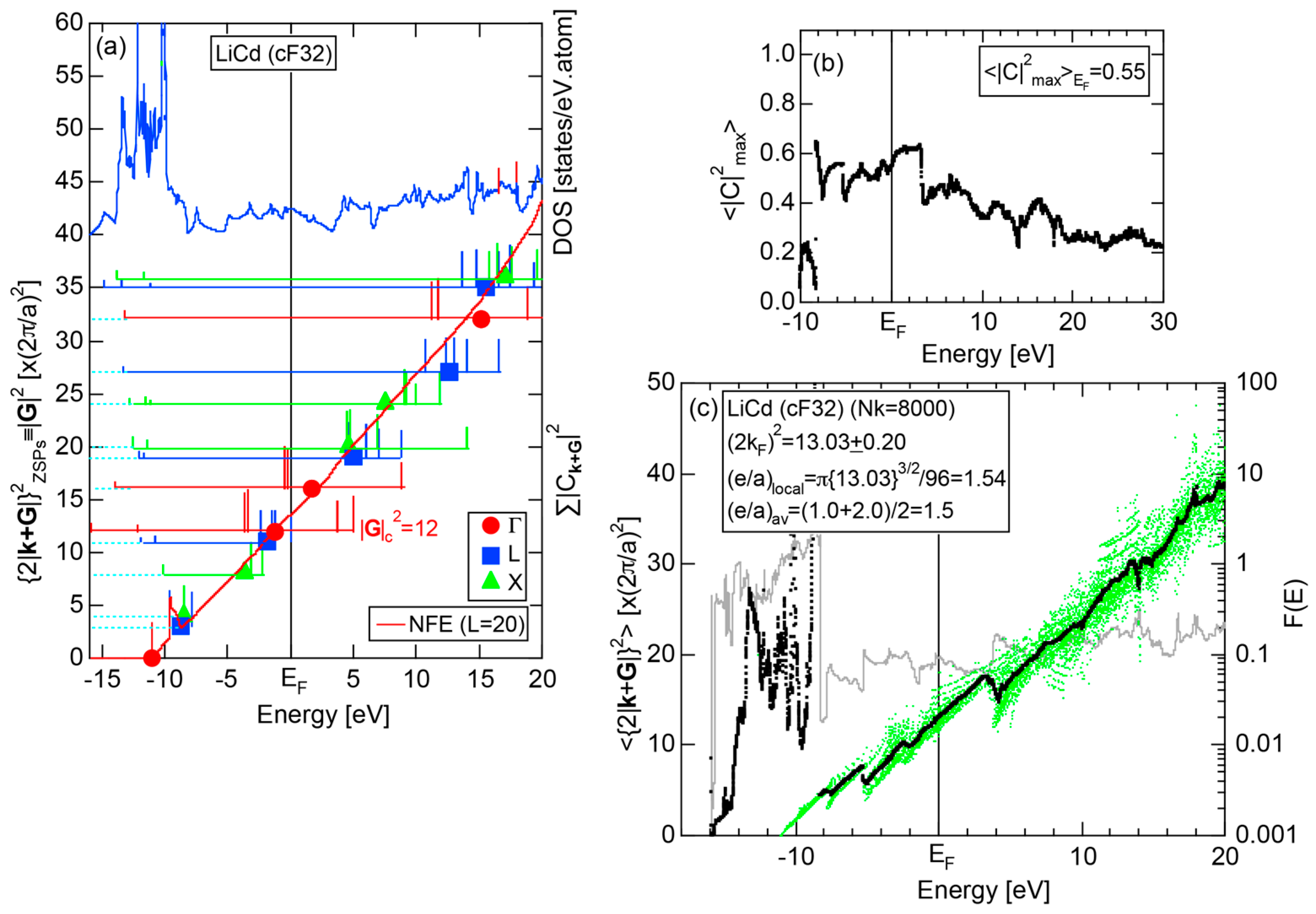
5.1. I-III-Type Zintl Compounds (cF32)
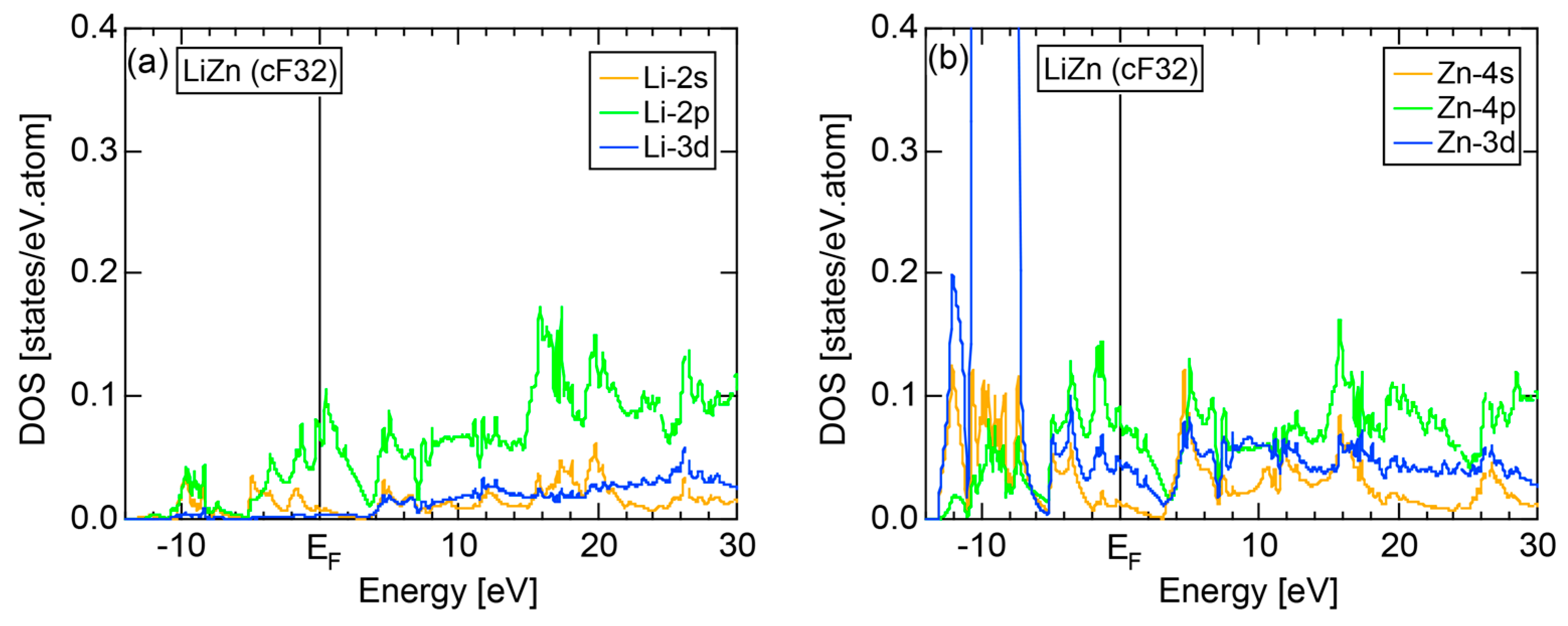
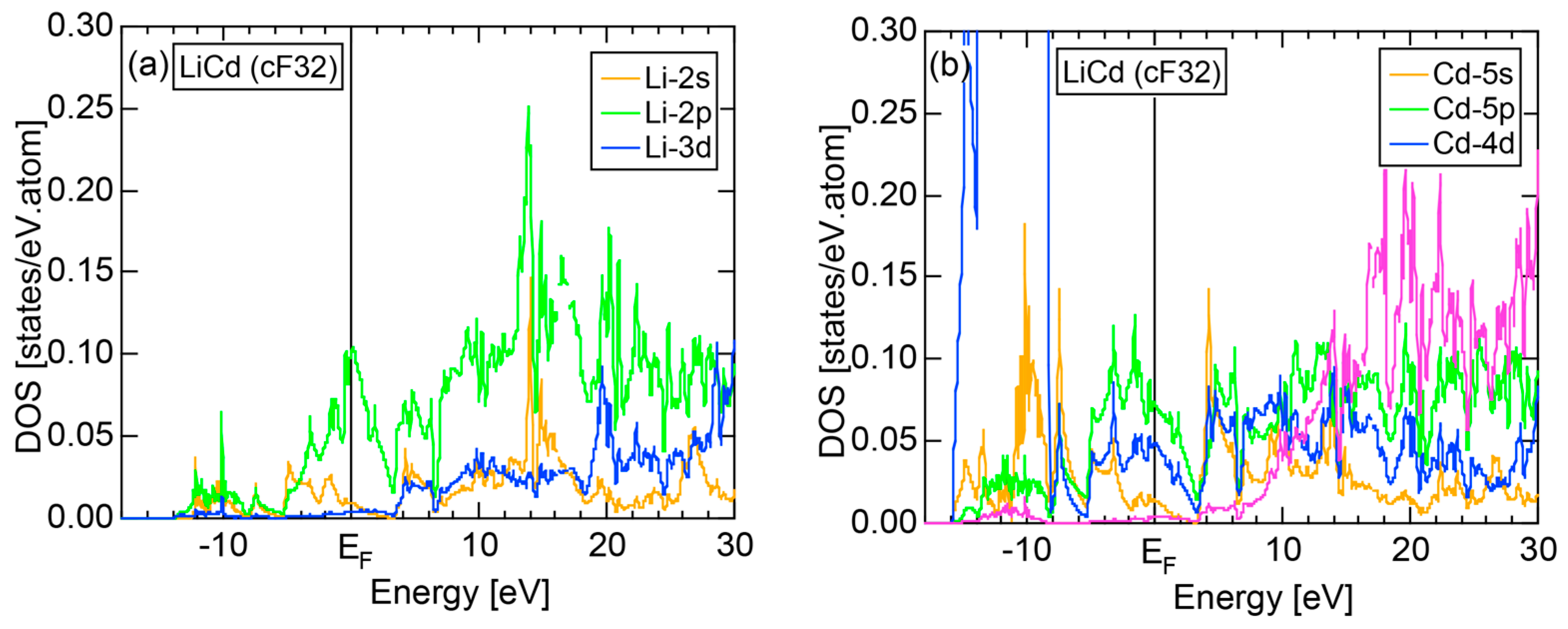
5.2. I-II-Type Zintl Compounds (cF32)
5.3. Hume-Rothery Electron Concentration Rule
6. Hume-Rothery Electron Concentration Rule in Phosphorus Compounds
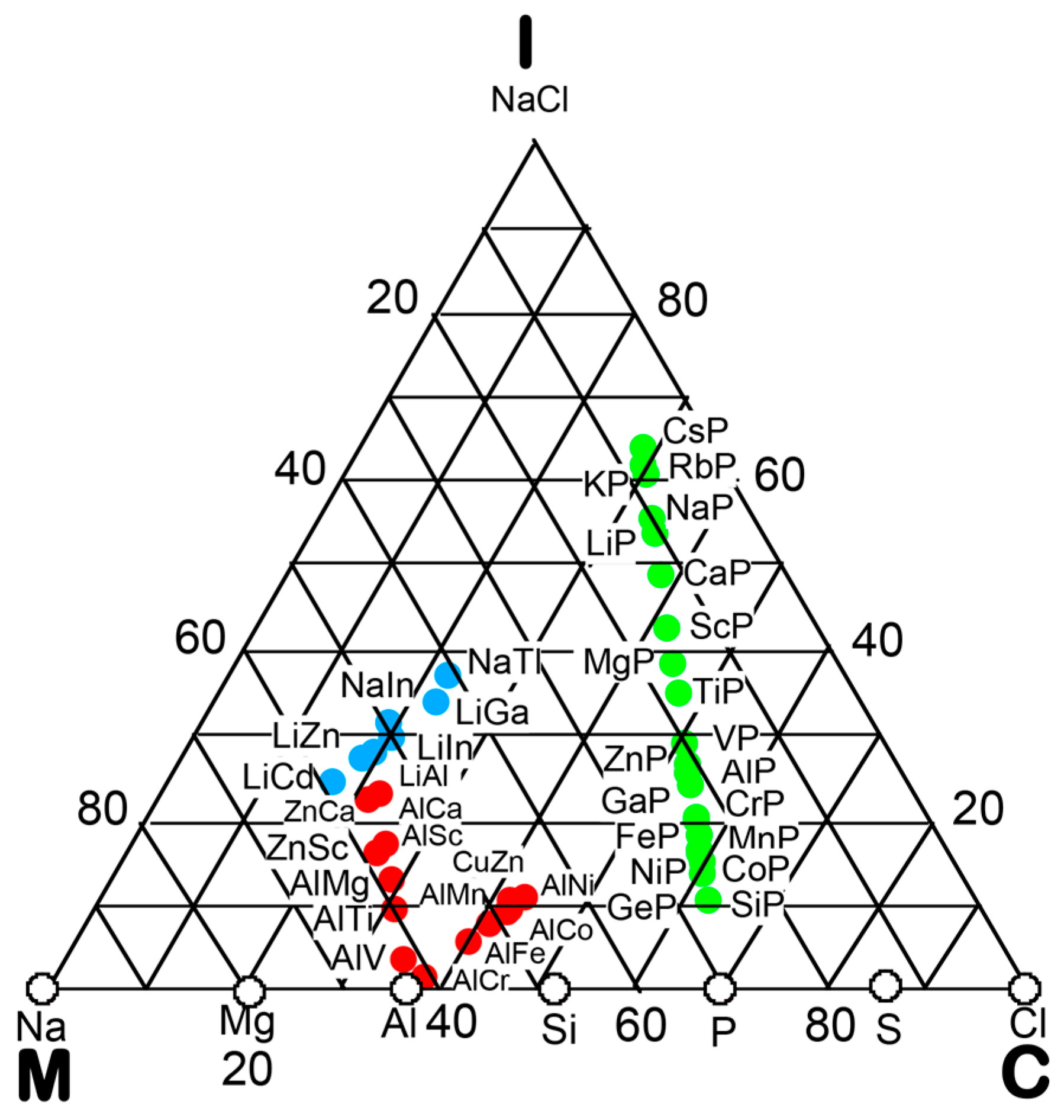
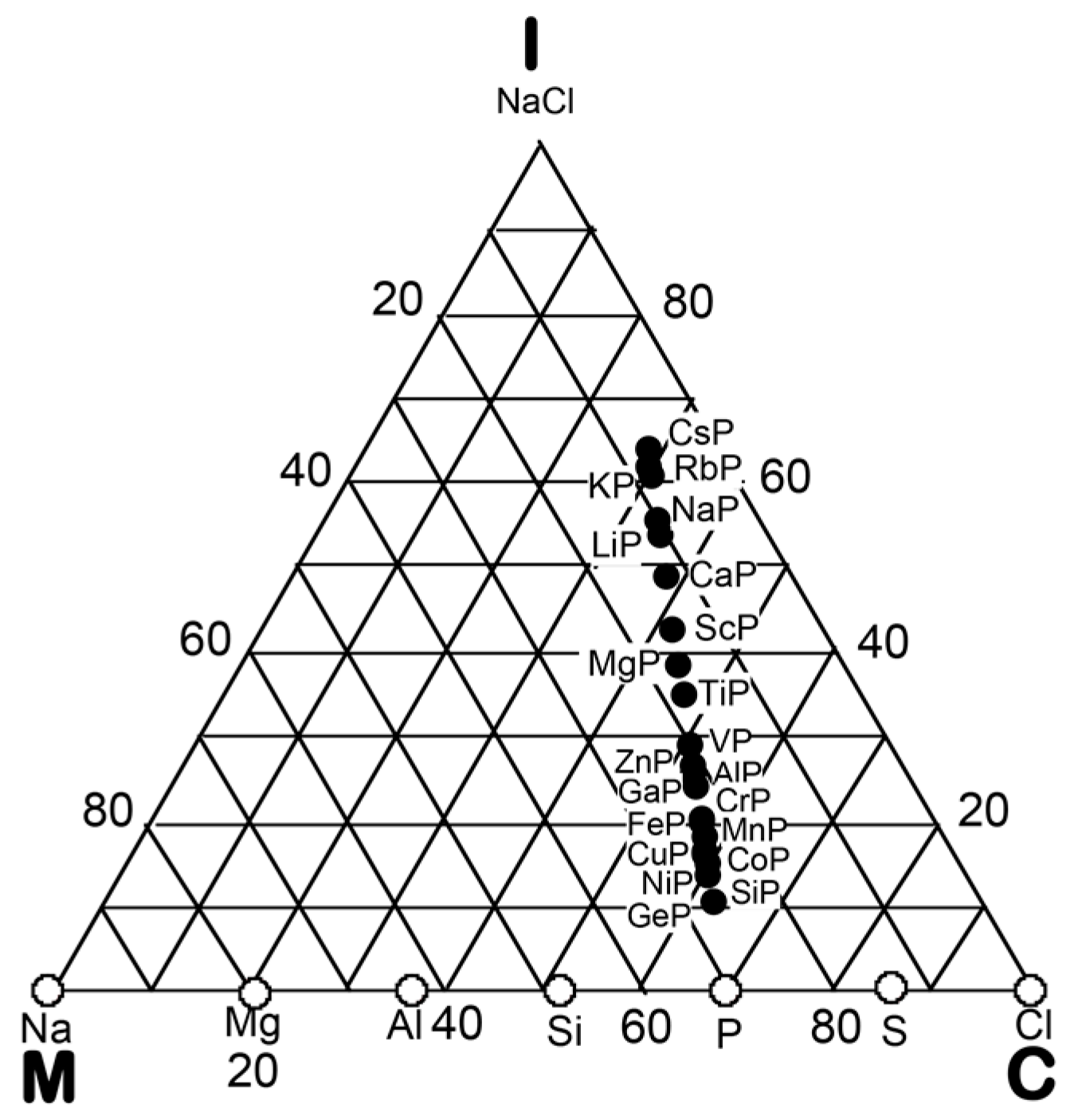
6.1. Equiatomic Phosphorus Compounds on the Van Arkel-Ketelaar Triangle Map
6.2. e/a Determination and Interference Condition for the Host Element P in Group 15
6.3. e/a Determination and Interference Condition of M-P Binary Compounds
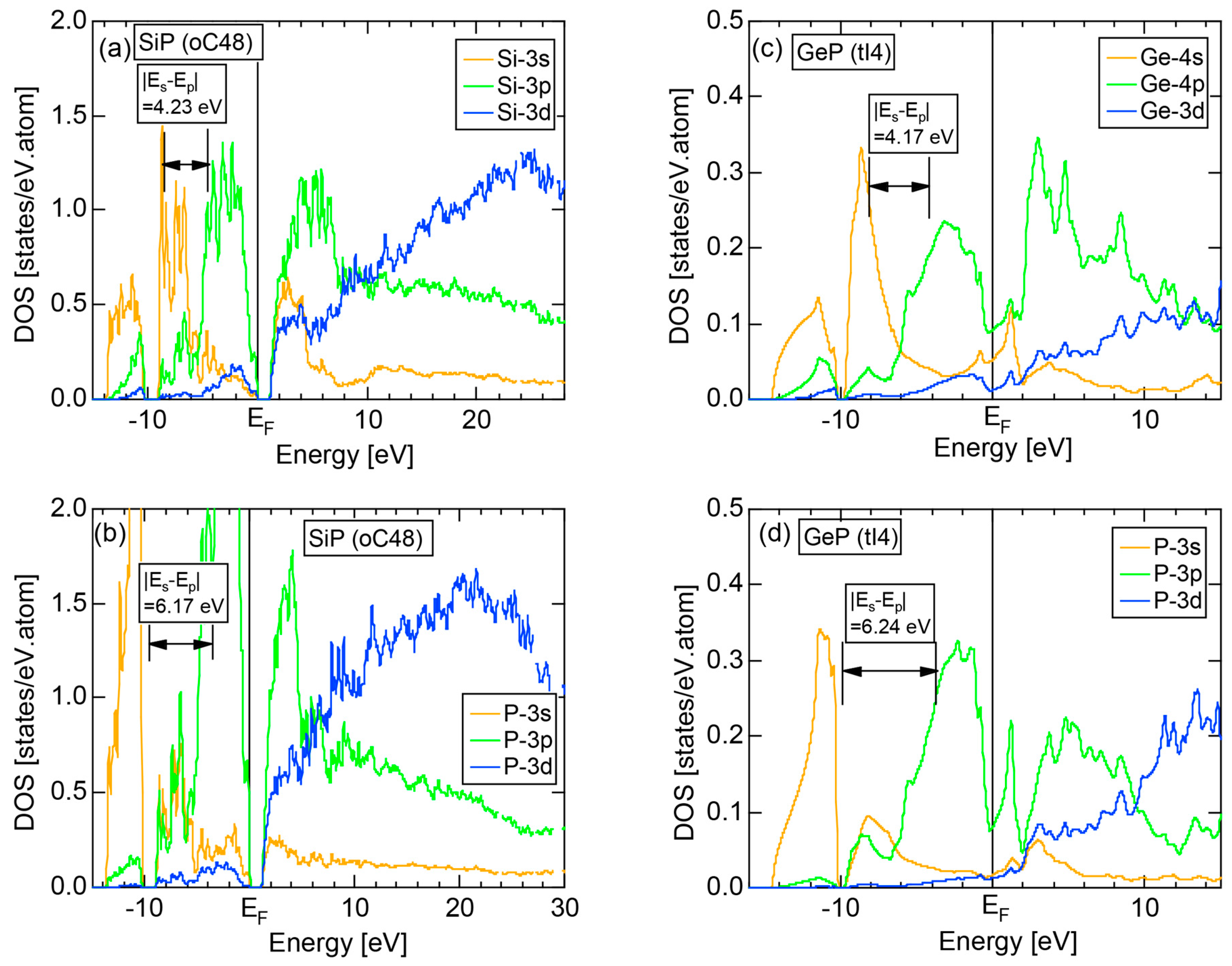
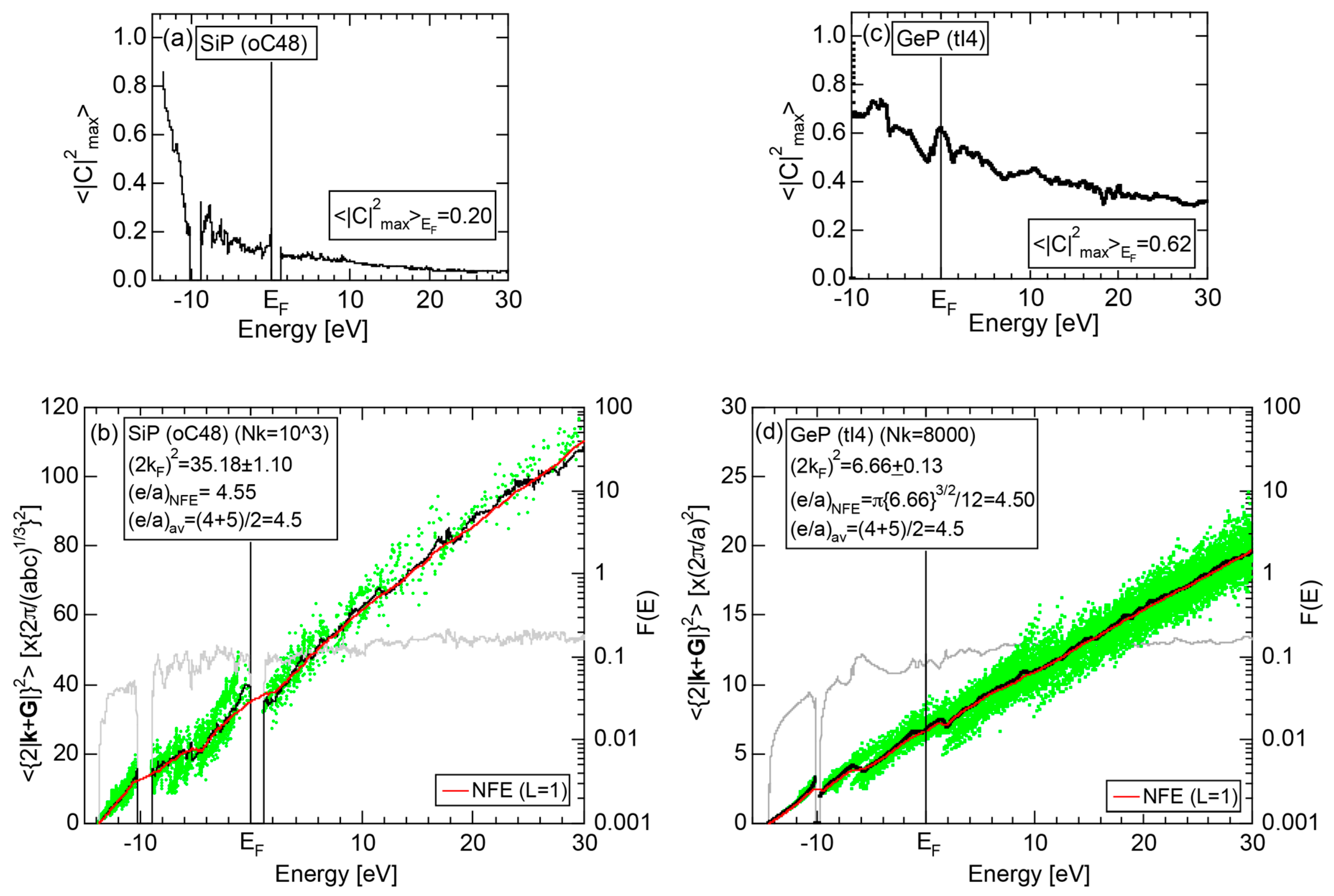
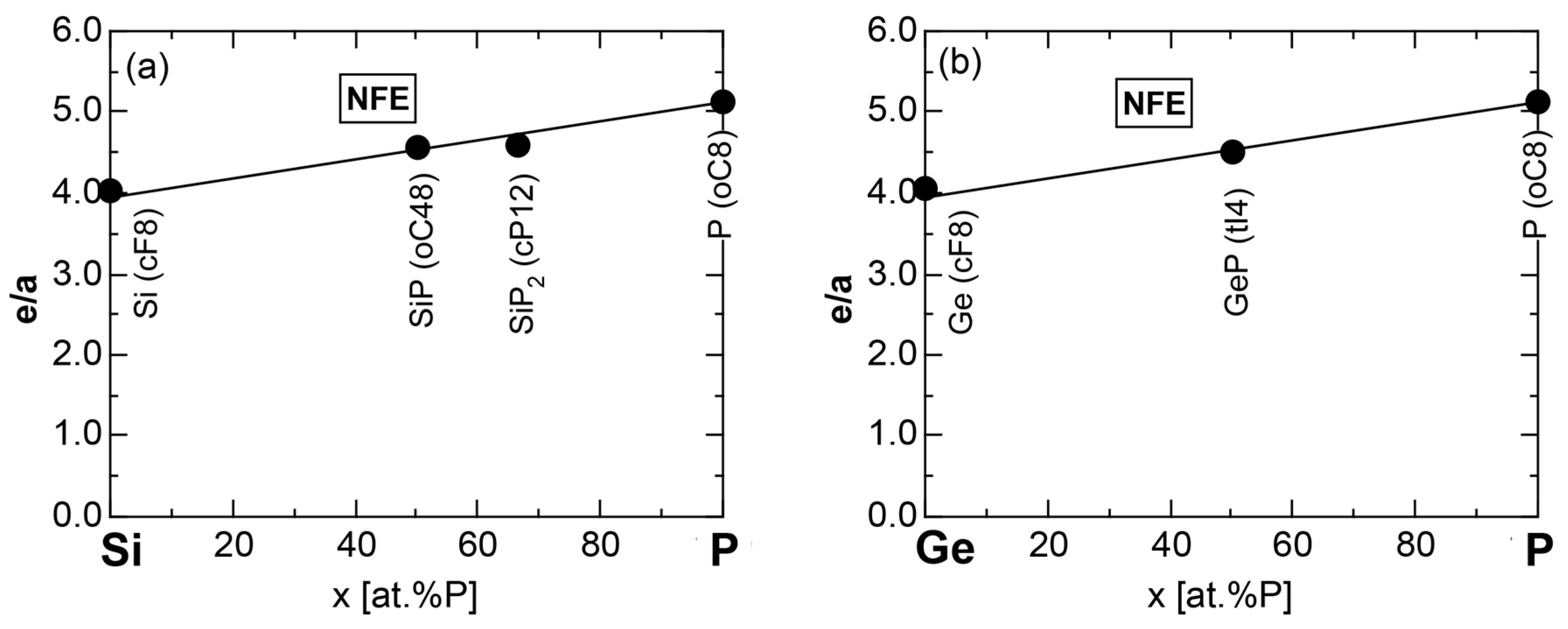
6.3.1. SiP and GeP Compounds
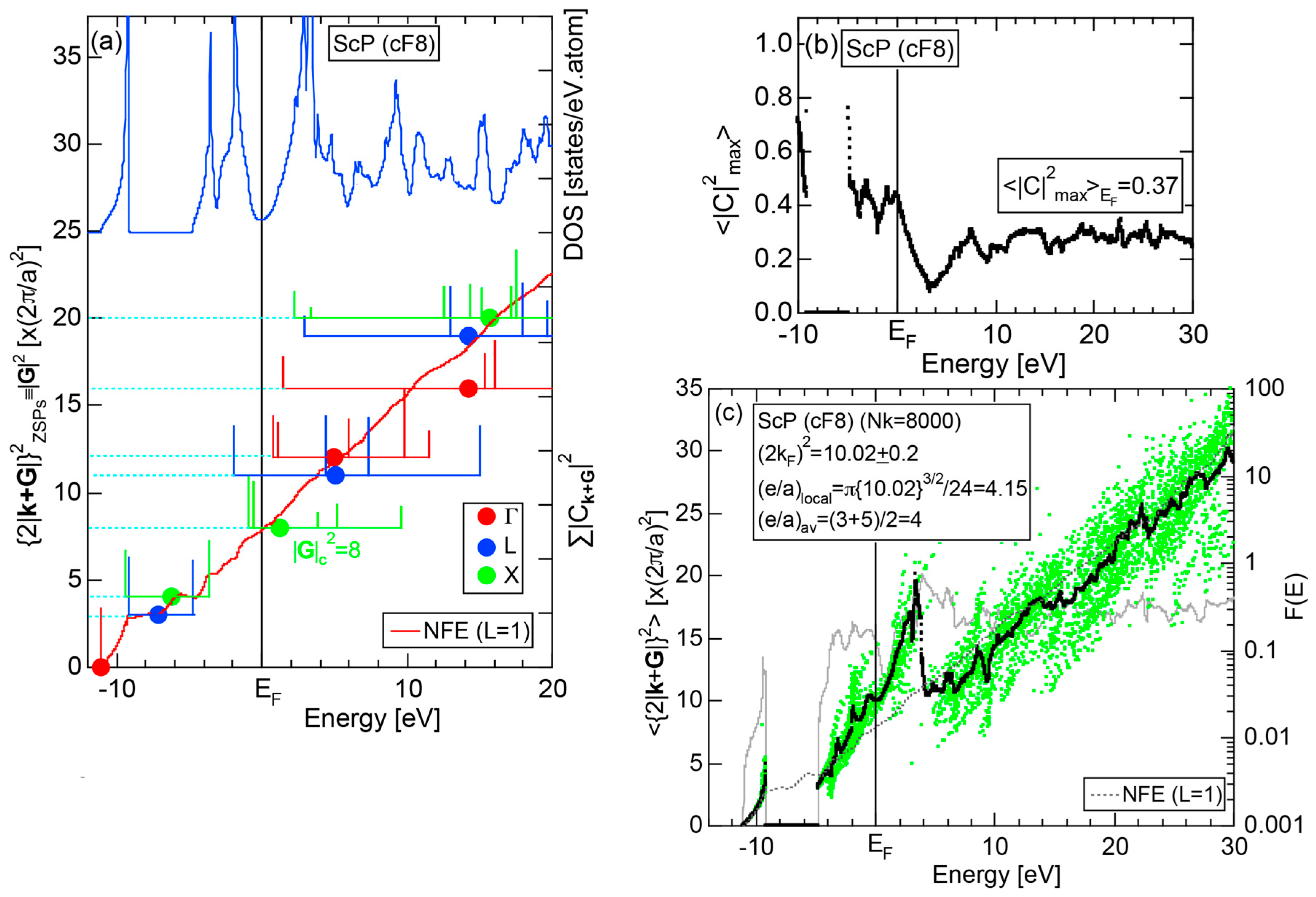
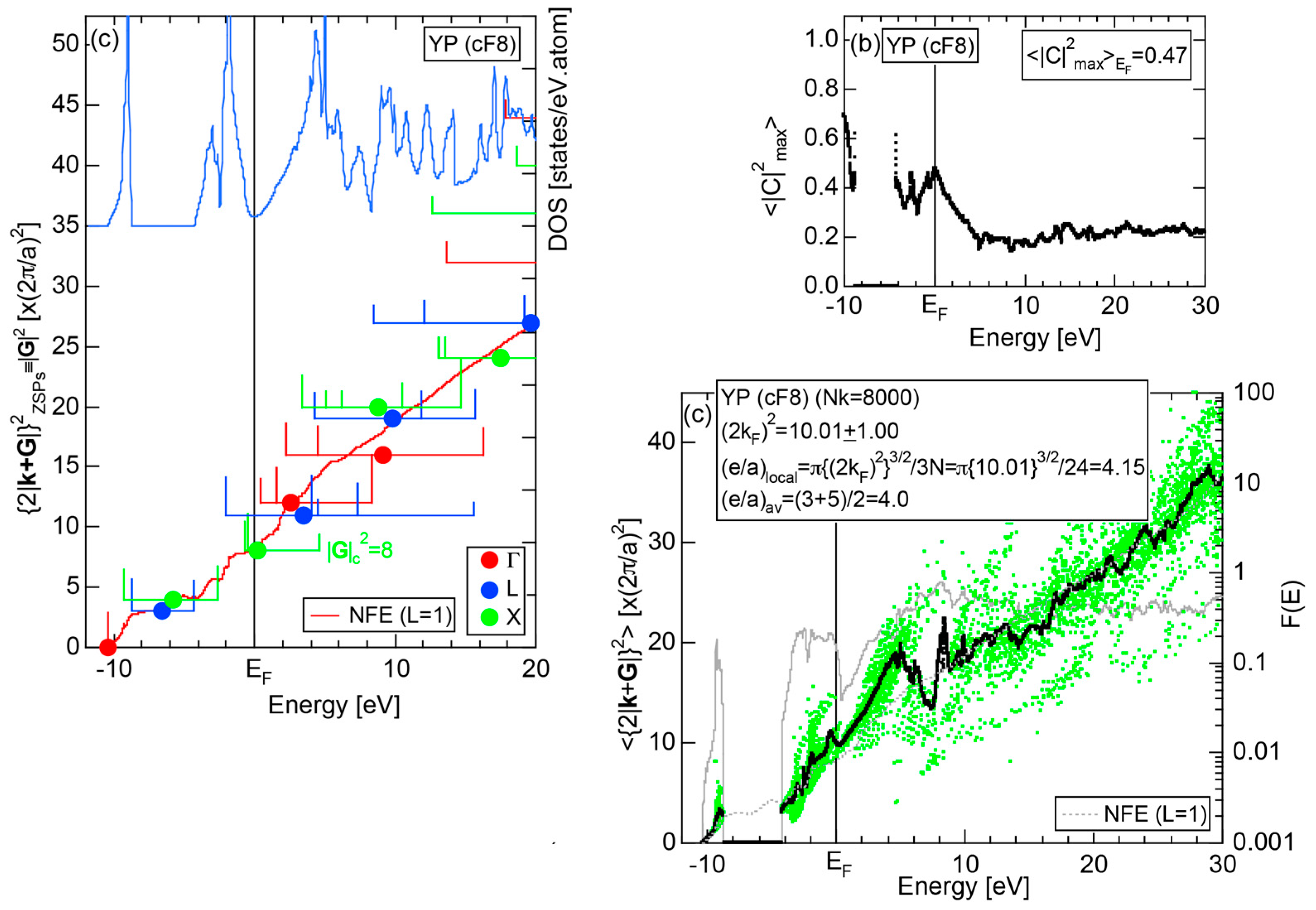
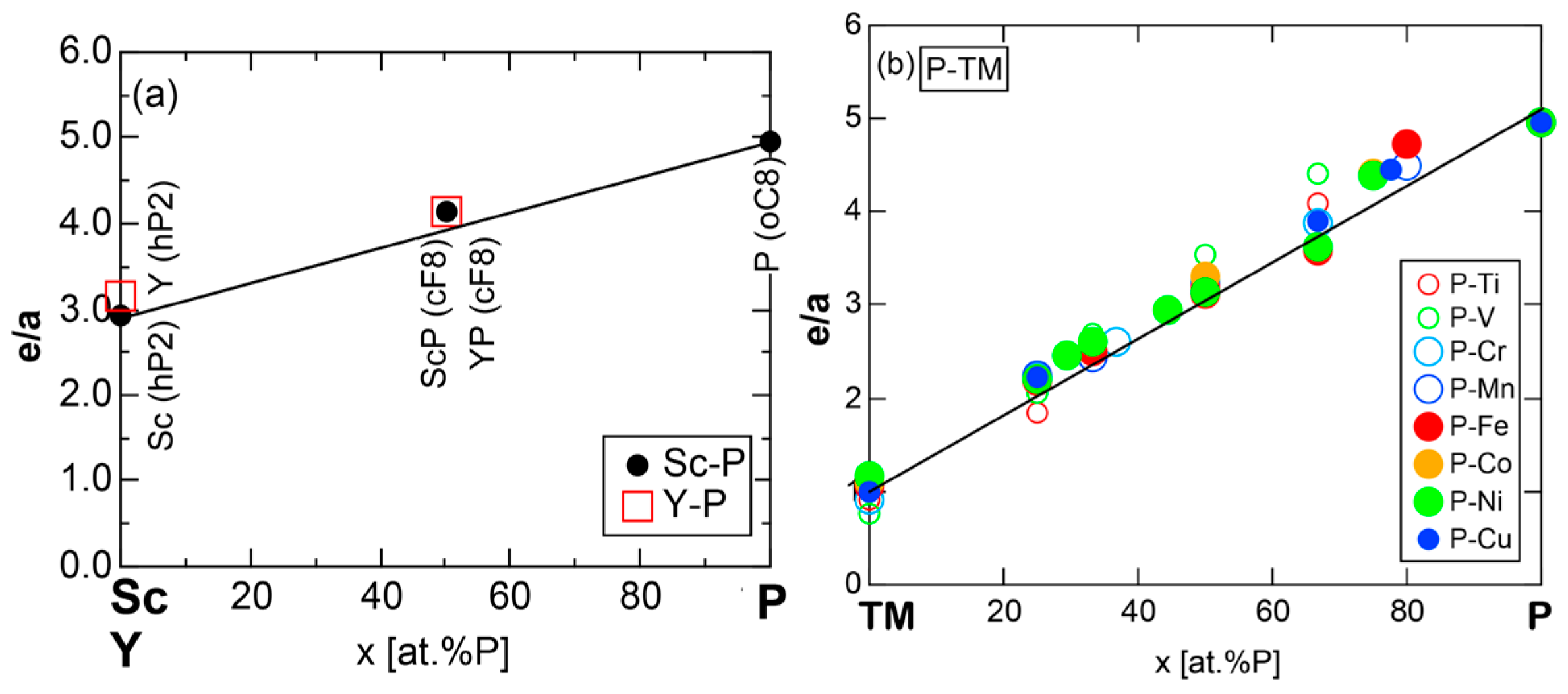
6.3.2. TM-P (TM = Sc to Ni) Compounds
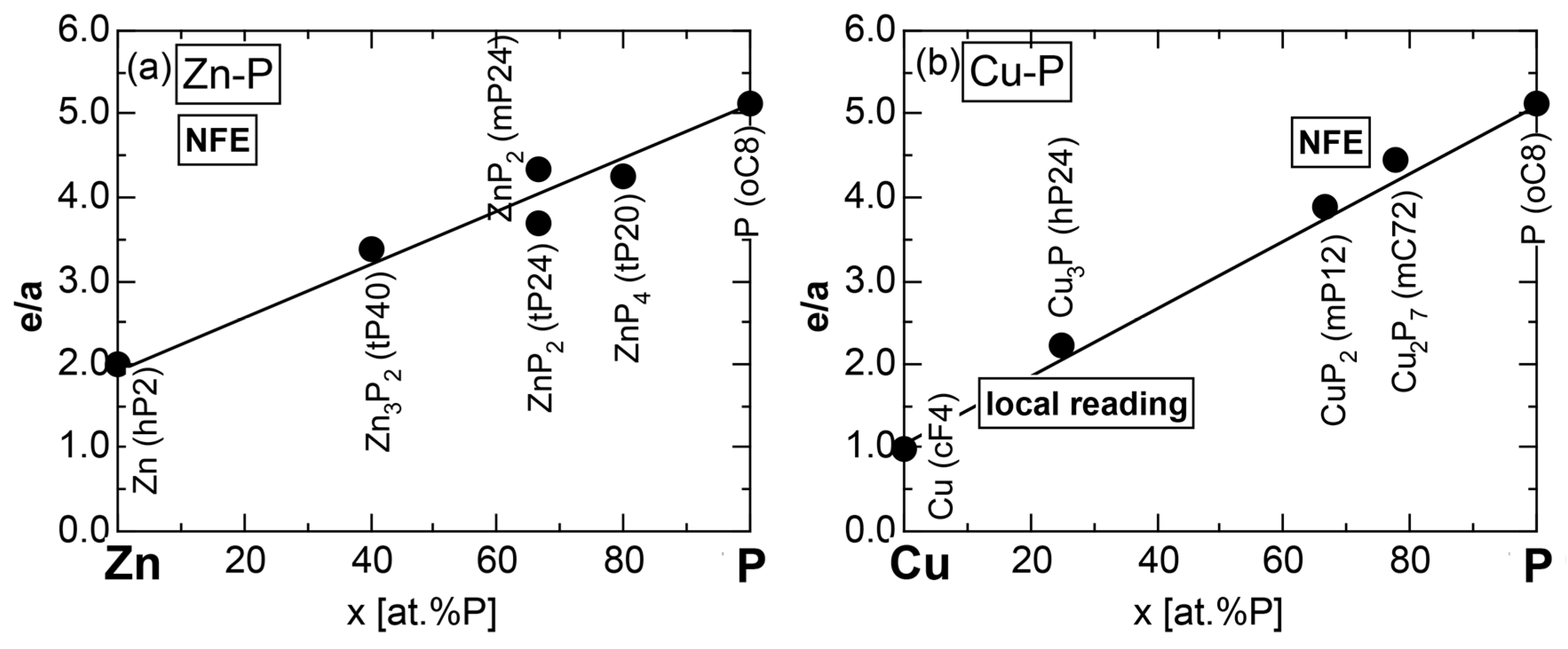
6.3.3. Mg-P, Ca-P, Zn-P and Cu-P Compounds
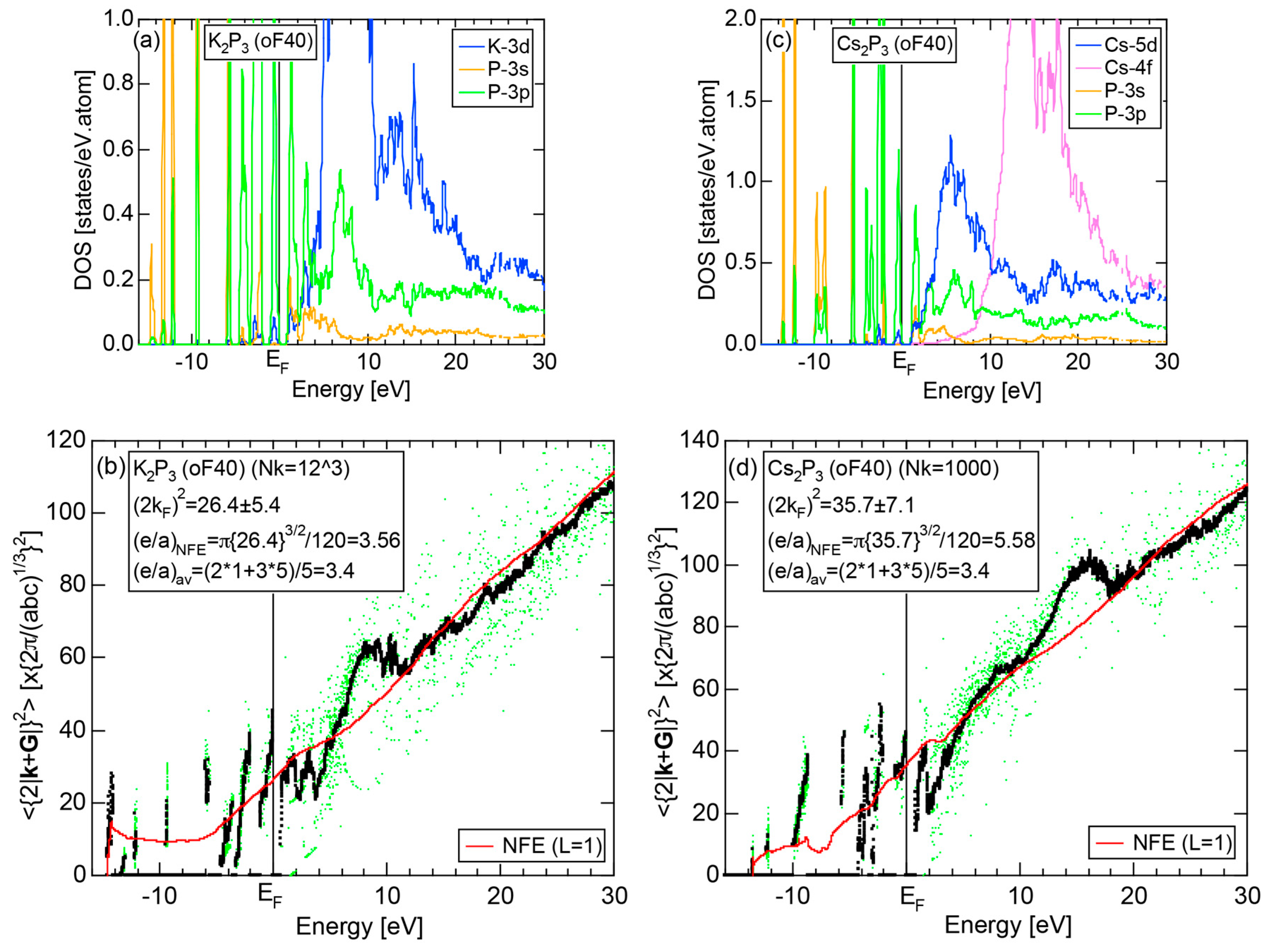
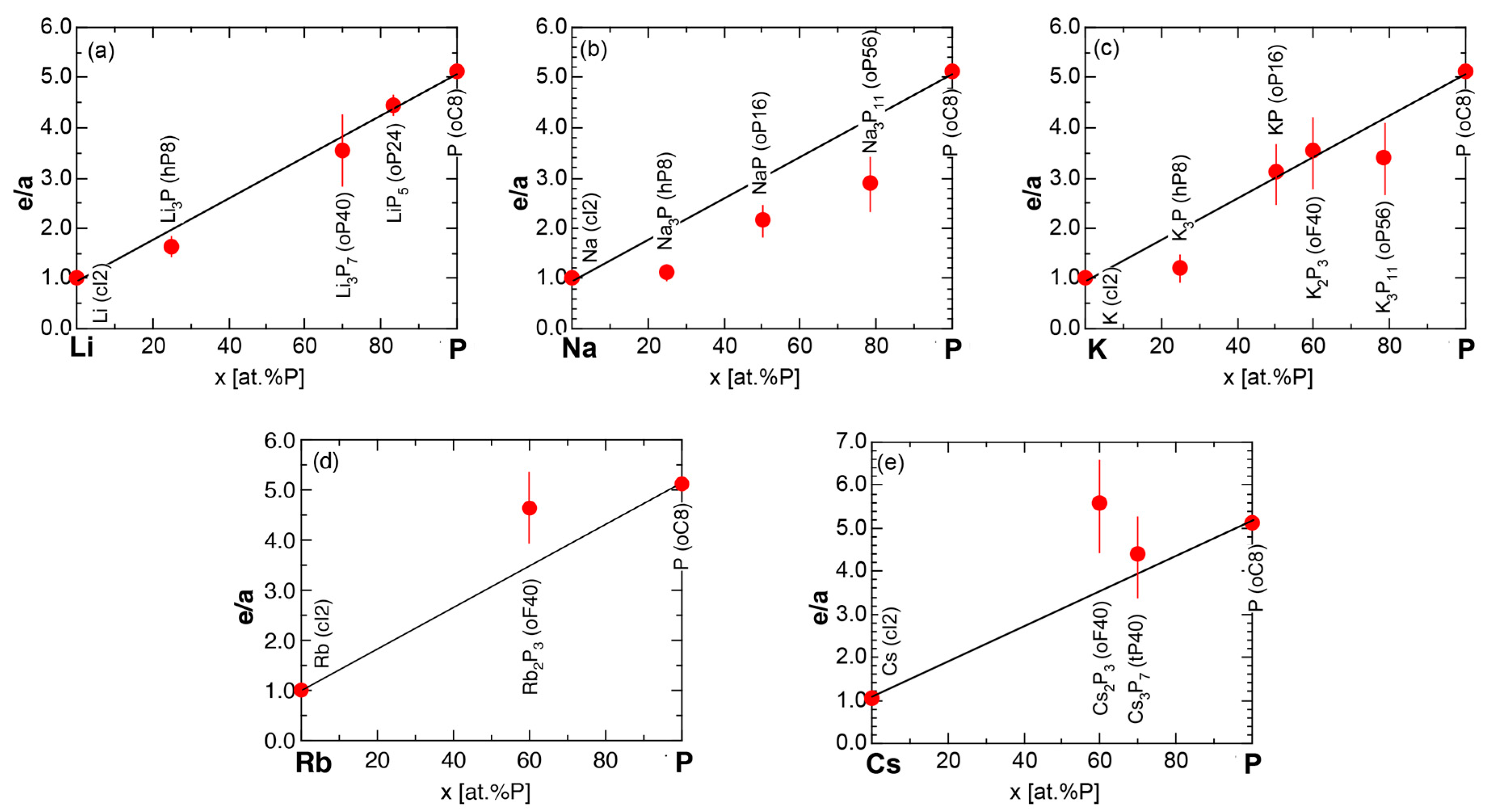
6.3.4. A-P (A = Li, Na, K, Rb and Cs) Compounds
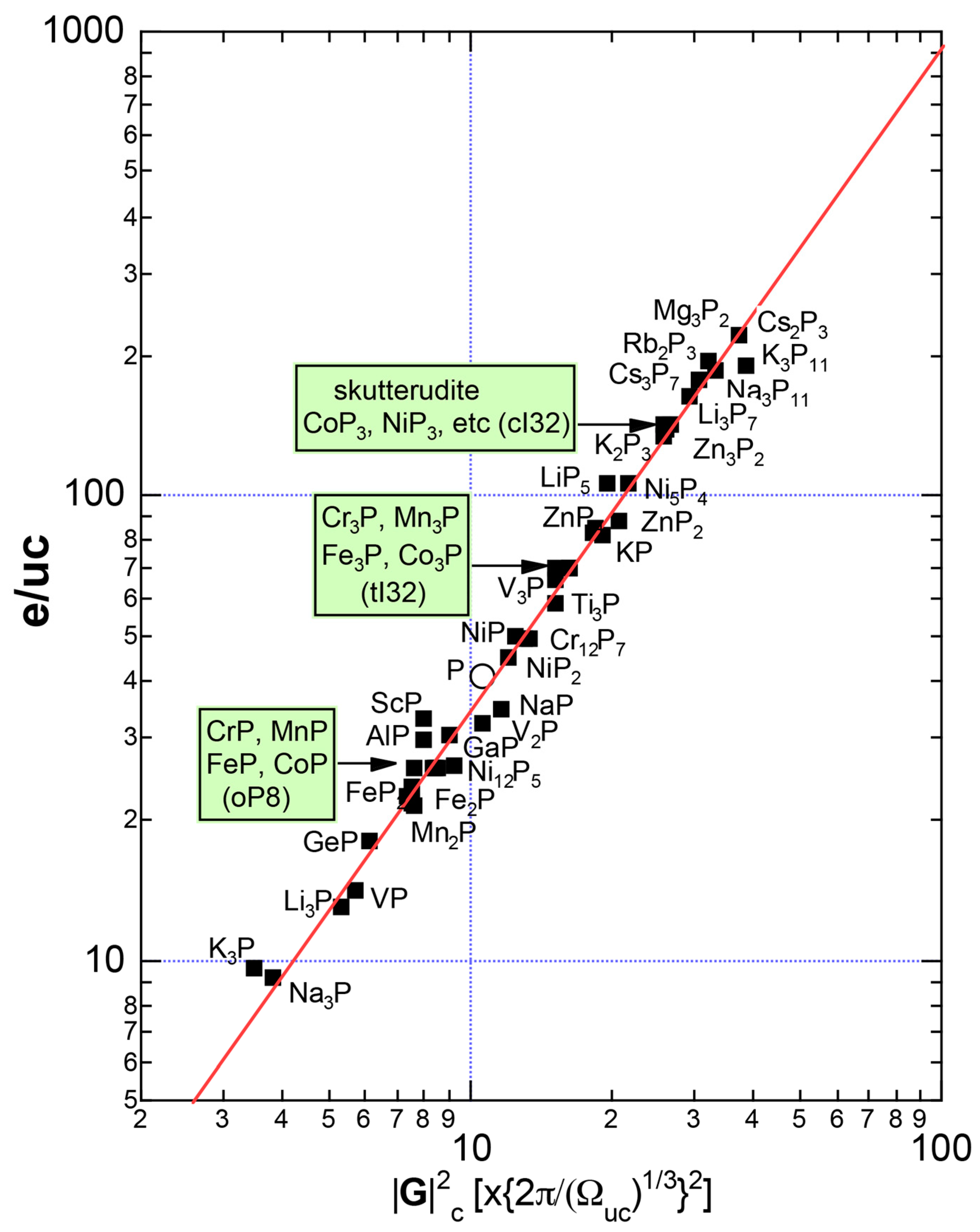
6.4. Hume-Rothery Electron Concentration Rule in Phosphorus-Based Compounds
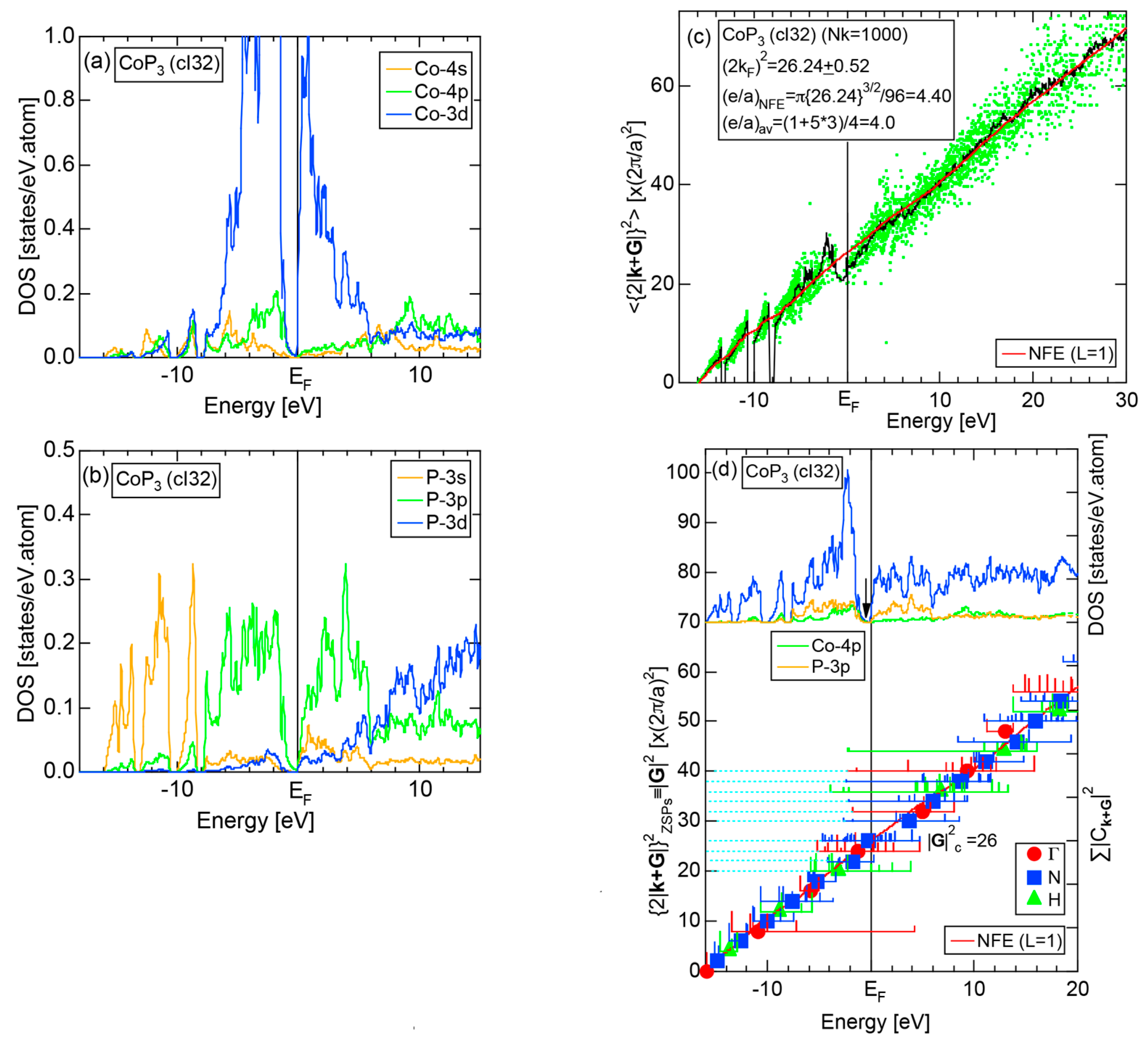
6.4.1. TMP3 (TM=Co, Ni, Rh and Ir), TMAs3 (TM=Co, Rh and Ir) and TMSb3 (TM=Co, Rh and Ir) Skutterudite Compounds (cI32)
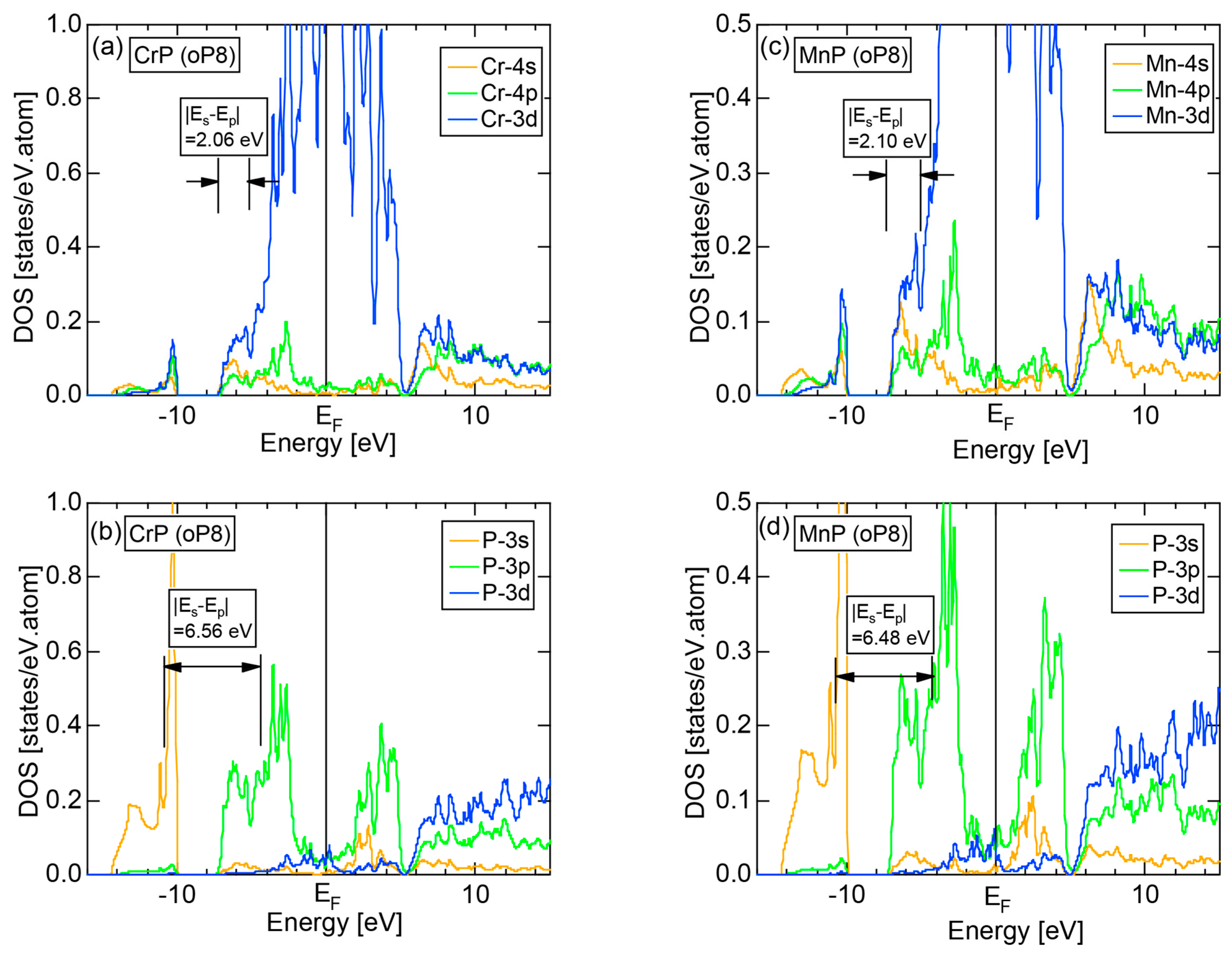
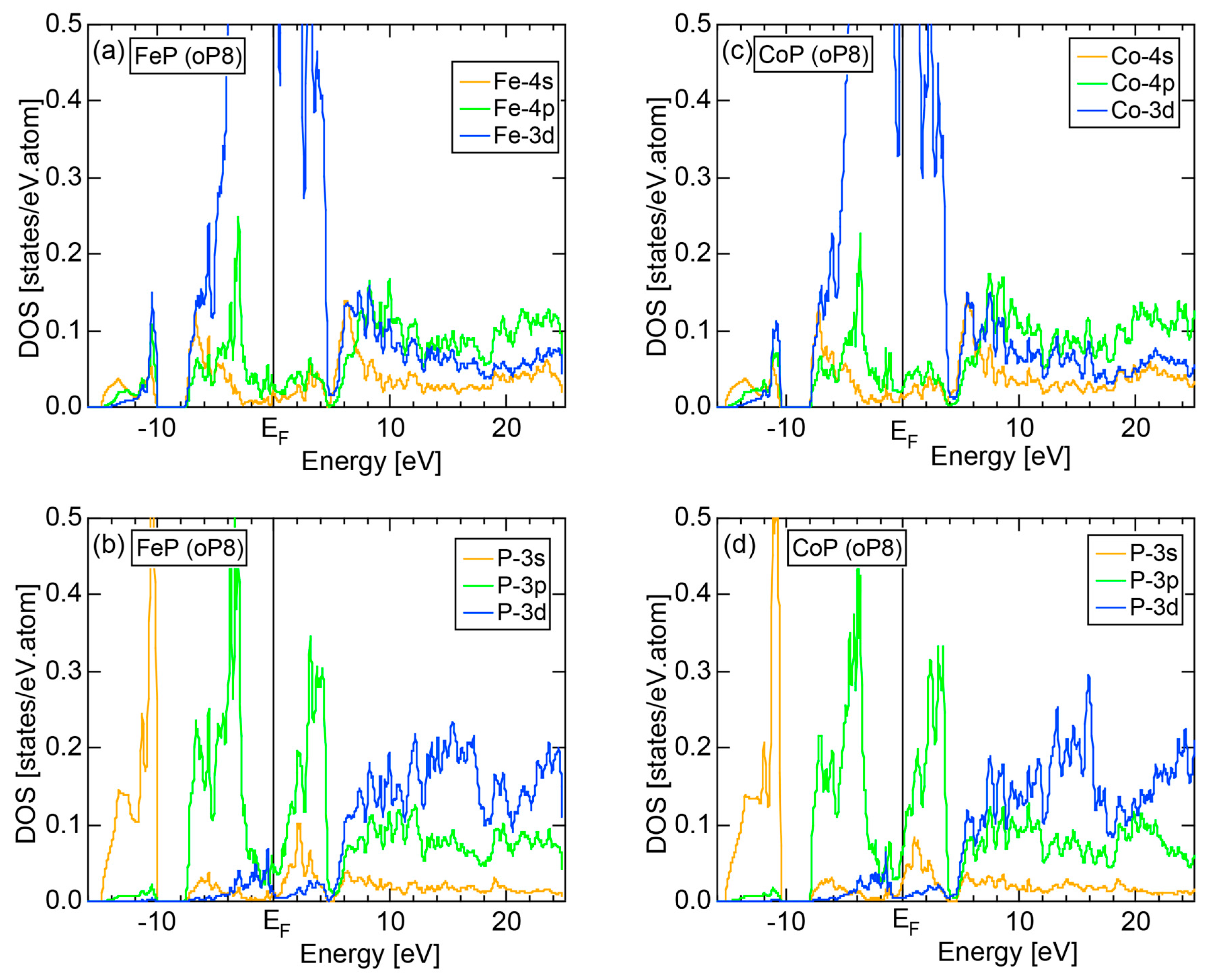
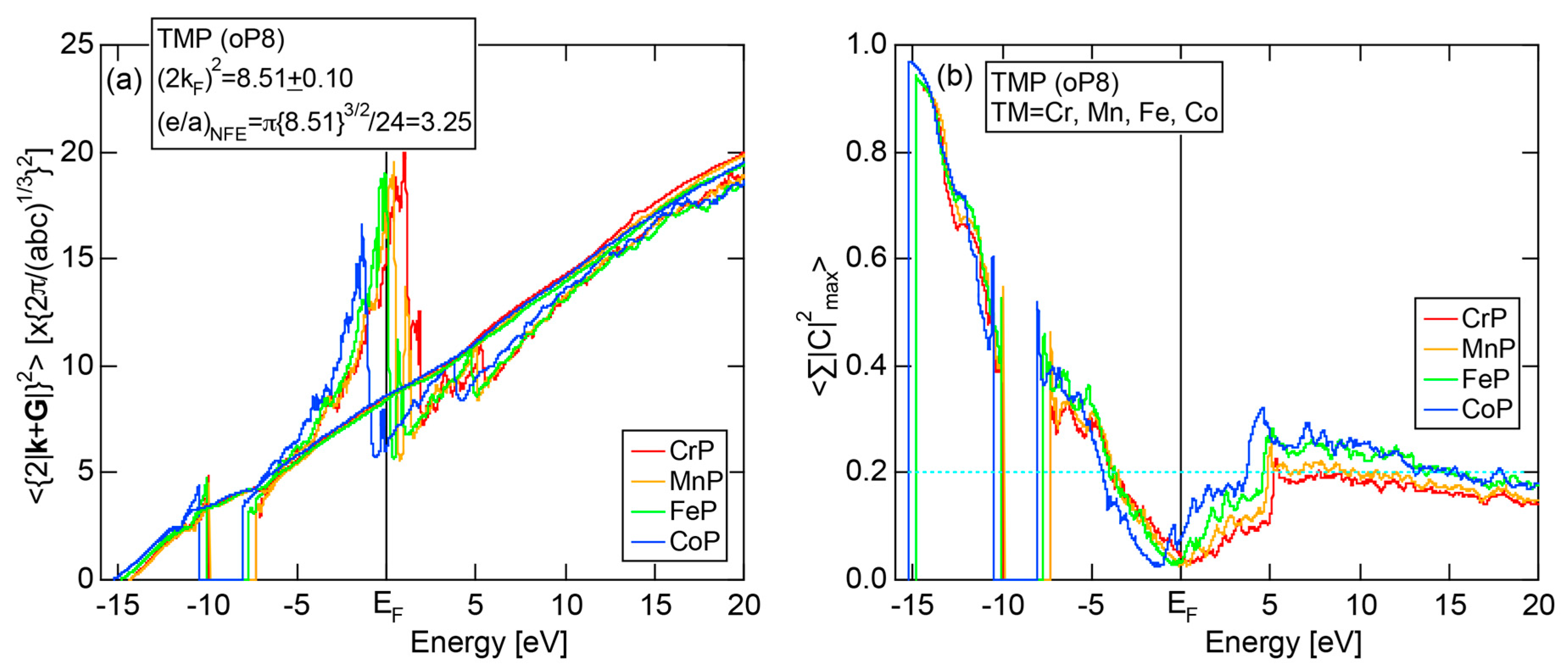
6.4.2. (TM)P (TM = Cr, Mn, Fe and Co) Compounds (oP8)
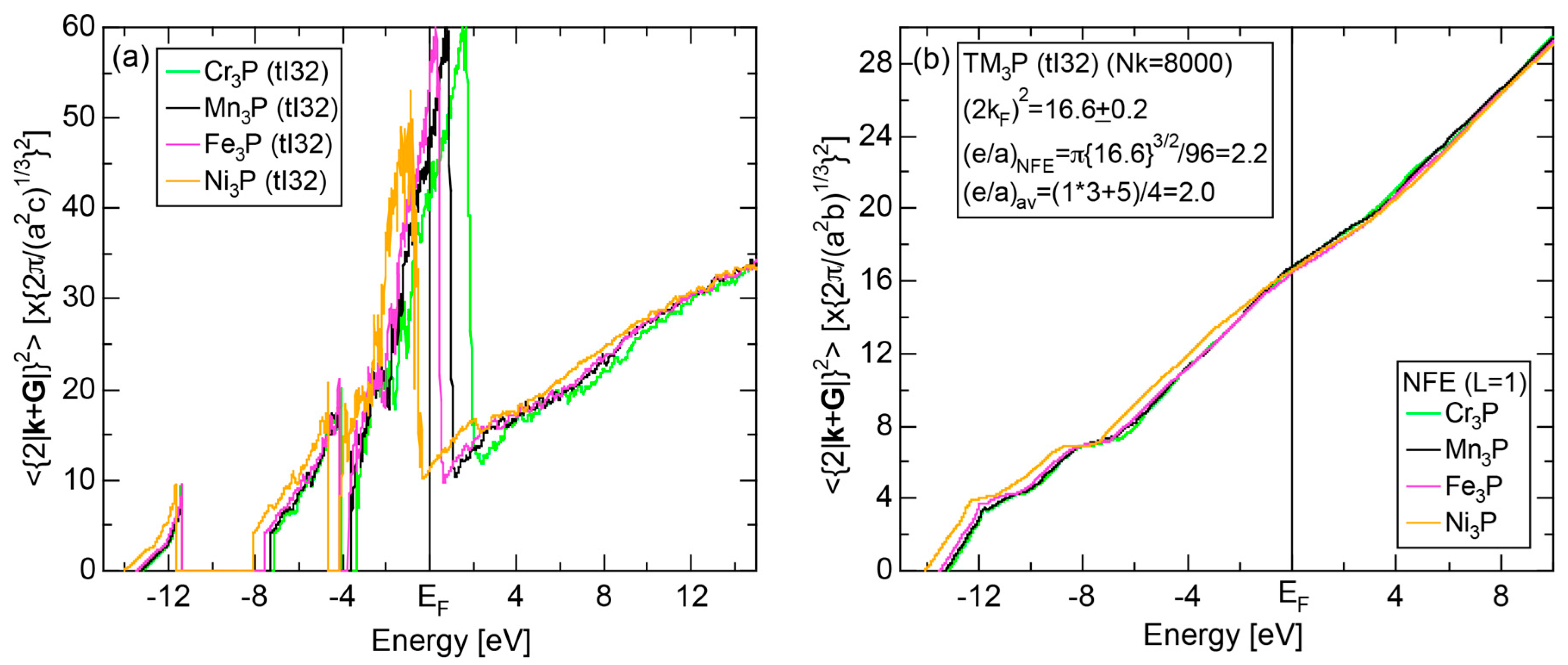
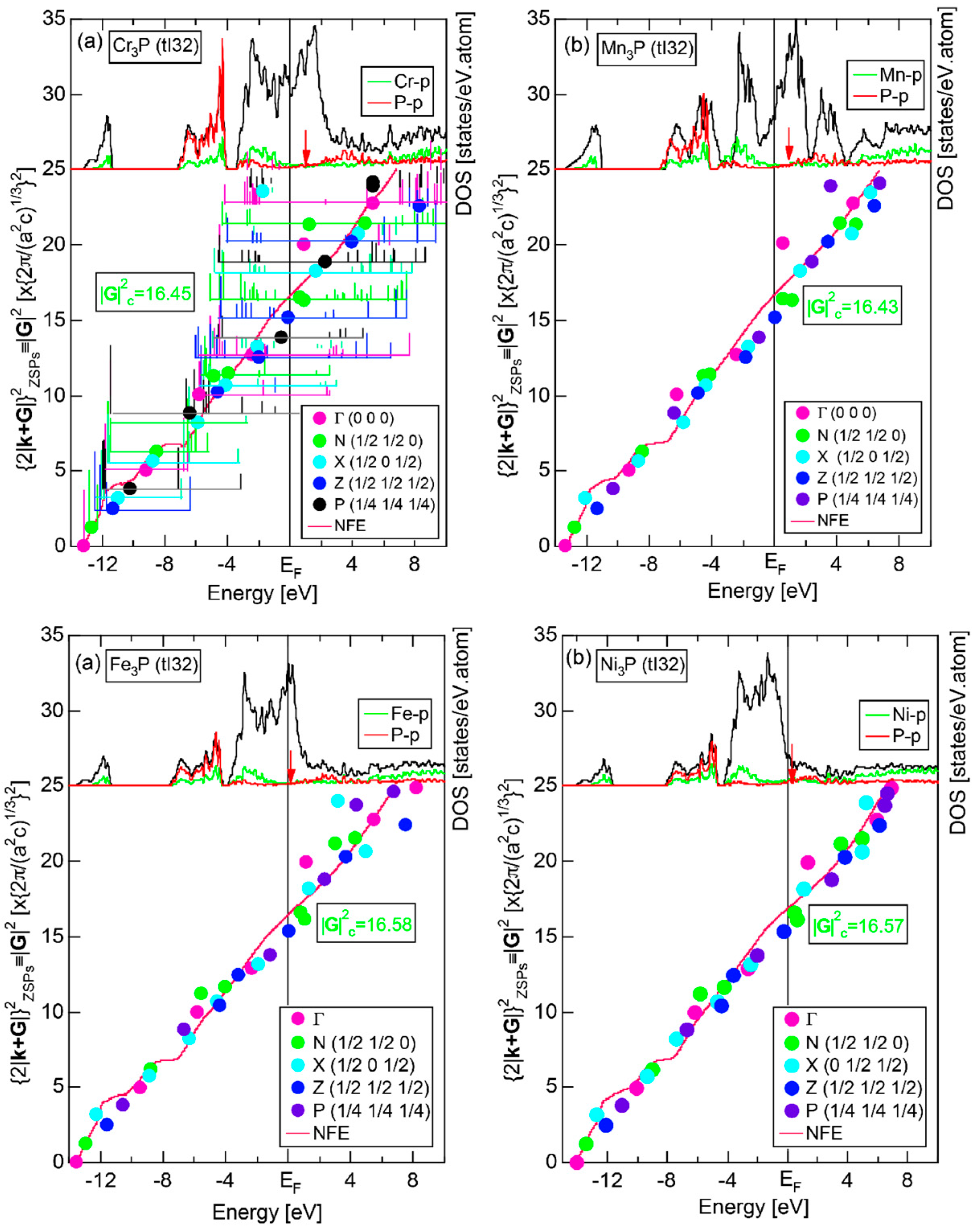
6.4.3. TM3P (TM = Cr, Mn, Fe and Ni) Compounds (tI32)
6.5. Interference Phenomenon for Phosphorus Compounds
6.6. Summary
7. Hume-Rothery Electron Concentration Rule in Inter-Transition Metal Compounds
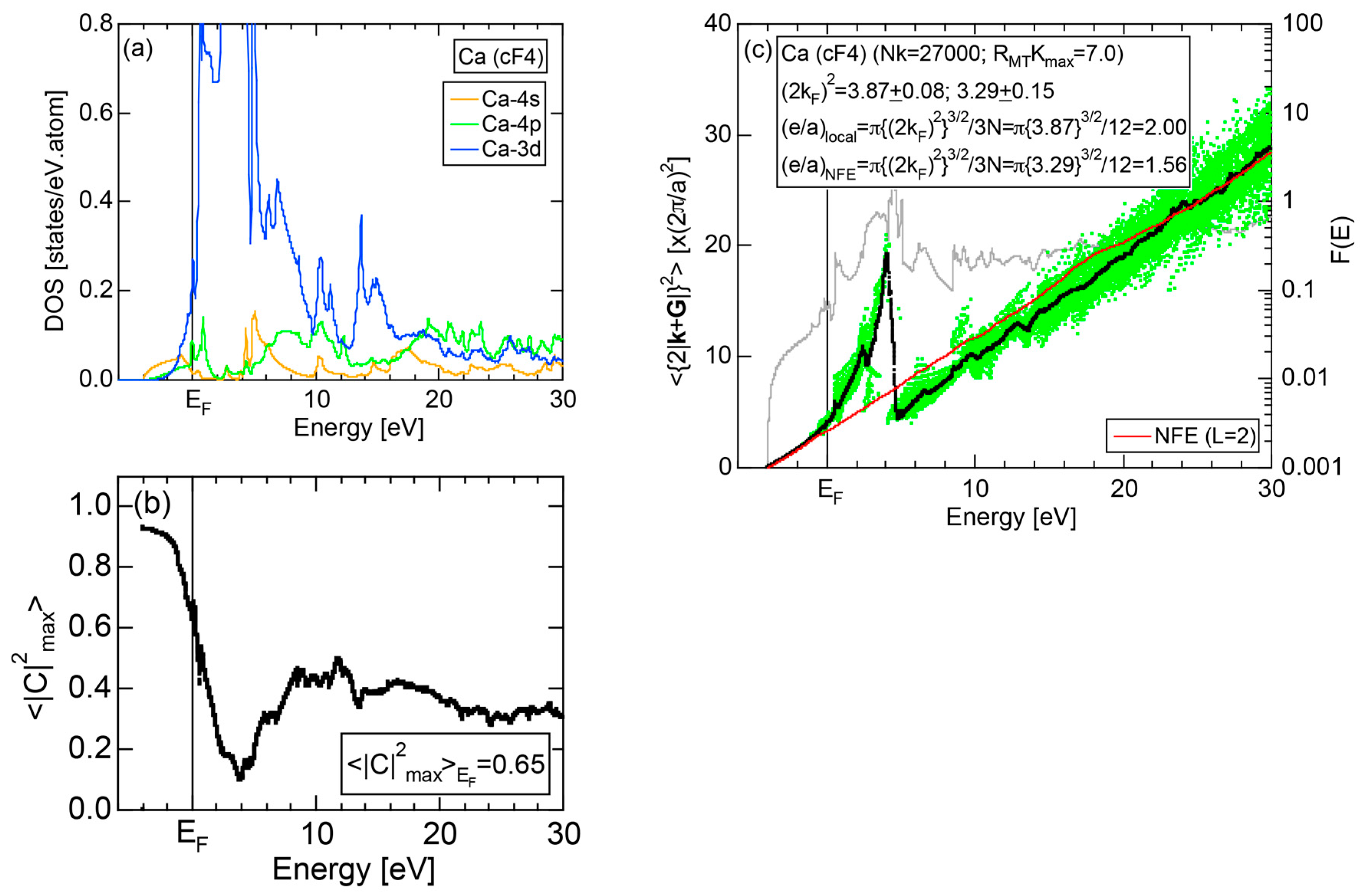
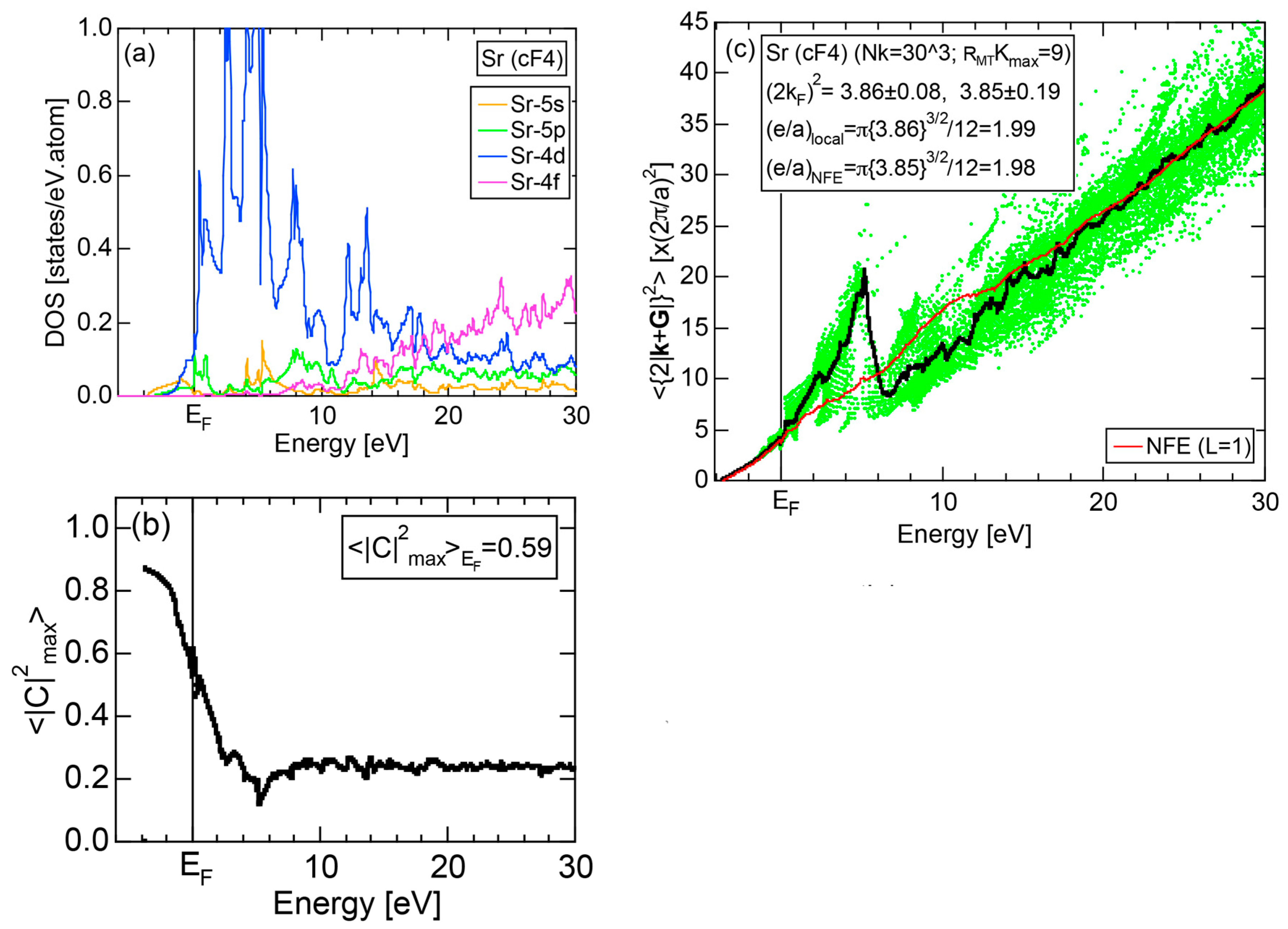
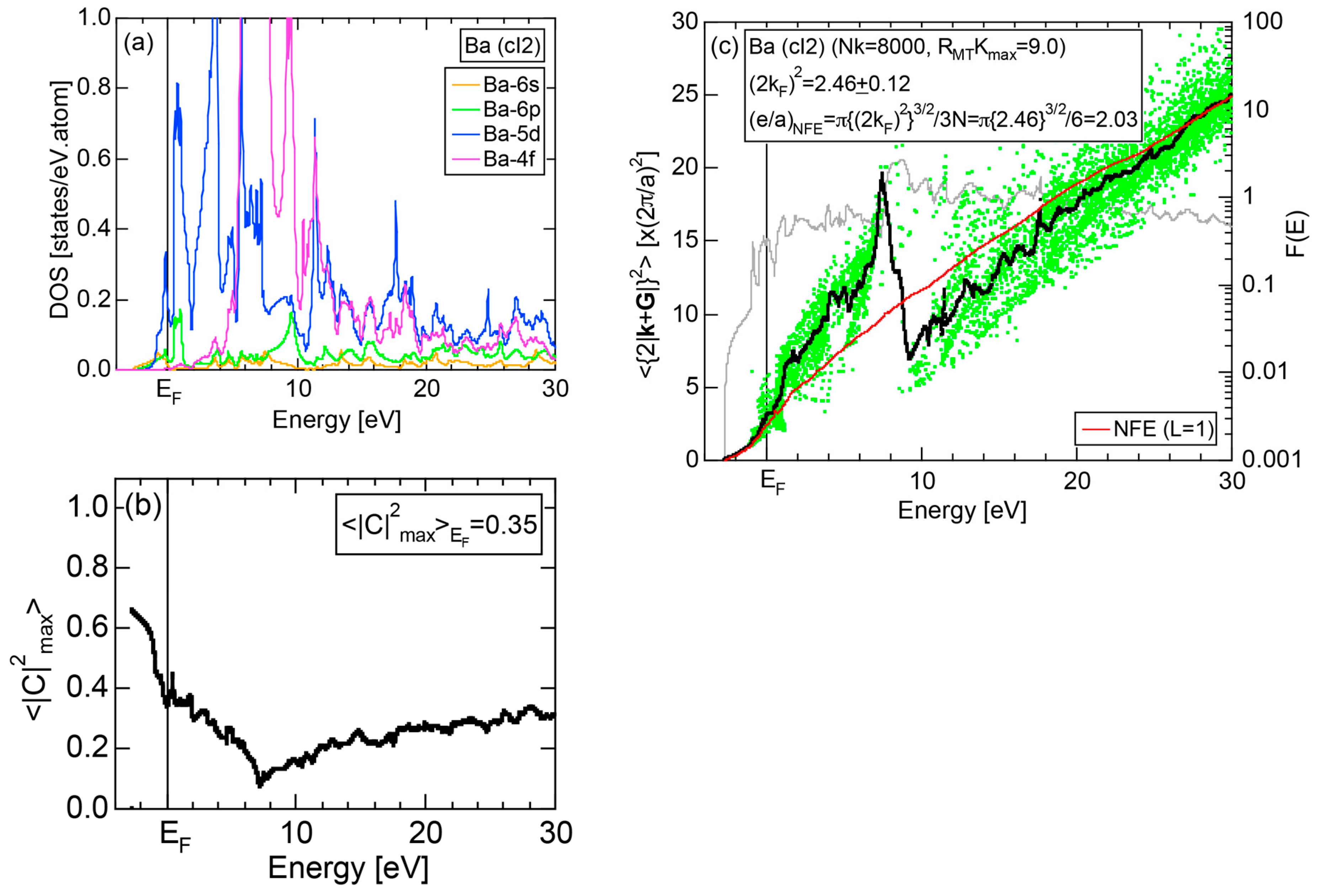
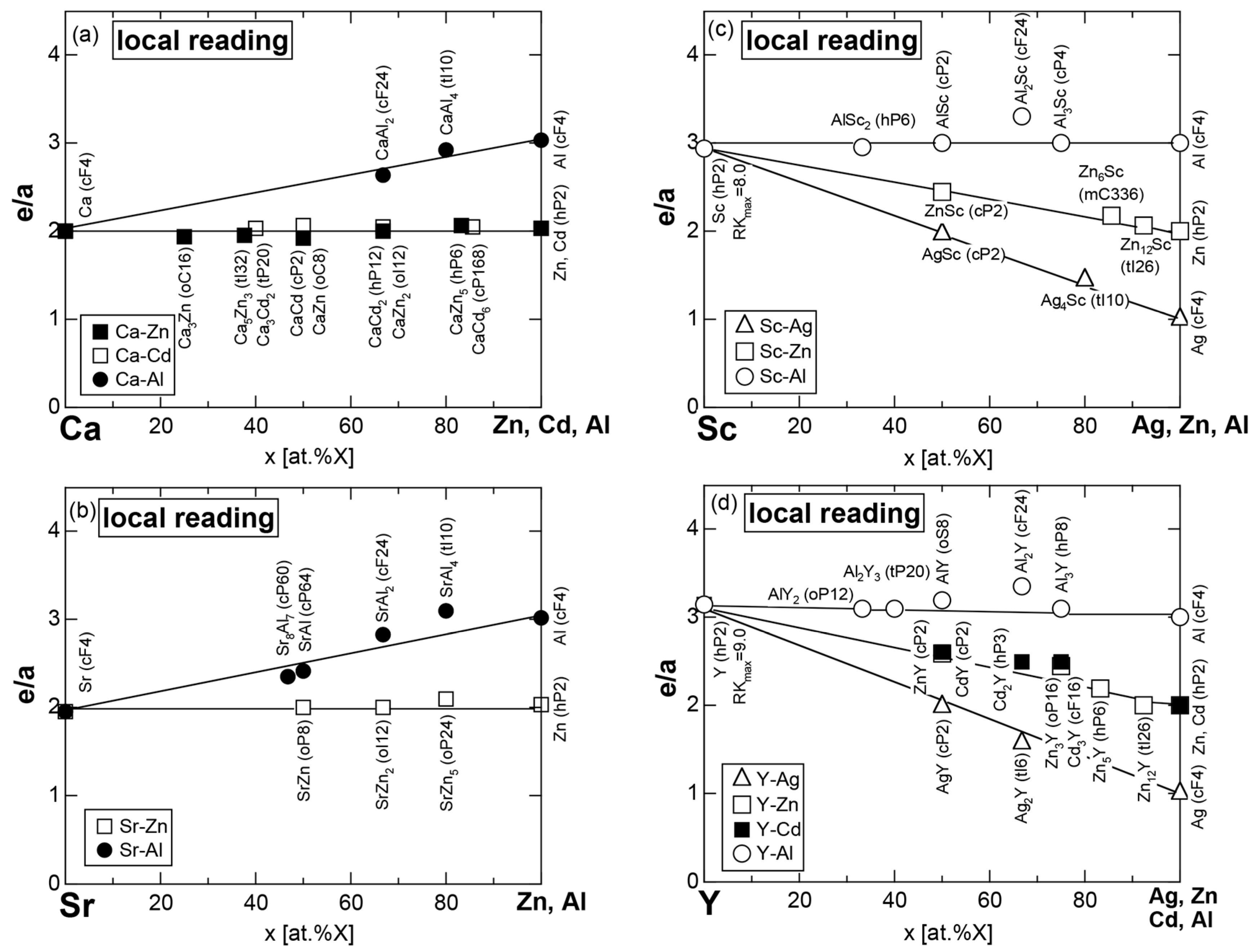
7.1. e/a Determination for Group 2 Elements Ca, Sr and Ba
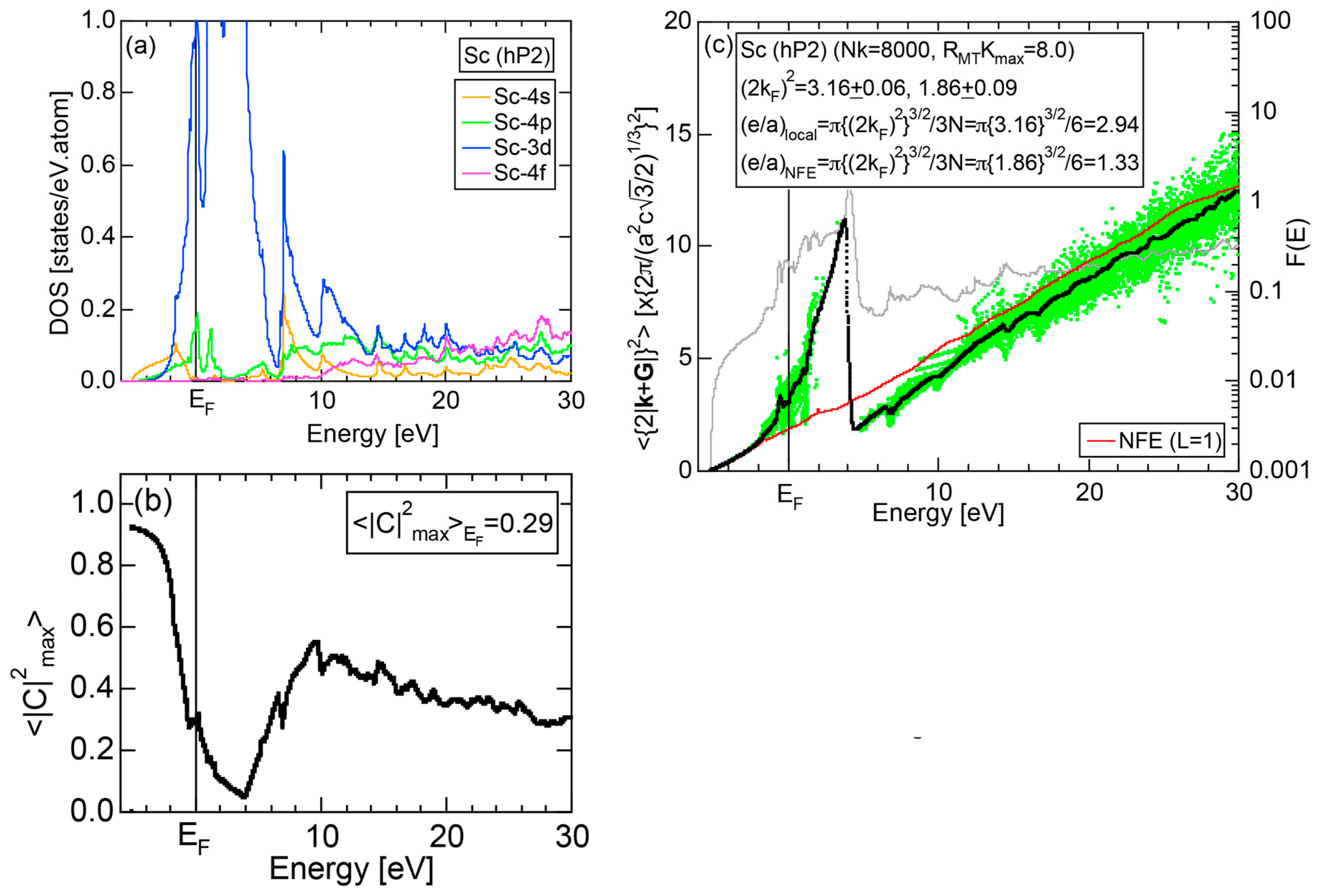
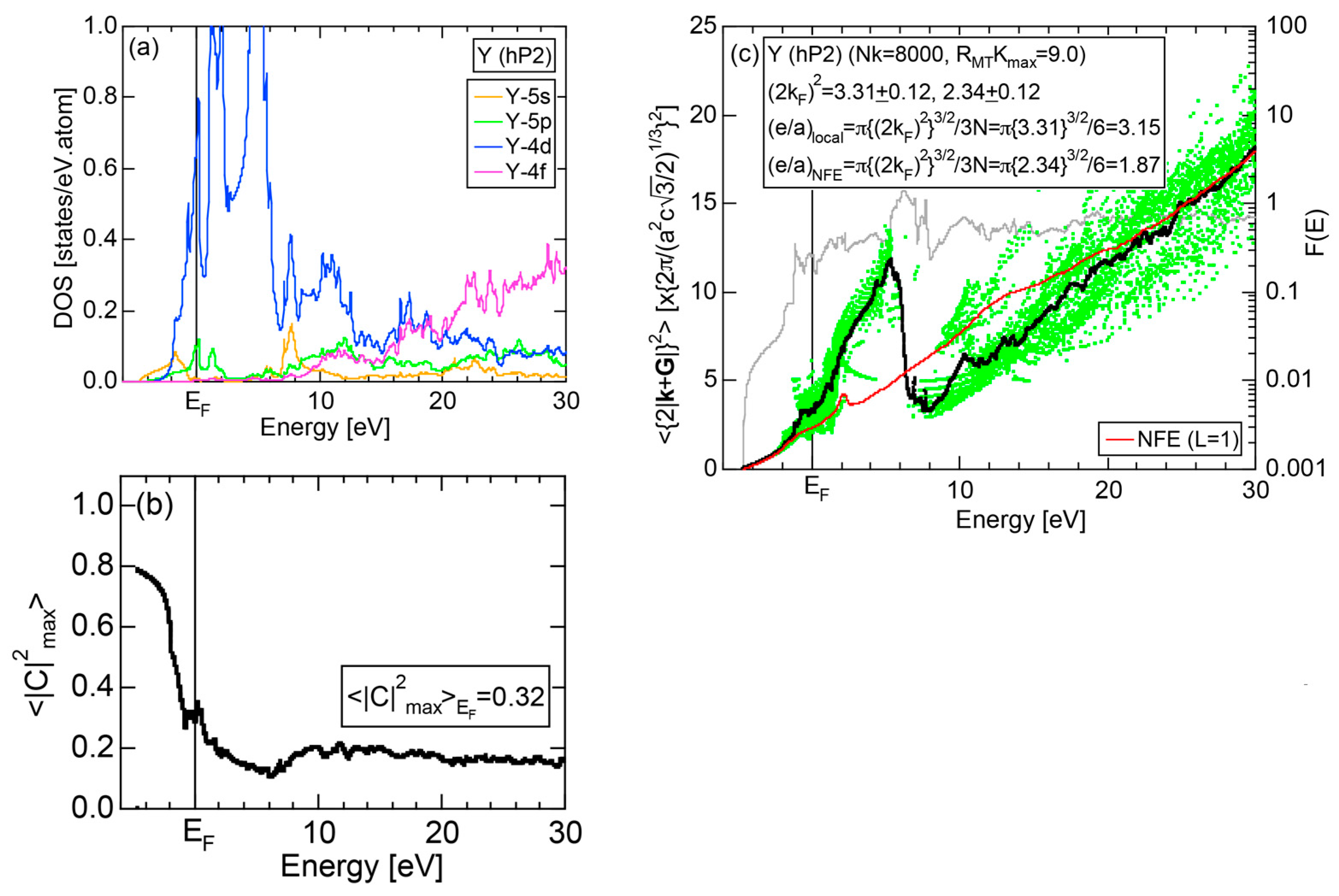
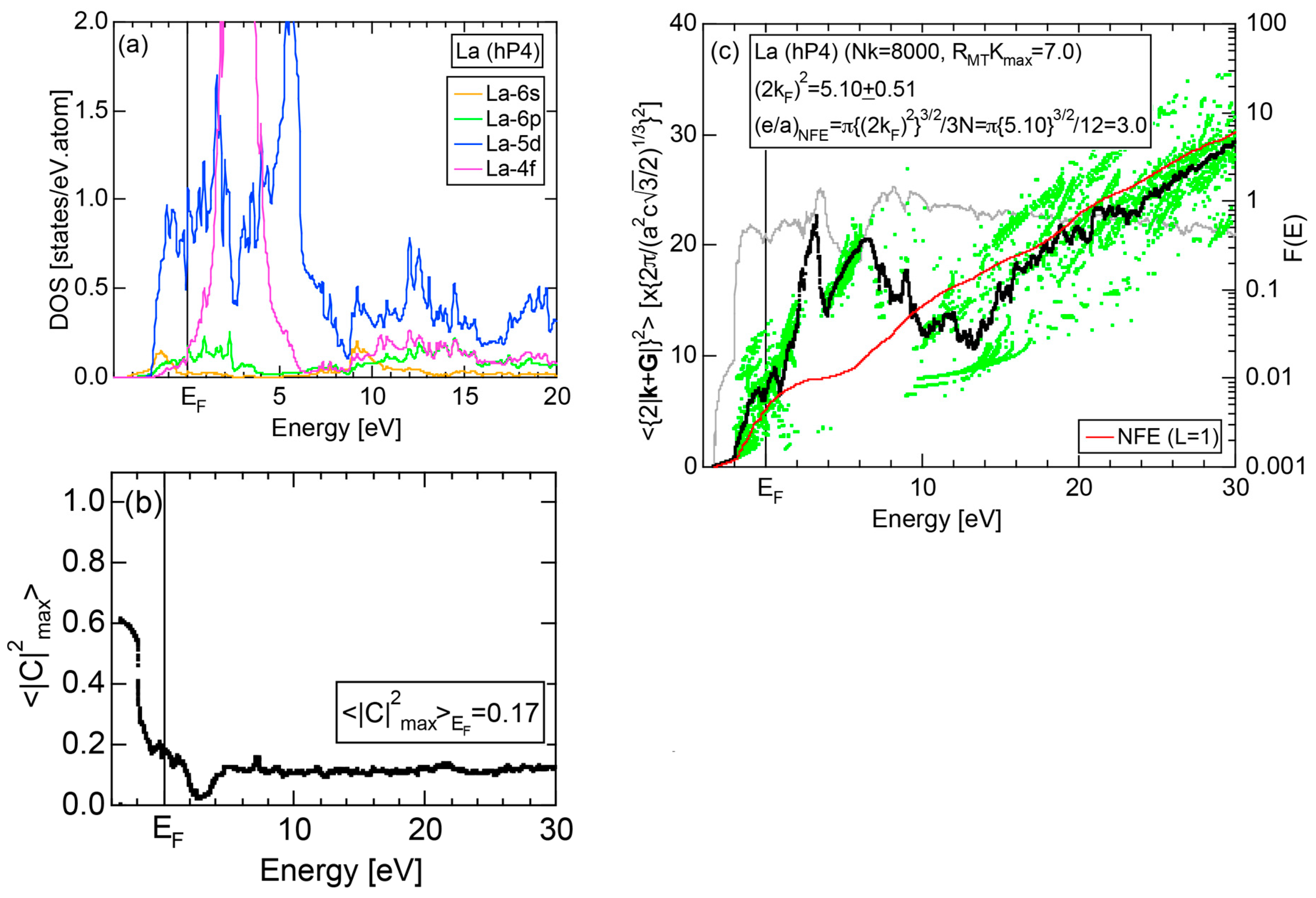
7.2. e/a Determination for Group 3 Elements Sc, Y and La
7.3. Alloying Environment Effects and the Linear Interpolation Rule
7.3.1. Ca-, Sr-, Sc- and Y-Compounds with Simple Elements
7.3.2. Ba- and La-Compounds with Simple Elements
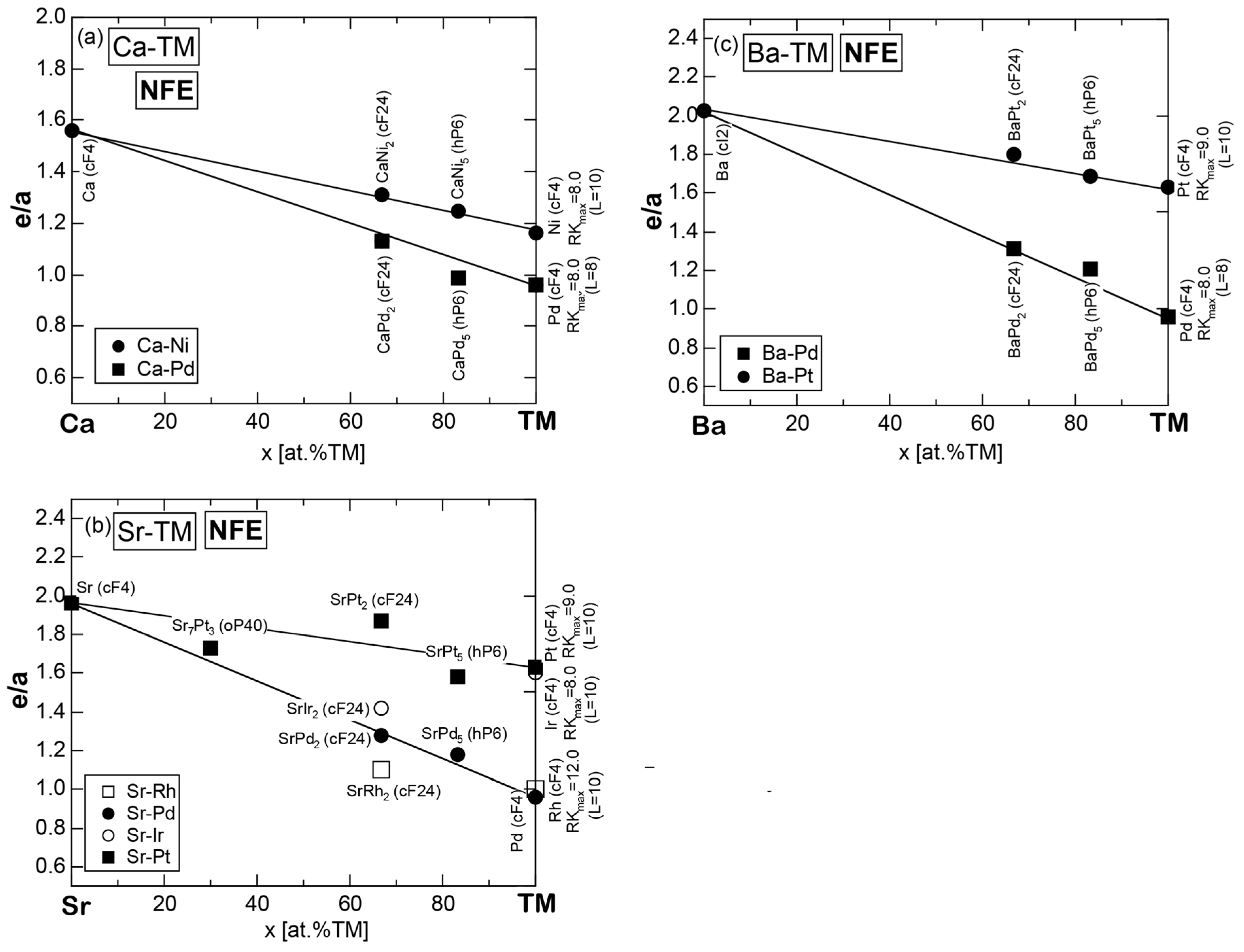
7.3.3. Ca-, Sr- and Ba-Compounds with TM Elements
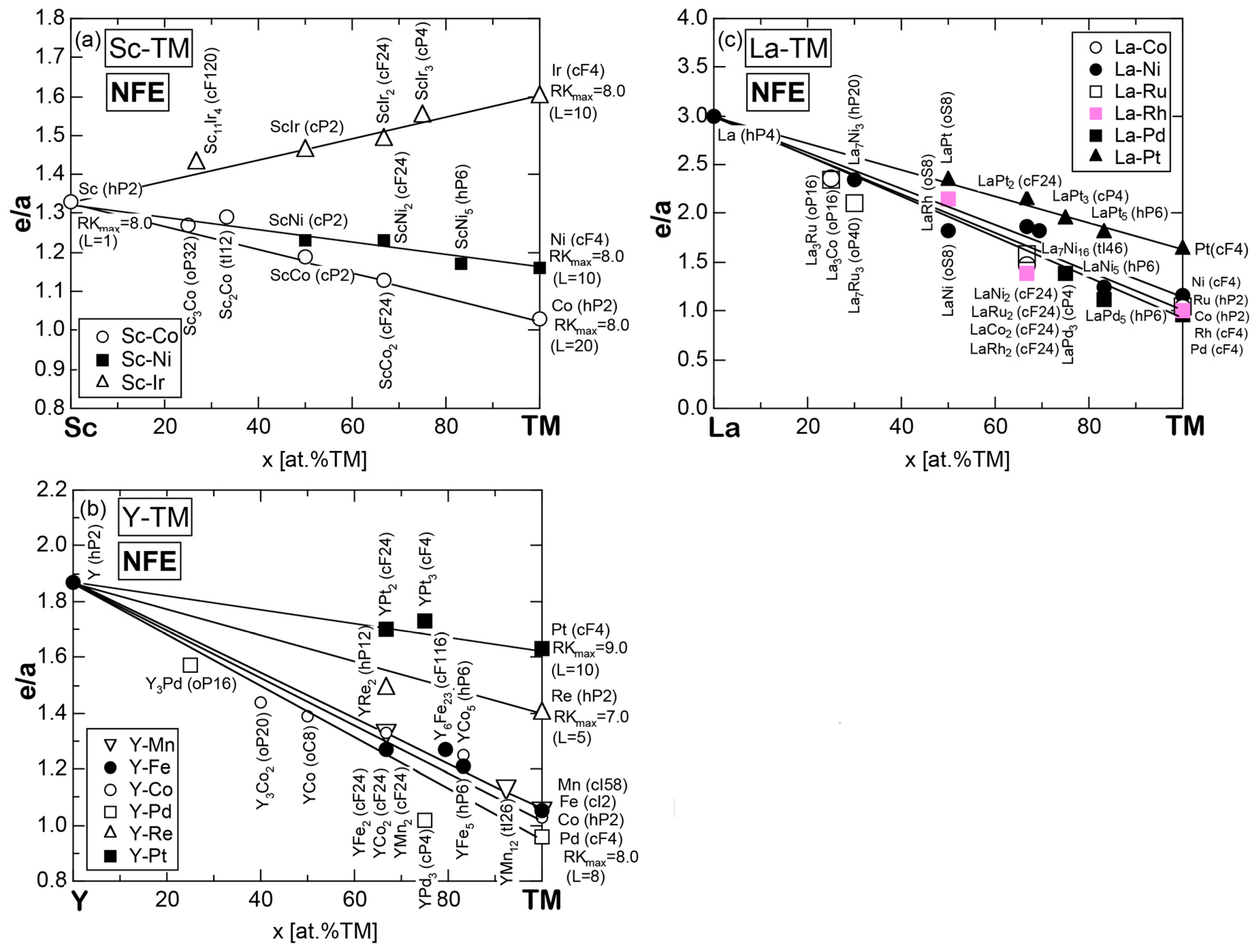
7.3.4. Sc-, Y- and La-Compounds with TM Elements
7.3.5. Inter-TM (Two TMs Selected from Group 4 to 10) Compounds
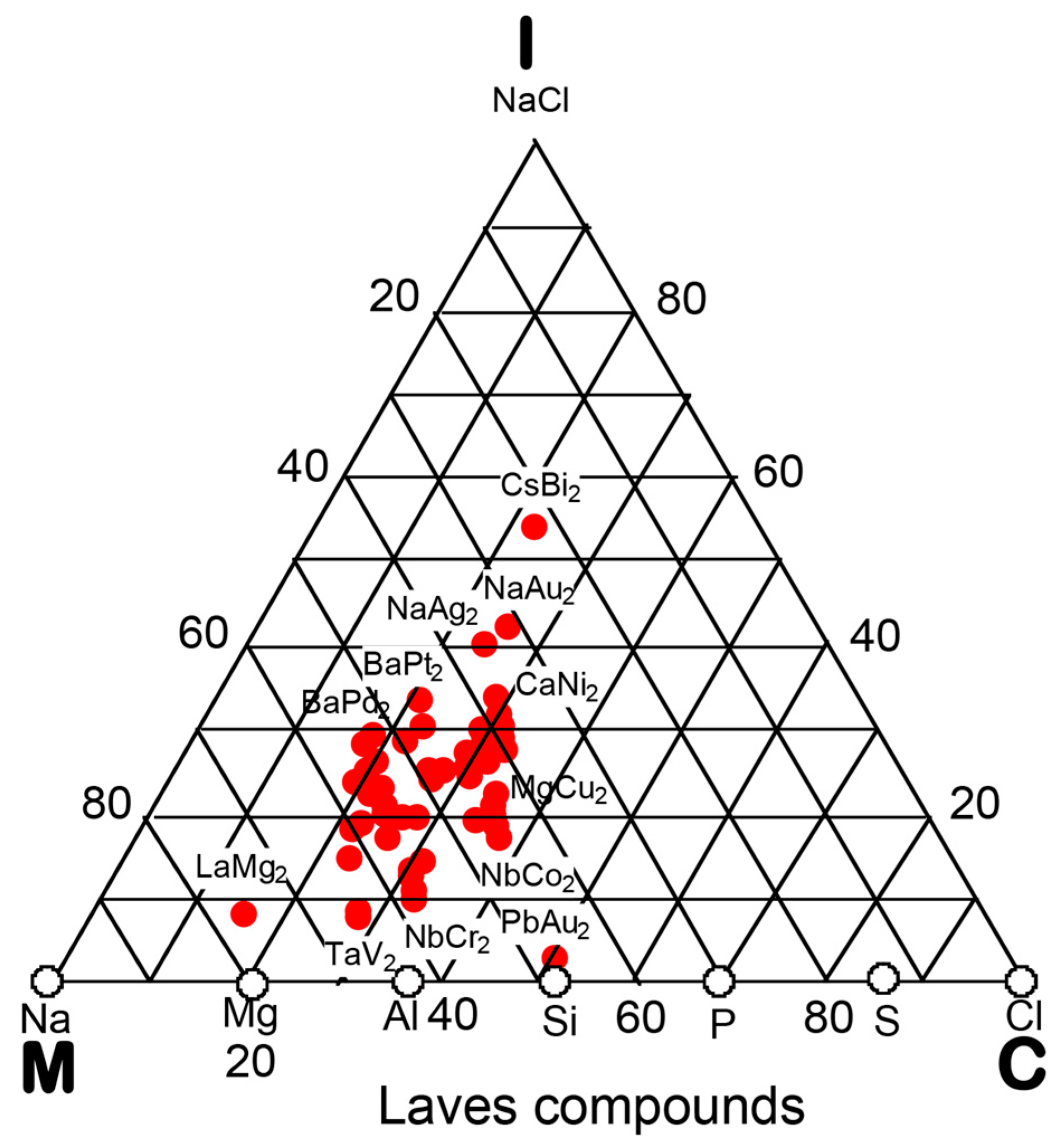
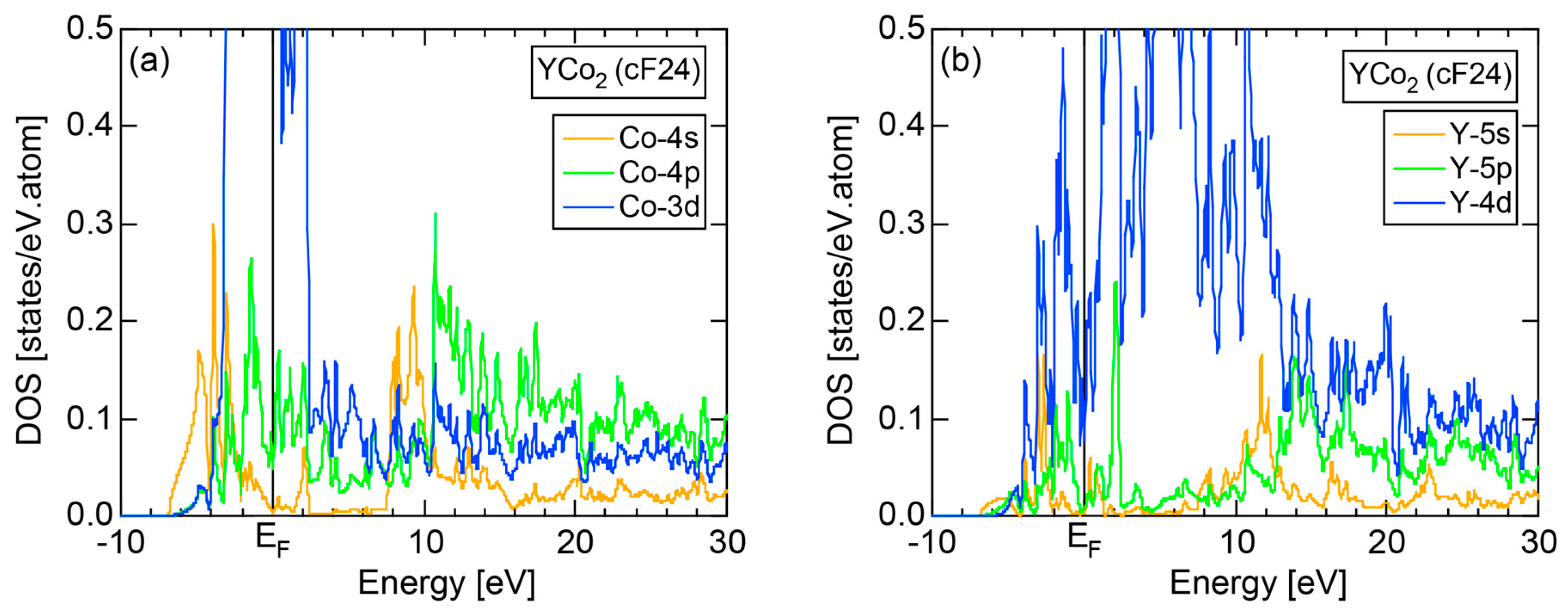
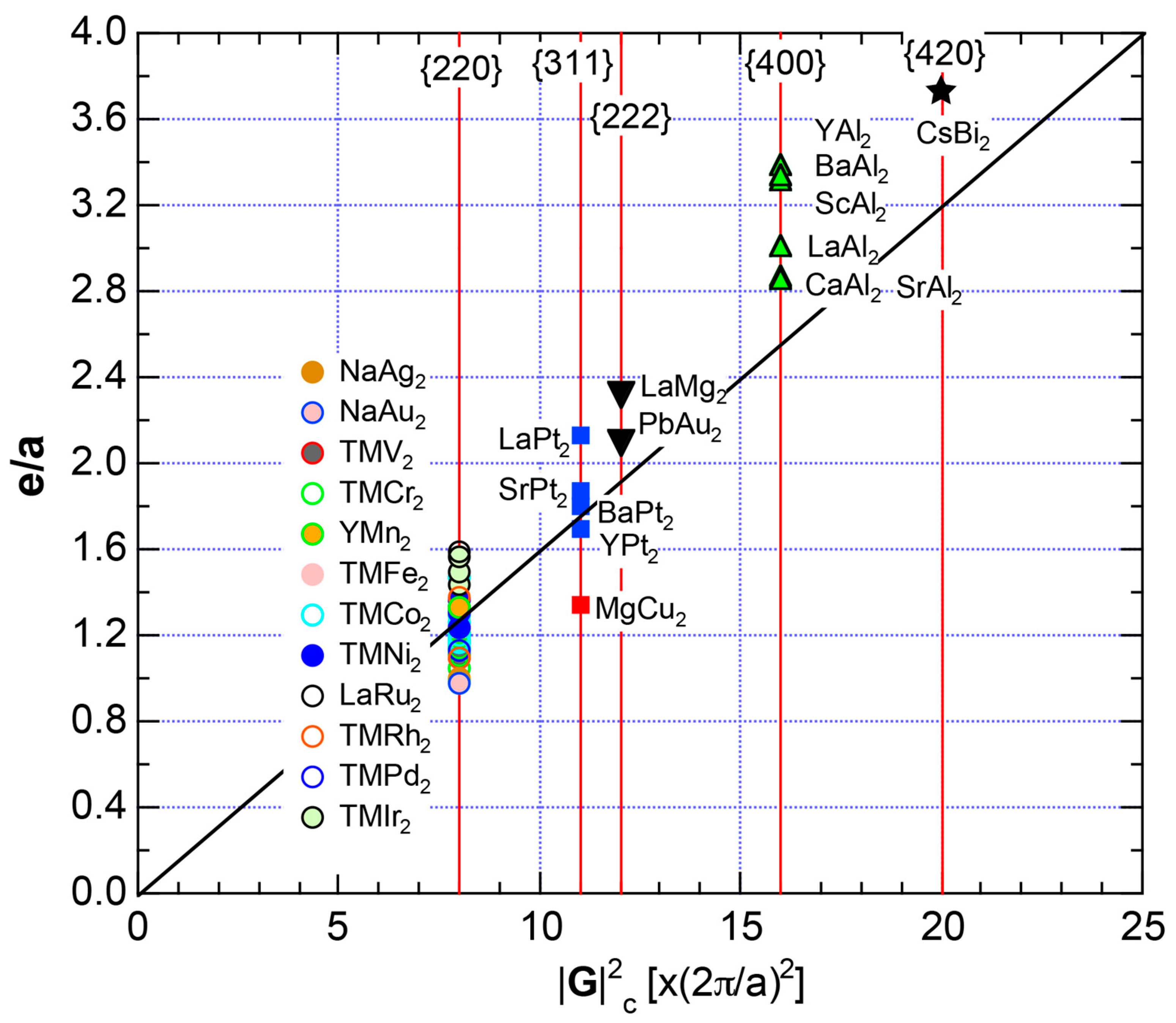
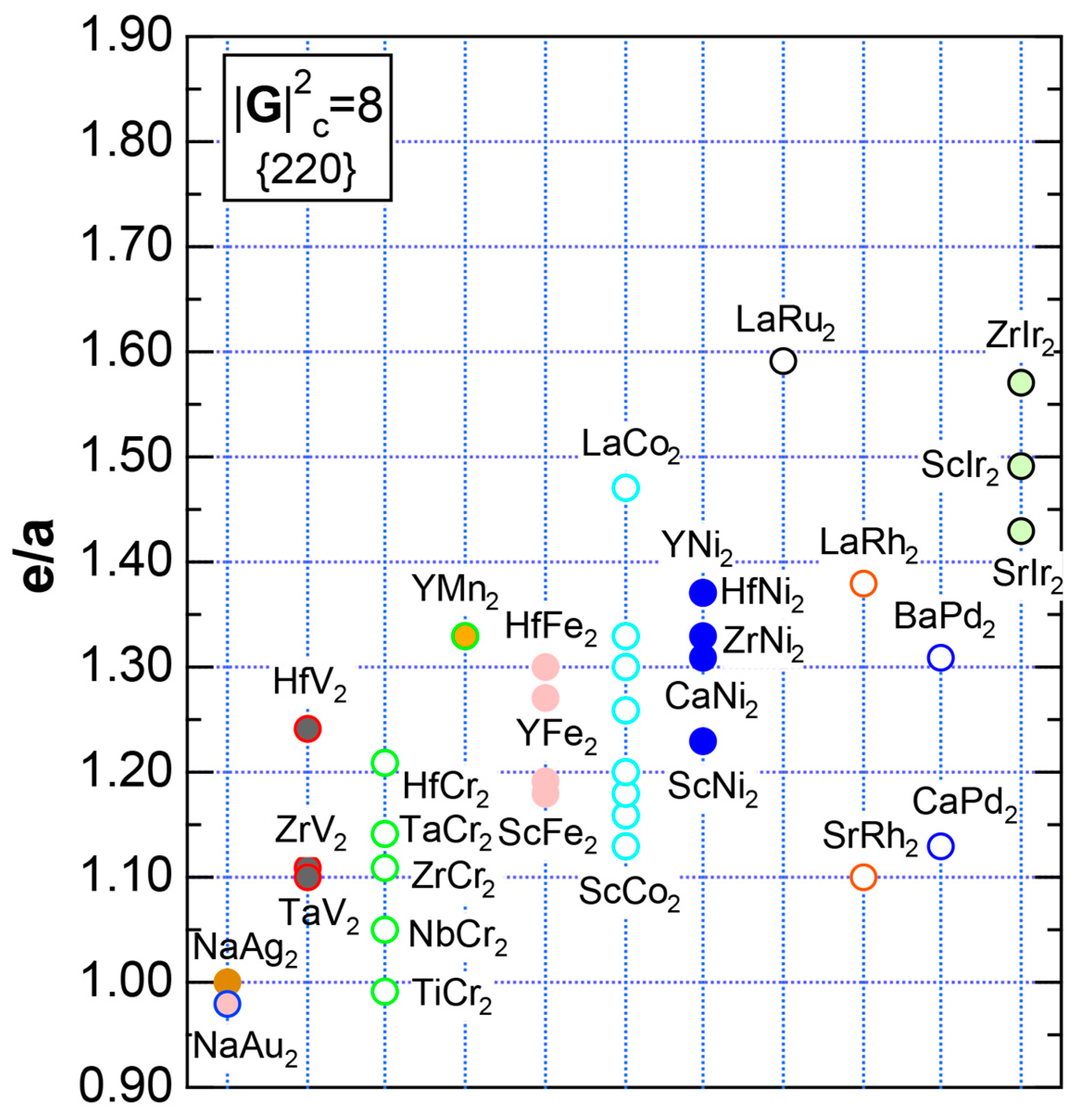
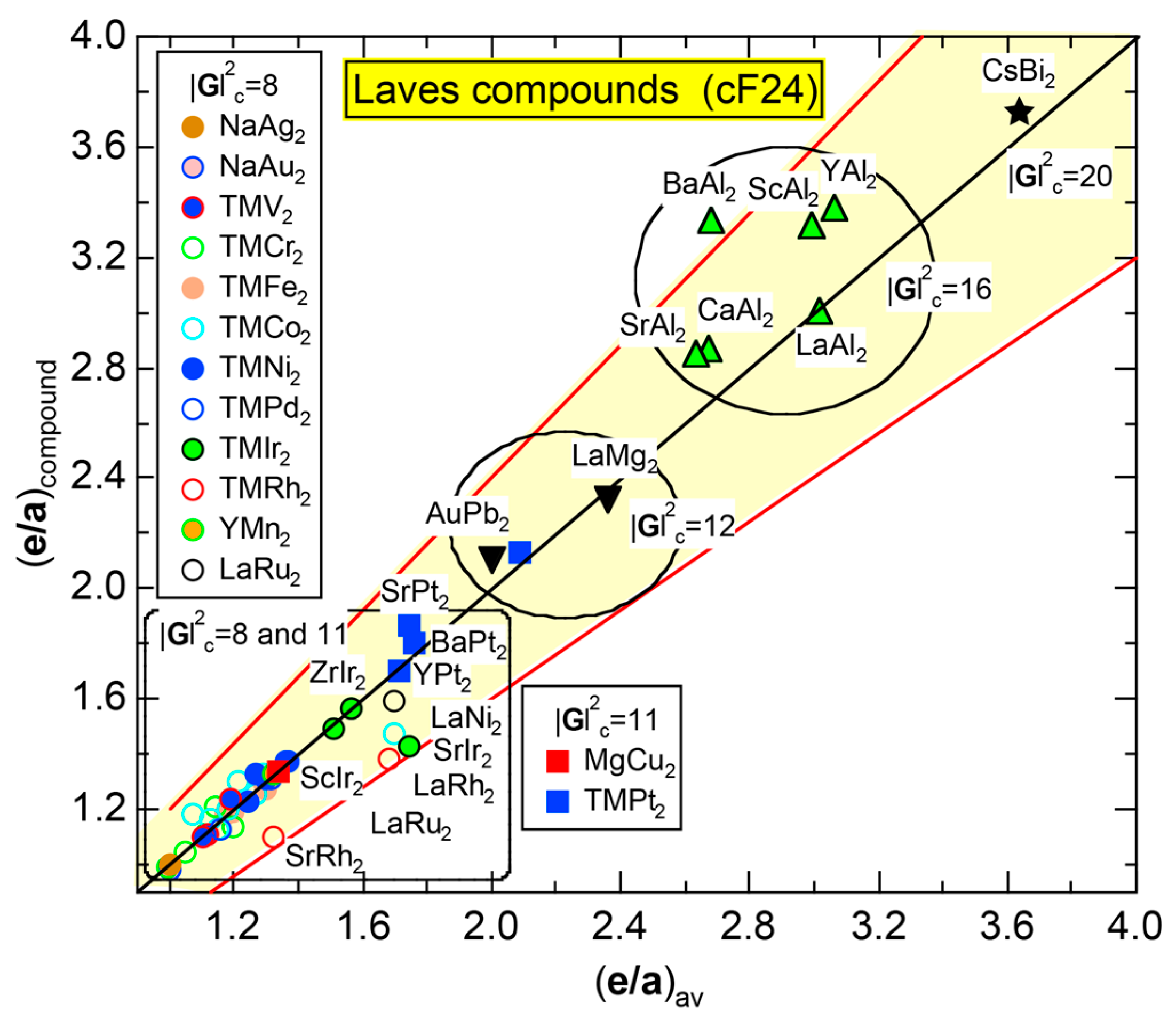
7.4. Hume-Rothery Electron Concentration Rule in Laves Compounds (cF24)
7.5. Stabilization Mechanism of Laves Compounds
8. The FLAPW-Fourier Theory to Develop New Functional Materials
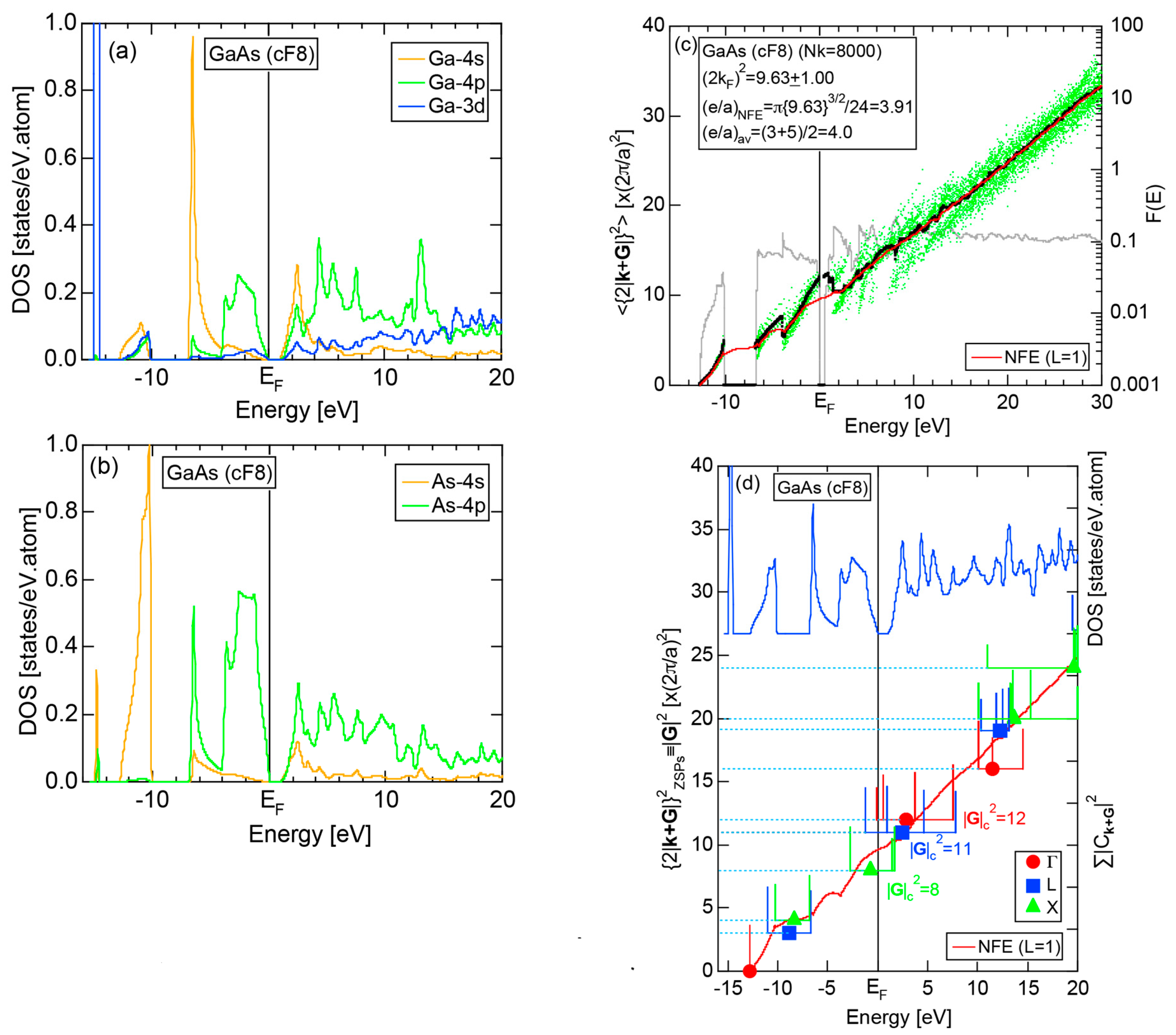
8.1. III-V Compounds
8.2. Development of New Electronic Functional Materials with e/a = 4
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Hume-Rothery, W. Researches on the nature, properties, and conditions of formation of intermetallic compounds, with special reference to certain compounds of tin-I-V. J. Inst. Met. 1926, 35, 295–361. [Google Scholar]
- Westgren, A.; Phragmén, G. Gesetzmäßigkeiten im Aufbau der Legierungen. Metallwirtschaft 1928, 7, 700–703. [Google Scholar]
- Mott, N.F.; Jones, H. The Theory of the Properties of Metals and Alloys; Clarendon Press: Oxford, UK, 1936; Dover Publications Inc.: New York, NY, USA, 1958.
- Tsai, A.P.; Inoue, A.; Masumoto, T. New stable icosahedral Al-Cu-Ru and Al-Cu-Os alloys. Jpn. J. Appl. Phys. 1988, 27, L1587–L1590. [Google Scholar] [CrossRef]
- Tsai, A.P.; Inoue, A.; Yokoyama, Y.; Masumoto, T. Stable icosahedral Al-Pd-Mn and Al-Pd-Re alloys. Mater. Trans. Jpn. Inst. Met. 1990, 31, 98–103. [Google Scholar]
- Yokoyama, Y.; Tsai, A.P.; Inoue, A.; Masumoto, T.; Chen, H.S. Formation criteria and growth morphology of quasicrystals in Al-Pd-TM (TM = Transition Metal) alloys. Mater. Trans. Jpn. Inst. Met. 1991, 32, 421–428. [Google Scholar] [CrossRef]
- Tsai, A.P. A test of Hume-Rothery rules for stable quasicrystals. J. Non-Cryst. Solids 2004, 334–335, 317–322. [Google Scholar] [CrossRef]
- Raynor, G.V. Progress in the theory of alloys. Prog. Met. 1949, 1, 1–76. [Google Scholar] [CrossRef]
- Zijlstra, E.S.; Bose, S.K.; Klanjšek, M.; Jeglič, P.; Dolinšek, J. Ab initio study of the Quandt-Elser model of icosahedral Al-Pd-Mn quasicrystals: Improved structural model, electric field gradients, apparent negative number of valence electrons of Mn. Phys. Rev. B 2005, 72, 174206. [Google Scholar] [CrossRef]
- Pauling, L. The nature of the interatomic forces in metals. Phys. Rev. 1938, 54, 899–904. [Google Scholar] [CrossRef]
- Mizutani, U.; Sato, H. The Physics of the Hume-Rothery Electron Concentration Rule; Uchida Rokakuho: Tokyo, Japan, 2015; pp. 1–231. (In Japanese) [Google Scholar]
- Mizutani, U.; Sato, H.; Inukai, M.; Nishino, Y.; Zijlstra, E.S. Electrons per atom ratio determination and Hume-Rothery electron concentration rule for P-based polar compounds studied by FLAPW-Fourier calculations. Inorg. Chem. 2015, 54, 930–946. [Google Scholar] [CrossRef] [PubMed]
- Mizutani, U.; Inukai, M.; Sato, H.; Zijlstra, E.S.; Lin, Q. e/a classification of Hume-Rothery Rhombic Triacontahedron-type approximants based on all-electron density functional theory calculations. Philos. Mag. 2014, 94, 2571–2594. [Google Scholar] [CrossRef]
- Mizutani, U.; Inukai, M.; Sato, M.; Zijlstra, E.S. Electron Theory of Complex Metallic Alloys. In Physical Metallurgy; Laughlin, D.E., Hono, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 103–202. [Google Scholar]
- Sato, H.; Inukai, M.; Zijlstra, E.S.; Mizutani, U. NFE approximation for the e/a determination for 3d-transition metal elements and their intermetallic compounds with Al and Zn. Philos. Mag. 2013, 93, 3029–3061. [Google Scholar] [CrossRef]
- Mizutani, U.; Sato, H.; Inukai, M.; Zijlstra, E.S. e/a determination for 4d- and 5d-transition metal elements and their intermetallic compounds with Mg, Al, Zn, Cd and In. Philos. Mag. 2013, 93, 3353–3390. [Google Scholar] [CrossRef]
- Mizutani, U.; Inukai, M.; Sato, H.; Zijlstra, E.S. Hume-Rothery stabilization mechanism and e/a determination for RT- and MI-type 1/1-1/1-1/1 approximants studied by FLAPW-Fourier analysis. Chem. Soc. Rev. 2012, 41, 6799–6820. [Google Scholar] [CrossRef] [PubMed]
- Mizutani, U.; Inukai, M.; Sato, H.; Zijlstra, E.S. Hume-Rothery stabilization mechanism and e/a determination in MI-type Al-Mn, Al-Re, Al-Re-Si, Al-Cu-Fe-Si and Al-Cu-Ru-Si 1/1-1/1-1/1 approximants—A proposal for a new Hume-Rothery electron concentration rule. Philos. Mag. 2012, 92, 1691–1715. [Google Scholar] [CrossRef]
- Mizutani, U. Hume-Rothery Rules for Structurally Complex Alloy Phases; CRC Press and Taylor & Francis: Boca Raton, FL, USA, 2011; pp. 1–342. [Google Scholar]
- Inukai, M.; Zijlstra, E.S.; Sato, H.; Mizutani, U. Origin of the DOS pseudogap and Hume-Rothery stabilization mechanism in RT-type Al48Mg64Zn48 and Al84Li52Cu24 1/1-1/1-1/1 approximants. Philos. Mag. 2011, 91, 4247–4263. [Google Scholar] [CrossRef]
- Ishimasa, T. Hume-Rothery rule as a formation condition of new icosahedral quasicrystals. In The Science of Complex Alloy Phases; Massalski, T.B., Turchi, P.E.A., Eds.; The Minerals, Metals & Materials Society: Pittsburgh, PA, USA, 2005; pp. 231–249. [Google Scholar]
- Kirihara, K.; Kimura, K. Composition dependence of thermoelectric properties of AlPdRe icosahedral quasicrystals. J. Appl. Phys. 2002, 92, 979–986. [Google Scholar] [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1954. [Google Scholar] [CrossRef]
- Dubois, J.M. Useful Quasicrystals; World Scientific: Singapore, 2005. [Google Scholar]
- Fujiwara, T. Electronic structure in the Al-Mn alloy crystalline analog of quasicrystals. Phys. Rev. B 1989, 40, 942–946. [Google Scholar] [CrossRef]
- Skriver, H.L. The LMTO Method; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1984. [Google Scholar]
- Blaha, P.; Schwarz, K.; Madsen, G.; Kvasnicka, D.; Luitz, J. WIEN2k. Available online: http://www.wien2k.at/ (accessed on 25 September 2016).
- Asahi, R.; Sato, H.; Takeuchi, T.; Mizutani, U. Verification of Hume-Rothery electron concentration rule in Cu5Zn8 and Cu9Al4γ brasses by ab initio FLAPW band calculations. Phys. Rev. B 2005, 71, 165103. [Google Scholar] [CrossRef]
- Villars, P. Pearson’s Handbook; ASM International: Materials Park, OH, USA, 1997. [Google Scholar]
- NIMS Materials Database “MatNavi”. Available online: http://mits.nims.go.jp/index_en.html (accessed on 25 September 2016).
- Luo, H.; Greene, R.G.; Ruoff, A.L. β-Po phase of sulfur at 162 GPa: X-ray diffraction study to 212 GPa. Phys. Rev. Lett. 1993, 71, 2943–2946. [Google Scholar] [CrossRef] [PubMed]
- Fujii, Y.; Hase, K.; Ohishi, Y.; Fujihisa, H.; Hamaya, N.; Takemura, K.; Shimomura, O.; Kikegawa, T.; Amemiya, Y.; Matsushita, T. Evidence for molecular dissociation in Bromine near 80 GPa. Phys. Rev. Lett. 1989, 63, 536–539. [Google Scholar] [CrossRef] [PubMed]
- Fujihisa, H. Structural Study of Pressure-Induced Molecular Dissociation in Solid Halogens. Ph.D. Thesis, University of Tsukuba, Tsukuba, Japan, 1993. Available online: http://dl.ndl.go.jp/info:ndljp/pid/3102873 (accessed on 25 September 2016). [Google Scholar]
- Van Arkel, A.E. Molecules and Crystals in Inorganic Chemistry; Interscience: New York, NY, USA, 1956. [Google Scholar]
- Ketelaar, J.A.A. Chemical Constitution, an Introduction to the Theory of the Chemical Bonds, 2nd ed.; Elsevier: New York, NY, USA, 1958. [Google Scholar]
- Allen, L.C.; Capitani, J.F.; Kolks, G.A.; Sproul, G.D. Van Arkel-Ketelaar triangles. J. Mol. Struct. 1993, 300, 647–655. [Google Scholar] [CrossRef]
- Mizutani, U.; Sato, H. Detrmination of electrons per atom ratio for transition metal compounds studied by FLAPW-Fourier calculations. Philos. Mag. 2016, 96, 3075–3096. [Google Scholar] [CrossRef]
- Allen, L.C. Electronegativity is the average one-electron energy of the valence-shell electrons in ground-state free atoms. J. Am. Chem. Soc. 1989, 111, 9003–9014. [Google Scholar] [CrossRef]
- Electronegativity. Wikipedia. Available online: http://en.wikipedia.org/wiki/Electronegativity (accessed on 25 September 2016).
- Sansonetti, J.E.; Martin, W.C. Handbook of Basic Atomic Spectroscopic Data; American Institute of Physics: College Park, MD, USA, 2005; Volume 34, No. 4; pp. 1559–2259. [Google Scholar]
- Mizutani, U.; Sato, H.; Inukai, M.; Zijlstra, E.S. Theoretical foundation for the Hume-Rothery electron concentration rule for structurally complex alloys. Acta Phys. Pol. A 2014, 126, 531–534. [Google Scholar] [CrossRef]
- Brandon, J.K.; Pearson, W.B.; Riley, P.W.; Chieh, C.; Stokhuyzen, R. γ-brasses with R cells. Acta Cryst. B 1977, 33, 1088–1095. [Google Scholar] [CrossRef]
- Hume-Rothery, W. Atomic Theory for Students of Metallurgy; Institute of Metals, Monograph and Report Series No. 3; The Institute of Metals: London, UK, 1962; p. 306. [Google Scholar]
- Gomez, C.P.; Lidin, S. Comparative structural study of the disordered MCd6 quasicrystal approximants. Phys. Rev. B 2003, 68, 024203. [Google Scholar] [CrossRef]
- Mizutani, U.; Inukai, M.; Sato, H.; Nozawa, K.; Zijlstra, E.S. Hume-Rothery Stabilization Mechanism in Tsai-Type Cd6Ca Approximant and e/a Determination of Ca and Cd Elements in the Periodic Table. In Aperiodic Crystals; Schmid, S., Withers, R.L., Lifshitz, R., Eds.; Springer: Heidelberg, Germany, 2013; Chapter 14; pp. 101–107. [Google Scholar]
- Nozawa, K.; Ishii, Y. First-principles studies for structural transitions in ordered phase of cubic approximant Cd6Ca. J. Phys. Condens. Matter 2008, 20, 315206. [Google Scholar] [CrossRef]
- Tamura, R.; Murao, Y.; Takeuchi, S.; Kiss, T.; Yokoya, T.; Shin, S. Comparative study of the binary icosahedral quasicrystal Cd5.7Yb and its crystalline approximant Cd6Yb by low-temperature ultrahigh-resolution photoemission spectroscopy. Phys. Rev. B 2002, 65, 224207. [Google Scholar] [CrossRef]
- Palenzona, A. The ytterbium-cadmium system. J. Less Common Met. 1971, 25, 367–372. [Google Scholar] [CrossRef]
- Ishimasa, T.; Kasano, Y.; Tachibana, A.; Kashimoto, S.; Osaka, K. Low-temperature phase of the Zn-Sc approximant. Philos. Mag. 2007, 87, 2887–2897. [Google Scholar] [CrossRef]
- Mizutani, U.; Inukai, M.; Sato, H.; Zijlstra, E.S. Hume-Rothery stabilization mechanism in low-temperature phase Zn6Sc approximant and e/a determination of Sc and Y in M-Sc and M-Y (M = Zn, Cd and Al) alloy systems. In Aperiodic Crystals; Schmid, S., Withers, R.L., Lifshitz, R., Eds.; Springer: New York, NY, USA, 2013; Chapter 15. [Google Scholar]
- Okamoto, H. Phase Diagrams for Binary Alloys; ASM International: Materials Park, OH, USA, 2000. [Google Scholar]
- Samson, S. The crystal structure of the phase β Mg2Al3. Acta Crystallogr. 1965, 19, 401–413. [Google Scholar] [CrossRef]
- Feuerbacher, M.; Thomas, C.; Makongo, J.P.A.; Hoffmann, S.; Carrillo-Cabrera, W.; Cardoso, R.; Grin, Y.; Kreiner, G.; Joubert, J.; Schenk, T.; et al. The Samson phase, β-Mg2Al3. Zeitschrift für Kristallographie 2007, 222, 259–288. [Google Scholar]
- Mizutani, U.; Kondo, Y.; Nishino, Y.; Inukai, M.; Feuerbacher, M.; Sato, H. Fermi surface-Brillouin zone-induced pseudogap in γ-Mg17Al12 and a possible stabilization mechanism of β-Al3Mg2. J. Phys. Condens. Matter 2010, 22, 485501. [Google Scholar] [CrossRef] [PubMed]
- Sevov, S.C. Zintl Phases. In Intermetalllic Compounds, Principles and Practice: Progress; Westbrook, J.H., Fleisher, R.L., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2002; Volume 3, pp. 113–132. [Google Scholar]
- Nesper, R. Structure and chemical bonding in Zintl-phases containing Lithium. Prog. Solid State Chem. 1990, 20, 1–45. [Google Scholar] [CrossRef]
- Stein, F.; Palm, M.; Sauthoff, G. Structure and stability of Laves phases. Part I. Critical assessment of factors controlling Laves phase stability. Intermetallics 2004, 12, 713–720. [Google Scholar] [CrossRef]
- Akasaki, I.; Amano, H. Breakthroughs in improving crystal quality of GaN and invention of the p-n junction blue-light-emitting diode. Jpn. J. Appl. Phys. 2006, 45, 9001–9010. [Google Scholar] [CrossRef]
- Nakamura, S.; Senoh, M.; Nagahama, S.; Iwasa, N.; Yamada, T.; Matushita, T.; Sugimoto, Y.; Kiyoku, H. Ridge-geometry InGaN multi-quantum-well-structure laser diodes. Appl. Phys. Lett. 1996, 69, 1477–1479. [Google Scholar] [CrossRef]
- Mizutani, U. Introduction to the Electron Theory of Metals; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]







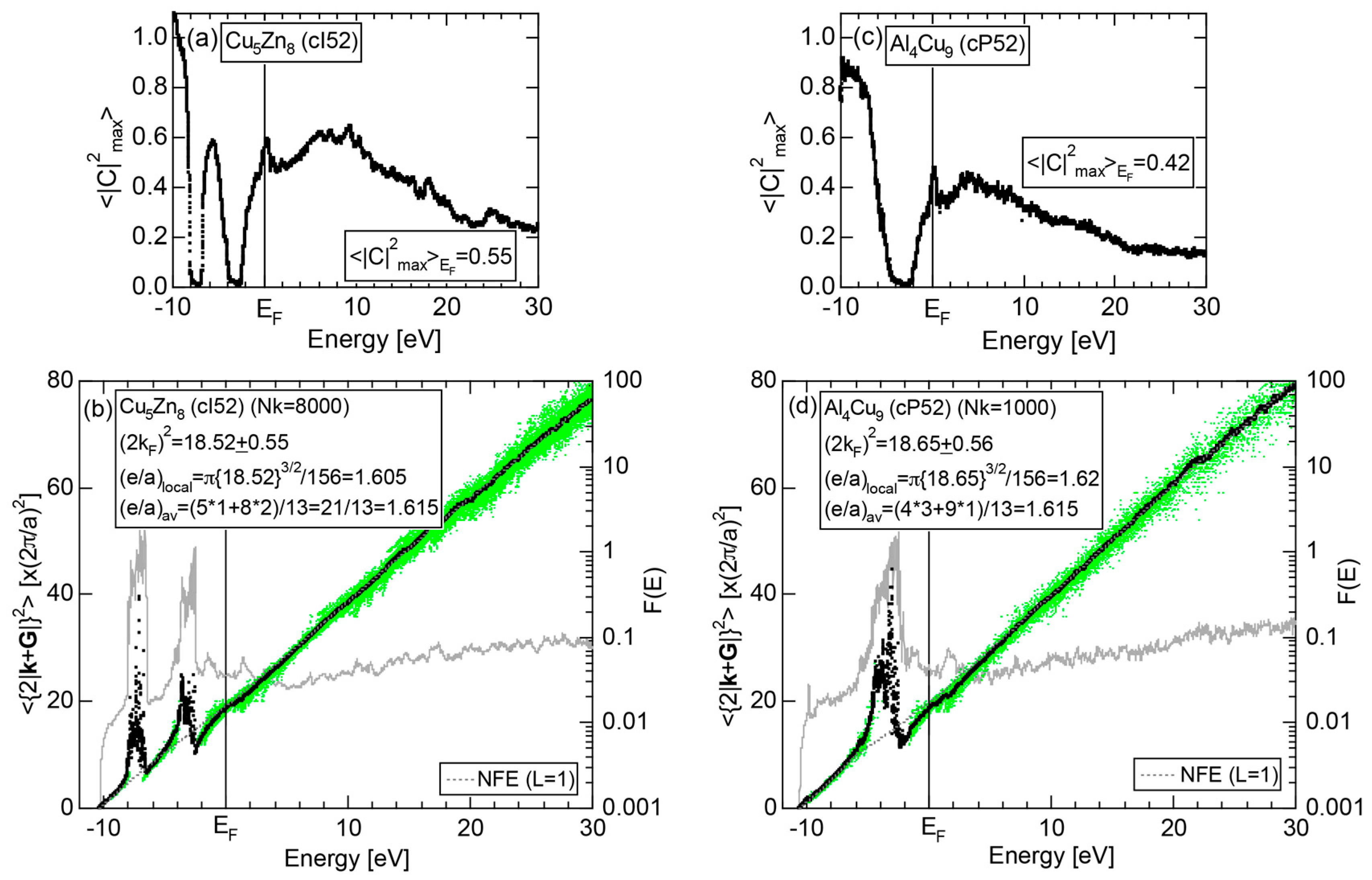
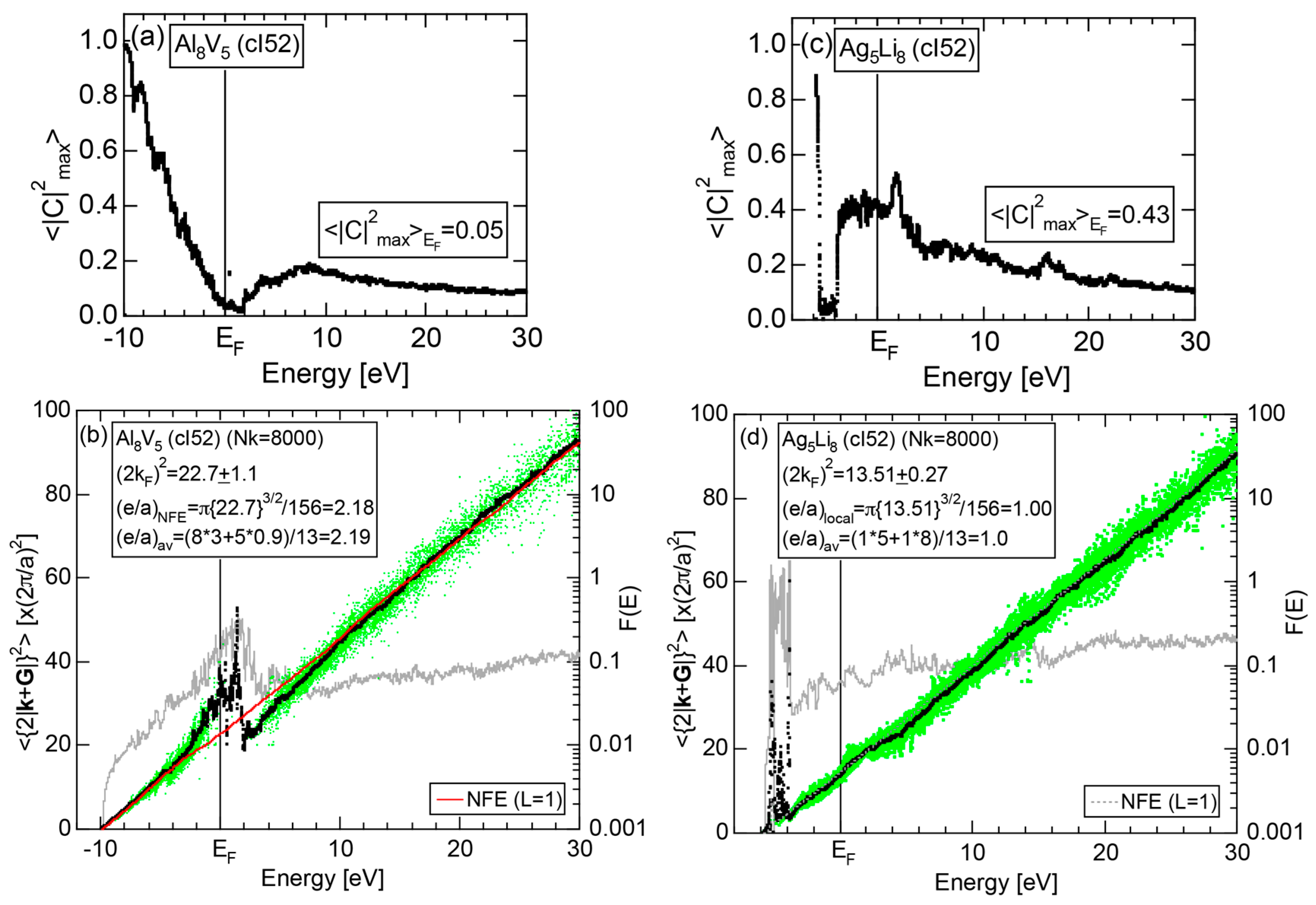

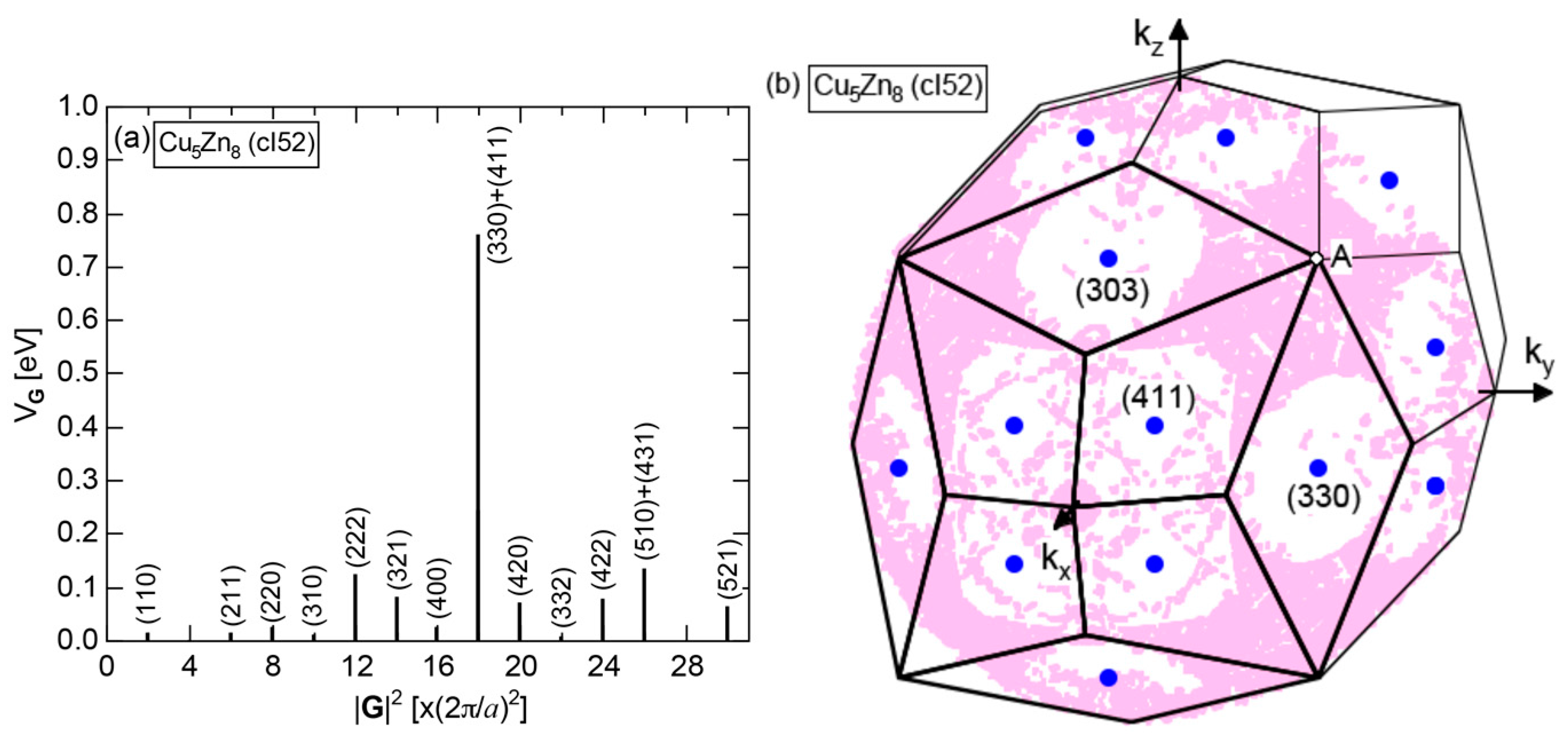
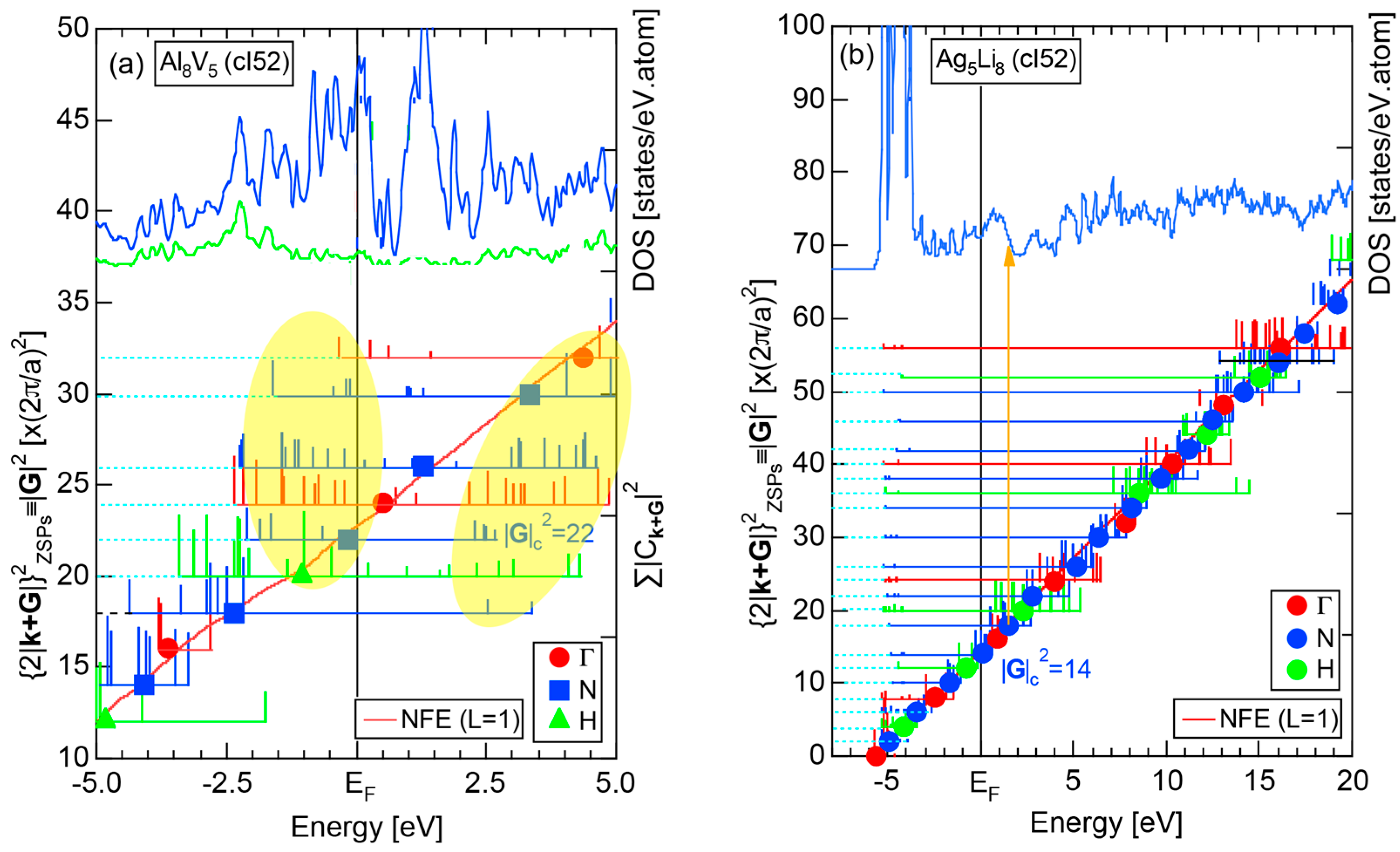


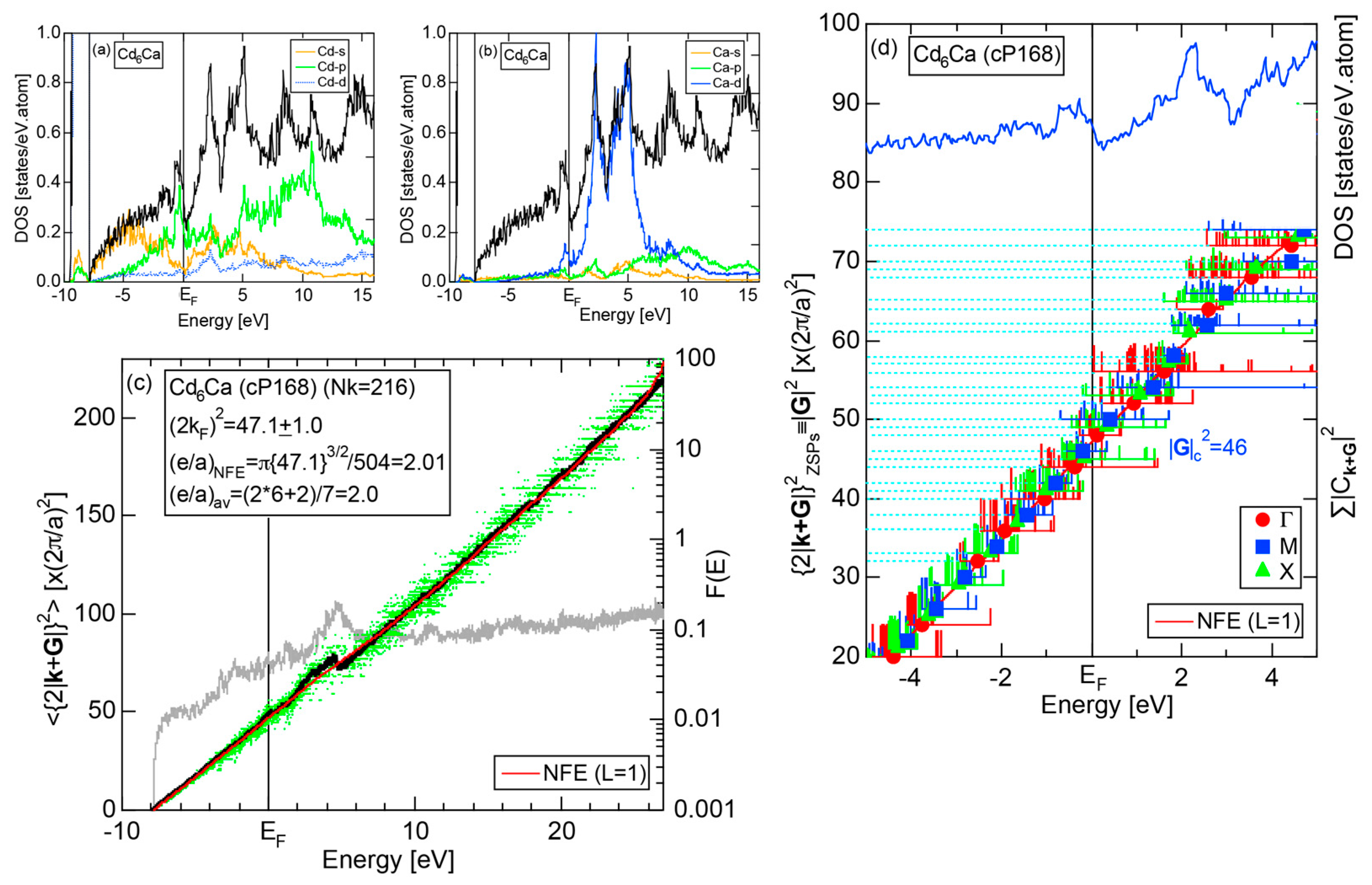
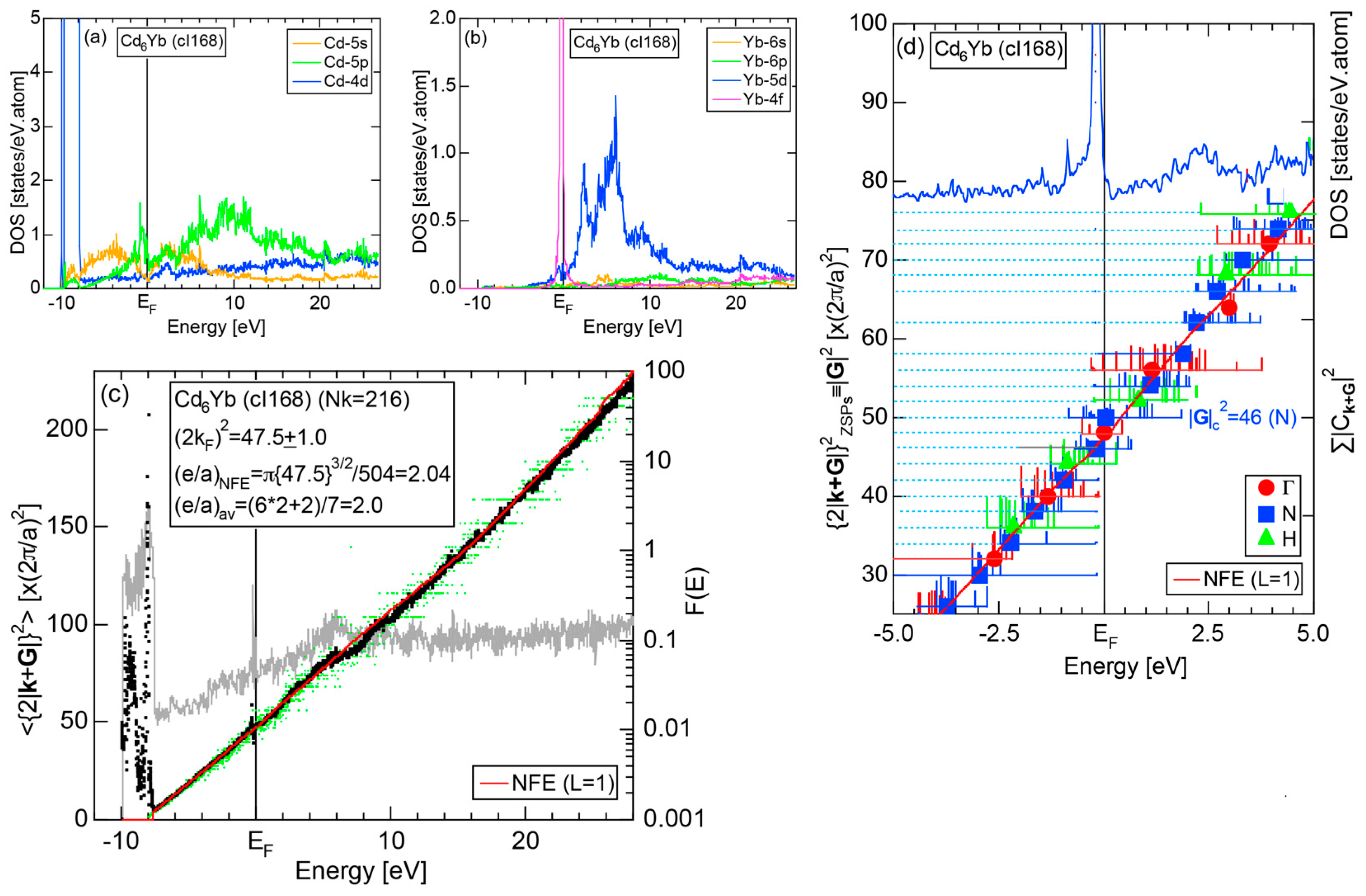
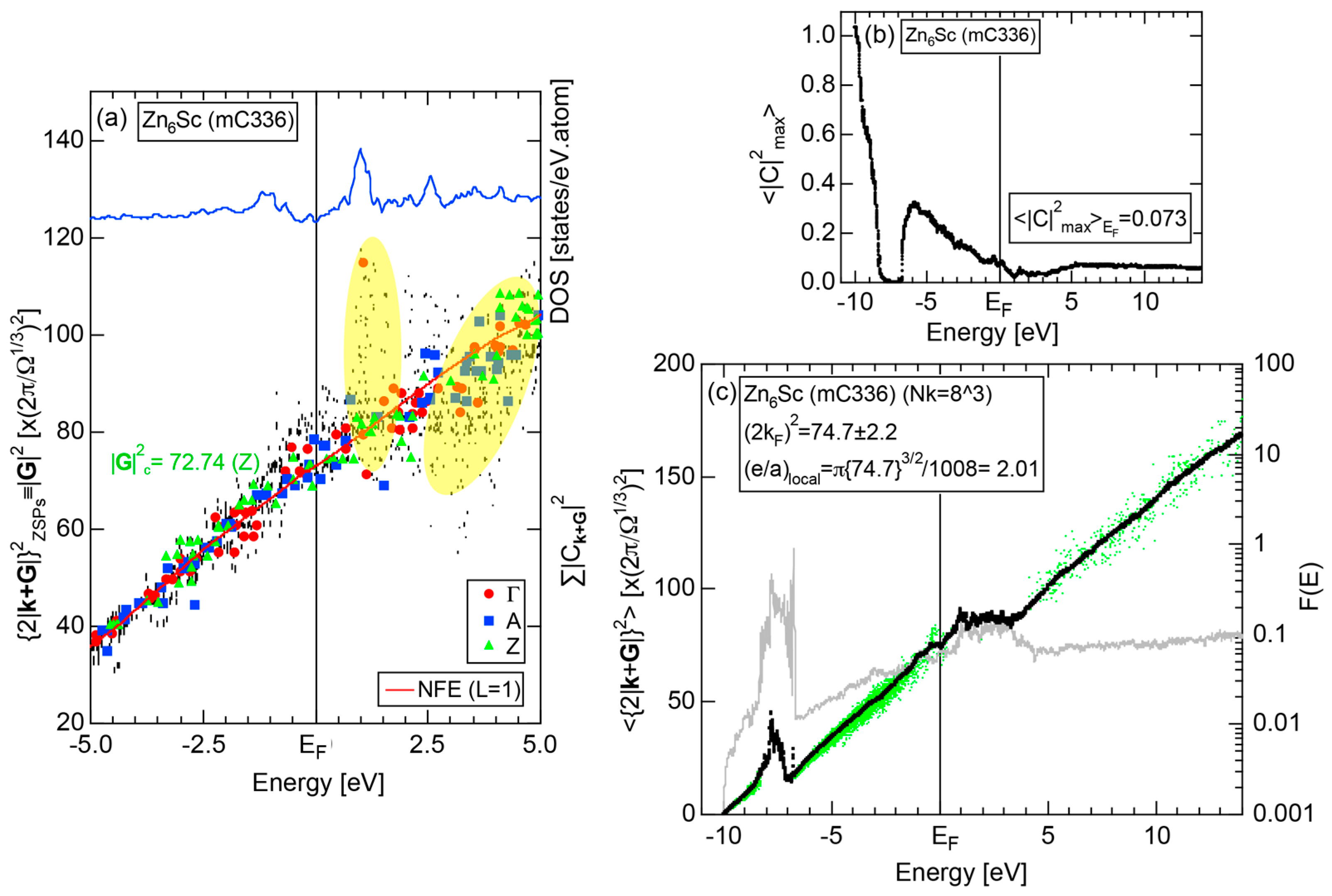













| Subgroup | System | N | (2kF)2 | e/a | e/uc | |G|2c | |
|---|---|---|---|---|---|---|---|
| × (2π/a)2 | × (2π/a)2 | ||||||
| gamma-brasses | 1 | Cu5Zn8 (cI52) | 52 | 18.5 ± 0.1 | 1.60 ± 0.02 | 83 | 18 |
| Ag5Zn8 (cI52) | 52 | 18.5 ± 0.1 | |||||
| Al4Cu9 (cP52) | 52 | 18.5 ± 0.1 | |||||
| In4Ag9 (cP52) | 52 | 18.5 ± 0.1 | |||||
| 2 | Al8V5 (cI52) | 52 | 22.7 ± 1.1 | 2.1 ± 0.1 | 109 | 22 | |
| Al8Cr5 (cI52) | 52 | 22.1 ± 1.1 | |||||
| 3 | Ag5Li8 (cI52) | 52 | 13.51 ± 0.27 | 1.00 ± 0.02 | 52 | 14 |
| Subgroup | Approximants | Space Group | N | |G|2c × (2π/a)2 | a Å | 2d Å | (2kF)2 × (2π/a)2 | e/a | e/uc | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1/1 | 1 | Al3Mg4Zn3 | Im-3 | 160 | 50 | 14.355 | 4.06 | 49.8 | 2.30 | 368 |
| Al9Mg8Ag3 | Im-3 | 160 | 50 | 14.4799 | 4.09 | 49.4 | 2.27 | 363 | ||
| 2 | Al21Li13Cu6 | Im-3 | 160 | 46 | 13.89 | 4.09 | 47.1 | 2.10 | 336 | |
| Ga21Li13Cu6 | Im-3 | 160 | 46 | 13.568 | 4.00 | 47.6 | 2.15 | 344 | ||
| 3 | Na26Au24Ga30 | Im-3 | 160 | 42 | 14.512 | 4.48 | 41.8 | 1.77 | 283 | |
| Na26Au37Ge18 | Im-3 | 162 | 42 | 14.581 | 4.50 | 41.4 | 1.72 | 278 | ||
| Na26Au37Sn18 | Im-3 | 162 | 42 | 15.009 | 4.63 | 41.1 | 1.70 | 275 | ||
| Na26Cd40Pb6 | Im-3 | 160 | 42 | 15.992 | 4.94 | 42.3 | 1.80 | 288 | ||
| 2/1 | 1 | Al13Mg27Zn45 | Pa-3 | 680 | 126 | 23.0349 | 4.10 | 124.0 | 2.13 | 1448 |
| 2 | Na27Au27Ga31 | Pa-3 | 680 | 110 | 23.446 | 4.47 | 109.2 | 1.76 | 1197 |
| Subgroup | Approximants | Space Group | N | |G|2c × (2π/a)2 | a Å | 2d Å | (2kF)2 × (2π/a)2 | e/a | e/uc | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1/1 | 1 | Al114Mn24 | Pm-3 | 138 | 50 | 12.68 | 3.59 | 48.9 | 2.59 | 357 |
| Al114Re24 | Pm-3 | 138 | 50 | 12.86 | 3.64 | 48.6 | 2.57 | 355 | ||
| Al102Re24Si12 | Pm-3 | 138 | 50 | 12.8603 | 3.64 | 51.0 | 2.76 | 381 | ||
| Al108Cu6Fe24Si6 | Pm-3 | 144 | 50 | 12.48 | 3.53 | 50.0 | 2.57 | 370 | ||
| Al108Cu6Ru24Si6 | Pm-3 | 144 | 50 | 12.6832 | 3.59 | 51.7 | 2.70 | 389 |
| Subgroup | Approximants | Space Group | N | |G|2c × (2π/a)2 | a Å | 2d Å | (2kF)2 × (2π/a)2 | e/a | e/uc | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1/1 | 1 | Zn6Sc | C2/c | 336 | 80 | a = 19.47 b = 13.79 c = 19.55 β = 89.931o | 79.0 ± 0.2 | 2.18 | 732 | |
| Cd6Ca | Pm-3 | 168 | 46 | 15.702 | 4.63 | 47.1 ± 1.0 | 2.01 | 338 | ||
| Cd6Yb | Im-3 | 168 | 46 | 15.638 | 4.61 | 47.5 ± 1.0 | 2.04 | 343 |
| Type | Compounds | Lattice Constant Å | N | |G|2c × (2π/a)2 | (2kF)2 × (2π/a)2 | e/a | e/uc |
|---|---|---|---|---|---|---|---|
| I-III cF32 Fd-3m | LiAl | 6.3757 | 32 | 16 | 16.29 ± 0.20 | 2.09 ± 0.06 | 67 |
| LiGa | 6.150 | 32 | 16 | 15.97 ± 0.20 | |||
| LiIn | 6.7920 | 32 | 16 | 15.75 ± 0.20 | |||
| NaIn | 7.332 | 32 | 16 | 15.99 ± 0.20 | |||
| NaTl | 7.473 | 32 | 16 | 16.12 ± 0.20 | |||
| I-II cF32 Fd-3m | LiZn | 6.209 | 32 | 12 | 13.00 ± 0.20 | 1.53 ± 0.02 | 49 |
| LiCd | 6.702 | 32 | 12 | 13.03 ± 0.20 |
| System | Space Group | Pearson Symbol | |G|2c × (2π/a)2 | (2kF)2 × (2π/a)2 | e/a | e/uc |
|---|---|---|---|---|---|---|
| P | Cmca | oC8 | 10.56 | 11.30 ± 0.33 | 4.97 | 40 |
| As | R-3m | hR2 | 4.74 | 4.45 ± 0.22 | 4.92 | 10 |
| Sb | R-3m | hR2 | 4.54 | 4.49 ± 0.22 | 4.99 | 10 |
| Bi | R-3m | hR2 | 4.53 | 4.46 ± 0.22 | 4.94 | 10 |
| Family | Subgroup | System | N | |G|2c × [2π/(Ωuc)1/3]2 | (2kF)2 × (2π/a)2 | e/a | e/uc |
|---|---|---|---|---|---|---|---|
| skutterudites (TM)M3 (TM = Co, Rh, Ir, Ni) (M = P, As, Sb) | 1 | CoAs3 (cI32) | 32 | 26 | 25.2 ± 0.2 | 4.34 ± 0.20 | 139 |
| RhAs3 (cI32) | 32 | 26 | 26.3 ± 0.2 | ||||
| IrAs3 (cI32) | 32 | 26 | 26.7 ± 0.2 | ||||
| CoSb3 (cI32) | 32 | 26 | 26.5 ± 0.2 | ||||
| RhSb3 (cI32) | 32 | 26 | 27.3 ± 0.2 | ||||
| IrSb3 (cI32) | 32 | 26 | 27.8 ± 0.2 | ||||
| NiP3 (cI32) | 32 | 26 | 25.1 ± 0.2 | ||||
| CoP3 (cI32) | 32 | 26 | 25.0 ± 0.2 | ||||
| RhP3 (cI32) | 32 | 26 | 25.9 ± 0.2 | ||||
| IrP3 (cI32) | 32 | 26 | 26.7 ± 0.2 | ||||
| (TM)P (TM = Cr, Mn, Fe, Co) | 1 | CrP (oP8) | 8 | 8.38 | 8.53 ± 0.43 | 3.25 ± 0.05 | 26 |
| MnP (oP8) | 8 | 8.49 | 8.47 ± 0.42 | ||||
| FeP (oP8) | 8 | 8.56 | 8.41 ± 0.42 | ||||
| CoP (oP8) | 8 | 8.29 | 8.60 ± 0.83 | ||||
| (TM)3P (TM = Cr, Mn, Fe, Ni) | 1 | Cr3P (tI32) | 32 | 16.3 | 16.67 ± 0.83 | 2.20 ± 0.05 | 70 |
| Mn3P (tI32) | 32 | 16.4 | 16.67 ± 0.83 | ||||
| Fe3P (tI32) | 32 | 16.2 | 16.47 ± 0.83 | ||||
| Ni3P (tI32) | 32 | 16.2 | 16.56 ± 0.33 |
| Compounds | Pearson Symbol | Energy Gap (eV) | (2kF)2 × (2π/a)2 | e/a | (e/a)av |
|---|---|---|---|---|---|
| SiP | oC48 | 1.2 | 35.2 | 4.55 | 4.56 |
| GeP | tI4 | pseudogap | 6.66 | 4.50 | 4.56 |
| ScP | cF8 | pseudogap | 10.02 | 4.15 | 4.03 |
| TiP2 | oP12 | pseudogap | 13.19 | 4.18 | 3.72 |
| VP2 | mC12 | pseudogap | 13.16 | 4.17 | 3.75 |
| CrP2 | mC12 | pseudogap | 12.55 | 3.88 | 3.72 |
| MnP4 | aP10 | 0.4 | 12.25 | 4.49 | 4.31 |
| CoP3 | cI32 | pseudogap | 26.24 | 4.2 | 4.12 |
| NiP3 | cI32 | pseudogap | 26.17 | 4.2 | 4.13 |
| CuP2 | mP12 | 0.84 | 12.59 | 3.9 | 3.75 |
| Cu2P7 | mC72 | 0.61 | 46.15 | 4.56 | 4.20 |
| Compounds | Pearson Symbol | Energy Gap (eV) | (2kF)2 × (2π/a)2 | e/a | (e/a)av |
|---|---|---|---|---|---|
| ZnP2 | mP24 | pseudogap | 21.47 | 4.34 | 4.0 |
| ZnP2 | tP24 | 1.63 | 19.28 | 3.69 | 4.0 |
| ZnP4 | tP20 | 0.63 | 18.7 | 4.24 | 4.4 |
| Mg3P2 | cI80 | 1.6 | 32.68 | 2.45 | 3.2 |
| MgP4 | mP10 | 0.50 | 11.65 | 4.16 | 4.4 |
| Ca5P8 | mC26 | 1.13 | 20.79 | 3.82 | 3.85 |
| CaP3 | aP8 | pseudogap | 10.7 | 4.58 | 4.25 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizutani, U.; Sato, H. The Physics of the Hume-Rothery Electron Concentration Rule. Crystals 2017, 7, 9. https://doi.org/10.3390/cryst7010009
Mizutani U, Sato H. The Physics of the Hume-Rothery Electron Concentration Rule. Crystals. 2017; 7(1):9. https://doi.org/10.3390/cryst7010009
Chicago/Turabian StyleMizutani, Uichiro, and Hirokazu Sato. 2017. "The Physics of the Hume-Rothery Electron Concentration Rule" Crystals 7, no. 1: 9. https://doi.org/10.3390/cryst7010009