Evolution in Time of Radiation Defects Induced by Negative Pions and Muons in Crystals with a Diamond Structure

Abstract

Evolution in time of radiation defects induced by negatively-charged pions and muons in crystals with diamond structures is considered. Negative pions and muons are captured by the nucleus and ionize an appropriate host atom, forming a positively-charged radiation defect in a lattice. As a result of an evolution in time, this radiation defect transforms into the acceptor center. An analysis of the full evolution process is considered for the first time. Formation of this acceptor center can be divided into three stages. At the first stage, the radiation defect interacts with a radiation trace and captures electrons. The radiation defect is neutralized completely in Si and Ge for a short time t $\le {10}^{-11}$ s, but in diamond, the complete neutralization time is very large t $\ge {10}^{-6}$ s. At the second stage, broken chemical bonds of the radiation defect are restored. In Si and Ge, this process takes place for the neutral radiation defect, but in diamond, it goes for a positively-charged state. The characteristic time of this stage is $t<{10}^{-8}$ s for Si and Ge and $t<{10}^{-11}$ s for diamond. After the chemical bonds’ restoration, the positively-charged, but chemically-bound radiation defect in diamond is quickly neutralized because of the electron density redistribution. The neutralization process is characterized by the lattice relaxation time. At the third stage, a neutral chemically-bound radiation defect captures an additional electron to saturate all chemical bonds and forms an ionized acceptor center. The existence of a sufficiently big electric dipolar moment leads to the electron capture. Qualitative estimates for the time of this process were obtained for diamond, silicon and germanium crystals. It was sown that this time is the shortest for diamond (≤${10}^{-8}$ s) and the longest for silicon (≤${10}^{-7}$ s)

1. Introduction

Radiation defects in diamond and silicon are examined actively because these semiconductors are widely used as detectors and some other devices in high energy physics. The main problem of these investigations is connected with their radiation hardness (see e.g., some recent works [1,2,3,4,5,6]). Radiation defects induced by protons, neutrons and heavier particles with kinetic energies $E\ge 100$ MeV are studied in most works. After slowing down to kinetic energies E less than ionization energies of host atoms in crystals, these impinging particles stop in the lattice, damaging it. If the recoil energy is higher than the lattice binding energy, a host atom will be displaced from its site. Numerical modeling of these processes is carried out, e.g., in [3,5]. In [7], many types of these radiation defects in diamond are well described. The second problem is implantation of ions in crystals for preparing necessary impurity atoms. Ion implantation is a commonly-used method for modifying properties of materials in the field of microelectronics. The application for diamond is represented, e.g., in [8].

For a number of reasons, radiation defects induced by light negatively-charged particles used to be out of interest in high energy physics experiments. First, these particles are secondary particles, as a rule, and, second, they cannot inflict many lattice damages compared to protons. Nevertheless, the interaction of these particles with crystals can be very important for many different applications of electronic devices.

We will consider in this article radiation defects induced by light negatively-charged particles like pions ($\pi$-mesons) and muons in crystals with a diamond structure. These particles do not destroy the crystal structure, like heavy particles, but can create specific defects in the lattice. Indeed, they are captured by a nucleus creating an impurity atom and, thus, can change the electronic properties of a crystal. Negative pions and muons are respectively long-lived particles: the lifetimes of charged pion and muon are ${\tau }_{{\pi }^{\pm }}\approx 2.6\times {10}^{-8}$ s and ${\tau }_{\mu }\approx 2.2\times {10}^{-6}$ s, respectively. Pions are born as usual when high energy protons are stopped in a target, and muons are born after the decay of pions:

$${\pi }^{\pm }\to {\mu }^{\pm }+{\nu }_{\mu },$$

where ${\nu }_{\mu }$ is a muon antineutrino for the negative muon and a neutrino for the positive one. This picture can be observed in cosmic rays. Negatively-charged pions and muons are stopped in a media very effectively because of the capture by nuclei.

The capture mechanism differs for pions and muons, but the result manifests in the same way in electronic properties, because they form finally the same acceptor impurity. Consider a capture of negative pions by stable nuclei of the main semiconductors: C, Si and Ge. In diamond, we have only one stable isotope C${}^{12}$, and a capture of a negative pion gives rise to the boron acceptor:

$${\mathrm{C}}^{12}+{\pi }^{-}\to {\mathrm{B}}^{11}+n,$$

where n is a decay neutron. The boron nucleus spin is $I=3/2$.

In silicon isotope Si${}^{28}$ (92% in nature, see e.g., [9]) can capture ${\pi }^{-}$ and than transform into the aluminum acceptor:

$${\mathrm{Si}}^{28}+{\pi }^{-}\to {\mathrm{Al}}^{27}+n.$$

Processes in germanium are more complicated, because it has only two stable isotopes with an atomic number equal to 70 and 72 with 21.2% and 22% in nature, respectively [9], which can capture a negative pion and decay to an appropriate gallium isotope. Therefore, we have:

$${\mathrm{Ge}}^{70}+{\pi }^{-}\to {\mathrm{Ga}}^{69}+n\mathrm{and}{\mathrm{Ge}}^{72}+{\pi }^{-}\to {\mathrm{Ga}}^{71}+n.$$

Both gallium isotopes possess a spin equal to 3/2. All isotopes B${}^{11}$, Al${}^{27}$, Ga${}^{69}$ and Ga${}^{71}$ are stable, and the capture of the negative pions irreversibly changes the concentration of the main acceptor impurities in semiconductors.

A capture process of negatively-charged muon in crystals strongly differs from the negative pion capture process. Consider this difference in more detail. Positively- and negatively-charged muons (${\mu }^{+}$ and ${\mu }^{-}$) are widely used for research of condensed matter in many different areas, for the simulation of the behavior of hydrogen-like light element impurities and chemical processes with atomic hydrogen (see e.g., [10]). The application of muons for materials’ investigation has become possible due to a well-developed $\mu$SR-technique based on the possibilities of supervision for a muon magnetic moment in the sample. Negatively- and positively-charged muons (${\mu }^{\mp }$) are unstable leptons with spin 1/2.

The negatively-charged muon (${\mu }^{-}$) decays according to the scheme:

$${\mu }^{-}\to e^{-}+{\nu }_{\mu }+{\tilde{\nu }}_e,$$

where ${\nu }_{\mu }$ and ${\tilde{\nu }}_e$ are muonic neutrino and electronic antineutrino, respectively. The escape probability of a decay electron depends on the angle between the electron momentum direction and the average muon spin s, due to what appears to be the possibility to study local fields of a target. A muon has a relatively high decay time of ${\tau }_{\mu }\approx 2.2\times {10}^{-6}$ s. The large lifetime allows investigating with a high precision the processes with a characteristic time $t<{10}^{-5}$ s, which provides the opportunity for a $\mu$SR-technique for the material property studies, well comparable with the possibilities of the widely-applied methods of NMR and ESR.

The behavior of ${\mu }^{+}$ and ${\mu }^{-}$ in a medium is radically different. From the chemical point of view, the positively-charged muon is a light element impurity modeling a light hydrogen isotope. The negatively-charged muon cascades into the ground $1s$-state forming a muonic atom ($\mu$-atom). The mass of a muon equals 207-times the mass of an electron, and therefore, its binding energy with an atomic nucleus is 207-times larger than that of the electron. After a muon capture, much energy is released, leading to a high ionization of a target atom due to the emission of Auger electrons. Further, the target Auger electrons are captured by the positively-charged radiation-induced defect. Due to a high muon mass value, the negative muon screens a nuclear charge Z, which is effectively becoming $Z-1$. After defect neutralization, a replacement impurity is formed, or a muonic atom, similar to an atom isotope with a nuclear charge $Z-1$.

This fact was well known since the initial stage of the muon research (see e.g., [11]) and gave rise to the foundation of the muon method of materials research ($\mu$SR). Systematic study of impurities’ formation with a nuclear charge equal to $Z-1$ in condensed matter was carried out at the early stages of the $\mu$SR-research [12,13,14]. The muonic atom formed inside a semiconductor lattice models an acceptor center. For example, in diamond ($Z=6$), the negative muon, as a result of capture by a nucleus, forms a pseudo-boron, or muonic boron, which can be designated as ${}_{\mu }$B. In Si ($Z=14$) and Ge ($Z=32$), the negative muon is captured by a nucleus forming the pseudo-aluminum ${}_{\mu }$Al with a nuclear charge equal to $Z=13$ and pseudo-gallium ${}_{\mu }$Ga with a nuclear charge equal to $Z=31$, respectively. These chemical elements are the main acceptor impurities in silicon and germanium semiconductors. Therefore, a radiation defect induced by a negative muon is unstable and disappears after its decay. However, nevertheless, this kind of defect is very interesting because it provides the possibility to study the evolution in time of the processes considered above.

The study of acceptor center properties using ${\mu }^{-}$ was suggested in [15]. The possibility to extract valuable information about the hyperfine structure and interactions with a lattice of acceptor centers in different semiconductors with the help of negative muons was shown in the works [16,17,18,19]. Recently, ${\mu }^{-}SR$research of synthetic diamond crystals were carried out in [20,21,22,23]. We will examine evolution in time of radiation defects induced by negative muons in the following, taking in mind that they are the same for negative pions, as well.

The total process of this kind of radiation defect formation can be separated into two principally different stages. At the first stage, a center with a large positive charge appears after the stopping of a negative muon or pion. This center interacts with electrons of a trace, created by the charged particle, when it is decelerated in a crystal. As a result of this interaction, the positively-charged center partially compensates its charge or becomes neutralized if it is possible. At the second stage, the center with a compensated charge restores broken chemical bonds with a lattice and then forms an acceptor center.

Now, we will outline briefly the main results of the first stage and show the difference between diamond and other diamond structure crystals following [24]. After that, we will consider the second stage in more detail.

2. Interaction with the Trace

When a negative pion is captured by a nucleus or a negative muon is captured to the K-shell of the muonic atom, substantial energy ($E\ge 1$ keV) is released. A totally ionized positively-charged center and Auger electron ionization environment appear, creating secondary electrons. This process takes short a time, $t\sim {10}^{-14}$ s. After the ionization, free electrons lose their energy; for a while, it will be of the order of the forbidden gap energy. This is a diffusion process, when ionized impurities and host atoms are neutralized, and it takes respectively a long time $t\le {10}^{-10}$ s. All of these findings were obtained as a result of a numerical modeling of a neutralization process of muonic atoms in a kinetic approximation for diamond and silicon crystals with different concentrations of impurities [24].

A different situation is observed in diamond and silicon already at this stage. The capture of a negative muon on a silicon nucleus creates the number of free charge carriers approximately at two orders more with respect to diamond. This result is connected with a difference in the number of Auger electrons, in ionization energies of impurities and a forbidden energy band for these two crystals.

Numerical calculations have shown that the recombination frequency of electrons with positively-charged ions in diamond reaches approximately ${10}^7$ s${}^{-1}$ only at a respectively short interval of time ${10}^{-10}$ s. In silicon, the recombination frequency reaches approximately ${10}^{11}$ s${}^{-1}$ for the same interval of time. As a result, all ionized impurities in silicon including a muonic atom ${}_{\mu }$Al are neutralized for a very short time $t\approx {10}^{-11}$ s. The probability of the neutralization of a muonic atom ${}_{\mu }$B is less than ${10}^{-3}$ for the interval $t\approx {10}^{-10}$ s. The recombination frequency in diamond sharply falls for $t>{10}^{-10}$ s, and the neutralization time in this process becomes more than both a muon lifetime and a characteristic time for chemical bonds’ restoration.

Thus numerical modeling has shown that a positively-charged radiation defect, created by a negative muon in silicon and germanium, must be quickly neutralized before chemical bonds with the lattice can be restored. In diamond, we observe other behavior. Namely, the radiation defect must restore chemical bonds with the lattice to be positively charged. Therefore, we need to consider different initial states of the radiation defect at the second stage for diamond and other crystals with the diamond structure.

The second stage of the radiation defect formation consists of a few steps that lead to an acceptor center formation. A neutral defect with restored chemical bonds is not an acceptor center yet, because there exist unsaturated chemical bonds. Therefore, we need to consider at least three steps of an acceptor center formation:

(1)

restoration of broken chemical bonds and neutralization of the radiation defect;

(2)

capture of a missing electron and saturation of chemical bonds of a neutral radiation defect in the lattice; formation of an ionized acceptor center;

(3)

formation of an acceptor center in the ground state.

The first two steps are discussed in this article.

3. Electron States of a Neutral Radiation Defect in Si and Ge

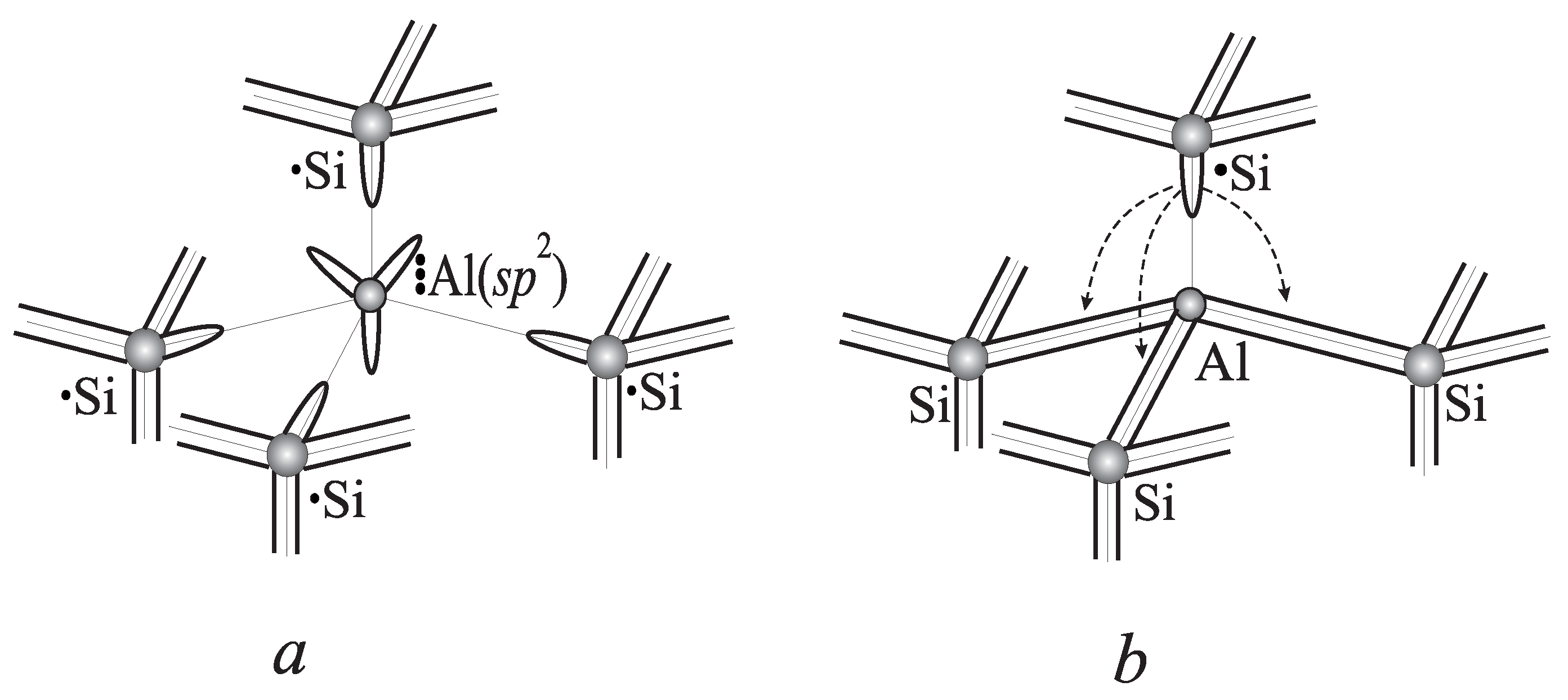
The muonic impurity atom is in an exited state just after formation because its chemical bonds with host atoms are broken. In accordance with the standard idea of quantum chemistry, only electrons with the same principal quantum number can create a chemical bond if they were on an unfilled energy level of the atom. In this case, they form hybridized states. For lattices with diamond structure electron states, $ns$ and $np$ are represented with equal probability, where $n=2,3$ and 4 relate to C, Si and Ge, respectively. Hybridized states are formed in atomic time, but chemical bonds’ formation is determined by exchange interactions that are weaker than Coulomb interactions, which form the appropriate atomic configuration.

When a chemical bond is formed, a significant energy (of the order of some eV) can be emitted. In gasses and liquids, this excess energy can be transferred to the third body. This kind of energy transfer in crystal must be connected with a phonon emission. One-phonon emission with the energy of ≥1 eV in covalent crystal is impossible. Therefore, a transfer of this energy value could be realized in the case of a multi-phonon process. This kind of process have a very small probability. Thus, a radiation transition with a photon emission seems to us more preferable with respect of the other processes.

In this section, we consider this process for a neutralized radiation defect in Si and Ge when three electrons are in hybridized states [25]. Consider an impurity atom with the nuclear charge $Z-1$, which is formed as a result of a neutralization process in an atomic time and has an atomic configuration where electrons at the external shell are in the “mixed”, but not in the ground, state:

$$|{\psi }_{\mathrm{in}}\rangle =|nsn{p}^2\rangle .$$

(1)

We assume that the electron configuration with the principal quantum number less then n is completely occupied, and the state of such electrons is described by the unperturbed wave function of the free atom. The initial state of the radiation defect in a silicon lattice is sketched in Figure 1a.

The mixed state (1) forms a chemical bond, if it possesses by maximal spin $S=3/2$, and a spacial part of its wave function one may represent in the view of equiprobable superposition of three Slater’s determinants:

$${\mathsf{\Psi }}_{s{p}^2}({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)=\frac{1}{\sqrt{3}}\left({\mathsf{\Psi }}_{+1}({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)+{\mathsf{\Psi }}_0({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)+{\mathsf{\Psi }}_{-1}({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)\right),$$

(2)

where:

$${\mathsf{\Psi }}_M({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)=\frac{1}{\sqrt{6}}\left(\begin{array}{ccc}{\psi }_{ns}\left({\mathbf{r}}_1\right)& {\psi }_{np,m}\left({\mathbf{r}}_1\right)& {\psi }_{np,m^{\prime }}\left({\mathbf{r}}_1\right)\\ {\psi }_{ns}\left({\mathbf{r}}_2\right)& {\psi }_{np,m}\left({\mathbf{r}}_2\right)& {\psi }_{np,m^{\prime }}\left({\mathbf{r}}_2\right)\\ {\psi }_{ns}\left({\mathbf{r}}_3\right)& {\psi }_{np,m}\left({\mathbf{r}}_3\right)& {\psi }_{np,m^{\prime }}\left({\mathbf{r}}_3\right)\end{array}\right).$$

(3)

Here, $M=m+m^{\prime }$, and $m,m^{\prime }=0,\pm 1$.

A spacial part of the wave function of the defect in a final state can be represented as a superposition of three hybridized states forming the chemical bond with host atoms of the lattice:

$${\mathsf{\Psi }}_{\mathrm{Cr}}({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)=\frac{1}{\sqrt{6}}\sum _{\mathcal{P}}{(-1)}^{\mathcal{P}}{\mathsf{\Psi }}_{{}_{\mu }\mathrm{A}}\left(\mathcal{P}({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)\right).$$

(4)

Here, summation is carried out over all permutations $\mathcal{P}$ of the valence electrons of the impurity and:

$$\begin{array}{ll}{\mathsf{\Psi }}_{{}_{\mu }\mathrm{A}}({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)& =\frac{1}{2}({\psi }_{{\mathbf{n}}_1}\left({\mathbf{r}}_1\right){\psi }_{{\mathbf{n}}_2}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_3}\left({\mathbf{r}}_3\right)+{\psi }_{{\mathbf{n}}_2}\left({\mathbf{r}}_1\right){\psi }_{{\mathbf{n}}_3}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_4}\left({\mathbf{r}}_3\right)\\ & +{\psi }_{{\mathbf{n}}_3}\left({\mathbf{r}}_1\right){\psi }_{{\mathbf{n}}_4}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_1}\left({\mathbf{r}}_3\right)+{\psi }_{{\mathbf{n}}_4}\left({\mathbf{r}}_1\right){\psi }_{{\mathbf{n}}_1}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_2}\left({\mathbf{r}}_3\right)).\end{array}$$

(5)

The unit vectors ${\mathbf{n}}_a$ are directed from the impurity to nearest neighbors (along the directions of the chemical bonds). The one-particle functions ${\psi }_{{\mathbf{n}}_a}\left(\mathbf{r}\right)$ are the hybridized states with directed bonds, and they can be written in a form (see e.g., [26,27]):

$${\psi }_{{\mathbf{n}}_a}\left(\mathbf{r}\right)={\alpha }_a{\psi }_{ns}\left(\mathbf{r}\right)+{\beta }_{{\mathbf{n}}_a}{\psi }_{np,{\mathbf{n}}_a}\left(\mathbf{r}\right)$$

(6)

and satisfy normalization conditions:

$$\int {\psi }_{{\mathbf{n}}_a}^{*}\left(\mathbf{r}\right){\psi }_{{\mathbf{n}}_b}\left(\mathbf{r}\right)d\mathbf{r}={\delta }_{ab}.$$

(7)

From this condition, we can obtain relations for the coefficients in the superposition (6):

$${\alpha }_a^2+{\beta }_{{\mathbf{n}}_a}^2=1,\sum _a{\alpha }_a^2=1,\sum _a{\beta }_{{\mathbf{n}}_a}^2=3,{\alpha }_a{\alpha }_b+{\beta }_{{\mathbf{n}}_a}{\beta }_{{\mathbf{n}}_b}\cos \left(\mathbf{n}\widehat{{}_a,}{\mathbf{n}}_b\right)=0.$$

(8)

4. Electron States of a Positively-Charged Radiation Defect in Diamond

A positively-charged radiation defect in diamond has the effective nuclear charge $Z=5$. Its atomic configuration contains only two electrons in an external (unfilled) electron shell, and they are in the “mixed” state [28]:

$$|{\psi }_{\mathrm{in}}\rangle =|2s2p\rangle .$$

(9)

We suppose also that the electronic configuration for the principle quantum number $n=1$ is completely filled, and electronic states of the external atomic shell are described by unperturbed wave functions of a free atom. The initial state of the radiation defect in a diamond lattice is shown schematically in Figure 2a.

The mixed state (9) forms a chemical bond with the nearest host atoms of the lattice. We express a wave function of the initial state (9) in distinguish from the state (1) in the form of superposition with all possible spin states:

$${\mathsf{\Psi }}_{sp}({\mathbf{r}}_1,{\mathbf{r}}_2)=A_0{\mathsf{\Psi }}_{sp}^{\left(0\right)}({\mathbf{r}}_1,{\mathbf{r}}_2)|0,0\rangle +A_1{\mathsf{\Psi }}_{sp}^{\left(1\right)}({\mathbf{r}}_1,{\mathbf{r}}_2)\sum _{M_S}|1,M_S\rangle ,$$

(10)

where:

$${\mathsf{\Psi }}_{sp}^{\left(S\right)}({\mathbf{r}}_1,{\mathbf{r}}_2)=\frac{1}{\sqrt{2}}\left({\psi }_{2s}\left({\mathbf{r}}_1\right){\psi }_{2p}\left({\mathbf{r}}_2\right)+{(-1)}^S{\psi }_{2p}\left({\mathbf{r}}_1\right){\psi }_{2s}\left({\mathbf{r}}_2\right)\right),$$

(11)

${\psi }_{2s}\left(\mathbf{r}\right)$ is the wave function of the $2s$-state. We assume that all p-states with different projections have equal probabilities:

$${\psi }_{2p}\left(\mathbf{r}\right)=\frac{1}{\sqrt{3}}\left({\psi }_{21,+1}\left(\mathbf{r}\right)+{\psi }_{21,0}\left(\mathbf{r}\right)+{\psi }_{21,-1}\left(\mathbf{r}\right)\right).$$

$S=0,1$ are the values of the total electron spin; $|S,M_S\rangle$ is the appropriate spin-state vector. Spin states with different projections are considered as having equal probabilities; so coefficients in the superposition (10) satisfy the following condition:

$$|A_0{|}^2+3{\left|A_1\right|}^2=1.$$

The space part of the defect wave function in the final state must correspond to the determined value of the total electron spin S, and this can be represented in the form of the superposition of hybridized states providing a chemical bond with the lattice host atoms:

$${\mathsf{\Psi }}_{\mathrm{Cr}}^{\left(S\right)}({\mathbf{r}}_1,{\mathbf{r}}_2)=\frac{1}{\sqrt{6}}\sum _{{\mathbf{n}}_a,{\mathbf{n}}_b}{\mathsf{\Psi }}_{{\mathbf{n}}_a{\mathbf{n}}_b}^{\left(S\right)}({\mathbf{r}}_1,{\mathbf{r}}_2),$$

(12)

where summation is carried out over all possible directions of the chemical bond of impurity valence electrons with the nearest neighbors of the lattice,

$${\mathsf{\Psi }}_{{\mathbf{n}}_a{\mathbf{n}}_b}^{\left(S\right)}({\mathbf{r}}_1,{\mathbf{r}}_2)=\frac{1}{\sqrt{2}}\left({\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right){\psi }_{{\mathbf{n}}_b}\left({\mathbf{r}}_2\right)+{(-1)}^S{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_b}\left({\mathbf{r}}_1\right)\right).$$

(13)

The unit vectors ${\mathbf{n}}_a$ are directed from the impurity to the neighbor atoms (along the direction of chemical bonds) like in (5). One-particle wave functions ${\psi }_{{\mathbf{n}}_a}\left(\mathbf{r}\right)$ of hybridized states with directed bonds are determined by Equations (6)–(8).

The final state of the charged impurity is described by a function similar to the superposition (10) where the wave functions with a determined spin must be replaced by Expression (13).

5. Formation of the Neutral Center (${}_{\mu }$A A${}_4{)}^0$ in Si and Ge

A lifetime of exited states (1) and (10) is determined by a rate of a radiation transition in a bond state and can be calculated by using Fermi’s “golden rule”:

$$dw=\frac{2\pi }{\hslash }{\left|\langle {\psi }_{in}|{\widehat{V}}_{\mathrm{rad}}|{\psi }_{Cr}\rangle \right|}^2\delta (E_f-E_i)d{\nu }_f.$$

(14)

The interaction operator is:

$${\widehat{V}}_{\mathrm{rad}}=\frac{e}{mc}\sum _a{\widehat{\mathbf{p}}}_a\mathbf{A}\left({\mathbf{r}}_a\right),$$

(15)

where $\mathbf{A}\left(\mathbf{r}\right)$ is the vector-potential of the free radiation field.

Let us consider now only the term for one electron with $a=1$ in the operator (14) to simplify the following calculations. In this case, matrix elements of the perturbation operator could be represented by the expression:

$$\langle {\psi }_{in}|{\widehat{\mathbf{p}}}_1{|{\psi }_{\mathrm{Cr}}\rangle }_{sa}=\int {\psi }_{ns}^{*}\left({\mathbf{r}}_1\right){\widehat{\mathbf{p}}}_1{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1\int {\psi }_{np,m}^{*}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_b}\left({\mathbf{r}}_2\right)d{\mathbf{r}}_2\int {\psi }_{np,m^{\prime }}^{*}\left({\mathbf{r}}_3\right){\psi }_{{\mathbf{n}}_c}\left({\mathbf{r}}_3\right)d{\mathbf{r}}_3$$

(16)

and:

$$\langle {\psi }_{in}|{\widehat{\mathbf{p}}}_1{|{\psi }_{\mathrm{Cr}}\rangle }_{pa}=\int {\psi }_{np,m}^{*}\left({\mathbf{r}}_1\right){\widehat{\mathbf{p}}}_1{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1\int {\psi }_{np,m^{\prime }}^{*}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_b}\left({\mathbf{r}}_2\right)d{\mathbf{r}}_2\int {\psi }_{ns}^{*}\left({\mathbf{r}}_3\right){\psi }_{{\mathbf{n}}_c}\left({\mathbf{r}}_3\right)d{\mathbf{r}}_3,$$

(17)

where the indexes are $a,b,c=1,2,3,4$.

If we direct the axis $z\left|\right|{\mathbf{n}}_1$, then the other three p-states in hybridized states (6) turn out as a result of the rotation of the state ${\psi }_{n1,0}\left(\mathbf{r}\right)$ in the state with a rotation moment projection equal to zero on the axes ${\mathbf{n}}_b$. In this case, we get the opportunity to calculate easy integrals incoming in Expressions (16) and (17):

$$\begin{array}{ccc}\hfill \int {\psi }_{ns}^{*}\left(\mathbf{r}\right){\psi }_{{\mathbf{n}}_a}\left(\mathbf{r}\right)dr& =& {\alpha }_a\langle ns|ns\rangle ={\alpha }_a;\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill \int {\psi }_{np,m}^{*}\left(\mathbf{r}\right){\psi }_{{\mathbf{n}}_a}\left(\mathbf{r}\right)dr& =& {\beta }_a\langle np,m|\widehat{R}({\theta }_a,{\phi }_a)|n1,0\rangle ,\hfill \end{array}$$

(19)

where $\widehat{R}({\theta }_a,{\phi }_a)$ is the rotation operator, and the matrix elements (19) are determined by the second column of the rotation matrix:

$$\langle n1,\pm 1|\widehat{R}({\theta }_a,{\phi }_a)|n1,0\rangle =\mp \frac{1}{\sqrt{2}}\sin {\theta }_a{e}^{-i{\phi }_a},\langle n1,0|\widehat{R}({\theta }_a,{\phi }_a)|n1,0\rangle =\cos {\theta }_a.$$

(20)

We put in Equation (18) the obvious expressions of the matrix elements of the rotation operator (see e.g., [29]).

Without reduction of the generality of the calculations, we consider a matrix element only for the z- projection of a momentum operator. Therefore, we have:

$$\begin{array}{ccc}\hfill \int {\psi }_{ns}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1& =& {\beta }_a\int {\psi }_{ns}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}\widehat{R}({\theta }_a,{\phi }_a){\psi }_{n1,0}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1={\beta }_a\cos {\theta }_a{I}_{sp}^{\left(n\right)},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill \int {\psi }_{np,m}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_{1}d{\mathbf{r}}_1& =& {\alpha }_a\int {\psi }_{n1,0}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}{\psi }_{ns}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1={\alpha }_a{I}_{sp}^{\left(n\right)*},\hfill \end{array}$$

(22)

where:

$$I_{sp}^{\left(n\right)}=\int {\psi }_{ns}^{*}\left(\mathbf{r}\right){\widehat{p}}_z{\psi }_{n1,0}\left(\mathbf{r}\right)d\mathbf{r}.$$

(23)

For clarity, we show some intermediate calculations. The total matrix element in Expression (14) consists of 72 different items corresponding to different matrix elements between states of the superpositions (2) and (4). However, it is enough to calculate only four of them. We give them below.

$$\begin{array}{ll}\langle {\mathsf{\Psi }}_{+1}|{\widehat{p}}_{1z}|{\mathsf{\Psi }}_{{\mathbf{n}}_1,{\mathbf{n}}_2,{\mathbf{n}}_3}\rangle & =-\frac{1}{4\sqrt{3}}{\beta }_1{\beta }_2{\beta }_3\left(\sin {\theta }_2\cos {\theta }_3{e}^{-i{\phi }_2}-\cos {\theta }_2\sin {\theta }_3{e}^{-i{\phi }_3}\right)I_{sp}^{\left(n\right)}\\ & +\frac{1}{4\sqrt{3}}{\alpha }_1\left({\beta }_2{\alpha }_3\sin {\theta }_2{e}^{-i{\phi }_2}-{\alpha }_2{\beta }_3\sin {\theta }_3{e}^{-i{\phi }_3}\right)I_{sp}^{\left(n\right)*}.\end{array}$$

(24)

The rest of the three matrix elements are determined by the other possible sets of ${\mathbf{n}}_a$ for the electrons with coordinates ${\mathbf{r}}_1,{\mathbf{r}}_2$ and ${\mathbf{r}}_3$:

$$\begin{array}{ll}\langle {\mathsf{\Psi }}_{+1}|{\widehat{p}}_{1z}|{\mathsf{\Psi }}_{{\mathbf{n}}_2,{\mathbf{n}}_3,{\mathbf{n}}_4}\rangle & =-\frac{1}{4\sqrt{3}}{\beta }_2{\beta }_3{\beta }_4\cos {\theta }_2\left(\sin {\theta }_3\cos {\theta }_4{e}^{-i{\phi }_3}-\cos {\theta }_3\sin {\theta }_4{e}^{-i{\phi }_4}\right)I_{sp}^{\left(n\right)}\\ & -\frac{1}{4\sqrt{3}}{\alpha }_2\left({\alpha }_3{\beta }_4\sin {\theta }_4{e}^{-i{\phi }_4}-{\beta }_3{\alpha }_4\sin {\theta }_3{e}^{-i{\phi }_3}\right)I_{sp}^{\left(n\right)*};\end{array}$$

(25)

$$\begin{array}{ccc}\hfill \langle {\mathsf{\Psi }}_{+1}\left|{\widehat{p}}_{1z}\right|{\mathsf{\Psi }}_{{\mathbf{n}}_3,{\mathbf{n}}_4,{\mathbf{n}}_1}\rangle & =& -\frac{1}{4\sqrt{3}}{\beta }_4\left({\beta }_1{\beta }_3\cos {\theta }_3{I}_{sp}^{\left(n\right)}-{\alpha }_1{\alpha }_3{I}_{sp}^{\left(n\right)*}\right)\sin {\theta }_4{e}^{-i{\phi }_4}\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill \langle {\mathsf{\Psi }}_{+1}\left|{\widehat{p}}_{1z}\right|{\mathsf{\Psi }}_{{\mathbf{n}}_4,{\mathbf{n}}_1,{\mathbf{n}}_2}\rangle & =& \frac{1}{4\sqrt{3}}{\beta }_2\left({\beta }_1{\beta }_4\cos {\theta }_4{I}_{sp}^{\left(n\right)}-{\alpha }_1{\alpha }_4{I}_{sp}^{\left(n\right)*}\right)\sin {\theta }_2{e}^{-i{\phi }_2}.\hfill \end{array}$$

(27)

It is easy to see that permutations of electrons in the superposition (5) do not change expressions for the matrix elements (24)–(27). Therefore, the number of permutations in the state (5) with similar expressions reduces the total number of items by six-times.

We get a very cumbersome expression for the arbitrary values of the parameters ${\alpha }_a,{\beta }_a,{\theta }_a$ and ${\phi }_a$. However, it is necessary to take into account that the system under consideration has a symmetry at less $C_{3v}$. In this case, the result could be essentially simplified. We examine the simplest case at first, when the system has a tetrahedral symmetry and all parameters in the hybridized states (6) are equal to each other:

$${\alpha }_a=\alpha =\frac{1}{2},{\beta }_a=\beta =\frac{\sqrt{3}}{2}.$$

(28)

If the vector ${\mathbf{n}}_4$ lies in the $xz$ plane, the angles ${\theta }_a,{\phi }_a$ are equal:

$${\theta }_1=0,{\theta }_2={\theta }_3={\theta }_4=\theta ,\cos \theta =-\frac{1}{3},{\phi }_2=-{\phi }_3=\frac{2\pi }{3},{\phi }_4=0.$$

(29)

In the case of symmetrical structure, we get the following expressions for the matrix elements:

$$\begin{array}{cc}\hfill \langle {\mathsf{\Psi }}_{+1}\left|{\widehat{p}}_{1z}\right|{\mathsf{\Psi }}_{{\mathbf{n}}_1,{\mathbf{n}}_2,{\mathbf{n}}_3}\rangle =& \frac{i}{8}\beta \left({\beta }^2\sin 2\theta I_{sp}^{\left(n\right)}-{\alpha }^2\sin \theta I_{sp}^{\left(n\right)*}\right),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \langle {\mathsf{\Psi }}_{+1}\left|{\widehat{p}}_{1z}\right|{\mathsf{\Psi }}_{{\mathbf{n}}_2,{\mathbf{n}}_3,{\mathbf{n}}_4}\rangle =& \frac{\sqrt{3}}{8}\left(1-\frac{1}{\sqrt{3}}\right)\beta \sin \theta \left({\beta }^2{\cos }^2\theta I_{sp}^{\left(n\right)}-{\alpha }^2{I}_{sp}^{\left(n\right)*}\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \langle {\mathsf{\Psi }}_{+1}\left|{\widehat{p}}_{1z}\right|{\mathsf{\Psi }}_{{\mathbf{n}}_3,{\mathbf{n}}_4,{\mathbf{n}}_1}\rangle =& \langle {\mathsf{\Psi }}_{+1}|{\widehat{p}}_{1z}|{\mathsf{\Psi }}_{{\mathbf{n}}_4,{\mathbf{n}}_1,{\mathbf{n}}_2}\rangle =-\frac{1}{4\sqrt{3}}\beta \sin \theta \left({\beta }^2\cos \theta I_{sp}^{\left(n\right)}-{\alpha }^2{I}_{sp}^{\left(n\right)*}\right).\hfill \end{array}$$

(32)

Adding up Expressions (30)–(32), we get:

$$\langle {\mathsf{\Psi }}_{+1}|{\widehat{p}}_{1z}|{\mathsf{\Psi }}_{\mathrm{Cr}}\rangle =-\frac{1-i\sqrt{3}}{8\sqrt{3}}{\beta }^3\sin 2\theta {\sin }^2\frac{\theta }{2}{I}_{sp}^{\left(n\right)}.$$

(33)

The matrix elements for the state with $M=-1$ are calculated by a similar way:

$$\langle {\mathsf{\Psi }}_{-1}|{\widehat{p}}_{1z}|{\mathsf{\Psi }}_{\mathrm{Cr}}\rangle =-\frac{1+i\sqrt{3}}{8\sqrt{3}}{\beta }^3\sin 2\theta {\sin }^2\frac{\theta }{2}{I}_{sp}^{\left(n\right)}.$$

(34)

For the state with $M=0$:

$$\langle {\mathsf{\Psi }}_0|{\widehat{p}}_{1z}|{\mathsf{\Psi }}_{\mathrm{Cr}}\rangle =-\frac{i}{2\sqrt{2}}{\beta }^3{\sin }^2\theta {\cos }^2\frac{\theta }{2}{I}_{sp}^{\left(n\right)}.$$

(35)

After substitution of the values o Parameters (28) and (29) and adding up Expressions (33)–(35), we have:

$$\langle {\mathsf{\Psi }}_{\mathrm{in}}|{\widehat{p}}_{1z}|{\mathsf{\Psi }}_{\mathrm{Cr}}\rangle =-\frac{{\beta }^3}{4\sqrt{3}}\left(\sin 2\theta {\sin }^2\frac{\theta }{2}+i\sqrt{2}{\sin }^2\theta {\cos }^2\frac{\theta }{2}\right)I_{sp}^{\left(n\right)}=\frac{1-i4}{72\sqrt{2}}{I}_{sp}^{\left(n\right)}.$$

(36)

For the calculation of the integral $I_{sp}$, we take the appropriate wave functions of the hydrogen-like atom with an effective nuclear charge equal to $\tilde{Z}$. In accordance with Slater [30], an effective charge is determined as $\tilde{Z}=Z-\sigma$, where Z is the real nuclear charge and $\sigma$ is a screening constant.

In a silicon crystal, an aluminum $\mu$-atom ${}_{\mu }$Al is formed. It has the principle quantum number $n=3$, and appropriate calculations for ${}_{\mu }$Al give the following results:

$$I_{sp}^{\left(3\right)}=-i\frac{10\tilde{Z}}{3\sqrt{6}},\mathrm{in}\mathrm{dimensional}\mathrm{units}{I}_{sp}^{\left(3\right)}=-i\frac{10}{3\sqrt{6}}\frac{\tilde{Z}\hslash }{a_0},$$

(37)

where $a_0$ is the Bohr radius.

In a germanium lattice, a gallium $\mu$-atom ${}_{\mu }$Ga with the principle quantum number $n=4$ must be formed. The unknown value of the matrix element for ${}_{\mu }$Ga is equal to:

$$I_{sp}^{\left(4\right)}=i\tilde{Z}\sqrt{5}{\left(\frac{3}{4}\right)}^2,\mathrm{correspondingly}{I}_{sp}^{\left(4\right)}=i\sqrt{5}{\left(\frac{3}{4}\right)}^2\frac{\tilde{Z}\hslash }{a_0}.$$

(38)

In the calculation of a transition probability per unit time, we will take into account that at least three electrons participate in the matrix element of the operator (19), and the number of spin states in Determinant (3) is $2S+1=4$:

$$d{w}_{\mathrm{hybr}}=\frac{2\pi }{{\hslash }^2}(2S+1){\left(\frac{e}{m{c}^2}\right)}^2\frac{2\pi \hslash c^2}{\omega }{\left|3\langle {\mathsf{\Psi }}_{\mathrm{in}}\left|{\widehat{p}}_{1z}\right|{\mathsf{\Psi }}_{\mathrm{Cr}}\rangle \right|}^2{\cos }^2\vartheta \delta ({\omega }_{if}-\omega )\frac{k^{2}dkd\mathsf{\Omega }}{{\left(2\pi \right)}^3}.$$

(39)

Here, ${\omega }_{if}$ appropriates the transition frequency of a neutral radiation defect from the energy level of the corresponding free atom state on the energy level corresponding to a hybridized state in a lattice.

After integration over the wavevector of photons and averaging over all angles, we get:

$$w_{\mathrm{hybr}}=\left\{\begin{array}{c}\left(17\times 5^2/2^3{3}^6\right){\tilde{Z}}_{\mathrm{Al}}^2{\alpha }^3{\omega }_{if}^{\mathrm{Si}}\approx 3.8\times {10}^8{s}^{-1}\mathrm{for}\mathrm{silicon},\hfill \\ \left(17\times 15/2^{12}\right){\tilde{Z}}_{\mathrm{Ga}}^2{\alpha }^3{\omega }_{if}^{\mathrm{Ge}}\approx 4.9\times {10}^8{s}^{-1}\mathrm{for}\mathrm{germanium},\hfill \end{array}\right.$$

(40)

where $\alpha =1/137$ is the fine structure constant. We have substituted here the effective charge ${\tilde{Z}}_{\mathrm{Al}}\approx 3.5$ and ${\tilde{Z}}_{\mathrm{Ga}}\approx 5.0$ in accordance with Slater [30].

6. Formation of Neutral Center (${}_{\mu }$B C${}_4{)}^0$ in Diamond

Formulae (16) and (17) must be modified for diamond in accordance with Equations (11) and (13) as follows:

$$\langle {\psi }_{in}|{\widehat{\mathbf{p}}}_1{|{\psi }_{\mathrm{Cr}}\rangle }_{sa}=\int {\psi }_{2s}^{*}\left({\mathbf{r}}_1\right){\widehat{\mathbf{p}}}_1{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1\int {\psi }_{2p}^{*}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_b}\left({\mathbf{r}}_2\right)d{\mathbf{r}}_2$$

(41)

and:

$$\langle {\psi }_{in}|{\widehat{\mathbf{p}}}_1{|{\psi }_{\mathrm{Cr}}\rangle }_{pa}=\int {\psi }_{2p}^{*}\left({\mathbf{r}}_1\right){\widehat{\mathbf{p}}}_1{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1\int {\psi }_{2s}^{*}\left({\mathbf{r}}_2\right){\psi }_{{\mathbf{n}}_b}\left({\mathbf{r}}_2\right)d{\mathbf{r}}_2,$$

(42)

To derive a common expression now, we consider that the Z-axis does not coincide with any of the bond directions ${\mathbf{n}}_a$. Therefore, as for (18) and (19), we have:

$$\begin{array}{cc}\hfill \int {\psi }_{2s}^{*}\left(\mathbf{r}\right){\psi }_{{\mathbf{n}}_b}\left(\mathbf{r}\right)d\mathbf{r}=& {\alpha }_b\langle 2s|2s\rangle ={\alpha }_b;\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill \int {\psi }_{2p}^{*}\left(\mathbf{r}\right){\psi }_{{\mathbf{n}}_b}\left(\mathbf{r}\right)d\mathbf{r}=& \frac{1}{3}{\beta }_b(2\cos {\phi }_b-i\sqrt{2}\sin {\theta }_b\sin {\phi }_b+\cos {\theta }_b).\hfill \end{array}$$

(44)

Without the reduction of the generality of the calculations, we consider a matrix element only for the z- projection of a momentum operator.

$$\begin{array}{c}\int {\psi }_{2s}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1=\hfill \\ \frac{{\beta }_a}{\sqrt{3}}\sum _m\langle 2,1,0|\widehat{R}\left({\mathbf{n}}_a\right)|2,1,m\rangle \int {\psi }_{2s}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}{\psi }_{21,0}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1=\frac{{\beta }_a}{\sqrt{3}}\cos {\theta }_a{I}_{sp}^{\left(2\right)},\hfill \end{array}$$

(45)

$$\begin{array}{c}\int {\psi }_{2p}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}{\psi }_{{\mathbf{n}}_a}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_{1}d{\mathbf{r}}_1=\frac{{\alpha }_a}{\sqrt{3}}\int {\psi }_{21,0}^{*}\left({\mathbf{r}}_1\right){\widehat{p}}_{1z}{\psi }_{2s}\left({\mathbf{r}}_1\right)d{\mathbf{r}}_1=\frac{{\alpha }_a}{\sqrt{3}}{I_{sp}^{\left(2\right)}}^{*},\hfill \end{array}$$

(46)

where $I_{sp}^{\left(2\right)}$ is determined by Equation (23) for $n=2$.

The interaction operator (15) conserves the total spin, and we need to calculate only matrix elements for the superpositions (10) and (12) between states with equal total spins. For states with a total electron spin $S=1$, the matrix elements of the interaction operator in Expression (14) are equal to zero because of the symmetry of the two-particle states (11) and (13). Therefore, contrary to calculations performed for neutral defects in Si and Ge, it is necessary to calculate matrix elements only for singlet states. Accordingly, a radiation transition in dipole approximation for triplet-states (with a maximum spin value of the (${}_{\mu }$B)${}^{+}$ defect) is forbidden. Note that singlet spin states constitute only 1/4 part of all spin states under the assumption of an equal probability of a population of all spin states. This fact leads to the reduction of a total probability transition by nine-times with respect to the probability transition between triplet states.

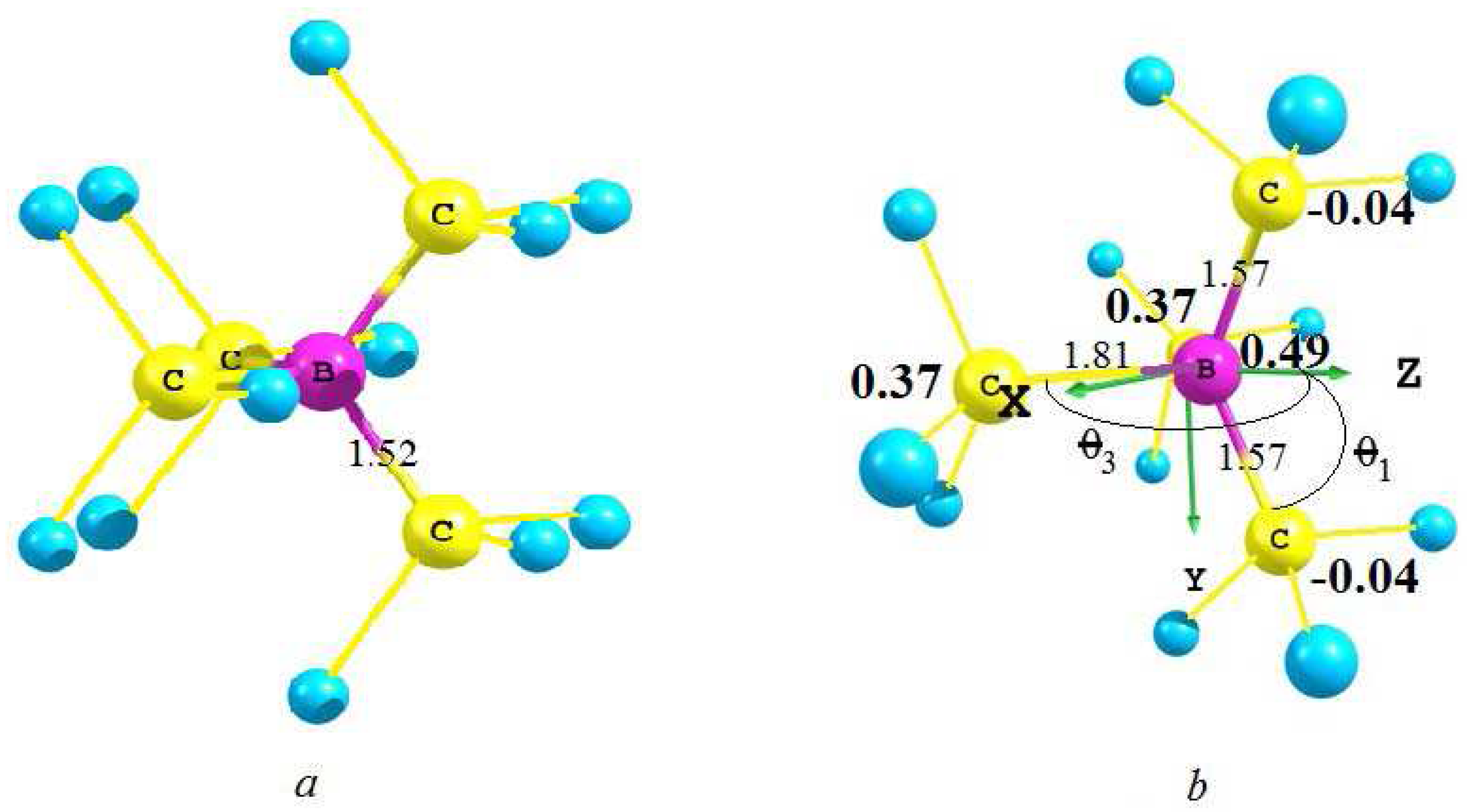
Taking into account a local symmetry $C_{2v}$ of the ${(}_{\mu }$B C${}_4{)}^{+}$ cluster, we direct axes as shown in Figure 2b and introduce the following designations: ${\theta }_1={\theta }_2\equiv {\theta }_1,{\theta }_3={\theta }_4\equiv {\theta }_3,{\phi }_1=\pi /2,$ ${\phi }_2=3\pi /2,$ ${\phi }_3=0,{\phi }_4=\pi$. We have, respectively, ${\beta }_1={\beta }_2\equiv {\beta }_1,{\alpha }_1={\alpha }_2\equiv {\alpha }_1,{\beta }_3={\beta }_4\equiv {\beta }_3,$ ${\alpha }_3={\alpha }_4\equiv {\alpha }_3$. After summation over all bonds, one obtains the expression:

$$\begin{array}{ll}\langle {\psi }_{in}|{\widehat{p}}_{1z}|{\psi }_{Cr}\rangle & =\frac{A_0}{3\sqrt{2}}\left\{\frac{1}{\sqrt{3}}{I}_{sp}^{*}\left({\beta }_1^2{\cos }^2{\theta }_1+4{\beta }_1{\beta }_3\cos {\theta }_1\cos {\theta }_3+{\beta }_3^2{\cos }^2{\theta }_3\right]\right.\\ & +\left.\left({\alpha }_1^2+4{\alpha }_1{\alpha }_3+{\alpha }_3^2\right)I_{sp}\right\}.\end{array}$$

(47)

We can determine superposition coefficients in (6). Taking into account the relations (8) as ${\alpha }_a^2=1-{\beta }_a^2$ and, respectively, ${\alpha }_1={\alpha }_2,{\beta }_1={\beta }_2,{\alpha }_3={\alpha }_4,{\beta }_3={\beta }_4$. Therefore, we have:

$${\beta }_{1,3}=\frac{1}{\sqrt{2}\sin {\theta }_{1,3}},{\alpha }_{1,3}=\frac{1}{\sqrt{2}}\sqrt{1-{\cot }^2{\theta }_{1,3}}.$$

(48)

Here, the condition $2{\alpha }_1^2+2{\alpha }_3^2=1$ and, respectively, $\cos \left(\mathbf{n}\widehat{{}_1,}{\mathbf{n}}_3\right)=\cos {\theta }_1\cos {\theta }_3$ were used.

Finally, the matrix element (47) can be written in the form:

$$\begin{array}{ll}\langle {\psi }_{in}|{\widehat{p}}_{1z}|{\psi }_{Cr}\rangle & =\frac{A_0}{3\sqrt{2}}\left\{\frac{1}{\sqrt{3}}{I}_{sp}^{*}\left({\cot }^2{\theta }_1+4\cot {\theta }_1\cot {\theta }_3+{\cot }^2{\theta }_3\right]\right.\\ & +\left.\left(2-{\cot }^2{\theta }_1-{\cot }^2{\theta }_3+4{\displaystyle \frac{\sqrt{\cos 2{\theta }_1\cos 2{\theta }_3}}{\sin {\theta }_1\sin {\theta }_3}}\right)I_{sp}\right\}.\end{array}$$

(49)

For the appropriate wave functions of the hydrogen-like atom with an effective nuclear charge equal to $\tilde{Z}$, the integral $I_{sp}^{\left(2\right)}$ is equal to:

$$I_{sp}^{\left(2\right)}=-i\tilde{Z},\mathrm{or}\mathrm{in}\mathrm{dimension}\mathrm{units}{I}_{sp}^{\left(2\right)}=-i\frac{\tilde{Z}m{e}^2}{\hslash }=-i\frac{\tilde{Z}\hslash }{a_0}.$$

(50)

An effective charge for a boron atom is equal to ${\tilde{Z}}_{\mathrm{B}}\approx 2.6$ [30].

In the calculation of the probability of a transition per unit time, we shall take into account that two electrons participate in the matrix element of the operator (15). Carrying out integration over a wavevector of photons and averaging over all angles, we obtain:

$$w_{\mathrm{hybr}}=\frac{16}{3}{\left|A_0\right|}^2{f}^2({\theta }_1,{\theta }_3){\tilde{Z}}^2{\alpha }^3{\omega }_{sp}.$$

(51)

Here, ${\omega }_{sp}$ corresponds to a transition frequency of the charged radiation defect from the energy level of the free ion (${}_{\mu }$B)${}^{+}$ to the energy level of the hybridized (bound) state in the lattice ${(}_{\mu }$B C${}_4{)}^{+}$.

In accordance with the matrix element (49) and the result of the matrix element (50) calculation, a configuration factor $f({\theta }_1,{\theta }_3)$ is equal to:

$$f({\theta }_1,{\theta }_3)=\frac{1+\sqrt{3}}{\sqrt{3}}\left({\cot }^2{\theta }_1+{\cot }^2{\theta }_3\right)+\frac{4}{\sqrt{3}}\cot {\theta }_1\cot {\theta }_3-4\frac{\sqrt{\cos 2{\theta }_1\cos 2{\theta }_3}}{\sin {\theta }_1\sin {\theta }_3}-2.$$

(52)

A transition frequency ${\omega }_{sp}$ and angles for a configuration factor $f({\theta }_1,{\theta }_3)$ were calculated numerically in [28] by the quantum-chemical methods. The crystalline chemical environment of clusters in Figure 2 has been taken into account by the procedure [31] based on a passivation of unnatural valences on a border of the cluster by hydrogen atoms. The variation of the geometrical position of the H* atoms, if it is possible, ensures the stoichiometry of the charge distribution on the carbon atoms of the model C${}_5$H*${}_{12}$ fragment (Figure 2a, where the B atom is substituted by the central C atom).

The initial state of the radiation (${}_{\mu }$B)${}^{+}$ defect in a diamond lattice is modeled by the tetrahedral structure of Figure 2a where the central carbon atom is substituted by the B atom, and the non- equilibrium length of four B–C bonds coincides with the equilibrium length of 1.523 Å for C–C bonds found by us earlier after geometry optimization of the central structural C${}_5$H*${}_{12}\left(T_d\right)$ fragment. As a result of a structural relaxation, the defect transits into the final hybridized state $|{\psi }_{Cr}\rangle$ described by the lowest in energy triplet structure of the [BC${}_4$H*${}_{12}{]}^{+}(T,C_{2v})$ cluster (Figure 2b). The energy of such a transition is calculated from the difference between the total energies of levels $|{\psi }_{in}\rangle$ and $|{\psi }_{Cr}\rangle$ to be equal to 1.17 eV.

The angles in the cluster are equal to ${\theta }_1\approx {65}^{\circ },{\theta }_3\approx {128}^{\circ }$. Calculations of a spin density at the center of the cluster give the value of the superposition parameter $A_0=\sqrt{7}/4$. The effective charge for $2s$ and $2p$ states of the boron atom is $\tilde{Z}=2.6$. Substituting the calculated values into Formulas (51) and (52), we obtain a numerical estimate of the radiation transition rate of the impurity center ${(}_{\mu }$B${)}^{+}$ into a hybridized state:

$$w_{\mathrm{hybr}}={\tau }_{+}^{-1}\approx 1.7\times {10}^{11}{s}^{-1}.$$

(53)

The obtained value confirms the validity of the assumption on the kinetics of a charged radiation defect ${(}_{\mu }$B${)}^{+}$ thermalization reported in [24]. The hybridization rate (53) is two orders of magnitude less than the rate of a non-hybridized charged center formation.

The hybridized charged center (${}_{\mu }$B)${}^{+}$ quickly, during characteristic lattice times, transfers into a neutral state. Therefore, the neutralization time of a charged defect formed by a negative muon in a diamond lattice is determined by the value of (53), and at least two order higher than that for silicon and germanium (40).

7. Formation of an Ionized Acceptor Center

In this section, we will consider the process of an electron capture on the neutral radiation defect with totally restored chemical bonds and the formation of an acceptor center in the ionized state.

According to our cluster calculations, the neutral ${[(}_{\mu }$B)C${}_4{]}^0$ defect has $C_{3v}$ symmetry and creates the substantial electric dipole moment, which is equal to 1.08D, in a diamond lattice. Here, D is Debye, the unit of an electric dipole moment in the atomic system of units (D$={10}^{-18}$CGSE). The dipole moment is directed along the symmetry axis. Therefore, we can suppose that any neutral cluster of a type ${[(}_{\mu }$A) A${}_4{]}^0$ in crystals with a diamond structure possesses an electric dipole moment of the order of 1D.

This electric dipole moment gives rise to an interaction necessary to capture a lattice electron and the form of an ionized acceptor center. The neutral center ${}_{\mu }$A has unsaturated chemical bonds because a crystal lattice turns out to be deformed. This deformation is a reason to change a phonon spectrum and the local phonon mode appearance. Chemical bounds are saturated after the missing electron capture. The new cluster is an ionized acceptor center and possesses a local crystal symmetry. When the ionized acceptor center is formed, an appropriate phonon of the local mode is radiated, and crystal deformations disappear. Therefore, the problem is very similar to the problem of the thermalization of molecular ions in molecular crystals and cryocrystals of noble atoms (see e.g., [32,33,34]). An exact solution of the problem taking into account a crystal symmetry is scarcely possible. However, qualitative estimations can be obtained in some approximations [35,36].

7.1. Effective Hamiltonian and Interaction Operator

Detailed calculations of an ionized acceptor center formation in diamond, silicon and germanium were carried out in [35,36], and here, we will present the main results. The electric dipole moment creates a scalar potential, and the interaction energy with lattice electrons is $\mathcal{U}=e\phi =e\left(\mathbf{d}\mathbf{r}\right)/\left(\epsilon r^3\right)$, where $\epsilon$ is a dielectric penetration. Therefore, taking into account the displacement $\mathbf{u}$ ($\mathbf{r}\to \mathbf{r}+\mathbf{u}$) and neglecting the changing of the denominator of the potential, we can write an electron-phonon interaction operator:

$${\widehat{V}}_{\mathrm{e}-\mathrm{ph}}\approx \frac{e\left(\mathbf{d}\widehat{\mathbf{u}}\right)}{\epsilon r^3}=\frac{ed}{\epsilon r^3}\cos \theta \widehat{u},$$

(54)

The operator of radial displacements can be determined in the approach of an isotropic elastic media. For this reason, we need to study vibrations of a sphere at the center of which is placed an electric dipolar moment $\mathbf{d}$. This dipolar moment creates an electric induction $\mathbf{D}$, and a displacement vector $\mathbf{u}$ satisfies the following equation:

$${\ddot{u}}_i-c_{\parallel }^2\Delta u_i-\frac{\varkappa }{{\epsilon }^2\rho }{D}_i{D}_k▵u_k=0,$$

(56)

where $c_{\parallel }$ is the longitudinal sound velocity, $\varkappa$ is the dielectric susceptibility and $\epsilon =1+4\pi \varkappa$, $\rho$ is the density of a media.

To solve Equation (55), we will take into account only radial vibrations of a deformed crystal lattice with respect to the center of the sphere. The center of this sphere coincides with our radiation defect. Therefore, we can introduce as usual for problems with central symmetry a radial displacement $\chi =ur$. In this case, we have the more simple equation for $\chi$:

$$\ddot{\chi }-\left(c_{\parallel }^2+\frac{4\varkappa d^2}{{\epsilon }^2\rho }\frac{1}{r^6}\right){\chi }^{″}=0,$$

(56)

where ${\chi }^{″}$ is the second derivative on the radial variable r. Making the one-dimensional Fourier transformation for the function $\chi (r,t)$:

$${\chi }_{\omega ,k}=2\underset{-\infty }{\overset{\infty }{\int }}dt{e}^{i\omega t}\underset{0}{\overset{\infty }{\int }}dr\sin \left(kr\right)\chi (r,t),$$

(57)

we obtain a dispersion relation in a long wavelength approximation:

$$({\omega }^2-k^2{c}_{\parallel }^2-{\mathsf{\Omega }}^2){\chi }_k=0,\mathsf{\Omega }=\frac{d}{\epsilon R_1^4}\sqrt{\frac{\varkappa }{6\pi \rho }},$$

(59)

where $R_1$ is the radius of the first coordination sphere. More detailed calculations are represented in Appendix A.

The numerical estimates for the frequency $\mathsf{\Omega }$ in diamond, silicon and germanium crystals are presented in

Table 1. Physical parameters of the C, Si and Ge crystals and the estimate of the frequency $\mathsf{\Omega }$.

Crystal	Density $\mathit{\rho }$, g cm${}^{-3}$	${\mathit{R}}_{\mathbf{1}}\mathbf{,}$ ${10}^{-8}$ cm	Dielectric Constant	$\mathsf{\Omega },$ ${10}^9$ s${}^{-1}$	Ionization Energy of the Acceptor, eV
Diamond	3.51	3.57	5.75	8.1 d	${}_{\mu }$B, 0.37
Silicon	2.33	5.43	11.97	1.4 d	${}_{\mu }$Al, 0.069
Germanium	5.323	5.66	16.0	0.66 d	${}_{\mu }$Ga, 0.011

(the parameters oft the crystals were taken from [37,38]). Since a dipole moment d is considered as an unknown parameter, the numerical estimates are presented in units of Debye.

Now, we can construct an effective Hamiltonian describing the radial vibrations of a lattice and determine the operator of radial displacements $\widehat{u}$ in Operator (54). Consider radial vibrations in a sphere with the radius $R_D$ with boundary conditions $u\left(R_D\right)=0$. Keeping a dependence on time t, we need to use discrete Fourier amplitudes ${\chi }_n$ instead of Equation (57):

$${\chi }_n=2\underset{0}{\overset{R_D}{\int }}dr\sin \left(k_{n}r\right)\chi (r,t),$$

(59)

where $k_n=\pi n/R_D$.

Therefore, ${\chi }_n$ and $\rho {\dot{\chi }}_n$ are generalized coordinates and the momentum of the system under consideration, respectively. The effective Hamiltonian for a system of independent oscillators can be written as:

$${\widehat{H}}_{ph}=\sum _n\frac{1}{2}\hslash {\omega }_n\left({\widehat{\mathcal{P}}}_n^2+{\widehat{\mathcal{Q}}}_n^2\right).$$

(60)

Here,

$${\omega }_n=\sqrt{c_{\parallel }^2{k}_n^2+{\mathsf{\Omega }}^2},$$

(61)

and the dimensionless generalized momentum and coordinate are defined as usual:

$${\widehat{\mathcal{P}}}_n=\rho {\widehat{\dot{\chi }}}_n/p_{0n},{\widehat{\mathcal{Q}}}_n={\widehat{\chi }}_n/q_{0n},$$

(62)

while the units of the generalized momentum and coordinate are equal to:

$$q_{0n}=\sqrt{\frac{\hslash }{{\omega }_n\rho R_D}},p_{0n}=\sqrt{\hslash {\omega }_n\rho R_D}.$$

Introducing, as usual, the annihilation and creation operators:

$${\widehat{b}}_n=\frac{1}{\sqrt{2}}\left({\widehat{\mathcal{Q}}}_n+i{\widehat{\mathcal{P}}}_n\right),{\widehat{b}}_n^{†}=\frac{1}{\sqrt{2}}\left({\widehat{\mathcal{Q}}}_n-i{\widehat{\mathcal{P}}}_n\right),[{\widehat{b}}_n,{\widehat{b}}_{n^{\prime }}^{†}]={\delta }_{n{n}^{\prime }},$$

(63)

we obtain the operator of radial displacements of a lattice, which must be substituted in Equation (54), in the form:

$$\widehat{u}=\frac{\widehat{\chi }}{r}=\frac{1}{r}\sum _n\sqrt{\frac{2\hslash }{\rho \omega \left(k_n\right)R_D}}\sin \left(k_{n}r\right)\left(b_n^{†}+b_n\right).$$

(64)

It is easy to see that the interaction operator (54) has a strong singularity at $r\to 0$, which leads to the divergence of matrix elements. However, Operator (54) is obtained in a dipolar approximation; its expression is valid for respectively large values of the radius vector and is not applicable at $r\to 0$. In this case, as usual (see e.g., [39]), the potential is taken as constant at $r<R_0$, where $R_0$ is a certain characteristic distance, i.e.,

$${\widehat{V}}_{\mathrm{e}-\mathrm{ph}}\approx \left\{\begin{array}{cc}\left(ed/\left(\epsilon r^3\right)\right)\cos \theta \widehat{u},\hfill & \mathrm{for}r>R_0,\hfill \\ \left(edr/\left(\epsilon R_0^4\right)\right)\cos \theta \widehat{u},\hfill & \mathrm{for}r<R_0.\hfill \end{array}\right.$$

(66)

In our case, we can take $R_0\ge r_0$, where $r_0$ is the length of chemical bonds in the lattice.

7.2. Electron Capture Rate

The probability of electron capture per unit time can be calculated with the well-known Fermi golden rule:

$$d{w}_{if}\equiv d{w}_{\mathrm{capt}}=\frac{2\pi }{\hslash }{\left|\langle f|{\widehat{V}}_{\mathrm{e}-\mathrm{ph}}|i\rangle \right|}^2\delta (E_f-E_i)d{\nu }_f\frac{d\mathbf{k}}{{\left(2\pi \right)}^3}.$$

(66)

We will consider a case of low temperature, and the initial state $|i\rangle =|\mathbf{k}\rangle |0_{\mathrm{ph}}\rangle$ corresponds to the free electron in the valence band with the wave-vector $\mathbf{k}$ and the absence of exited radial phonons. The final state is determined by the captured electron to the $|ns\rangle$ or $|np\rangle$ hybridized state of the cluster and by the excitation of the radial phonon with the wavevector ${\mathbf{k}}_{\mathrm{ph}}$:

$$|f\rangle =\left(\begin{array}{c}|ns\rangle \\ |np\rangle \end{array}\right)|{\mathbf{k}}_{\mathrm{ph}}\rangle .$$

Here, $n=2,3$ and 4 for C, Si and Ge, respectively. Equation (66) takes into account that all electrons having wavevectors in the interval from $\mathbf{k}$ to $\mathbf{k}+d\mathbf{k}$ can be captured by the cluster.

The volume element of the final states in the case of one-dimensional motion is equal to:

$$d{\nu }_f=R_D\frac{d{k}_{\mathrm{ph}}}{2\pi }do,$$

where $do$ is the element of the solid angle into which a phonon is emitted. The energies of the initial and final states are:

$$E_i=E_0+\frac{{\hslash }^2{k}^2}{2m^{*}},E_f=E_{-}+\hslash \omega \left(k_{\mathrm{ph}}\right),E_0-E_{-}=\hslash ▵,$$

$m^{*}$ is the effective mass of the electron. To obtain numerical results, the ionization energy of the cluster (acceptor) is taken for $\hslash ▵$.

Integration of (66) over k gives:

$$d{w}_{\mathrm{capt}}=\frac{m^{*}}{{\left(2\pi \hslash \right)}^2}\frac{2}{3\rho }{\left(\frac{ed}{\epsilon }\right)}^2{\left|{}_e\langle f\left|F\left(r\right)e^{i{k}_{\mathrm{ph}}r}\right|{\mathbf{k}}_0\rangle \right|}^2\frac{k_0}{\omega \left(k_{\mathrm{ph}}\right)}d{k}_{\mathrm{ph}}d\mathsf{\Omega },$$

(67)

where a vector of the final state ${|f\rangle }_e$ takes into account electron states only, and according to Equation (65),

$$F\left(r\right)=\left\{\begin{array}{cc}{r}^{-4},\hfill & \mathrm{for}r>R_0,\hfill \\ R_0^{-4},\hfill & \mathrm{for}r<R_0.\hfill \end{array}\right.$$

(68)

Here:

$$k_0^2=\frac{2m^{*}}{\hslash }(▵-{\omega }_{\mathrm{ph}}).$$

(69)

For the further analysis, it is convenient to introduce the dimensionless parameters and variables:

$$x=\frac{\tilde{Z}}{n{a}_0}r,{\tilde{k}}_{\mathrm{ph}}=\frac{n{a}_0}{\tilde{Z}}{k}_{\mathrm{ph}},{\tilde{k}}_0=\frac{n{a}_0}{\tilde{Z}}{k}_0,$$

(70)

where $n=2,3$ and 4 for C, Si and Ge, respectively. The estimated characteristic parameters for considered crystals are summarized in

Table 2. Characteristic parameters estimated for C, Si and Ge.

Crystal	${\mathit{r}}_0$, ${10}^{-8}$ cm	$\tilde{\mathit{Z}}$	${\tilde{\mathit{r}}}_0$	${\mathit{\omega }}_0$, ${10}^{14}$c${}^{-1}$	${\mathit{k}}_{0,\mathit{max}}$, ${10}^7$ cm${}^{-1}$	${\tilde{\mathit{k}}}_{0,\mathit{max}}{\tilde{\mathit{r}}}_0$	${\mathit{k}}_{\mathbf{ph},\mathit{max}}$, ${10}^8$ cm${}^{-1}$	${\tilde{\mathit{k}}}_{\mathbf{ph},\mathit{max}}{\tilde{\mathit{r}}}_0$
C	1.54	2.6	3.78	3.32	3.1	0.48	4.2	15.9
Si	2.34	3.5	5.15	1.05	1.34	0.31	1.18	2.78
Ge	2.44	5.0	5.75	1.24	0.54	0.13	0.32	0.77

.

All considered crystals are anisotropic, and the sound velocity $c_{\parallel }$ in the dispersion relation (58) depends on the direction of a phonon propagation. To take this into account, we will use, as usual, the average value of the longitudinal velocity of sound $\langle c_{\parallel }\rangle$, neglecting the effects of anisotropy.

We define a characteristic frequency:

$${\omega }_0=\langle c_{\parallel }\rangle \frac{\tilde{Z}}{n{a}_0}$$

(71)

and corresponding dimensionless frequencies $\tilde{\omega }={\omega }_{\mathrm{ph}}/{\omega }_0,\widetilde{▵}=▵/{\omega }_0$ and $\tilde{\mathsf{\Omega }}=\mathsf{\Omega }/{\omega }_0$. Taking into account the dispersion relation of the radial phonons (58), we can write the electron capture rate in the form:

$$w_{\mathrm{capt}}=G_n\int \frac{d\mathsf{\Omega }}{4\pi }\underset{\tilde{\mathsf{\Omega }}}{\overset{\widetilde{▵}}{\int }}\frac{{\left|{\tilde{k}}_0\mathcal{A}({\tilde{k}}_{\mathrm{ph}},{\tilde{k}}_0)\right|}^2}{\sqrt{(\widetilde{▵}-\tilde{\omega })({\tilde{\omega }}^2-{\tilde{\mathsf{\Omega }}}^2)}}d\tilde{\omega },$$

(73)

where:

$$G_n=\frac{1}{6\pi \rho m^{*}}{\left(\frac{2m^{*}}{\hslash \langle c_{\parallel }\rangle }\right)}^{3/2}{\left(\frac{ed}{\epsilon }\right)}^2{\left(\frac{\tilde{Z}}{n{a}_0}\right)}^{13/2}.$$

(73)

The dimensionless matrix element $\mathcal{A}$ is determined by Function (68):

$$\mathcal{A}({\tilde{k}}_{\mathrm{ph}},{\tilde{k}}_0){=}_e\langle f\left|F\left(x\right)e^{i{\tilde{k}}_{\mathrm{ph}}x}\right|{\tilde{\mathbf{k}}}_0\rangle .$$

(74)

Equation (72) shows that the electron can be captured both in s- and p-states of the hybridized state of the cluster. As was shown in [36], the capture rate to the p-state $w^p$ is approximately two orders less than the capture rate to s-state $w^s$. Therefore, in the following, we can consider the electron capture to the s-state. In this case, the matrix element (74) is given by the expression:

$${\mathcal{A}}_n^s({\tilde{k}}_{\mathrm{ph}},{\tilde{k}}_0)=\frac{1}{\sqrt{2}\pi {\tilde{k}}_0}\underset{0}{\overset{\infty }{\int }}F\left(x\right)R_{n0}\left(x\right)e^{i{\tilde{k}}_{\mathrm{ph}}x}\sin ({\tilde{k}}_{0}x)xdx={\tilde{k}}_0^{-1}(I_1^{\left(n\right)}\left(\tilde{\omega }\right)-i{I}_2^{\left(n\right)}\left(\tilde{\omega }\right)),$$

(75)

where $I_1\left(\tilde{\omega }\right)$ and $I_2\left(\tilde{\omega }\right)$ are the real and imaginary parts of the matrix element, respectively. Finally, the capture rate (72) has the form:

$$w_{\mathrm{capt}}\approx w^s=G_n\underset{\tilde{\mathsf{\Omega }}}{\overset{\widetilde{▵}}{\int }}\frac{{(I_1^{\left(n\right)}\left(\tilde{\omega }\right))}^2+{(I_2^{\left(n\right)}\left(\tilde{\omega }\right))}^2}{\sqrt{(\widetilde{▵}-\tilde{\omega })({\tilde{\omega }}^2-{\tilde{\mathsf{\Omega }}}^2)}}d\tilde{\omega },$$

(76)

Obtained Formula (76) determines the formation rate of the ionized acceptor center through the capture of the electron of the medium on the neutral radiation defect induced by the negative muon or pion in crystals. Analytical expressions depend on well-known characteristic parameters of the medium except for two parameters of the cluster, namely, the electric dipolar moment d and the parameter $R_0$ in Equation (65). The dependence on d of the integral in Equation (75) is weak and can assume that $w_{\mathrm{capt}}\propto d^2$. Unfortunately, the dependence of the results on the parameter $R_0$ is more critical, because the matrix elements exponentially depend on the lower integration limit. Nevertheless, the parameter $R_0$ cannot be smaller than the length of the chemical bound in the lattice. We can determine the upper limit also $R_0⩽R_1$, the radius of the first coordination sphere.

Numerical calculation were performed for several different values of the uncertain parameters d and $R_0$. The results are summarized in

Table 3. Estimate of the formation rate of ionized acceptor centers ${{(}_{\mu }A)}^{-}$ in the C, Si and Ge crystals.

d	${\mathit{x}}_0$, C	${\mathit{w}}_{\mathbf{capt}}$, C$·{10}^8$ s${}^{-1}$	${\mathit{x}}_0$, Si	${\mathit{w}}_{\mathbf{capt}}$, Si $·{10}^8$ s ${}^{-1}$	${\mathit{x}}_0$, Ge	${\mathit{w}}_{\mathbf{capt}}$, Ge $·{10}^8$ s ${}^{-1}$
1.0	3.78	22.0	5.12	0.71	5.76	14.3
0.5	3.78	5.9	5.12	0.19	5.76	3.8
0.2	3.78	0.98	5.12	0.034	5.76	0.65
1.0	5.5	2.2	7.5	0.095	7.5	2.4
0.5	5.5	0.58	7.5	0.024	7.5	0.64
0.2	5.5	0.09	7.5	2.6$·{10}^{-3}$	7.5	0.11

.

According to the obtained results in the considered range of the uncertain parameters $R_0$ and d, the spread of the estimates of the capture rates is about two orders of magnitude and seems at first unsatisfactory. However, it is not surprising because both the dipole approximation and the dispersion relation for the radial phonons (58) are quite rough for $r\sim R_1$. Nevertheless, the considered interaction mechanism is fairly justified and describes the process of the electron capture on the neutral defect of the lattice with the formation of the ionized state of the acceptor center.

8. Discussion

We have considered the total process of an acceptor center formation in crystals with the diamond structure, which appears as a radiation defect induced by negative pions or muons. It was shown that the evolution of this kind of radiation defects can be divided into two physically different stages. At the first stage, the negatively-charged particle is stopped in the crystal and captured by a nucleus with the charge Z (in the case of ${\pi }^{-}$) or at the K-shell of a muonic atom (in the case of ${\mu }^{-}$). Both negative pions and muons create a host nucleus with an effective charge $Z-1$. This strongly-charged center interacts with trace electrons and captures them. This stage of radiation defect neutralization exists because of Coulomb interaction. Numerical calculations show that this stage of neutralization strongly differs in diamond and other crystals. Namely, the radiation defect is completely neutralized in Si and Ge for a relatively short time ${\tau }_n\le {10}^{-11}$ s. In diamond, this radiation defect can be completely neutralized for a long time ${\tau }_n>{10}^{-6}$ s.

The second stage of evolution of this radiation defect is connected with restoration of chemical bonds with the lattice as the first step and formation of an appropriate acceptor center as the final step. Chemical bonds in Si and Ge are restored for neutral radiation defects and in C chemical bonds can be formed for a single-fold charged center. Formation of a chemically-bound radiation defect is accompanied with sufficiently large energy emission. Therefore, the process of chemical bonds’ formation can be described with the help of radiation transition. Our estimates gave rather a long time for this step: ${\tau }_{\mathrm{hybr}}\approx 2.6\times {10}^{-9}$ s for Si and ${\tau }_{\mathrm{hybr}}\approx 2.0\times {10}^{-9}$ s for Ge. Charged radiation defect in C forms chemical bonds very quickly: ${\tau }_{\mathrm{hybr}}\approx 0.6\times {10}^{-11}$ s. We can see that this time is many orders shorter than ${\tau }_n$. Therefore, the radiation defect in diamond is neutralized in the chemically-bound state. This time cannot be strictly estimated, but we can suppose that it is determined by characteristic electronic times in the lattice and must be of the order of ${10}^{-10}$ s. We can conclude that the first step of the formation of a chemically-bound neutral radiation defect is approximately two orders shorter in diamond with respect to silicon and germanium.

The second step finishes the formation of an acceptor center in the ionized state. This step is similar in all of the above-mentioned crystals, but very complicated for obtaining good quantitative results. We can see that the chemically-bound neutral radiation defect is a cluster with unsaturated chemical bonds. This unsaturated chemical bond can be saturated if an electron of a valence band of the crystal is captured by the cluster. What kind of interaction gives an opportunity to capture a missing electron? The neutral cluster possesses a relatively large electric dipole moment, which interacts with lattice electrons. This interaction can be qualitatively described in the dipolar approximation. Our analytical and numerical calculations show that:

$$\begin{array}{cc}\hfill 0.5\times {10}^{-10}\mathrm{s}& \le {\tau }_{\mathrm{capt}}\le 2\times {10}^{-8}\mathrm{s}\mathrm{for}\mathrm{diamond},\hfill \\ \hfill 1.4\times {10}^{-8}\mathrm{s}& \le {\tau }_{\mathrm{capt}}\le 2\times {10}^{-7}\mathrm{s}\mathrm{for}\mathrm{silicon},\hfill \\ \hfill 0.5\times {10}^{-9}\mathrm{s}& \le {\tau }_{\mathrm{capt}}\le 1.7\times {10}^{-8}\mathrm{s}\mathrm{for}\mathrm{germanium}.\hfill \end{array}$$

The total time for the acceptor center formation in the ionized state as a result of a radiation defect induced by negative pions and muons is the sum of times for all steps:

$${\tau }_{{\mathrm{ac}}^{-}}={\tau }_n+{\tau }_{\mathrm{hybr}}+{\tau }_{\mathrm{capt}},$$

and is determined by the longest item. The final step is slower with respect to the first two steps, and we can conclude that the formation time of the ionized acceptor center is the shortest for diamond (≤$2\times {10}^{-8}$ s) and the longest for silicon (≤$2\times {10}^{-7}$ s). These values are comparable with characteristic times in semiconductor devices.

The ionized acceptor center is neutralized through the mechanism of Coulomb capture of the hole from the valence band. This process is well studied in many articles (see e.g., [39,40,41]), and we will not concern ourselves with this problem here.

9. Conclusions

The obtained results will be useful both for $\mu$SR experiments and research of different radiation defects in semiconductors. The considered approach can be applied to crystals with the sphalerite-type structure (A${}_{III}$B${}_V$ semiconductors, e.g., GaAs, InSb, CdS), which are widely used in electronic devices. Unfortunately, these crystals are more complicated for analysis because of the large variety of possible impurity centers. In addition, the model of chemical bonds must be modified for some calculations.