Shifting the Shear Paradigm in the Crystallographic Models of Displacive Transformations in Metals and Alloys
Abstract
:1. The Origin of the Concept of Simple Shear
2. Shears Used in the Theories of Deformation Twinning
3. Shears Used in the Theories of Martensitic Transformations
3.1. Early Models of Martensitic Transformations
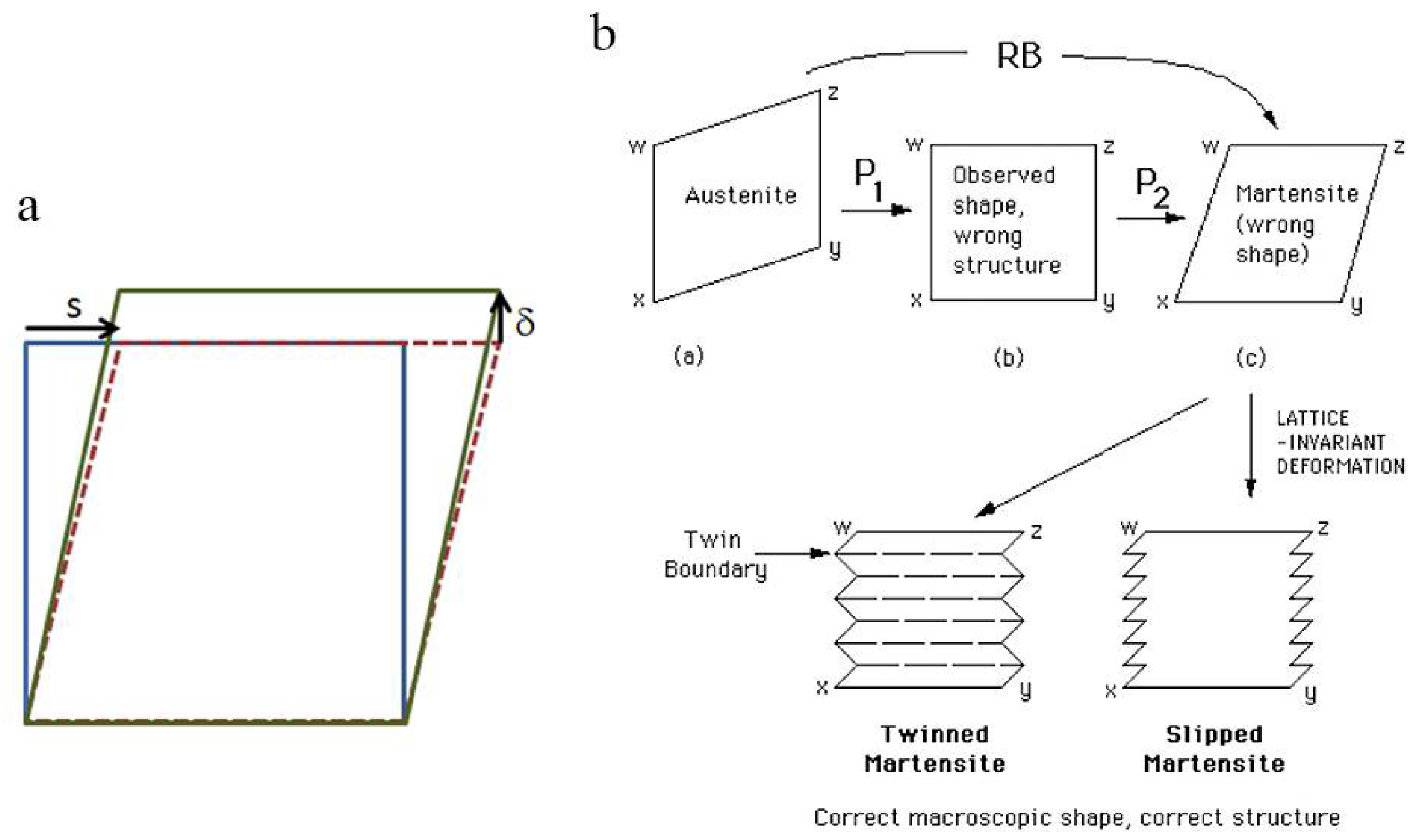
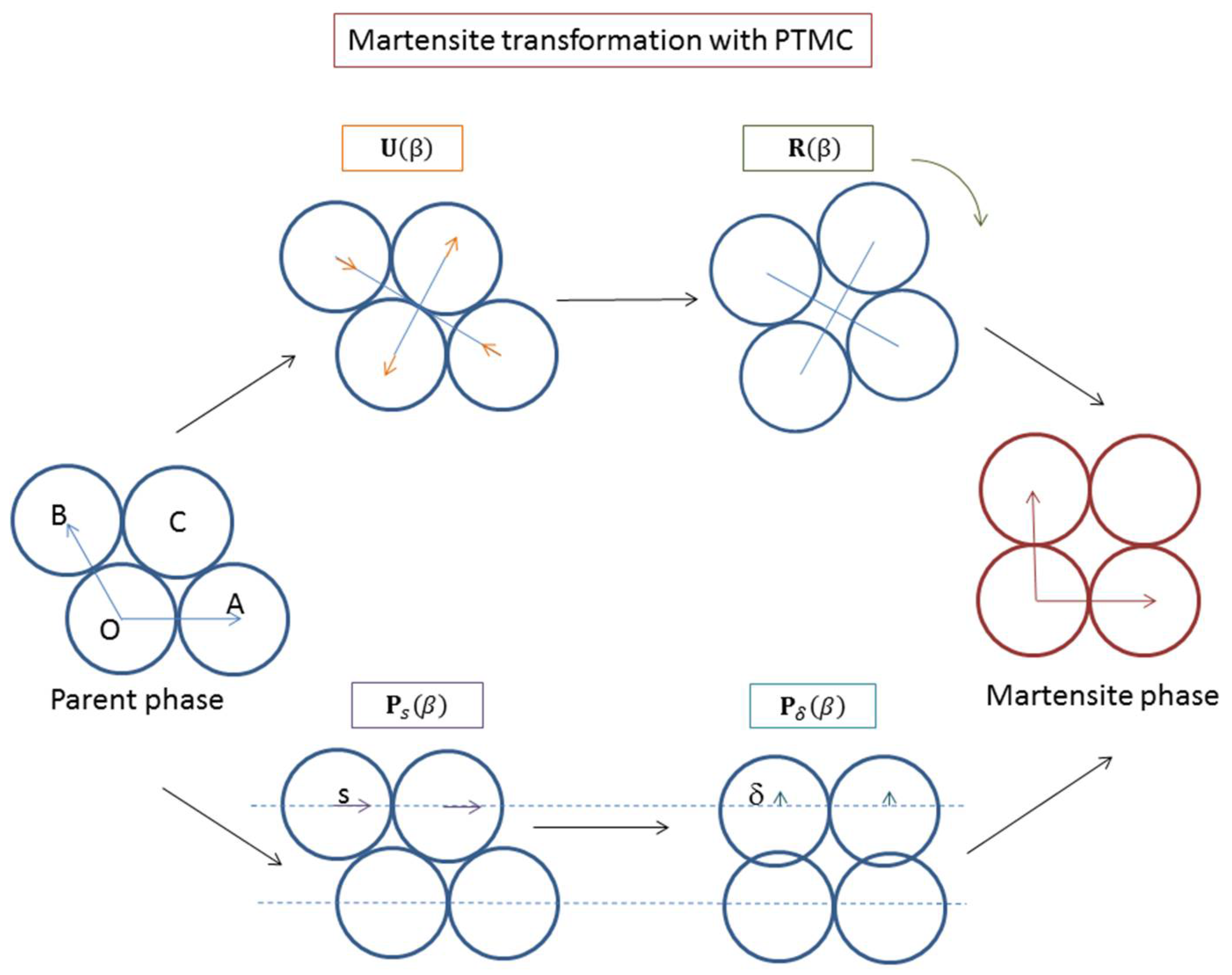
3.2. The Phenomenological Theory of Martensite Crystallography (PTMC)
3.3. Bogers and Burgers’ Model
4. Simple Shear Saved by the Dislocations/Disconnections?
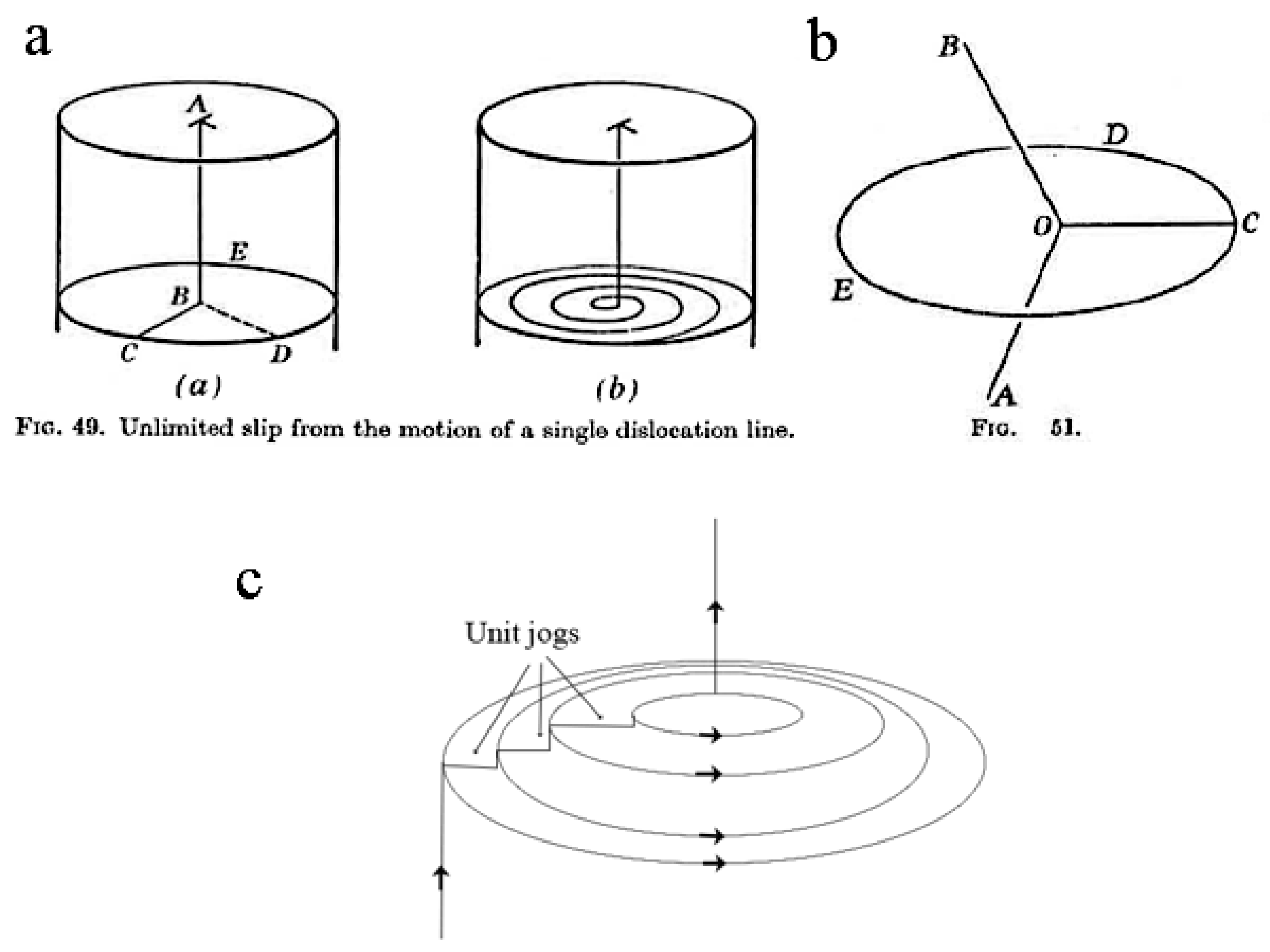
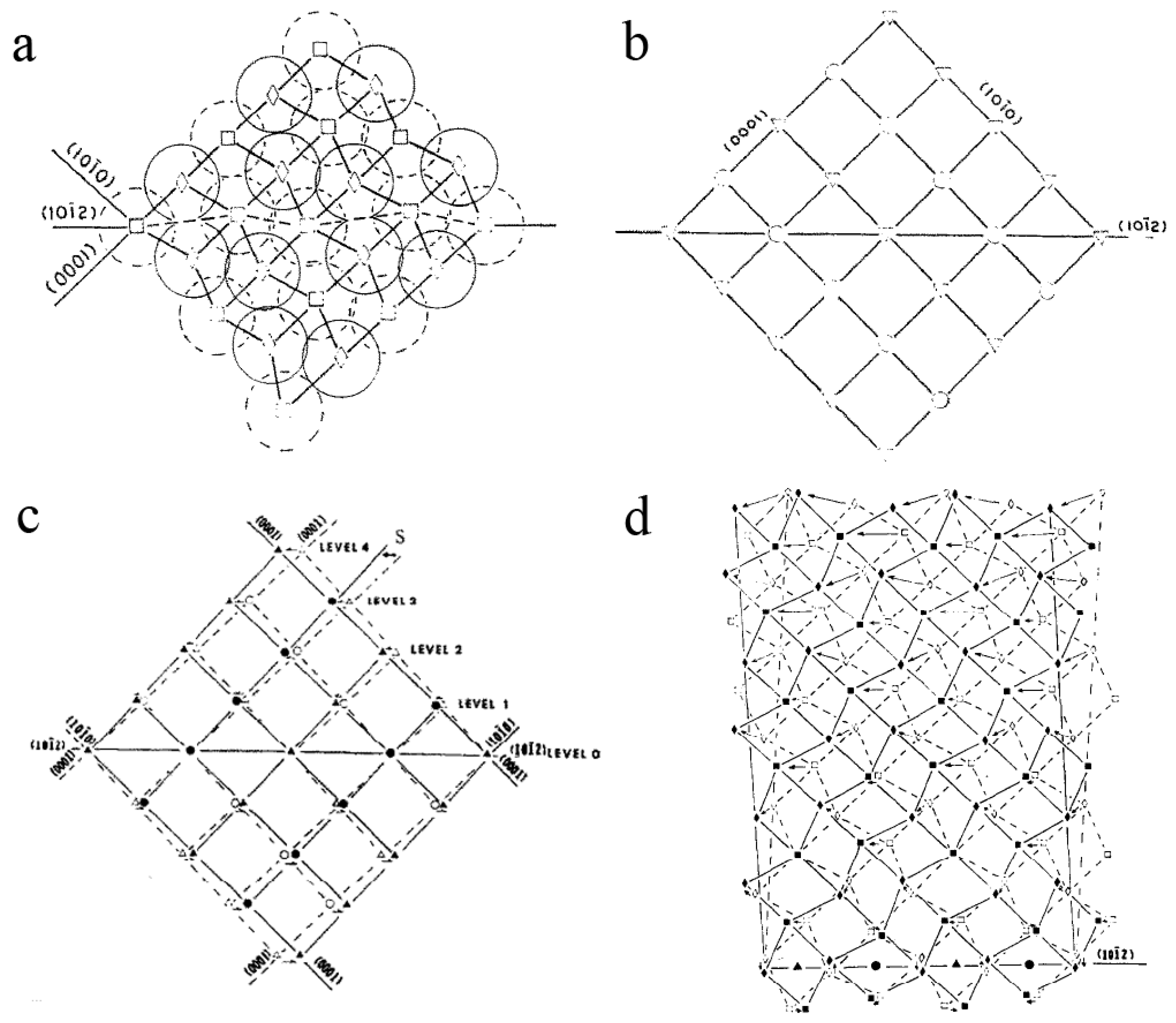
Frank and Read’s model, mentioned by Cottrell, was explained a little earlier in his book; it is a former model of what is now known as “Frank–Read” source of dislocations. In this model, Frank and Read imagined a dislocation rotating around a point, producing a new slip for each revolution, as explained by Cottrell in the Figure 49 of his book [54] reported in Figure 10a,b. Cottrell made a parallel with the spirals formed at the surface of a growing crystal, even if it was clearly stated that this spiral dislocation results from growth and not from deformation. The Frank-Read model used by Cottrell to explain twinning was the ancestor of the “pole mechanism” model. It was followed by Cottrell and Bilby’s model [71], refined by Sleeswyk [69,72] and again later by Venables [73] (Figure 10c). Sleeswyk [69] also imagined how the twinning dislocations at the interface could dissociate at the interface and move away, and he introduced the concept of “emissary dislocations”. General considerations on twinning mechanisms and twinning dislocations in metals can be found in Ref. [2,3]. An updated review was recently published by Mahato et al., in Section 4 of [74].Since a new configuration is produced by twinning, the dislocations that cause it must be imperfect. While it is usually not difficult to discover a suitable imperfect dislocation to cause the required shear of neighbouring planes as it passes between them, the problem is to explain how twinning develops homogeneously through successive planes. The homogeneous shear required a twinning dislocation on every plane without exception, which seems unlikely, or the motion of a single dislocation from plane to plane in a regular manner. Cottrell and Bilby have recently suggested a mechanism, based on that of Frank and Read, whereby the latter process can occur in certain crystals containing dislocations. Figure 51 [reported in Figure 10b] illustrated the mechanism. Here OA, OB, and OC, represent three dislocation lines and CDE is a slip or twinning plane. The dislocation OC (“the sweeping” dislocation) and its Burgers vector both lie in this plane (the “sweeping” plane) and the dislocation can rotate in the plane about the point O. If it is a unit dislocation and remains in the plane as it rotates a slip band is formed. The requirements for twinning (or a shear transformation) to occur are as follows: 1. The sweeping dislocation must be imperfect and produce the correct shear displacement on the sweeping plane; 2. Successive sweeping planes must be joined to form a helical surface.[54]
5. Angular Distortive Transformations
5.1. Twinning Dislocations Replaced by Transformation Waves and Dislocations Induced by Twinning
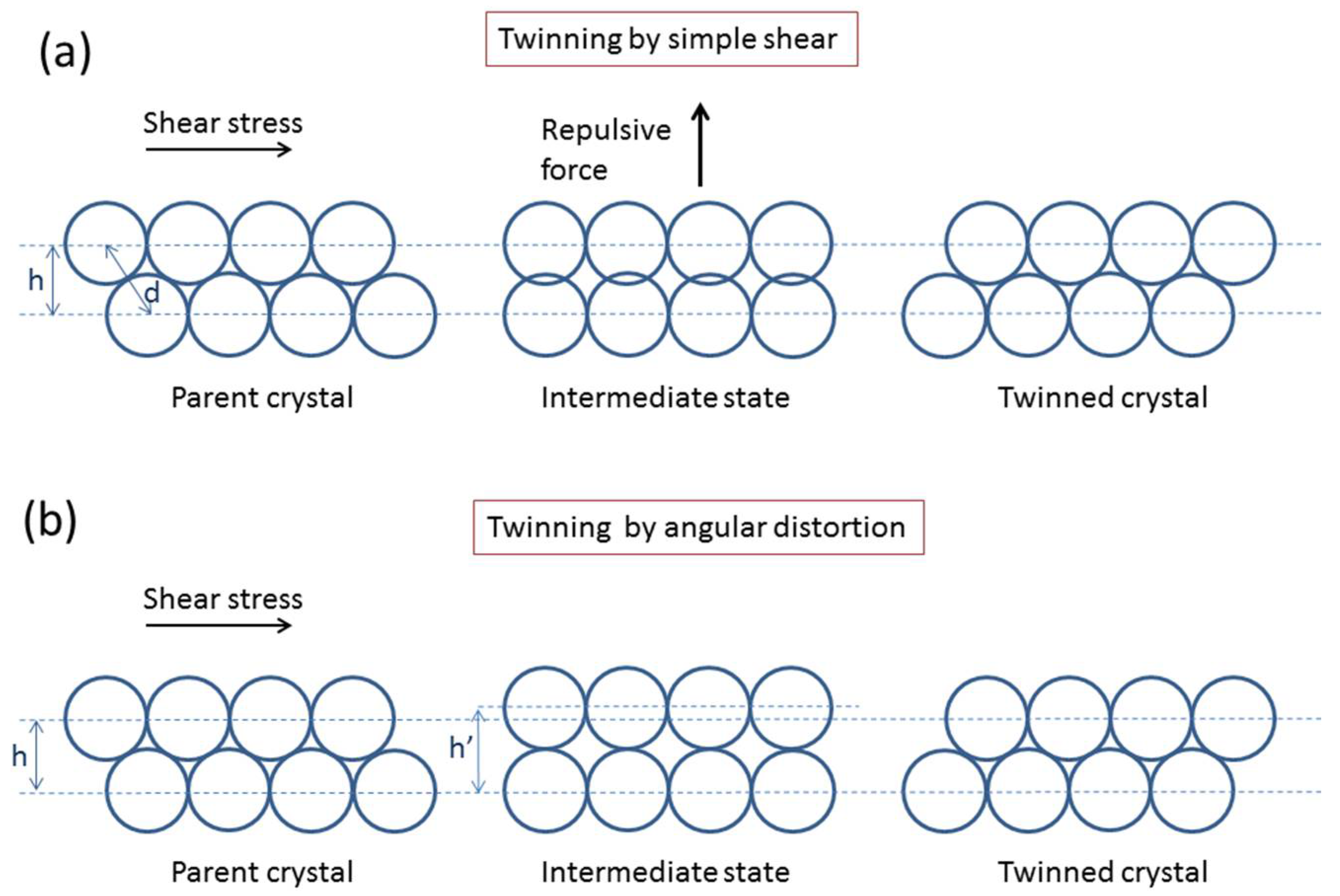
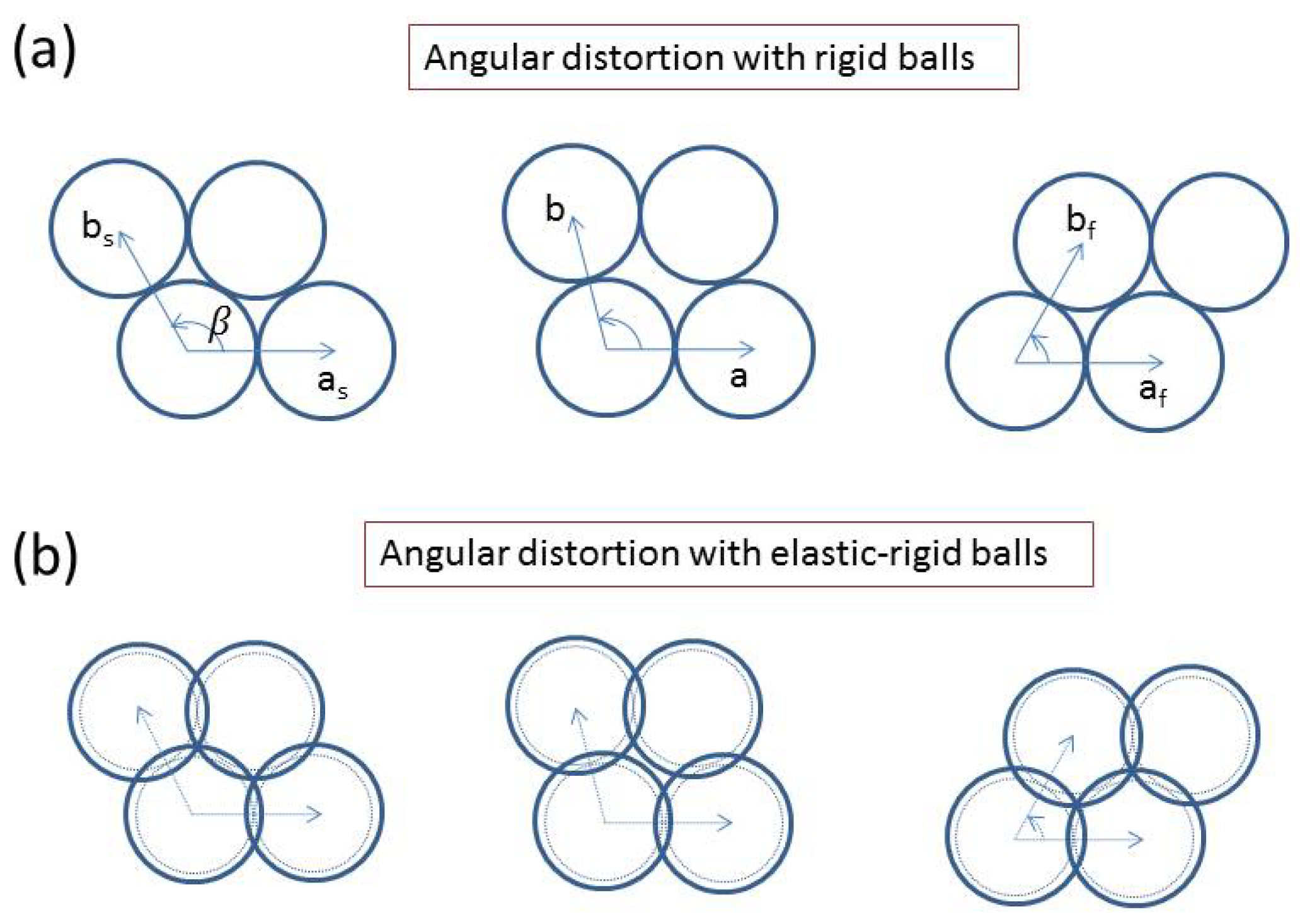
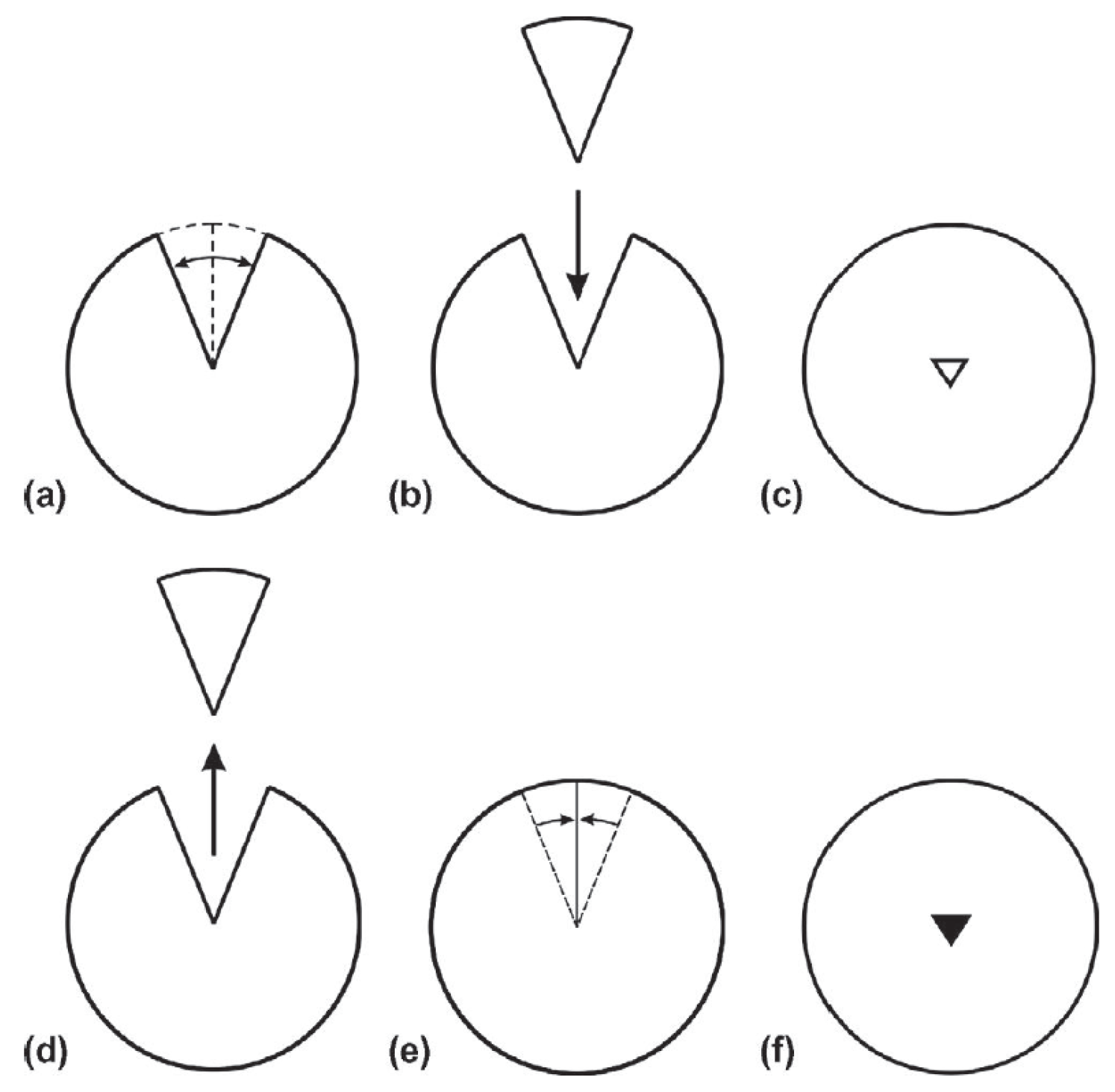
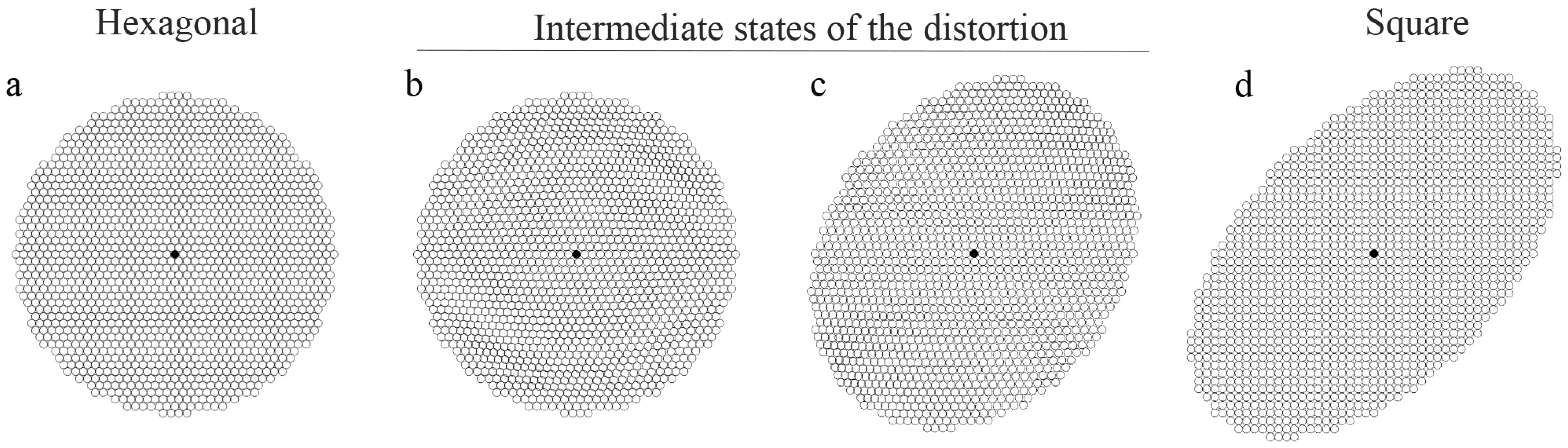
5.2. The Concept of Angular Distortion
5.3. Accommodation Dislocations and Disclinations
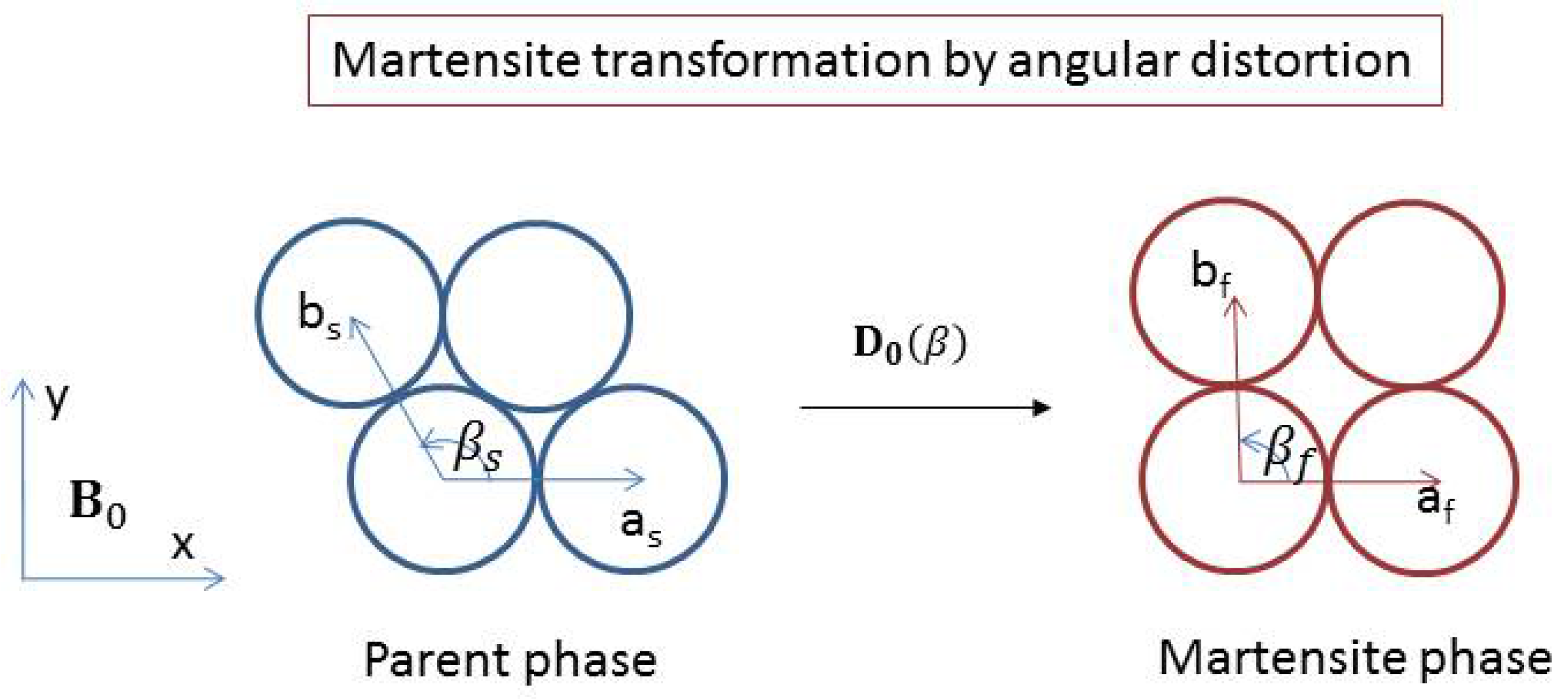
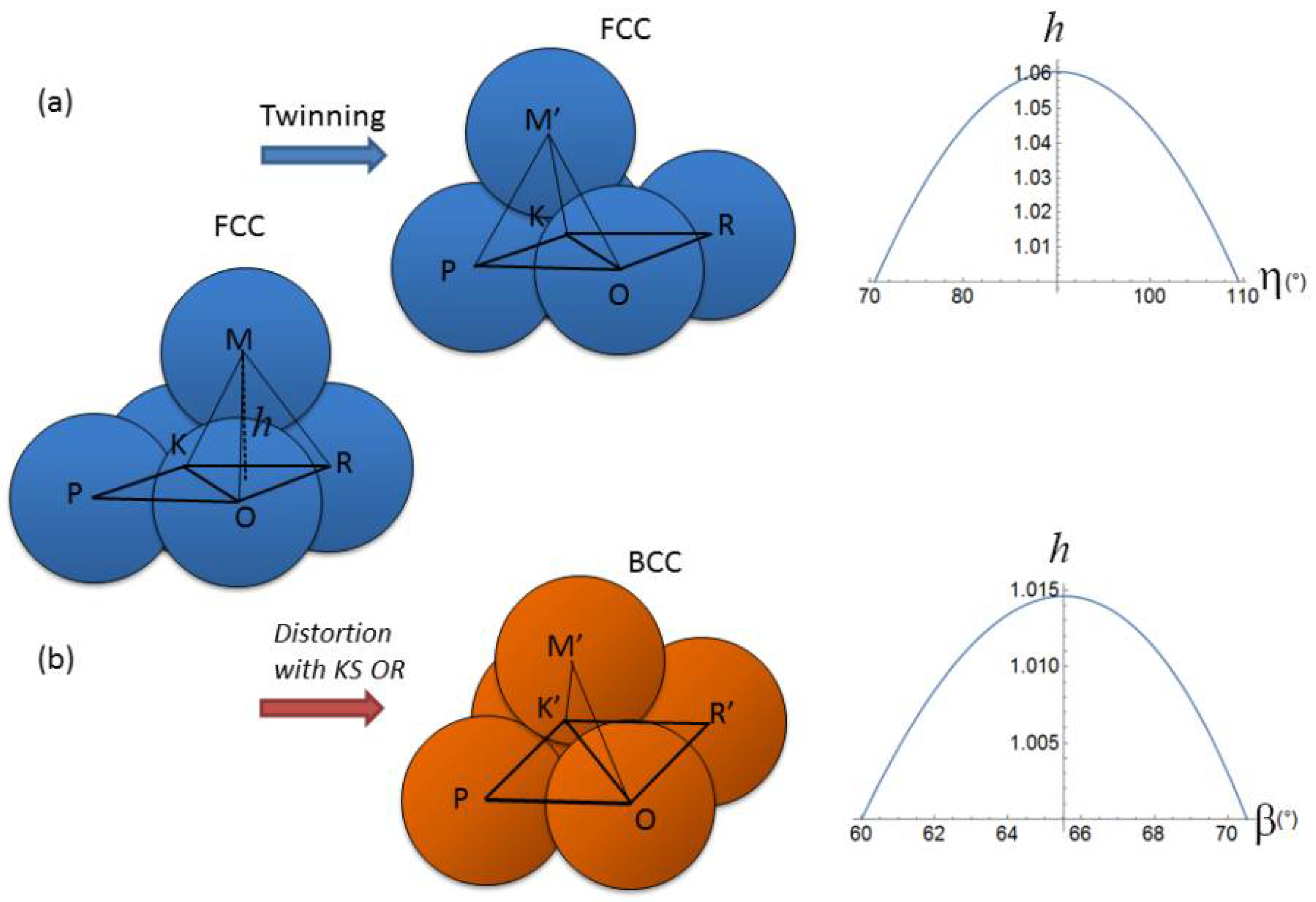
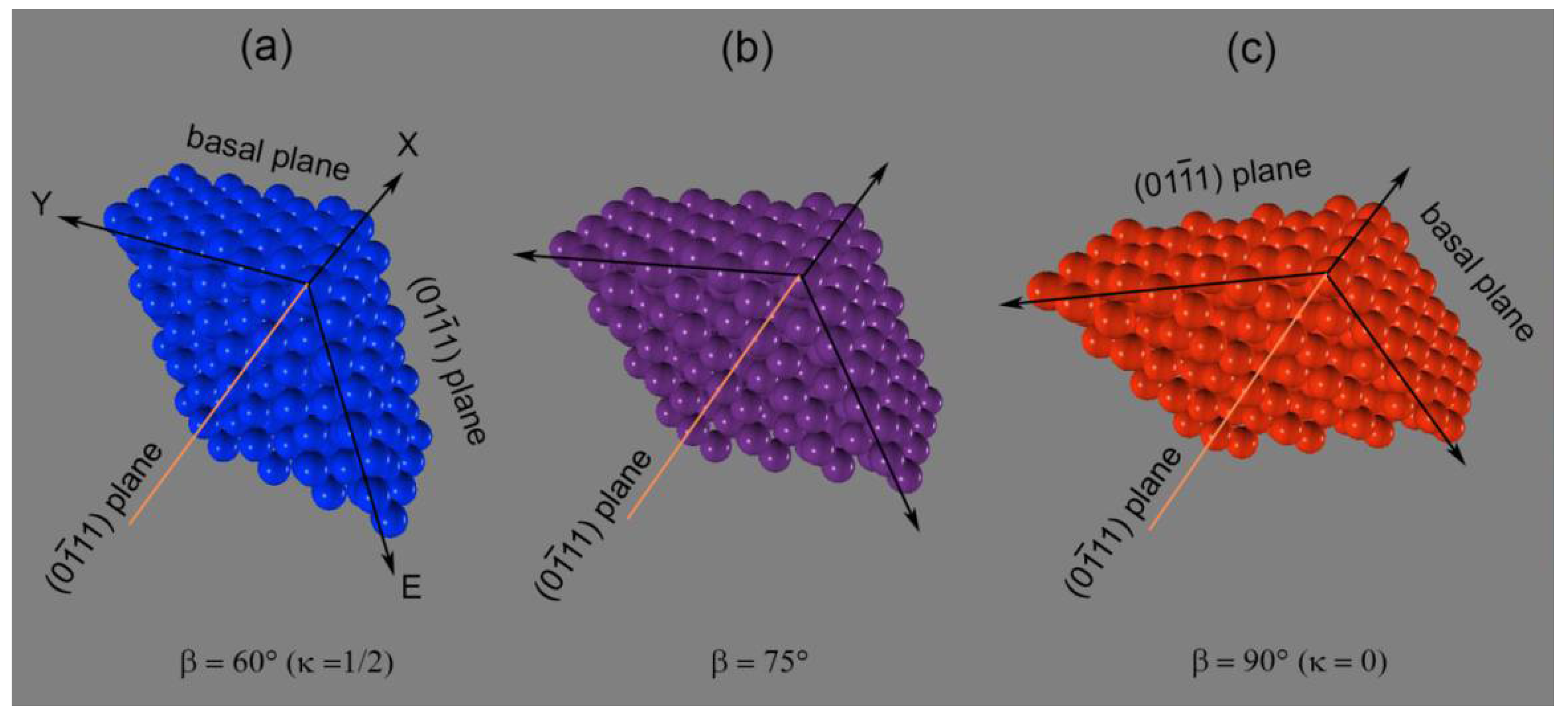
6. Angular Distortion versus the Phenomenological Theory of Martensite Crystallography, Illustrated with a Simple Example
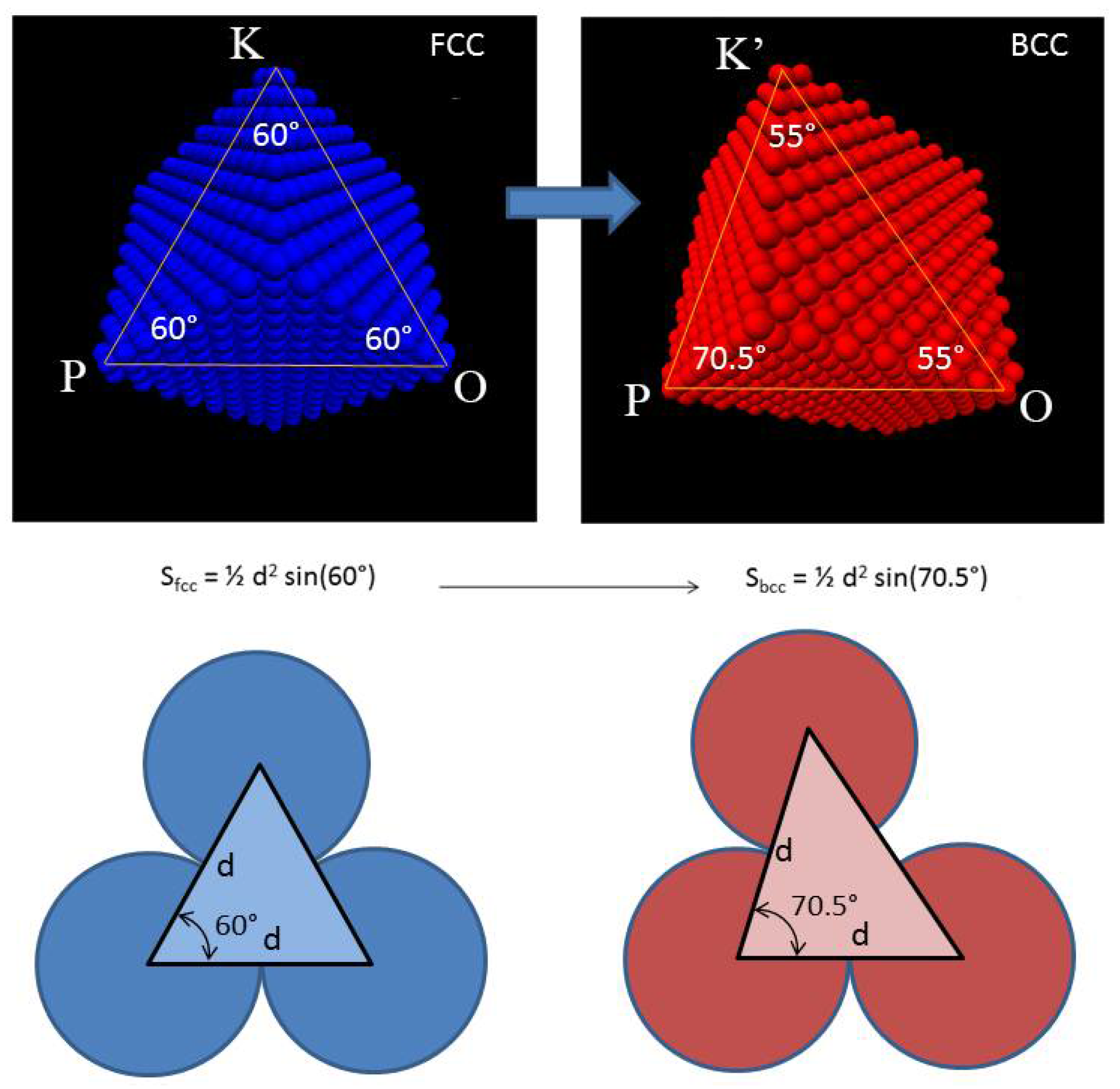
7. The Angular Distortive Model for Face-Centered Cubic–Body-Centered Cubic Martensitic Transformation
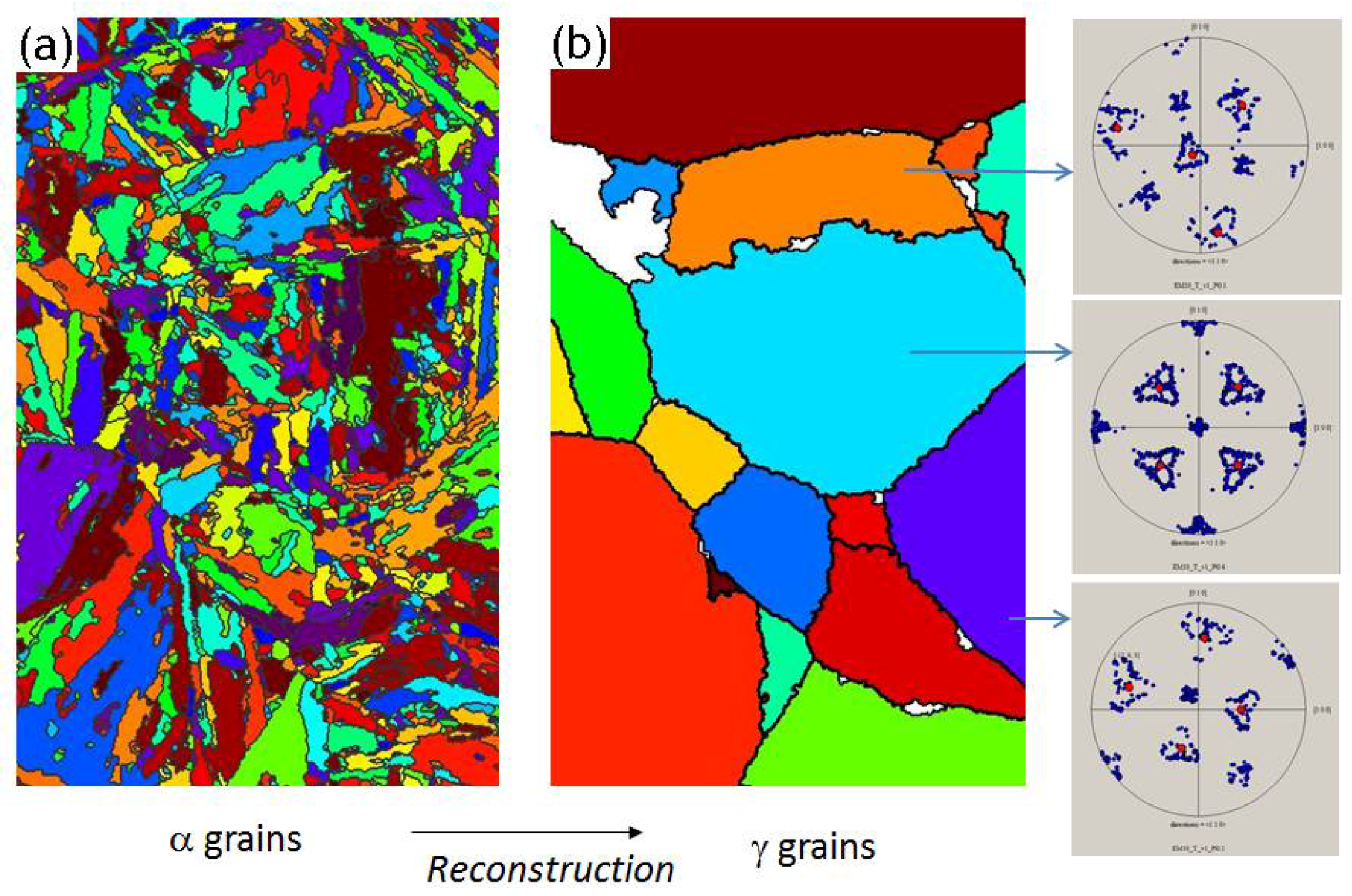
7.1. The Intriguing Continuities in the Pole Figures
7.2. A Two-Step Model Developed to Explain the Continuous Features
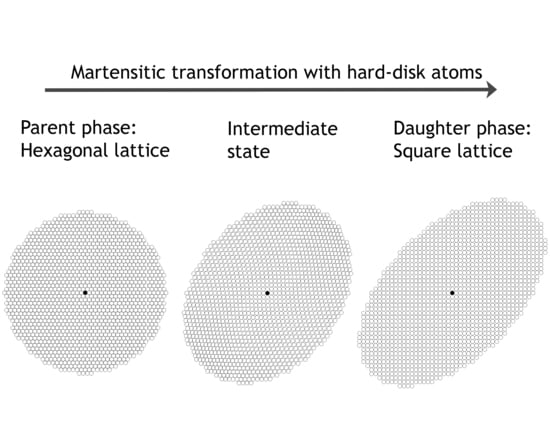
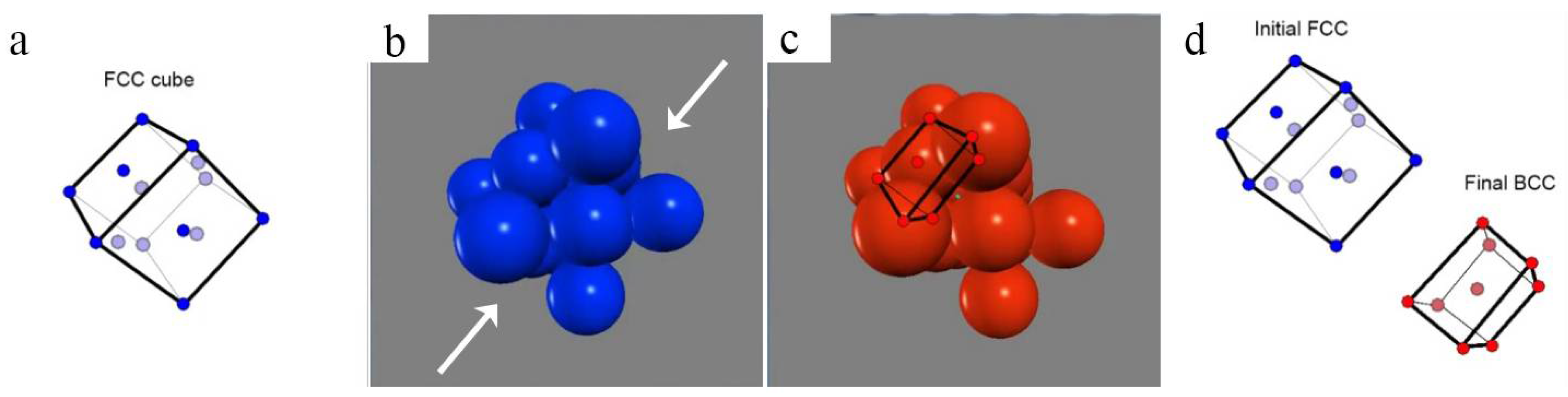
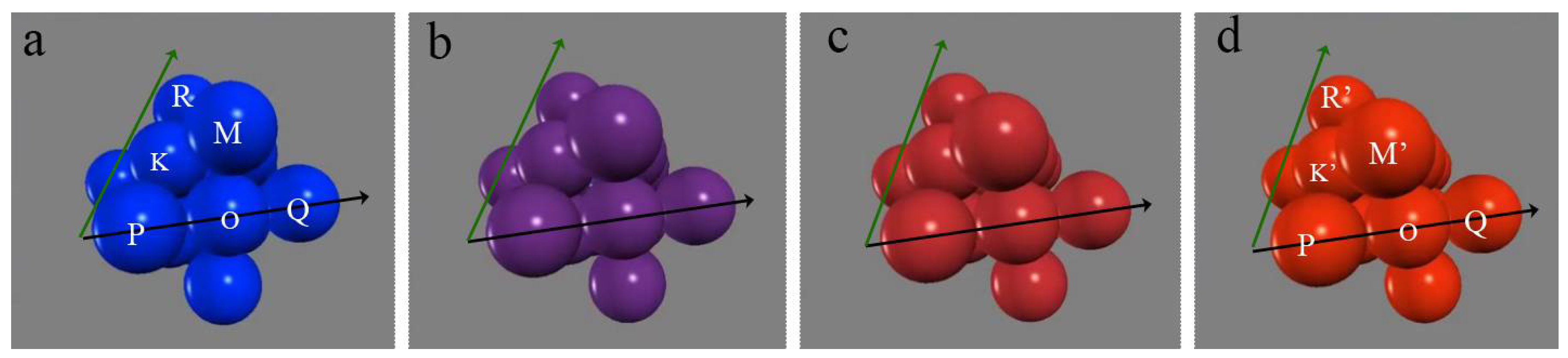
7.3. One-Step Hard-Sphere Model with Pitsch OR
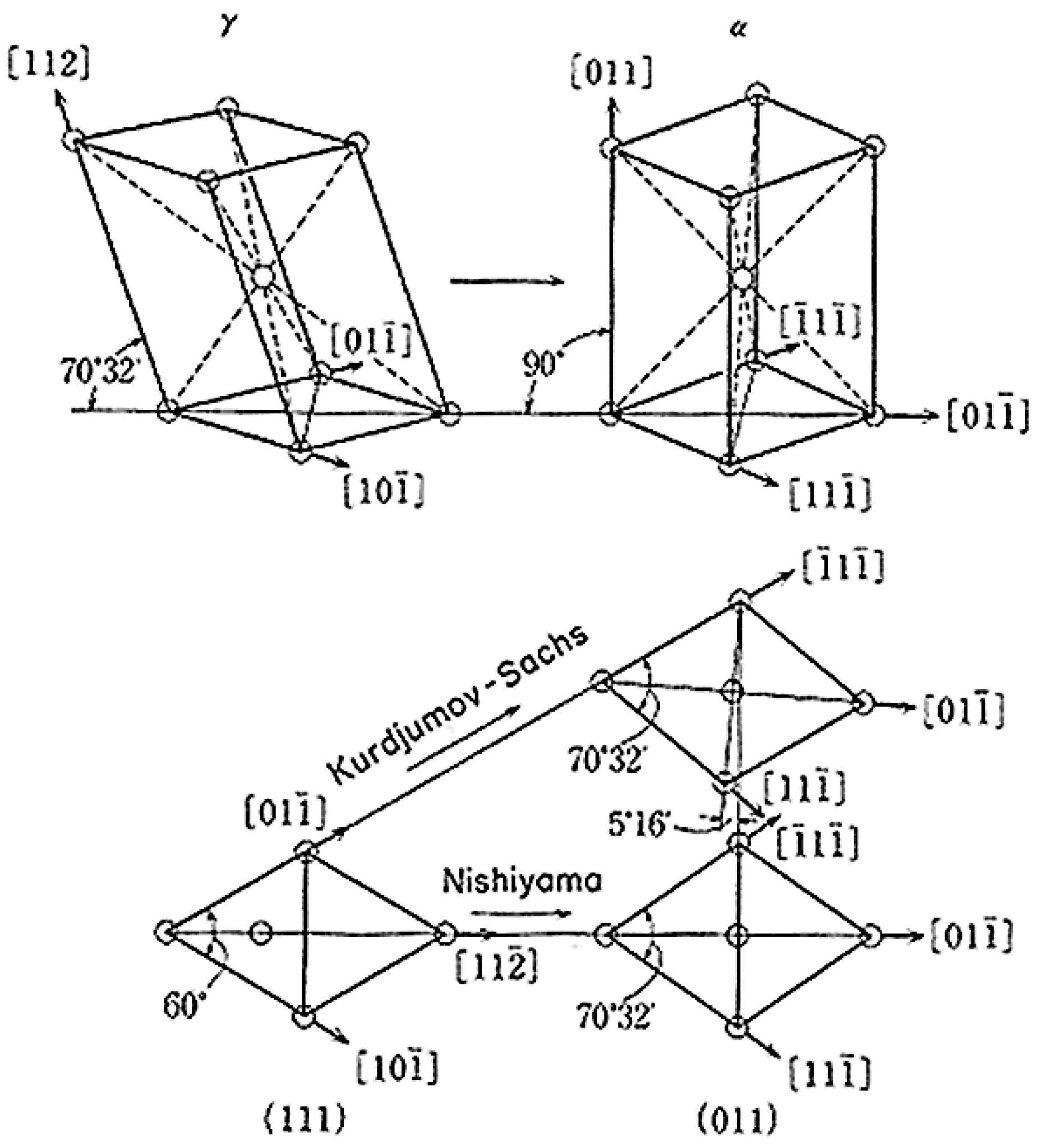
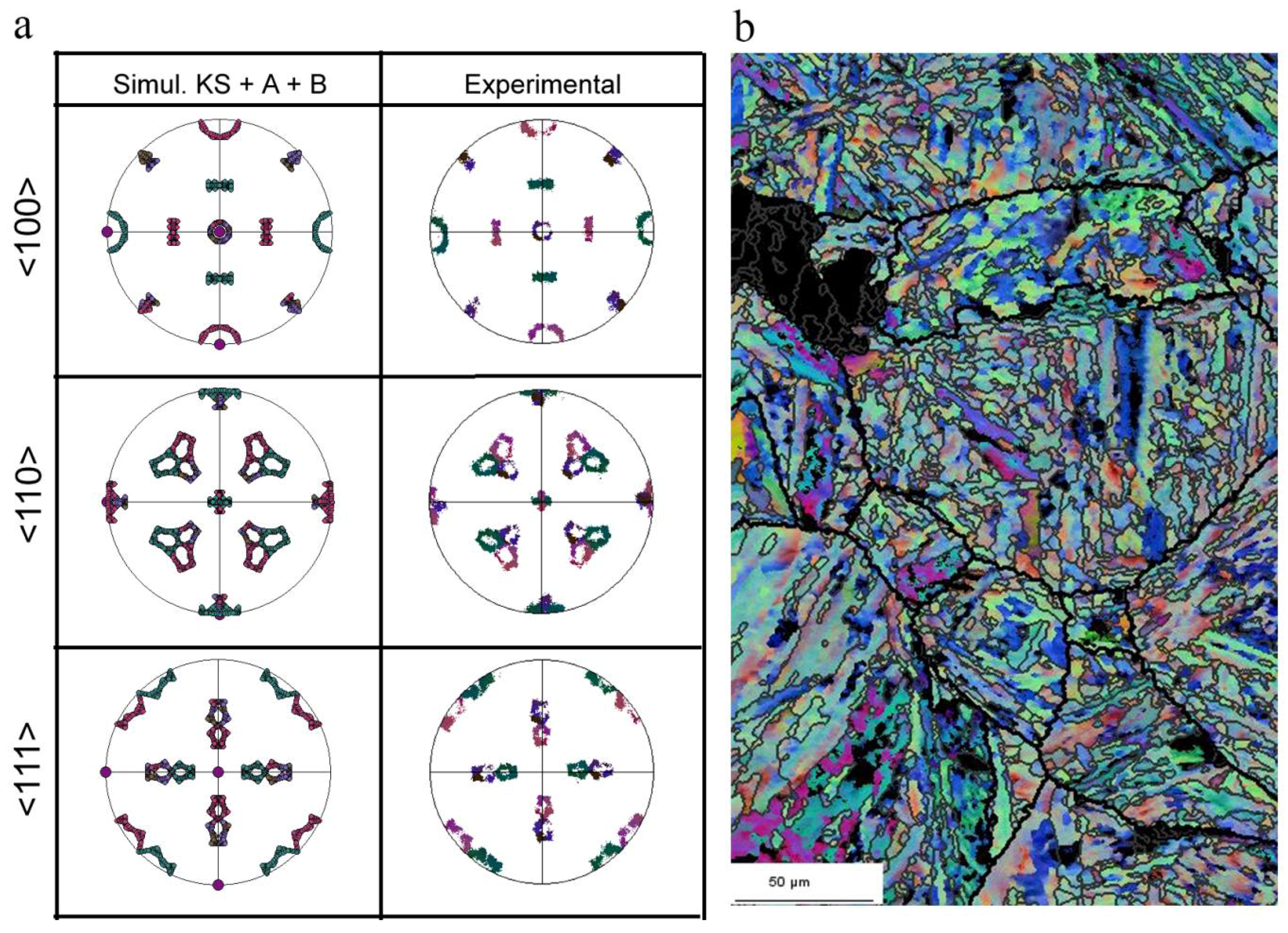
7.4. One-Step Hard-Sphere Model with KS OR
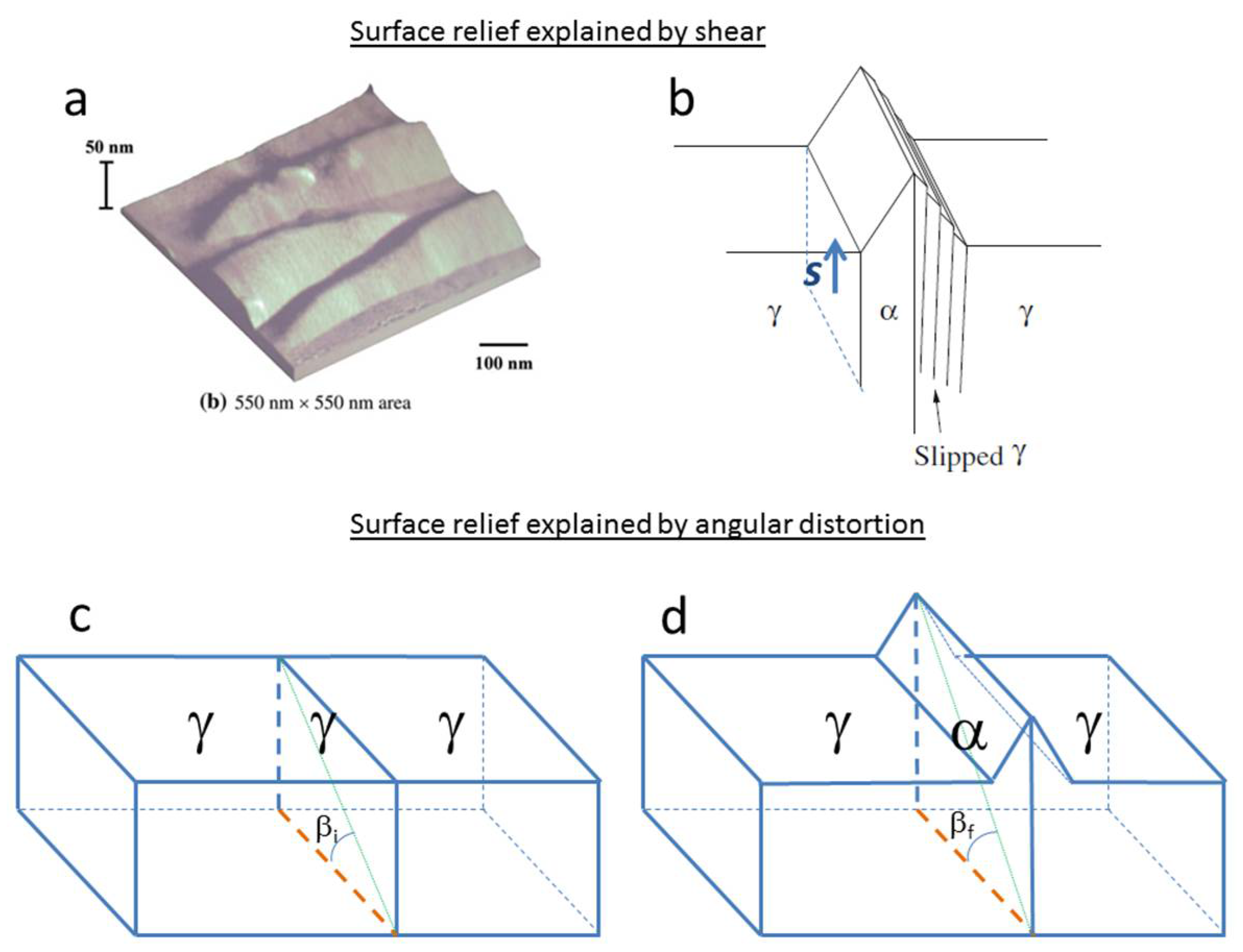
7.5. Habit Plane and Surface Relief
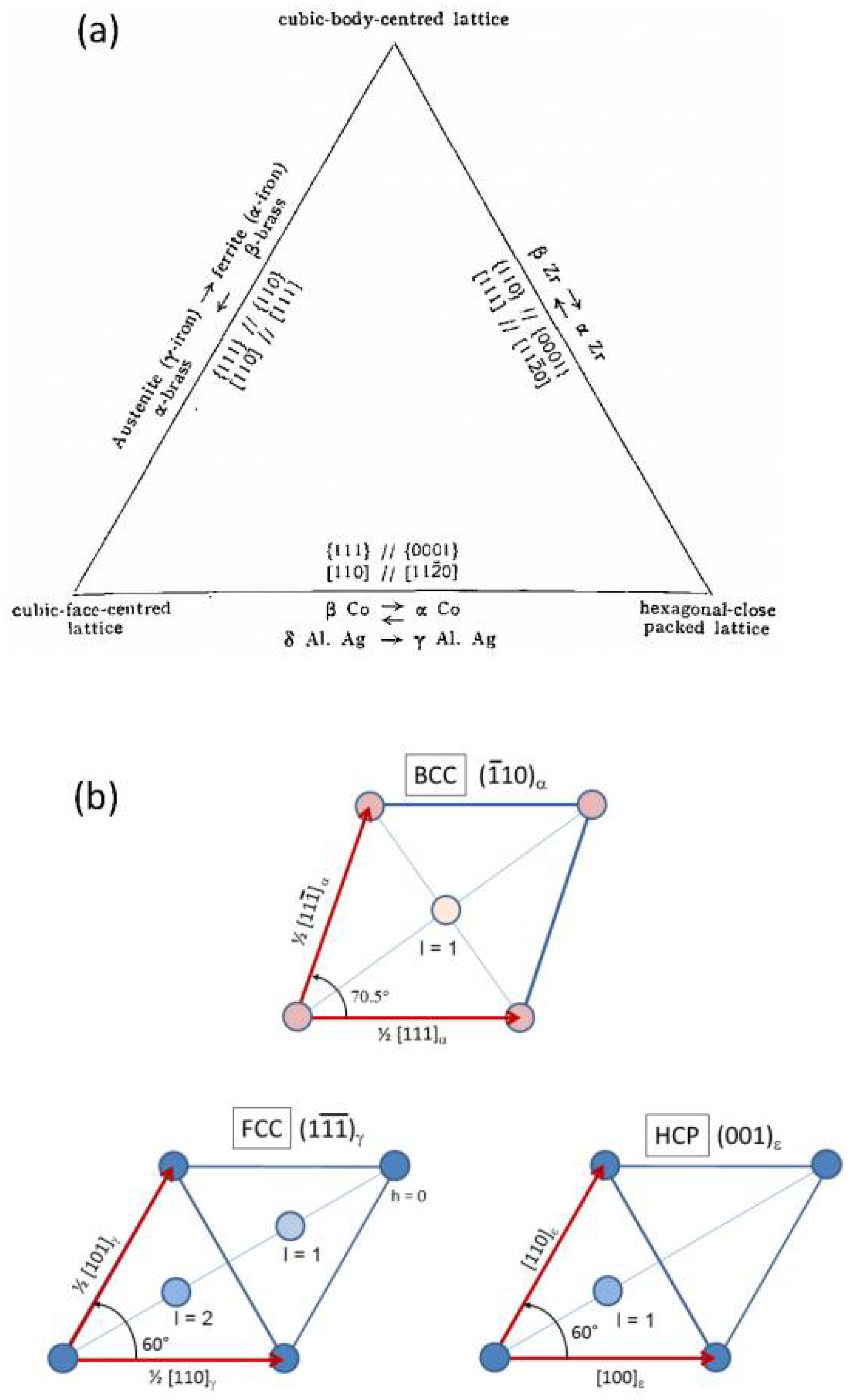
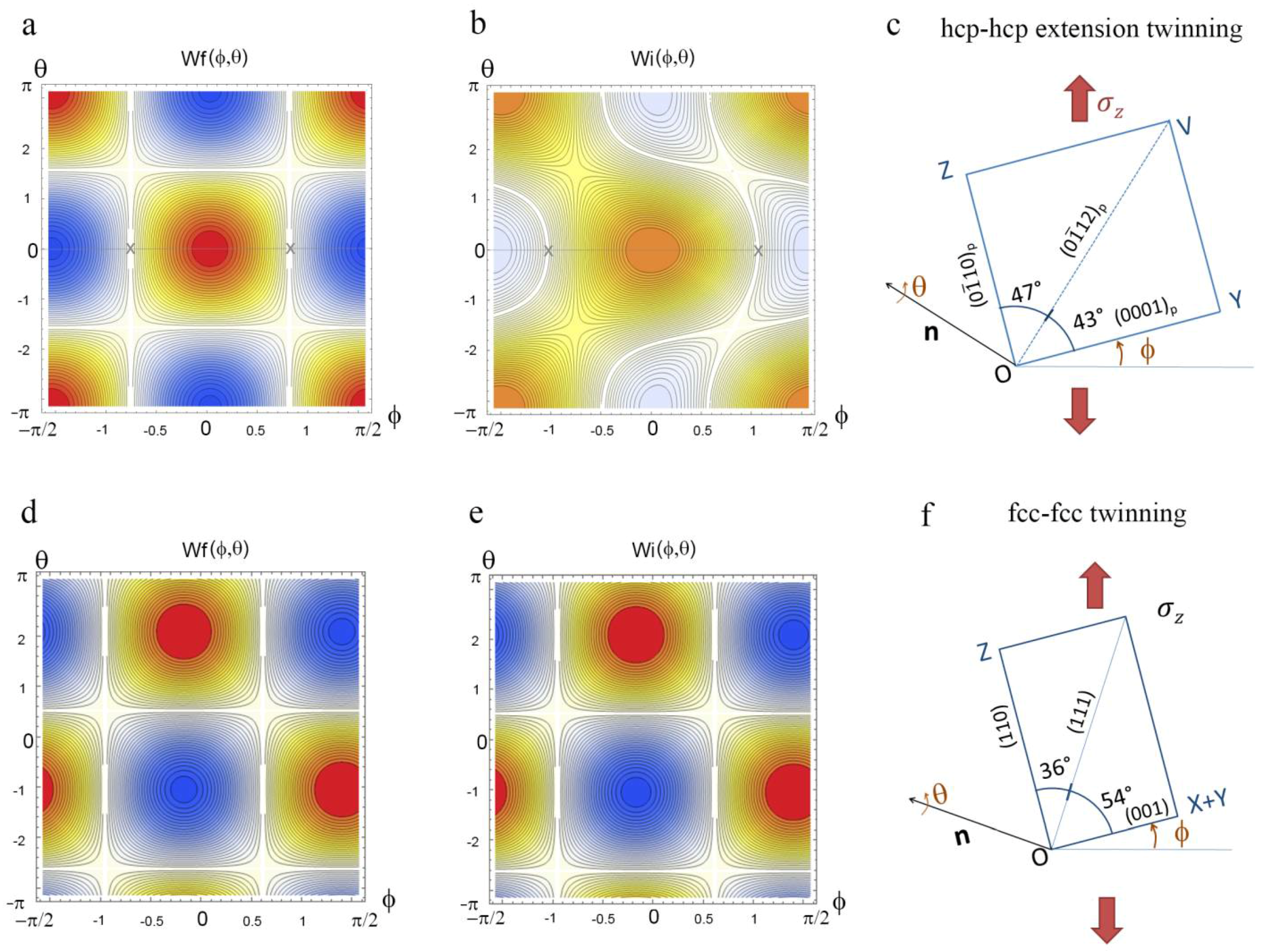
8. Generalization of the Angular Distortive Model to Face-Centered Cubic–Body-Centered Cubic–Hexagonal Close-Packed Martensitic Transformations, and to Face-Centered Cubic–Face-Centered Cubic Deformation Twinning
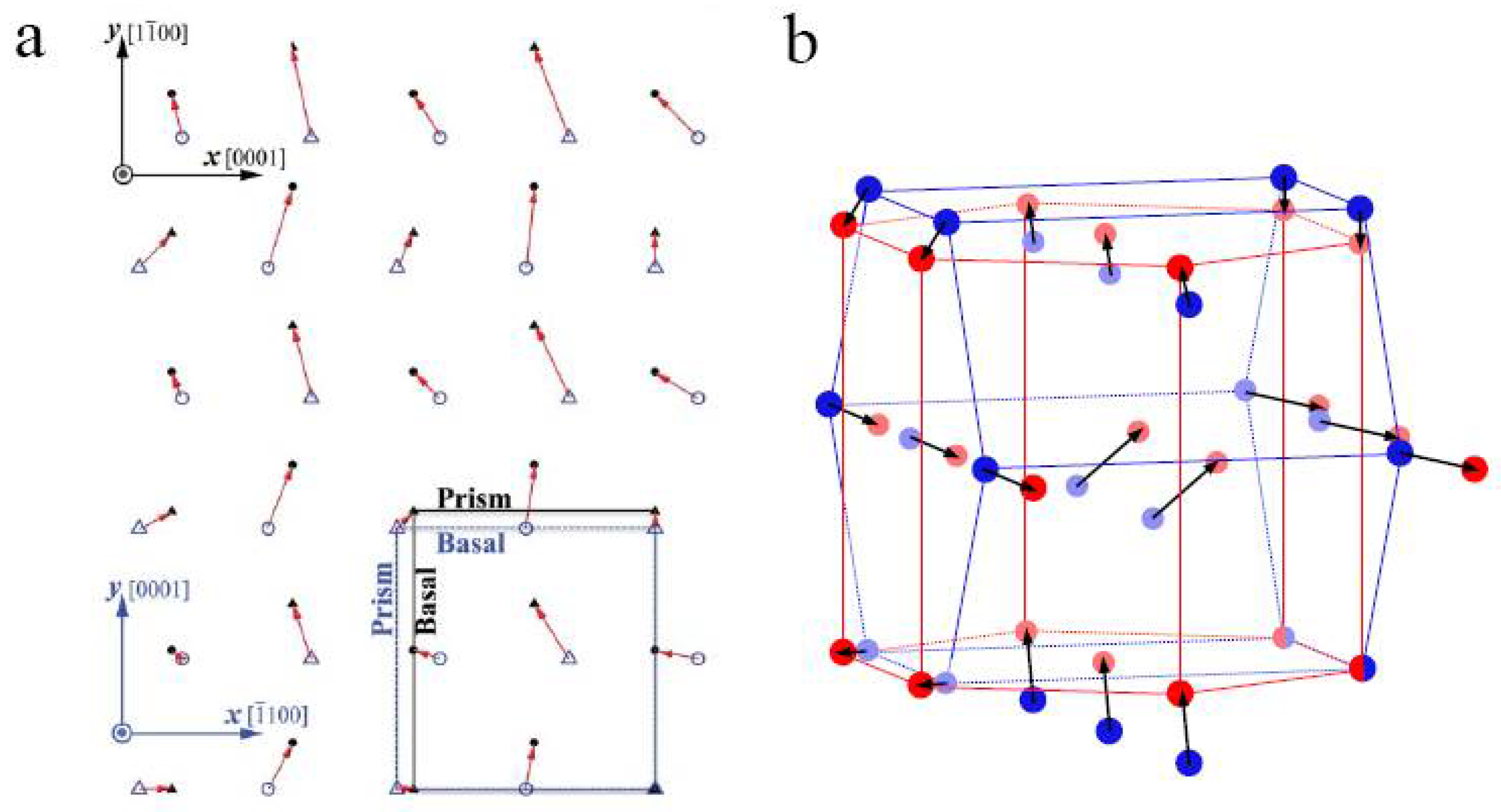
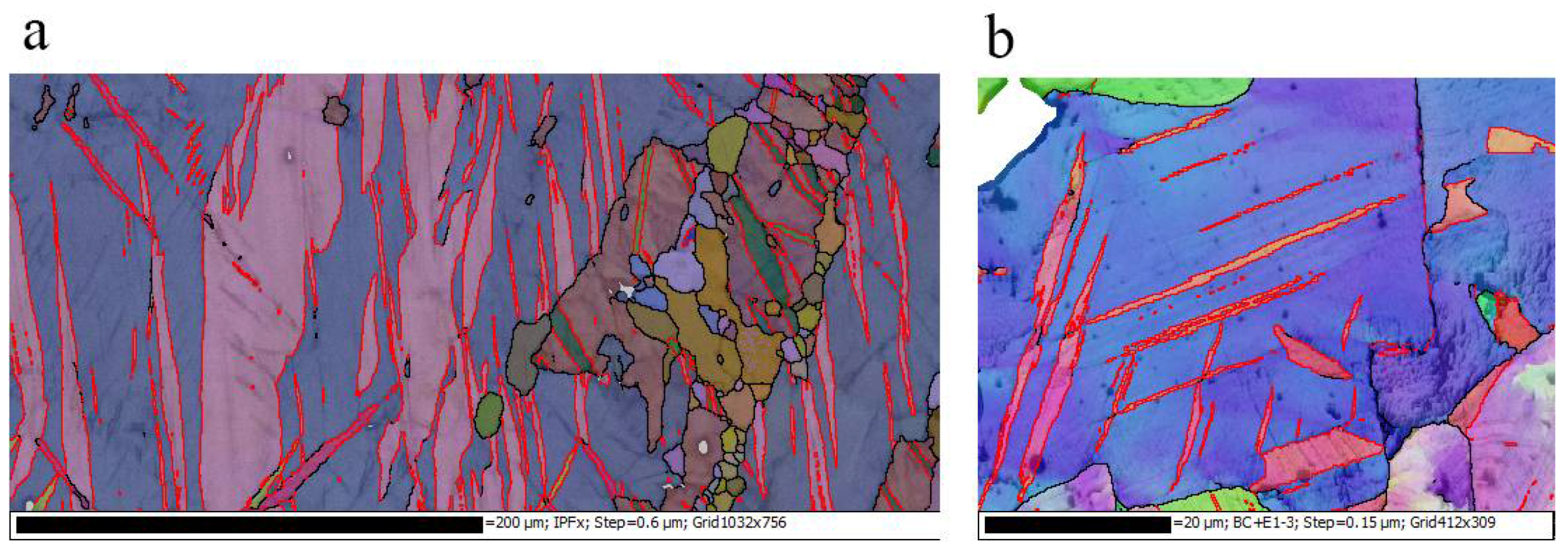
9. Angular Distortive Model for Deformation Twinning in Hexagonal Close-Packed Metals
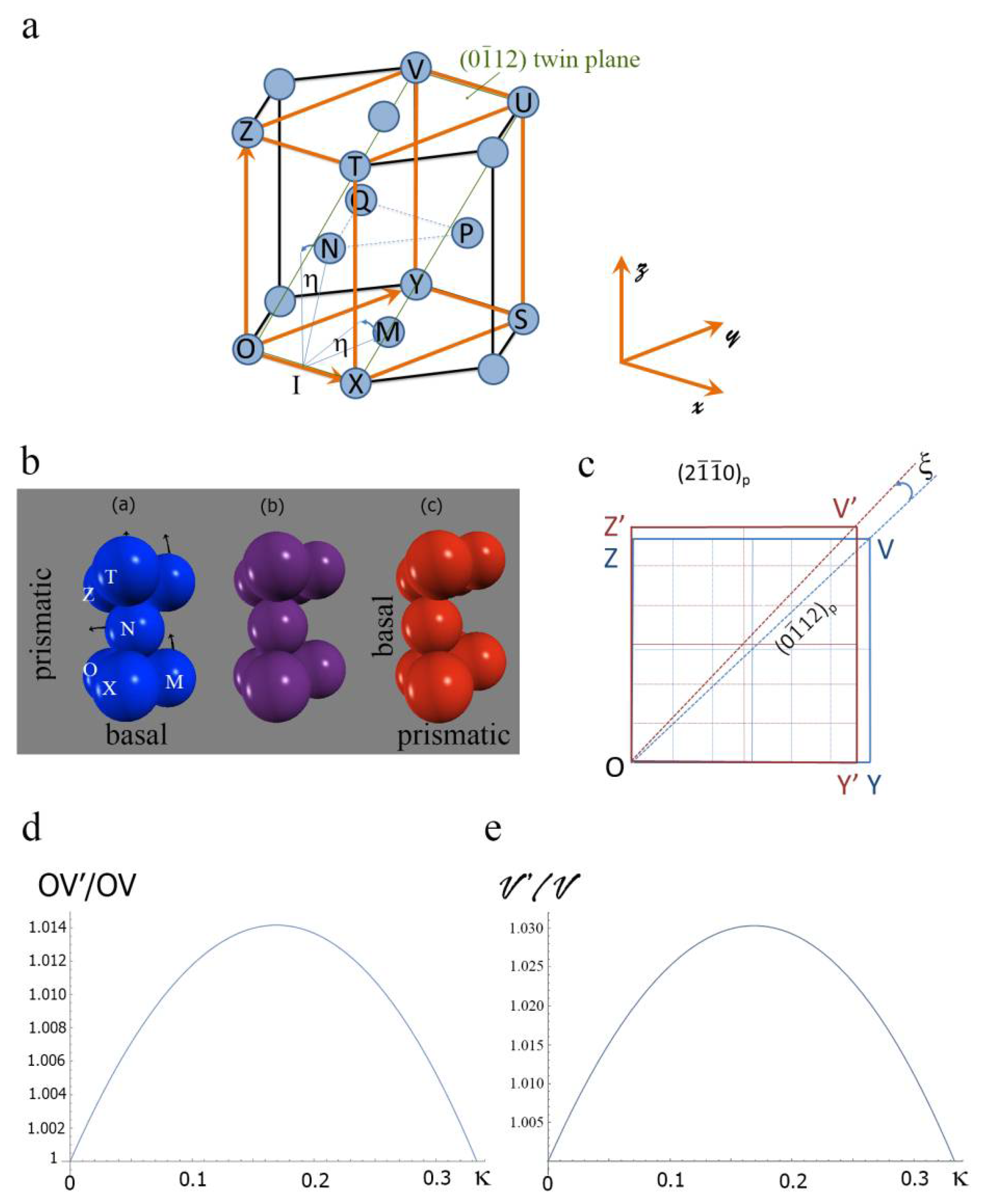
9.1. Application to Extension Twinning
9.2. Comparison with the Pure-Shuffle Model
9.3. Application of the Distortive Model to Other Twinning Modes
9.4. Comparison with Earlier Atomistic Models of Hexagonal Close-Packed Twinning
10. Future Works and Perspectives
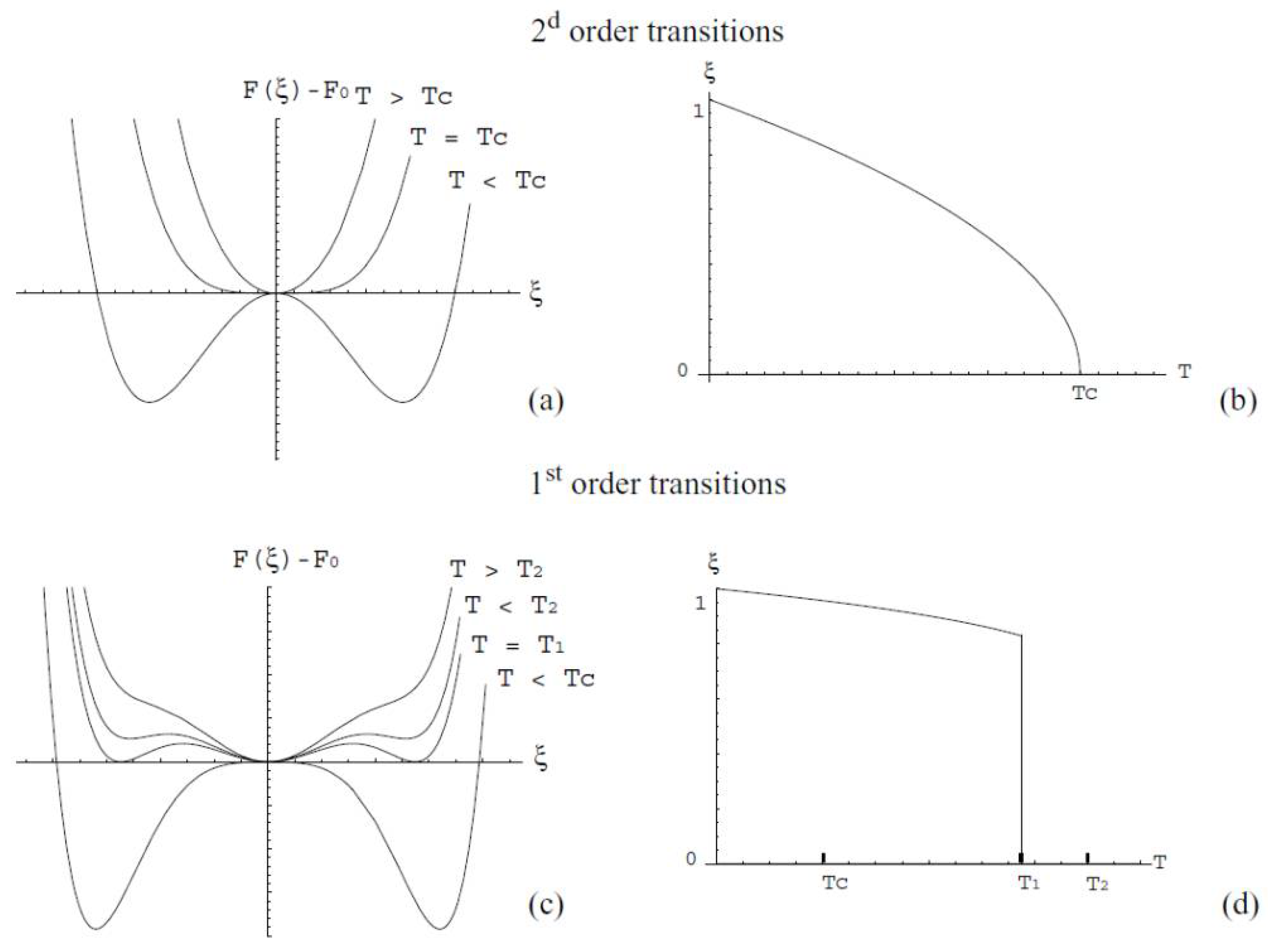
10.1. The Distortion Angle As a Natural Order Parameter
Different order parameters have been proposed beside the “volume fraction” mentioned by Clapp. For example, Flack [95], and more recently Clayton and Knap [162], proposed to use the shear strain(s). Beside the problem of defining the order parameter, Landau’s theory is based on the idea that the transition is a loss of symmetry, and thus cannot be applied directly to first-order transitions. Indeed, in metallurgy, many transformations are in between very distinct phases without group–subgroup relations, for example fcc-bcc transformations. Some symmetry elements are lost, but others are created. These transitions are also called in physics “reconstructive” (the meaning here is different from that used in metallurgy, where it is synonymous of “diffusive”). An interesting and powerful generalization of Landau’s theory of reconstructive transitions was proposed by Tolédano and Dmitriev [163]. The effective order parameter is a variation of a density function that is a sum of wave functions. The periodic form of this parameter permits one to decompose the free energy as a truncated Fourier series of the order parameter (and no longer a Taylor series). Many examples of applications from crystal to quasicrystals are studied and described in [163]. The density-wave description is an important element of generalization that establishes a first link with the wave propagation mode. However, the systematic use of a latent lattice, relevant for order–disorder transitions, would require more physical justifications for martensitic transformations. Besides, Tolédano and Dmitriev’s book [163] aims at physicists, but it does not use the classical vocabulary and concepts of metallurgy, and it does not respond to some basic questions raised by metallurgists—for example, about orientation relationships and the habit planes.Certainly one of the stumbling blocks in defining a martensitic transformation is that there is no obvious order parameter" associated with it, such as one has with ferromagnetic transformations (magnetic moment), order-disorder (long range order parameter), etc. Of course, one always has the possibility of using the volume fraction transformed as such an order parameter, analogous to the use of the fractional density of superconducting electrons for superconducting transformations, but this is a much more erratic quantity (markedly dependent on sample history) in the case of interest here.[161]
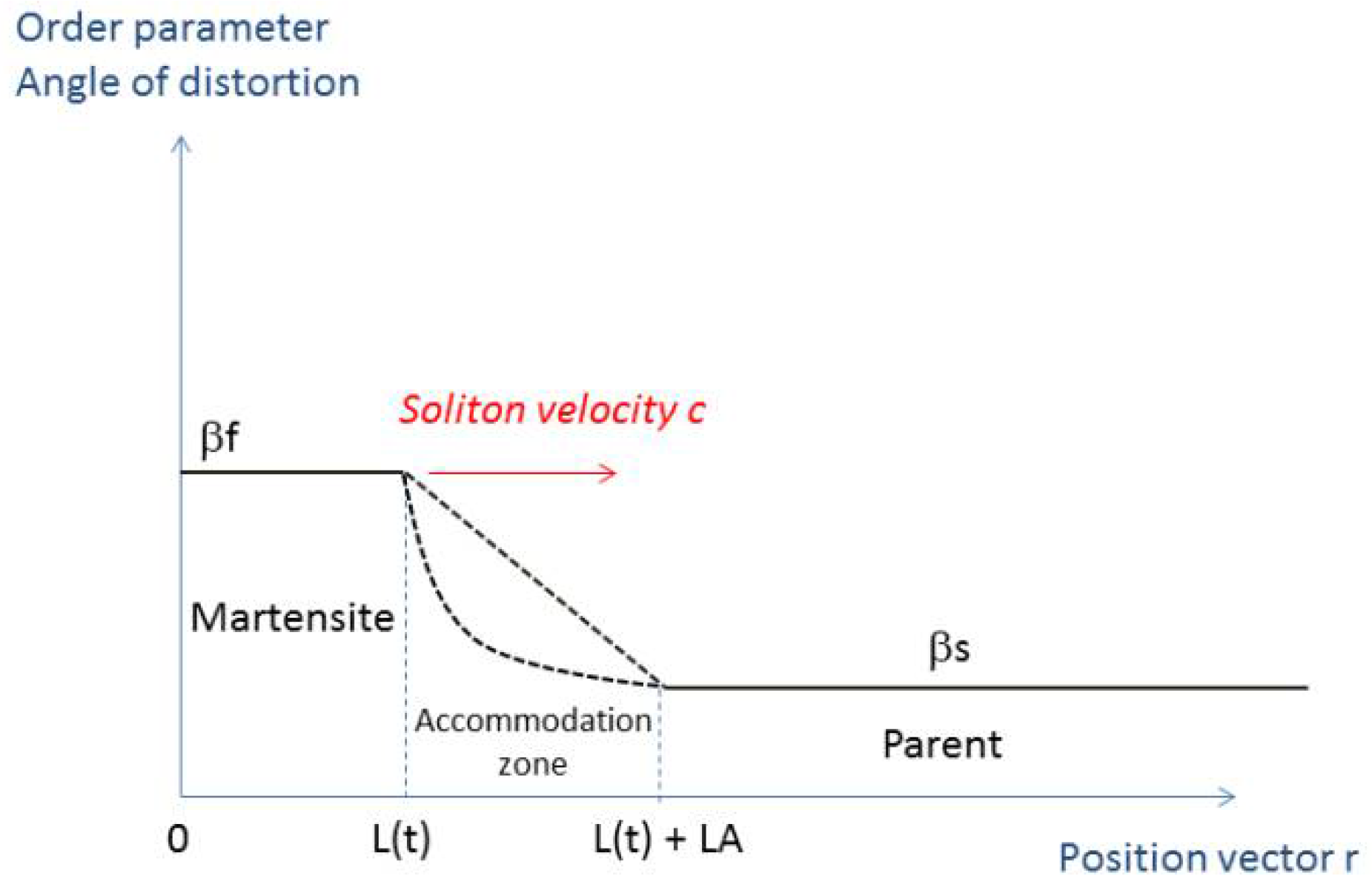
10.2. Dynamics of Phase Transformation and Accommodation Phenomena
11. Conclusions
Acknowledgments
Conflicts of Interest
References
- Cahn, R.W. Twinned crystals. Adv. Phys. 1954, 3, 363–444. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation Twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Mahajan, S.; Williams, D.F. Deformation Twinning in Metals and Alloys. Int. Metal. Rev. 1973, 18, 43–61. [Google Scholar] [CrossRef]
- Hardouin Duparc, O.B.M. A review of some elements for the history of mechanical twinning centred on its German origins until Otto Mügge’s K1 and K2 invariant plane notation. J. Mater. Sci. 2017, 52, 4182–4196. [Google Scholar] [CrossRef]
- Thomson, W.; Tait, P.G. Treatise on Natural Philosophy; pp. 123–124 in the Second Edition 1879, §§149–150 in the Elements of Natural Philosophy, a Simplified Version of the Treatise; Clarendon Press: Cambridge, UK, 1867; Volume 1, pp. 105–106, 170–171. [Google Scholar]
- Mügge, O. Ueber homogene Deformationen (einfache Schiebungen) an den triklinen Doppelsalzen BaCdCl4.4aq. Neues Jahrbuch Mineralogie Geologie und Palaeontologie Beilage 1889, 6, 274–304. [Google Scholar]
- Haüy, R.J. Traité de Minéralogie 1801. Five Volumes. Available online: http://catalogue.bnf.fr/ark:/12148/cb373669857.public (accessed on 16 April 2018).
- Barlow, W. Probable Nature of the Internal Symmetry of Crystals. Nature 1883, 29, 186–188. [Google Scholar] [CrossRef]
- Bragg, L.; Nye, J.F. A Dynamical Model of a Crystal Structure. Proc. R. Soc. Lond. A 1947, 190, 474–481. [Google Scholar] [CrossRef]
- Hall, E.O. Twinning and Diffusionless Transformations in Metals; Butterworths Scientific Publications: London, UK, 1954. [Google Scholar]
- Kihô, H. The Crystallographic Aspect of the Mechanical Twinning in Metals. J. Phys. Soc. Jpn. 1954, 9, 739–747. [Google Scholar] [CrossRef]
- Jaswon, M.A.; Dove, D.B. The Crystallography of Deformation Twinning. Acta Crystallogr. 1960, 13, 232–240. [Google Scholar] [CrossRef]
- Bilby, B.A.; Crocker, A.G. The Theory of the Crystallography of Deformation Twinning. Proc. R. Soc. Lond. A 1965, 288, 240–255. [Google Scholar] [CrossRef]
- Bevis, M.; Crocker, A.G. Twinning Shears in Lattices. Proc. R. Soc. Lond. A 1968, 304, 123–134. [Google Scholar] [CrossRef]
- Crocker, A.G.; Bevis, M. The Science Technology and Application of Titanium; Jaffee, R., Promisel, N., Eds.; Pergamon Press: Oxford, UK, 1970; pp. 453–458. [Google Scholar]
- Niewczas, M. Lattice correspondence during twinning in hexagonal close-packed crystals. Acta Mater. 2010, 58, 5848–5857. [Google Scholar] [CrossRef]
- Schmid, E.; Boas, W. Kristallplastizität: Mit Besonderer Berücksichtigung der Metalle, 1st ed.; Springer: Berlin, Germany, 1935; ISBN 978-3662342619. [Google Scholar]
- Barrett, C.D.; El Kadiri, H.; Tschopp, M.A. Breakdown of the Schmid law in homogeneous and heterogeneous nucleation events of slip and twinning in magnesium. J. Mech. Phys. Solids 2012, 60, 2084–2099. [Google Scholar] [CrossRef]
- Kumar, M.A.; Beyerlein, I.J.; Tomé, C.N. Effect of local stress fields on twin characteristics in HCP metals. Acta Mater. 2016, 116, 143–154. [Google Scholar] [CrossRef]
- Taylor, G.I. The deformation of crystals of beta-brass. Proc. R. Soc. Lond. A 1928, 118, 1–24. [Google Scholar] [CrossRef]
- Christian, J.W. Some Surprising Features of the Plastic Deformation of Body-Centered Cubic Metals and Alloys. Metall. Trans. A 1983, 14, 1237–1256. [Google Scholar] [CrossRef]
- Gröger, R.; Bailey, A.G.; Vitek, V. Multiscale modeling of plastic deformation of molybdenum and tungsten: I. Atomistic studies of the core structure and glide of ½<111> screw dislocations at 0 K. Acta Mater. 2008, 56, 5401–5411. [Google Scholar] [CrossRef]
- Wayman, C.M. Shear Transformations and Microstructures. Metallography 1975, 8, 105–130. [Google Scholar] [CrossRef]
- Bain, E.C. The nature of martensite. Trans. AIME 1924, 70, 25–35. [Google Scholar]
- Young, J. The Crystal Structure of Meteoric Iron as determined by X-ray Analysis. R. Soc. Proc. Lond. A 1926, 112, 630–642. [Google Scholar] [CrossRef]
- Kurdjumov, G.; Sachs, G. Über den Mechanismus der Stahlhärtung. Z. Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Wassermann, G. Einfluß der α-γ-Umwandlung eines irreversiblen Nickelstahls auf Kristallorientierung und Zugfestigkeit. Steel Res. Int. 1933, 6, 347–351. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray Investigation of the Mechanism of the Transformation from Face-Centred Cubic Lattice to Body-Centred Cubic. Sci. Rep. Tohoku Univ. 1934, 23, 637–668. [Google Scholar]
- Burgers, W.G. On the process of transition of the cubic-body-centered modification into the hexagonal-close-packed modification of zirconium. Physica 1934, 1, 561–586. [Google Scholar] [CrossRef]
- Kelly, A.; Groves, G.W. Crystallography and Crystal Defects, 1st ed.; John Wiley & Sons: London, UK, 1970. [Google Scholar]
- Greninger, A.B.; Troiano, A.R. The Mechanism of Martensite Formation. Metals Trans. 1949, 185, 590–598. [Google Scholar] [CrossRef]
- Jaswon, M.A.; Wheeler, J.A. Atomic displacements in austenite-martensite transformation. Acta Crystallogr. 1948, 1, 216–224. [Google Scholar] [CrossRef]
- Weschler, M.S.; Liebermann, D.S.; Read, T.A. On the theory of the formation of martensite. Trans. AIME 1953, 197, 1503–1515. [Google Scholar]
- Bowles, J.S.; Mackenzie, J.K. The crystallography of martensitic transformations I. Acta Metall. 1954, 2, 129–137. [Google Scholar] [CrossRef]
- Bowles, J.S.; Mackenzie, J.K. The crystallography of martensitic transformations II. Acta Metall. 1954, 2, 138–147. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformations in Metals and Alloys; Last Version, 2002; Pergamon Press: Oxford, UK, 1965; ISBN 9780080440194. [Google Scholar]
- Nishiyama, Z. Martensite Transformation; Fine, M.E., Meshii, M., Waymann, C.M., Eds.; Materials Science Series, English Edition; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Bhadeshia, H.K.D.H. Worked Examples in the Geometry of Crystals, 2nd ed.; The Institute of Metals: Brookfield, VT, USA, 1987. [Google Scholar]
- Bhadeshia, H.K.D.H.; Honeycombe, R. Steels: Microstructure and Properties; Butterworth-Heinemann: Oxford, UK, 2006; ISBN 978-0750680844. [Google Scholar]
- Nishiyama, Z.; Shimizu, K. On the sub-bands in a martensite plate. Microscopy 1956, 4, 51. [Google Scholar]
- Shimizu, K. Japanese great pioneer and leader, Zenji Nishiyama, on studies of martensitic transformations. J. Phys. IV 2003, 112, 11–16. [Google Scholar] [CrossRef]
- Machlin, E.S.; Cohen, M. Habit Phenomenon in the Martensite Transformation. Trans. AIME 1951, 191, 1019–1029. [Google Scholar]
- Bowles, J.S.; Dunne, D.P. The role of plastic accommodation in the (225) martensite transformation. Acta Metall. 1969, 17, 677–685. [Google Scholar] [CrossRef]
- Dunne, D.P.; Wayman, C.M. The assessment of the double shear theory as applied to ferrous martensitic transformations. Acta Metall. 1971, 19, 425–438. [Google Scholar] [CrossRef]
- Wayman, C.M. The growth of martensite since E.C. Bain (1924)-Some Milestones. Mater. Sci. Forum 1990, 56, 1–32. [Google Scholar] [CrossRef]
- Dunne, D.P. An historical account of the development of the Bowles-Mackenzie theory of the crystallography of martensitic transformation. In Proceedings of the 12th International Conference on Martensitic Transformations (ICOMAT-08), Santa Fe, NM, USA, 29 June–5 July 2008; Olson, G.B., Lieberman, D.S., Saxena, A., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2009; pp. 47–53. [Google Scholar]
- Zhang, M.X.; Kelly, P.M. Crystallographic features of phase transformations in solids. Prog. Mater. Sci. 2009, 54, 1101–1170. [Google Scholar] [CrossRef]
- Bowles, J.S.; Barrett, C.S. Crystallography of Transformations. Prog. Met. Phys. 1952, 31–41. [Google Scholar] [CrossRef]
- Kelly, P.M. Crystallography of Lath Martensite in Steels. Mater. Trans. JIM 1992, 33, 235–242. [Google Scholar] [CrossRef]
- Qi, L.; Khachaturyan, A.G.; Morris, J.W., Jr. The microstructure of dislocated martensitic steel: Theory. Acta Mater. 2014, 76, 23–39. [Google Scholar] [CrossRef]
- Mackenzie, J.K.; Bowles, J.S. The crystallography of martensitic transformation IV Body-centred cubic to orthorhombic transformations. Acta Metall. 1957, 5, 137–149. [Google Scholar] [CrossRef]
- Williams, A.J.; Cahn, R.W.; Barrett, C.S. The crystallography of the β→α transformation in titanium. Acta Metall. 1954, 2, 117–128. [Google Scholar] [CrossRef]
- Bogers, A.J.; Burgers, W.G. Partial dislocations on the {110} planes in the bcc lattice and the transition of the fcc into the bcc lattice. Acta Metall. 1964, 12, 255–261. [Google Scholar] [CrossRef]
- Cottrell, A.H. Dislocations and Plastic Flow in Crystals, 1st ed.; Oxford Clarendon Press: New York, NY, USA, 1953. [Google Scholar]
- Zener, C. Elasticity and Anelasticity of Metals; University Press: Chicago, IL, USA, 1948. [Google Scholar]
- Olson, G.B.; Cohen, M.A. Mechanism for the strain-induced nucleation of martensitic transformations. J. Less Common Met. 1972, 28, 107–118. [Google Scholar] [CrossRef]
- Olson, G.B.; Cohen, M.A. General mechanism of martensitic nucleation: Part II. FCC→BCC and other martensitic transformations. Metall. Mater. Trans. A 1976, 7, 1905–1914. [Google Scholar]
- Le Lann, A.; Dubertret, A. A structural Description of the F.C.C.→B.C.C. Martensitic Transformation in Terms of {011} <11> f.c.c Simulation Double Shear. Phys. Status Solidi 1983, 78, 309–321. [Google Scholar] [CrossRef]
- Frenkel, J. Zur theorie der elastizit. atsgrenze und der festigkeit kristallinischer kцrper. Z. Phys. 1926, 37, 572–609. [Google Scholar] [CrossRef]
- Smallman, R.E.; Bishop, R.J. Modern Physical Metallurgy & Materials Engineering, 6th ed.; Chapter 4 “Defects in Solids”; Butterworth-Heinemann: Oxford, UK, 1999. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Chapter 21 “Dislocations”; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Peierls, R. The Size of a Dislocation. Proc. Phys. Soc. 1940, 52, 34–37. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. Dislocations in a simple cubic lattice. Proc. Phys. Soc. 1947, 59, 256–272. [Google Scholar] [CrossRef]
- Bragg, L.; Lomer, W.M. A dynamical model of a crystal structure II. Proc. R. Soc. Lond. A 1949. [Google Scholar] [CrossRef]
- Hirth, J.P. A Brief History of Dislocation Theory. Metall. Trans. A 1985, 16, 2085–2090. [Google Scholar] [CrossRef]
- Seitz, F.; Read, W.T. Theory of plasticity of solids III. J. Appl. Phys. 1941, 12, 470–486. [Google Scholar] [CrossRef]
- Vladimirskii, K.V. Twinning in calcite. Zh. Eksp. Teor. Fiz. 1947, 17, 530. (In Russian) [Google Scholar]
- Frank, F.C.; van der Merwe, J.H. One dimensional dislocations I. Statistic theory. Proc. R. Soc. Lond. A 1949, 198, 205–216. [Google Scholar] [CrossRef]
- Sleeswyk, A.W. 1/2⟨1 1 1⟩ screw dislocations and the nucleation of {1 1 2}⟨1 1 1⟩ twins in the b.c.c. lattice. Philos. Mag. 1963, 8, 1467–1486. [Google Scholar] [CrossRef]
- Christian, J.W. Twinning and martensitic transformation. J. Phys. Colloq. 1974, 35, C7-65–C7-76. [Google Scholar] [CrossRef]
- Cottrell, A.H.; Bilby, B.A. A mechanism for the growth of deformation twins in crystals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 573–581. [Google Scholar] [CrossRef]
- Sleeswyk, A.W. Perfect dislocation pole models for twinning in f.c.c and b.c.c lattices. Philos. Mag. 1974, 29, 407–421. [Google Scholar] [CrossRef]
- Venables, J.A. On dislocation pole models for twinning. Philos. Mag. 1974, 30, 1165–1169. [Google Scholar] [CrossRef]
- Mahato, B.; Sahu, T.; Shee, S.K.; Sahu, P.; Sawaguchi, T.; Kömi, J.; Karjalainen, L.P. Simultaneous twinning nucleation mechanisms in an Fe-Mn-Si-Al twinning induced plasticity steel. Acta Mater. 2017, 132, 264–275. [Google Scholar] [CrossRef]
- Thomas, G.; Whelan, M.J. Helical dislocations in quenched aluminium-4% copper alloys. Philos. Mag. 1959, 4, 511–527. [Google Scholar] [CrossRef]
- Venables, J.A. The electron microscopy of deformation twinning. J. Phys. Chem. Solids 1964, 25, 685–692. [Google Scholar] [CrossRef]
- Mahajan, S. Nucleation and growth of deformation twins in Mo-35 at.% Re alloy. Philos. Mag. 1972, 26, 161–171. [Google Scholar] [CrossRef]
- Mahajan, S.; Chin, G.Y. Formation of deformation twins in f.c.c. crystals. Acta Metal. 1973, 21, 1353–1363. [Google Scholar] [CrossRef]
- Zárubová, N.; Ge, Y.; Heczko, O.; Hannula, S.P. In situ TEM study of deformation twinning in Ni-Mn-Ga non-modulated martensite. Acta Mater. 2013, 61, 5290–5299. [Google Scholar] [CrossRef]
- Bergeon, N.; Guenin, G.; Esnouf, C. Microstructural analysis of the stress-induced ε martensite in a Fe-Mn-Si-Cr-Ni shape memory alloy: Part I—Calculated description of the microstructure. Mater. Sci. Eng. A 1998, 242, 77–86. [Google Scholar] [CrossRef]
- Weitz, T.; Karnthaler, H.P. Transformation strains in martensitic phase transitions of Co alloys. Phase Transit. 1999, 67, 695–705. [Google Scholar] [CrossRef]
- Zhao, H.; Song, M.; Ni, S.; Shao, S.; Wang, J.; Liao, X. Atomic-scale understanding of stress-induced phase transformation in cold-rolled Hf. Acta Mater. 2017, 131, 271–279. [Google Scholar] [CrossRef]
- Zhao, H.; Hu, X.; Song, M.; Ni, S. Mechanisms for deformation induced hexagonal close-packed structure to face-centered cubic structure transformation in zirconium. Scr. Mater. 2017, 132, 63–67. [Google Scholar] [CrossRef]
- Hirth, J.P.; Pond, R.C. Steps, Dislocations and disconnections as interface defects relating to structure and phase transformations. Acta Mater. 1996, 44, 4749–4763. [Google Scholar] [CrossRef]
- Pond, R.C.; Ma, X.; Hirth, J.P. Geometrical and physical models of martensitic transformations in ferrous alloys. J. Mater. Sci. 2008, 43, 3881–3888. [Google Scholar] [CrossRef]
- Howe, J.M.; Pond, R.C.; Hirth, J.P. The role of disconnections in phase transformations. Prog. Mater. Sci. 2009, 54, 792–938. [Google Scholar] [CrossRef]
- Pond, R.C.; Hirth, J.P.; Serra, A.; Bacon, D.J. Atomic displacements accompanying deformation twinning: Shear and shuffles. Mater. Res. Lett. 2016. [Google Scholar] [CrossRef]
- Hirth, J.P.; Wang, J.; Tomé, C.N. Disconnections and other defects associated with twin interfaces. Prog. Mater. Sci. 2016, 83, 417–471. [Google Scholar] [CrossRef]
- Capolungo, L.; Beyerlein, I.J. Nucleation and stability of twins in hcp metals. Phys. Rev. B 2008, 78, 024117. [Google Scholar] [CrossRef]
- Wang, J.; Zeng, Z.; Weinberger, C.R.; Zhang, Z.; Zhu, T.; Mao, S.X. In situ atomic-scale observation of twinning dominated deformation in nanoscale body-centred cubic tungsten. Nat. Mater. 2015, 14, 594–600. [Google Scholar] [CrossRef] [PubMed]
- Wilson, K.G. Problems in Physics with Many Scales of Length. Sci. Am. 1979, 158–179. [Google Scholar] [CrossRef]
- Meyers, M.A. On the growth of lenticular martensite. Acta Metall. 1980, 28, 757–770. [Google Scholar] [CrossRef]
- Barsch, G.R.; Krumhansl, J.A. Twin Boundaries in Ferroelastic Media with Interface Dislocations. Phys. Rev. Lett. 1984, 53, 1069–1072. [Google Scholar] [CrossRef]
- Barsch, G.R.; Horovitz, B.; Krumhansl, J.A. Dynamics of Twin Boundaries in Martensites. Phys. Rev. Lett. 1987, 59, 1251–1254. [Google Scholar] [CrossRef] [PubMed]
- Flack, F. Ginzburg-Landau Theory and Solitary Waves in Shape-Memory Alloys. Z. Phys. B Condens. Matter 1984, 54, 159–167. [Google Scholar]
- Kashchenko, M.P.; Chashchina, V.G. Key Role of Transformation Twins in Comparison of Results of Crystal Geometric and Dynamic Analysis for Thin Plate Martensite. Phys. Met. Metallogr. 2013, 114, 821–825. [Google Scholar] [CrossRef]
- Volterra, V. Sur l’équilibre des corps élastiques multiplement connexes. In Annales Scientifiques de l'École Normale Supérieure; Gauthier-Villars: Paris, France, 1907; Volume 24, pp. 401–518. [Google Scholar]
- Romanov, A.E. Mechanics and physics of dislinations in solids. Eur. J. Mech. A Solids 2003, 22, 727–741. [Google Scholar] [CrossRef]
- Kleman, M.; Friedel, J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev. Mod. Phys. 2008, 82, 61–115. [Google Scholar] [CrossRef]
- Klimanek, P.; Klemm, V.; Romanov, A.E.; Seefeldt, M. Disclinations in Plastically Deformed Metallic Materials. Adv. Eng. Mater. 2001, 3, 877–884. [Google Scholar] [CrossRef]
- Müllner, P.; Romanov, A.E. Internal Twinning in deformation twinning. Acta Mater. 2000, 48, 2323–2337. [Google Scholar] [CrossRef]
- Müllner, P.; King, A.H. Deformation of hierarchically twinned martensite. Acta Mater. 2010, 58, 5242–5261. [Google Scholar] [CrossRef]
- Kelly, P.M. Martensite Crystallography—The Apparent Controversy between the Infinitesimal Deformation Approach and the Phenomenological Theory of Martensitic Transformations. Metall. Mater. Trans. A 2003, 34, 1783–1786. [Google Scholar] [CrossRef]
- Gey, N.; Humbert, M. Specific analysis of EBSD data to study the texture inheritance due to the β→α phase transformation. J. Mater. Sci. 2003, 38, 1289–1294. [Google Scholar] [CrossRef]
- Cayron, C. Groupoid of orientational variants. Acta Crystallogr. Sect. Found. Crystallogr. 2006, 62, 21–40. [Google Scholar] [CrossRef] [PubMed]
- Cayron, C.; Artaud, B.; Briottet, L. Reconstruction of parent grains from EBSD data. Mater. Charact. 2006, 57, 386–401. [Google Scholar] [CrossRef]
- Cayron, C. ARPGE: A computer program to automatically reconstruct the parent grains from electron backscatter diffraction data. J. Appl. Crystallogr. 2007, 40, 1183–1188. [Google Scholar] [CrossRef] [PubMed]
- Bunge, H.J.; Weiss, W.; Klein, H.; Wcislak, L.; Garbe, U.; Schneider, J.R. Orientation relationship of Widmannstätten plates in an iron meteorite measured with high-energy synchrotron radiation. J. Appl. Crystallogr. 2003, 36, 137–140. [Google Scholar] [CrossRef]
- Nolze, G.; Geist, V.; Saliwan Neumann, R.; Buchheim, M. Investigation of orientation relationships by EBSD and EDS on the example of the Watson iron meteorite. Cryst. Res. Technol. 2005, 40, 791–804. [Google Scholar] [CrossRef]
- Cayron, C.; Barcelo, F.; de Carlan, Y. The mechanism of the fcc-bcc martensitic transformation revealed by pole figures. Acta Mater. 2010, 58, 1395–1402. [Google Scholar] [CrossRef]
- Cayron, C.; Barcelo, F.; de Carlan, Y. Reply to “Comments on ‘The mechanism of the fcc-bcc martensitic transformation revealed by pole figures’”. Scr. Mater. 2011, 64, 103–106. [Google Scholar] [CrossRef]
- Thiaudière, D.; Hennet, L.; King, A.; de Carlan, Y.; Béchade, J.L.; Cayron, C. Soleil and ESRF ultra-fast in situ X-ray diffraction experiments to track the hcp phases in martensitic steels. Unpublished work. 2012. [Google Scholar]
- Pitsch, W. The Martensite Transformation in Thin Foils of Iron-Nitrogen Alloys. Philos. Mag. 1959, 4, 577–584. [Google Scholar] [CrossRef]
- Cayron, C. One-step model of the face-centred-cubic to body-centred-cubic martensitic transformation. Acta Crystallogr. Sect. Found. Crystallogr. 2013, 69, 498–509. [Google Scholar] [CrossRef]
- Cayron, C. EBSD imaging of orientation relationships and variants groupings in different martensitic alloys and Widmanstätten iron meteorites. Mater. Charact. 2014, 94, 93–110. [Google Scholar] [CrossRef]
- Maki, T.; Wayman, C.M. Transmission electron Microscopy Studies of Thin Fold Martensite in Fe-Ni and Fe-Ni-C alloys. Acta Metall. 1977, 25, 681–693. [Google Scholar] [CrossRef]
- Cayron, C. Continuous atomic displacements and lattice distortion during fcc-bcc martensitic transformation. Acta Mater. 2015, 96, 189–202. [Google Scholar] [CrossRef]
- Kong, L.T. Phonon dispersion measured directly from molecular dynamics simulations. Comput. Phys. Commun. 2011, 182, 2201–2207. [Google Scholar] [CrossRef]
- Sinclair, C.W.; Hoagland, R.G. A molecular dynamics study of the fcc→bcc transformation at fault intersections. Acta Mater. 2008, 56, 4160–4171. [Google Scholar] [CrossRef]
- Sandoval, L.; Hurbassek, H.M. The Bain versus Nishiyama-Wassermann path in the martensitic transformation of Fe. New J. Phys. 2009, 11, 103027. [Google Scholar] [CrossRef]
- Wang, B.; Sak-Saracino, E.; Gunkelmann, N.; Urbassek, H.M. Molecular-dynamics study of the α→γ phase transition in Fe-C. Comput. Mater. Sci. 2014, 82, 399–404. [Google Scholar] [CrossRef]
- Meiser, J.; Urbassek, H.M. Martensitic transformation of pure iron at a grain boundary: Atomistic evidence for a two-step Kurdjumov-Sachs–Pitsch pathway. AIP Adv. 2013, 6, 085017. [Google Scholar] [CrossRef]
- Cayron, C. Angular distortive matrices of phase transitions in the fcc-bcc-hcp system. Acta Mater. 2016, 111, 417–441. [Google Scholar] [CrossRef]
- Baur, A.P.; Cayron, C.; Logé, R.E. {225}γ habit planes in martensitic steels: From the PTMC to a continuous model. Sci. Rep. 2017, 7, 40938. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K.; Oka, M.; Wayman, C.M. The association of martensite platelets with austenite stacking faults in an Fe-8Cr-1C alloy. Acta Metall. 1970, 18, 1005–1011. [Google Scholar] [CrossRef]
- Shibata, A.; Murakami, T.; Morito, S.; Furuhara, T.; Maki, T. The Origin of Midrib in Lenticular Martensite. Mater. Trans. 2008, 49, 1242–1248. [Google Scholar] [CrossRef]
- Cayron, C.; Baur, A.P.; Logé, R.E. A Crystallographic Model of the {557} Habit Planes in Low-Carbon Martensitic Steels. Available online: https://arxiv.org/abs/1606.04257 (accessed on April 2018).
- Peet, M.J.; Bhadeshia, H.K.D.H. Surface Relief Due to Bainite Transformation at 473K (200 °C). Metall. Mater. Trans. A 2011, 42, 3344–3348. [Google Scholar] [CrossRef]
- Sowa, H. Sphere packing as tool for a description of martensitic transformations. Acta Crystallogr. A Found. Adv. 2017, 73, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Cayron, C. Hard-sphere displacive model of extension twinning in magnesium. Mater. Des. 2017, 119, 361–375. [Google Scholar] [CrossRef]
- Liu, B.-Y.; Wang, J.; Li, B.; Lu, L.; Zhang, X.-Y.; Shan, Z.-W.; Li, J.; Jia, C.-L.; Sun, J.; Ma, E. Twinning-like lattice reorientation without a crystallographic plane. Nat. Commun. 2014, 5, 3297. [Google Scholar] [CrossRef] [PubMed]
- Barnett, M.R.; Keshavarz, Z.; Beer, A.G.; Ma, X. Non-Schmid behavior during secondary twinning in a polycrystalline magnesium alloy. Acta Mater. 2008, 56, 5–15. [Google Scholar] [CrossRef]
- Luo, J.R.; Godfrey, A.; Liu, W.; Liu, Q. Twinning behavior of a strongly basal textured AZ31 Mg alloy during warm rolling. Acta Mater. 2012, 60, 1986–1998. [Google Scholar] [CrossRef]
- Jonas, J.J.; Mu, S.; Al-Samman, T.; Gottstein, G.; Jiang, L.; Martin, E. The role of strain accommodation during the variant selection of primary twins in magnesium. Acta Mater. 2011, 59, 2046–2056. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Capolungo, L.; Marshall, P.E.; McCabe, R.J.; Tomé, C.N. Statistical analyses of deformation twinning in magnesium. Philos. Mag. 2010, 90, 2161–2190. [Google Scholar] [CrossRef]
- Li, B.; Ma, E. Atomic Shuffling Dominated Mechanism for Deformation Twinning in Magnesium. Phys. Rev. Lett. 2009, 103, 035503. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yadav, S.K.; Hirth, J.P.; Tomé, C.N.; Beyerlein, I.J. Pure-Shuffle Nucleation of Deformation Twins in Hexagonal-Close-Packed Metals. Mater. Res. Lett. 2013, 1, 126–132. [Google Scholar] [CrossRef]
- Liu, B.-Y.; Wan, L.; Wang, J.; Ma, E.; Shan, Z-W. Terrace-like morphology of the boundary created through basal-prismatic transformation in magnesium. Scr. Mater. 2015, 100, 86–89. [Google Scholar] [CrossRef]
- Li, B.; Zhang, X.Y. Twinning with zero shear. Scr. Mater. 2016, 125, 73–79. [Google Scholar] [CrossRef]
- Christian, J.W.; Olson, G.B.; Cohen, M. Classification of Displacive Transformations: What is a Martensitic Transformation? J. Phys. IV 1995, 5, 3–10. [Google Scholar] [CrossRef]
- Chowdhury, P.; Sehitoglu, H. Deformation physics of shape memory alloys—Fundamentals at atomistic frontier. Prog. Mater. Sci. 2017, 88, 49–88. [Google Scholar] [CrossRef]
- Wang, H.L.; Hao, Y.L.; He, S.Y.; Du, K.; Li, T.; Obbard, E.G.; Hudspeth, J.; Wang, J.G.; Wang, Y.D.; Wang, Y.; et al. Tracing the coupled atomic shear and shuffle for a cubic to a hexagonal crystal transition. Scr. Mater. 2017, 133, 70–74. [Google Scholar] [CrossRef]
- Delaey, L. Diffusionless Transformations. In Phase Transformations in Materials; Kostorz, G., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2001. [Google Scholar] [CrossRef]
- Ishii, A.; Li, J.; Ogata, S. Shuffling-controlled versus strain-controlled deformation twinning: The case for HCP Mg twin nucleation. Int. J. Plast. 2016, 82, 32–43. [Google Scholar] [CrossRef]
- Ogawa, K.; Kajiwara, S. High-resolution electron microscopy study of ledge structures and transition lattices at the austenite-martensite interface in Fe-based alloys. Philos. Mag. 2004, 84, 2919–2947. [Google Scholar] [CrossRef]
- Tu, J.; Zhang, S. On the {102} twinning growth mechanism in hexagonal close-packed metals. Mater. Des. 2016, 96, 143–149. [Google Scholar] [CrossRef]
- Cayron, C. Hard-sphere displacive model of deformation twinning in hexagonal close-packed metals. Revisiting the case of the (56°, a) contraction twins in magnesium. Acta Crystallogr. A Found. Adv. 2017, 73, 346–356. [Google Scholar] [CrossRef] [PubMed]
- Serra, A.; Pond, R.C.; Bacon, D.J. Computer Simulation of the Structure and Mobility of Twinning Dislocations in H.C.P. Metals. Acta Metall. Mater. 1991, 39, 1469–1480. [Google Scholar] [CrossRef]
- Serra, A.; Pond, R.C.; Bacon, D.J. The Crystallography and Core Structure of Twinning Dislocations in H.C.P. Metals. Acta Metall. Mater. 1988, 36, 3183–3203. [Google Scholar] [CrossRef]
- Cayron, C.; Logé, R.E. Unconventional Twinning Modes in Magnesium. Available online: https://arxiv.org/abs/1707.00490 (accessed on April 2018).
- Cayron, C. A one-step mechanism for new twinning modes in magnesium and titanium alloys modelled by the obliquity correction of a (58°, a + 2b) prototype stretch twin. Acta Crystallogr. A Found. Adv. 2018, 74, 44–53. [Google Scholar] [CrossRef] [PubMed]
- Le Lann, A.; Dubertret, A. A Development of Kronberg’s Model for {102} Twins in H.C.P. Metals. Phys. Status Solidi A 1979, 51, 497–507. [Google Scholar]
- Dubertret, A.; Le Lann, A. Development of a New Model for Atom Movement in Twinning. Phys. Status Solidi A 1980, 60, 145–151. [Google Scholar] [CrossRef]
- Kronberg, M.L. A structural mechanism for the twinning process on {102} in hexagonal close packed metals. Acta Metall. 1968, 16, 29–34. [Google Scholar] [CrossRef]
- Qin, R.S.; Bhadeshia, H.K. Phase field method. Mater. Sci. Technol. 2010, 26, 803–811. [Google Scholar] [CrossRef]
- Levitas, V.I. Thermodynamically consistent phase field approach to phase transformations with interface stresses. Acta Mater. 2013, 61, 4305–4319. [Google Scholar] [CrossRef]
- Mnyukhm, Y. Second-Order Phase Transitions, L. Landau and His Successors. Am. J. Condens. Matter Phys. 2013, 3, 25–30. [Google Scholar]
- Landau, L. On the theory of phase transitions. Zh. Eksp. Teor. Fiz. 1937, 7, 19–32. [Google Scholar] [CrossRef]
- Wigner, E. Gruppentheorie und Ihre Anwendung auf die Quantenmechanik der Atomspektren; Springer Fachmedien Wiesbaden GmbH: Wiesbaden, Germany, 1931. [Google Scholar]
- Weyl, H. Gruppentheorie Und Quantenmechanik; S. Hirzel: Leipzig, Germany, 1931. [Google Scholar]
- Clapp, P.C. How would we Recognize a Martensitic Transformation if it Bumper us on a Dark and Austy Night? J. Phys. IV 1995, 5, 11–19. [Google Scholar]
- Clayton, J.D.; Knap, J. A phase field model of deformation twinning: Nonlinear theory and numerical simulations. Phys. D Nonlinear Phenom. 2011, 240, 841–858. [Google Scholar] [CrossRef]
- Tolédano, J.C.; Dmitriev, V. Reconstructive Phase Transitions in Crystals and Quasicrystals; World Scientific: Singapore, 1996. [Google Scholar]
- Janovec, V. Group analysis of domains and domain pairs. Czechoslov. J. Phys. B. 1972, 22, 975–994. [Google Scholar] [CrossRef]
- Janovec, V.; Dvorakova, E. The coset and double coset decomposition of the 32 crystallographic point groups. Acta Crystallogr. A Found. Adv. 1989, 45, 801–802. [Google Scholar] [CrossRef]
- Kalonji, G.; Cahn, J.W. Symmetry constraints on the orientation dependence of interfacial properties: The group of the Wulff plot. J. Phys. 1982, 43, 25–31. [Google Scholar] [CrossRef]
- Brandt, W. Über eine Verallgemeinerung des Gruppenbegriffes. Math. Ann. 1926, 96, 360–366. [Google Scholar] [CrossRef]
- Brown, R. From groups to groupoids: A brief survey. Bull. Lond. Math. Soc. 1987, 19, 113–134. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 1950, 20, 1064–1082. [Google Scholar]








© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cayron, C. Shifting the Shear Paradigm in the Crystallographic Models of Displacive Transformations in Metals and Alloys. Crystals 2018, 8, 181. https://doi.org/10.3390/cryst8040181
Cayron C. Shifting the Shear Paradigm in the Crystallographic Models of Displacive Transformations in Metals and Alloys. Crystals. 2018; 8(4):181. https://doi.org/10.3390/cryst8040181
Chicago/Turabian StyleCayron, Cyril. 2018. "Shifting the Shear Paradigm in the Crystallographic Models of Displacive Transformations in Metals and Alloys" Crystals 8, no. 4: 181. https://doi.org/10.3390/cryst8040181