2.1. Box Size Adjustment for Free Energy Optimization
As explained above (and in the Appendix), the SCF free energy features segment potentials and segment densities that are mutually dependent. The optimization of it leads to rules of which the fixed point is known as the SCF solution. Let us now assume that we have such an SCF solution, and we can evaluate the free energy using Equation (A4). One can easily see that, for an SCF solution, Equation (A4) can be simplified resulting in:
where the free energy of the homogeneous reference (the bulk) as the reference as usual,
q is the single chain partition function, which can be computed with the propagator formalism from the segment potentials,
V the system volume and
is the value of the Lagrange field that takes values such that the system is incompressible at each coordinate, i.e.,
. To compare systems with different size and structure to each other, it is appropriate to evaluate the free energy density for each of these systems:
Typically, the free energy density is negative because the microphase segregated state develops spontaneously from the homogeneous state. The system with the lowest free energy is the preferred one.
Inspection of the procedure reveals that we should fix the values of
,
and
before we can start solving the SCF equations. Hence, we end up with a free energy density that is a function of the specified spacing
D, i.e.,
. There is no guarantee that, for an arbitrary choice of the system size, the optimized SCF free energy density is at its minimal value. Therefore, we need to vary the value of
in the lamellar phase, or the combination of
and
in the hexagonal phase or the value of
in (e.g.) the gyroid case to find the optimal spacing
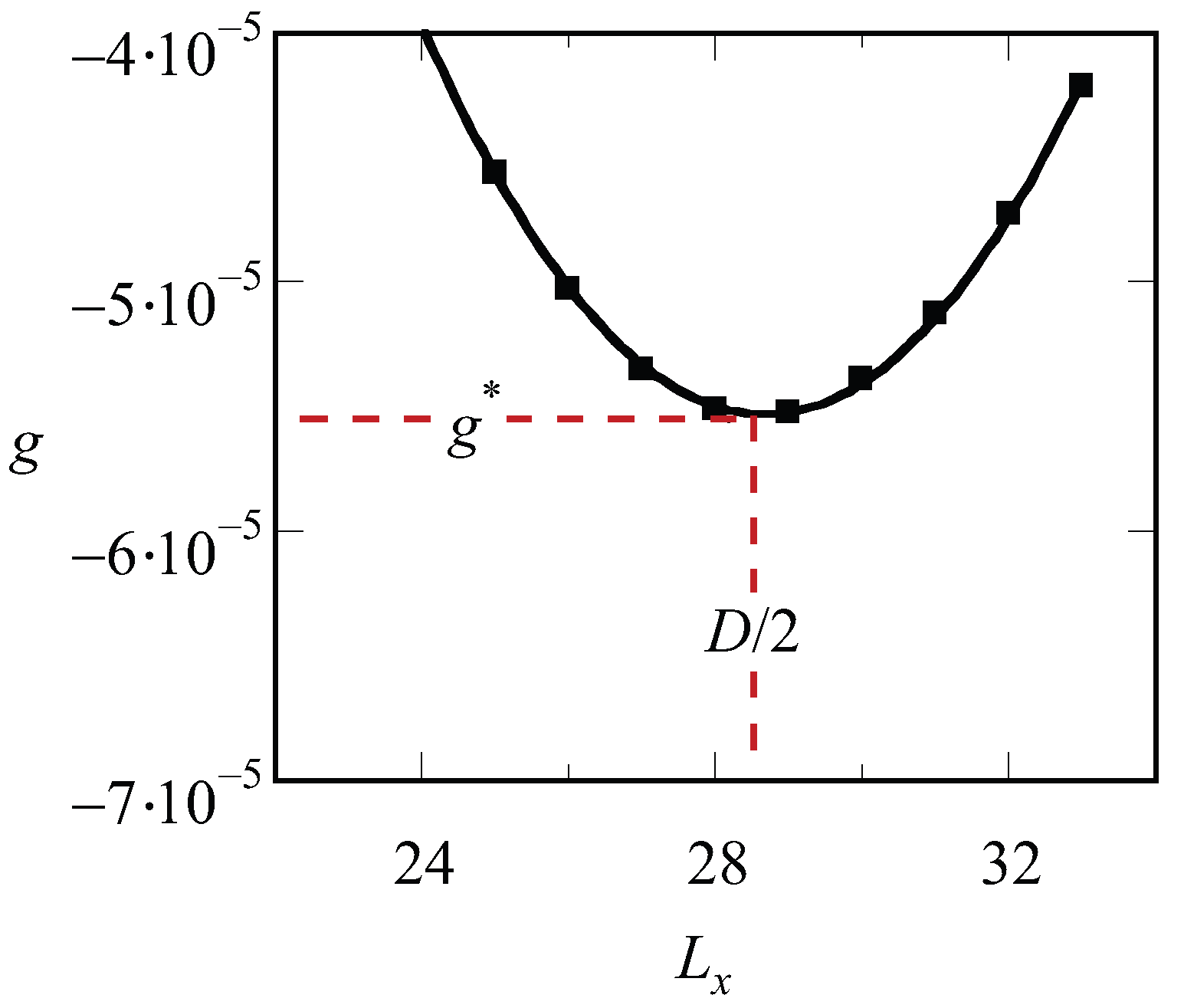
. A typical result of such procedure for a lamellar phase is presented in
Figure 1. The free energy that is optimized with respect to the spacing is labeled by an asterisk,
.
Apart from the system size we need, though the choice of the number of gradient directions and the type of boundary condition, to specify the phase of choice of considerations. To illustrate this, we will visit the topologies that are used below, namely the LAM, HEX, SG, DG, DD and HPL phases in order.
2.2. The Lamellar Phase
For a LAM phase, we reduce the calculations to the one-gradient case
and the mean field approximation is applied in
y- and
z-directions. The system size is given by
and we use reflecting boundary conditions:
All other quantities that are a function of the spatial coordinate, such as the segment potentials, the end-point distributions follow these rules. In this case, the free energy G is per unit area and the free energy density is found by . Typically, we will have one A–B interface somewhere half-way in the ‘box’ (depending on f) and the lamellar spacing is given by . We select the A-rich domain to be at low x-values and the B-rich domain at high x-values by means of an initial guess for the segment potentials.
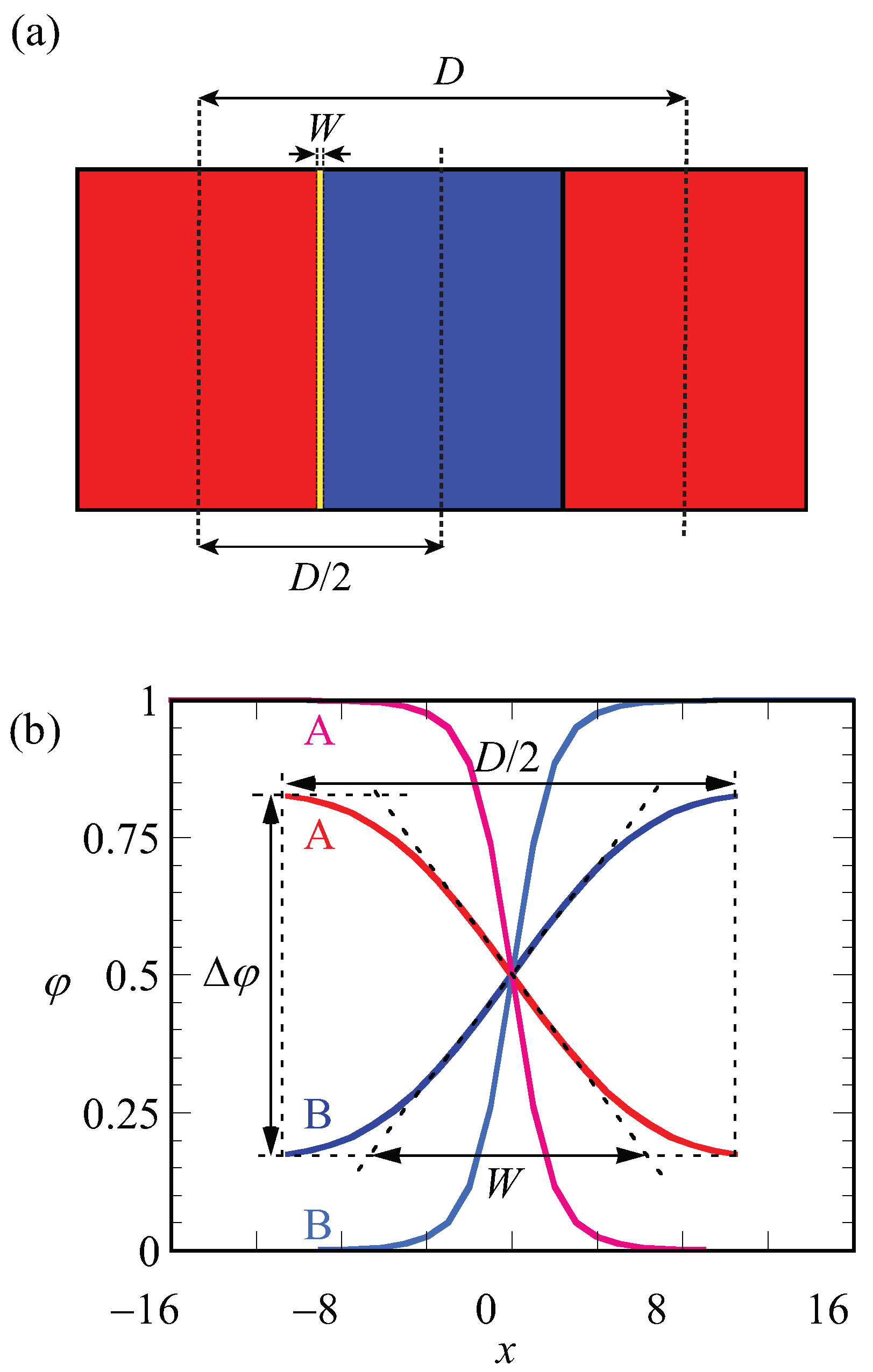
A schematic representation of the LAM phase and the optimized (with respect to the spacing) density profile are given in
Figure 2a,b. In
Figure 2a, red and blue regions belong to the A and B blocks, respectively. The spacing (
D) and width of the interface (
W) are indicated on the lamellae. The same parameters (
D and
W) are defined more precisely on the density profiles
and
shown in
Figure 2b. In this graph, the density difference
, which
is also the volume fraction midway in the A-rich phase, is indicated. As the coordinate
is fixed to the position of the steepest gradients in the density, the evaluation of the density difference takes place at
:
. Finally, the width of the interface, as graphically illustrated in
Figure 2, is computed from the profiles according to
In
Figure 2b, the curves in black belong to the density profiles of A and B blocks for
in the weak segregation regime where the optimized spacing is
, whereas density profiles shown in light gray belong to the A and B blocks of a copolymer in the strong segregation region of
with optimized spacing
. For weakly segregated block copolymers,
easily deviates highly from unity and its value approaches zero in the limit towards the critical point, whereas it approaches unity for strong segregation limits. From its definition (Equation (
5)), it is easily seen that the width of the interface
W is small for strong segregation and increases upon the approach towards weak segregation. Obviously,
W cannot exceed
.
2.4. Various Mesophases That Require Three-Gradient SF-SCF
There are many three-gradient solutions of the SCF equations. Some of these, e.g., the
cubic phase, require reflecting boundary conditions [
13]. Here, our interest is in, e.g., SG and DG structures that lack symmetry planes. For such structures, one requires periodic boundary conditions. We restrict our analysis to three-gradient SF-SCF computations with equal sizes in the three gradient directions:
. The periodic boundaries are implemented by realizing that coordinates 1 and
L are ‘neighbors’ where it is understood that the potentials and end-point distributions follow the same rules:
Next, similarly as in other systems, we vary
L systematically to find the optimal spacing. Here, we choose the spacing
for which the free energy density is minimized with respect to
L. The SG phase has many interesting aspects that are well documented in the literature [
21,
22,
23,
24]. Our result for the SG phase closely follows all these features. As mentioned already, the SG lacks mirror symmetry. There only exists a three-fold symmetry axis along one of the diagonals of the unit cell as is easily seen from the profile given in
Figure 4a. Other various features of SG appear when we multiply the unit cell a few times. As the majority phase is made transparent, we notice spherical holes with a hexagonal pattern when viewed from the view direction given in
Figure 4b. From other view directions (not shown), one can see the holes in a square packing.
As proven below, the SG is metastable as one can easily find for either a HEX phase or a LAM phase for which the free energy density is lower. The reason for this relatively high free energy density is clear. The majority phase fills up 2/3 of the volume, whereas the minority phase fills the remainder of the volume in a gyroid-like. The interface in between the A and B rich domains deviates from the being a minimal surface (zero mean curvature throughout the interface), which is only expected for the SG gyroid phase with . Such balanced SG phase does not exist as for the lamellar phase is the lowest in free energy.
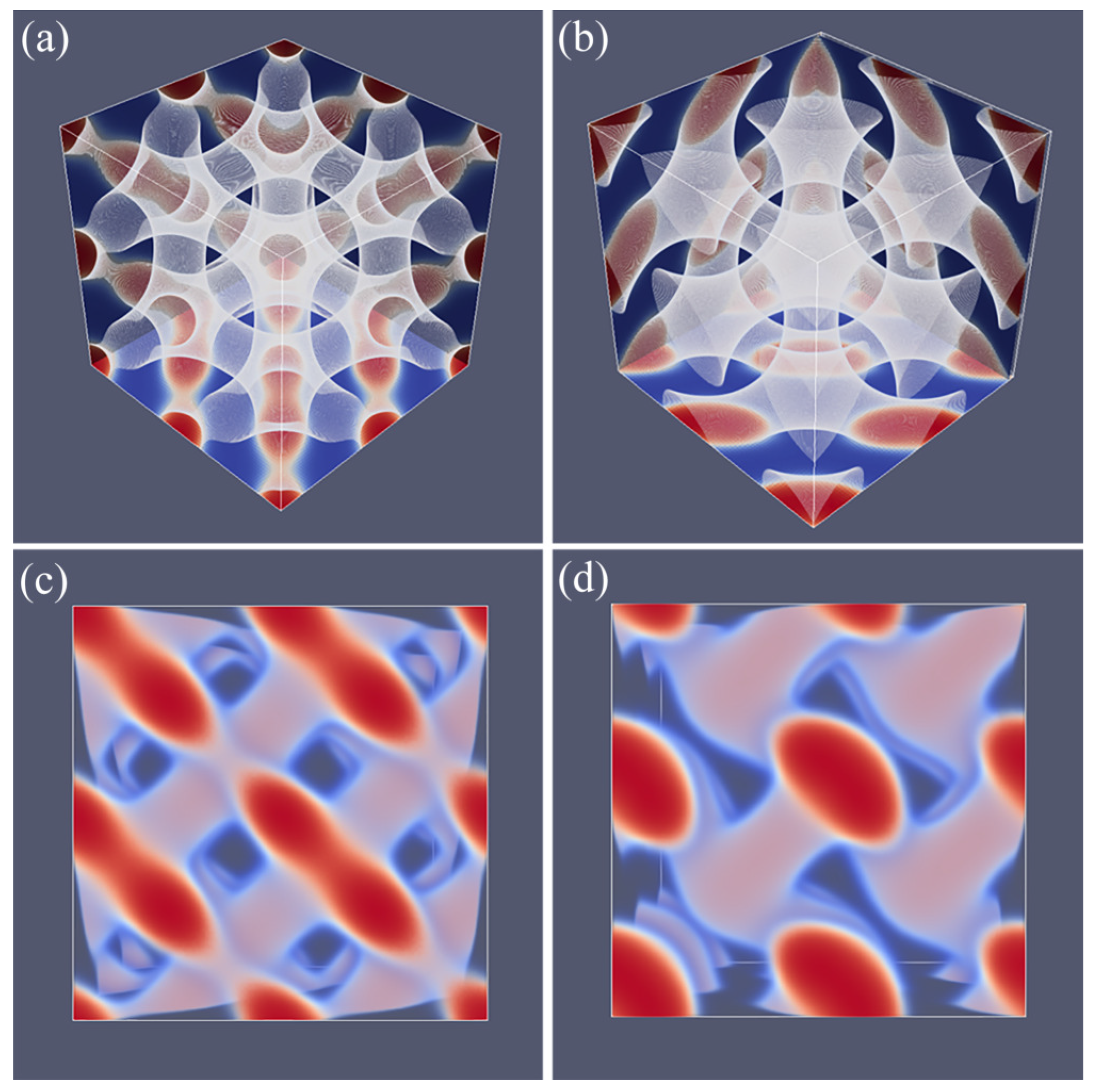
A typical unit cell of a DG phase is depicted in
Figure 4c. The viewgraph of eight unit cells (
Figure 4d) now lacks the ‘holes’ because these holes are now the place in which the second gyroidal labyrinth of the minority phase is placed. Below, we show that the DG phase is a candidate ground state as it is lower in free energy than the HEX and the LAM for a small region of
f values.
As compared to the SG, the DG has two gyroidal labyrinths with equal volume and the majority phase is in between the two and in this sense the symmetry is restored. From the perspective of the majority phase, the two sub-phases of the minority phase are spaced symmetrically around it even though . As compared to the SG, the optimal spacing of the DG increased almost by a factor of two as it went up from for SG to for DG. Again, the DG has no symmetry planes and only one three-fold symmetry axis. Interestingly, the two minority phases only have three-fold junction points where three tubular domains come together. This appears sufficient to generate a so-called triply periodic structure, i.e., one can travel inside a minority phase in any of the three directions, x, y and z throughout the system.
As explained above, we do not impose a particular symmetry for a particular segregated state during the SF-SCF optimization procedure, but instead implement an initial guess and apply appropriate boundary conditions. By accident, one of the calculations targeted for a SG phase deferred to a HPL phase. A possible reason for this unforeseen result was found posteriori by the observation that the HPL is competitive free-energy wise with the SG for the
f value that was selected in the computations (see also below). Upon inspection of the HPL phase, a strong resemblance with the DD was found and therefore we present these phases side by side in
Figure 5. For both phases, we employed periodic boundary conditions, and again for both phases, we have systematically varied the box size
L and present the resulting structure for the optimal spacing
D.
Referring to
Figure 5a,c we present the DD morphology from two perspectives: (a) a view from along one of the diagonals from which the three symmetry planes can be seen and (c) a view with any of the planes of the unit cell placed perpendicular to the viewing direction. The DD morphology has often been described in the literature [
36,
37] and the phase that was predicted by SF-SCF is completely in line with this. The structure has three symmetry planes that are rotated with respect to each other by 60
. Similarly as for the DG, the minority phase forms two non-intersecting triply periodic regions with opposite handedness, while the majority phase is draped in between the minority labyrinths. The morphology of DD (space group
) is characterized by four-fold junctions similarly as in the tetragonal C-network in diamond (or the structure of methane).
In
Figure 5b,d, we show the typical HPL phase with an optimized spacing for an asymmetry fraction of
for which the free energy density is lower than that of the corresponding SG (see below). The two viewgraphs show the structure from two viewpoints identical to the ones given for DD: (b) gives the view in the direction along the axis of the unit cell. For this point, the three symmetry-planes can be seen, and (d) gives the view face-on with one of the planes of the unit cell perpendicular to the view direction. The comparison between panels (a), and (b) as well as (c) and (d) in
Figure 5 are apparent and informative. Comparing HPL and DD, we notice that the curvatures of the interfaces are clearly similar. There are, however, important differences. As the DD has four-fold connections, in the HPL phase, there are only three-fold connections (as in gyroids). (This is not easily recognized from the viewgraphs, but this is better observed by inspection of the HPL from many viewing directions). As compared to the DD, the fourth connection is ‘broken’. As a consequence, the HPL phase is lamellar and not triply-periodic: one can peel off one layer after another layer from the HPL phase, which is best seen from the images of (b) and (d) in Figure 11. (b) and (d) correspond to the morphology when we have the compositions of
and
, respectively. The layers together feature holes in hexagonally organized patterns. In (b) at low
f, the hexagonally ordered pores are more apparent because the lower volume of the minority phase does not alter the visibility of the holes. In between the holes, lamellae strongly bend toward a neighboring layer in the direction of the missing connector. Two neighboring lamellae have opposite bending characteristics; hence, there are two types of layers in the HPL phase which alternate, each having inversed curvatures. These two types of layers resemble the two networks with opposite handedness in DG or DD phases. Characteristic for the HPL phase is that the odd layers almost touch each other across the pores of the even layers and vice versa. Indeed, if at these places, the odd layers would re-establish their connection and when similar connections were made between the even layers, we restore exactly the DD phase without the need to modify the curvatures of the interfaces much (as is best seen from close inspection of the differences between
Figure 5c,d). The reason for the HPL phase to have lamellae with locally strong curves is to ensure a homogeneous distance between the lamellae in the presence of pores in the lamellae. Such homogeneity in interlamellar distances is a desired property as this ensures homogeneous stretching of the copolymer blocks.
2.5. Systematic Dependences
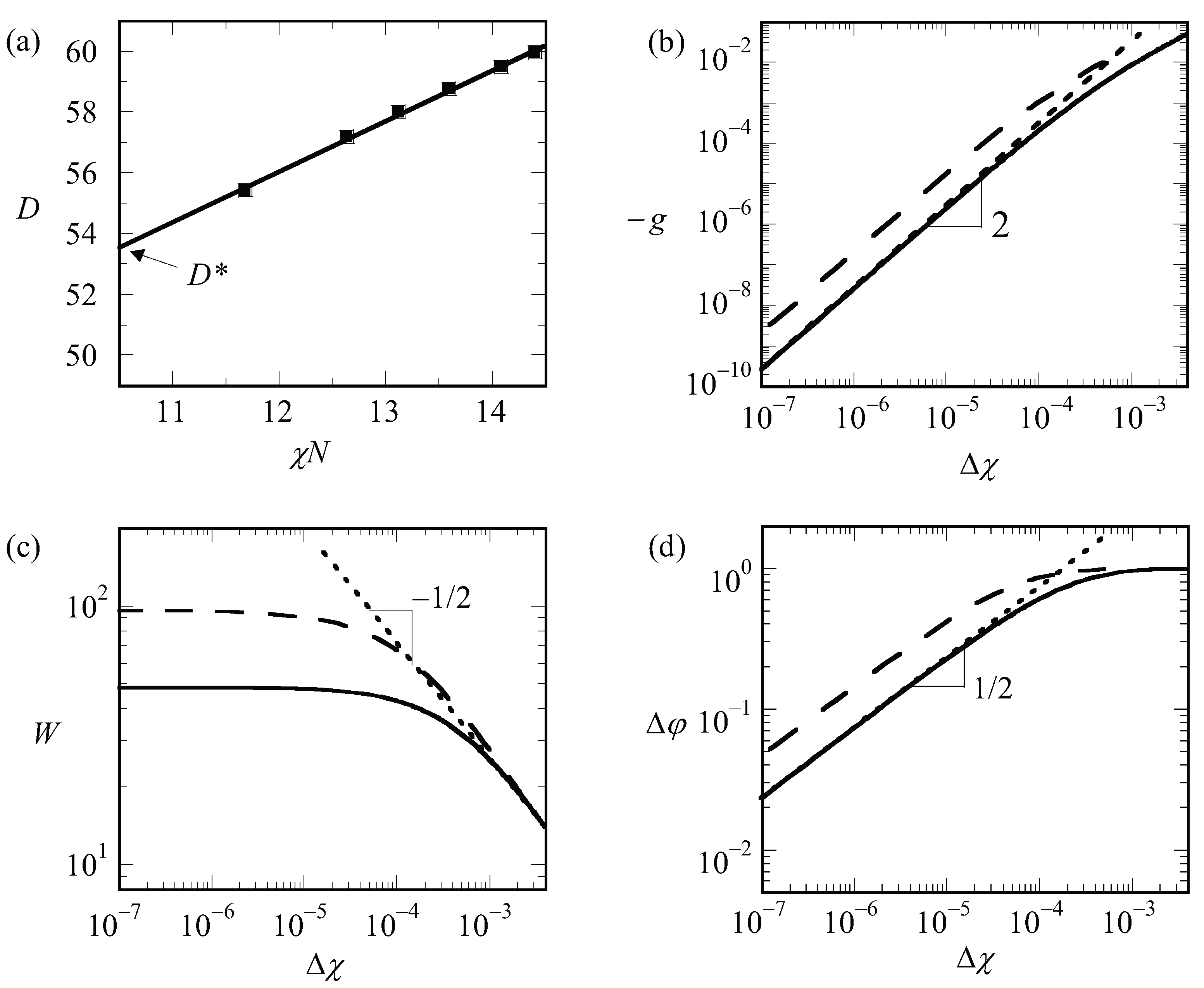
By examining finite chain length effects near the critical region, we are faced with a problem. In order to find
, we need to have an accurate guess for the optimal spacing at the critical point, which we will refer to as
. The latter we can only find by extrapolation. The (approximate) procedure that we followed is illustrated by referring to
Figure 6a. In this graph, we present the optimal spacing of the lamellar phase with
for a given overall chain length of
as a function of the product
. Hence, for this graph, we varied the
only and each point on the graph is the result from an optimization of the box size. We find
by extrapolation to
. It would have been better if we would have extrapolated to the exact critical value for the chain length
(which we will find below slightly lower than 10.5); however, the error in
that is introduced in this way is negligible. We can collect
as a function of chain length but which is presented later. We first analyze how the LAM phase is changed when we approach the critical point. These results are shown in
Figure 6b–d, wherein we present the free energy density, the width of the interface and the density difference, respectively, as a function of
for a lamellar phase with
for which
is very close to an integer number. Hence, for such a case, we know that in the limit of
, we enforce an optimal spacing to the system. For systems away from the critical region, one possibly would have acquired slightly different
D values, but this requirement cannot be implemented in a lattice model.
As can be seen from
Figure 6b,d, we obtain power-law dependences for both
as well as
. Indeed, these scaling dependences have been employed to identify
: the value of
was adjusted until the best power-law scaling was observed in
Figure 6b,d in the limit of
. Inspection of
Figure 6b shows that we find
. This value should be contrasted to the well-known result for the interfacial tension mentioned above for the liquid–liquid interface for macroscopic phase separation for which the coefficient is 3/2. We attribute the increase in the exponent to the observation that the width of the interface does not diverge (see
Figure 6c). At high value of
, the free energy density
tend to level off a bit as it becomes more linearly dependent on
.
Inspection of
Figure 6d shows that
in the limit of
and goes to the constant value of unity for large values of the interaction parameter. The scaling exponent near critical is identical to the one found for macrophase segregation.
The width of the interface has a more complex behavior as illustrated in
Figure 6c. It was already mentioned above that the width of the interface cannot exceed
. Hence, the width should level off in the limit of
. In this case, the solid line is for
13,000 while the dashed line is for
50,000. The corresponding values for
are 76 and 150, respectively. Upon inspection of the limiting value of the width, we notice that the width goes to approximately 2/3 of the value of
. Interestingly, for rather high values of
, the width of the interface follows approximately
, similar to that in the macrophase segregation problem. Apparently as long as
, we witness an increase of the interfacial width as if the two blocks would have been disconnected.
We have collected the optimal spacing at the critical point
for a wide range of chain lengths and present these results in
Figure 7a. To a good approximation, the results are represented by
, which is consistent with early predictions of Leibler [
15]. Next, we collected the critical interaction parameter
again for a wide range of chain lengths and present the results in
Figure 7b. In this graph, we have plotted
as a function of
and found to a good approximation as a straight line. The fitting result is indicated in the legend of
Figure 7b. Within the accuracy of the fitting procedure, we thus find
. These results are compatible with finite chain length corrections for the critical point found in the literature [
17].
We may use a simple Flory-like argument to elaborate on the scaling of the spacing with the chain length. In this argument, we can balance the entropic penalty for stretching of the chains, written as
(ignoring numerical coefficients) with the free energy to enlarge the contact area between the A and B blocks,
, where
is the interfacial free energy associated with this surface and
a is the area per molecule. The latter can be estimated from the filling of the system by chains, hence
and thus the free energy per chain is
where the free energy per chain is in units of
and that numerical coefficients are ignored. Optimization with respect to
D gives
. The interfacial energy of an A–B interface is known to depend on the square root of the interaction energy,
[
42]. Using the result that at the critical point
, we notice that
. We can apply the same argument to systems that are not close to the critical point. In
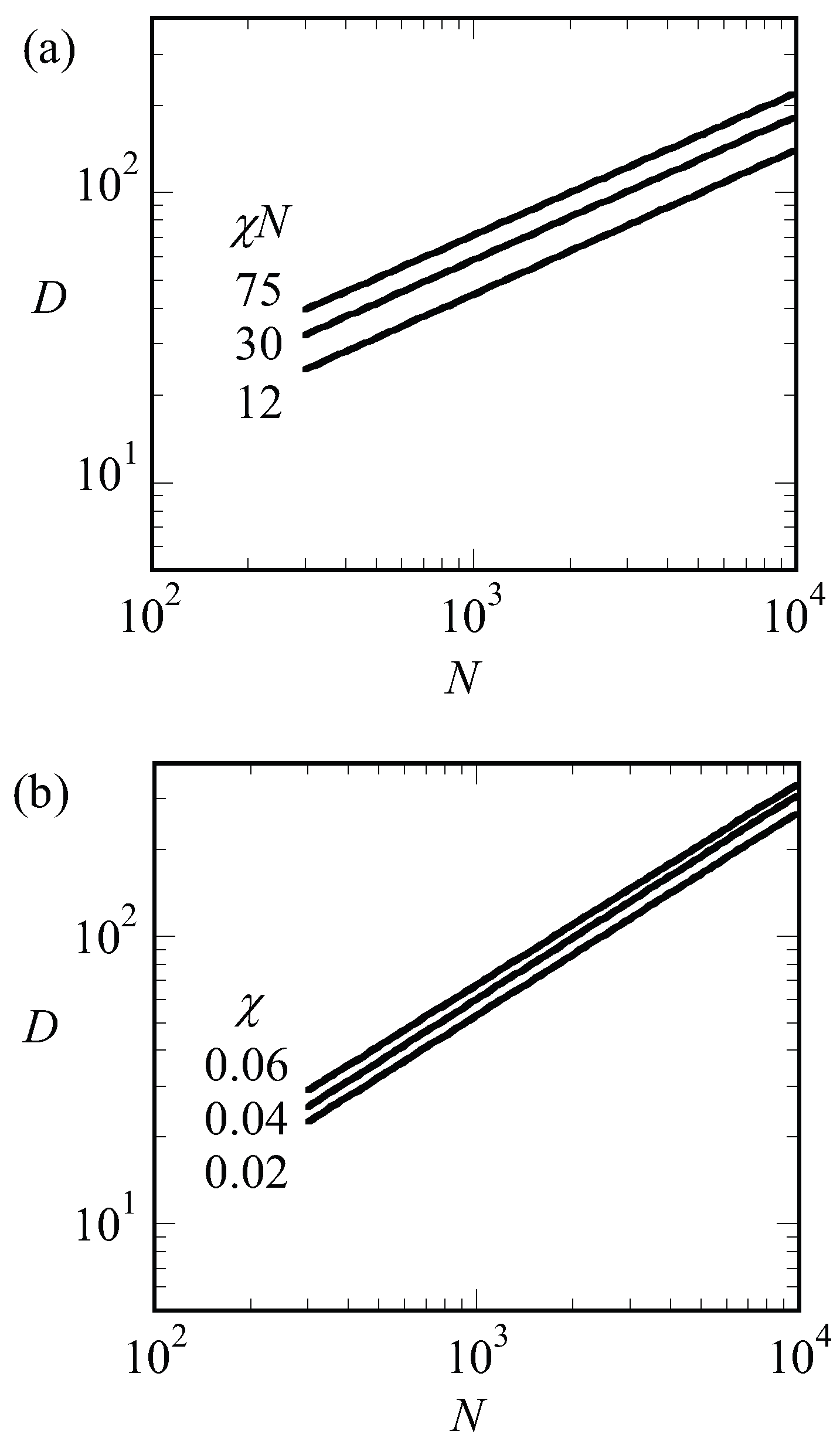
Figure 7a, we present the optimal spacing for LAM phase with
for low, intermediate and strong segregation regions of
and 75, respectively, as a function of the chain length
N. Hence for each of the lines, we varied
such to keep
fixed. Again, we find that the spacings obeyed
to a good approximation. This must be contrasted to the results presented in
Figure 8b. In this figure, we present the optimal spacing for the symmetric LAM phase (
) as a function of the chain length for fixed value of the interaction parameter. Hence, in these cases, we only changed
N and the interfacial energy
was approximately constant. As a result, the spacings obeyed
to a good approximation.
Next, we present the optimal spacing
D as a function of
f for LAM and HEX in
Figure 9 for a given value of
and
. When changing
f, we will pass the phase boundary around
. Hence, in
Figure 9, we showed the data points of the stable phases as filled dots and squares for LAM and HEX, respectively, and data points for the non-stable phases were shown as empty. With increasing
f, we find an increase in the optimal spacing. For the LAM phase, the slight increase in the spacing to a plateau region was successfully fitted by
. This is the expected dependence when the two blocks independently find the optimal width. A significantly stronger dependence for
was found for the HEX phase where to a reasonable approximation
. This result must be attributed to the decreased space occupied by the minority block in the cylindrical domains.
We would like to report on the chain length dependence of the HEX to LAM phase transition at a finite value of . We tried to obtain such result for . We tested a range of chain lengths of . Within the numerical noise of our procedure, we could not detect the expected chain length dependence for . This may be attributed to the noise in the data, which was amplified slightly because we could not satisfy the box dimensions for the HEX phase with enough precision. Instead, we focused on the stability of the various mesophases in the neighborhood of .
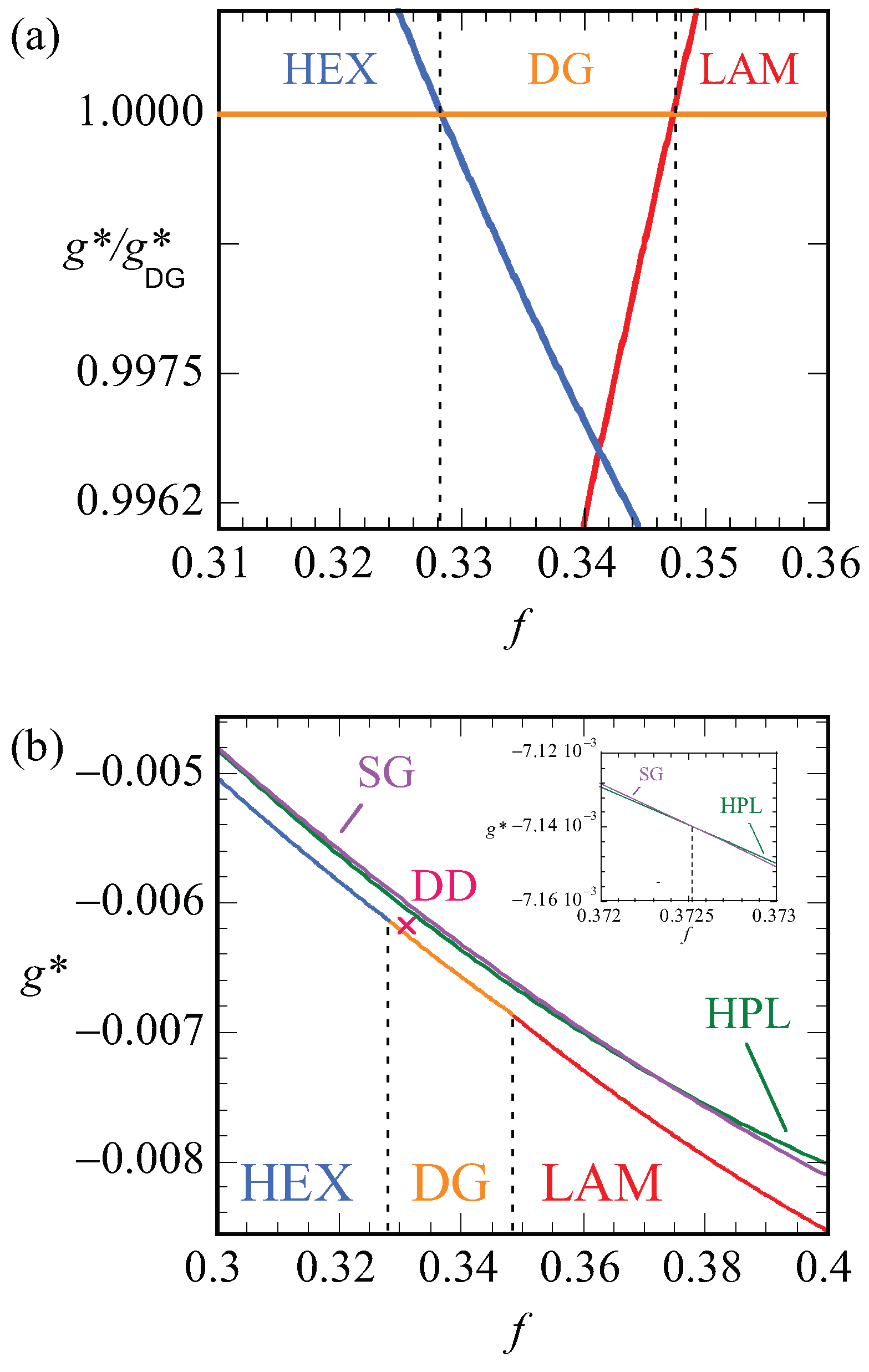
Let us focus next on the stability of various mesophases near
. For all phases, we have computed the optimized free energy density as a function of the asymmetry ratio,
. Plotting these free energy densities as a function of the asymmetry fractions results in lines that are nearly parallel (cf.
Figure 10b). The results are more easily discussed when we take the ratio
as a function of
f. Obviously, this dependence results in unity for the DG phase. Recalling that the free energy densities are negative, we find that when the ratio is smaller than unity, i.e., when
the DG is preferred and when
the other phase is stable. In
Figure 10a, we show this ratio as a function of
f for the HEX, the LAM and the DG phases. Literature points to a stability domain for the DG phase between
[
6]. We found DG as the most stable phase between
. These results are consistent with each other also considering the fact that the SF-SCF results are for a fixed chain length
.
In
Figure 10b, the bottom line presents the lowest free energy values that were obtained, i.e., it connects the data of the HEX phase to those of the DG and then to the LAM phase. The vertical dashed lines present the phase boundaries. The point X gives the free energy density of the DD phase, which is indeed slightly larger than the DG at the same
f value. The two top lines are the free energy densities of the HPL and the SG phases. Both these phases are metastable as their free energy density is higher than the HEX, DG, LAM phase boundary. As shown in the inset, the free energy densities of the HPL and SG cross each other around
. For smaller
f values, the HPL is preferred over SG and, above this crossing point, the SG is more stable.
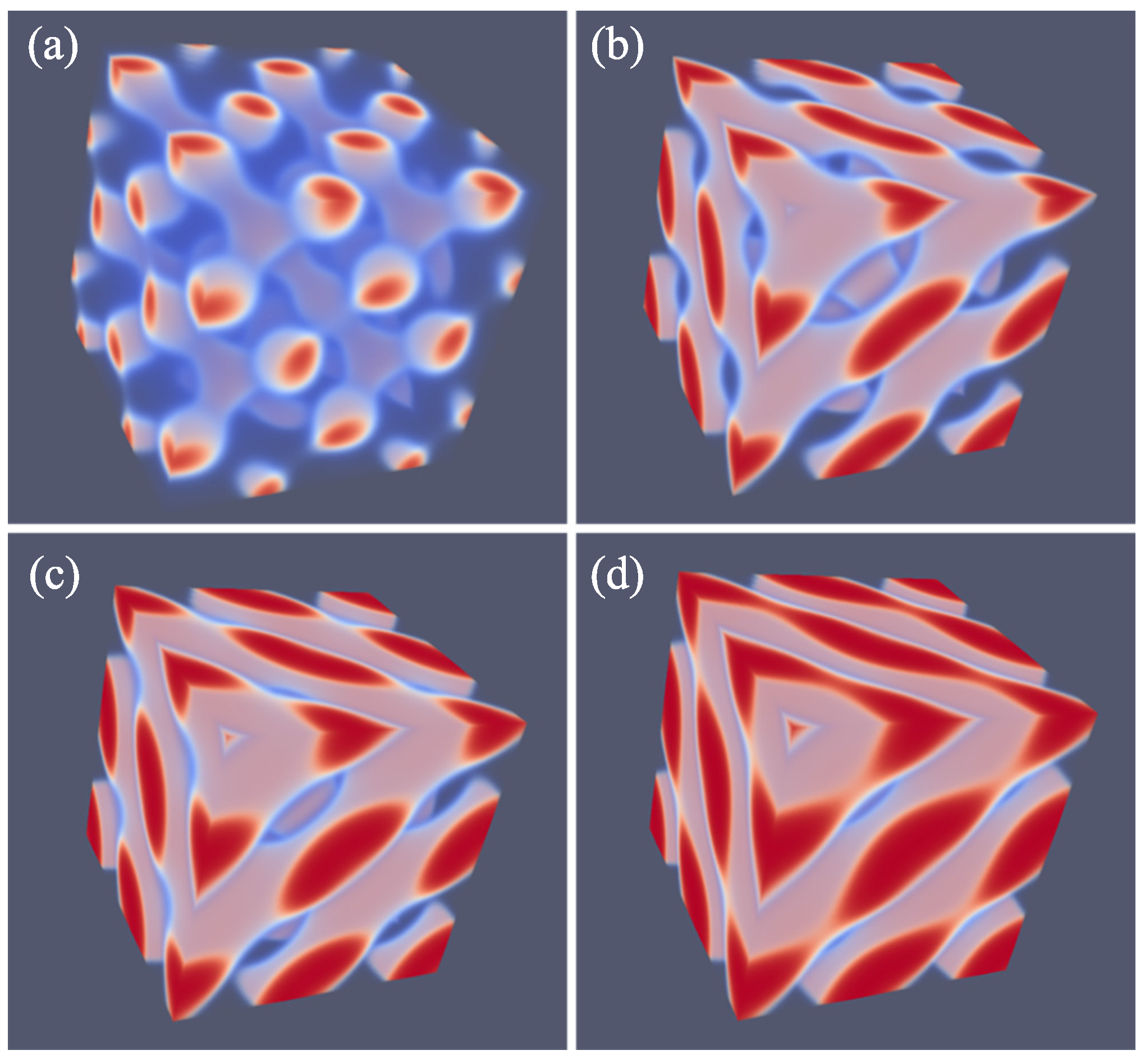
Of all phases that we have considered, the HPL phase is possibly the most novel one. It turned out that the phase is computationally highly robust and it was quite easy to find HPL phases for various values of
f covering the whole relevant range from the region where the LAM phase is stable (e.g.,
) to near the order–disorder line for
. In
Figure 11, we put four variants of the HPL phase for
, 0.30, 0.37 and 0.50 side by side. The first one is the HPL in the region where spherical phase is the preferred state; (b) is near the region where the HEX is the stable phase; (c) is a transition state between HEX and LAM, e.g., DG; (d) is the HPL for the case where obviously the LAM phase is the ground state. It is noticed that at large values of
f, the lamellae of the HPL are close to planar (
, i.e., (d)) and the hexagonally ordered holes are relatively small. The holes become bigger when
f decreases. At the same time, the layers become more strongly curved (
, i.e., (b)). Now, the connection points are more apparent as three cylindrical domains come together. When
f is decreased even more (
, i.e., (a)), the cylindrical domains are no longer homogeneous in thickness. Instead, the tubular fragments develop similarly to spherical regions with a neck in between. This is consistent with spherical detached domains being preferred for systems with such low
f values. For small
f values, the minority phase becomes smaller and smaller in volume and therefore the holes where the majority phase exists in the HPL phase grow larger and larger. In other words, the tubular regions that keep the layers intact become thinner and thinner. The lamellae also become more curved and the direction of the thin tubular fragments are almost perpendicular to the planar lamellae found close to
.
In
Figure 12, we present our results for the strong segregation,
. We kept the chain length at
, and thus increased the interaction parameter. Here, we plot the free energy density
normalized by this value for the DG (similarly as in
Figure 10a) as a function of the
f value. Again, only when this ratio is smaller than unity do we expect the DG to be stable (recall that the free energy density is negative). Inspection of
Figure 12 proves that the ratios are larger than unity for both the HEX as well as the LAM phase. This proves that the DG phase is metastable for these high values of the interaction parameter. The free energy densities of the HEX and LAM phases cross at
, which is below the value found for the HEX-LAM transition region for
. This is in line with the general knowledge of the phase diagram that the phase transitions all move slightly to smaller
f values with increasing
. We note that the ratio
are just of order 1.0015, which means that the free energy differences are minor. Nevertheless, the differences are significantly larger than the noise in the data (data point not shown are exactly on the lines), and we believe that these results are sufficiently accurate.
A typical value for the optimal D for the DG at , was . The optimal spacing for the DG at for near was found to be . This growth with a factor 1.36 in optimal spacing is a bit larger than expected from , which implies and hence a growth by only a factor 1.26. We also investigated the free energy density of the HPL phase for the strong segregation . In line with the results at lower segregation, the HPL phase is also metastable and indeed the DG phase outperforms the HPL phase also at as (the DG free energy density while that of the HPL is for the corresponding f values).