Nonlinear Analyses of Adobe Masonry Walls Reinforced with Fiberglass Mesh
Abstract
:1. Introduction
2. Summary of Experimental Outcomes
2.1. Test Setup
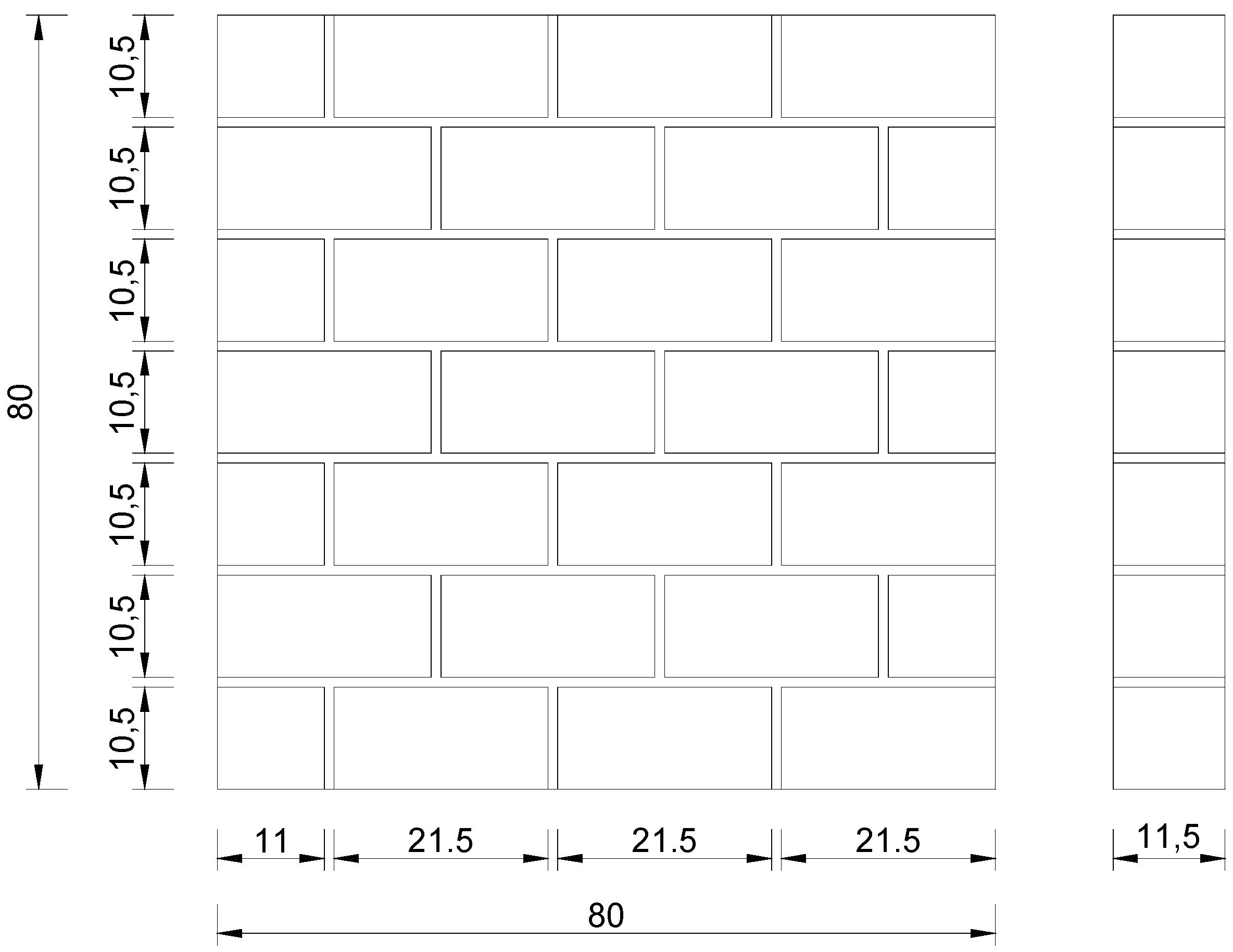
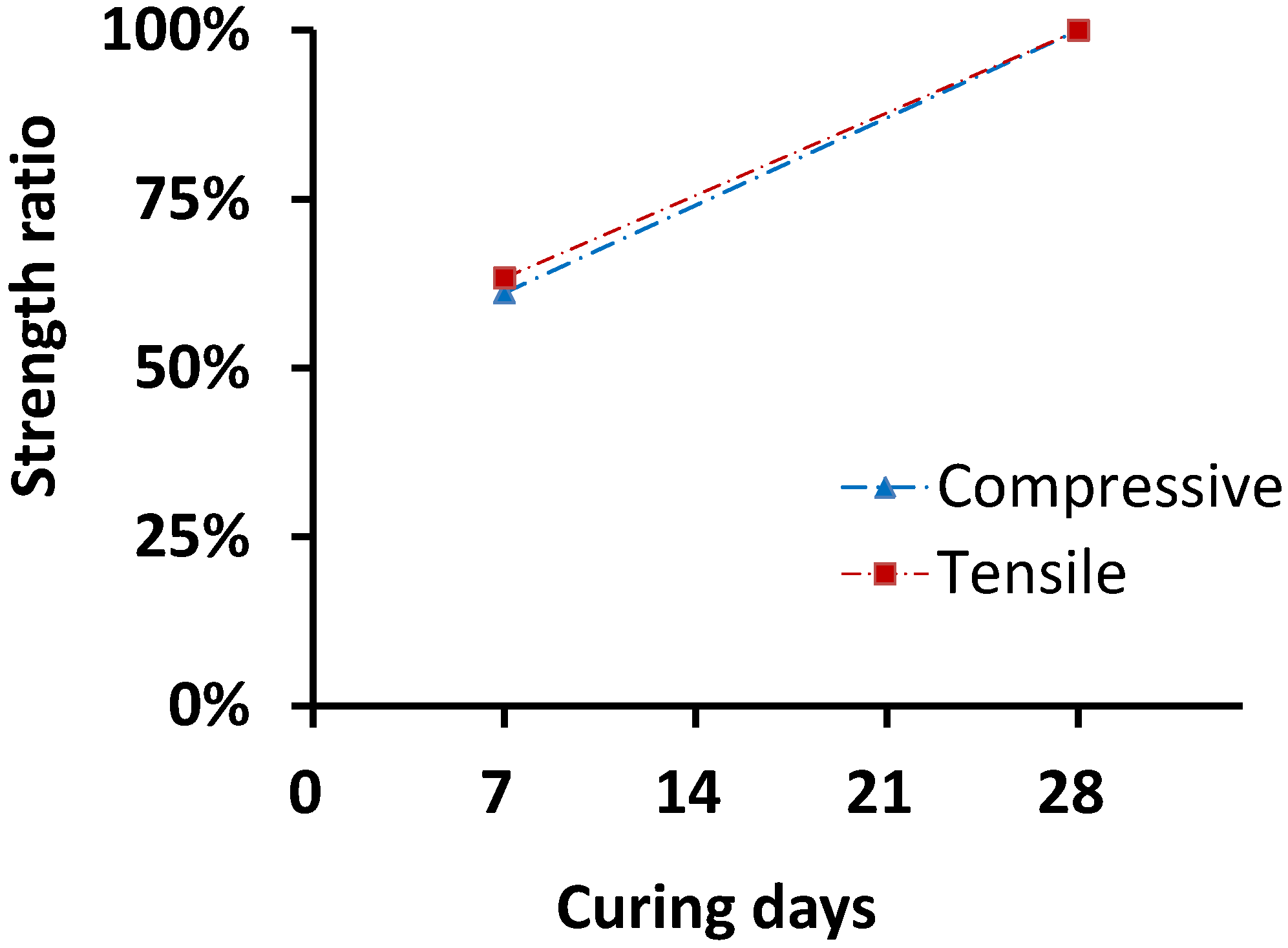
2.2. Material Characterization
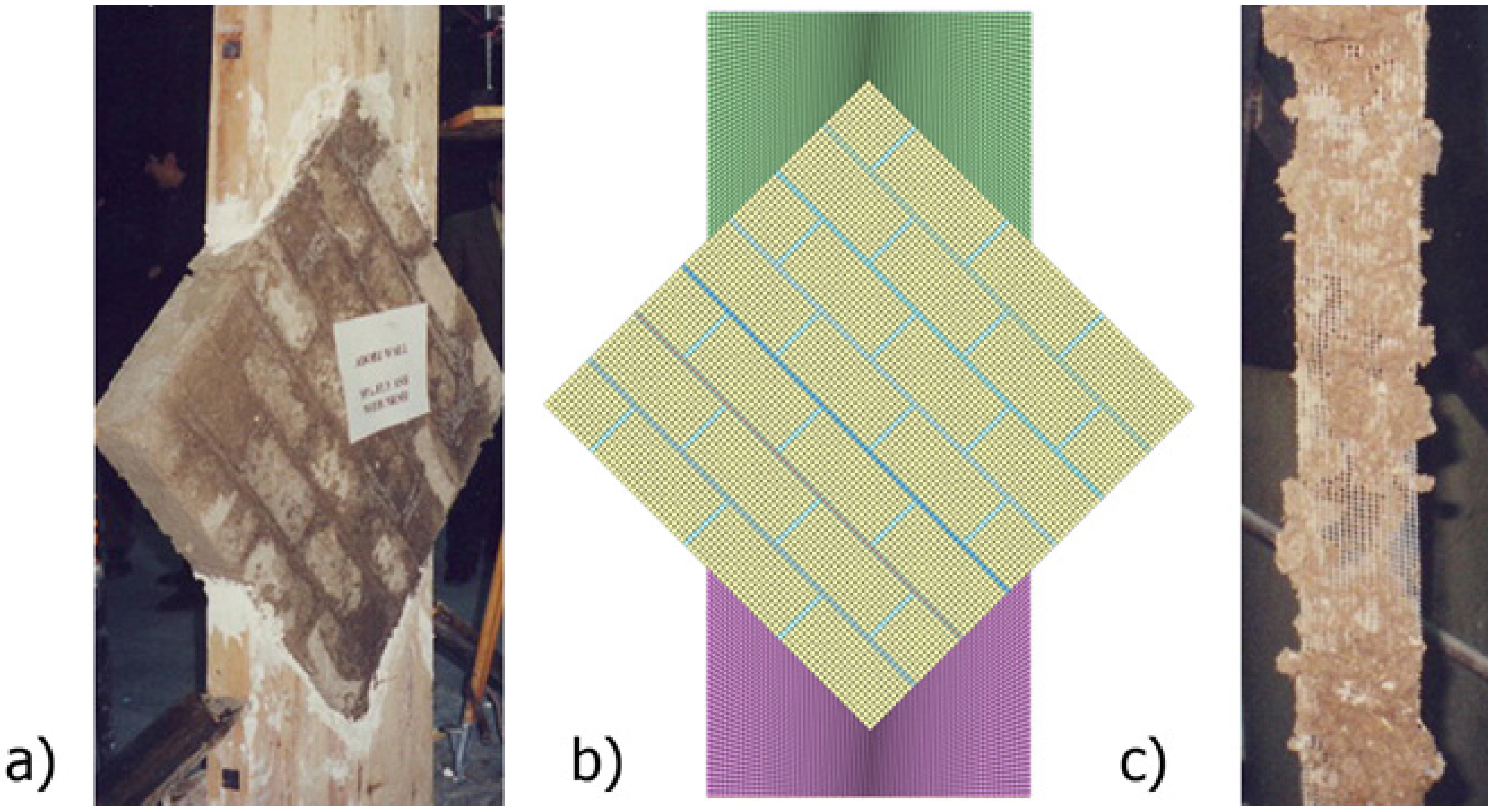
3. Nonlinear Numerical Analyses
3.1. Finite Element Method
| Properties | Fresh plain soil | Plain soil | Plain soil | Mortar B |
|---|---|---|---|---|
| Curing time (days) | 0 | 28 | >28 | 0 |
| Tensile strength (kPa) | 39.2 | 78.4 | 98 | 98 |
| Compressive strength (MPa) | 3.32 | 6.64 | 8.30 | 8.30 |
3.2. Numerical Program
- Plain tested: the wall is made of plain adobe bricks, 28 days curing and fresh plain mortar (i.e., 0 day curing), the elastic modulus for both materials is 20 MPa based on experimental data fitting;
- Long-term curing (LTC): this wall, not tested in reality, is made of plain adobe bricks and plain mortar after a long curing time (i.e., a curing time higher than about 28 days); elastic moduli were the same as the first case, for comparison purposes;
- Mortar B (MB): this wall, not tested in reality, is considered only for comparison purposes with the plain tested wall; the wall is made of plain adobe bricks, 28 days curing and a better mortar compared to plain soil; elastic moduli were the same as the first case, for comparison purposes.
| FEM model | Brick tensile strength (kPa) | Mortar tensile strength (kPa) | Brick compressive strength (MPa) | Mortar compressive strength (MPa) |
|---|---|---|---|---|
| Plain | 78.4 | 39.2 | 6.64 | 3.32 |
| LTC | 98.0 | 98.0 | 8.30 | 8.30 |
| MB | 78.4 | 98.0 | 6.64 | 8.3 |
4. Outcomes of Numerical Analyses
4.1. Experimental Theoretical Comparison
4.2. FEM Models: Validation
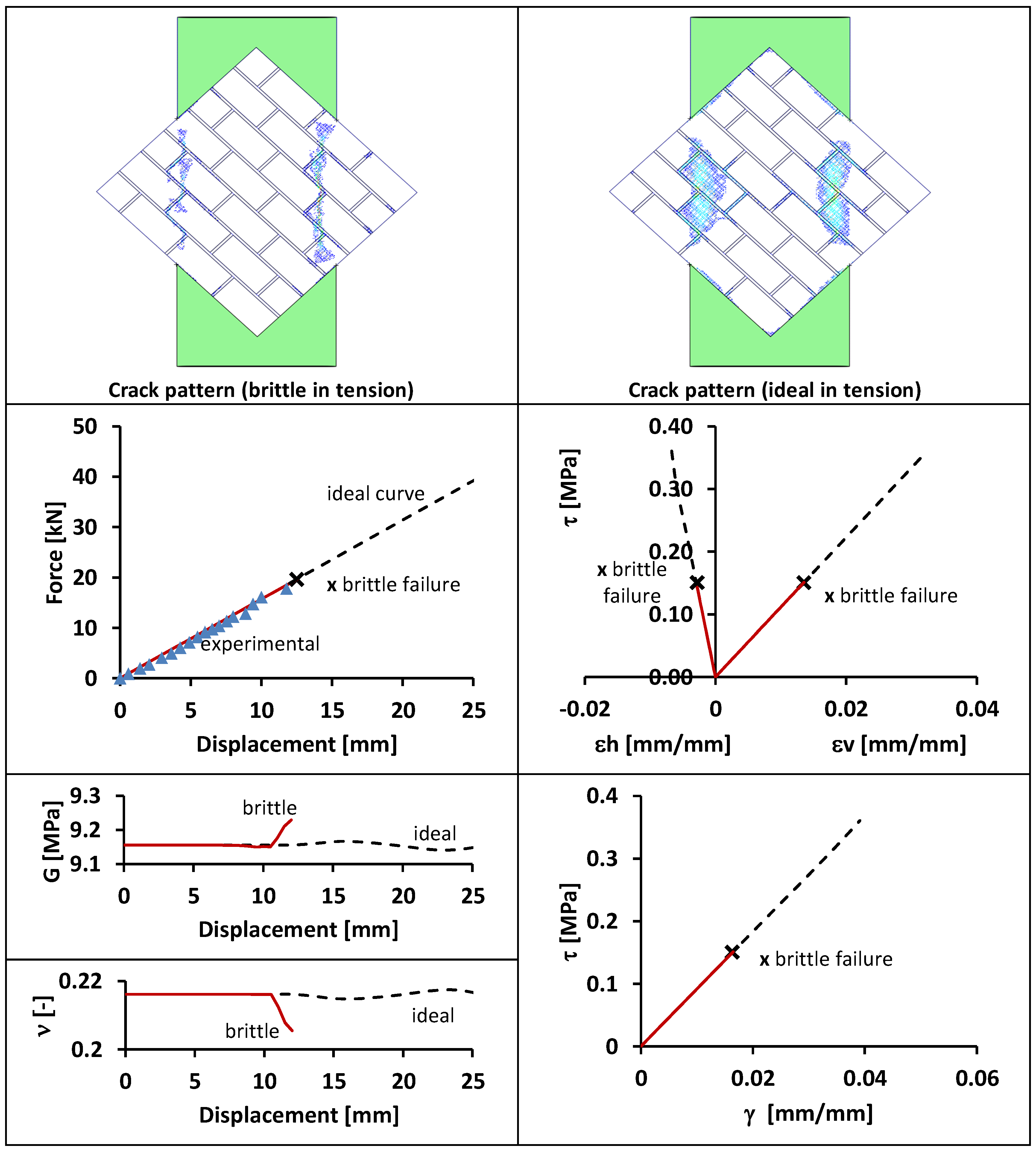

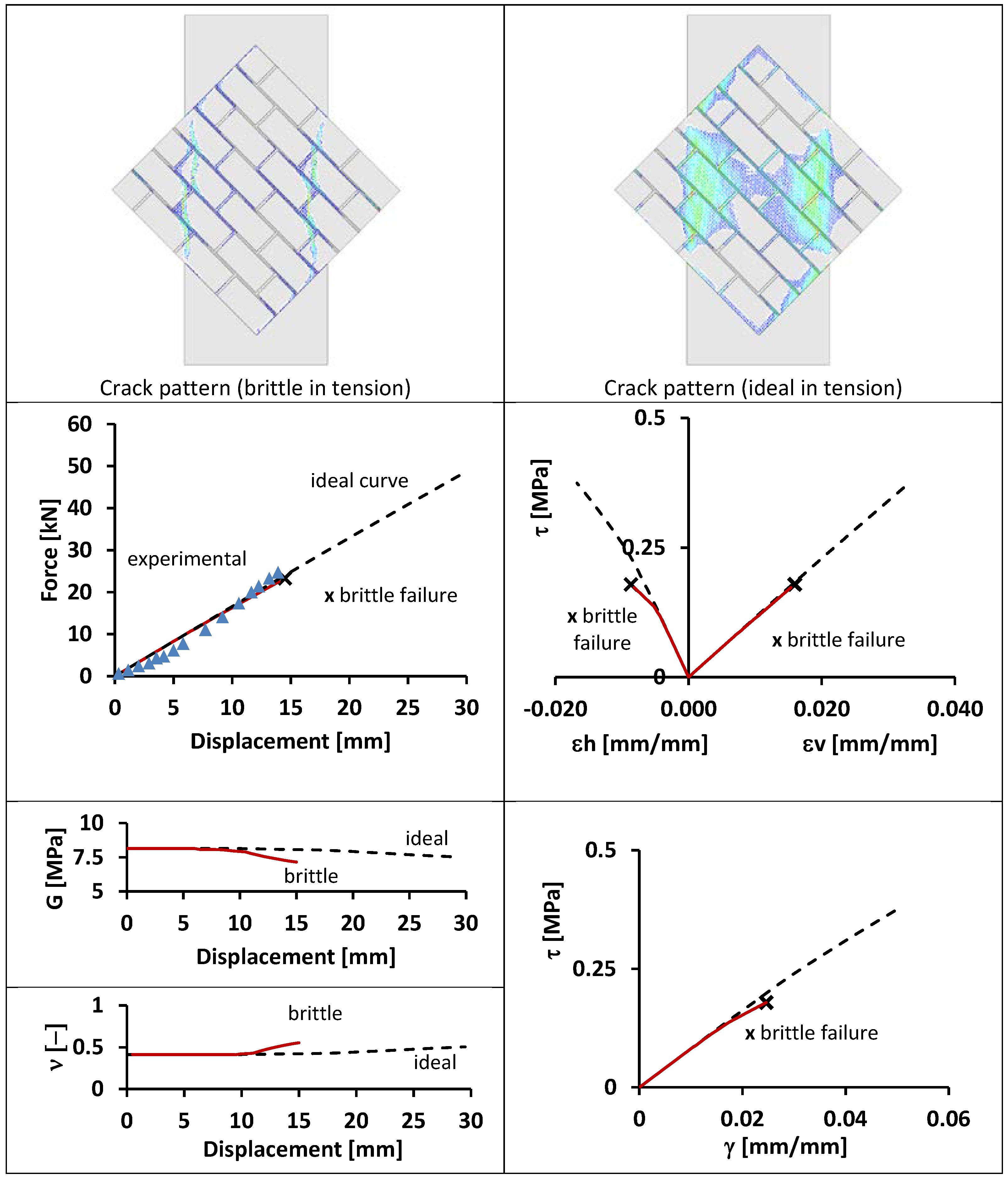
4.3. FEM Models: Long-Term Curing (LTC)
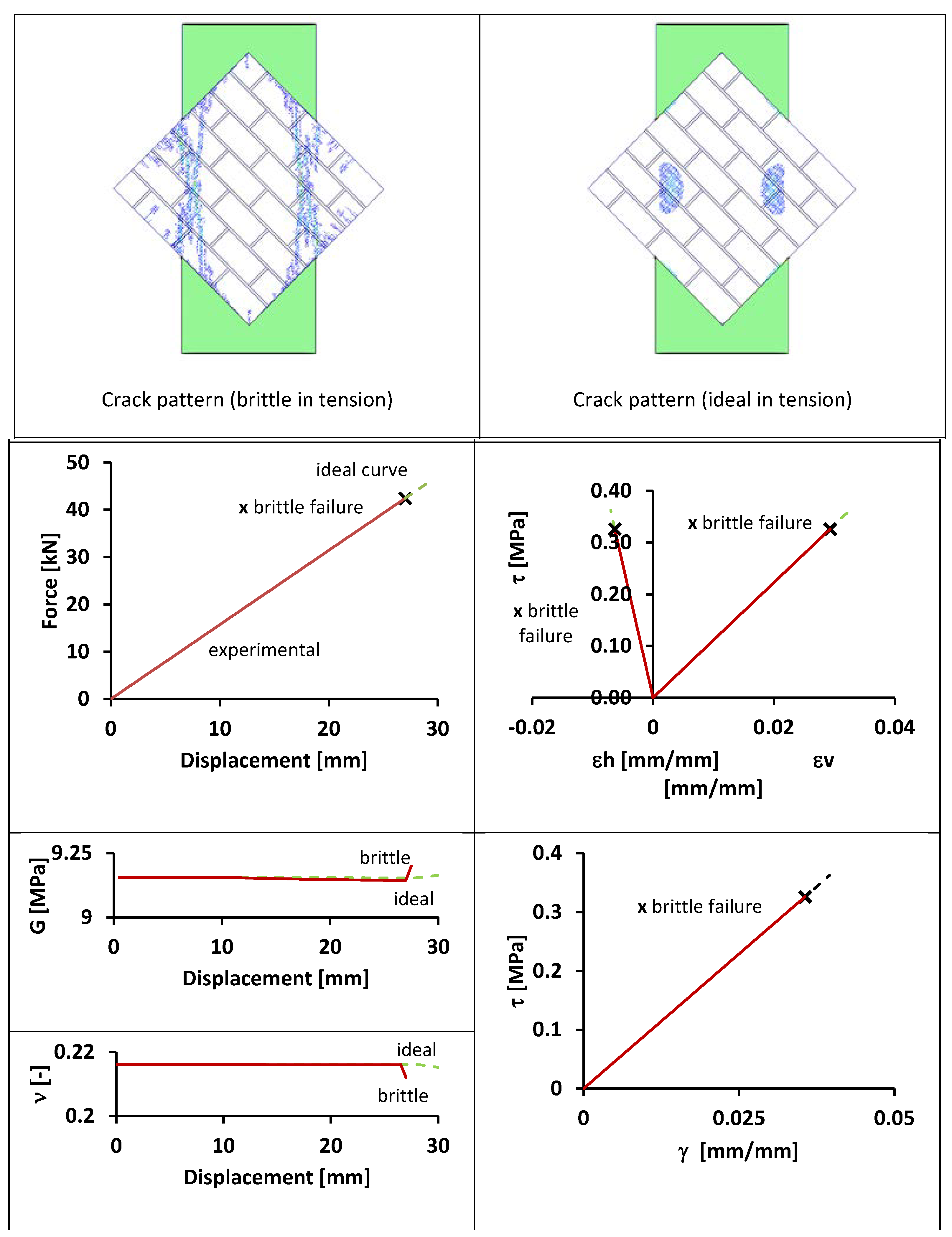
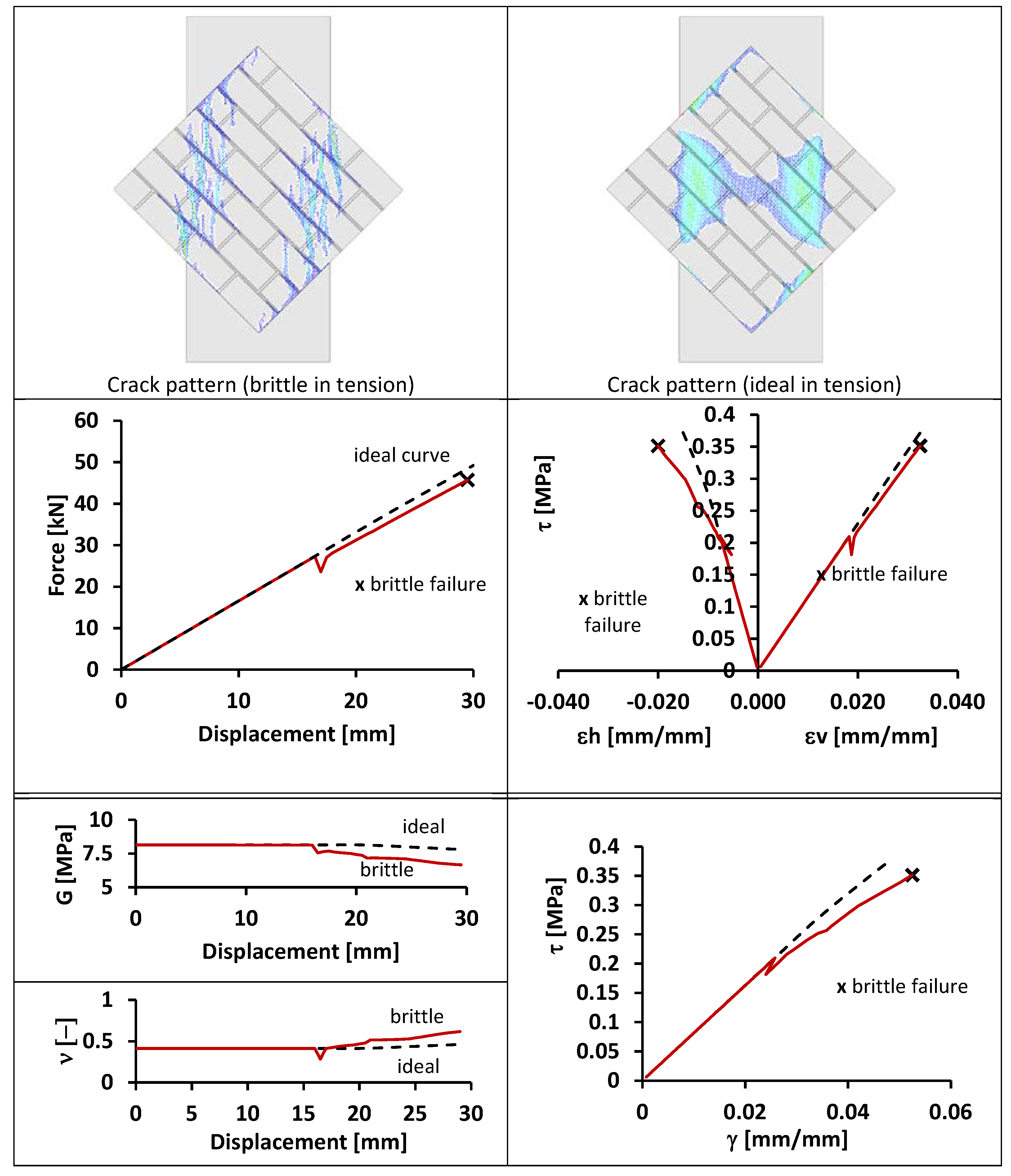
4.4. FEM Models: Mortar B (MB)

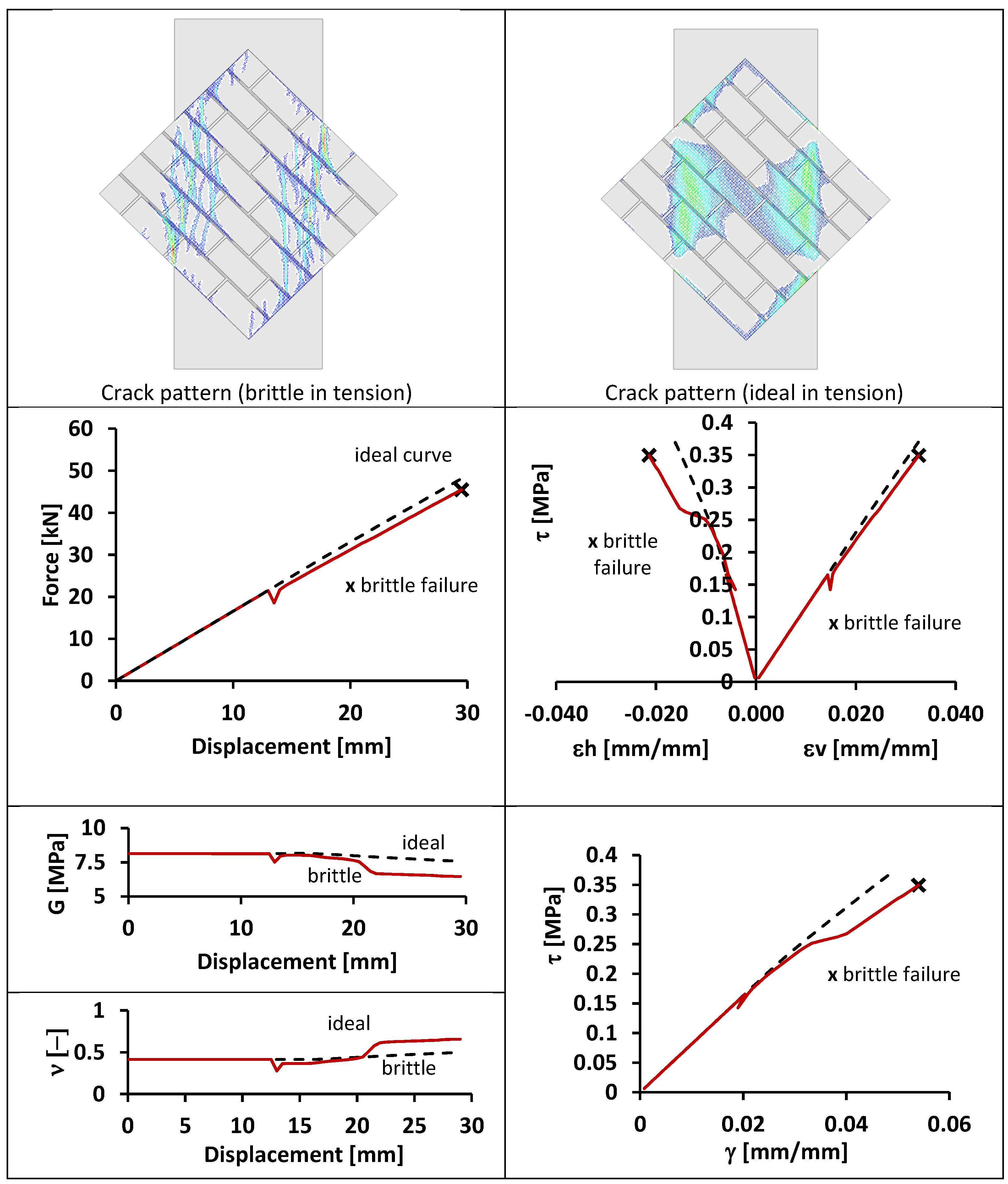
5. Conclusions
| FEM model | Material level (input data) | Global level (outcomes) | |||
|---|---|---|---|---|---|
| Brick strength ratio | Mortar strength ratio | G (MPa) | τ (MPa) | τ ratio | |
| Plain (unreinforced) | 1 | 1 | 9.17 | 0.15 | 1.00 |
| Plain (reinforced) | 1 | 1 | 8.14 | 0.19 | 1.26 |
| LTC (unreinforced) | 1.25 | 2.5 | 9.17 | 0.32 | 2.20 |
| LTC (reinforced) | 1.25 | 2.5 | 8.14 | 0.35 | 2.31 |
| MB (unreinforced) | 1 | 2.5 | 9.17 | 0.25 | 1.70 |
| MB (reinforced) | 1 | 2.5 | 8.14 | 0.34 | 2.31 |
Acknowledgments
Conflicts of Interest
References
- Revuelta-Acosta, J.D.; Garcia-Diaz, A.; Soto-Zarazua, G.M.; Rico-Garcia, E. Adobe as a sustainable material: A thermal performance. J. Appl. Sci. 2010, 10, 2211–2216. [Google Scholar] [CrossRef]
- Binici, H.; Aksogan, O.; Bakbak, D.; Kaplan, H.; Isik, B. Sound insulation of fibre reinforced mud brick walls. Constr. Build. Mater. 2009, 23, 1035–1041. [Google Scholar] [CrossRef]
- Houben, H.; Guillaud, H. Earth Construction a Comprehensive Guide; Intermediate Technology Publications: London, UK, 1994. [Google Scholar]
- Tolles, L.E.; Krawinkler, H. Seismic Studies on Small-Scale Models on Adobe Houses; The John A. Blume Earthquake Engineering Center, Department of Civil Engineering, Stanford University: Stanford, CA, USA, 1990. [Google Scholar]
- Standard Test Method for Diagonal Tension (Shear) in Masonry Assemblages; ASTM E519-02; American Society for Testing Materials (ASTM): West Conshohocken, PA, USA, 1981.
- Lignola, G.P.; Prota, A.; Manfredi, G. Nonlinear analyses of tuff masonry walls strengthened with cementitious matrix-grid composites. J. Compos. Constr. 2009, 13, 243–251. [Google Scholar] [CrossRef]
- Turanli, L.; Saritas, A. Strengthening the structural behavior of adobe walls through the use of plaster reinforcement mesh. Constr. Build. Mater. 2001, 25, 1747–1752. [Google Scholar] [CrossRef]
- Turanli, L. Evaluation of Some Physical and Mechanical Properties of Plain and Stabilized Adobe Blocks. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 1985. [Google Scholar]
- Manie, J.; Kikstra, W.P. DIANA Finite Element Analysis: User’s Manual release 9.4.3. Available online: https://support.tnodiana.com/manuals/d943/Diana.html (accessed on 13 February 2014).
- Lignola, G.P.; Prota, A.; Manfredi, G. Numerical investigation on the influence of FRP retrofit layout and geometry on the in-plane behavior of masonry walls. J. Compos. Constr. 2012, 16, 712–723. [Google Scholar] [CrossRef]
- Parisi, F.; Lignola, G.P.; Augenti, N.; Prota, A.; Manfredi, G. Rocking response assessment of in-plane laterally-loaded masonry walls with openings. Eng. Struct. 2013, 56, 1234–1248. [Google Scholar] [CrossRef]
- Parisi, F.; Lignola, G.P.; Augenti, N.; Prota, A.; Manfredi, G. Nonlinear behavior of a masonry sub-assemblage before and after strengthening with inorganic matrix-grid composites. J. Compos. Constr. 2011, 15, 821–832. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Giamundo, V.; Lignola, G.P.; Prota, A.; Manfredi, G. Nonlinear Analyses of Adobe Masonry Walls Reinforced with Fiberglass Mesh. Polymers 2014, 6, 464-478. https://doi.org/10.3390/polym6020464
Giamundo V, Lignola GP, Prota A, Manfredi G. Nonlinear Analyses of Adobe Masonry Walls Reinforced with Fiberglass Mesh. Polymers. 2014; 6(2):464-478. https://doi.org/10.3390/polym6020464
Chicago/Turabian StyleGiamundo, Vincenzo, Gian Piero Lignola, Andrea Prota, and Gaetano Manfredi. 2014. "Nonlinear Analyses of Adobe Masonry Walls Reinforced with Fiberglass Mesh" Polymers 6, no. 2: 464-478. https://doi.org/10.3390/polym6020464





