Nonlinear Progressive Damage Analysis of Notched or Bolted Fibre-Reinforced Polymer (FRP) Laminates Based on a Three-Dimensional Strain Failure Criterion
Abstract
:1. Introduction
2. Progressive Damage Analysis Methodology
2.1. Progressive Damage Analysis Procedure
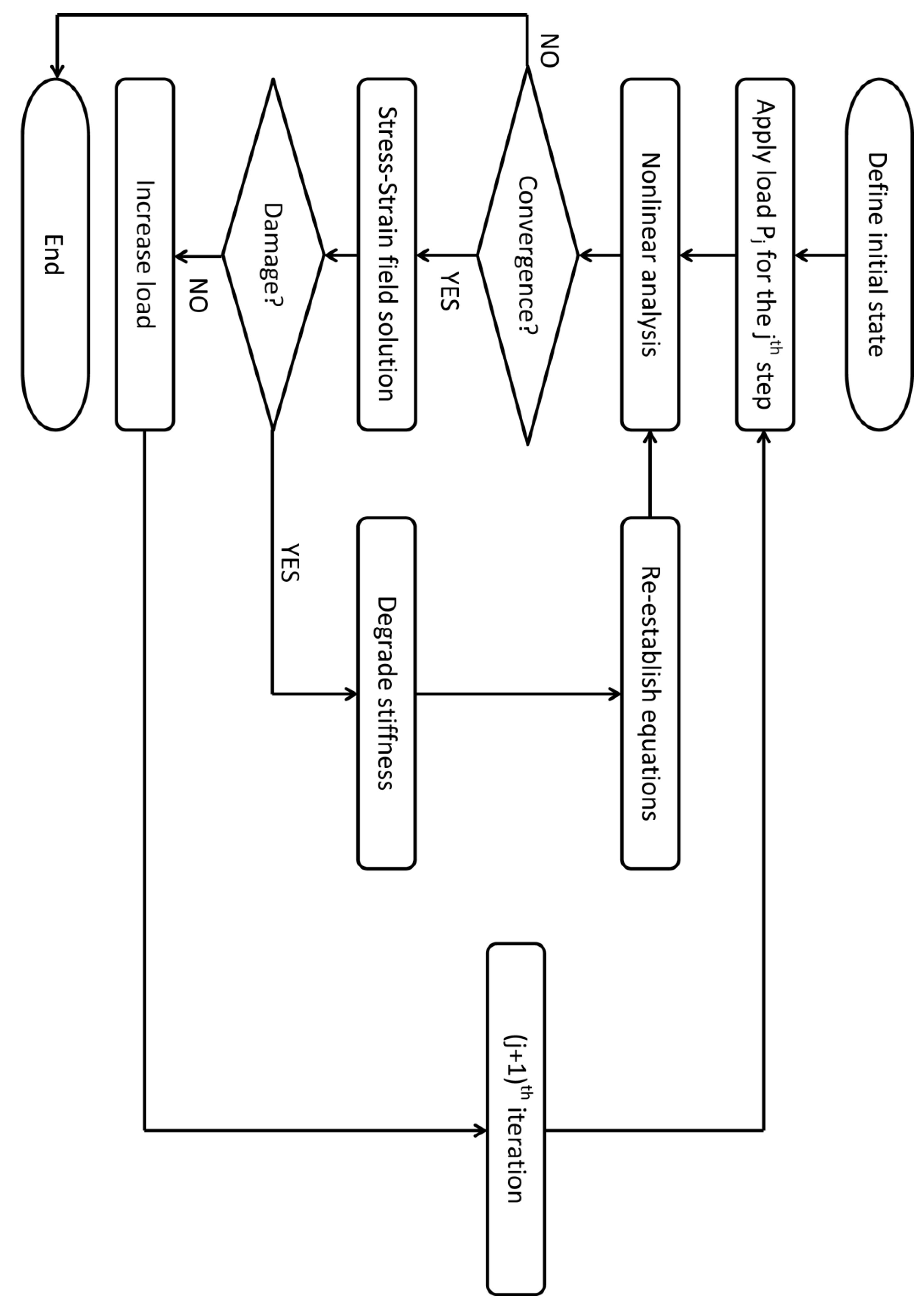
2.2. Material Strength Criterion
| Damage mode | Graphic representation | Strength criterion inequality |
|---|---|---|
| Fibre damage |  |  |
| Matrix damage |  |  |
| Delamination damage |  |  |
2.3. Constitutive Relation for Damaged Orthotropic Material
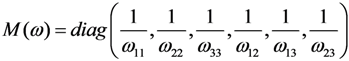
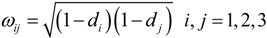
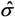 and apparent stress σ results in
and apparent stress σ results in
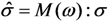
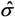 and σ are first-order tensors containing six stress components.
and σ are first-order tensors containing six stress components.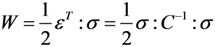
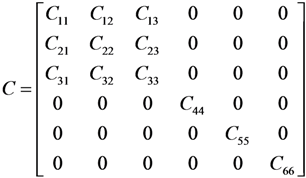
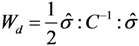
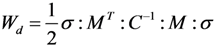
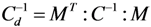
2.4. Method for Solving Stress
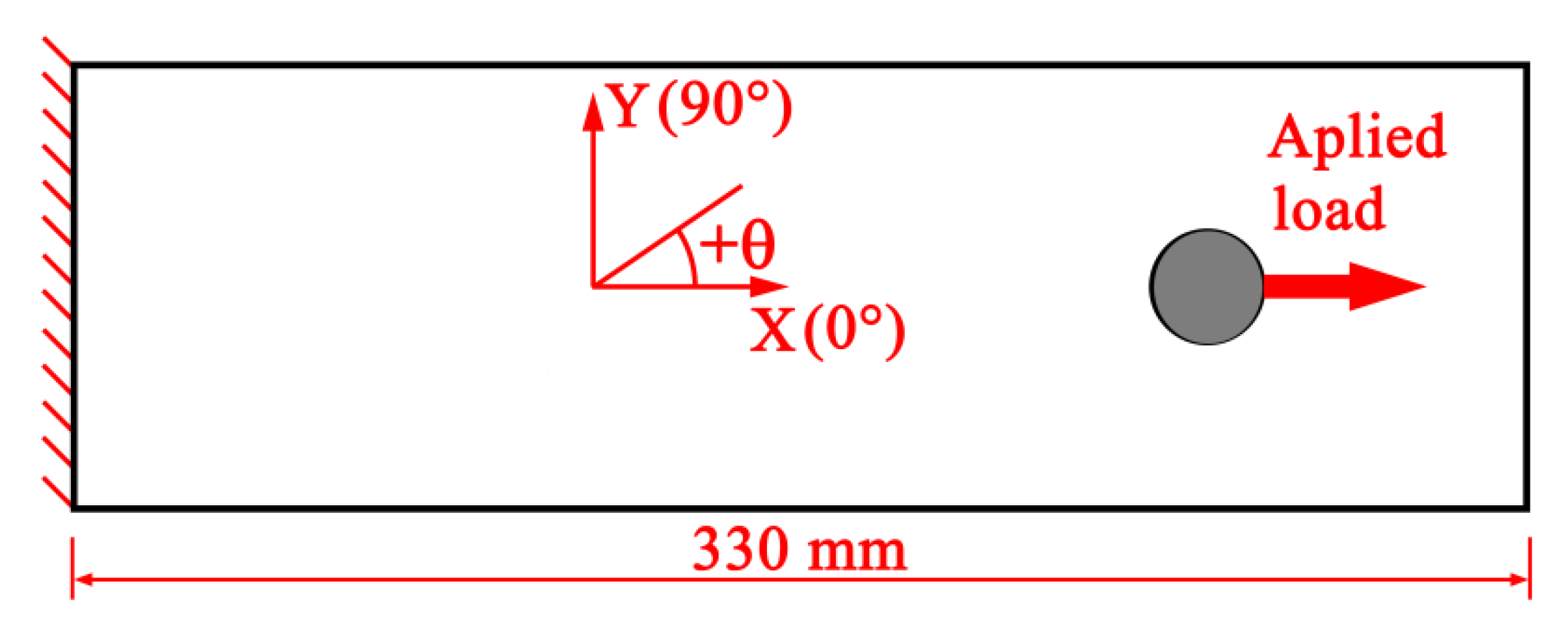
3. Case Study 1: Notched FRP Laminate under Unidirectional Tension
3.1. Geometry and Material Properties

| Elastic property | Value | Strength property * | Value |
|---|---|---|---|
| E1 | 52,000 MPa |  | 1,840 MPa |
| E2 = E3 | 8,000 MPa |  | 1,580 MPa |
| G12= G13 | 3,000 MPa |  | 44 MPa |
| G23 | 2,900 MPa |  | 172 MPa |
| v12 = v13 | 0.28 | S12= S13 | 39 MPa |
| v23 | 0.34 | S23 | 32 MPa |
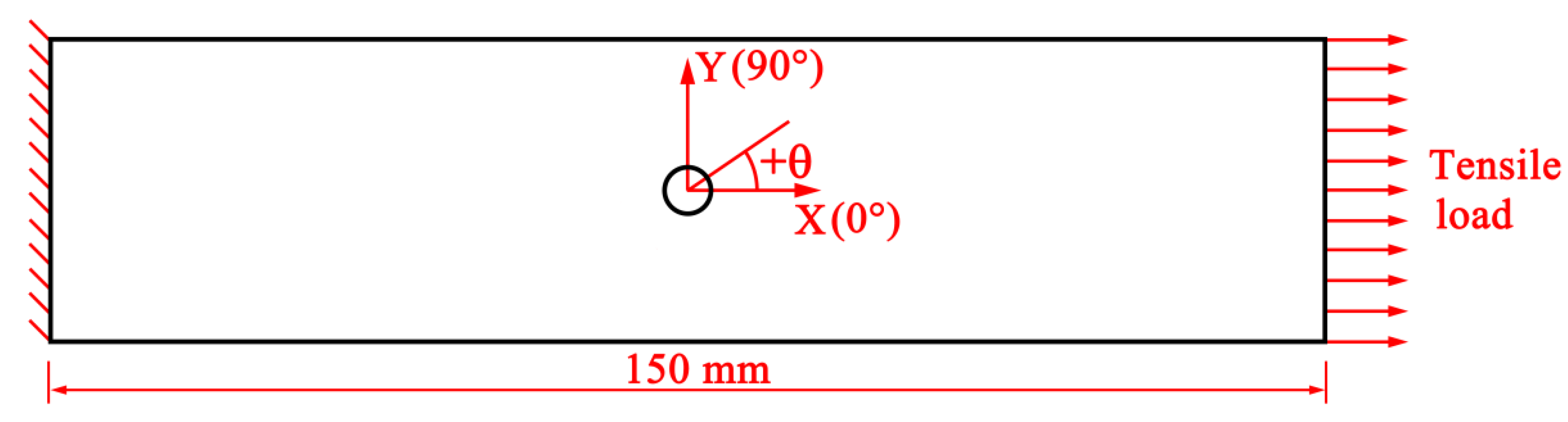
3.2. Finite Element Model

3.3. Selection of the Damage Factors
3.3.1. Constant Damage Factors
| Damage mode | Damage factor | Value |
|---|---|---|
| Fibre damage | d1 | 0.99 |
| Matrix damage | d2 | 0.95 |
| Delamination damage | d3 | 0.95 |
3.3.2. Two Types of CDM-Based Exponential Damage Factors
 for
for  results in:
results in:
 :
:
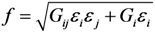

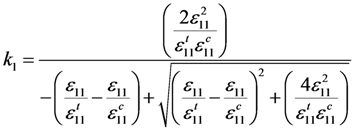
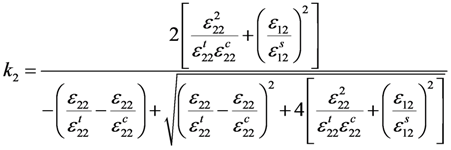
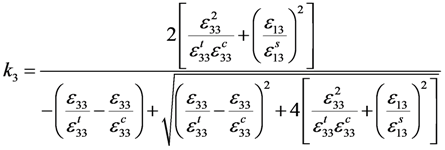
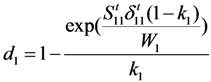
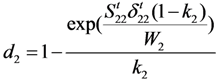
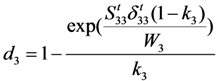
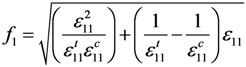
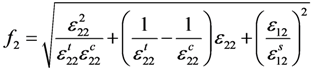
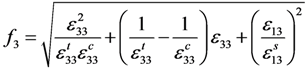
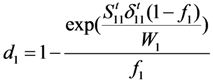
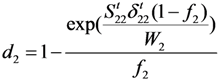
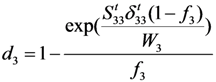
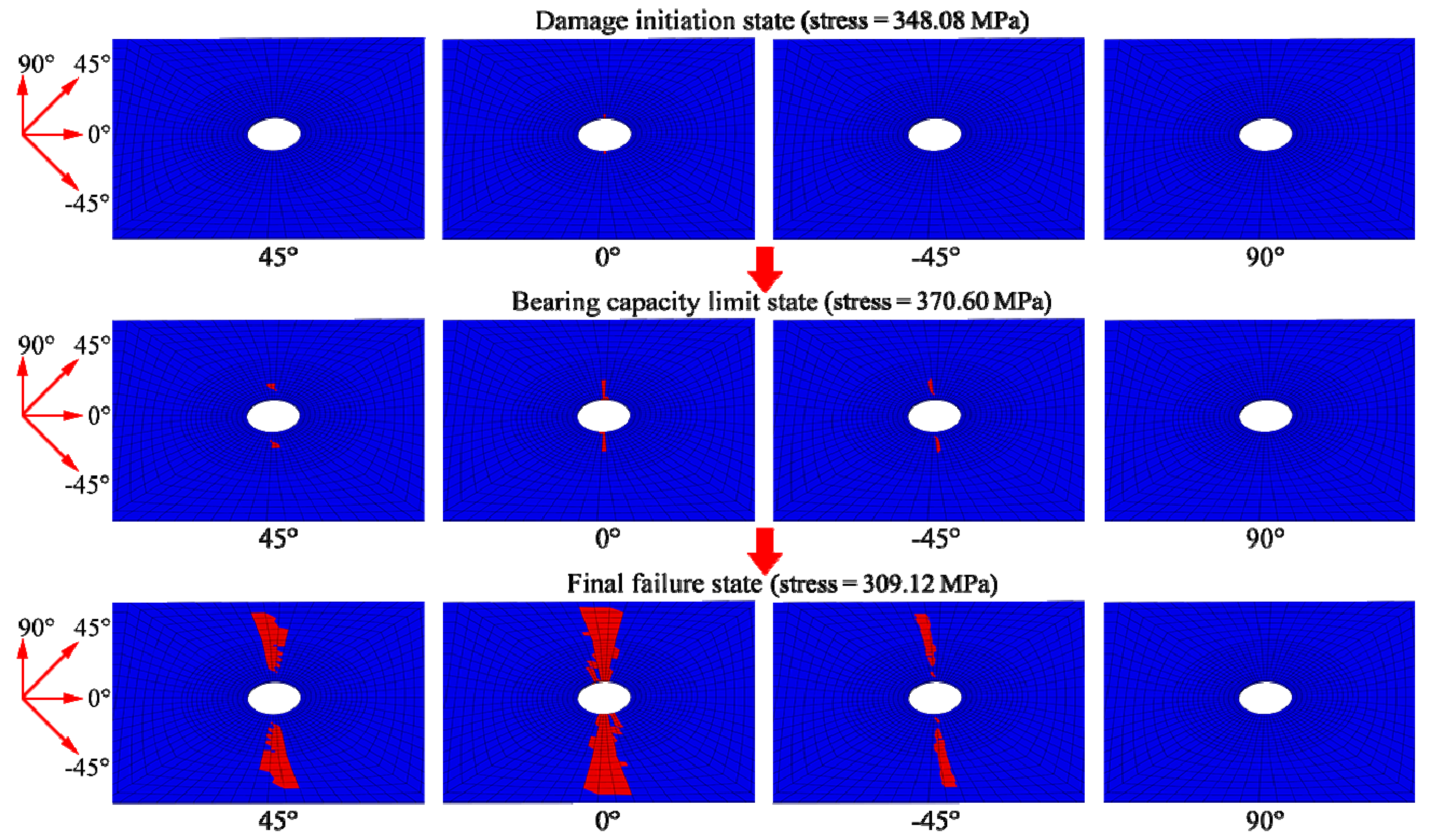
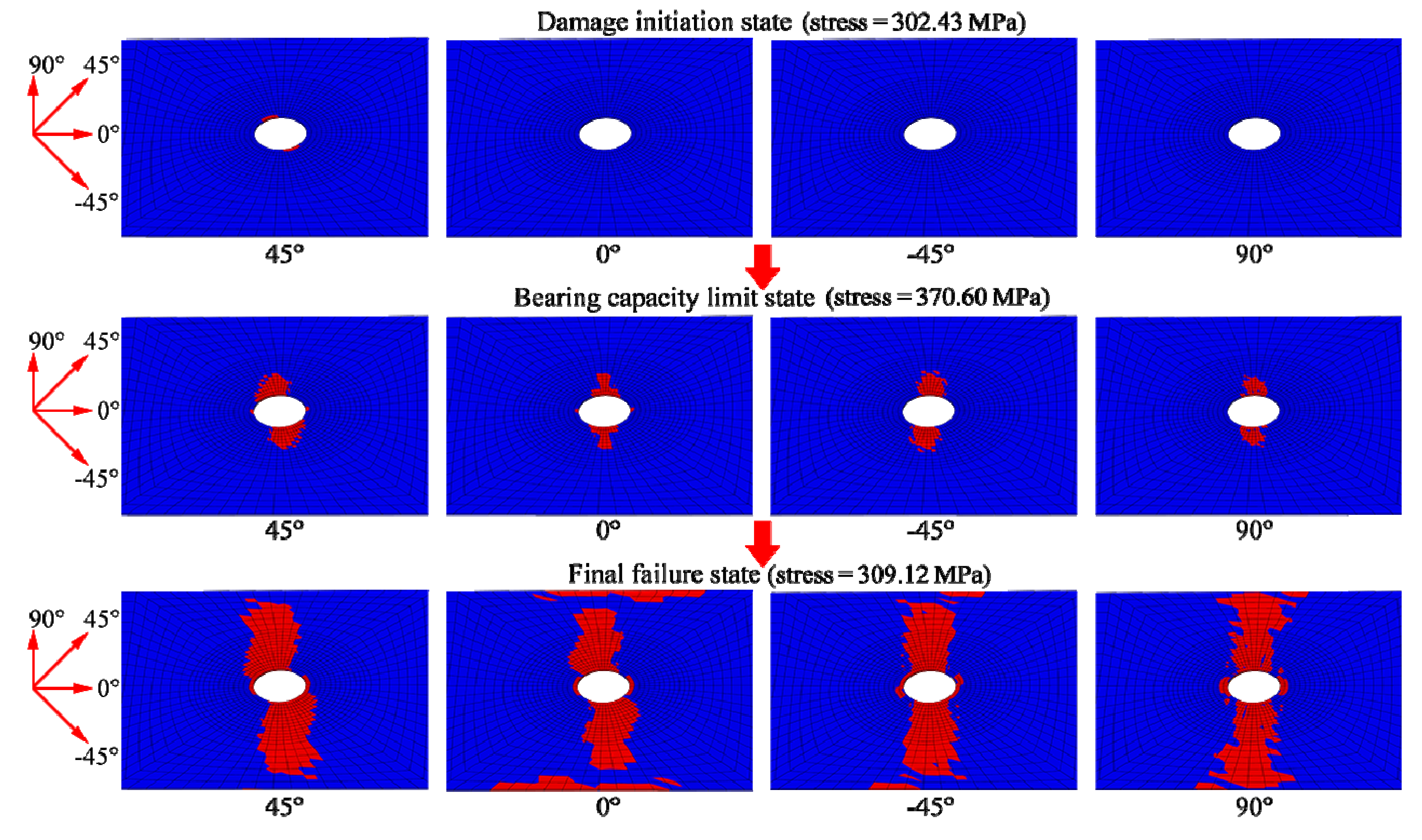
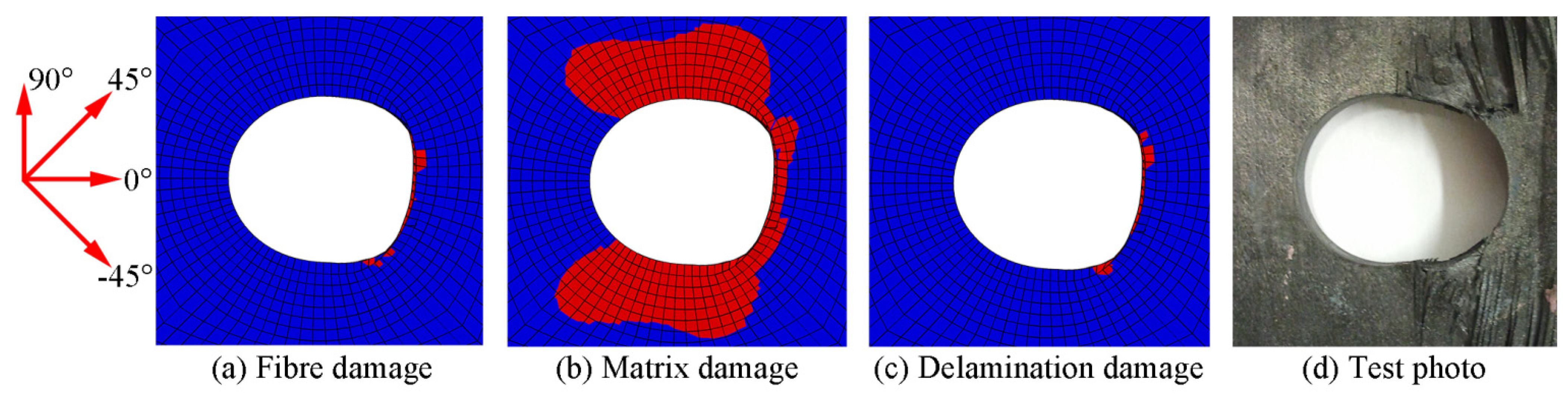
3.4. Comparison of Numerical and Experimental Results

| Damage factor | Numerical result | Experimental result | Error |
|---|---|---|---|
| Constant | 385.23 MPa | 350 MPa | 10.07% |
| Exponential (square index) | 376.94 MPa | 7.70% | |
| Exponential (damage index) | 370.60 MPa | 5.89% |


4. Case Study 2: Bolted FRP Laminate under Unidirectional Tension
4.1. Geometry and Material Properties
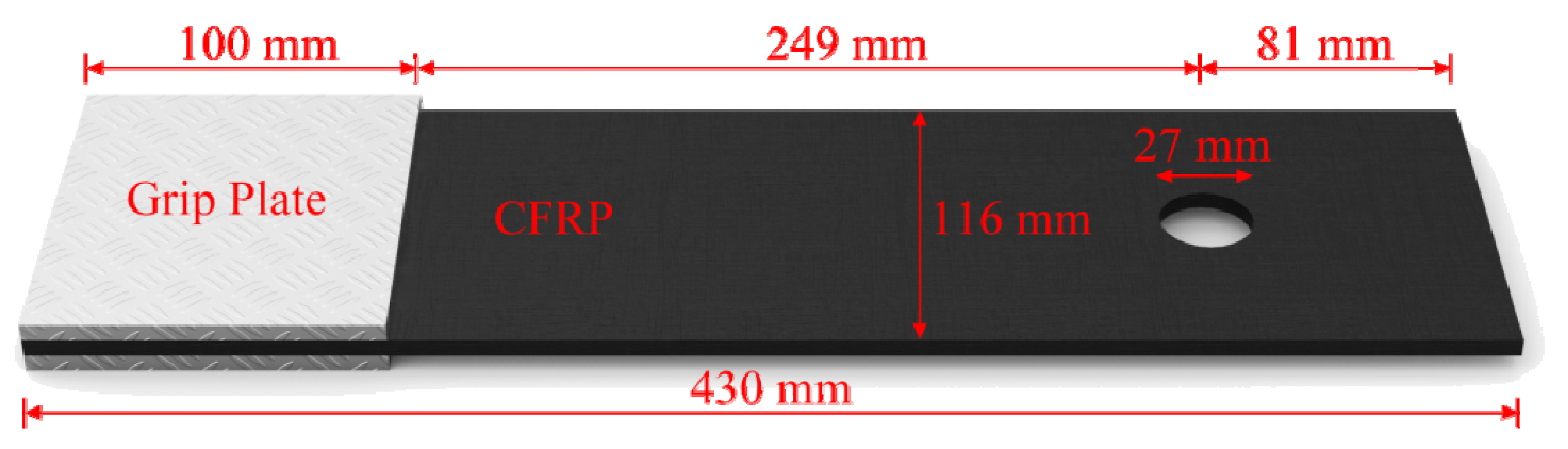
 . The thickness of each ply was 0.25 mm, and the total thickness of the laminate was 5.25 mm. The material properties of a single ply are listed in Table 5.
. The thickness of each ply was 0.25 mm, and the total thickness of the laminate was 5.25 mm. The material properties of a single ply are listed in Table 5.| Elastic property | Value | Strength property * | Value |
|---|---|---|---|
| E1 | 116,000 MPa |  | 2,160 MPa |
| E2 = E3 | 7,500 MPa |  | 1,900 MPa |
| G12= G13 | 3,000 MPa |  | 80 MPa |
| G23 | 2,800 MPa |  | 210 MPa |
| v12 = v13 | 0.3 | S12= S13 | 110 MPa |
| v23 | 0.33 | S23 | 90 MPa |
4.2. Experimental Set-Up

4.3. Finite Element Model

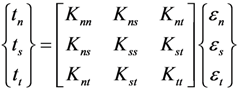
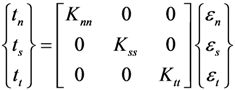
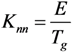
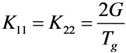
 and
and  . The cohesive element damage initiation was controlled by the ABAQUS built-in quadratic nominal strain criterion:
. The cohesive element damage initiation was controlled by the ABAQUS built-in quadratic nominal strain criterion:
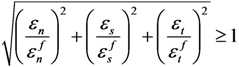
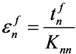 ,
, 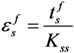 and
and 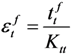 .
.
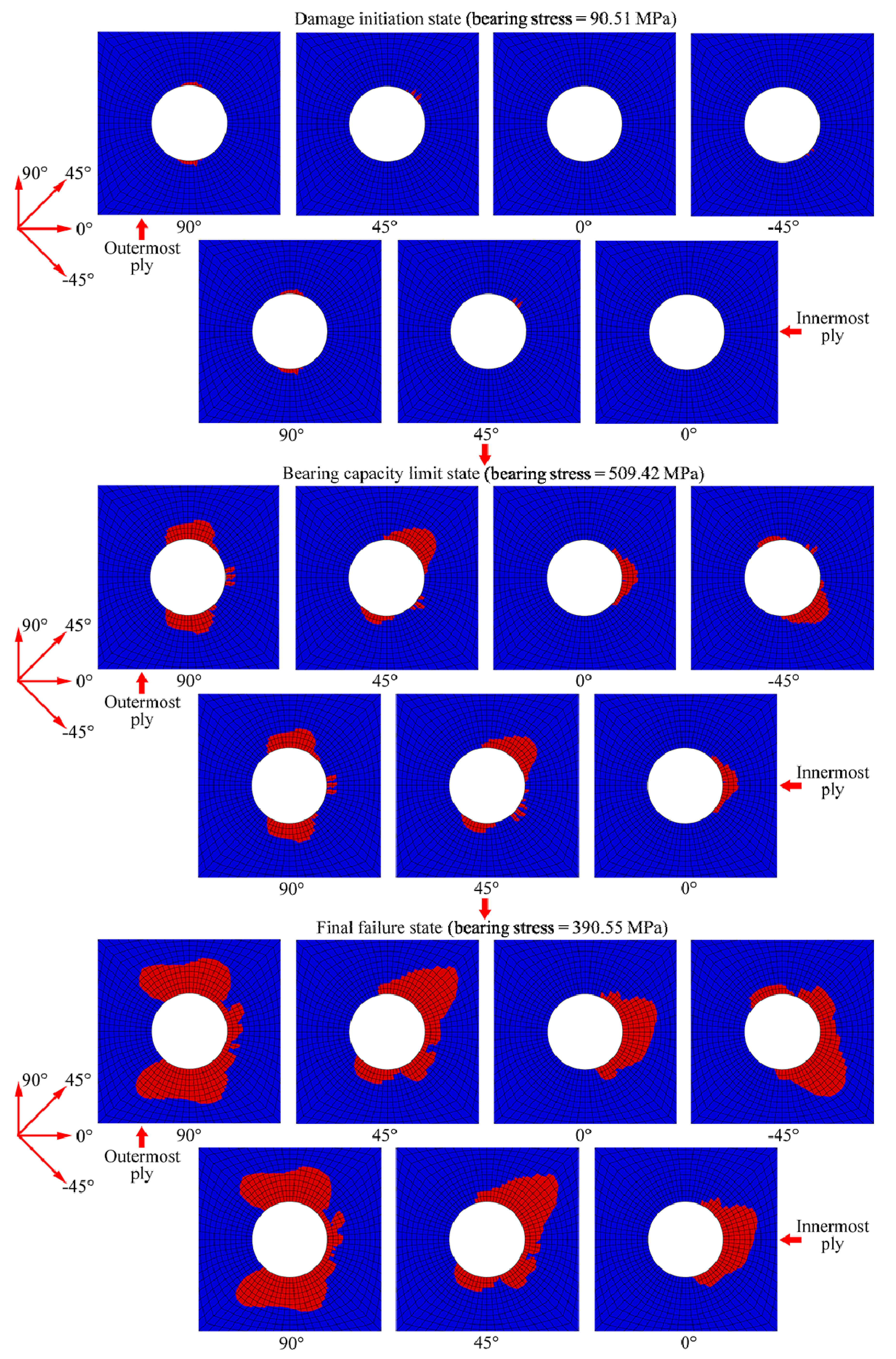
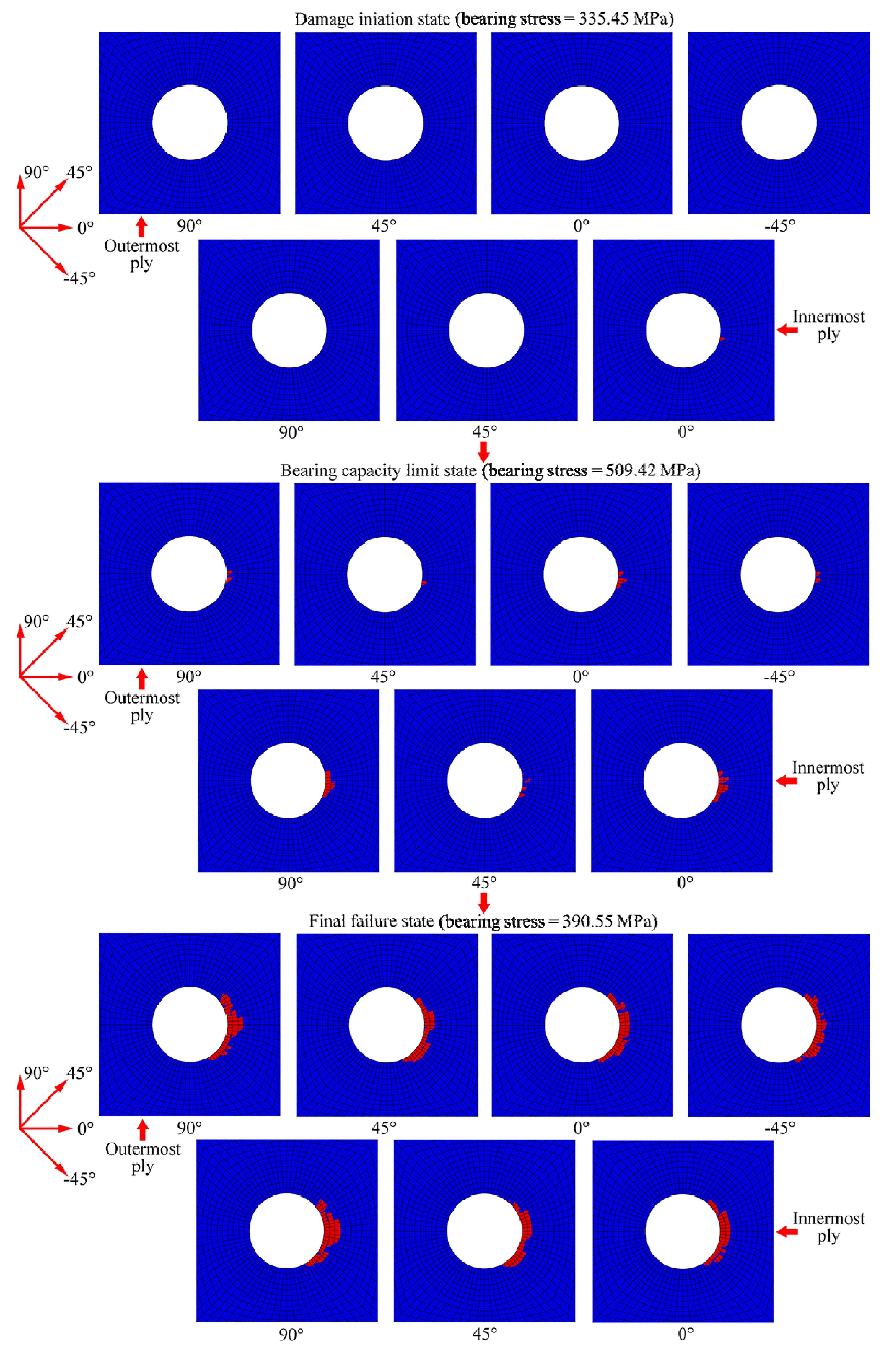
4.4. Comparison of Numerical and Experimental Results
 , where P is the applied load, d is the hole diameter and h is the specimen thickness. The bearing strain is defined as εBr = δ / d, where δ is the bolt displacement. The bearing strength is defined as
, where P is the applied load, d is the hole diameter and h is the specimen thickness. The bearing strain is defined as εBr = δ / d, where δ is the bolt displacement. The bearing strength is defined as  , where Pultimate is the ultimate load [22].
, where Pultimate is the ultimate load [22].
| FE model | Numerical result | Test 1 result | Error 1 | Test 2 result | Error 2 |
|---|---|---|---|---|---|
| Without cohesive layers | 509.42 MPa | 498.98 MPa | 2.09% | 540.32 MPa | −5.72% |
| With cohesive layers | 502.22 MPa | 0.65% | −7.05% |

4. Conclusions
- The numerical results based on the three-dimensional strain strength criterion proposed in this paper are in good agreement with the experimental results. This shows that this succinct strain strength criterion is suitable for using in industry and research to predict the ultimate strengths of notched or bolted FRP laminates.
- The damage tensor used in this paper, which is strictly derived from the basic theory of damage mechanics, consists of damage factors. It is suitable for degrading the FRP material properties according to different damage modes. It was also found that the CDM-based exponential damage factors using the damage index as the independent variable are preferable to the similar CDM-based exponential damage factors using the square index as the independent variable and the conventional constant damage factors. This preferred type of exponential damage factors was controlled by the damage index k as well as the fracture energy. These factors gave the best accuracy and convergence in the numerical model compared to the results gained by the exponential damage factors using the square index f, which has no clear physical concept, and the constant damage factors, which are set empirically.
- Many existing studies demonstrate that the calculation model for composite materials with cohesive layers probably performs better than the model without cohesive layers, particularly in some complex cases. However, in the case of in-plane FRP laminate loading, such as notched or bolted FRP laminates under unidirectional tension, the three-dimensional strain strength criterion proposed in this paper shows sufficient accuracy. Adding cohesive layers to the model to simulate the delamination damage will considerably increase the amount of work necessary for pre-processing and post-processing, with limited increase in calculation accuracy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mallick, P. Fiber-Reinforced Composites: Materials, Manufacturing, and Design, 2nd ed.; CRC Press: New York, NY, USA, 1993; pp. 6–7. [Google Scholar]
- Schlaich, M.; Zwingmann, B.; Liu, Y.; Goller, R. CFRP tension elements and their anchorages. Bautechnik 2012, 89, 841–849. [Google Scholar] [CrossRef]
- Hinton, M.J.; Soden, P.D. Predicting failure in composite laminates: The background to the exercise. Composit. Sci. Technol. 1998, 58, 1001–1010. [Google Scholar] [CrossRef]
- Hinton, M.J.; Kaddour, A.S. The background to part b of the second world-wide failure exercise: Evaluation of theories for predicting failure in polymer composite laminates under three-dimensional states of stress. J. Composit. Mater. 2013, 47, 643–652. [Google Scholar] [CrossRef]
- Whitney, J.M.; Nuismer, R.J. Stress fracture criteria for laminated composites containing stress-concentrations. J. Composit. Mater. 1974, 8, 253–265. [Google Scholar] [CrossRef]
- Karlak, R.F. Hole effects in a related series of symmetrical laminates. In Proceedings of the Conference on Failure Modes in Composite (IV), Chicago, IL, USA, 1–3 January 1977.
- Pipes, R.B.; Wetherhold, R.C.; Gillespie, J.W. Notched strength of composite-materials. J. Composit. Mater. 1979, 13, 148–160. [Google Scholar] [CrossRef]
- Echaabi, J.; Trochu, F.; Gauvin, R. Review of failure criteria of fibrous composite materials. Polym. Composit. 1996, 17, 786–798. [Google Scholar] [CrossRef]
- Chamis, C.C. Polymer composite mechanics review—1965 to 2006. J. Reinf. Plast. Composit. 2007, 26, 987–1019. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. Trans. Asme 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Puck, A. A failure criterion shows the direction. Kunststoffe-German Plast. 1992, 82, 607–610. [Google Scholar]
- Chang, F.K.; Chang, K.Y. A progressive damage model for laminated composites containing stress-concentrations. J. Composit. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]
- Chang, F.K.; Lessard, L.B. Damage tolerance of laminated composites containing an open hole and subjected to compressive loadings: 1. Analysis. J. Composit. Mater. 1991, 25, 2–43. [Google Scholar]
- Tan, S.C. A progressive failure model for composite laminates containing openings. J. Composit. Mater. 1991, 25, 556–577. [Google Scholar]
- Tan, S.C.; Perez, J. Progressive failure of laminated composites with a hole under compressive loading. J. Reinf. Plast. Composit. 1993, 12, 1043–1057. [Google Scholar] [CrossRef]
- Camanho, P.P.; Matthews, F.L. A progressive damage model for mechanically fastened joints in composite laminates. J. Composit. Mater. 1999, 33, 2248–2280. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, part i: Modeling. J. Composit. Mater. 2000, 34, 1056–1080. [Google Scholar]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, part ii: Material characterization and model verification. J. Composit. Mater. 2000, 34, 1081–1116. [Google Scholar]
- Tserpes, K.I.; Labeas, G.; Papanikos, P.; Kermanidis, T. Strength prediction of bolted joints in graphite/epoxy composite laminates. Composit. B Eng. 2002, 33, 521–529. [Google Scholar] [CrossRef]
- Lapczyk, I.; Hurtado, J.A. Progressive damage modeling in fiber-reinforced materials. Composit. A Appl. Sci. Manuf. 2007, 38, 2333–2341. [Google Scholar] [CrossRef]
- Linde, P.; de Boer, H. Modelling of inter-rivet buckling of hybrid composites. Composit. Struct. 2006, 73, 221–228. [Google Scholar] [CrossRef]
- Frizzell, R.M.; McCarthy, C.T.; McCarthy, M.A. Simulating damage and delamination in fibre metal laminate joints using a three-dimensional damage model with cohesive elements and damage regularisation. Composit. Sci. Technol. 2011, 71, 1225–1235. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar] [CrossRef]
- Needleman, A. A continuum model for void nucleation by inclusion debonding. J. Appl. Mech. Trans. Asme 1987, 54, 525–531. [Google Scholar] [CrossRef]
- Needleman, A. An analysis of tensile decohesion along an interface. J. Mech. Phys. Solids 1990, 38, 289–324. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical simulation of mixed-mode progressive delamination in composite materials. J. Composit. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Systèmes, D. ABAQUS 6.10: Analysis User’s Manual; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2010. [Google Scholar]
- Goutianos, S.; Sørensen, B.F. Path dependence of truss-like mixed mode cohesive laws. Eng. Fract. Mech. 2012, 91, 117–132. [Google Scholar] [CrossRef]
- McGarry, J.P.; Ó Máirtín, É.; Parry, G.; Beltz, G.E. Potential-based and non-potential-based cohesive zone formulations under mixed-mode separation and over-closure. Part I: Theoretical analysis. J. Mech. Phys. Solids 2014, 63, 336–362. [Google Scholar] [CrossRef]
- Máirtín, ÉÓ; Parry, G.; Beltz, G.E.; McGarry, J.P. Potential-based and non-potential-based cohesive zone formulations under mixed-mode separation and over-closure—part ii: Finite element applications. J. Mech. Phys. Solids 2014, 63, 363–385. [Google Scholar] [CrossRef]
- Perugini, P.; Riccio, A.; Scaramuzzino, F. Three-dimensional progressive damage analysis of composite joints. In Proceedings of the 8th International Conference on Civil and Structural Engineering Computing, Vienna, Austria, 19–21 September 2001.
- Tserpes, K.; Papanikos, P.; Kermanidis, T. A three-dimensional progressive damage model for bolted joints in composite laminates subjected to tensile loading. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 663–675. [Google Scholar] [CrossRef]
- Tsai, S.W. Theory of Composites Design; Think Composites: Dayton, OH, USA, 1992. [Google Scholar]
- Krajcinovic, D. Damage Mechanics; Elsevier: Waltham, MA, USA, 1996; Volume 41. [Google Scholar]
- Ladevèze, P.; Simmonds, J.G. Nonlinear Computational Structural Mechanics: New Approaches and Non-incremental Methods of Calculation; Springer: Berlin, Germany, 1999; pp. 11–12. [Google Scholar]
- Liu, P.F.; Zheng, J.Y. Recent developments on damage modeling and finite element analysis for composite laminates: A review. Mater. Des. 2010, 31, 3825–3834. [Google Scholar] [CrossRef]
- Burr, A.; Hild, F.; Leckie, F.A. Micromechanics and continuum damage mechanics. Arch. Appl. Mech. 1995, 65, 437–456. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method: Solid Mechanics, 6rd ed.; Butterworth-heinemann: Oxford, UK, 2000; Volume 2, pp. 4–37. [Google Scholar]
- O’Higgins, R.M.; McCarthy, M.A.; McCarthy, C.T. Comparison of open hole tension characteristics of high strength glass and carbon fibre-reinforced composite materials. Composit. Sci. Technol. 2008, 68, 2770–2778. [Google Scholar] [CrossRef]
- Wang, Y.; Tong, M.; Zhu, S. Three-dimensional nonlinear progressive damage analysis on composite laminates based on continuum damage mechanics. J. Nanjing Univ. Aeronaut. Astronaut. 2009, 6, 709–714. [Google Scholar]
- ASTM Standard D5766/D5766M-02. Standard test method for open hole tensile strength of polymer matrix composite laminates. In Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2002; Volume: 15.03.
- Deutsches Institut für Normung. DIN EN 14399: High-Strength Structural Bolting Assemblies for Preloading; Beuth: Berlin, Germany, 2005. [Google Scholar]
- Jin, Z.-H.; Sun, C. Cohesive zone modeling of interface fracture in elastic bi-materials. Eng. Fract. Mech. 2005, 72, 1805–1817. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H. Computational implementation of the ppr potential-based cohesive model in abaqus: Educational perspective. Eng. Fract. Mech. 2012, 93, 239–262. [Google Scholar] [CrossRef]
- Alves, J.L.; Roehl, D. A new cohesive zone model for shell. In Proceedings of the 12th Pan-American Congress of Applied Mechanics, Port of Spain, Trinidad, 2–6 January 2012.
- Daudeville, L.; Allix, O.; Ladeveze, P. Delamination analysis by damage mechanics—Some applications. Compos. Eng. 1995, 5, 17–24. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, Y.; Zwingmann, B.; Schlaich, M. Nonlinear Progressive Damage Analysis of Notched or Bolted Fibre-Reinforced Polymer (FRP) Laminates Based on a Three-Dimensional Strain Failure Criterion. Polymers 2014, 6, 949-976. https://doi.org/10.3390/polym6040949
Liu Y, Zwingmann B, Schlaich M. Nonlinear Progressive Damage Analysis of Notched or Bolted Fibre-Reinforced Polymer (FRP) Laminates Based on a Three-Dimensional Strain Failure Criterion. Polymers. 2014; 6(4):949-976. https://doi.org/10.3390/polym6040949
Chicago/Turabian StyleLiu, Yue, Bernd Zwingmann, and Mike Schlaich. 2014. "Nonlinear Progressive Damage Analysis of Notched or Bolted Fibre-Reinforced Polymer (FRP) Laminates Based on a Three-Dimensional Strain Failure Criterion" Polymers 6, no. 4: 949-976. https://doi.org/10.3390/polym6040949




