Prediction of Flow Effect on Crystal Growth of Semi-Crystalline Polymers Using a Multi-Scale Phase-Field Approach
Abstract
:1. Introduction
2. Mathematical Formulation
2.1. Modeling Flow Induced Molecular Structure
2.2. Modeling Nucleation upon Oriented Molecular Structure
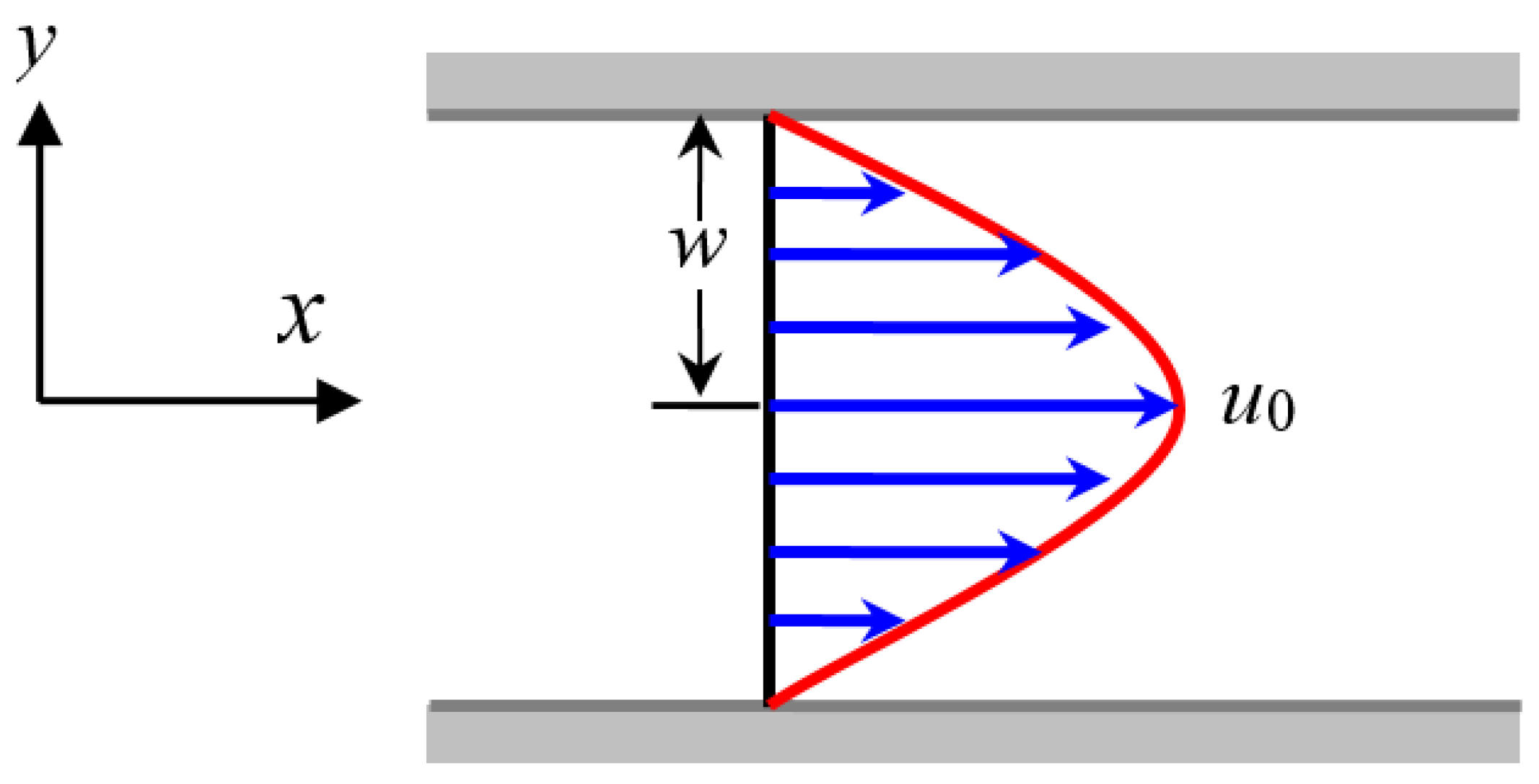
2.3. Modeling Crystal Growth with Melt Flow
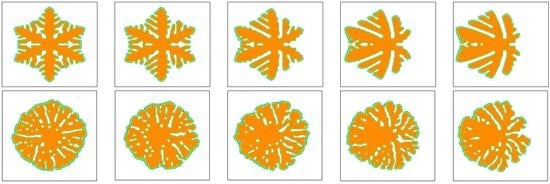
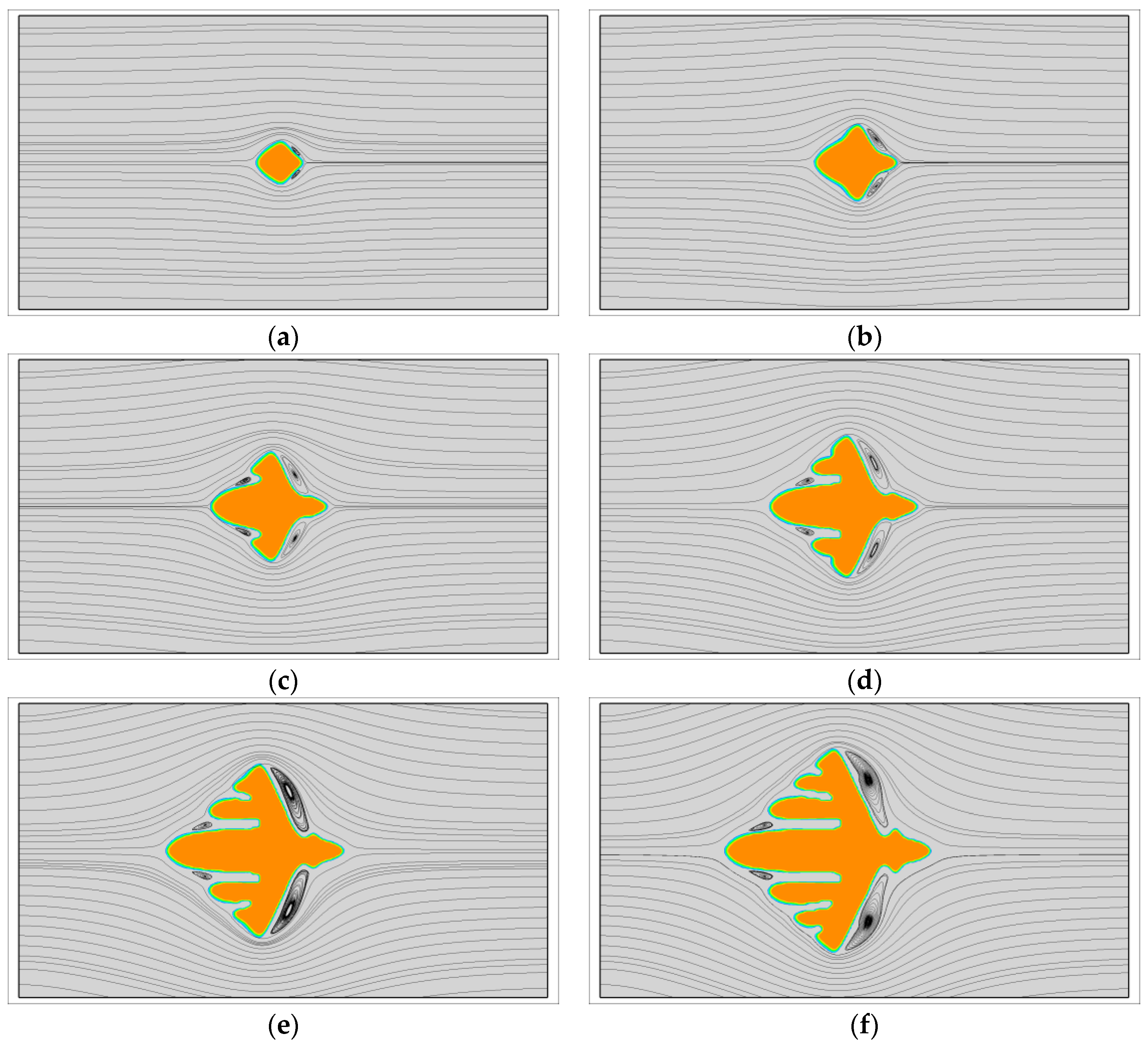
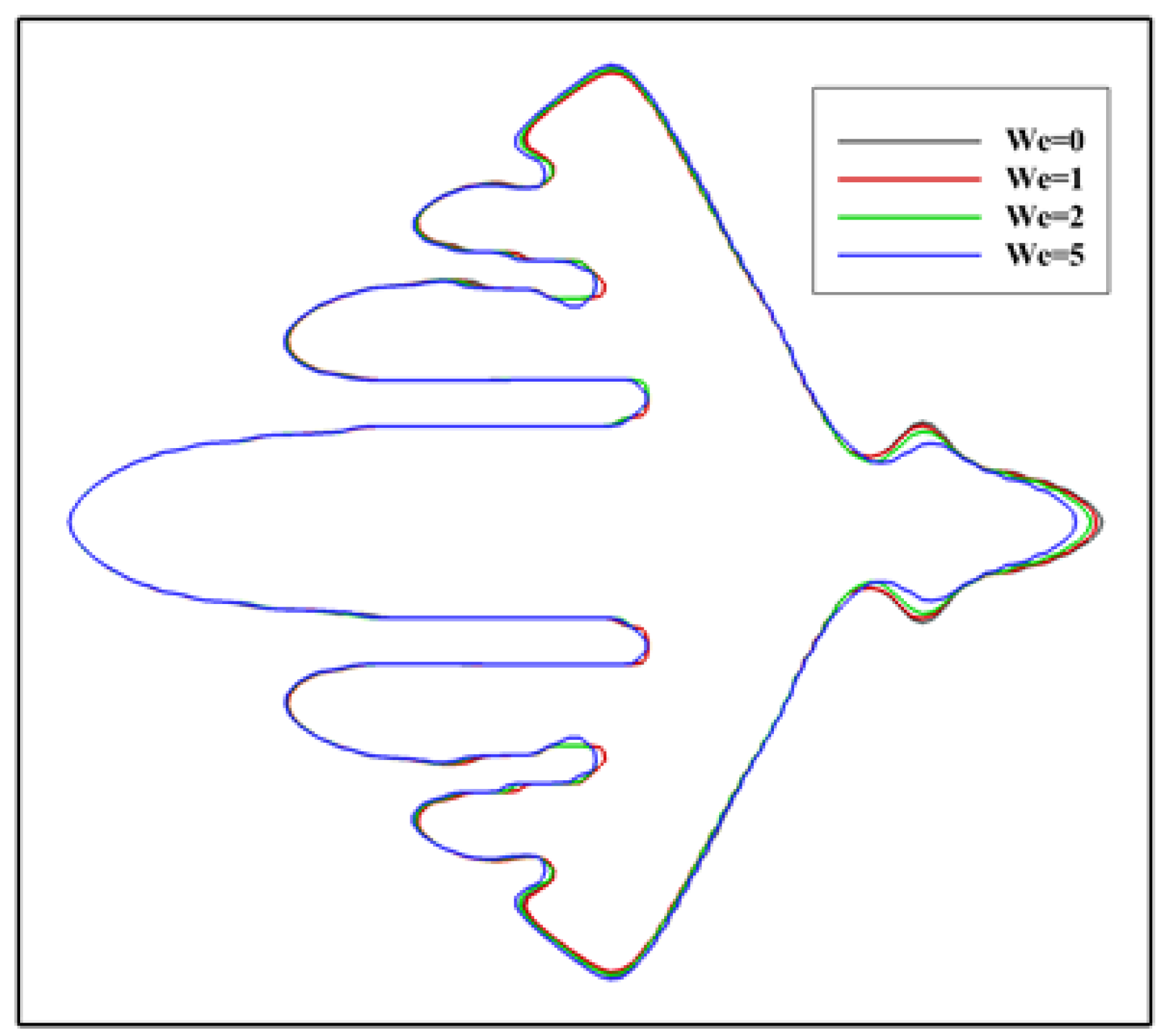
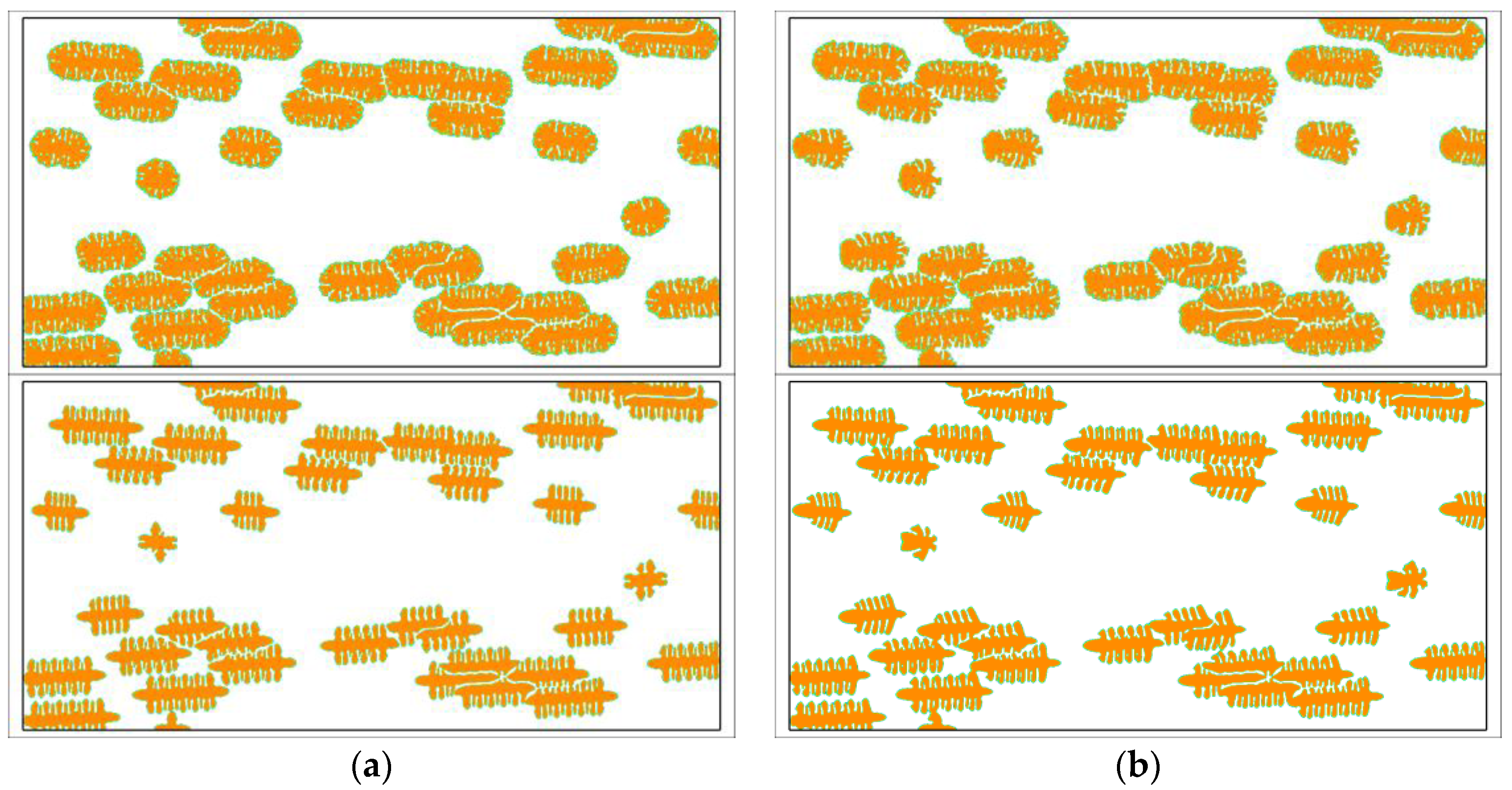
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Nondimensionalization of the Models
Appendix B. Method for the Molecular Structure Model
Appendix C. Method for the Crystal Growth Model
Appendix D. Summarization of the Whole Simulation Process
- (1)
- For given , calculate the density of activated nuclei by Equations (11)–(14);
- (2)
- Determine the center of each nucleus in the simulation area by a random number generator;
- (3)
- Calculate the orientation and aspect ratio of each nucleus by Equations (11)–(20) according to the molecular configuration at the position where the nucleus is located;
- (4)
- Generate the oriented nuclei upon the simulation lattice;
- (1)
- Given model parameters and initial conditions for the crystal growth model;
- (2)
- For given and , compute by Equation (A23);
- (3)
- For given , , , and , compute by Equation (A24);
- (4)
- For given , and , compute the intermediate velocity by Equations (A25) and (A26);
- (5)
- For given , compute the pressure by Equation (A27);
- (6)
- For given , correct the velocity by Equations (A28) and (A29);
- (7)
- For given and , compute by Equations (A30)–(A32);
- (8)
- Compute from by Equations (A33)–(A35);
- (9)
- If the terminal time is not reached, update by and return to (2).
References
- Janeschitz-Kriegl, H.; Ratajski, E. Some fundamental aspects of the kinetics of flow-induced crystallization of polymers. Colloid Polym. Sci. 2010, 288, 1525–1537. [Google Scholar] [CrossRef]
- Ratajski, E.; Janeschitz-Kriegl, H. Flow-induced crystallization in polymer melts: On the correlation between nucleation and specific work. Polym. Bull. 2012, 68, 1723–1730. [Google Scholar] [CrossRef]
- Liu, S.Y.; Zhang, F.F.; Zheng, G.Q.; Dai, K.; Liu, C.T.; Shen, C.Y.; Guo, J.Z. Direct microscopic observation of shish-kebab structuren high-temperature electrospun iPP fibers. Mater. Lett. 2016, 172, 149–152. [Google Scholar] [CrossRef]
- Kumaraswamy, G.; Issaian, A.M.; Kornfield, J.A. Shear-Enhanced Crystallization in Isotactic Polypropylene. 1. Correspondence between in Situ Rheo-Optics and ex Situ Structure Determination. Macromolecules 1999, 32, 7537–7547. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Turng, L.S.; Shen, C.Y. Morphological evolution and orientation development of stretched iPP films: Influence of draw ratio. J. Polym. Sci. B Polym. Phys. 2010, 48, 1223–1234. [Google Scholar] [CrossRef]
- Hsiao, B.S.; Yang, L.; Somani, R.H.; Avila-Orta, C.A.; Zhu, L. Unexpected shish-kebab structure in a sheared polyethylene melt. Phys. Rev. Lett. 2005, 94, 117802. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; He, H.P.; Cao, W.; Shen, C.Y.; Chen, J.B. Multi-scale molding and numerical simulation of the flow-induced crystallization of polymer. Comput. Mater. Sci. 2013, 67, 35–39. [Google Scholar] [CrossRef]
- Mu, Y.; Zhao, G.Q.; Chen, A.B.; Dong, G.W.; Li, S. Numerical investigation of the crystallization and orientation behavior in polymer processing with a two-phase model. Comput. Chem. Eng. 2014, 63, 91–107. [Google Scholar] [CrossRef]
- Spina, R.; Spekowius, M.; Hopmann, C. Multiphysics simulation of thermoplastic polymer crystallization. Mater. Des. 2016, 95, 455–469. [Google Scholar] [CrossRef]
- Anwar, M.; Schilling, T. Crystallization of polyethylene: A molecular dynamics simulation study of the nucleation and growth mechanisms. Polymer 2015, 76, 307–312. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics of polymer crystallization revisited: Crystallization from the melt and the glass in longer polyethylene. J. Chem. Phys. 2013, 139, 054903. [Google Scholar] [CrossRef] [PubMed]
- Baig, C.; Edwards, B.J. Atomistic simulation of crystallization of a polyethylene melt in steady uniaxial extension. J. Non-Newton. Fluid Mech. 2010, 165, 992–1004. [Google Scholar] [CrossRef]
- Nie, Y.J.; Zhang, R.J.; Zheng, K.S.; Zhou, Z.P. Nucleation details of nanohybrid shish-kebabs in polymer solutions studied by molecular simulations. Polymer 2015, 76, 1–7. [Google Scholar] [CrossRef]
- Hu, W.; Frenkel, D.; Mathot, V.B.F. Simulation of shish-kebab crystallite induced by a single prealigned macromolecule. Macromolecules 2002, 35, 7172–7174. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Turng, L.S.; Shen, C.Y. Modeling and prediction of morphology and crystallinity for cylindrical-shaped crystals during polymer processing. Polym. Eng. Sci. 2010, 50, 1226–1235. [Google Scholar] [CrossRef]
- Ruan, C.L.; Liu, C.T.; Zheng, G.Q. Monte Carlo simulation for the morphology and kinetics of spherulites and shish-kebabs in isothermal polymer crystallization. Math. Probl. Eng. 2015, 2015, 506204. [Google Scholar] [CrossRef]
- Graham, R.S.; Olmsted, P.D. Coarse-grained simulations of flow-induced nucleation in semicrystalline polymers. Phys. Rev. Lett. 2009, 103, 115702. [Google Scholar] [CrossRef] [PubMed]
- Jolley, K.; Graham, R.S. A fast algorithm for simulating flow-induced nucleation in polymers. J. Chem. Phys. 2011, 134, 164901. [Google Scholar] [CrossRef] [PubMed]
- Graham, R.S. Modelling flow-induced crystallisation in polymers. Chem. Commun. 2014, 50, 3531–3545. [Google Scholar] [CrossRef] [PubMed]
- Piorkowska, E.; Billon, N.; Haudin, J.M.; Gadzinowska, K. Spherulitic Structure development during crystallization in confined space II. Effect of spherulite nucleation at borders. J. Appl. Polym. Sci. 2005, 97, 2319–2329. [Google Scholar] [CrossRef]
- Raabe, D.; Godara, A. Mesoscale simulation of the kinetics and topology of spherulite growth during crystallization of isotactic polypropylene (iPP) by using a cellular automaton. Model. Simul. Mater. Sci. Eng. 2005, 13, 733–751. [Google Scholar] [CrossRef]
- Xu, H.J.; Matkar, R.; Kyu, T. Phase-field modeling on morphological landscape of isotactic polystyrene single crystals. Phys. Rev. E 2005, 72, 011804. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Shi, T.F.; Chen, J.Z. Simulated morphological landscape of polymer single crystals by phase field model. J. Chem. Phys. 2008, 129, 194903. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.D.; Ouyang, J.; Su, J.; Zhou, W. Phase field modeling of the ring-banded spherulites of crystalline polymers: The role of thermal diffusion. Chin. Phys. B 2014, 23, 126103. [Google Scholar] [CrossRef]
- Wang, X.D.; Ouyang, J.; Su, J.; Zhou, W. A phase-field model for simulating various spherulite morphologies of semi-crystalline polymers. Chin. Phys. B 2013, 22, 106103. [Google Scholar] [CrossRef]
- Huang, T.; Kamal, M.R. Morphological Modeling of Polymer Solidification. Polym. Eng. Sci. 2000, 40, 1796–1808. [Google Scholar] [CrossRef]
- Criscione, A.; Kintea, D.; Tuković, Ž.; Jakirlić, S.; Roisman, I.V.; Tropea, C. Crystallization of supercooled water: A level-set-based modeling of the dendrite tip velocity. Int. J. Heat Mass Transf. 2013, 66, 830–837. [Google Scholar] [CrossRef] [Green Version]
- López, J.; Gómez, P.; Hernández, J. A volume of fluid approach for crystal growth simulation. J. Comput. Phys. 2010, 229, 6663–6672. [Google Scholar] [CrossRef]
- Liu, Z.J.; Ouyang, J.; Zhou, W.; Wang, X.D. Numerical simulation of the polymer crystallization during cooling stage by using level set method. Comput. Mater. Sci. 2015, 97, 245–253. [Google Scholar] [CrossRef]
- Kobayashi, R. Modeling and numerical simulations of dendritic crystal growth. Physica D 1993, 63, 410–423. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys. Rev. E 1998, 57, 4323–4349. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase-field simulation of solidification. Annu. Rev. Mater. Res. 2002, 32, 163–194. [Google Scholar] [CrossRef]
- Gránásy, L.; Pusztai, T.; Warren, J.A. Modelling polycrystalline solidification using phase field theory. J. Phys. Condens. Mat. 2004, 16, R1205–R1235. [Google Scholar] [CrossRef]
- Gránásy, L.; Rátkai, L.; Szállás, A.; Korbuly, B.; Tóth, G.; Környei, L.; Pusztai, T. Phase-field modeling of polycrystalline solidification: From needle crystals to spherulites-A Review. Metall. Mater. Trans. A 2014, 45, 1694–1719. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhang, H.X.; Zhou, W.; Ouyang, J. A 3D phase-field model for simulating the crystal growth of semi-crystalline polymers. Int. J. Heat Mass Transf. 2017, 115, 194–205. [Google Scholar] [CrossRef]
- Xu, H.J.; Keawwattana, W.; Kyu, T. Effect of thermal transport on spatiotemporal emergence of lamellar branching morphology during polymer spherulitic growth. J. Chem. Phys. 2005, 123, 124908. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Jin, Z.K.; Xing, Y.; Gao, H.; Wang, X.K. Simulated rhythmic growth of targeted single crystal by polymer phase-field model. Comput. Mater. Sci. 2013, 68, 23–26. [Google Scholar] [CrossRef]
- Wang, X.D.; Ouyang, J.; Su, J.; Zhou, W. Investigating the role of oriented nucleus in polymer shish-kebab crystal growth via phase-field method. J. Chem. Phys. 2014, 140, 114102. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Beckermann, C.; Karma, A.; Li, Q. Phase-field simulations of dendritic crystal growth in a forced flow. Phys. Rev. E 2001, 63, 061601. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.K.; Zhu, M.F.; Pan, S.Y.; Yang, C.R.; Raabe, D. Lattice Boltzmann modeling of dendritic growth in forced and natural convection. Comput. Math. Appl. 2011, 61, 3585–3592. [Google Scholar] [CrossRef]
- De Gennes, P.G. Coil-stretch transition of dilute flexible polymers under ultrahigh velocity gradients. J. Chem. Phys. 1974, 60, 5030–5042. [Google Scholar] [CrossRef]
- Azzurri, F.; Alfonso, G.C. Insights into formation and relaxation of shearinduced nucleation precursors in isotactic polystyrene. Macromolecules 2008, 41, 1377–1383. [Google Scholar] [CrossRef]
- Cavallo, D.; Azzurri, F.; Balzano, L.; Funari, S.S.; Alfonso, G.C. Flow memory and stability of shear-induced nucleation precursors in isotactic polypropylene. Macromolecules 2010, 43, 9394–9400. [Google Scholar] [CrossRef]
- Hamad, F.G.; Colby, R.H.; Milner, S.T. Lifetime of flow-induced precursors in isotactic polypropylene. Macromolecules 2015, 48, 7286–7299. [Google Scholar] [CrossRef]
- Guo, X.; Isayev, A.I.; Guo, L. Crystallinity and microstructure in injection molding of isotactic polypropylenes Part 1: A new approach to modeling and model parameters. Polym. Eng. Sci. 1999, 39, 2096–2114. [Google Scholar] [CrossRef]
- Boutaousa, M.; Bourgin, P.; Zinet, M. Thermally and flow induced crystallization of polymers at low shear rate. J. Non-Newton. Fluid Mech. 2010, 165, 227–237. [Google Scholar] [CrossRef]
- Yu, F.Y.; Zhang, H.B.; Wang, Z.G.; Yu, W.; Zhou, C.X. Overshoots in stress and free energy change during the flow-induced crystallization of polymeric melt in shear flow. Chin. J. Polym. Sci. 2010, 28, 657–666. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Isayev, A.I.; Shen, S.F. Transient shear flow behavior of polymeric fluids according to the Leonov model. Rheol. Acta 1981, 20, 443–457. [Google Scholar] [CrossRef]
- Herrchen, M.; Öttinger, H.C. A detailed comparison of various FENE dumbbell models. J. Non-Newton. Fluid Mech. 1997, 68, 17–42. [Google Scholar] [CrossRef]
- Wang, X.D.; Ouyang, J.; Zhou, W.; Liu, Z.J. A phase field technique for modeling and predicting flow induced crystallization morphology of semi-crystalline polymers. Polymers 2016, 8, 230. [Google Scholar] [CrossRef]
- Koscher, E.; Fulchiron, R. Influence of shear on polypropylene crystallization: Morphology development and kinetics. Polymer 2002, 43, 6931–6942. [Google Scholar] [CrossRef]
- Charbon, C.; Swaminarayan, S. A multiscale model for polymer crystallization. II. Solidification of a macroscopic part. Polym. Eng. Sci. 1998, 38, 644–656. [Google Scholar] [CrossRef]
- Pantani, R.; De Santis, F.; Speranza, V.; Titomanlio, G. Modelling morphology evolution during solidification of IPP in processing conditions. AIP Conf. Proc. 2014, 1593, 636–640. [Google Scholar]
- Anderson, D.M.; McFadden, G.B.; Wheeler, A.A. A phase-field model of solidification with convection. Phys. D 2000, 135, 175–194. [Google Scholar] [CrossRef]
- Tönhardt, R.; Amberg, G. Phase-field simulation of dendritic growth in a shear flow. J. Cryst. Growth 1998, 194, 406–425. [Google Scholar] [CrossRef]
- Tönhardt, R.; Amberg, G. Dendritic growth of randomly oriented nuclei in a shear flow. J. Cryst. Growth 2000, 213, 161–187. [Google Scholar] [CrossRef]
- Beckermann, C.; Diepers, H.J.; Steinbach, I.; Karma, A.; Tong, X. Modeling melt convection in phase-field simulations of solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Pantani, R.; Coccorullo, I.; Speranza, V.; Titomanlio, G. Modeling of morphology evolution in the injection molding process of thermoplastic polymers. Prog. Polym. Sci. 2005, 30, 1185–1222. [Google Scholar] [CrossRef]
- Katayama, K.; Yoon, M.G. Polymer Crystallization in Melt Spinning: Mathematical Simulation; High-speed fiber spinning; John Wiley & Sons: Hoboken, NJ, USA, 1985; pp. 207–223. [Google Scholar]
- Najafi, N.; Heuzey, M.C.; Carreau, P.; Therriault, D. Quiescent and shear-induced crystallization of linear and branched polylactides. Rheol. Acta 2015, 54, 831–845. [Google Scholar] [CrossRef]
- Zhang, C.G.; Hu, H.Q.; Wang, D.J.; Yan, S.K.; Han, C.C. In situ optical microscope study of the shear-induced crystallization of isotactic polypropylene. Polymer 2005, 46, 8157–8161. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Dong, X.; Zhou, Y.; Wang, D.; Han, C.C. Shear-induced orientation in the crystallization of an isotactic polypropylene nanocomposite. Polymer 2009, 50, 2465–2471. [Google Scholar] [CrossRef]
- Su, J.; Ouyang, J.; Wang, X.D.; Yang, B.X. Lattice Boltzmann method coupled with the Oldroyd-B constitutive model for a viscoelastic fluid. Phys. Rev. E 2013, 88, 053304. [Google Scholar] [CrossRef] [PubMed]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Ouyang, J.; Liu, Y. Prediction of Flow Effect on Crystal Growth of Semi-Crystalline Polymers Using a Multi-Scale Phase-Field Approach. Polymers 2017, 9, 634. https://doi.org/10.3390/polym9120634
Wang X, Ouyang J, Liu Y. Prediction of Flow Effect on Crystal Growth of Semi-Crystalline Polymers Using a Multi-Scale Phase-Field Approach. Polymers. 2017; 9(12):634. https://doi.org/10.3390/polym9120634
Chicago/Turabian StyleWang, Xiaodong, Jie Ouyang, and Ying Liu. 2017. "Prediction of Flow Effect on Crystal Growth of Semi-Crystalline Polymers Using a Multi-Scale Phase-Field Approach" Polymers 9, no. 12: 634. https://doi.org/10.3390/polym9120634