Design Analysis of Adhesively Bonded Structures

Abstract

The existing analytical solutions for the peeling and shearing stresses in polymeric adhesively bonded structures are either too inaccurate or too complex for adoption by practicing engineers. This manuscript presents a closed-form solution that is reasonably accurate yet simple and concise enough to be adopted by practicing engineers for design analysis and exploration. Analysis of these concise solutions have yielded insightful design guidelines: (i) the magnitude of peeling stress is generally higher than that of shearing stress; (ii) the peeling stress in a balanced structure may be reduced most effectively by reducing the elastic modulus of the adherends or by increasing the adhesive-to-adherend thickness ratio and less effectively by reducing the elastic modulus of the adhesive; and (iii) the peeling stress in an unbalanced structure may be reduced by increasing the in-plane compliance of the structure, which may be implemented most effectively by reducing the thicknesses of the adherends and less effectively by reducing the elastic modulus of the adherends.

1. Introduction

The polymeric adhesive in many bonded structures is much more structurally compliant than the adherends, leading to a significantly lower magnitude of in-plane stress in the adhesive. Completely ignoring this in-plane stress in the adhesive substantially reduces the complexity of the analysis and allows the formulation of closed-form solutions. The first of such analyses was presented by Volkersen (1938) [1], who modelled the adhesive layer in a single lap-shear structure as having only shear stiffness and the adherends as capable of only in-plane stretching. A more sophisticated analysis was presented by Goland and Reissner (1944) [2], who modelled the adhesive as having stiffness in shearing and transverse stretching and the adherends as capable of in-plane stretching and bending.

Goland and Reissner [2] assumed the adherends to have negligible shear and transverse-normal compliances, which may not be valid for bonded structures with relatively large ratios of adherends-to-adhesive thicknesses. Assuming a linear distribution of shear stress along the thickness of the adherends—An overly simplistic assumption—Tsai et al. (1998) [3] incorporated shear compliance of the adherends into the formulation of Goland and Reissner [2]. But before Tsai et al. [3], Suhir (1986, 1989) has evaluated the shear compliance [4] and the transverse compliance [5] of the adherends using Ribiere Solution for a long-and-narrow strip [6].

Besides assuming nil in-plane stress in the adhesive, the above authors and many others [7,8,9,10,11,12] have also conveniently assumed that the shear and the transverse stresses are unvarying over the thickness of the adhesive. Ojalo and Eidinoff (1978) [13] were believed to be the first to challenge this assumption; assuming linear variation of the in-plane and the transverse deformations of the adhesive along its thickness, they concluded that the shear stress varies linearly while the transverse stress is unvarying along the thickness of the adhesive. More recently, Wang and Zhang (2009) [14] assumed that transverse stress in the adhesive exhibits a step-jump in magnitude while shear stress is unvarying along its thickness. These assumptions invariably violate the differential equation of equilibrium:

$$\begin{array}{l}\frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{xz}}{\partial z}=0\\ \frac{\partial {\sigma }_z}{\partial z}+\frac{\partial {\tau }_{xz}}{\partial x}=0\end{array}$$

(1)

Except for [14], these strength-of-material solutions have also failed to satisfy the condition that there shall be no shear stress at the free edges of the adhesive, thus leading to gross underestimation of the magnitude of peeling stress at the free edge [15].

Moreover, the strength-of-material solution of Goland and Reissner [2] was restricted to balanced structures—That is, structures in which the adherends are identical in geometry and materials—For which the resultant differential equations for the shear and the transverse stresses in the adhesive are uncoupled and can be solved with relative ease. Delale et al. (1981) [8], Bigwood and Crocombe (1989) [9], Liu et al. (2014) [11], Zhao et al. (2011) [16], and Zhang et al. (2015) [17] have analysed unbalanced structures experiencing arbitrary edge loading such that the differential equations are heavily coupled. The resultant closed-formed solutions are immensely chunky and complex.

A “theory of elasticity” solution that is based on variational formulation was presented by Allman (1977) [18]. The solution satisfied Equation (1) while also ensuring that the free-edge condition of nil-shear stress was satisfied. Similar approach was followed by Chen and Cheng (1983) [19], Yin (1991) [20], Adams and Mallick (1992) [21], and Wu and Zhao (2013) [22]. The solutions are not only complex but highly restrictive—The boundary conditions are embedded within the governing differential equation, thus limiting the generality of the solutions.

From the perspective of practicing engineers, the current state of closed-form solutions for adhesively bonded structures is far from satisfactory—These solutions are either too inaccurate or too complex for practical adoption. It is the objective of this manuscript to offer a closed-form solution that is reasonably accurate yet simple and concise enough to be adopted by practicing engineers for design analysis and exploration.

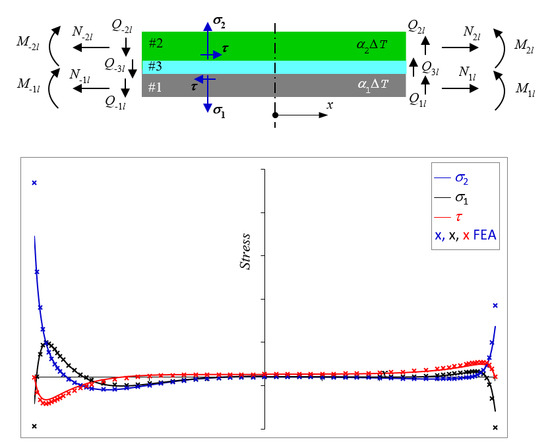
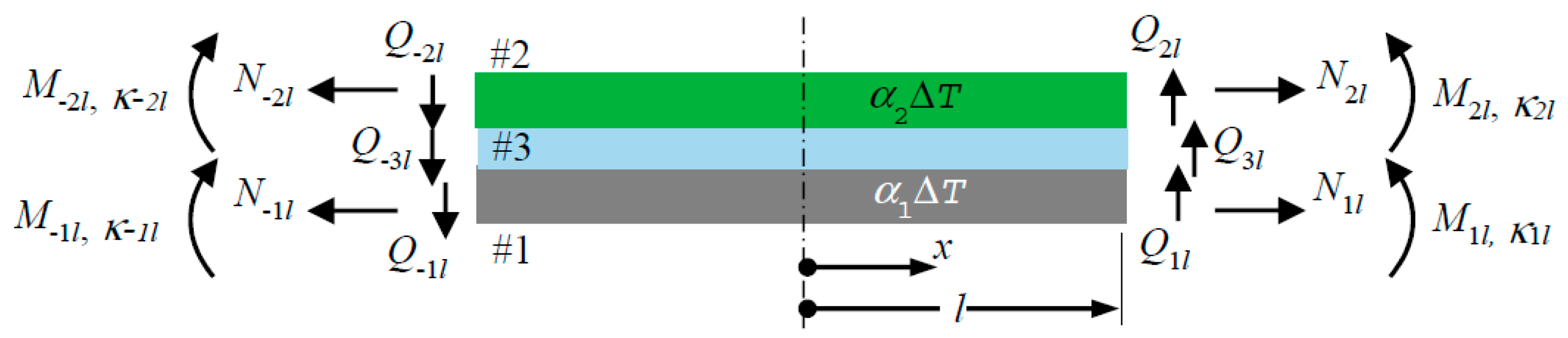
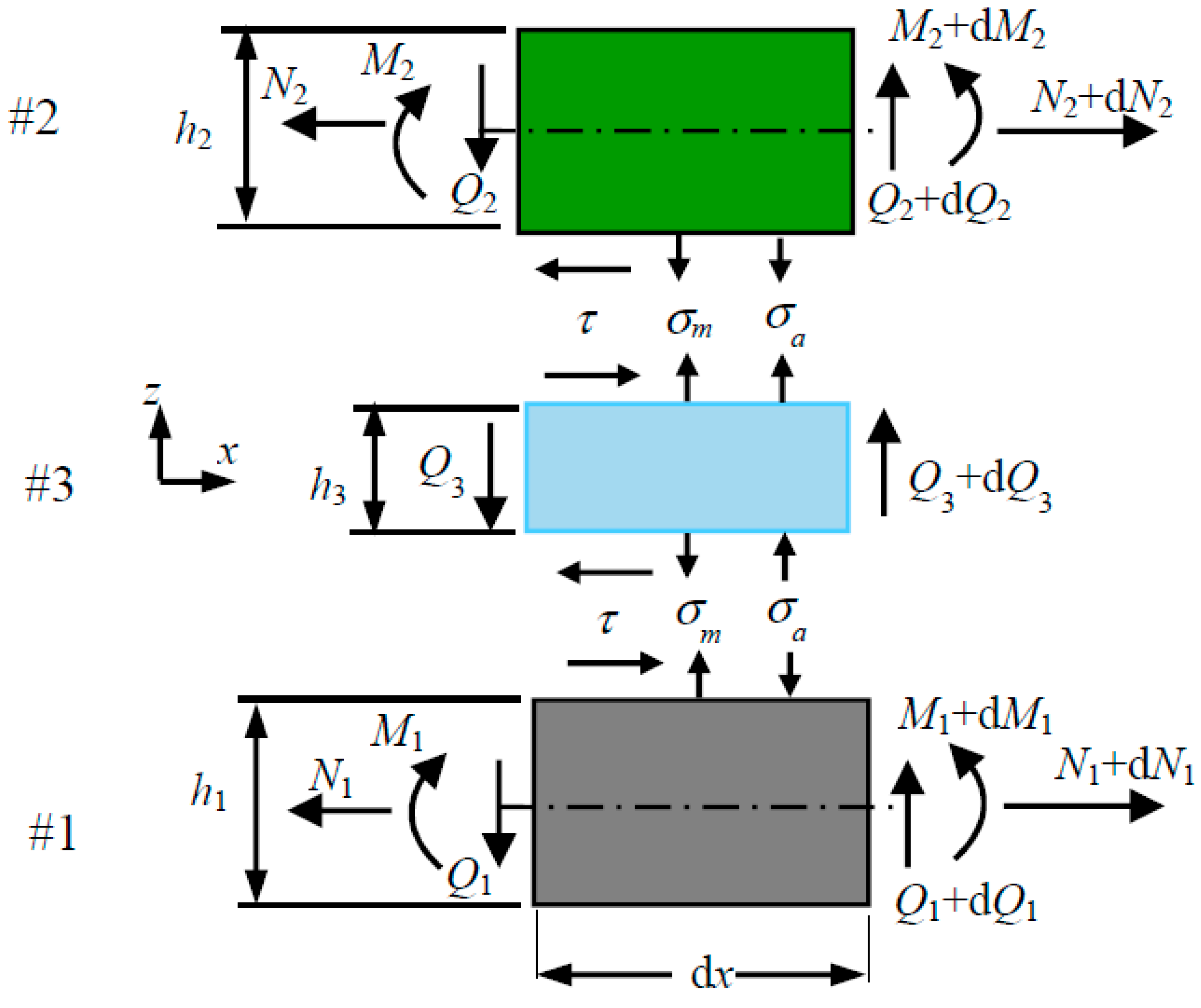
2. Analytical Equations

Figure 1 shows a bonded structure made up of adherend #1, adherend #2, and adhesive #3. The structure experiences a mismatched thermal expansion between the adherends and stretching, shearing, and bending at their edges. Note the notations and positive directions of the in-plane stretching forces N_±il, the shear forces Q_±il, moments M_±il, and curvatures κ_±il, at x = ±l, where l is the half-length of the adhesive. The height, Young’s modulus, shear modulus, flexural stiffness, and thermal coefficient of expansion of member #i are denoted as h_i, E_i, G_i, D_i, and α_i, respectively. The shear, in-plane (x), transverse (z), and flexural compliances of the bonded structure are denoted as κ_s, λ_x, λ_z, and $\overline{D}$, respectively. The corresponding compliances of member #i are denoted as κ_si, λ_xi, λ_zi, and $\overline{D_i}$, respectively. The formulas for computing these compliances are collected under the heading “basic formula” at the front of this article. The derivations of these formulas may be found in Refs. [15,23].

The adhesive is assumed to experience negligible in-plane stress, σ_x. The differential equation of equilibrium, Equation (1), then suggests an nonvarying shear stress, τ_xz, and a linearly varying transverse stress, σ_z, along the thickness of the adhesive. Denoting σ_m and σ_a respectively as the mean and amplitude of variation of the transverse stress along the thickness of the adhesive, the peeling stress at the two interfaces of the adhesive with adherend #i is given by

$${\sigma }_{pi}={\sigma }_m\mp {\sigma }_a, i=1,2$$

(2)

Unless otherwise stated in this manuscript, the upper and the lower signs in $\mp$ are associated with adherend #1 and adherend #2 respectively. These stresses, together with the interfacial shear stress, τ, on an elemental representation of a bonded structure are shown in Figure 2. Substituting ∂σ_z/∂z as σ_a/(2h₃) into Equation (1) gives

$${\sigma }_a=-\frac{h_3}{2}\frac{d\tau }{dx}$$

(3)

The derivations of the differential equations for τ and σ_m are elaborated upon in Appendix A.

2.1. Balanced Structures

Referring to Equation (A5) and with the parameter, µ_σ, equates to nil for a balanced bonded structure, the differential equation for the interfacial shear stress is given by

$$\frac{d^3\tau }{d{x}^3}-{\beta }^2\frac{d\tau }{dx}=0$$

(4)

where ${\beta }^2={\lambda }_x/{\kappa }_s$. For structures of reasonably large length, say βl > 3, the solution is given approximately by

$$\tau (x)=A_c{e}^{\beta (x-l)}+A_3, x> 0$$

(5)

The boundary conditions κ_sdτ(l)/dx = ε_T + ε_Nl + ε_Ml and ${{\displaystyle \int }}_{-l}^l\tau dx=N_{2l}-N_{-2l}$ return

$$\begin{array}{l}{A}_{\pm c}=\frac{{\epsilon }_T+{\epsilon }_{\pm Nl}+{\epsilon }_{\pm Ml}}{\beta {\kappa }_s}\\ A_3=\frac{N_{2l}-N_{-2l}}{2l}-\frac{A_c-A_{-c}}{2\beta l}=\frac{N_{2l}-N_{-2l}}{2l}-\frac{{\epsilon }_{Nl}-{\epsilon }_{-Nl}+{\epsilon }_{Ml}-{\epsilon }_{-Ml}}{2{\lambda }_{x}l}\end{array}$$

(6)

where

$$\begin{array}{l}{\epsilon }_T=\left({\alpha }_2-{\alpha }_1\right)∆T\\ {\epsilon }_{\pm Nl}=N_{\pm 2l}{\lambda }_{x2}-N_{\pm 1l}{\lambda }_{x1}\\ {\epsilon }_{\pm Ml}=\frac{1}{2}\left(\left(h_1+h_3\right){\kappa }_{\pm 1l}+\left(h_2+h_3\right){\kappa }_{\pm 2l}\right)\end{array}$$

(7)

Referring to Equation (A6) and with the parameter, µ_τ, equates to nil for a balanced bonded structure, the differential equation for the mean of the peeling stress is given by

$$\frac{d^4{\sigma }_m}{d{x}^4}+4{\alpha }^4{\sigma }_m=0$$

(8)

where $4{\alpha }^4=\overline{D}/{\lambda }_z$. For structures of reasonably large length, say αl > 3, the solution is given approximately by

$${\sigma }_m(x)=e^{\alpha (x-l)}\left[B_{1c}\cos \alpha (x-l)+B_{2c}\sin \alpha (x-l)\right], x > 0.$$

(9)

The boundary conditions ${\mathsf{\lambda }}_z{d}^2{\mathsf{\sigma }}_m/d{x}^2=M_{2l}/D_2-M_{1l}/D_1={\widehat{M}}_{21l}$ and ${\mathsf{\lambda }}_z{d}^3{\mathsf{\sigma }}_m/d{x}^3=-(Q_{2l}/D_2-Q_{1l}/D_1)=-{\widehat{Q}}_{21l}$ return

$$B_{1c}=\frac{{\widehat{Q}}_{21l}}{2{\alpha }^3{\lambda }_z}+B_{2c},B_{2c}=\frac{{\widehat{M}}_{21l}}{2{\alpha }^2{\lambda }_z}$$

(10)

Substituting Equation (5) into Equation (3) yields the amplitude of the peeling stress:

$${\sigma }_a(x)=-\frac{A_s\beta h_3}{2}{e}^{\beta (x-l)} \mathrm{for} x > 0.$$

(11)

2.2. Unbalanced Structures

2.2.1. Non-Free Edge Solutions

Combining Equations (A5) and (A6) gives rise to a seventh-order differential equation for τ(x) and a sixth-order differential equation for σ_m(x) [5,7,8,9,11]. The resulting solutions are far too complex to be attractive to practicing engineers. Instead, solving Equations (A5) and (A6) iteratively would lead to approximate solutions of τ(x) and σ_m(x) that are far simpler, thus enabling insights and encouraging application by practicing engineers. Designating the subscripts c and p as complimentary and particular solutions, respectively, the approximate solution involves solving for the complementary solutions for the interfacial shear stress, τ_c, and the mean of the peeling stress, σ_mc—these are given by Equations (5) and (9)—followed by substituting σ_mc into Equation (A5) to obtain τ =τ_c + τ_p, and τ_c into Equation (A6) to obtain σ_m = σ_mc + σ_mp.

The interfacial shear and peel stresses have been evaluated as

$$\begin{array}{l}\tau (x)=A_s{e}^{\beta (x-l)}+A_4+e^{\alpha (x-l)}\left[A_{p1}\cos \alpha (x-l)+A_{p2}\sin \alpha (x-l)\right]\\ {\sigma }_m(x)=e^{\alpha (x-l)}\left[B_1\cos \alpha (x-l)+B_2\sin \alpha (x-l)\right]+B_p{e}^{\beta (x-l)}\\ {\sigma }_a(x)=-\frac{h_3}{2}\left[\beta A_s{e}^{\beta (x-l)}+\alpha e^{\alpha (x-l)}\left[\left(A_{p1}+A_{p2}\right)\cos \alpha (x-l)-\left(A_{p1}-A_{p2}\right)\sin \alpha (x-l)\right]\right]\end{array}$$

(12)

where

$$\begin{array}{l}{A}_s=A_c-\frac{\alpha \left(A_{p1}+A_{p2}\right)}{\beta }\\ A_4=A_3-\frac{1}{2l}\left(\frac{1}{2\alpha }-\frac{\alpha }{{\beta }^2}\right)\left(A_{p1}-A_{-p1}\right)+\frac{1}{2l}\left(\frac{1}{2\alpha }+\frac{\alpha }{{\beta }^2}\right)\left(A_{p2}-A_{-p2}\right)\\ A_{\pm p1}=\frac{{\mu }_{\sigma }}{{\kappa }_s}\frac{\left(2{\alpha }^3+\alpha {\beta }^2\right)B_{\pm 1c}+\left(2{\alpha }^3-\alpha {\beta }^2\right)B_{\pm 2c}}{2{\alpha }^2\left(4{\alpha }^4+{\beta }^4\right)},A_{p2}=\frac{{\mu }_{\sigma }}{{\kappa }_s}\frac{\left(2{\alpha }^3+\alpha {\beta }^2\right)B_{\pm 2c}-\left(2{\alpha }^3-\alpha {\beta }^2\right)B_{\pm 1c}}{2{\alpha }^2\left(4{\alpha }^4+{\beta }^4\right)}\\ B_{\pm 1c}=\frac{{\widehat{Q}}_{\pm 21l}}{2{\alpha }^3{\lambda }_z}+B_{\pm 2c},B_{\pm 2c}=\frac{{\widehat{M}}_{\pm 21l}}{2{\alpha }^2{\lambda }_z}\\ B_1=\frac{{\beta }^3{B}_p+{\widehat{Q}}_{21l}/{\lambda }_z}{2{\alpha }^3}+B_2,B_2=\frac{-{\beta }^2{B}_P+{\widehat{M}}_{21l}/{\lambda }_z}{2{\alpha }^2}\\ B_P=\frac{{\mu }_{\tau }{A}_c}{{\lambda }_z}\frac{\beta }{4{\alpha }^4+{\beta }^4}\end{array}$$

(13)

It is worth noting that in the case of an unbalanced bonded structure experiencing only mismatched thermal expansion and/or differential stretching between the adherends, the magnitude of σ_m is negligibly small compared to that of τ and σ_a [23]. Ignoring σ_m, the differential equation for τ is given by Equation (4); and τ(x) and σ_a(x) are given by Equations (5) and (11), respectively.

2.2.2. Free Edge Solutions

The expression of shear stress in Equation (12) does not satisfy the free edge condition, τ(l) = 0, which is essential for accurate modelling of σ_a(l). The free edge condition may be enforced artificially through the introduction of a decay function, 1 − e^nβ(x−l) [15,23]. The derivation of the factor n is explained in Appendix B. The expressions of τ(x), σ_m(x), and σ_a(x) with the free edge condition enforced are given by

$$\tau (x)=\left\{A_s{e}^{\beta (x-l)}+A_4+e^{\alpha (x-l)}\left[A_{p1}\cos \alpha (x-l)+A_{p2}\sin \alpha (x-l)\right]\right\}\left[1-e^{n\beta (x-l)}\right]$$

(14)

$$\begin{array}{ll}{\sigma }_m(x)& =e^{\alpha (x-l)}\left[B_{1n}\cos \alpha (x-l)+B_{2n}\sin \alpha (x-l)\right]+B_p{e}^{\beta (x-l)}-B_{pn1}{e}^{(n+1)\beta (x-l)}-B_{pn2}{e}^{n\beta (x-l)}\\ & \approx e^{\alpha (x-l)}\left[B_{1n}\cos \alpha (x-l)+B_{2n}\sin \alpha (x-l)\right]+B_p{e}^{\beta (x-l)}\end{array}$$

(15)

$${\sigma }_a(x)=-\frac{h_3}{2}\left\{\begin{array}{l}\left(1-e^{n\beta (x-l)}\right)\left\{\beta A_s{e}^{\beta (x-l)}+\alpha e^{\alpha (x-l)}\left[\left(A_{p1}+A_{p2}\right)\cos \alpha (x-l)-\left(A_{p1}-A_{p2}\right)\sin \alpha (x-l)\right]\right\}-\\ n\beta e^{n\beta (x-l)}\left\{A_s{e}^{\beta (x-l)}+A_4+e^{\alpha (x-l)}\left[A_{p1}\cos \alpha (x-l)+A_{p2}\sin \alpha (x-l)\right]\right\}\end{array}\right\}$$

(16)

where

$$\begin{array}{l}{B}_{1n}=\frac{{\beta }^3\left(B_p-{(n+1)}^3{B}_{pn1}-n^3{B}_{pn2}\right)+{\widehat{Q}}_{21l}/{\lambda }_z}{2{\alpha }^3}+B_{2n},B_{2n}=\frac{-{\beta }^2\left(B_p-{(n+1)}^2{B}_{pn1}-n^2{B}_{pn2}\right)+{\widehat{M}}_{21l}/{\lambda }_z}{2{\alpha }^2}\\ B_{pn1}=\frac{{\mu }_{\tau }{A}_c}{{\lambda }_z}\frac{(n+1)\beta }{4{\alpha }^4+{(n+1)}^4{\beta }^4},B_{pn2}=\frac{{\mu }_{\tau }{A}_3}{{\lambda }_z}\frac{n\beta }{4{\alpha }^4+n^4{\beta }^4}\end{array}$$

(17)

3. Numerical Validations

Equations (5), (9), and (11) for the balanced structures [15] and for unbalanced bonded structure experiencing only mismatched thermal expansion and/or differential stretching between the adherends [23] have been validated in previous publications. Hence, only the equations for unbalanced structures experiencing the general state of edge loading shall be validated. The material properties, dimensions of the bonded structure, thermomechanical loads, and finite element model used in this study are shown in Figure 3a. The domain of the bonded structure was modelled using more than 100,000 eight-node quadrilateral elements. The domain around the free edge was discretised at 75 divisions per mm. The adhesive was assigned with anisotropic properties of negligible E_x, rendering it consistent with the assumption in the analytical solutions that the adhesive experiences negligible σ_x. The compliances (assuming plane stress), characteristic parameters (α, β), free-edge parameters (ϕ, n) which are computed using Equations (A9) and (A10), coupling parameters (µ_σ, µ_τ), and the coefficients in the stress equations are tabulated in

Table 1. Numerical validation: characteristics of the unbalanced structure.

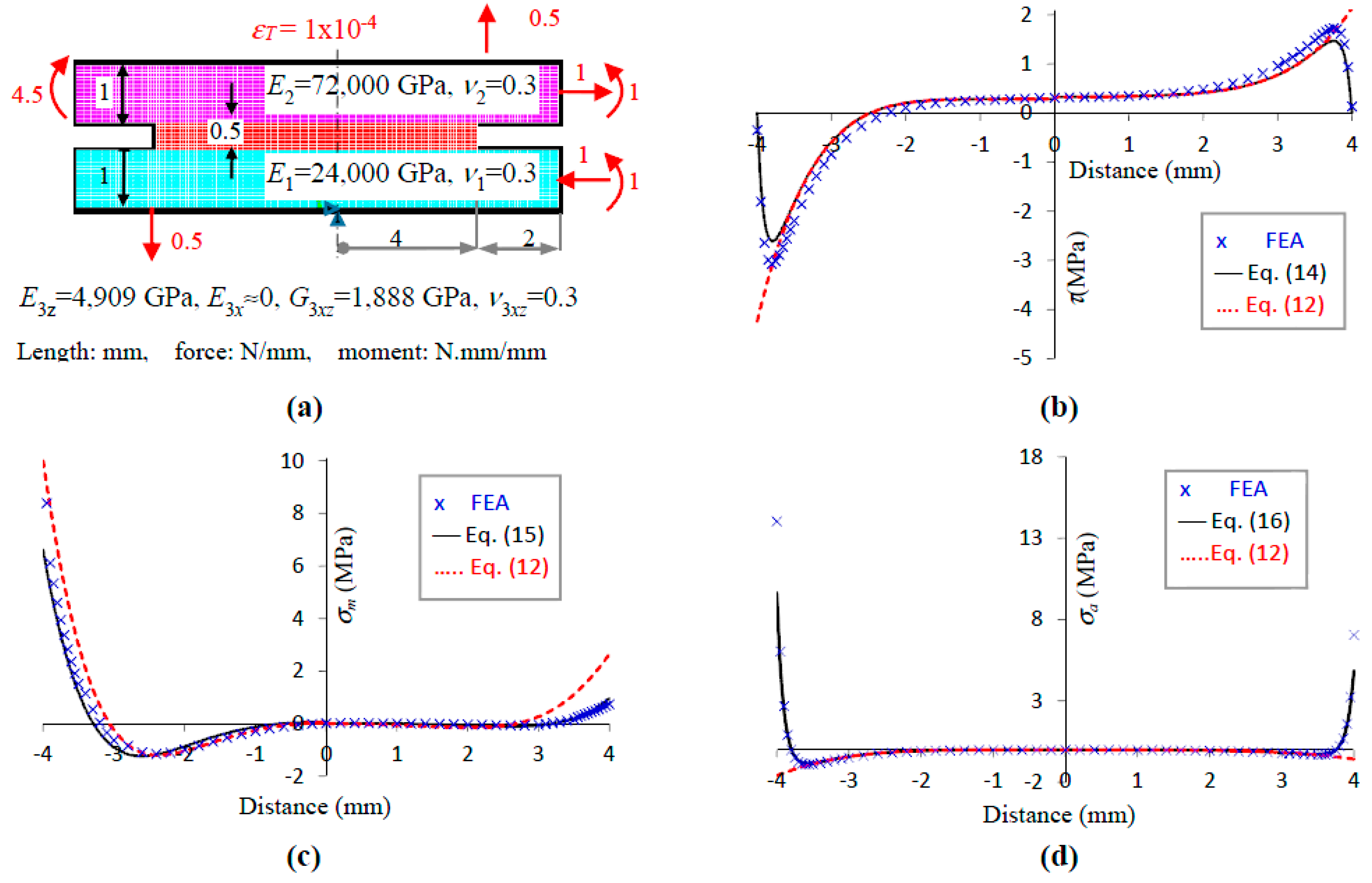
Compliances		Characteristic parameters (mm−1)				Free edge parameters
κs	2.83 × 10−4	α		1.08		ϕ	0.45
λx	4.31 × 10−4	β		1.23		n	7.4
λz	1.21 × 10−4	Coupling parameters (N−1)
		µσ		1.67 × 10−4		µτ	2.50 × 10−4
Stress coefficients (N. mm−2)
Domain	As	A4	Ap1	Ap2	B1n	B2n	Bp
−l ≤ x ≤ 0	3.23	0.31	1.33	0.83	4.94	7.23	1.67
0 ≤ x ≤ l	1.53		0.3	0.1	0.35	0.98	0.61

κ_s, λ_z (N⁻¹.mm³), λ_x (N⁻¹.mm).

. It is noted that (i) βl, αl ≥ 4, thus justifying the use of the reduced form of solutions as presented in Section 2; (ii) the magnitudes of the coupling parameters are significantly large, reflecting the significant difference in the stiffness between the two adherends; and (iii) the relatively strong coupling has led to the relatively large magnitudes of the particular stress coefficients (A_p1, A_p2, B_p) compared to that of the complementary stress coefficients (A_s, B_1n, B_2n).

Figure 3b shows the shear stress, τ(x), for (i) the analytical solution that enforces the nil-shear stress free-edge condition, Equation (14), (ii) the analytical solution that does not enforce the above free-edge condition, Equation (12), and (iii) the finite element analysis (FEA) solution. The analytical solution, Equation (14), agrees reasonably well with the FEA solution for the entire length of the bonding although the magnitude of the former is consistently at approximately 85% that of the FEA. The free-edge parameter at ϕ = 0.45 is in reasonable agreement with that extracted from FEA at ϕ_FEA = 0.40 and 0.48 for −l ≤ x ≤ 0 and 0 ≤ x ≤ −l, respectively.

Figure 3c shows the mean of the transverse stress, σ_m(x), for (i) the analytical solution that enforces the nil-shear stress free-edge condition, Equation (15), (ii) the analytical solution that does not enforce the above free-edge condition, Equation (12), and (iii) the FEA solution. The free-edge solution, Equation (15), agrees well with the FEA solution, especially if the FEA solutions at x = ±l, which are susceptible to numerical error, are ignored.

Figure 3d shows the amplitude of the transverse stress, σ_a(x), for (i) the analytical solution that enforces the nil-shear stress free-edge condition, Equation (16), (ii) the analytical solution that does not enforce the above free-edge condition, Equation (12), and (iii) the FEA solution. Both Equation (16) and the FEA show the magnitude of σ_a increases rapidly near the free edge. In contrast, Equation (12) shows a very mild increase in magnitude near the free edge, in the opposite direction.

4. Design Analysis

4.1. Balanced Structures

The shear stress in the adhesive for a balanced structure is given by Equation (5). For simplicity, we shall assume A_c » A₃, the maximum magnitude of shear stress is given by

$${\tau }_{\max }\approx A_c=\frac{{\epsilon }_T+{\epsilon }_{Nl}+{\epsilon }_{Ml}}{\sqrt{{\lambda }_x{\kappa }_s}}$$

(18)

For the same magnitude of the applied strains, the magnitude of shear stress may be reduced by increasing the x-compliance and the shear compliances of the bonded structure. We shall analyse two extreme cases; case I: the ratio h_adhesive/h_adherend is significant such that the shear compliance of the structure is dominated by that of the adhesive; that is, κ_s ≈ h₃/G₃, and case II: h_adhesive/h_adherend is insignificantly small, such that the shear compliance of the structure is dominated by that of the adherends; that is, κ_s ≈ h₁/4G₁. The product λ_xκ_s for the two extreme cases (for plane stress) are given by

$${\lambda }_x{\kappa }_s=\{\begin{array}{cc}\frac{2h_3/h_1}{E_1{G}_3}\left(4+3h_3/h_1\right)\hfill & \hfill \mathrm{Case}\mathrm{I}\\ \frac{2}{E_1{G}_1}\hfill & \hfill \mathrm{Case}\mathrm{II}\end{array}$$

(19)

Thus, for Case I, the magnitude of shear stress in the adhesive may be reduced by reducing the elastic moduli of the adherends and the adhesive while increasing the thickness ratio of adhesive-to-adherend. For Case II, the magnitude of shear stress in the adhesive may be reduced by reducing the elastic modulus of the adherends.

The mean of the transverse stress in the adhesive, σ_m, for a balanced structure is given by Equation (9). The maximum magnitude of σ_m occurs at x = l and is given by

$${\sigma }_{m,\max }=B_{1c}=\frac{1}{2{\alpha }^2{\lambda }_z}\left(\frac{{\widehat{Q}}_{21l}}{\alpha }+{\widehat{M}}_{21l}\right)$$

(20)

Noting that 2α²λ_z = $\sqrt{{\lambda }_z\overline{D}}$, ${\widehat{Q}}_{21l}=Q_{2l}/D_2-Q_{1l}/D_1$, ${\widehat{M}}_{21l}=M_{2l}/D_2-M_{1l}/D_1$ and D₁ = D₂, for the same magnitude of the normalised edge forces, (Q_2l − Q_1l)/α, and the edge moments, M_2l-M_1l, the magnitude of σ_m,max may be reduced by increasing the product λ_z$\overline{D}$D₁² = 2λ_zD₁; that is, by increasing the z-compliance and the flexural stiffness of the structure. We shall analyse the same two extreme cases described for shear stress : λ_z ≈ h₃/E₃ for Case I and λ_z ≈ 13h₁/16E₁ for Case II. The product λ_zD₁ for the two extreme cases (for plane stress) are given by

$${\lambda }_z{D}_1=\{\begin{array}{c}\frac{h_1{}^3{h}_3{E}_1/E_3}{12}\mathrm{Case}\mathrm{I}\\ \frac{13h_1{}^4}{192}\mathrm{Case}\mathrm{II}\end{array}$$

(21)

Thus, for Case I, the magnitude of σ_m,max may be reduced most effectively by increasing the thickness of the adherends and less effectively by increasing the thickness of the adhesive or the ratio of E_adherend-to-E_adhesive. For Case II, the magnitude of σ_m,max may be reduced very effectively by increasing the thickness of the adherends.

The amplitude of the transverse stress in the adhesive, σ_a, for a balanced structure is given by Equation (11), which however ought to be modified to include the free-edge condition:

$${\sigma }_a(x)=-\frac{h_3}{2}\left\{\left(1-e^{n\beta (x-l)}\right)\beta A_c{e}^{\beta (x-l)}-n\beta e^{n\beta (x-l)}\left[A_c{e}^{\beta (x-l)}+A_3\right]\right\}$$

(22)

The maximum magnitude of σ_m occurs at x = l. For simplicity, we shall assume A_c » A₃; the maximum magnitude of σ_a, after substituting the exponential factor n with Equation B(2) is given approximately by

$${\sigma }_{a,\max }\approx \frac{n\beta h_3{A}_c}{2}\approx \frac{0.72A_c}{{\varphi }^{1.4}{\left(\beta h_3\right)}^{0.4}}\approx \frac{0.72}{{\varphi }^{1.4}}\frac{{\epsilon }_T+{\epsilon }_{Nl}+{\epsilon }_{Ml}}{\sqrt[4]{{\lambda }_x{}^3{\kappa }_s{h}_3{}^2}}$$

(23)

Assuming ϕ to be a constant, then for the same magnitudes of the applied strains, the magnitude of σ_a,max may be reduced by increasing the product λ_x³κ_sh₃², which for the two extreme cases: κ_s ≈ h₃/G₃ for Case I and κ_s ≈ h₁/4G₁ for Case II - are given by (for plane stress)

$${\lambda }_x{}^3{\kappa }_s{h}_3{}^2=\{\begin{array}{c}\frac{8{\left(h_3/h_1\right)}^3{\left(4+3h_3/h_1\right)}^3}{E_1{}^3{G}_3}\mathrm{Case}\mathrm{I}\\ \frac{128{\left(h_3/h_1\right)}^2}{E_1{}^3{G}_1}\mathrm{Case}\mathrm{II}\end{array}$$

(24)

Thus, for Case I, the magnitude of σ_a,max may be reduced most effectively by reducing the elastic modulus of the adherends or by increasing the thickness ratio of adhesive-to-adherend and less effectively by reducing the elastic modulus of the adhesive. For Case II, the magnitude of σ_m,max may be reduced most effectively by reducing the elastic modulus of the adherends and less effectively by increasing the thickness ratio of adhesive-to-adherend.

It is clear from the above that the design guidelines do not concurrently minimise τ_max, σ_a,max, and σ_m,max. In other words, the design guidelines for minimizing the magnitudes of τ_max, σ_a,max, and σ_m,max are contradictory. We shall examine the relative magnitudes of these components of stress. Equation (25) presents the ratio of σ_a,max/τ_max. It is noted that the magnitude of σ_a,max is almost always larger than that of τ_max. This, together with the fact that the peeling strength of a bonded joint is generally weaker than its shear strength, suggests that it is more important to minimise the magnitudes of σ_a,max and σ_m,max than the magnitude of τ_max.

$$\begin{array}{ll}\frac{{\sigma }_{a,\max }}{{\tau }_{\max }}& =\frac{n\beta h_3}{2}\approx \frac{0.72}{{\phi }^{1.4}{\left(\beta h_3\right)}^{0.4}}\approx \frac{2}{{\left(\beta h_3\right)}^{0.4}}\mathrm{assuming}\phi =0.5\\ & \approx 2{\left[\frac{E_1{h}_1}{2G_3{h}_3\left(4+3h_3/h_1\right)}\right]}^{0.2}\mathrm{for}\mathrm{Case}\mathrm{I}\\ & \approx 3\mathrm{to}4\mathrm{for}{E}_1{h}_1/G_3{h}_3\mathrm{between}60\mathrm{to}250\end{array}$$

(25)

Equation (26) presents the ratio of σ_a,max/σ_m,max. Noting that σ_m,max ≈ 0 for adherends experiencing only thermal strain and/or stretching strain, σ_a,max is much larger than σ_m,max for these cases. Noting that σ_a,max ≈ 0 for adherends experiencing only edge shear forces, Q_il, σ_a,max is much smaller than σ_m,max for this case. Thus, σ_a,max may be larger or smaller than σ_m,max for a general loading condition. For the case of single lap-joints (SLJ) that are dominated by stretching and bending through a single adherend, i.e., ε_T = 0, ${\widehat{Q}}_{21l}\approx 0$, κ_1l = 0, while N_2l and M_2l are positive, σ_a,max is almost always larger than σ_m,max. It is therefore advisable to give more weight to the design guidelines that minimize the magnitude of σ_a,max.

$$\begin{array}{ll}\frac{{\sigma }_{a,\max }}{{\sigma }_{m,\max }}& =\frac{n\beta h_3}{2}\sqrt{\frac{{\lambda }_z\overline{D}}{{\lambda }_x{\kappa }_s}}\frac{{\epsilon }_T+{\epsilon }_{Nl}+{\epsilon }_{Ml}}{{\widehat{Q}}_{21l}/\alpha +{\widehat{M}}_{21l}}\\ & \approx \frac{n\beta h_3}{4}\sqrt{\frac{6}{\left(4+3h_3/h_1\right)\left(1+\nu \right)}}\left(\frac{N_{2l}{h}_1}{6M_{2l}}+1+h_3/h_1\right)>1\mathrm{for}\mathrm{SLJ}\mathrm{and}\mathrm{Case}\mathrm{I}\end{array}$$

(26)

4.2. Unbalanced Structures

In light of the coupling of τ(x) and σ_m(x) for the unbalanced structures, it is improbable to find a universal guideline for the optimum design of unbalanced structures that can be expressed in the simple forms of Equations (19), (21) and (24).

The shear stress in the adhesive of an unbalanced structure is given by Equation (14). For simplicity, we shall assume A_s » A₄ while also ignoring the decay function, 1 − e^nβ(x−l), the maximum magnitude of shear stress is then given by

$$\begin{array}{ll}{\tau }_{\max }& \approx A_s+A_{p1}=A_c-\frac{\alpha }{\beta }\left(A_{p1}+A_{p2}\right)+A_{p1}\\ & =\frac{{\epsilon }_T+{\epsilon }_{Nl}+{\epsilon }_{Ml}}{\sqrt{{\lambda }_x{\kappa }_s}}+\frac{{\mu }_{\sigma }\left[\left(2{\alpha }^3-2{\alpha }^2\beta +\alpha {\beta }^2\right){\widehat{Q}}_{21l}/\alpha +\left(-4{\alpha }^4/\beta +4{\alpha }^3-2{\alpha }^2\beta \right){\widehat{M}}_{21l}\right]}{4{\alpha }^4\left(4{\alpha }^4+{\beta }^4\right){\lambda }_z{\kappa }_s}\end{array}$$

(27)

The magnitude of A_c may be reduced by increasing the x-compliance and the shear compliance of the structure. Equation (27) suggests that the magnitude of the particular solution may be reduced by increasing the product $\left(4{\alpha }^4+{\beta }^4\right){\lambda }_z{\kappa }_s$, which implies increasing the x-compliance and the flexural compliance of the structure. While increasing the x-compliance of the structure would reduce the magnitudes of both the complimentary and particular solutions, this does not imply that it will always lead to reduced magnitude of the τ_max of the unbalanced structure. This is because ε_T, ε_Nl, ε_Ml, ${\widehat{Q}}_{21l}$, ${\widehat{M}}_{21l}$ and µ_σ could be either positive or negative and hence the particular solution may not act in the same direction as the complementary solution. Nevertheless, increasing the x-compliance of the structure is more likely than not to reduce the τ_max of an unbalanced structure. In the same breath, it should be noted that the magnitude of τ_max in an unbalanced structure may not always be larger than that in a balanced structure assuming both structures have identical characteristic parameters.

The mean of the transverse stress in the adhesive, σ_m, for an unbalanced structure is given by Equation (15). For the reason of simplicity, we shall ignore those terms associated with the decay function. The maximum magnitude of σ_m occurs at x = l and is given by

$$\begin{array}{ll}{\sigma }_{m,\max }& \approx B_1+B_p=B_{1c}+\left(\frac{{\beta }^3}{2{\alpha }^3}-\frac{{\beta }^2}{2{\alpha }^2}+1\right)B_p\\ & =\frac{1}{\sqrt{\overline{D}{\lambda }_z}}\left[\frac{{\widehat{Q}}_{21l}}{\alpha }+{\widehat{M}}_{21l}+\frac{{\mu }_{\tau }\left({\beta }^4/\alpha -{\beta }^3+2{\alpha }^2\beta \right)}{4{\alpha }^4+{\beta }^4}\frac{{\epsilon }_T+{\epsilon }_{Nl}+{\epsilon }_{Ml}}{\beta {\kappa }_s}\right]\end{array}$$

(28)

Noting that ${\widehat{Q}}_{21l}=Q_{2l}/D_2-Q_{1l}/D_1$ and ${\widehat{M}}_{21l}=M_{2l}/D_2-M_{1l}/D_1$, for the same magnitudes of Q_il and M_il, the magnitude of B₁ may be reduced by increasing the z-compliance while reducing the flexural compliance of the structures. Equation (28) suggests that the magnitude of the particular solution may be reduced by increasing the magnitudes of the characteristic parameter, α, which implies increasing the flexural compliance of the structure while reducing the z-compliance of the structure. This is in reverse to the trend for B_p.

The amplitude of the transverse stress in the adhesive, σ_a, for an unbalanced structure is given by Equation (16). Assuming A_s » A₄, the maximum magnitude of σ_a is given by:

$${\sigma }_{a,\max }\approx \frac{n\beta h_3\left(A_s+A_{p1}\right)}{2}\approx \frac{n\beta h_3}{2}{\tau }_{\max }\approx \frac{0.72}{{\phi }^{1.4}{\left(\beta h_3\right)}^{0.4}}{\tau }_{\max }$$

(29)

which again suggests that the magnitude of σ_a,max is likely to be reduced by increasing the x-compliance of the structure.

It has been argued in the previous section that the magnitude of σ_a,max is almost always larger than that of τ_max for balanced structures. Comparing Equations (23) and (29), it is reasonably safe to suggest that this will also be the case for unbalanced structures. It has been established in the previous section that the ratio of σ_a,max to σ_m,max for balanced SLJ is larger than unity. If the ratio for the particular solutions is also larger than unity then one can safely assume that the ratio of σ_a,max to σ_m,max for unbalanced SLJ is also larger than unity. The ratio for the particular solutions is given by

$$\frac{{\sigma }_{a,\max }}{{\sigma }_{m,\max }}\approx \frac{n\beta h_3}{2}\frac{{\mu }_{\sigma }\left(-2{\alpha }^2/\beta +2\alpha -\beta \right){\kappa }_{2l}}{{\mu }_{\tau }\left({\beta }^3/\alpha -{\beta }^2+2{\alpha }^2\right)\frac{{\epsilon }_{Nl}+{\epsilon }_{Ml}}{\sqrt{{\lambda }_x{\kappa }_s}}}$$

(30)

which is not necessary larger than unity. Thus, σ_a,max is only conditionally larger than σ_m,max for unbalanced SLJ.

Given the loadings and the design space, the optimum designs of unbalanced structure that gives rise to a minimum τ_max, a minimum σ_m,max, and a minimum σ_a,max, respectively, can be readily established using Equations (27)–(29).

5. Conclusions

Strength-of-material solutions for the shear stress, τ, the mean, σ_m, and amplitude, σ_a, of the peeling stress in both balanced and unbalanced structures have been derived and used for design analysis. Design guidelines for balanced structures have been established. The magnitude of σ_a,max for balanced structures is almost always larger than that of τ_max and the magnitude of σ_a,max for balanced single-lap-joints is also almost always larger than σ_m,max. The magnitude of σ_a,max for balanced structures may be reduced most effectively by reducing the elastic modulus of the adherends or by increasing the thickness ratio of adhesive-to-adherend and less effectively by reducing the elastic modulus of the adhesive. The simple expressions of τ_max, σ_m,max and σ_a,max established in this manuscript for the unbalanced structures will help practicing engineers find the optimum design within the given design space.