Entropic Interactions between Two Knots on a Semiflexible Polymer
Abstract
:1. Introduction
2. Model and Methods
2.1. Potentials and Mapping onto DNA
2.2. Constrained vs. Free Chains
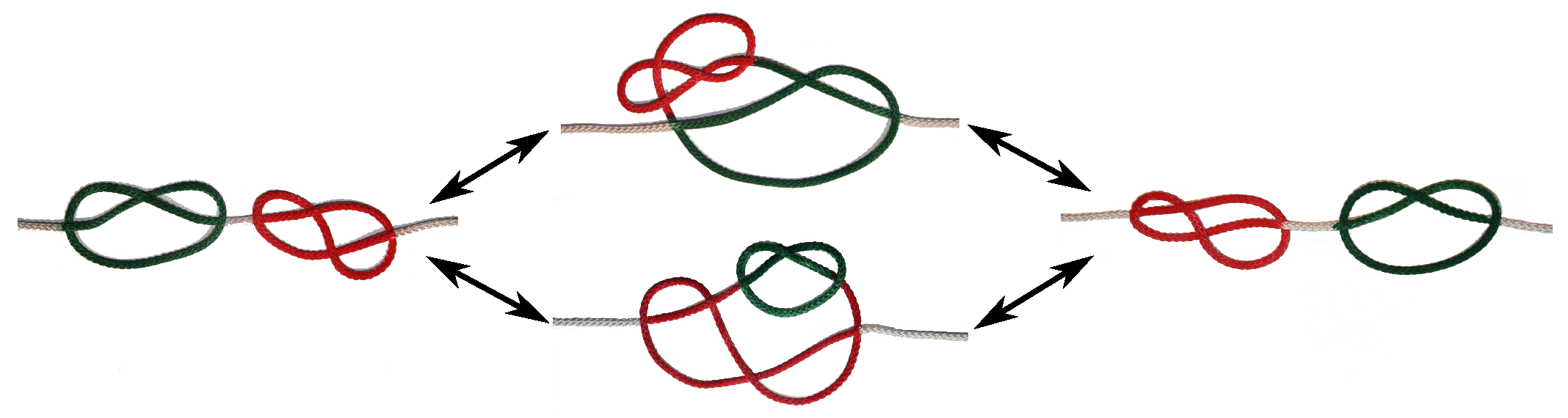
2.3. Knot Analysis
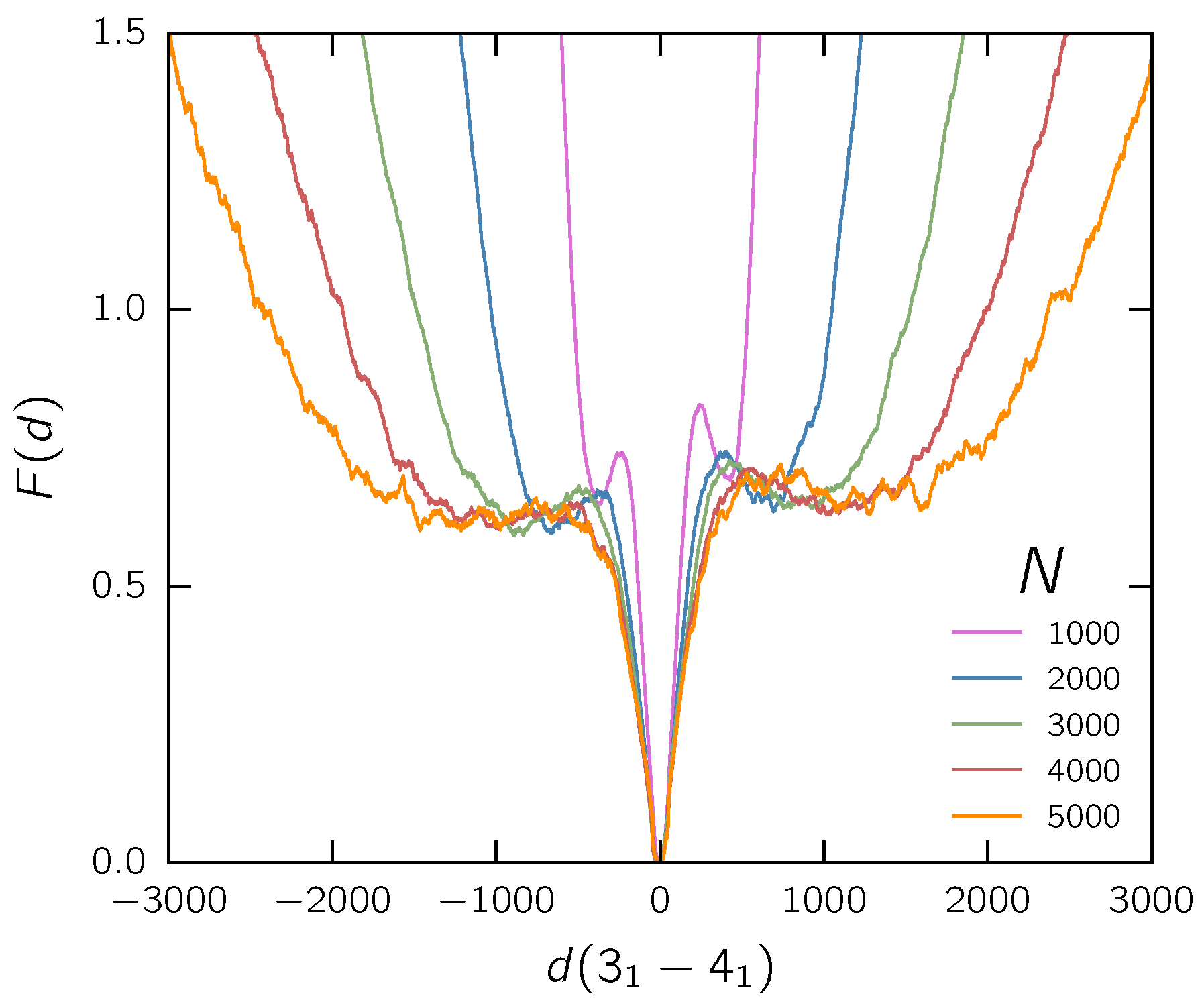
3. Results
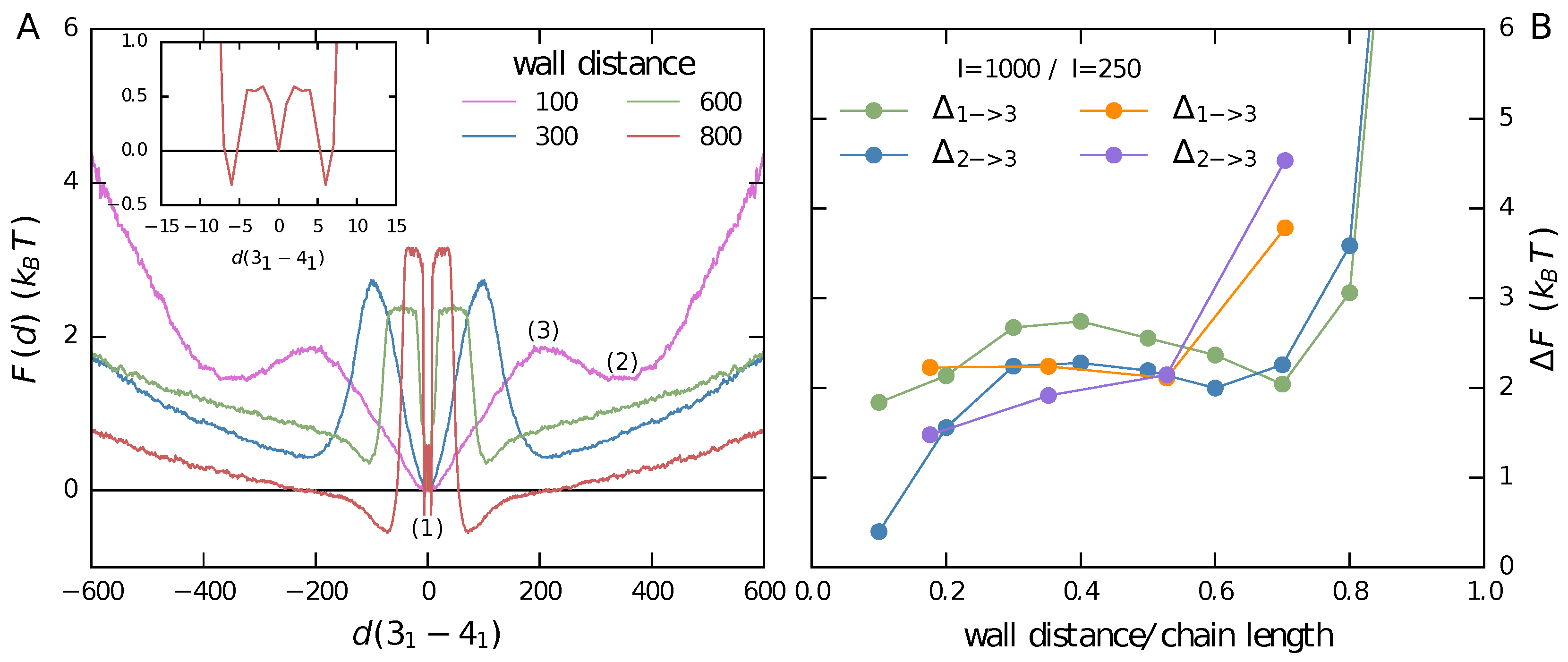
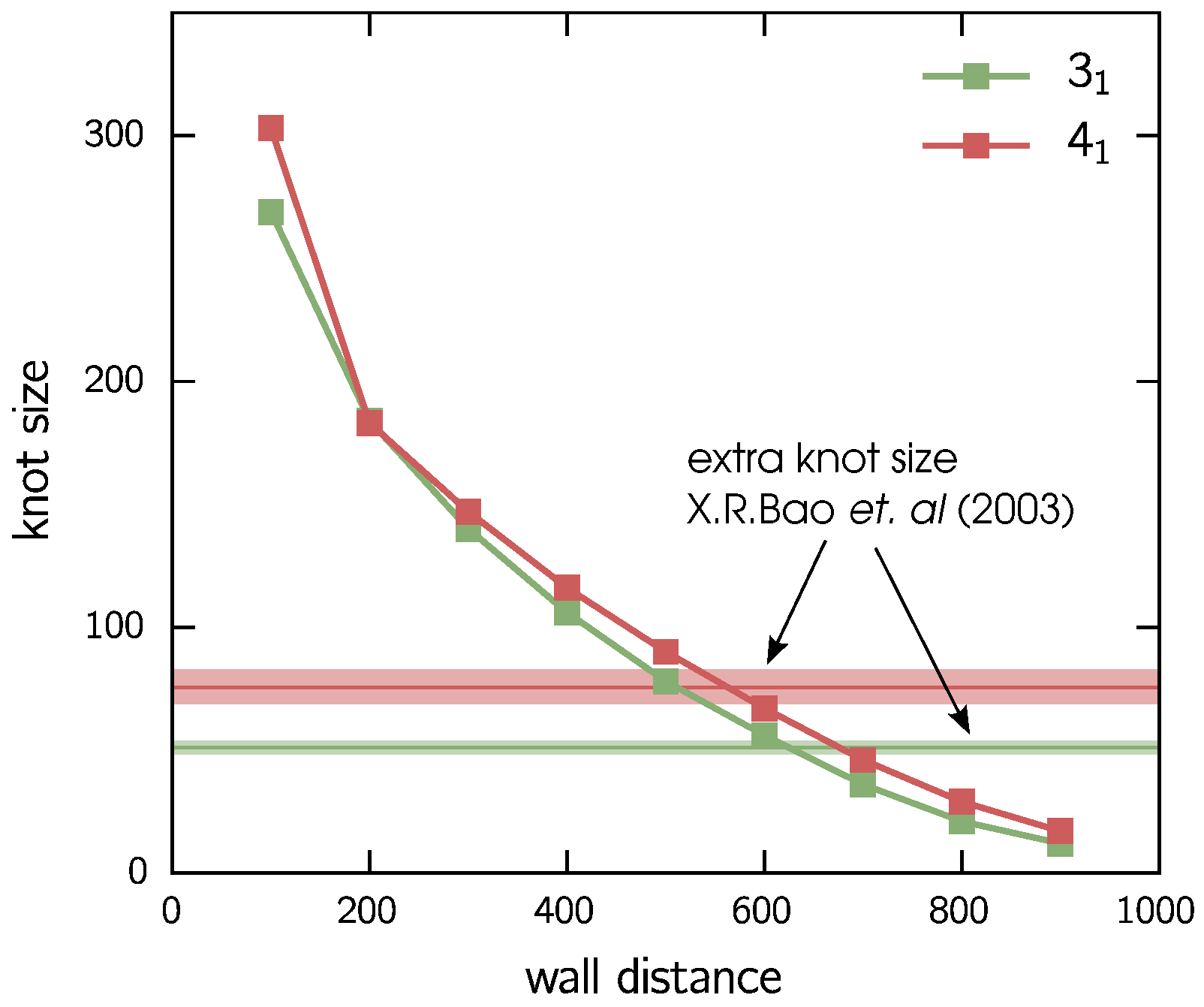
3.1. Two Knots Constrained between Walls
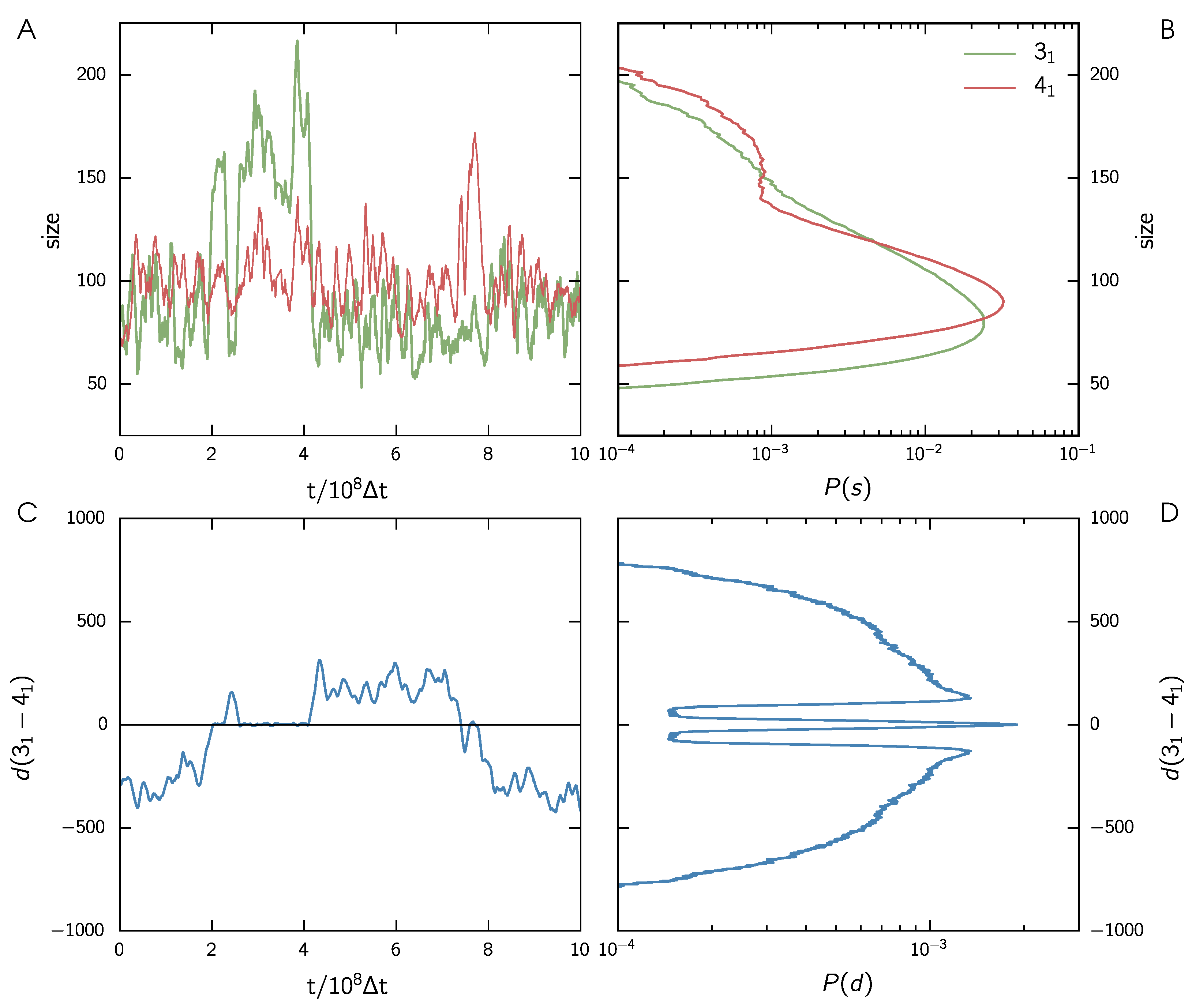
3.2. Two Knots on a Free Chain
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Epple, M. Die Entstehung der Knotentheorie: Kontexte und Konstruktionen Einer Modernen Mathematischen Theorie; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Thomson, W., II. On vortex atoms. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1867, 34, 15–24. [Google Scholar] [CrossRef]
- Taite, P.G. On knots I,II,III. Sci. Pap. 1900, 1, 237–347. [Google Scholar]
- Frisch, H.L.; Wasserman, E. Chemical topology. J. Am. Chem. Soc. 1961, 83, 3789–3795. [Google Scholar] [CrossRef]
- Delbrück, M. Knotting problems in biology. Proc. Symp. Appl. Math. 1962, 14, 55–63. [Google Scholar]
- MacGregor, H.; Vlad, M. Interlocking and knotting of ring nucleoli in amphibian oocytes. Chromosoma 1972, 39, 205–214. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.F.; Depew, R.E.; Wang, J.C. Knotted single-stranded DNA rings: A novel topological isomer of circular single-stranded DNA formed by treatment with Escherichia coli ω protein. J. Mol. Biol. 1976, 106, 439–452. [Google Scholar] [CrossRef]
- Dean, F.; Stasiak, A.; Koller, T.; Cozzarelli, N. Duplex DNA knots produced by escherichia-coli topoisomerase-I—Structure and requirements for formation. J. Biol. Chem. 1985, 260, 4975–4983. [Google Scholar] [PubMed]
- Shaw, S.Y.; Wang, J.C. Knotting of a DNA chain during ring-closure. Science 1993, 260, 533–536. [Google Scholar] [CrossRef] [PubMed]
- Rybenkov, V.V.; Cozzarelli, N.R.; Vologodskii, A.V. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl. Acad. Sci. USA 1993, 90, 5307–5311. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; Trigueros, S.; Sumners, D.W.; Roca, J. Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc. Natl. Acad. Sci. USA 2002, 99, 5373–5377. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Sumners, D.W.; Roca, J. DNA knots reveal a chiral organization of DNA in phage capsids. Proc. Natl. Acad. Sci. USA 2005, 102, 9165–9169. [Google Scholar] [CrossRef] [PubMed]
- Plesa, C.; Verschueren, D.; Pud, S.; van der Torre, J.; Ruitenberg, J.W.; Witteveen, M.J.; Jonsson, M.P.; Grosberg, A.Y.; Rabin, Y.; Dekker, C. Direct observation of DNA knots using a solid-state nanopore. Nat. Nanotechnol. 2016, 11, 1093–1097. [Google Scholar] [CrossRef] [PubMed]
- Dietrich-Buchecker, C.O.; Sauvage, J.P. A synthetic molecular trefoil knot. Angew. Chem. Int. Ed. Engl. 1989, 28, 189–192. [Google Scholar] [CrossRef]
- Forgan, R.S.; Sauvage, J.P.; Stoddart, J.F. Chemical topology: Complex molecular knots, links, and entanglements. Chem. Rev. 2011, 111, 5434–5464. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, M.L. Are There Knots in Proteins. Nat. Struct. Biol. 1994, 1, 213–214. [Google Scholar] [CrossRef] [PubMed]
- Takusagawa, F.; Kamitori, S. A real knot in protein. J. Am. Chem. Soc. 1996, 118, 8945–8946. [Google Scholar]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef] [PubMed]
- Virnau, P.; Mirny, L.A.; Kardar, M. Intricate knots in proteins: Function and evolution. PLoS Comput. Biol. 2006, 2, 1074–1079. [Google Scholar] [CrossRef] [PubMed]
- Kolesov, G.; Virnau, P.; Kardar, M.; Mirny, L.A. Protein knot server: Detection of knots in protein structures. Nucleic Acids Res. 2007, 35, W425–W428. [Google Scholar] [CrossRef] [PubMed]
- Jamroz, M.; Niemyska, W.; Rawdon, E.J.; Stasiak, A.; Millett, K.C.; Sułkowski, P.; Sulkowska, J.I. KnotProt: A database of proteins with knots and slipknots. Nucleic Acids Res. 2015. [Google Scholar] [CrossRef] [PubMed]
- King, N.P.; Jacobitz, A.W.; Sawaya, M.R.; Goldschmidt, L.; Yeates, T.O. Structure and folding of a designed knotted protein. Proc. Natl. Acad. Sci. USA 2010, 107, 20732–20737. [Google Scholar] [CrossRef] [PubMed]
- Bölinger, D.; Sulkowska, J.I.; Hsu, H.P.; Mirny, L.A.; Kardar, M.; Onuchic, J.N.; Virnau, P. A Stevedore’s Protein Knot. PLoS Comput. Biol. 2010, 6, e1000731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Virnau, P.; Mallam, A.; Jackson, S. Structures and folding pathways of topologically knotted proteins. J. Phys. Condens. Matter 2011, 23, 033101. [Google Scholar] [CrossRef] [PubMed]
- Vologodskii, A.; Lukashin, A.; Frankkam, M.; Anshelev, V. Knot problem in statistical-mechanics of polymer-chains. Zhurnal Eksperimentalnoi I Teoreticheskoi Fiziki 1974, 66, 2153–2163. [Google Scholar]
- Frank-Kamenetskii, M.D.; Lukashin, A.V.; Vologodskii, A.V. Statistical mechanics and topology of polymer chains. Nature 1975, 258, 398–402. [Google Scholar] [CrossRef] [PubMed]
- Koniaris, K.; Muthukumar, M. Knottedness in ring polymers. Phys. Rev. Lett. 1991, 66, 2211–2214. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, M.L. Knots in Hamilton cycles. Macromolecules 1994, 27, 5924–5926. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Critical exponents for random knots. Phys. Rev. Lett. 2000, 85, 3858. [Google Scholar] [CrossRef] [PubMed]
- Virnau, P.; Kantor, Y.; Kardar, M. Knots in globule and coil phases of a model polyethylene. J. Am. Chem. Soc. 2005, 127, 15102–15106. [Google Scholar] [CrossRef] [PubMed]
- Marenduzzo, D.; Orlandini, E.; Stasiak, A.; Sumners, D.; Tubiana, L.; Micheletti, C. DNA-DNA interactions in bacteriophage capsids are responsible for the observed DNA knotting. Proc. Natl. Acad. Sci. USA 2009, 106, 22269–22274. [Google Scholar] [CrossRef] [PubMed]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E. Polymers with spatial or topological constraints: Theoretical and computational results. Phys. Rep. 2011, 504, 1–73. [Google Scholar] [CrossRef]
- Reith, D.; Cifra, P.; Stasiak, A.; Virnau, P. Effective stiffening of DNA due to nematic ordering causes DNA molecules packed in phage capsids to preferentially form torus knots. Nucleic Acids Res. 2012, 40, 5129–5137. [Google Scholar] [CrossRef] [PubMed]
- Wüst, T.; Reith, D.; Virnau, P. Sequence determines degree of knottedness in a coarse-grained protein model. Phys. Rev. Lett. 2015, 114, 028102. [Google Scholar] [CrossRef] [PubMed]
- Rieger, F.C.; Virnau, P. A Monte Carlo study of knots in long double-stranded DNA chains. PLoS Comput. Biol. 2016, 12, e1005029. [Google Scholar] [CrossRef] [PubMed]
- Marenz, M.; Janke, W. Knots as a topological order parameter for semiflexible polymers. Phys. Rev. Lett. 2016, 116, 128301. [Google Scholar] [CrossRef] [PubMed]
- Suma, A.; Rosa, A.; Micheletti, C. Pore translocation of knotted polymer chains: how friction depends on knot complexity. ACS Macro Lett. 2015, 4, 1420–1424. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Stella, A.L. The entropic cost to tie a knot. J. Stat. Mech. Theory Exp. 2010, 2010, P06012. [Google Scholar] [CrossRef]
- Tubiana, L.; Rosa, A.; Fragiacomo, F.; Micheletti, C. Spontaneous knotting and unknotting of flexible linear polymers: Equilibrium and kinetic aspects. Macromolecules 2013, 46, 3669–3678. [Google Scholar] [CrossRef]
- Tubiana, L. Computational study on the progressive factorization of composite polymer knots into separated prime components. Phys. Rev. E 2014, 89, 052602. [Google Scholar] [CrossRef] [PubMed]
- Tsurusaki, K.; Deguchi, T. Fractions of particular knots in gaussian random polygons. J. Phys. Soc. Jpn. 1995, 64, 1506–1518. [Google Scholar] [CrossRef]
- Trefz, B.; Siebert, J.; Virnau, P. How molecular knots can pass through each other. Proc. Natl. Acad. Sci. USA 2014, 111, 7948–7951. [Google Scholar] [CrossRef] [PubMed]
- Najafi, S.; Podgornik, R.; Potestio, R.; Tubiana, L. Role of bending energy and knot chirality in knot distribution and their effective interaction along stretched semiflexible polymers. Polymers 2016, 8, 347. [Google Scholar] [CrossRef]
- Najafi, S.; Tubiana, L.; Podgornik, R.; Potestio, R. Chirality modifies the interaction between knots. Europhys. Lett. 2016, 114, 50007. [Google Scholar] [CrossRef]
- Rosa, A.; Di Ventra, M.; Micheletti, C. Topological jamming of spontaneously knotted polyelectrolyte chains driven through a nanopore. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Anderson, J.A.; Lorenz, C.D.; Travesset, A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 2008, 227, 5342–5359. [Google Scholar] [CrossRef]
- Glaser, J.; Nguyen, T.D.; Anderson, J.A.; Lui, P.; Spiga, F.; Millan, J.A.; Morse, D.C.; Glotzer, S.C. Strong scaling of general-purpose molecular dynamics simulations on GPUs. Comput. Phys. Commun. 2015, 192, 97–107. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, H.S. Efficient chain moves for Monte Carlo simulations of a wormlike DNA model: Excluded volume, supercoils, site juxtapositions, knots, and comparisons with random-flight and lattice models. J. Chem. Phys. 2008, 128, 145104. [Google Scholar] [CrossRef] [PubMed]
- Freyd, P.; Yetter, D.; Hoste, J.; Lickorish, W.R.; Millett, K.; Ocneanu, A. A new polynomial invariant of knots and links. Bull. Am. Math. Soc. 1985, 12, 239–246. [Google Scholar] [CrossRef]
- Jenkins, R.J. Knot Theory, Simple Weaves, and an Algorithm for Computing the HOMFLY Polynomial. Master’s Thesis, Carnegie Mellon University (CMU), Pittsburgh, PA, USA, 1989. [Google Scholar]
- Virnau, P. Detection and visualization of physical knots in macromolecules. Phys. Procedia 2010, 6, 117–125. [Google Scholar] [CrossRef]
- Bao, X.R.; Lee, H.J.; Quake, S.R. Behavior of complex knots in single DNA molecules. Phys. Rev. Lett. 2003, 91, 265506. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richard, D.; Stalter, S.; Siebert, J.T.; Rieger, F.; Trefz, B.; Virnau, P. Entropic Interactions between Two Knots on a Semiflexible Polymer. Polymers 2017, 9, 55. https://doi.org/10.3390/polym9020055
Richard D, Stalter S, Siebert JT, Rieger F, Trefz B, Virnau P. Entropic Interactions between Two Knots on a Semiflexible Polymer. Polymers. 2017; 9(2):55. https://doi.org/10.3390/polym9020055
Chicago/Turabian StyleRichard, David, Stefanie Stalter, Jonathan Tammo Siebert, Florian Rieger, Benjamin Trefz, and Peter Virnau. 2017. "Entropic Interactions between Two Knots on a Semiflexible Polymer" Polymers 9, no. 2: 55. https://doi.org/10.3390/polym9020055




