Theoretical Methods for Studying DNA Structural Transitions under Applied Mechanical Constraints
Abstract
:1. Introduction
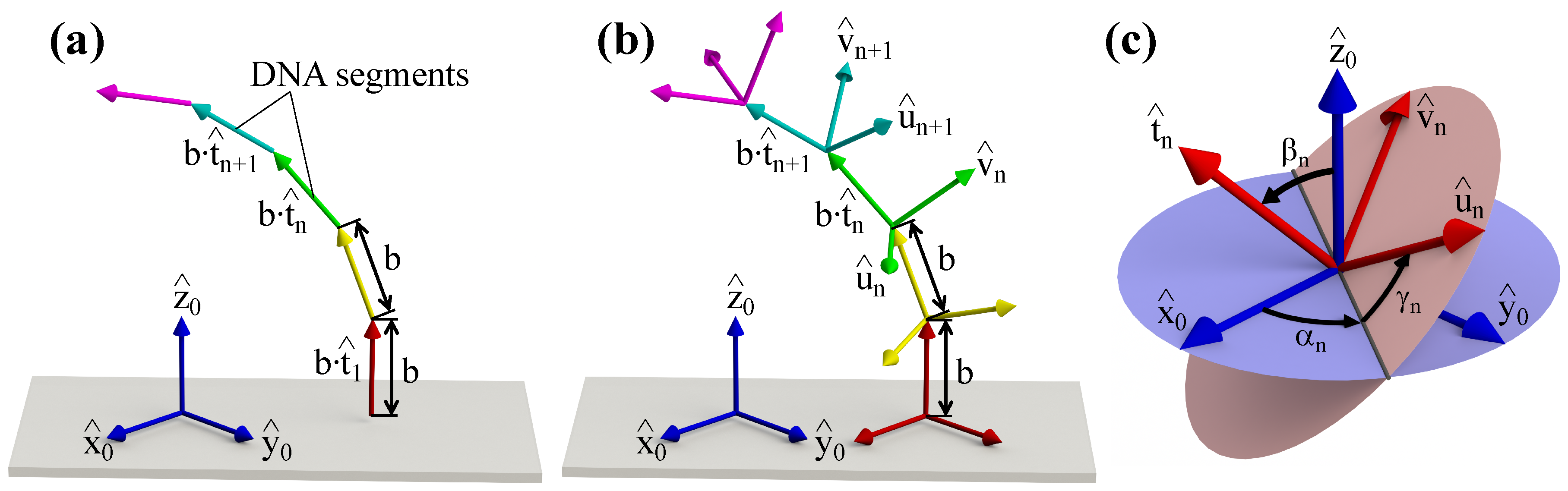
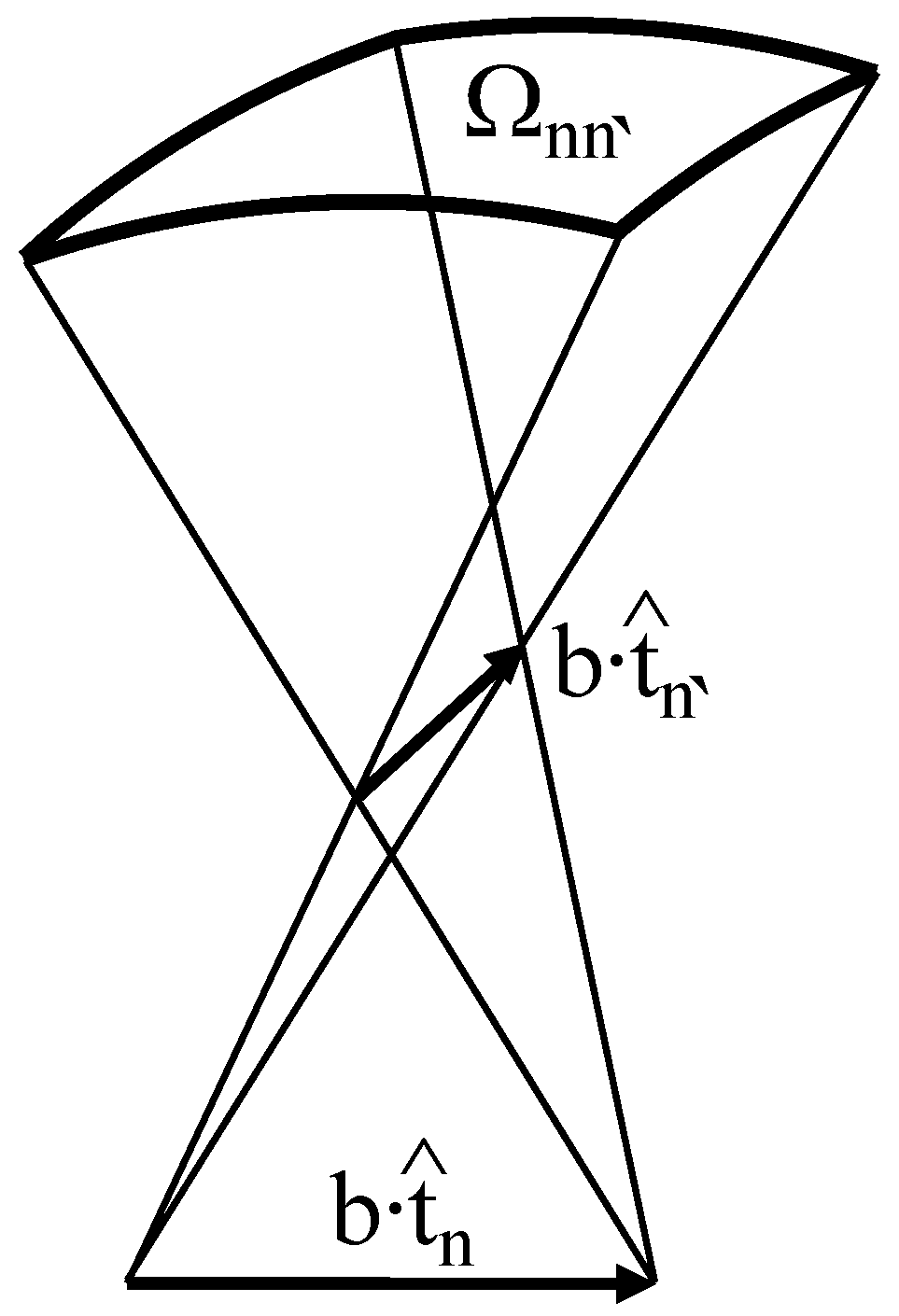
2. Conformational Energy of DNA
3. Mechanically-Stretched Homogeneous DNA
4. Homogeneous DNA Subjected to Both Force and Torque Constraints
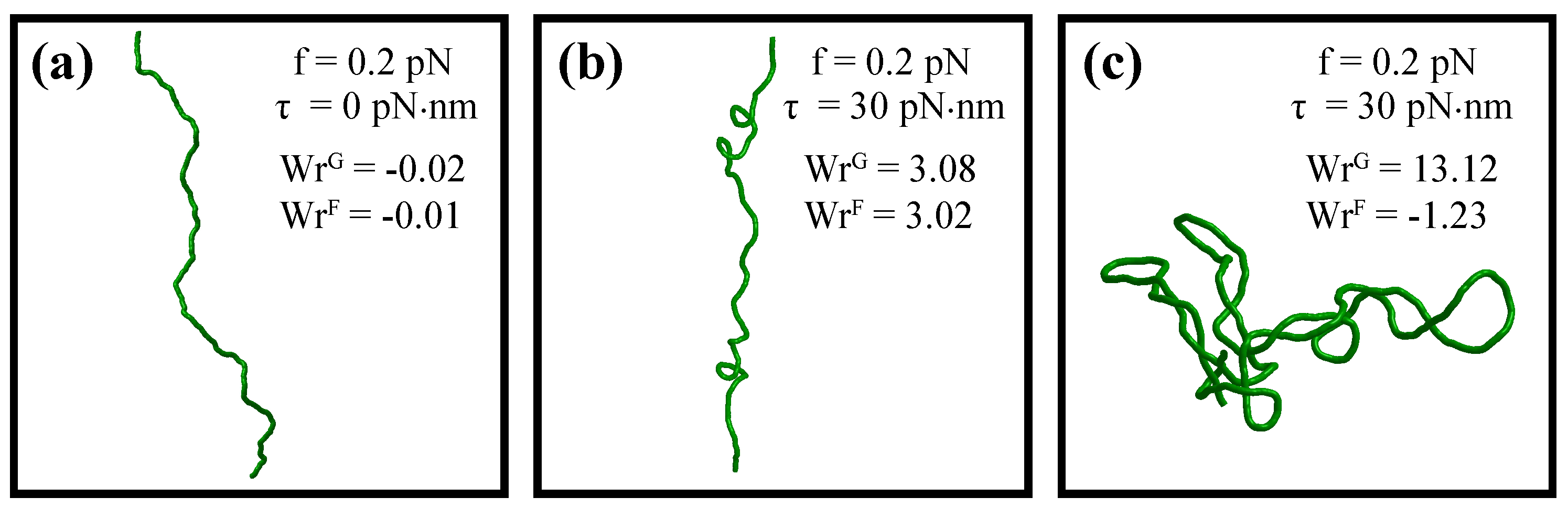
5. Metropolis-Monte Carlo Simulations
6. Transfer-Matrix Formalism
6.1. Transfer-Matrix Calculations of the DNA Partition Function
6.2. Description of the DNA Structural Transitions Using the Transfer-Matrix Formalism
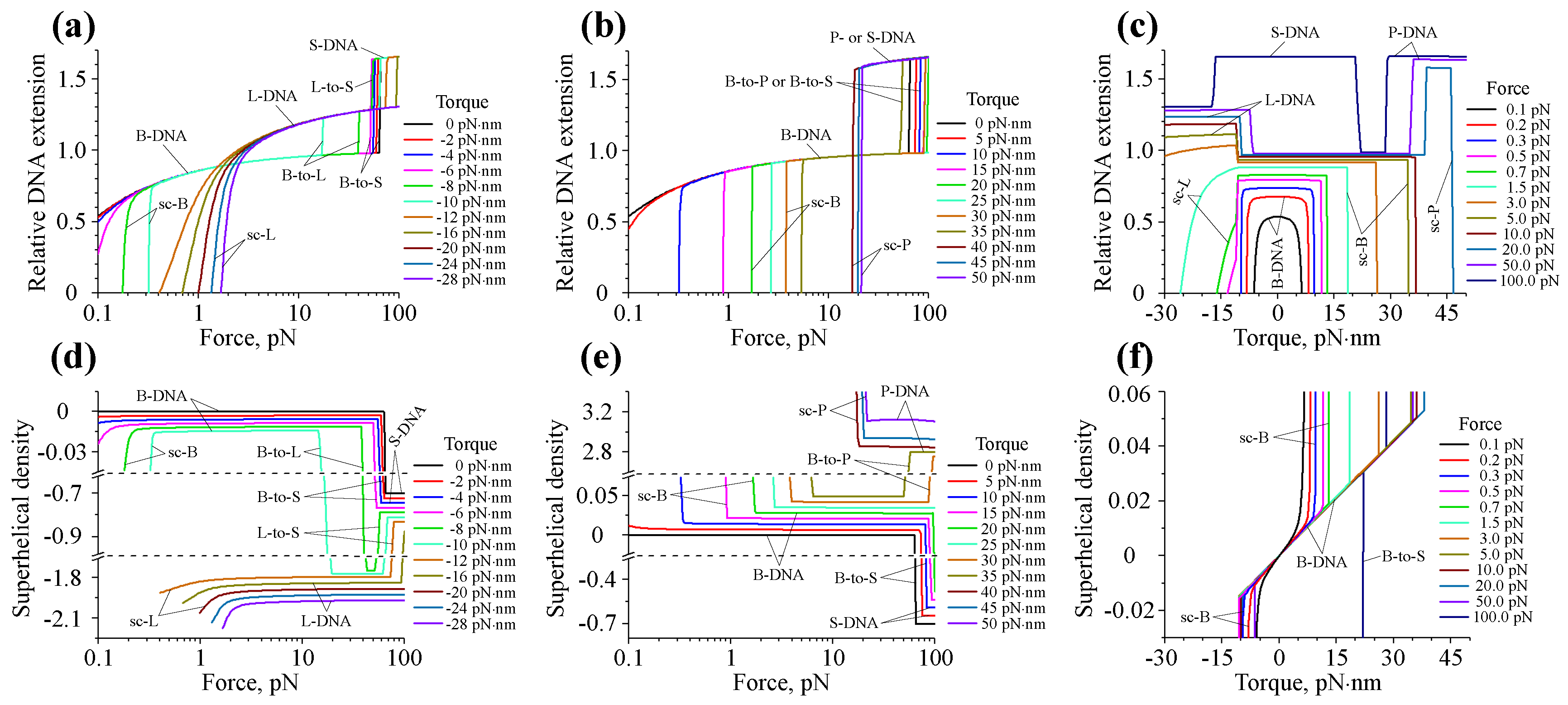
7. Force- and Torque-Dependent DNA Structural Transitions
8. Other Potential Applications of the Transfer-Matrix Formalism
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DNA | deoxyribonucleic acid |
| bp | base-pair |
| FJC model | freely-jointed chain model |
| WLC model | worm-like chain model |
| sc-B, sc-L and sc-P | supercoiled B-, L- and P-DNA, respectively |
| B-to-L, B-to-P, B-to-S and L-to-S | structural transitions between the corresponding DNA states (B, L, P and S) |
References
- Franklin, R.E.; Gosling, R.G. Molecular configuration in sodium thymonucleate. Nature 1953, 171, 740–741. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.C. Helical repeat of DNA in solution. Proc. Natl. Acad. Sci. USA 1979, 76, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Rich, A.; Nordheim, A.; Wang, A.H.-J. The chemistry and biology of left-handed Z-DNA. Ann. Rev. Biochem. 1984, 53, 791–846. [Google Scholar] [CrossRef] [PubMed]
- Bryant, Z.; Stone, M.D.; Gore, J.; Smith, S.B.; Cozzarelli, N.R.; Bustamante, C. Structural transitions and elasticity from torque measurements on DNA. Nature 2003, 424, 338–341. [Google Scholar] [CrossRef] [PubMed]
- Sheinin, M.Y.; Forth, S.; Marko, J.F.; Wang, M.D. Underwound DNA under tension: Structure, elasticity, and sequence-dependent behaviors. Phys. Rev. Lett. 2011, 107, 108102. [Google Scholar] [CrossRef] [PubMed]
- Oberstrass, F.C.; Fernandes, L.E.; Bryant, Z. Torque measurements reveal sequence-specific cooperative transitions in supercoiled DNA. Proc. Natl. Acad. Sci. USA 2012, 109, 6106–6111. [Google Scholar] [CrossRef] [PubMed]
- Cluzel, P.; Lebrun, A.; Heller, C.; Lavery, R.; Viovy, J.L.; Chatenay, D.; François, C. DNA: An extensible molecule. Science 1996, 271, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science 1996, 271, 795–798. [Google Scholar] [CrossRef] [PubMed]
- Léger, J.F.; Romano, G.; Sarkar, A.; Robert, J.; Bourdieu, L.; Chatenay, D.; Marko, J.F. Structural transitions of a twisted and stretched DNA molecule. Phys. Rev. Lett. 1999, 83, 1066–1069. [Google Scholar] [CrossRef]
- Allemand, J.F.; Bensimon, D.; Lavery, R.; Croquette, V. Stretched and overwound DNA forms a Pauling-like structure with exposed bases. Proc. Natl. Acad. Sci. USA 1998, 95, 14152–14157. [Google Scholar] [CrossRef] [PubMed]
- Sheinin, M.Y.; Wang, M.D. Twist-stretch coupling and phase transition during DNA supercoiling. Phys. Chem. Chem. Phys. 2009, 11, 4800–4803. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Neukirch, S. Global force-torque phase diagram for the DNA double helix: Structural transitions, triple points and collapsed plectonemes. Phys. Rev. E 2013, 88, 062722. [Google Scholar] [CrossRef] [PubMed]
- Kłysik, J.; Stirdivant, S.M.; Larson, J.E.; Hart, P.A.; Wells, R.D. Left-handed DNA in restriction fragments and a recombinant plasmid. Nature 1981, 290, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Nordheim, A.; Lafer, E.M.; Peck, L.J.; Wang, J.C.; Stellar, D.; Rich, A. Negatively supercoiled plasmids contain left-handed Z-DNA segments as detected by specific antibody binding. Cell 1982, 31, 309–318. [Google Scholar] [CrossRef]
- Peck, L.J.; Wang, J.C. Energetics of B-to-Z transition in DNA. Proc. Natl. Acad. Sci. USA 1983, 80, 6206–6210. [Google Scholar] [CrossRef] [PubMed]
- Strick, T.R.; Croquette, V.; Bensimon, D. Homologous pairing in stretched supercoiled DNA. Proc. Natl. Acad. Sci. USA 1998, 95, 10579–10583. [Google Scholar] [CrossRef] [PubMed]
- Yakovchuk, P.; Protozanova, E.; Frank-Kamenetskii, M.D. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res. 2006, 34, 564–574. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Chen, H.; Marko, J.F.; Yan, J. Two distinct overstretched DNA states. Nucleic Acids Res. 2006, 38, 5594–5600. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Qu, Y.; Chen, H.; Rouzina, I.; Zhang, S.; Doyle, P.S.; Yan, J. Interconversion between three overstretched DNA structures. J. Am. Chem. Soc. 2014, 136, 16073–16080. [Google Scholar] [CrossRef] [PubMed]
- Franklin, R.E.; Gosling, R.G. The structure of sodium thymonucleate fibres. I. The influence of water content. Acta Cryst. 1953, 6, 673–677. [Google Scholar] [CrossRef]
- Strick, T.R.; Allemand, J.-F.; Bensimon, D.; Bensimon, A.; Croquette, V. The elasticity of a single supercoiled DNA molecule. Science 1996, 271, 1835–1837. [Google Scholar] [CrossRef] [PubMed]
- Deufel, C.; Forth, S.; Simmons, C.R.; Dejgosha, S.; Wang, M.D. Nanofabricated quartz cylinders for angular trapping: DNA supercoiling torque detection. Nat. Methods 2007, 4, 223–225. [Google Scholar] [CrossRef] [PubMed]
- Forth, S.; Deufel, C.; Sheinin, M.Y.; Daniels, B.; Sethna, J.P.; Wang, M.D. Abrupt buckling transition observed during the plectoneme formation of individual DNA molecules. Phys. Rev. Lett. 2008, 100, 148301. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Chen, H.; Zhang, X.; Qu, Y.; Marko, J.F.; Yan, J. Transition dynamics and selection of the distinct S-DNA and strand unpeeling modes of double helix overstretching. Nucleic Acids Res. 2011, 39, 3473–3481. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, H.; Fu, H.; Doyle, P.S.; Yan, J. Two distinct overstretched DNA structures revealed by single-molecule thermodynamics measurements. Proc. Natl. Acad. Sci. USA 2012, 109, 8103–8108. [Google Scholar] [CrossRef] [PubMed]
- King, G.A.; Gross, P.; Bockelmann, U.; Modesti, M.; Wuite, G.J.L.; Peterman, E.J.G. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching using fluorescence microscopy. Proc. Natl. Acad. Sci. USA 2013, 110, 3859–3864. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, H.; Le, S.; Rouzina, I.; Doyle, P.S.; Yan, J. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching by single-molecule calorimetry. Proc. Natl. Acad. Sci. USA 2013, 110, 3865–3870. [Google Scholar] [CrossRef] [PubMed]
- Mosconi, F.; Allemand, J.F.; Bensimon, D.; Croquette, V. Measurement of the torque on a single stretched and twisted DNA using magnetic tweezers. Phys. Rev. Lett. 2009, 102, 078301. [Google Scholar] [CrossRef] [PubMed]
- Vologodskii, A.V.; Cozzarelli, N.R. Conformational and thermodynamic properties of supercoiled DNA. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 609–643. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F. Biophysics of protein-DNA interactions and chromosome organization. Physica A 2015, 418, 126–153. [Google Scholar] [CrossRef] [PubMed]
- Luger, K.; Mäder, A.W.; Richmond, R.K.; Sargent, D.F.; Richmond, T.J. Crystal structure of the nucleosome core particle at 2.8Å resolution. Nature 1997, 389, 251–260. [Google Scholar] [PubMed]
- Skoko, D.; Wong, B.; Johnson, R.C.; Marko, J.F. Micromechanical analysis of the binding of DNA-bending proteins HMGB1, NHP6A, and HU reveals their ability to form highly stable DNA-protein complexes. Biochemistry 2004, 43, 13867–13874. [Google Scholar] [CrossRef] [PubMed]
- Van Noort, J.; Verbrugge, S.; Goosen, N.; Dekker, C.; Dame, R.T. Dual architectural roles of HU: Formation of flexible hinges and rigid filaments. Proc. Natl. Acad. Sci. USA 2004, 101, 6969–6974. [Google Scholar] [CrossRef] [PubMed]
- Swinger, K.K.; Rice, P.A. IHF and HU: Flexible architects of bent DNA. Curr. Opin. Struct. Biol. 2004, 14, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, H.; Kenney, L.J.; Yan, J. A divalent switch drives H-NS/DNA-binding conformations between stiffening and bridging modes. Genes Dev. 2010, 24, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Chen, H.; Dröge, P.; Yan, J. Physical organization of DNA by multiple non-specific DNA-binding modes of integration host factor (IHF). PLoS ONE 2012, 7, e49885. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.J.; Whang, Y.R.; Kenney, L.J.; Yan, J. Gene silencing H-NS paralogue StpA forms a rigid protein filament along DNA that blocks DNA accessibility. Nucleic Acids Res. 2012, 40, 3316–3328. [Google Scholar] [CrossRef] [PubMed]
- Winardhi, R.S.; Fu, W.; Castang, S.; Li, Y.; Dove, S.L.; Yan, J. Higher order oligomerization is required for H-NS family member MvaT to form gene-silencing nucleoprotein filament. Nucleic Acids Res. 2012, 40, 8942–8952. [Google Scholar] [CrossRef] [PubMed]
- Le, S.; Chen, H.; Cong, P.; Lin, J.; Dröge, P.; Yan, J. Mechanosensing of DNA bending in a single specific protein-DNA complex. Sci. Rep. 2013, 3, 3508. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Lim, C.J.; Whang, Y.R.; Liu, J.; Yan, J. Mechanism of DNA organization by Mycobacterium tuberculosis protein Lsr2. Nucleic Acids Res. 2013, 41, 5263–5272. [Google Scholar] [CrossRef] [PubMed]
- Winardhi, R.S.; Gulvady, R.; Mellies, J.L.; Yan, J. Locus of enterocyte effacement-encoded regulator (Ler) of pathogenic Escherichia coli competes off histone-like nucleoid-structuring protein (H-NS) through noncooperative DNA binding. J. Biol. Chem. 2014, 289, 13739–13750. [Google Scholar] [CrossRef] [PubMed]
- Efremov, A.K.; Qu, Y.; Maruyama, H.; Lim, C.J.; Takeyasu, K.; Yan, J. Transcriptional repressor TrmBL2 from Thermococcus kodakarensis forms filamentous nucleoprotein structures and competes with histones for DNA binding in a salt- and DNA supercoiling-dependent manner. J. Biol. Chem. 2015, 290, 15770–15784. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.U.D.; Waege, I.; Hausner, W.; Thomm, M.; Boos, W.; Diederichs, K.; Welte, W. Structural insights into nonspecific binding of DNA by TrmBL2, an archaeal chromatin protein. J. Mol. Biol. 2015, 427, 3216–3229. [Google Scholar] [CrossRef] [PubMed]
- Shivashankar, G.V. Mechanosignaling to the cell nucleus and gene regulation. Annu. Rev. Biophys. 2011, 40, 361–378. [Google Scholar] [CrossRef] [PubMed]
- Iyer, K.V.; Pulford, S.; Mogilner, A.; Shivashankar, G.V. Mechanical activation of cells induces chromatin remodeling preceding MKL nuclear transport. Bipohys. J. 2012, 103, 1416–1428. [Google Scholar] [CrossRef] [PubMed]
- Mammoto, A.; Mammoto, T.; Ingber, D.E. Mechanosensitive mechanisms in transcriptional regulation. J. Cell Sci. 2012, 125, 3061–3073. [Google Scholar] [CrossRef] [PubMed]
- Tajik, A.; Zhang, Y.; Wei, F.; Sun, J.; Jia, Q.; Zhou, W.; Singh, R.; Khanna, N.; Belmont, A.S.; Wang, N. Transcription upregulation via force-induced direct stretching of chromatin. Nat. Mater. 2016, 15, 1287–1296. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Odijk, T. Stiff chains and filaments under tension. Macromolecules 1995, 28, 7016–7018. [Google Scholar] [CrossRef]
- Fain, B.; Rudnick, J.; Östlund, S. Conformations of linear DNA. Phys. Rev. E 1997, 55, 7364–7368. [Google Scholar] [CrossRef]
- Moroz, J.D.; Nelson, P. Entropic elasticity of twist-storing polymers. Macromolecules 1998, 31, 6333–6347. [Google Scholar] [CrossRef]
- Bouchiat, C.; Mézard, M. Elasticity model of a supercoiled DNA molecule. Phys. Rev. Lett. 1998, 80, 1556–1559. [Google Scholar] [CrossRef]
- Bouchiat, C.; Mézard, M. Elastic rod model of a supercoiled DNA molecule. Eur. Phys. J. E 2000, 2, 377–402. [Google Scholar] [CrossRef]
- Wang, M.D.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Stretching DNA with optical tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef]
- Gross, P.; Laurens, N.; Oddershede, L.B.; Bockelmann, U.; Peterman, E.J.G.; Wuite, G.J.L. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011, 7, 731–736. [Google Scholar] [CrossRef]
- Bustamante, C.; Marko, J.F.; Siggia, E.D.; Smith, S. Entropic elasticity of lambda-phage DNA. Science 1994, 265, 1599–1600. [Google Scholar] [CrossRef] [PubMed]
- Olson, W.K. Simulating DNA at low resolution. Curr. Opin. Struct. Biol. 1996, 6, 242–256. [Google Scholar] [CrossRef]
- Olson, W.K.; Gorin, A.A.; Lu, X.J.; Hock, L.M.; Zhurkin, V.B. DNA sequence-dependent deformability deduced from protein–DNA crystal complexes. Proc. Natl. Acad. Sci. USA 1998, 95, 11163–11168. [Google Scholar] [CrossRef] [PubMed]
- Lankaš, F.; Šponer, J.; Langowski, J.; Cheatham, T.E., III. DNA basepair step deformability inferred from molecular dynamics simulations. Biophys. J. 2003, 85, 2872–2883. [Google Scholar] [CrossRef]
- Lankaš, F.; Gonzalez, O.; Heffler, L.M.; Stoll, G.; Moakher, M.; Maddocks, J.H. On the parameterization of rigid base and basepair models of DNA from molecular dynamics simulations. Phys. Chem. Chem. Phys. 2009, 11, 10565–10588. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, O.; Petkevičiūtė, D.; Maddocks, J.H. A sequence-dependent rigid-base model of DNA. J. Chem. Phys. 2013, 138, 055102. [Google Scholar] [CrossRef] [PubMed]
- Călugăreanu, G. Sur les classes d’isotopie des noeuds tridimensionels et leurs invariants. Czechoslov. Math. J. 1961, 11, 588–625. [Google Scholar]
- White, J.H. Self-linking and the Gauss integral in higher dimensions. Am. J. Math. 1969, 91, 693–728. [Google Scholar] [CrossRef]
- Fuller, F.B. The writhing number of a space curve. Proc. Natl. Acad. Sci. USA 1971, 68, 815–819. [Google Scholar] [CrossRef] [PubMed]
- Crick, F.H.C. Linking numbers and nucleosomes. Proc. Natl. Acad. Sci. USA 1976, 73, 2639–2643. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Siggia, E.D. Statistical mechanics of supercoiled DNA. Phys. Rev. E 1995, 52, 2912–2938. [Google Scholar] [CrossRef]
- Fuller, F.B. Decomposition of the linking number of a closed ribbon: A problem from molecular biology. Proc. Natl. Acad. Sci. USA 1978, 75, 3557–3561. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Marko, J.F. Effects of DNA-distorting proteins on DNA elastic response. Phys. Rev. E 2003, 68, 011905. [Google Scholar] [CrossRef] [PubMed]
- Efremov, A.K.; Winardhi, R.S.; Yan, J. Transfer-matrix calculations of DNA polymer micromechanics under tension and torque constraints. Phys. Rev. E 2016, 94, 032404. [Google Scholar] [CrossRef] [PubMed]
- Levitt, M. Protein folding by restrained energy minimization and molecular dynamics. J. Mol. Biol. 1983, 170, 723–764. [Google Scholar] [CrossRef]
- Klenin, K.; Langowski, J. Computation of writhe in modeling of supercoiled DNA. Biopolymers 2000, 54, 307–317. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Vologodskii, A.V.; Marko, J.F. Extension of torsionally stressed DNA by external force. Biophys. J. 1997, 73, 123–132. [Google Scholar] [CrossRef]
- Vologodskii, A.V.; Levene, S.D.; Klenin, K.V.; Frank-Kamenetskii, M.; Cozzarelli, N.R. Conformational and thermodynamic properties of supercoiled DNA. J. Mol. Biol. 1992, 227, 1224–1243. [Google Scholar] [CrossRef]
- Marko, J.F. Torque and dynamics of linking number relaxation in stretched supercoiled DNA. Phys. Rev. E 2007, 76, 021926. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.M.T.; van der Heijden, G.H.M.; Neukirch, S. Supercoiling of DNA plasmids: Mechanics of the generalized ply. Proc. R. Soc. Lond. A 2002, 458, 959–985. [Google Scholar] [CrossRef]
- Sarkar, A.; Léger, J.-F.; Chatenay, D.; Marko, J.F. Structural transitions in DNA driven by external force and torque. Phys. Rev. E 2001, 63, 051903. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Marko, J.F. Localized single-stranded bubble mechanism for cyclization of short double helix DNA. Phys. Rev. Lett. 2004, 93, 108108. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Kawamura, R.; Marko, J.F. Statistics of loop formation along double helix DNAs. Phys. Rev. E 2005, 71, 061905. [Google Scholar] [CrossRef] [PubMed]
- Ranjith, P.; Kumar, P.B.S.; Menon, G.I. Distribution functions, loop formation probabilities, and force-extension relations in a model for short double-stranded DNA molecules. Phys. Rev. Lett. 2005, 94, 138102. [Google Scholar] [CrossRef] [PubMed]
- Gel’fand, I.M.; Minlos, R.A.; Shapiro, Z.Y. Representations of the Rotation and Lorentz Groups and Their Applications; Pergamon Press: New York, NY, USA, 1963. [Google Scholar]
- Storm, C.; Nelson, P.C. Theory of high-force DNA stretching and overstretching. Phys. Rev. E 2003, 67, 051906. [Google Scholar] [CrossRef] [PubMed]
- Neukirch, S. Extracting DNA twist rigidity from experimental supercoiling data. Phys. Rev. Lett. 2004, 93, 198107. [Google Scholar] [CrossRef] [PubMed]
- Purohit, P.K. Plectoneme formation in twisted fluctuating rods. J. Mech. Phys. Solids 2008, 56, 1715–1729. [Google Scholar] [CrossRef]
- Daniels, B.C.; Forth, S.; Sheinin, M.Y.; Wang, M.D.; Sethna, J.P. Discontinuities at the DNA supercoiling transition. Phys. Rev. E 2009, 80, 040901. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Neukirch, S. Competition between curls and plectonemes near the buckling transition of stretched supercoiled DNA. Phys. Rev. E 2012, 85, 011908. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Marko, J.F. Intrinsic and force-generated cooperativity in a theory of DNA-bending proteins. Phys. Rev. E 2010, 82, 051906. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Marko, J.F. Range of interaction between DNA-bending proteins is controlled by the second-longest correlation length for bending fluctuations. Phys. Rev. Lett. 2010, 109, 248301. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Le, S.; Muniyappa, K.; Yan, J. Dynamics and regulation of RecA polymerization and de-polymerization on double-stranded DNA. PLoS ONE 2013, 8, e66712. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.Y.; Lim, C.J.; Dröge, P.; Yan, J. Regulation of bacterial DNA packaging in early stationary phase by competitive DNA binding of Dps and IHF. Sci. Rep. 2013, 5, 18146. [Google Scholar] [CrossRef] [PubMed]
- Winardhi, R.S.; Yan, J.; Kenney, L.J. H-NS regulates gene expression and compacts the nucleoid: Insights from single-molecule experiments. Biophys. J. 2015, 109, 1321–1329. [Google Scholar] [CrossRef] [PubMed]

| DNA form, u | Bending persistence | Twisting persistence | Contour length relative | DNA helical | Base-pairing energy relative | |
|---|---|---|---|---|---|---|
| length, (nm) | length, (nm) | to B-DNA form | repeat, (bp) | to B-DNA form, () | ||
| B-DNA | 50 [54,56] | 95 [4,23,28] | 1 | 10.4 [2] | 0 | 4.3 [69] |
| L-DNA | 7 [5,12] | 15 [5,6,12] | 1.35 [5,12] | 16 [4,5,6] | 5.0 [69] | 4.3 [69] |
| P-DNA | 15 [12] | 25 [12] | 1.7 [9,10,12] | 3 [4,9,10,11,12] | 17.8 [69] | [69] |
| S-DNA | 15 [12,83] | 20 [12] | 1.7 [4,8,9] | 35 [4,9] | 5.1 (this study) | 4.3 (this study) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Efremov, A.K.; Winardhi, R.S.; Yan, J. Theoretical Methods for Studying DNA Structural Transitions under Applied Mechanical Constraints. Polymers 2017, 9, 74. https://doi.org/10.3390/polym9020074
Efremov AK, Winardhi RS, Yan J. Theoretical Methods for Studying DNA Structural Transitions under Applied Mechanical Constraints. Polymers. 2017; 9(2):74. https://doi.org/10.3390/polym9020074
Chicago/Turabian StyleEfremov, Artem K., Ricksen S. Winardhi, and Jie Yan. 2017. "Theoretical Methods for Studying DNA Structural Transitions under Applied Mechanical Constraints" Polymers 9, no. 2: 74. https://doi.org/10.3390/polym9020074




