Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuous Air Entrainment
Abstract
:1. Introduction
2. Numerical Modeling and Meshing
2.1. Governing Equations
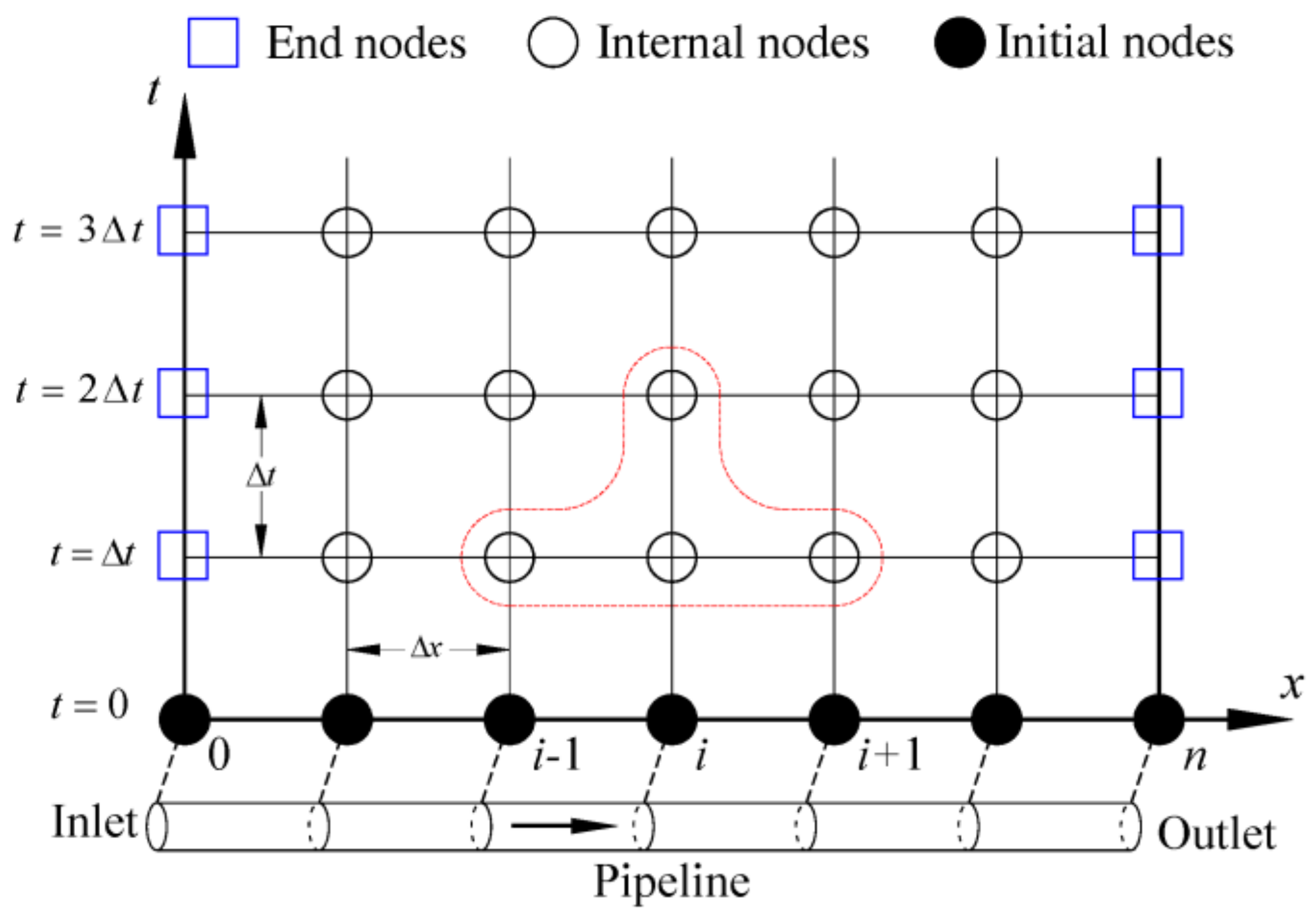
2.2. Discretization Model
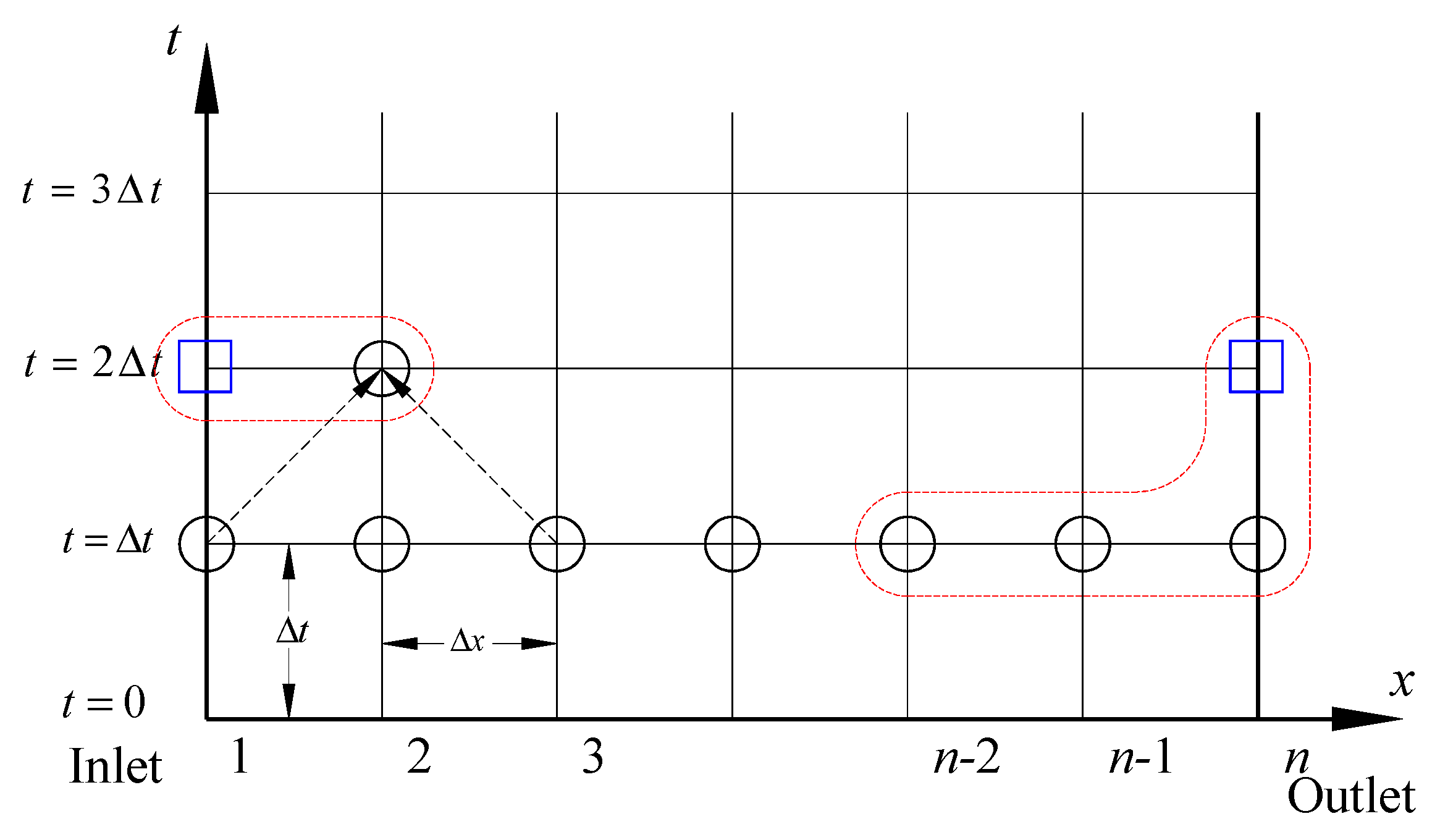
2.3. Meshing and Advancement
2.4. Boundary Conditions
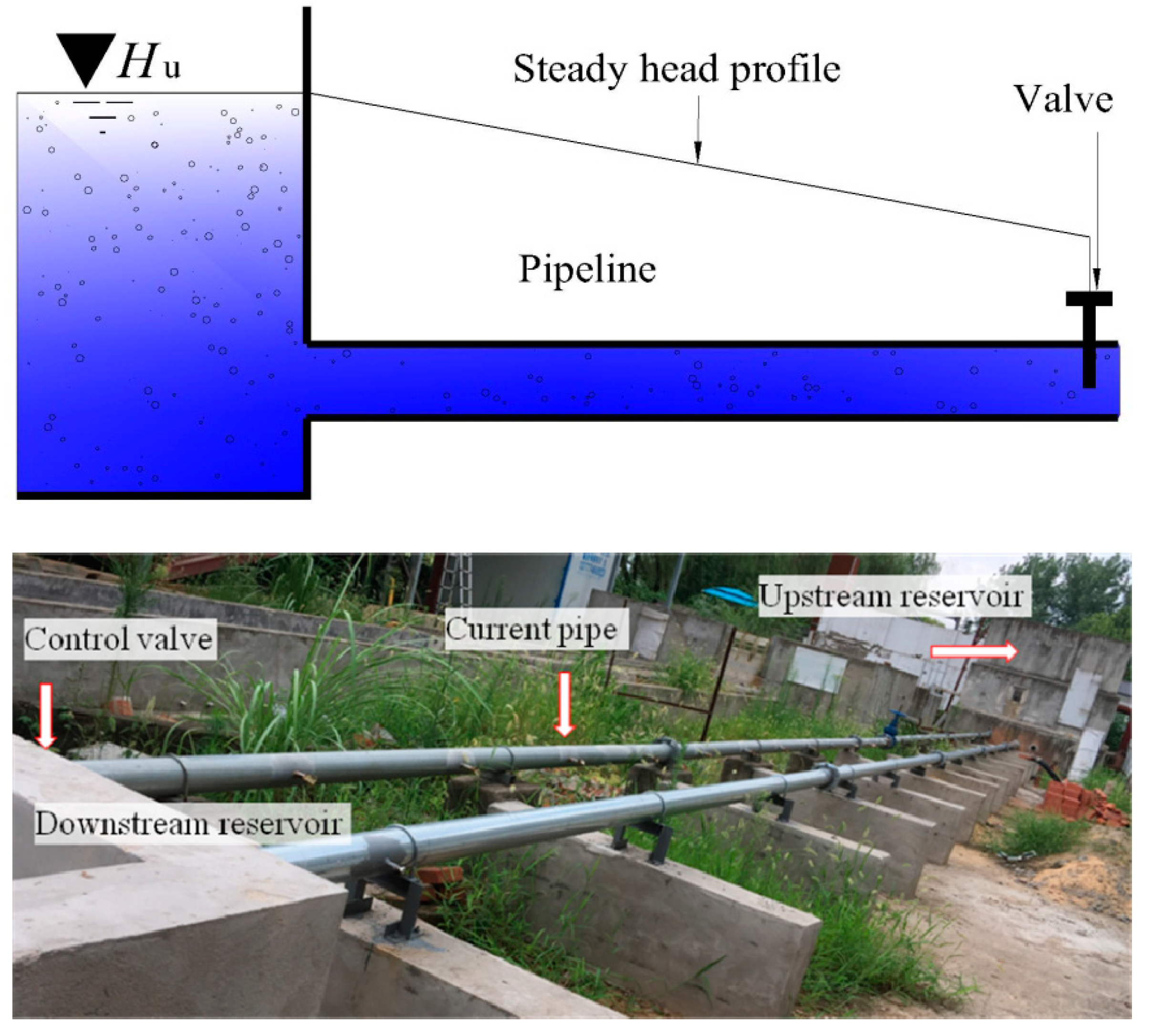
2.4.1. Upstream Boundary Model
2.4.2. Downstream Boundary Model
3. Experimental Measurement
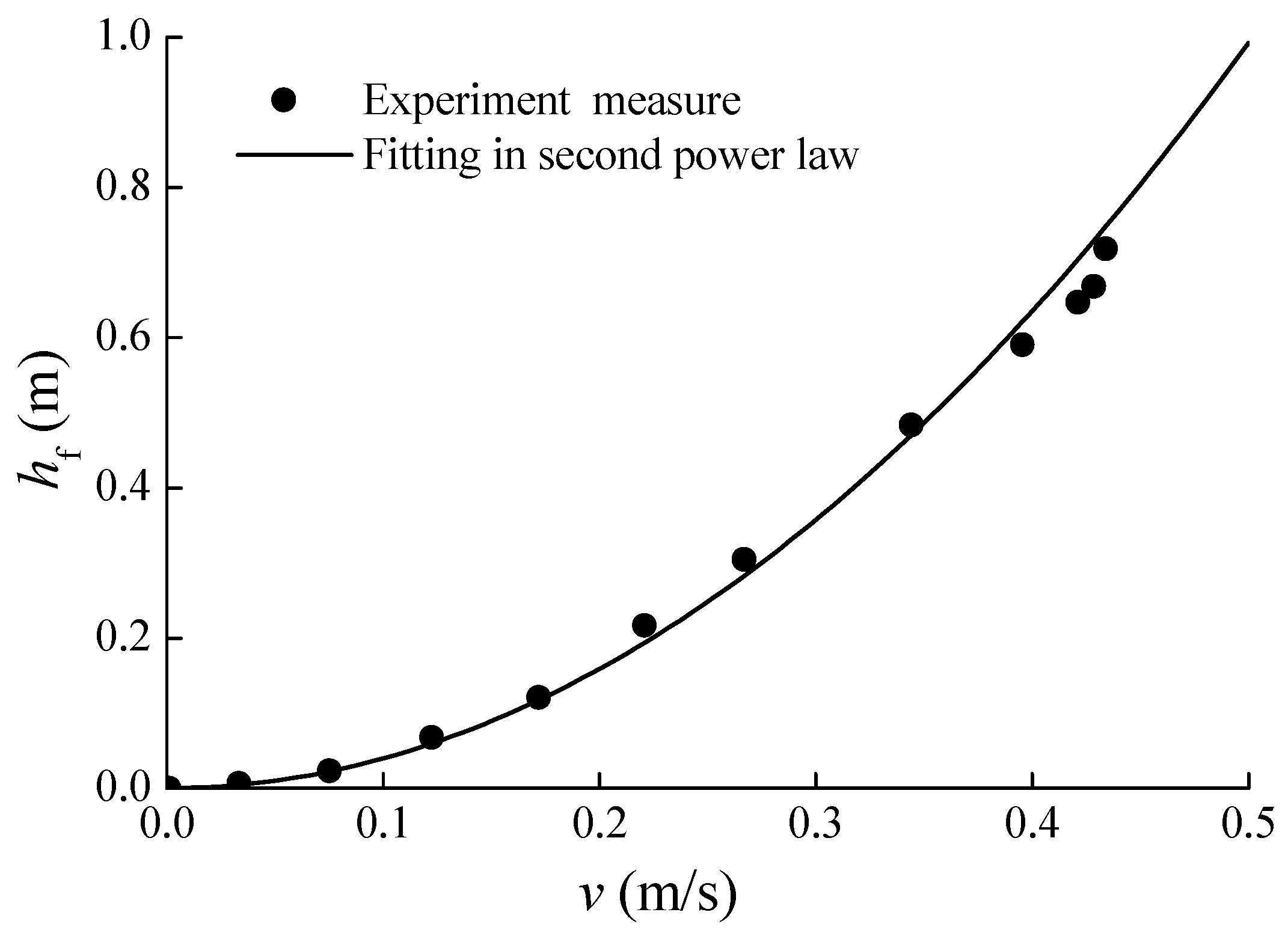
3.1. Steady Hydraulic Friction
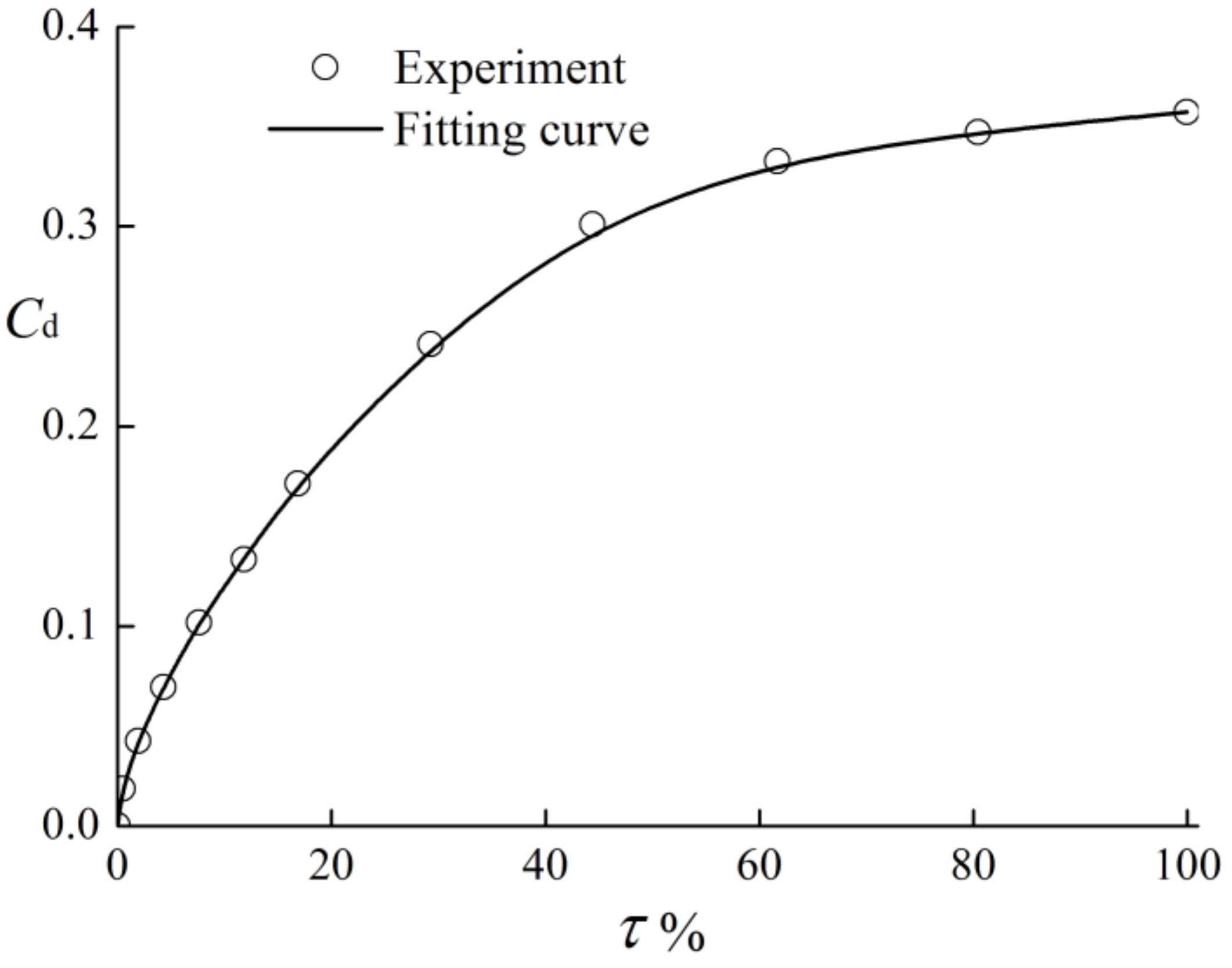
3.2. Valve Performance
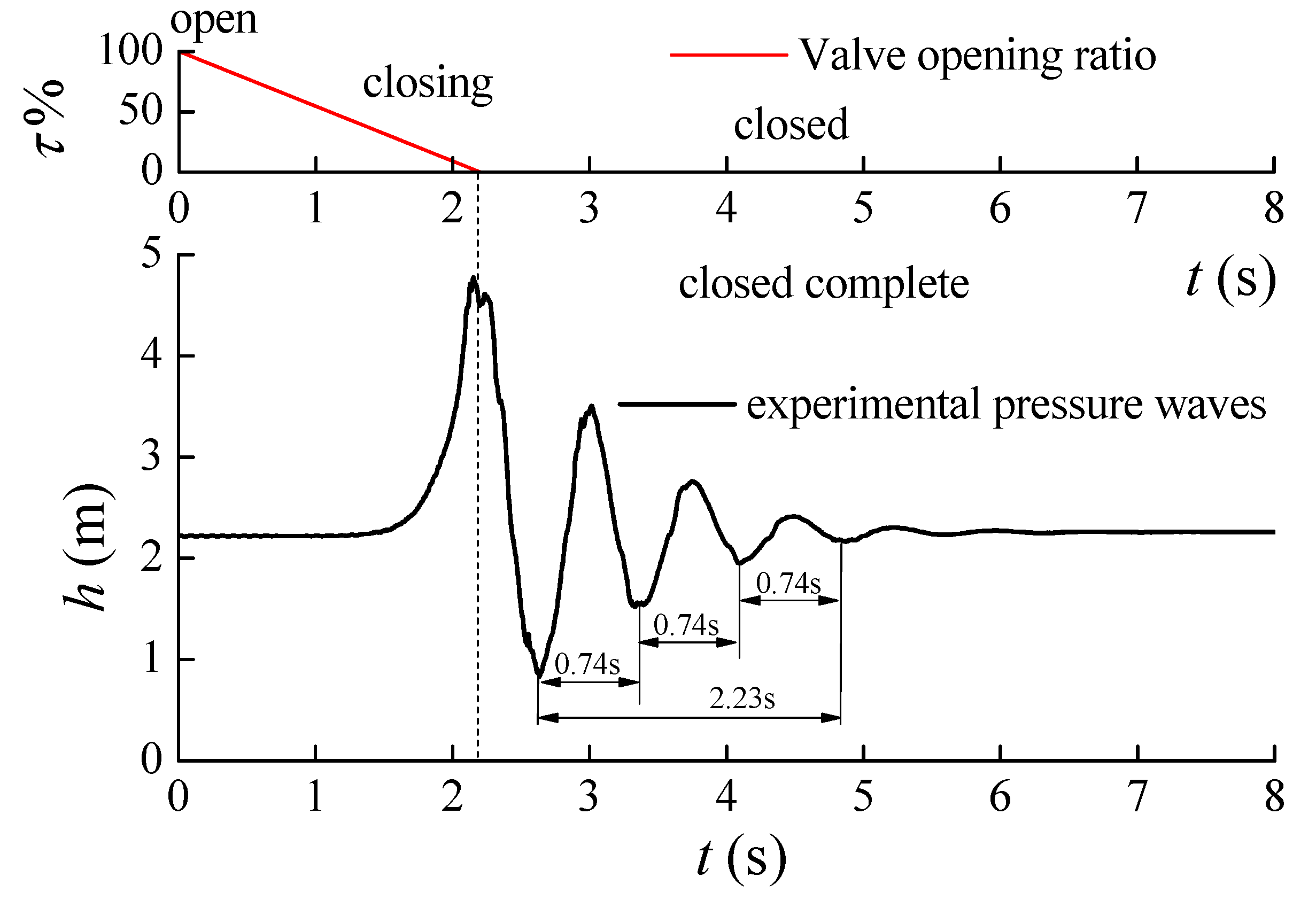
3.3. Water Hammer Measurements
4. Simulation and Analysis
4.1. Simulation and Comparison
4.2. Improvement to Approximate the Attenuation
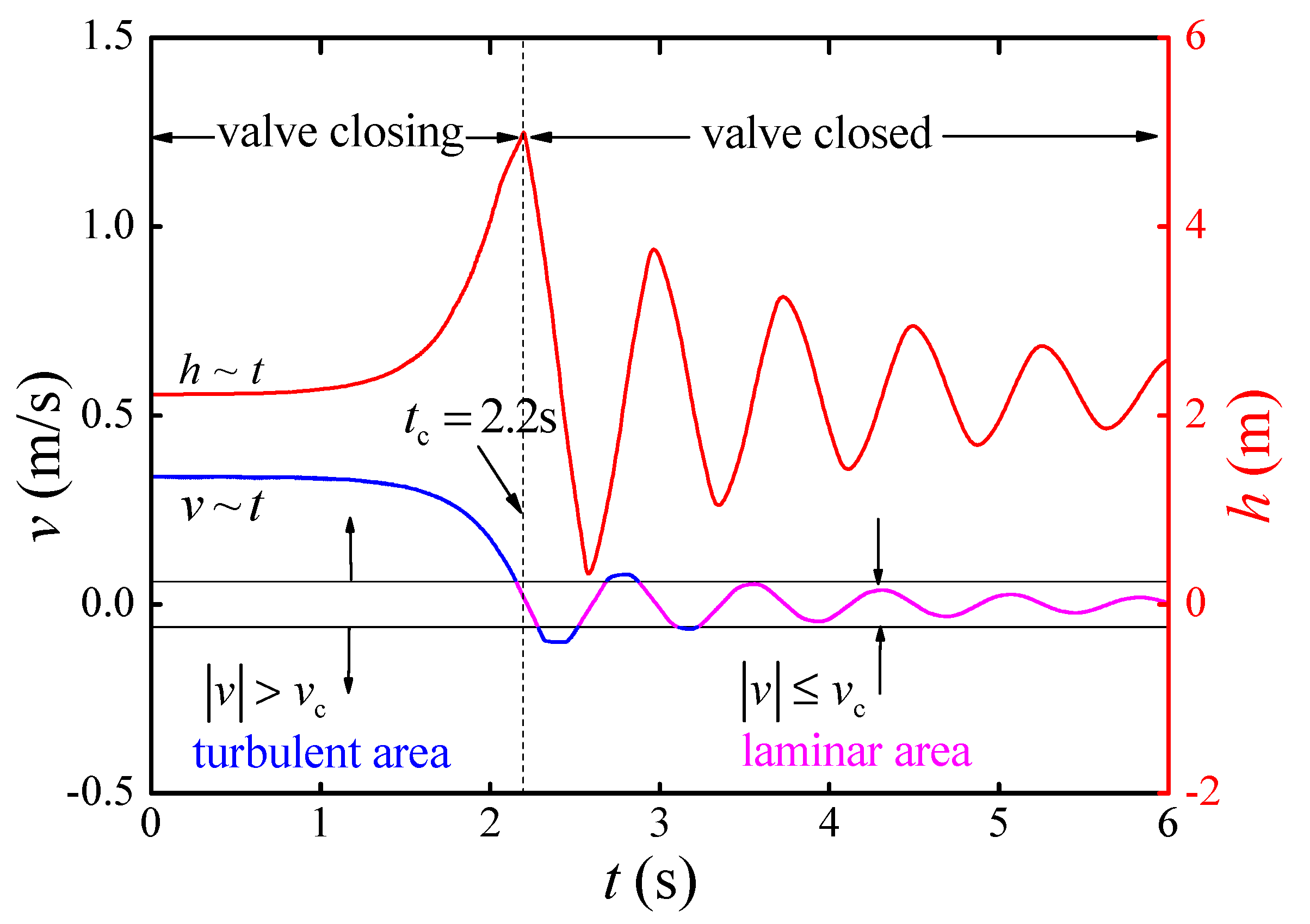
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| = | acceleration of gravity (m/s2) | |
| = | pressure head (m) | |
| = | distance along pipe from inlet (m) | |
| = | time, as subscript to denote time (s) | |
| = | flow velocity (m/s) | |
| = | Darcy friction factor | |
| = | main pipe diameter (m) | |
| = | the angle between pipe and the horizontal plane. | |
| = | speed of pressure wave (m/s) | |
| = | serial number of nodes (s) | |
| = | time step (s) | |
| = | number of sections | |
| = | length of segment (m) | |
| = | head of upstream reservoir (m) | |
| = | discharge coefficient | |
| = | the height of reference plane | |
| = | head drop due to friction along the pipe (m) | |
| = | valve opening ratio | |
| = | volume modulus | |
| = | density (kg/m3) | |
| = | elasticity modulus of steel pipe | |
| = | thickness of steel pipe (m) | |
| = | air content occupied in mixed fluid | |
| = | thermodynamics constant (J/(mol∙K)) | |
| = | temperature (K) | |
| = | absolute pressure (pa) | |
| = | additional friction factor in two-phase flow | |
| = | length of the pipe (m) | |
| = | additional friction factor after valve closed completely | |
| = | time of valve closing operation | |
| = | coefficient in additional friction function | |
| = | kinematic viscosity of water (m2/s) | |
| = | hydraulic radius (m) | |
| = | the critical flow velocity between laminar and turbulent flow (m/s) | |
| = | residuals between experimental and simulated peaks (m) | |
| = | the sum of squared residuals | |
| = | experimental positive peak (m) | |
| = | experimental negative peak (m) | |
| = | experimental positive peak (m) | |
| = | experimental negative peak (m) |
Acronyms
| MOC | = | Method of Characteristics |
| LWM | = | Lax-Wendroff Method |
References
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Yu, X.D.; Zhang, J.; Miao, D. Innovative Closure Law for Pump-Turbines and Field Test Verification. J. Hydraul. Eng. 2015, 141, 9. [Google Scholar] [CrossRef]
- Chaudhry, M. Applied Hydraulic Transients; Van Nostrana Reinhold Co.: New York, NY, USA, 1987. [Google Scholar]
- Besharat, M.; Viseu, M.T.; Ramos, H.M. Experimental Study of Air Vessel Behavior for Energy Storage or System Protection in Water Hammer Events. Water 2017, 9, 63. [Google Scholar] [CrossRef]
- Coronado-Hernandez, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Experimental and Numerical Analysis of a Water Emptying Pipeline Using Different Air Valves. Water 2017, 9, 98. [Google Scholar] [CrossRef]
- Wood, D.J. Waterhammer analysis-Essential and easy (and efficient). J. Environ. Eng.-Asce 2005, 131, 1123–1131. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Anderson, A. Thomas Young’s research on fluid transients: 200 years on. In Proceedings of the 10th International Conference on Pressure Surges, Edinburgh, UK, 14–16 May 2008; Hunt, S., Ed.; BHR Group Limited: Cranfield, UK, 2008. [Google Scholar]
- Tijsseling, A.S.; Anderson, A. A Precursor in Waterhammer Analysis-Rediscovering Johannes von Kries. In Proceedings of the 9th International Conference on Pressure Surges, Chester, UK, 24–26 March 2004; Murray, S.J., Ed.; BHR Group Limited: Cranfield, Bedfordshire, UK, 2004. [Google Scholar]
- Ghidaoui, M.S.; Zhao, M.; McInnis, D.A.; Axworthy, D.H. A review of water hammer theory and practice. Appl. Mech. Rev. 2005, 58, 49–76. [Google Scholar] [CrossRef]
- Triki, A. Dual-technique-based inline design strategy for water hammer control in pressurized pipe flow. Acta Mech. 2018, 229, 2019–2039. [Google Scholar] [CrossRef]
- Zhang, X.X.; Cheng, Y.G.; Xia, L.S.; Yang, J.D. CFD simulation of reverse water hammer induced by collapse of draft-tube cavity in a model pump-turbine during runaway process. In Proceedings of the 28th Iahr Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016. [Google Scholar]
- Chaudhry, M.; Hussaini, M. Second-order accurate explicit finite-difference schemes for waterhammer analysis. J. Fluids Eng. 1985, 107, 523–529. [Google Scholar] [CrossRef]
- Kochupillai, J.; Ganesan, N.; Padmanabhan, C. A new finite element formulation based on the velocity of flow for water hammer problems. Int. J. Press. Ves. Pip. 2005, 82, 1–14. [Google Scholar] [CrossRef]
- Tian, W.X.; Su, G.H.; Wang, G.P.; Qiu, S.Z.; Xia, Z.J. Numerical simulation and optimization on valve-induced water hammer characteristics for parallel pump feedwater system. Ann. Nuclear Energy 2008, 35, 2280–2287. [Google Scholar] [CrossRef]
- Schmitt, C.; Pluvinage, G.; HADJ-TAIEB, E.; Akid, R. Water pipeline failure due to water hammer effects. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 1075–1082. [Google Scholar] [CrossRef]
- Karadžić, U.; Bulatović, V.; Bergant, A. Valve-Induced Water Hammer and Column Separation in a Pipeline Apparatus. Stroj. Vestn.-J. Mech. Eng. 2014, 60, 742–754. [Google Scholar]
- Izquierdo, J.; Iglesias, P.L. Mathematical modelling of hydraulic transients in simple systems. Math. Comput. Modell. 2002, 35, 801–812. [Google Scholar] [CrossRef]
- Bazargan-Lari, M.R.; Kerachian, R.; Afshar, H.; Bashi-Azghadi, S.N. Developing an optimal valve closing rule curve for real-time pressure control in pipes. J. Mech. Sci. Technol. 2013, 27, 215–225. [Google Scholar] [CrossRef]
- Wan, W.; Li, F. Sensitivity Analysis of Operational Time Differences for a Pump-Valve System on a Water Hammer Response. J. Press. Vess. Technol. 2016, 138, 011303. [Google Scholar] [CrossRef]
- Sibetheros, I.A.; Holley, E.R.; Branski, J.M. Spline Interpolations for Water Hammer Analysis. J. Hydraul. Eng.-ASCE 1991, 117, 1332–1351. [Google Scholar] [CrossRef]
- Gong, J.Z.; Lambert, M.F.; Simpson, A.R.; Zecchin, A.C. Detection of Localized Deterioration Distributed along Single Pipelines by Reconstructive MOC Analysis. J. Hydraul. Eng. 2014, 140, 190–198. [Google Scholar] [CrossRef] [Green Version]
- Travas, V.; Basara, S. A mixed MOC/FDM numerical formulation for hydraulic transients. Tehn. Vjesn.-Techn. Gazette 2015, 22, 1141–1147. [Google Scholar]
- Evangelista, S.; Leopardi, A.; Pignatelli, R.; de Marinis, G. Hydraulic Transients in Viscoelastic Branched Pipelines. J. Hydraul. Eng. 2015, 141, 04015016. [Google Scholar] [CrossRef]
- Covas, D.; Stoianov, I.; Mano, J.F.; Ramos, H.; Graham, N.; Maksimovic, C. The dynamic effect of pipe-wall viscoelasticity in hydraulic transients. Part I-experimental analysis and creep characterization. J. Hydraul. Res. 2004, 42, 516–530. [Google Scholar] [CrossRef]
- Wood, D.J.; Lingireddy, S.; Boulos, P.F.; Karney, B.W.; McPherson, D.L. Numerical methods for modeling transient flow in distribution systems. J. Am. Water Work Assoc. 2005, 97, 104–115. [Google Scholar] [CrossRef]
- Guo, L.L.; Geng, J.; Shi, S.; Du, G.S. Study of the Phenomenon of Water Hammer Based on Sliding Mesh Method. In Development of Industrial Manufacturing; Choi, S.B., Hamid, F.S., Han, L., Eds.; Scientific.net: Zurich, Switzerland, 2014; Volume 525, pp. 236–239. [Google Scholar]
- Hwang, Y.H. Development of a particle method of characteristics (PMOC) for one-dimensional shock waves. Shock Waves 2018, 28, 379–399. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Liu, D.Y.; Ma, J.J.; Wang, P.; Xia, L. A second-order Finite Volume Method for pipe flow with water column separation. J. Hydrol.-Environ. Res. 2017, 17, 47–55. [Google Scholar] [CrossRef]
- Bergant, A.; Tusseling, A.S.; Vitkovsky, J.P.; Covas, D.I.C.; Simpson, A.R.; Lambert, M.F. Parameters affecting water hammer wave attenuation, shape and timing—Part 1: Mathematical tools. J. Hydraul. Res. 2008, 46, 373–381. [Google Scholar] [CrossRef]
- Bergant, A.; Tijsseling, A.S.; Vitkovsy, J.P.; Covas, D.I.C.; Simpson, A.R.; Lambert, M.F. Parameters affecting water hammer wave attenuation, shape and timing-Part 2: Case studies. J. Hydraul. Res. 2008, 46, 382–391. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.E.; Asce, M.; Steffler, P.M. Transient flow in a rapidly filling horizontal pipe containing trapped air. J. Hydraul. Eng.-ASCE 2002, 128, 625–634. [Google Scholar] [CrossRef]
- Anderson, J.D. Computational Fluid Dynamics: The Basics with Applications; McGrawhill Inc.: New York, NY, USA, 1995. [Google Scholar]
- Manopoulos, C.G.; Mathioulakis, D.S.; Tsangaris, S.G. One-dimensional model of valveless pumping in a closed loop and a numerical solution. Phys. Fluids 2006, 18, 017106. [Google Scholar] [CrossRef]
- Himr, D. Numerical simulation of water hammer in low pressurized pipe: comparison of SimHydraulics and Lax-Wendroff method with experiment. In Proceedings of the EPJ Web of Conferences, Hradec Králové, Czech Republic, 20–23 November 2012; Dancova, P., Novonty, P., Eds.; Technical University of Liberec: Liberec, Czech Republic, 2012. [Google Scholar]
- Wan, W.Y.; Zhu, S.; Hu, Y.J. Attenuation analysis of hydraulic transients with laminar-turbulent flow alternations. Appl. Math. Mech. 2010, 31, 1209–1216. [Google Scholar] [CrossRef]
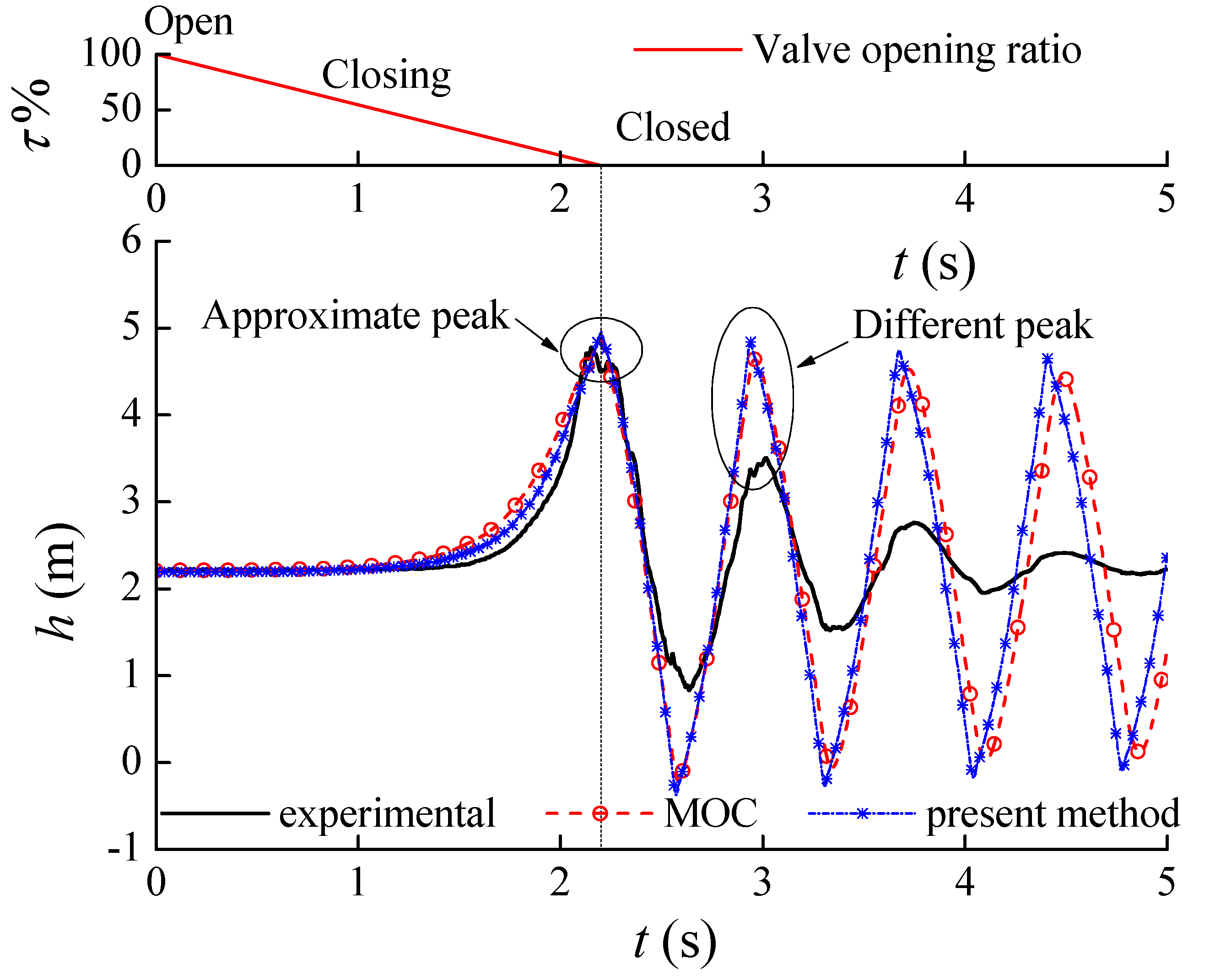
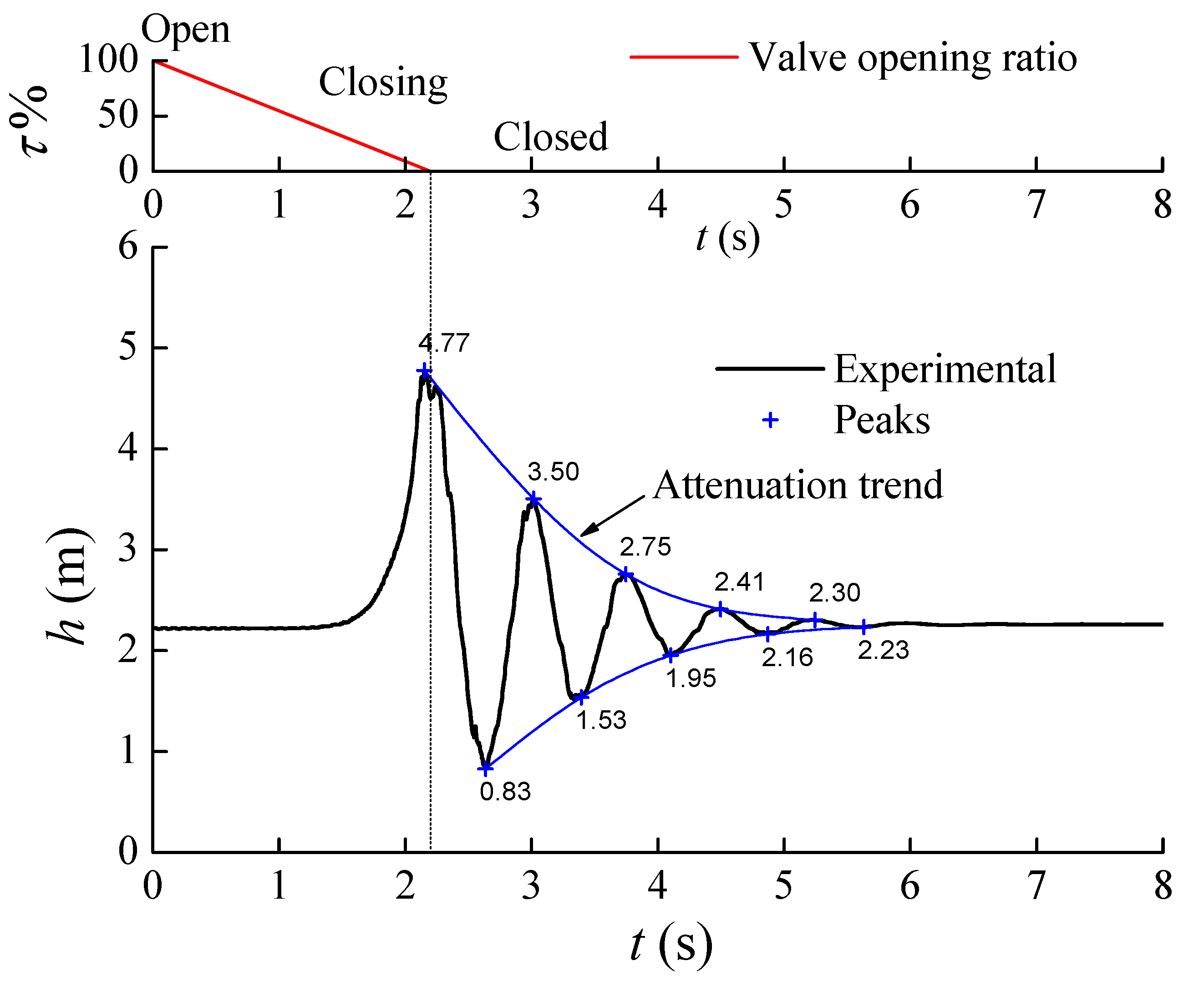

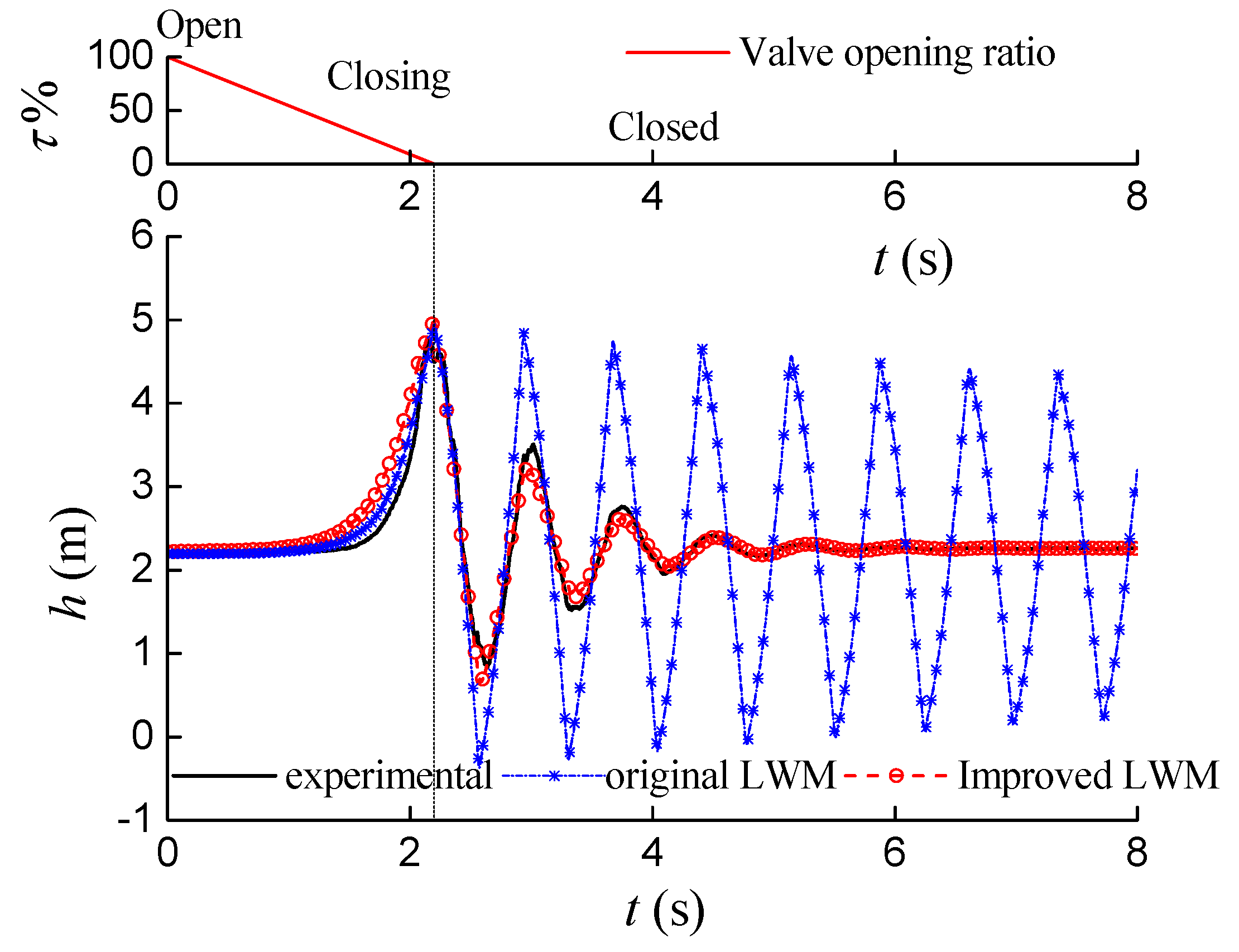
| Periods | Experimental | Original | Improved | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LM | TM | CM | ||||||||
| 1st | 4.77 | 0.83 | 4.96 | −0.38 | 4.93 | 0.66 | 4.94 | 1.01 | 4.93 | 0.66 |
| 2nd | 3.50 | 1.53 | 4.84 | −0.27 | 3.22 | 1.68 | 3.08 | 1.65 | 3.23 | 1.68 |
| 3rd | 2.75 | 1.95 | 4.74 | −0.17 | 2.61 | 2.04 | 2.74 | 1.86 | 2.62 | 2.04 |
| 4th | 2.41 | 2.16 | 4.65 | −0.09 | 2.39 | 2.18 | 2.60 | 1.96 | 2.39 | 2.18 |
| 5th | 2.30 | 2.23 | 4.56 | 0.00 | 2.31 | 2.23 | 2.52 | 2.02 | 2.31 | 2.23 |
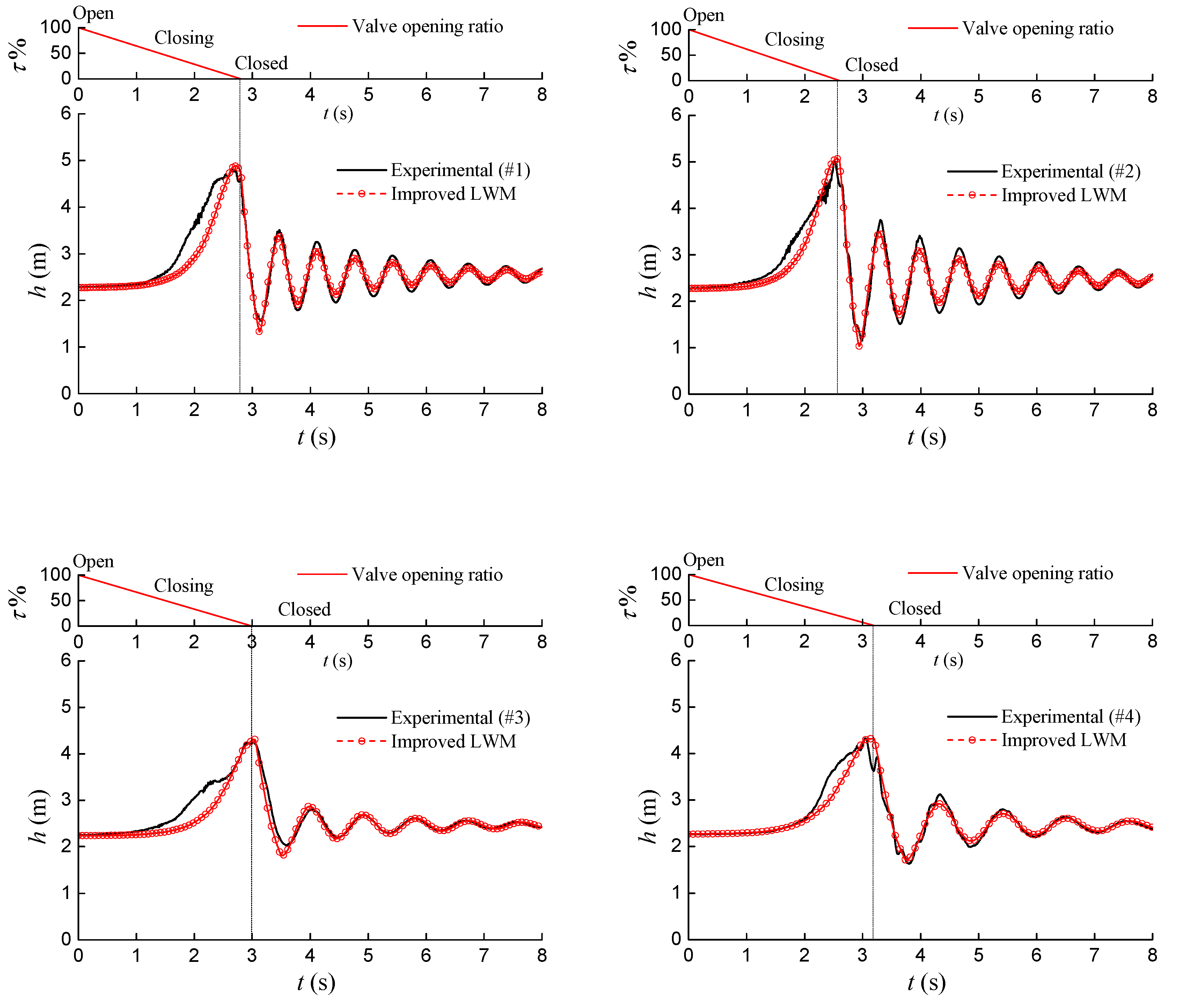
| Case | Wave Speed (m∙s−1) | m | Air Content (%) | Closing Time (s) |
|---|---|---|---|---|
| #1 | 183 | 0.139 | 0.308 | 2.8 |
| #2 | 175 | 0.152 | 0.338 | 2.6 |
| #3 | 132 | 0.269 | 0.598 | 3.0 |
| #4 | 110 | 0.388 | 0.864 | 3.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Wan, W.; Shi, M. Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuous Air Entrainment. Water 2018, 10, 928. https://doi.org/10.3390/w10070928
Zhang B, Wan W, Shi M. Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuous Air Entrainment. Water. 2018; 10(7):928. https://doi.org/10.3390/w10070928
Chicago/Turabian StyleZhang, Boran, Wuyi Wan, and Mengshan Shi. 2018. "Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuous Air Entrainment" Water 10, no. 7: 928. https://doi.org/10.3390/w10070928





