Best Fit and Selection of Theoretical Flood Frequency Distributions Based on Different Runoff Generation Mechanisms
Abstract
:1. Introduction
2. Derived Flood Frequency Distributions
2.1. IF Model
2.2. Two Component IF Model (TCIF)
- -
- “L-type” (frequent) response, occurring when a lower threshold fa,L is exceeded, and responsible of ordinary floods likely produced by a relatively small portion of the basin aL:
- -
- “H-type” (rare) response, occurring when a higher threshold fa,H is exceeded, and providing extraordinary floods mostly characterized by larger contributing areas aH:
3. Case Studies and Application

| n. | A (km2) | I | (m3/s) | Cv | Cs | N | |
|---|---|---|---|---|---|---|---|
| Carapelle at Carapelle | 1 | 715 | -0.23 | 283.7 | 057 | 1.34 | 36 |
| Bradano at Ponte Colonna | 2 | 462 | -0.08 | 201.6 | 0.76 | 1.21 | 32 |
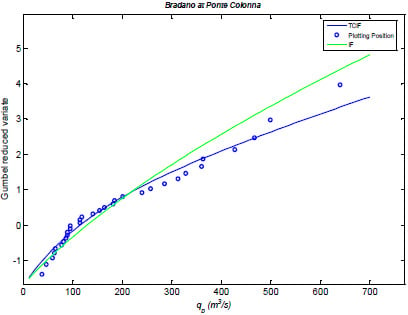
Parameter Estimation and Results
| Site | qo (m3/s) | E[iA,τ] (mm/h) | ε | Λp | k | τA(h) | ξ | β | ε’ | Λq |
|---|---|---|---|---|---|---|---|---|---|---|
| Carapelle at Carapelle | 7.0 | 0.20 | 0.39 | 44.6 | 0.8 | 9.2 | 0.7 | 4 | 0.5 | 10.5 |
| Bradano at Ponte Colonna | 5.0 | 0.45 | 0.33 | 21.0 | 0.8 | 4.3 | 0.7 | 4 | 0.5 | 5.0 |
| Site | fA (mm/h) | r | εL | ε H | ΛL | ΛH | fA,L (mm/h) | fA,H (mm/h) | rL | rH |
| Carapelle at Carapelle | 1.01 | 0.45 | 0.5 | 0.5 | 9.86 | 0.66 | 1.01 | 3.86 | 0.41 | 0.99 |
| Bradano at Ponte Colonna | 2.02 | 0.30 | 0.5 | 0.5 | 3.98 | 1.04 | 2.01 | 5.08 | 0.15 | 0.99 |

4. Model Selection Procedure
| Site | LLC | AICc | BIC | LLR | |||
|---|---|---|---|---|---|---|---|
| IF | TCIF | IF | TCIF | IF | TCIF | ( IF, TCIF ) | |
| Carapelle at Carapelle | 453.12 | 452.94 | 457.48 | 462.23 | 460.28 | 467.27 | 0.18 |
| Bradano at Ponte Colonna | 397.29 | 395.66 | 401.71 | 405.14 | 404.23 | 409.52 | 1.63 |
| Carapelle at Carapelle | Bradano at Ponte Colonna | ||||||
|---|---|---|---|---|---|---|---|
| N1 | N2 | μ(δp) | σ(δp) | N1 | N2 | μ(δp) | σ(δp) |
| 18 | 18 | −0.17 | −4.04 | 16 | 16 | −0.89 | −1.61 |
5. Conclusions
List of Model Parameters, Units (Parameters without Units are Dimensionless), and Short Description
| A (km2) | basin area |
| τA (h) | lag-time of basin area A |
| ξ | routing factor |
| β | scale parameter of Gamma distribution |
| E[iA,τ] (mm/h) | average rainfall intensity referred to the entire basin area A |
| ε | scale parameter of the relationship between average rainfall intensity E[ia,τ] and source area a |
| qo (m3/s) | base flow |
| Λp | mean annual number of independent rainfall events |
| k | shape parameter of the Weibull distribution of the rainfall intensity |
| fA (mm/h) | average hydrologic loss referred to the entire basin area A |
| ε’ | scale parameter of the relationship between average hydrologic loss (fa) and source area a |
| r | ratio of the mean contributing area E[a] to the total basin area A |
| Λq | mean annual number of independent flood events |
| fA,L (mm/h) | lower runoff threshold referred to the entire basin area A |
| fA,H (mm/h) | higher runoff threshold referred to the entire basin area A |
| εL | scale parameter of the relationship between average hydrologic loss (fa,L) and source area a |
| εH | scale parameter of the relationship between average hydrologic loss (fa,H) and source area a |
| rL | ratio of the L-type mean contributing area E[aL] to the total basin area A |
| rH | ratio of the H-type mean contributing area E[aH] to the total basin area A |
| ΛL | mean annual number of independent flood events for L-type |
| ΛH | mean annual number of independent flood events for H-type |
Appendix
- both random variables a and ua are controlled by: (i) rainfall intensity, duration and areal extension; (ii) runoff concentration; (iii) hydrological losses.
- The runoff peak per unit area, ua, is linearly dependent on the areal net rainfall intensity in a time interval equal to τa with a constant routing factor ξ. Then, the probability distribution of ua, can be derived from the probability distribution of rainfall intensity ia,t conditional on a duration equal to τa, lag-time of a.
- The areal rainfall intensity ia,t is assumed Weibull distributed with two parameters θa,τ and k. The mean areal rainfall intensity is:
- The routing factor ξ is a key model parameter which in reality appeared very stable. In fact, ξ, it was found to vary in a narrow range (0.6, 0.8) with an average value close to 0.7 which has been used in all the applications of the IF and TCIF models made since they were introduced.
- The lag-time τa scales with a according to a power law with exponent 0.5.
- The variable contributing area a follows a mixed distribution with a continuous part which is a two parameter gamma distribution, valid for 0 < a< A and a discrete probability PA
- The gamma function arises as the distribution of the sum of β stochastic (independent) variables exponentially distributed with equal mean value α.
- Thus, being any flood peak due to the superposition of flows coming from sub-basins whose expected number is equal to the number Nω of sub-basins of Horton order immediately smaller than that of the whole basin, we identified β to E[Nω]. Nω tends to be invariant at any scale and assumes values ranging between 3 and 5 [50] with expected value close to 4 [51].
- The annual maximum floods arise from a compound Poisson process and the following relationships hold for the flood peak qp, the peak of direct streamflow Q, and the exceedance probability function of the peak of direct streamflow GQ’(q):with base flow qo
Acknowledgements
References and Notes
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; O’Connell, P.E.; Oki, T.; Pomeroy, J.W.; Schertzer, D.; Uhlenbrook, S.; Zehe, E. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar]
- Abdulla, F.A.; Lettenmaier, D.P. Development of regional parameter estimation equations for a macro scale hydrologic model. J. Hydrol. 1997, 197, 30–57. [Google Scholar]
- Seibert, J. Regionalisation of parameters of a conceptual rainfall-runoff model. Agric. For. Meteorol. 1999, 98-99, 279–293. [Google Scholar]
- Fernandez, W.; Vogel, R.M.; Sankarasubramanian, A. Regional calibration of a watershed model. Hydrol. Sci. J. 2000, 45, 689–707. [Google Scholar] [CrossRef]
- Hundecha, Y.; Bardossy, A. Modeling of the effect of land use changes on the runoff generation of a river basin through parameter regionalization of a watershed model. J. Hydrol. 2004, 292, 281–295. [Google Scholar] [CrossRef]
- Merz, B.; Blöschl, G. Regionalisation of watershed model parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef]
- Wagener, T.; Wheater, H.S. Parameter estimation and regionalization for continuous rainfall-runoff models including uncertainty. J. Hydrol. 2006, 320, 132–154. [Google Scholar] [CrossRef]
- Heuvelmans, G.; Muys, B.; Feyen, J. Regionalisation of the parameters of a hydrological model: Comparison of linear regression models with artificial neural nets. J. Hydrol. 2006, 319, 245–265. [Google Scholar] [CrossRef]
- Post, D.A.; Jakeman, A.J. Predicting the daily streamflow of ungauged watersheds in S.E. Australia by regionalizing the parameters of a lumped conceptual rainfall-runoff model. Ecol. Model. 1999, 123, 91–104. [Google Scholar]
- Wagener, T.; Wheater, H.S.; Gupta, H.V. Rainfall-runoff Modelling in Gauged and Ungauged Catchments; Imperial College Press: London, UK, 2004; p. 300. [Google Scholar]
- Wagener, T.; Sivapalan, M.; McDonnell, J.J.; Hooper, R.; Lakshmi, V.; Liang, X.; Kumar, P. Predictions in ungauged basins (PUB)—A catalyst for multi-disciplinary hydrology. Eos. Trans. AGU 2004, 85, 451–452. [Google Scholar] [CrossRef]
- McIntyre, N.; Lee, H.; Wheater, H.S.; Young, A.; Wagener, T. Ensemble predictions of runoff in ungauged catchments. Water Resour. Res. 2005, 41, W12434. [Google Scholar]
- Young, A.R. Stream flow simulation within UK ungauged watersheds using a daily rainfall-runoff model. J. Hydrol. 2006, 320, 155–172. [Google Scholar]
- McDonnell, J.J.; Woods, R. On the need for catchment classification. J. Hydrol. 2004, 299, 2–3. [Google Scholar] [CrossRef]
- Eagleson, P. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Gottschalk, L.; Weingartner, R. Distribution of peak flow derived from a distribution of rainfall volume and runoff coefficient, and a unit hydrograph. J. Hydrol. 1998, 208, 148–162. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M. Derived distribution of floods based on the concept of partial area coverage with a climatic appeal. Water Resour. Res. 2000, 36, 469–482. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G. On the derived flood frequency distribution: Analytical formulation and the influence of antecedent soil moisture condition. J. Hydrol. 2002, 262, 245–258. [Google Scholar] [CrossRef]
- Franchini, M.; Galeati, G.; Lolli, M. Analytical derivation of the flood frequency curve through partial duration series analysis and a probabilistic representation of the runoff coefficient. J. Hydrol. 2005, 303, 1–15. [Google Scholar] [CrossRef]
- Gioia, A.; Iacobellis, V.; Manfreda, S.; Fiorentino, M. Runoff thresholds in derived flood frequency distributions. Hydrol. Earth Syst. Sci. 2008, 12, 1295–1307. [Google Scholar]
- Strupczewski, W.G.; Singh, V.P.; Weglarczyk, S. Physics of Environmental Frequency Analysis. In Integrated Technologies for Environmental Monitoring and Information Production; Harmancioglu, N.B., Ozkul, S.D., Fistikoglu, O., Geerders, P., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; NATO Science Series: IV: Earth and Environmental Sciences; Vol. 23, pp. 195–172. [Google Scholar]
- Sivapalan, M.; Wood, E.F.; Beven, K.J. On hydrologic similarity, 3. A dimensionless flood frequency model using a generalized geomorphologic unit hydrograph and partial area runoff generation. Water Resour. Res. 1990, 26, 43–58. [Google Scholar]
- Vander Kwaak, J.E.; Loague, K. Hydrologic-response simulations for the R-5 catchment with a comprehensive physics-based model. Water Resour. Res. 2001, 37, 999–1013. [Google Scholar] [CrossRef]
- Allamano, P.; Claps, P.; Laio, F. An analytical model of the effects of catchment elevation on the flood frequency distribution. Water Resour. Res. 2009, 45, W01402. [Google Scholar] [CrossRef]
- Waylen, P.; Woo, M. Prediction of annual floods generated by mixed processes. Water Resour. Res. 1982, 18, 1283–1286. [Google Scholar] [CrossRef]
- Rossi, F.; Fiorentino, M.; Versace, P. Two-component extreme value distribution for flood frequency analysis. Water Resour. Res. 1984, 20, 847–856. [Google Scholar] [CrossRef]
- Buishand, T.; Demaré, G. Estimation of the annual maximum distribution from samples of maxima in separate seasons. Stochastic Hydrol. Hydraul. 1990, 4, 89–103. [Google Scholar] [CrossRef]
- Alila, Y.; Mtiraoui, A. Implications of heterogeneous flood-frequency distributions on traditional stream-discharge prediction techniques. Hydrol. Proc. 2002, 16, 1065–1084. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G.; Merz, R.; Gutknecht, D. Linking flood frequency to long-term water balance: Incorporating effects of seasonality. Water Resour. Res. 2005, 41, W06012. [Google Scholar]
- Rahman, A.; Weinmann, P.; Hoang, T.; Laurenson, E. Monte Carlo simulation of flood frequency curves from rainfall. J. Hydrol. 2002, 256, 196–210. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Fiorentino, M.; Manfreda, S.; Iacobellis, V. Peak runoff contributing area as hydrological signature of the probability distribution of floods. Adv. Water Resour. 2007, 30, 2123–2134. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modeling—The Primer; Wiley: Chichester, UK, 2001. [Google Scholar]
- Wagener, T.; Gupta, H.V. Model identification for hydrological forecasting under uncertainty. Stoch. Environ. Res. Risk Assess. 2005, 19, 378–387. [Google Scholar] [CrossRef]
- Laio, F.; Di Baldassarre, G.; Montanari, A. Model selection techniques for the frequency analysis of hydrological extremes. Water Resour. Res. 2009, 45, W07416. [Google Scholar] [CrossRef]
- Busemeyer, J.R.; Wang, Y.M. Model comparisons and model selections based on generalization criterion methodology. J. Math. Psychol. 2000, 44, 171–189. [Google Scholar] [CrossRef] [PubMed]
- Kottegoda, N.T.; Rosso, R. Statistics, Probability and Reliability for Civil and Environmental Engineers; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Am. Geograph. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Fiorentino, M.; Iacobellis, V. New insights about the climatic and geologic control on the probability distribution of floods. Water Resour. Res. 2001, 37, 721–730. [Google Scholar] [CrossRef]
- Fiorentino, M.; Gioia, A.; Iacobellis, V.; Manfreda, S. Regional analysis of runoff thresholds behaviour in Southern Italy based on theoretically derived distributions. Adv. Geosci. 2010, (in press). [Google Scholar]
- Matalas, N.C.; Slack, J.R.; Wallis, J.R. Regional skew in search of a parent. Water Resour. Res. 1975, 11, 815–826. [Google Scholar] [CrossRef]
- Cunnane, C. Review of statistical models for flood frequency estimation. In Proceedings of the International Symposium on Flood Frequency and Risk Analysis, Louisiana State University, Baton Rouge, LA, USA, 14–17 May 1986.
- Mosier, C.I. Problems and designs of cross-validation. Educ. Psychol. Meas. 1951, 11, 5–11. [Google Scholar] [CrossRef]
- Camstra, A.; Boomsma, A. Cross-validation in regression and covariance structure analysis: An overview. Sociol. Method. Res. 1992, 21, 89–115. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory, Tsahkadsor, Armenia, 2–8 September 1971; Petrov, B.N., Csaki, F., Eds.; Akademiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Stone, M. On asymptotic equivalence of choice of model by cross-validation and Akaike’s criterion. J. Roy. Stat. Soc. Ser. B 1977, 39, 44–47. [Google Scholar]
- Browne, M.; Cudeck, W. Single Sample cross-validation indices for covariance structures. Multivariate Behav. Res. 1989, 24, 445–455. [Google Scholar]
- Linhart, H.; Zucchini, W. Model Selection; John Wiley: Hoboken, NJ, USA, 1986. [Google Scholar]
- Sugiura, N. Further analysis of the data by Akaike’s information criterion and the finite corrections. Commun. Stat. Theory Methods 1978, A7, 13–26. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Iacobellis, V.; Fiorentino, M.; Gioia, A.; Manfreda, S. Best Fit and Selection of Theoretical Flood Frequency Distributions Based on Different Runoff Generation Mechanisms. Water 2010, 2, 239-256. https://doi.org/10.3390/w2020239
Iacobellis V, Fiorentino M, Gioia A, Manfreda S. Best Fit and Selection of Theoretical Flood Frequency Distributions Based on Different Runoff Generation Mechanisms. Water. 2010; 2(2):239-256. https://doi.org/10.3390/w2020239
Chicago/Turabian StyleIacobellis, Vito, Mauro Fiorentino, Andrea Gioia, and Salvatore Manfreda. 2010. "Best Fit and Selection of Theoretical Flood Frequency Distributions Based on Different Runoff Generation Mechanisms" Water 2, no. 2: 239-256. https://doi.org/10.3390/w2020239