Integrated Application of Remote Sensing, GIS and Hydrological Modeling to Estimate the Potential Impact Area of Earthquake-Induced Dammed Lakes
Abstract
:1. Introduction
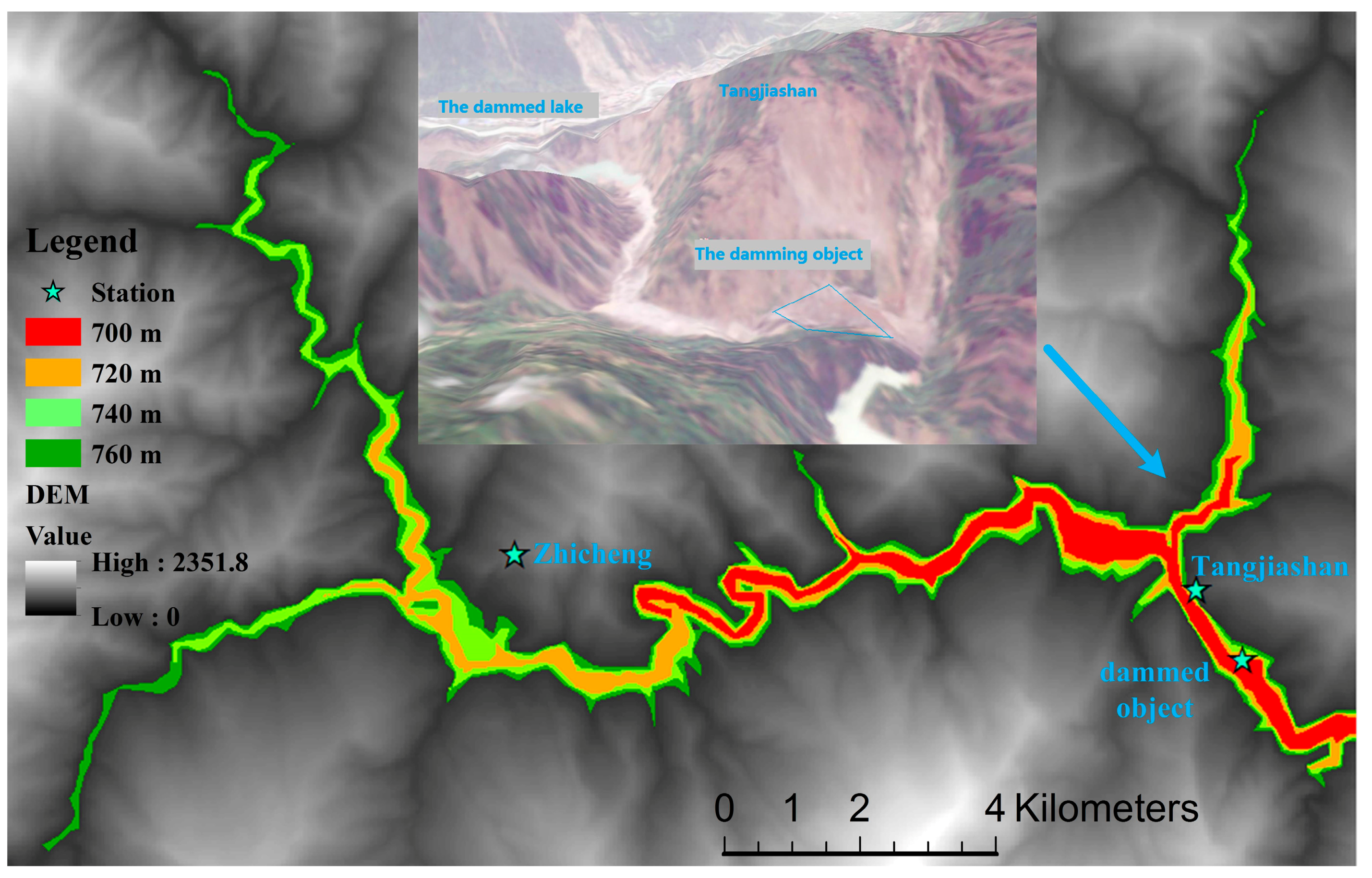
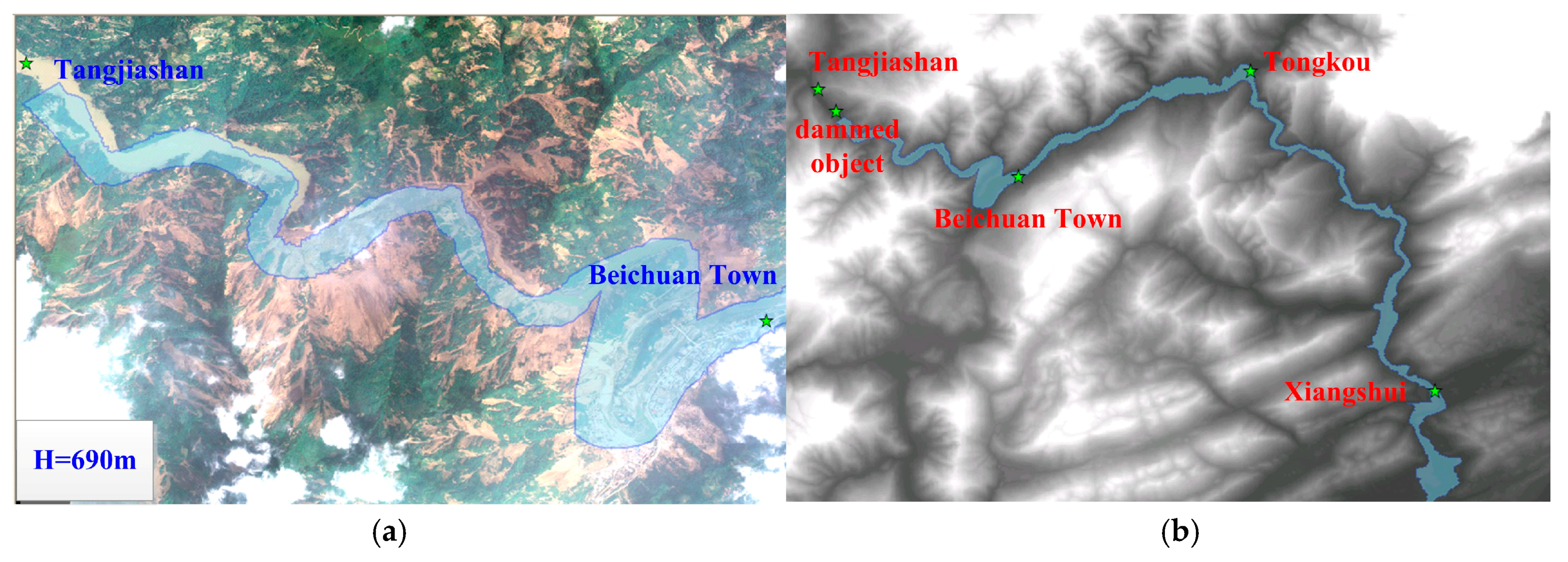
2. Study Area and Dataset
3. Methodology
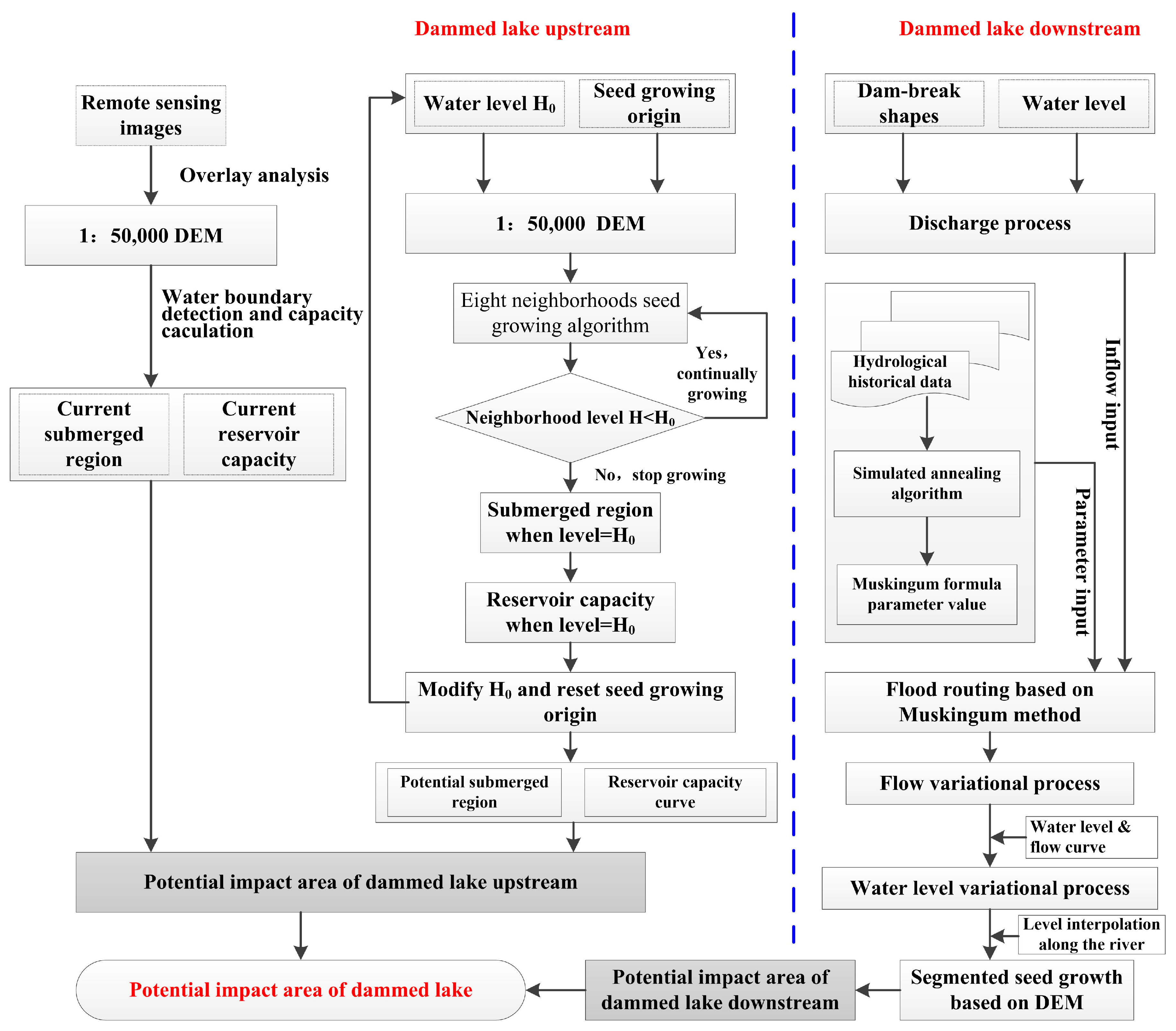
3.1. Extraction and Calculation of Dammed Lake Parameters
3.2. Dam-Break Flow Calculation
3.3. Flood Routing with an Improved Muskingum Method
3.3.1. Muskingum Method
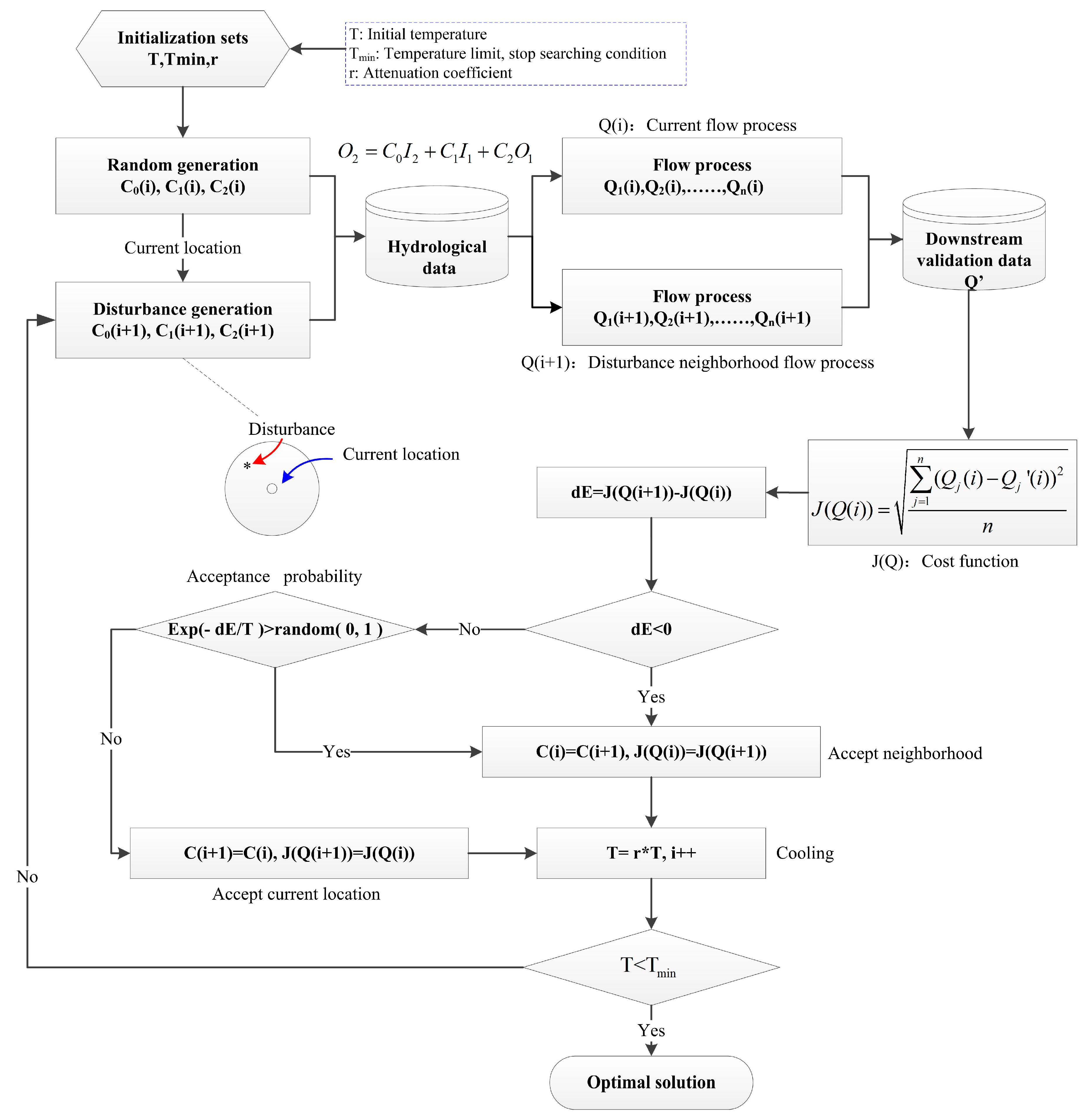
3.3.2. Parameter Optimization with Simulated Annealing
3.4. Estimation for Potential Impact Area
3.4.1. The Runoff vs. Elevation Curve
3.4.2. Estimation for Dam-Break Damage based on Remote Sensing Image and DEM
4. Calculation Example and Analysis
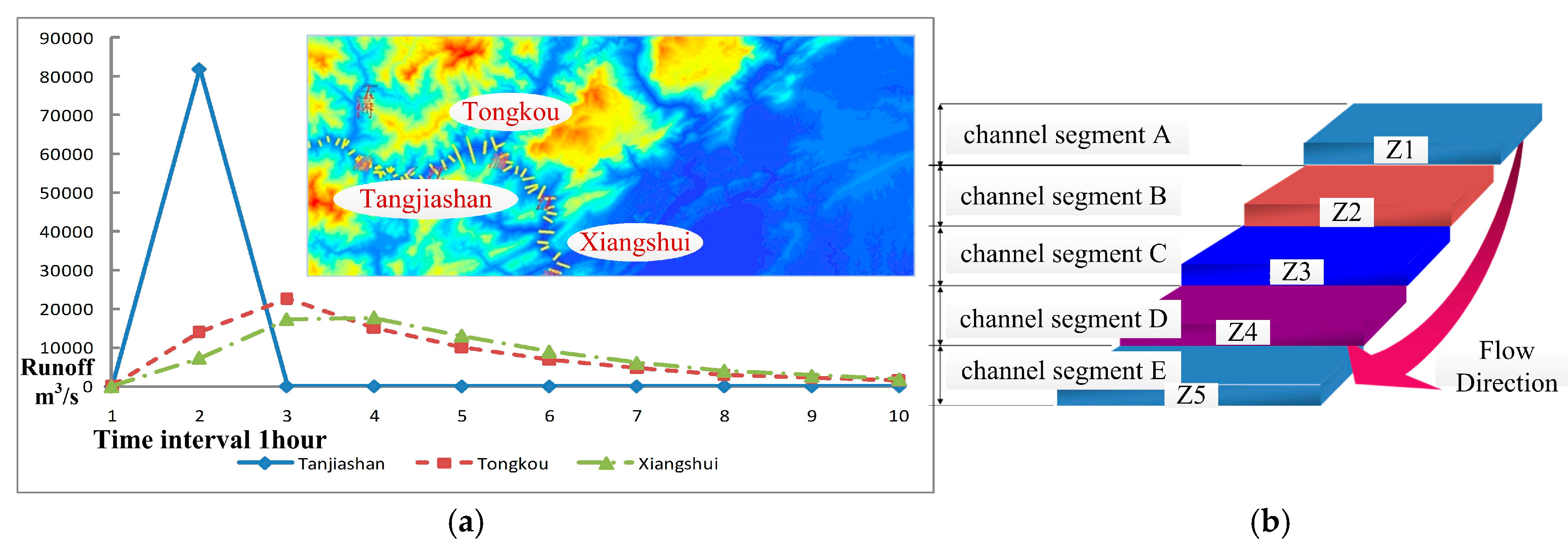
4.1. Dammed Lake Parameters based on DEM and Remote Sensing Images
4.2. Dam-Break Flow Calculation Result (H = 700 m)
4.3. Flood Routing Result (H = 700 m) with an Improved Muskingum Method
4.3.1. Muskingum Parameters Calculation with the Simulated Annealing Method
4.3.2. Validation of the Muskingum Parameters
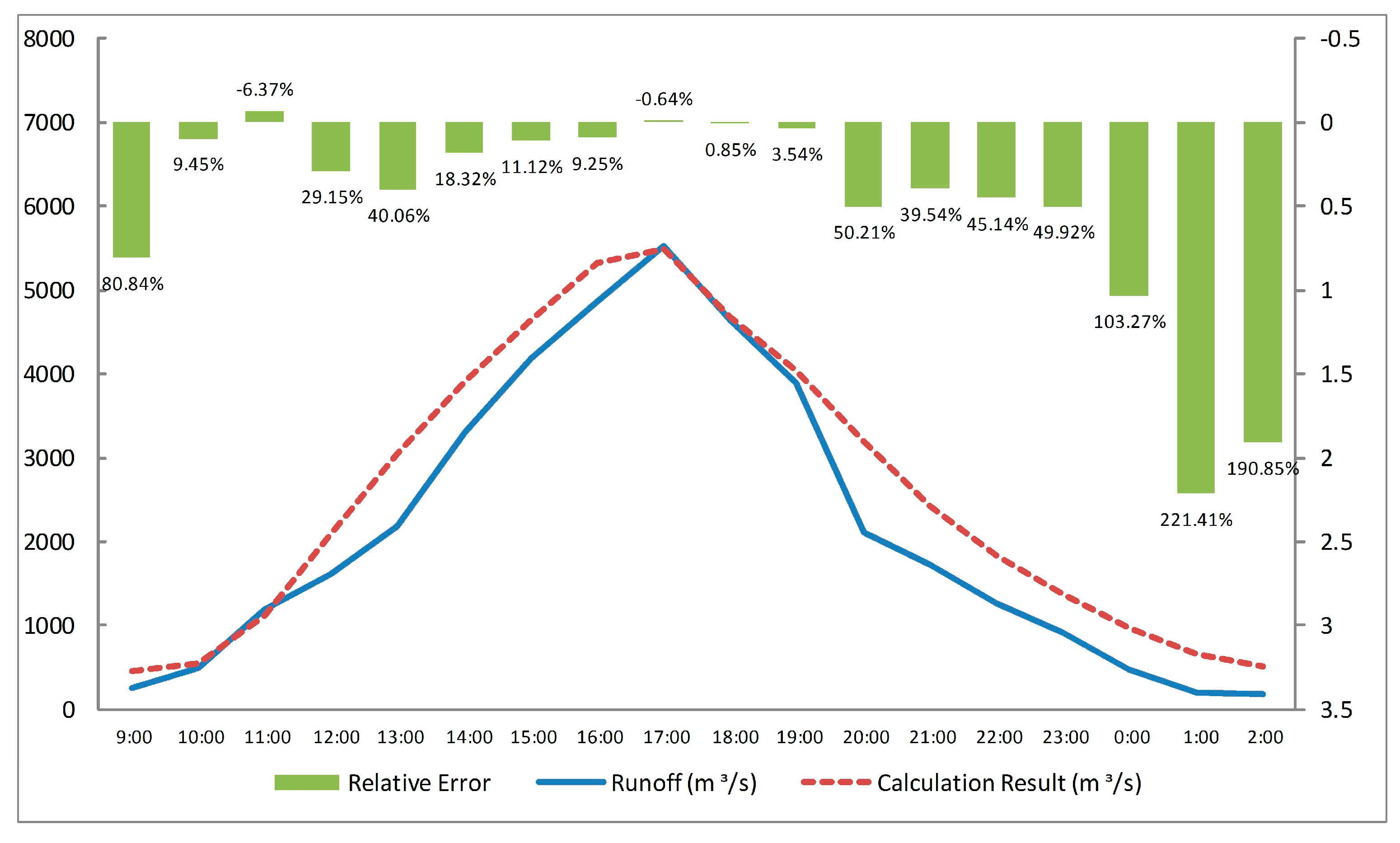
4.3.3. Flood Routing Result (H = 700 m)
4.4. Estimation for Potential Impact Area (H = 700 m)
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mckillop, R.J.; Clague, J.J. Statistical, remote sensing-based approach for estimating the probability of catastrophic drainage from moraine-dammed lakes in southwestern British Columbia. Glob. Planet. Chang. 2007, 56, 153–171. [Google Scholar] [CrossRef]
- Zhou, J.W.; Cui, P.; Fang, H. Dynamic process analysis for the formation of Yangjiagou landslide-dammed lake triggered by the Wenchuan earthquake, China. Landslides 2013, 10, 331–342. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Schumann, J.P.; Neal, J.C.; Mason, D.C.; Bates, P.D. The accuracy of sequential aerial photography and SAR data for observing urban flood dynamics, a case study of the UK summer 2007 floods. Remote Sens. Environ. 2011, 115, 2536–2546. [Google Scholar] [CrossRef]
- Sheng, Y.; Gong, P.; Xiao, Q. Quantitative dynamic flood monitoring with NOAA AVHRR. Int. J. Remote Sens. 2001, 22, 1709–1724. [Google Scholar] [CrossRef]
- Ling, F.; Du, Y. Monitoring river discharge with remotely sensed imagery using river island area as an indicator. J. Appl. Remote Sens. 2012, 6, 063564. [Google Scholar] [CrossRef]
- Van Dijk, A.; Renzullo, L.J. Water resource monitoring systems and the role of satellite observations. HESS 2010, 7, 2360–2364. [Google Scholar] [CrossRef]
- Jain, S.K.; Saraf, A.K.; Goswami, A.; Ahmad, T. Flood inundation mapping using NOAA AVHRR data. Water Resour. Manag. 2006, 20, 949–959. [Google Scholar] [CrossRef]
- Lu, S.; Wu, B.; Yan, N.; Wang, H. Water body mapping method with HJ-1A/B satellite imagery. Int. J. Appl. Earth Obs. 2011, 13, 428–434. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Tateishi, R. A water index for rapid mapping of shoreline changes of five East African Rift Valley lakes: An empirical analysis using Landsat TM and ETM+ data. Int. J. Remote Sens. 2006, 27, 3153–3181. [Google Scholar] [CrossRef]
- Sun, F.; Sun, W.; Chen, J.; Gong, P. Comparison and improvement of methods for identifying waterbodies in remotely sensed imagery. Int. J. Remote Sens. 2012, 33, 6854–6875. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, C.; Xu, K.; Watanabea, M. Flood disaster monitoring and evaluation in China. Environ. Hazard. 2002, 4, 33–43. [Google Scholar]
- Stephens, E.M.; Batesa, P.D.; Freera, J.E.; Masonb, D.C. The impact of uncertainty in satellite data on the assessment of flood inundation models. J. Hydrol. 2012, 414, 162–173. [Google Scholar] [CrossRef]
- Kuenzer, C.; Guo, H.; Huth, J.; Leinenkugel, P.; Li, X.; Dech, S. Flood Mapping and Flood Dynamics of the Mekong Delta: ENVISAT-ASAR-WSM Based Time Series Analyses. Remote Sens. 2013, 5, 687–715. [Google Scholar] [CrossRef] [Green Version]
- Amini, J. A method for generating floodplain maps using IKONOS images and DEMs. Int. J. Remote Sens. 2010, 31, 2441–2456. [Google Scholar] [CrossRef]
- Zheng, D.; Bastiaanssen, W.G.M. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar]
- Othman, A.A.; Gloaguen, R. River Courses Affected by Landslides and Implications for Hazard Assessment: A High Resolution Remote Sensing Case Study in NE Iraq–W Iran. Remote Sens. 2013, 5, 1024–1044. [Google Scholar] [CrossRef]
- Van Genderen, J.L. Atlas of remote sensing of the Wenchuan earthquake. Int. J. Digit. Earth 2009, 4, 91–92. [Google Scholar] [CrossRef]
- Furuya, M.; Wahr, J.M. Water level changes at an ice-dammed lake in west Greenland inferred from InSAR data. Geophys. Res. Lett. 2005, 32, 301–320. [Google Scholar] [CrossRef]
- Pan, S.; Li, X.; Song, X. Using Remote Sensing Data to Monitor Landslide-dammed Lakes Caused by Wenchuan Earthquake. J. Geo-Inf. Sci. 2009, 11, 299–304. (In Chinese) [Google Scholar] [CrossRef]
- Fan, J.; Tian, B.; Cheng, G.; Tao, H.; Zhang, J.; Yan, D.; Su, F.; Liu, B. Investigation on Damming Object Induced by the Earthquake of Wenchuan on May 12 Based on Multi-platform Remote Sensing. J. Mt. Sci-Engl. 2008, 26, 257–262. (In Chinese) [Google Scholar]
- Gorum, T.; Fan, X.; Westen, C.J.V.; Huang, R.Q. Distribution pattern of earthquake-induced landslides triggered by the 12 May 2008 Wenchuan earthquake. Geomorphology 2011, 133, 152–167. [Google Scholar] [CrossRef]
- Ehrlich, D.; Guo, H.D.; Molch, K.; Ma, J.W.; Pesaresi, M. Identifying damage caused by the 2008 Wenchuan earthquake from VHR remote sensing data. Int. J. Digit. Earth 2009, 2, 309–326. [Google Scholar] [CrossRef]
- Yinsung, H.; Yuhsiung, H. Impact of earthquake-induced dammed lakes on channel evolution and bed mobility: Case study of the Tsaoling landslide dammed lake. J. Hydrol. 2009, 374, 43–55. [Google Scholar]
- Bookhagen, B.; Haselton, K.; Trauth, M.H. Hydrological modelling of a Pleistocene landslide-dammed lake in the Santa Maria Basin, NW Argentina. Palaeogeogr. Palaeoclimatol. 2001, 169, 113–127. [Google Scholar] [CrossRef]
- Conesa-Garcia, C.; Caselles-Miralles, V.; Sanchez Tomas, J.M.; Garcia-Lorenzo, R. Hydraulic Geometry, GIS and Remote Sensing, Techniques against Rainfall-Runoff Models for Estimating Flood Magnitude in Ephemeral Fluvial Systems. Remote Sens. 2010, 2, 2607–2628. [Google Scholar] [CrossRef]
- Xue, Y.; Xu, W.; Luo, S.; Chen, H.; Li, N.; Xu, L. Experimental study of dam-break flow in cascade reservoirs with steep bottom slope. J. Hydrodyn. 2011, 23, 491–497. [Google Scholar] [CrossRef]
- Cui, P.; Dang, C.; Zhuang, J.Q.; You, Y.; Chen, X.Q. Landslide-dammed lake at Tangjiashan, Sichuan province, China (triggered by the Wenchuan Earthquake, May 12, 2008): Risk assessment, mitigation strategy, and lessons learned. Environ. Earth Sci. 2012, 65, 1055–1065. [Google Scholar] [CrossRef]
- Peng, C.; Zhu, Y.Y.; Han, Y.S.; Chen, X.Q.; Zhuang, J.Q. The 12 May Wenchuan earthquake-induced landslide lakes: Distribution and preliminary risk evaluation. Landslides 2009, 6, 209–223. [Google Scholar]
- Peng, M.; Zhang, L.M. Analysis of human risks due to dam break floods—Part 2: Application to Tangjiashan landslide dam failure. Nat. Hazards 2012, 64, 1899–1923. [Google Scholar] [CrossRef]
- Yang, S.H.; Pan, Y.W.; Dong, J.J.; Yeh, K.C.; Liao, J.J. A systematic approach for the assessment of flooding hazard and risk associated with a landslide dam. Nat. Hazards 2013, 65, 41–62. [Google Scholar] [CrossRef]
- Chen, X.Q.; Cui, P.; Li, Y.; Zhao, W.Y. Emergency response to the Tangjiashan landslide-dammed lake resulting from the 2008 Wenchuan Earthquake, China. Landslides 2011, 8, 91–98. [Google Scholar] [CrossRef]
- Liu, J.; Ma, C.; Liu, C.; Qin, D.; Gu, X. An extended maxima transform-based region growing algorithm for convective cell detection on satellite images. Remote Sens. Lett. 2014, 5, 971–980. [Google Scholar] [CrossRef]
- Zhan, D.J.; Ye, S.Z. Engineering Hydrology, 17th ed.; China Water & Power Press: Beijing, China, 2000; pp. 122–125. [Google Scholar]
- Bahrami, S.; Ardejani, F.D.; Baafi, E. Application of artificial neural network coupled with genetic algorithm and simulated annealing to solve groundwater inflow problem to an advancing open pit mine. J. Hydrol. 2016, 536, 471–484. [Google Scholar] [CrossRef]
| Data | Acquisition Date | Resolution | Format | Region |
|---|---|---|---|---|
| Formosat-2 | 20 May 2008 | 2 m | TIFF | Tanjiashan Dammed Lake |
| Aerial photograph | 18 May 2008 | 0.15 m | TIFF | Beichuan Town |
| Envisat | 20 May 2008 | 30 m | TIFF | Tanjiashan Dammed Lake |
| DEM | 2003 | 1:50,000 | TIFF | Xun River Basin |
| Water Level (m) | Reservoir Capacity (108 m3) | Area (km2) |
|---|---|---|
| 690 | 0.248 | 1.591 |
| 695 | 0.338 | 1.958 |
| 700 | 0.445 | 2.430 |
| 705 | 0.572 | 2.680 |
| 710 | 0.714 | 2.975 |
| 715 | 0.872 | 3.380 |
| 720 | 1.076 | 4.538 |
| 725 | 1.318 | 5.077 |
| 730 | 1.587 | 5.671 |
| 735 | 1.888 | 6.276 |
| 740 | 2.229 | 7.223 |
| 745 | 2.607 | 7.883 |
| 750 | 3.018 | 8.564 |
| Dam-Break Time | Flood Peak | Peak Appearance Time | Ending Flow |
|---|---|---|---|
| 1 h | 83,620 m3/s | 17 min | 76 ms3/s |
| Reach | C0 | C1 | C2 |
|---|---|---|---|
| Tangjiashan to Tongkou | 0.1722 | 0.1615 | 0.6663 |
| Tongkou to Xiangshui | 0.5197 | 0.2819 | 0.1984 |
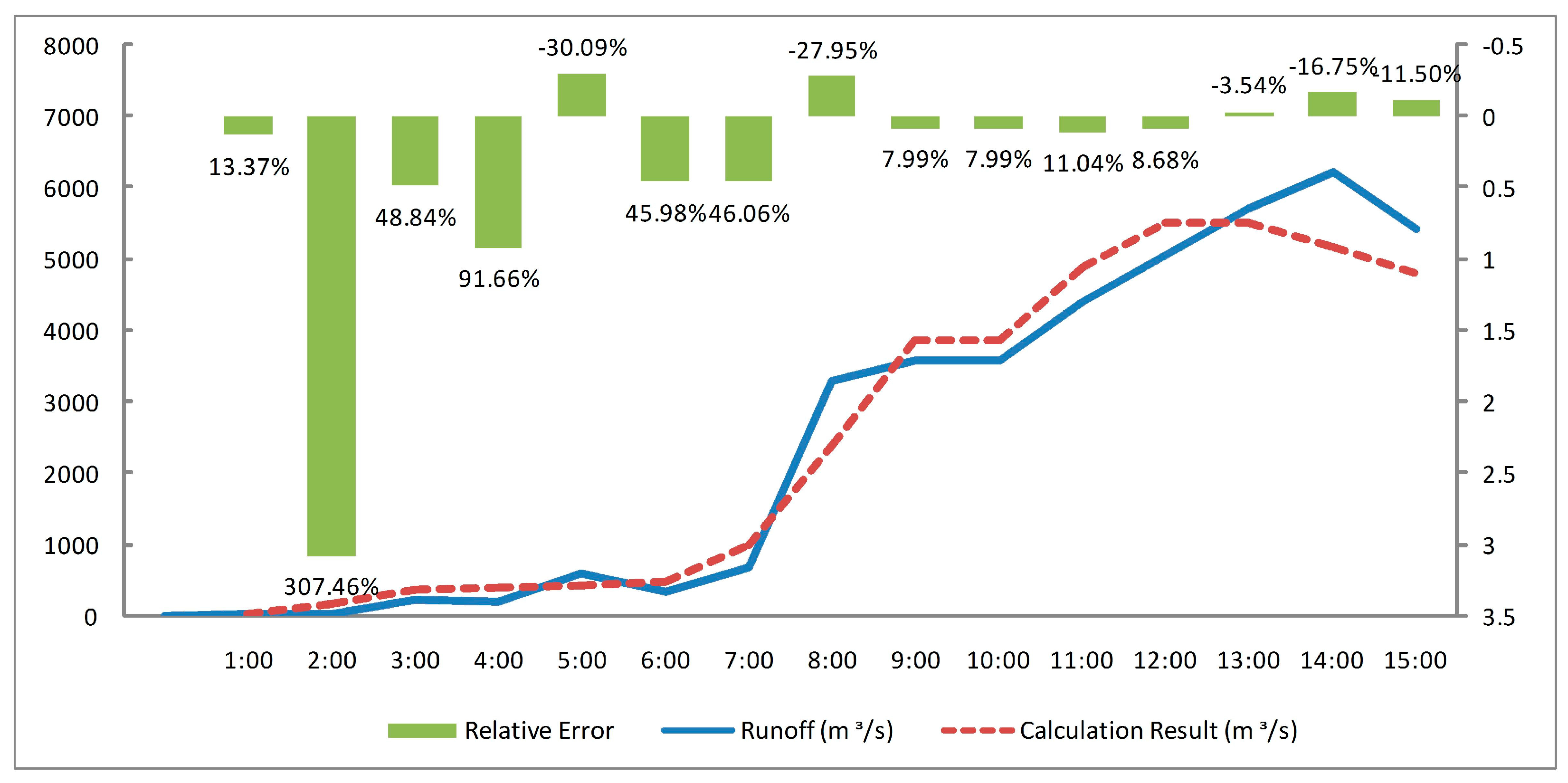
| Time (h) Tangjiashan | Water Level (m) | Runoff Q (m3/s) | Time (h) Tongkou | Water Level (m) | Runoff Q′ (m3/s) | Flood Routing Result | Relative Error % |
|---|---|---|---|---|---|---|---|
| 0:00 | 620.90 | 33.1 | 0:00 | 535.31 | 23 | ||
| 1:00 | 621.05 | 64.3 | 1:00 | 535.36 | 28 | 31.743 | +13.37% |
| 2:00 | 622.75 | 858 | 2:00 | 535.52 | 44 | 179.282 | +307.46% |
| 3:00 | 622.25 | 576 | 3:00 | 537.19 | 240 | 357.210 | +48.84% |
| 4:00 | 621.93 | 415 | 4:00 | 537.1 | 210 * | 402.496 | +91.66% |
| 5:00 | 622.03 | 465 | 5:00 | 538.27 | 594 | 415.279 | −30.09% |
| 6:00 | 622.62 | 780 | 6:00 | 537.33 | 333 | 486.114 | +45.98% |
| 7:00 | 625.90 | 3240 | 7:00 | 538.57 | 690 | 1007.800 | +46.06% |
| 8:00 | 629.54 | 6870 | 8:00 | 545.05 | 3300 | 2377.770 | −27.95% |
| 9:00 | 629.54 | 6870 | 9:00 | 545.65 | 3590 | 3876.827 | +7.99% |
| 10:00 | 629.54 | 6870 | 10:00 | 545.65 | 3590 | 3876.827 | +7.99% |
| 11:00 | 629.59 | 6930 | 11:00 | 547.16 | 4400 | 4885.981 | +11.04% |
| 12:00 | 629.23 | 6530 | 12:00 | 548.25 | 5060 | 5499.190 | +8.68% |
| 13:00 | 627.34 | 4640 | 13:00 | 549.20 | 5720 | 5517.713 | −3.54% |
| 14:00 | 626.94 | 4320 | 14:00 | 549.73 | 6210 | 5169.716 | −16.75% |
| 15:00 | 626.47 | 3800 | 15:00 | 548.80 | 5420 | 4796.622 | −11.5% |
| Reach Parameters | I2 (m3/s) | I1 (m3/s) | O1 (m3/s) | O2 (m3/s) |
|---|---|---|---|---|
| Tangjiashan to Tongkou | 83,620 | 3.2 | 4 | 14,402.6 |
| C0 = 0.1722 | 76 | 83,620 | 14,402.6 | 23,114.1 |
| C1 = 0.1615 | 76 | 76 | 23,114.1 | 15,426.3 |
| C2 = 0.6663 | 76 | 76 | 15,426.3 | 10,303.9 |
| 76 | 76 | 10,303.9 | 6890.9 | |
| 76 | 76 | 6890.9 | 4616.7 | |
| 76 | 76 | 4616.7 | 3101.5 | |
| 76 | 76 | 3101.5 | 2091.9 | |
| 76 | 76 | 2091.9 | 1419.2 |
| Reach Parameters | I2 (m3/s) | I1 (m3/s) | O1 (m3/s) | O2 (m3/s) |
|---|---|---|---|---|
| Tongkou to Xiangshui | 14,402.6 | 4 | 2 | 7486.6 |
| C0 = 0.5197 | 23,114.1 | 14,402.6 | 7486.6 | 17,557.8 |
| C1 = 0.2819 | 15,426.3 | 23,114.1 | 17,557.8 | 18,016.4 |
| C2 = 0.1984 | 10,303.9 | 15,426.3 | 18,016.4 | 13,278.1 |
| 6890.9 | 10,303.9 | 13,278.1 | 9120.2 | |
| 4616.7 | 6890.9 | 9120.2 | 6151.3 | |
| 3101.5 | 4616.7 | 6151.3 | 4133.7 | |
| 2091.9 | 3101.5 | 4133.7 | 2781.6 | |
| 1419.2 | 2091.9 | 2781.6 | 1879.1 |
| Hydrologic Stations | The Runoff (y) vs. Elevation (x) Curve | Flood Peak | Elevation Maximum |
|---|---|---|---|
| Tongkou | y = 20.9186473861676x2 − 22,283.2134587244x + 5,934,150.94321418 | 23,114.1 m3/s | 565.89 m |
| R2 = 0.986247730187266 | |||
| Xiangshui | y = 7.26568228353629x3 − 11,429.4504515713x2 + 5,993,229.82457408x − 1,047,570,044.59771 | 18,016.4 m3/s | 537.47 m |
| R2 = 0.997800010971559 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, B.; Yang, S.; Ye, S. Integrated Application of Remote Sensing, GIS and Hydrological Modeling to Estimate the Potential Impact Area of Earthquake-Induced Dammed Lakes. Water 2017, 9, 777. https://doi.org/10.3390/w9100777
Cao B, Yang S, Ye S. Integrated Application of Remote Sensing, GIS and Hydrological Modeling to Estimate the Potential Impact Area of Earthquake-Induced Dammed Lakes. Water. 2017; 9(10):777. https://doi.org/10.3390/w9100777
Chicago/Turabian StyleCao, Bo, Shengmei Yang, and Song Ye. 2017. "Integrated Application of Remote Sensing, GIS and Hydrological Modeling to Estimate the Potential Impact Area of Earthquake-Induced Dammed Lakes" Water 9, no. 10: 777. https://doi.org/10.3390/w9100777





