Transient Modeling of Flow in Unsaturated Soils Using a Novel Collocation Meshless Method
Abstract
:1. Introduction
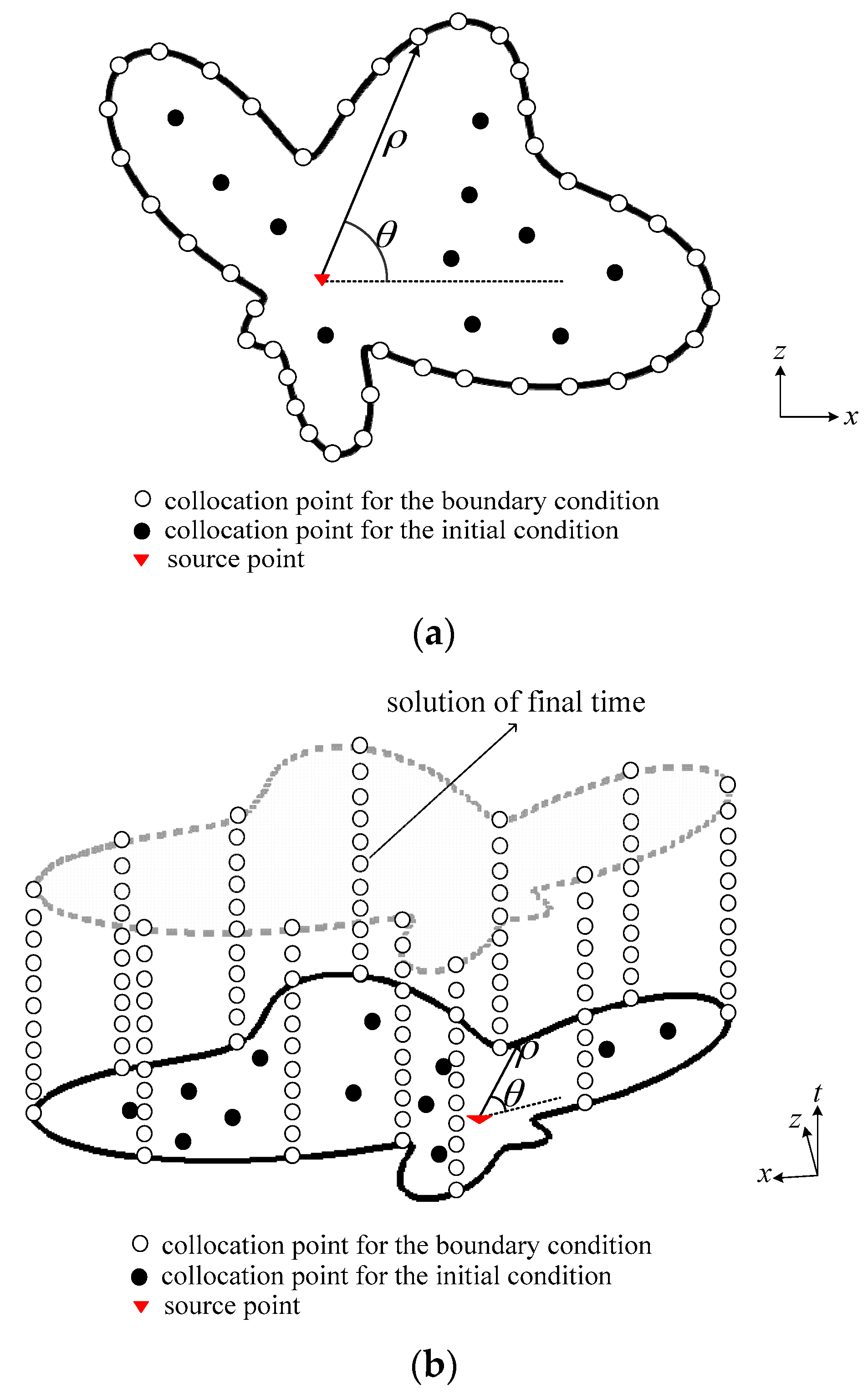
2. Trefftz Method for Modeling Subsurface Flow in Unsaturated Soils
2.1. The Linearized Richards Equation
2.2. The Trefftz Method in Euclidean Space
2.3. The T Basis Function for Steady-State Linearized Richards Equation
2.4. The Trefftz Method in Minkowski Spacetime
3. Numerical Examples
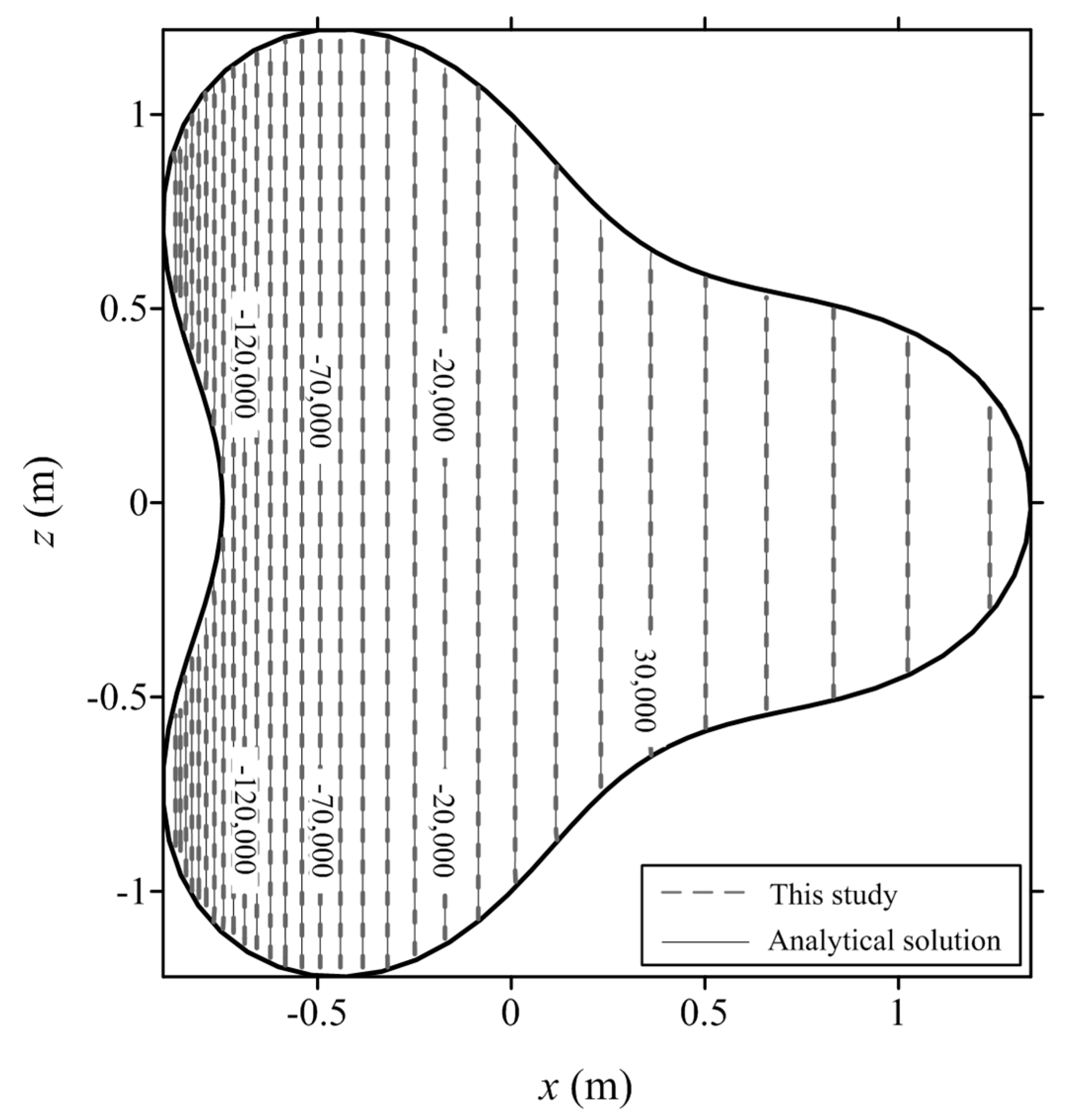
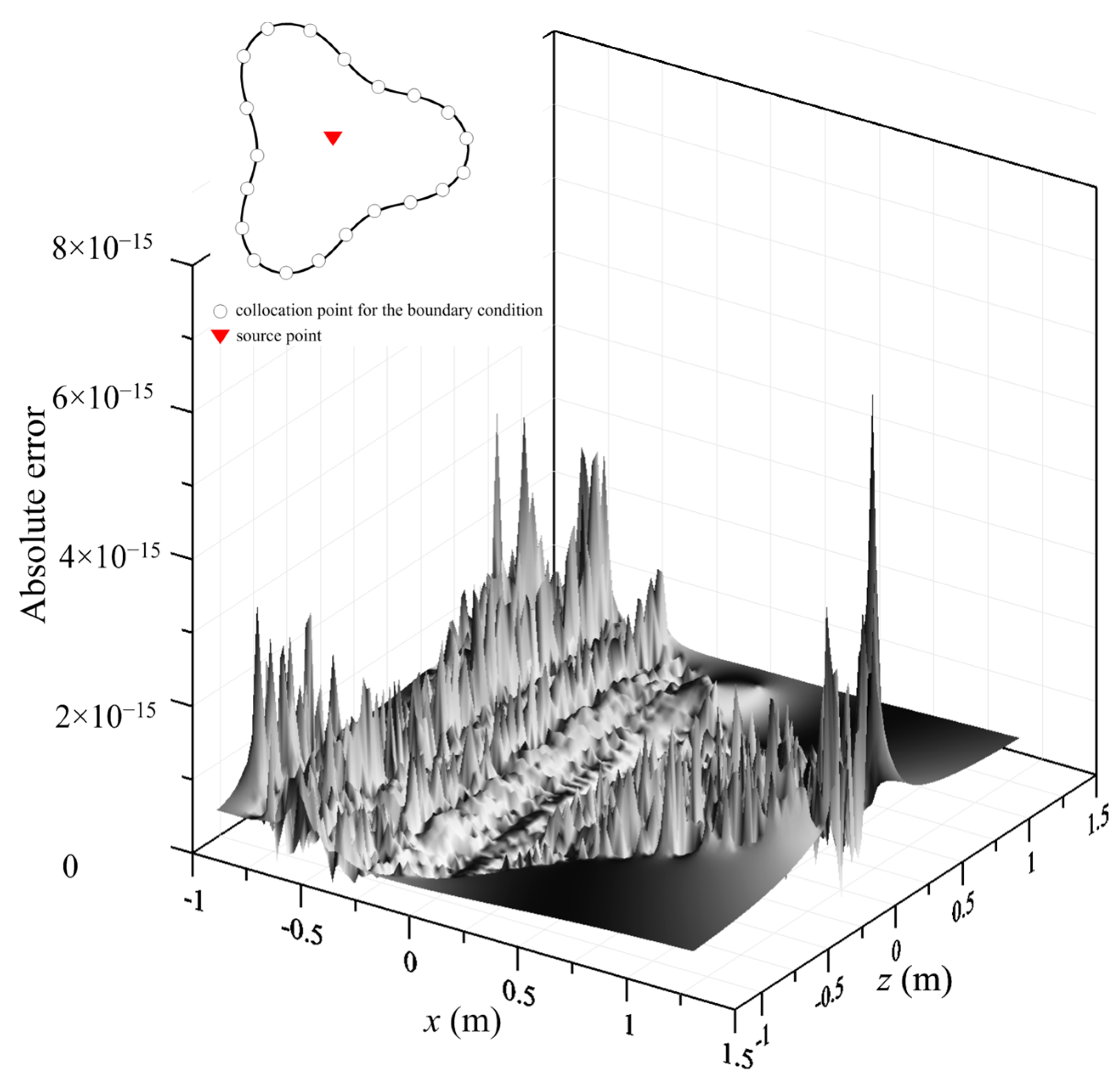
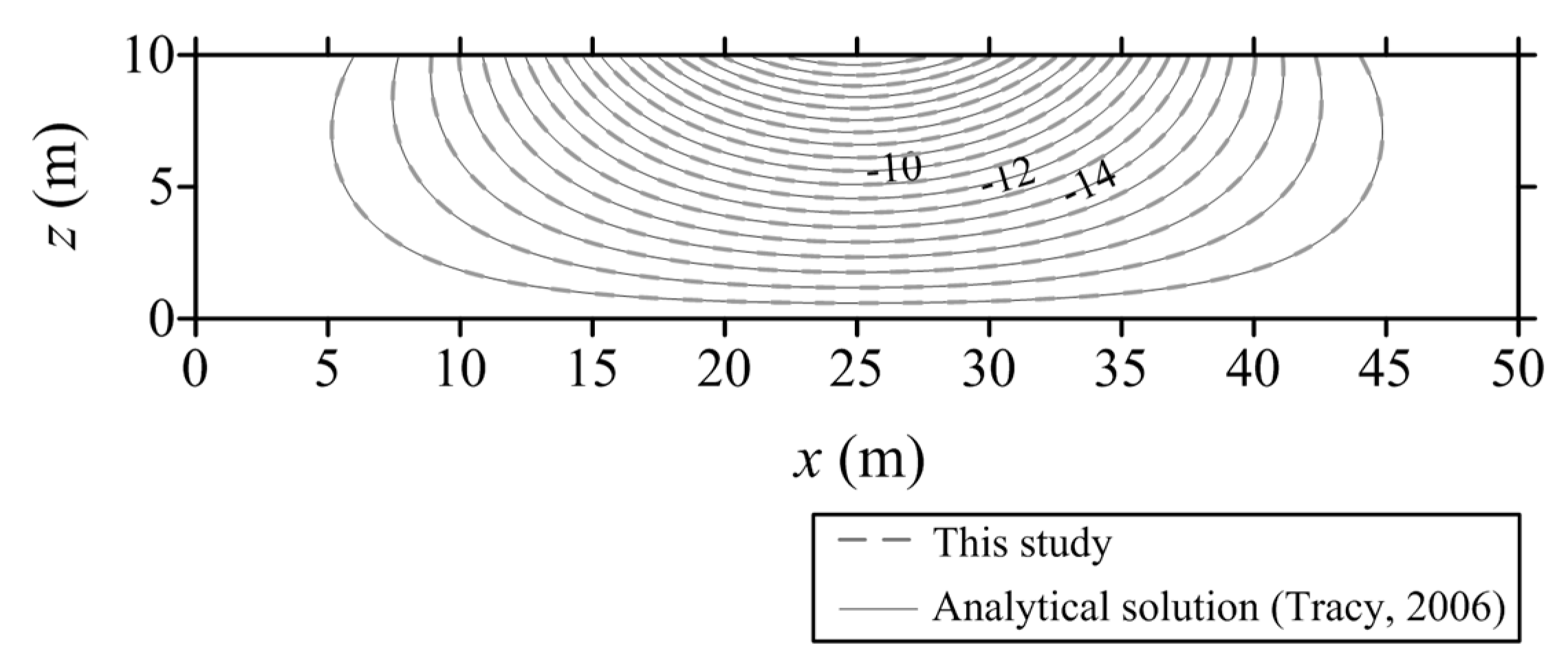
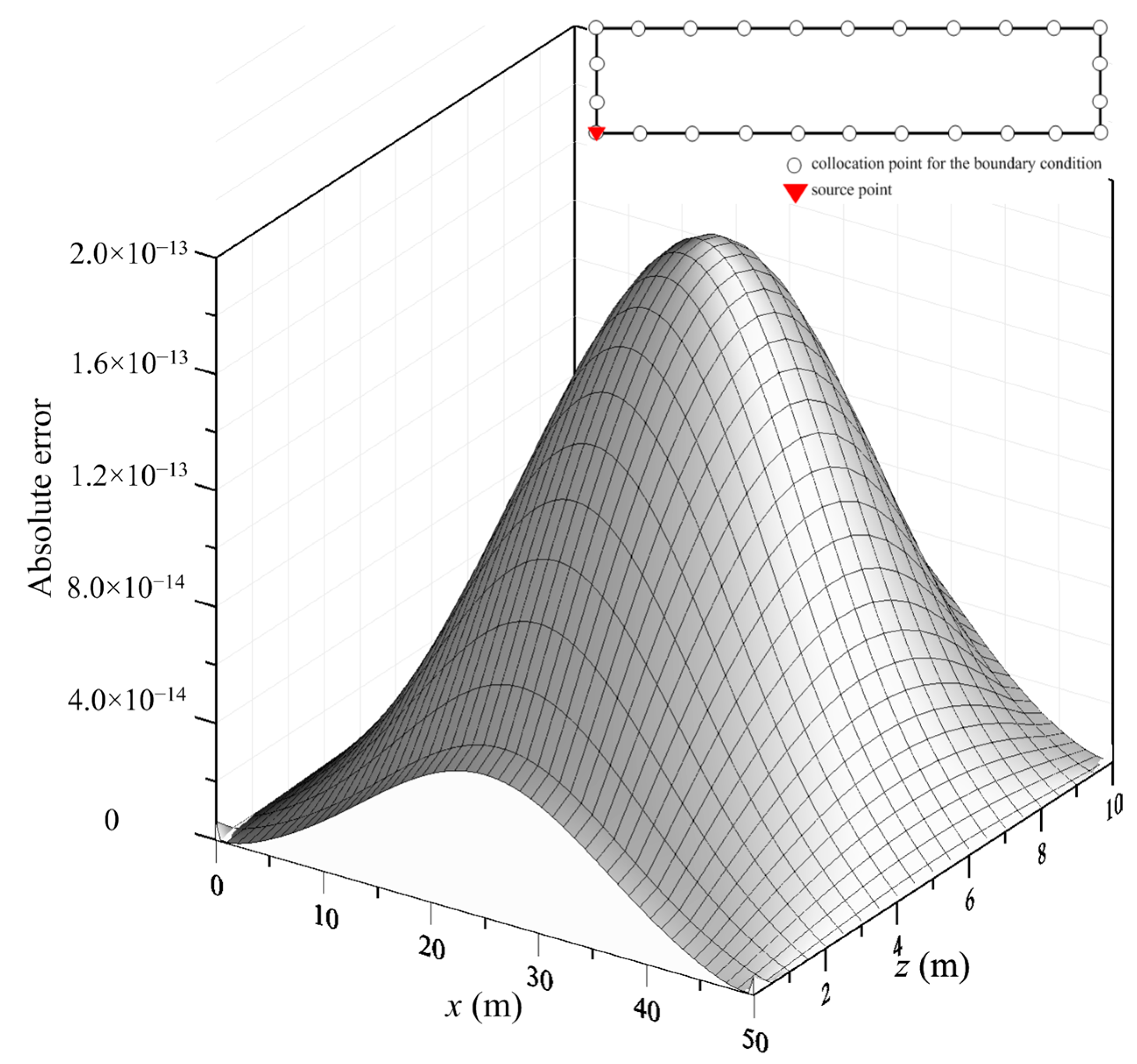
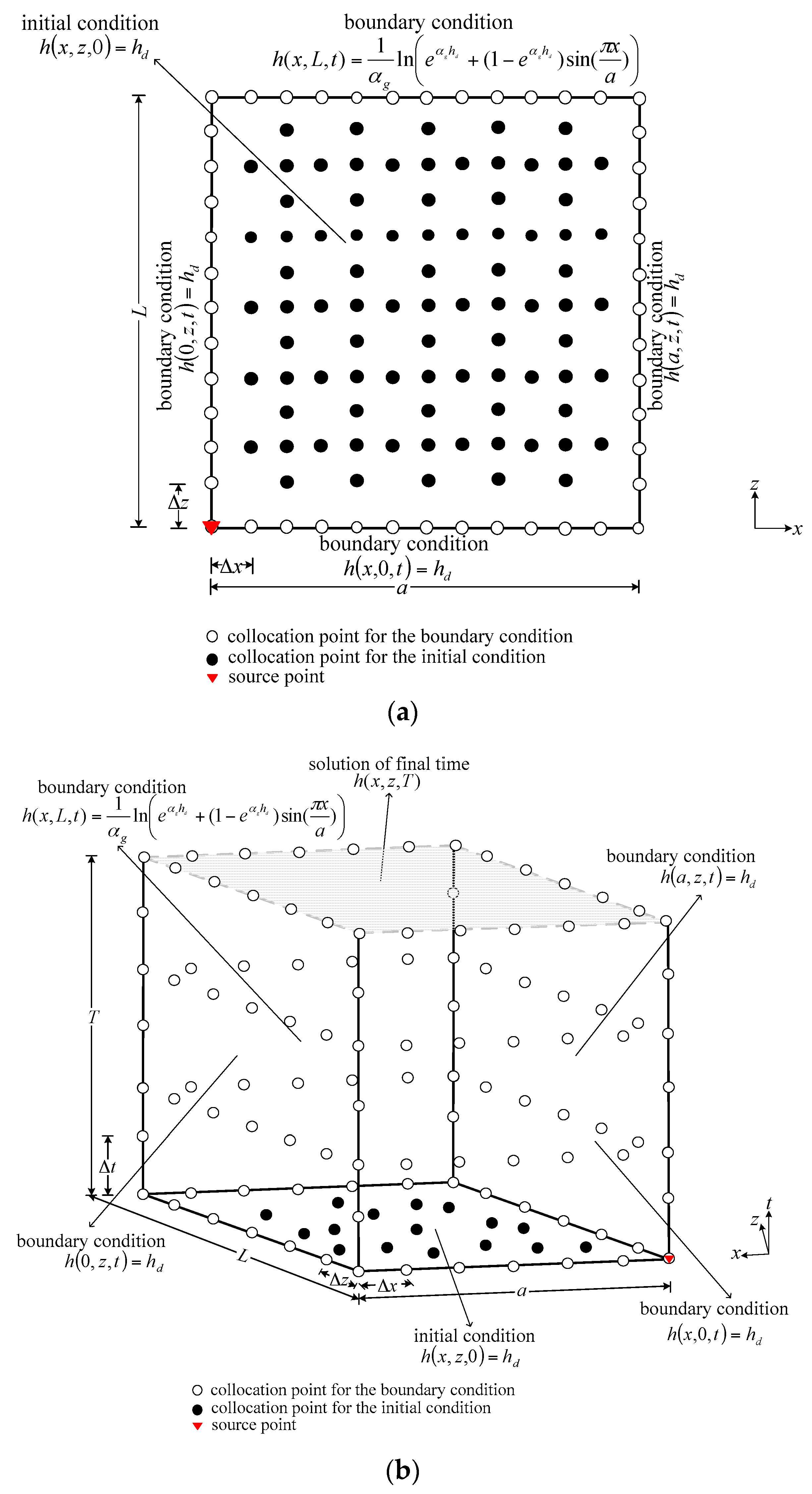
3.1. Steady-State Modeling of Two-Dimensional Subsurface Flow in Unsaturated Soil
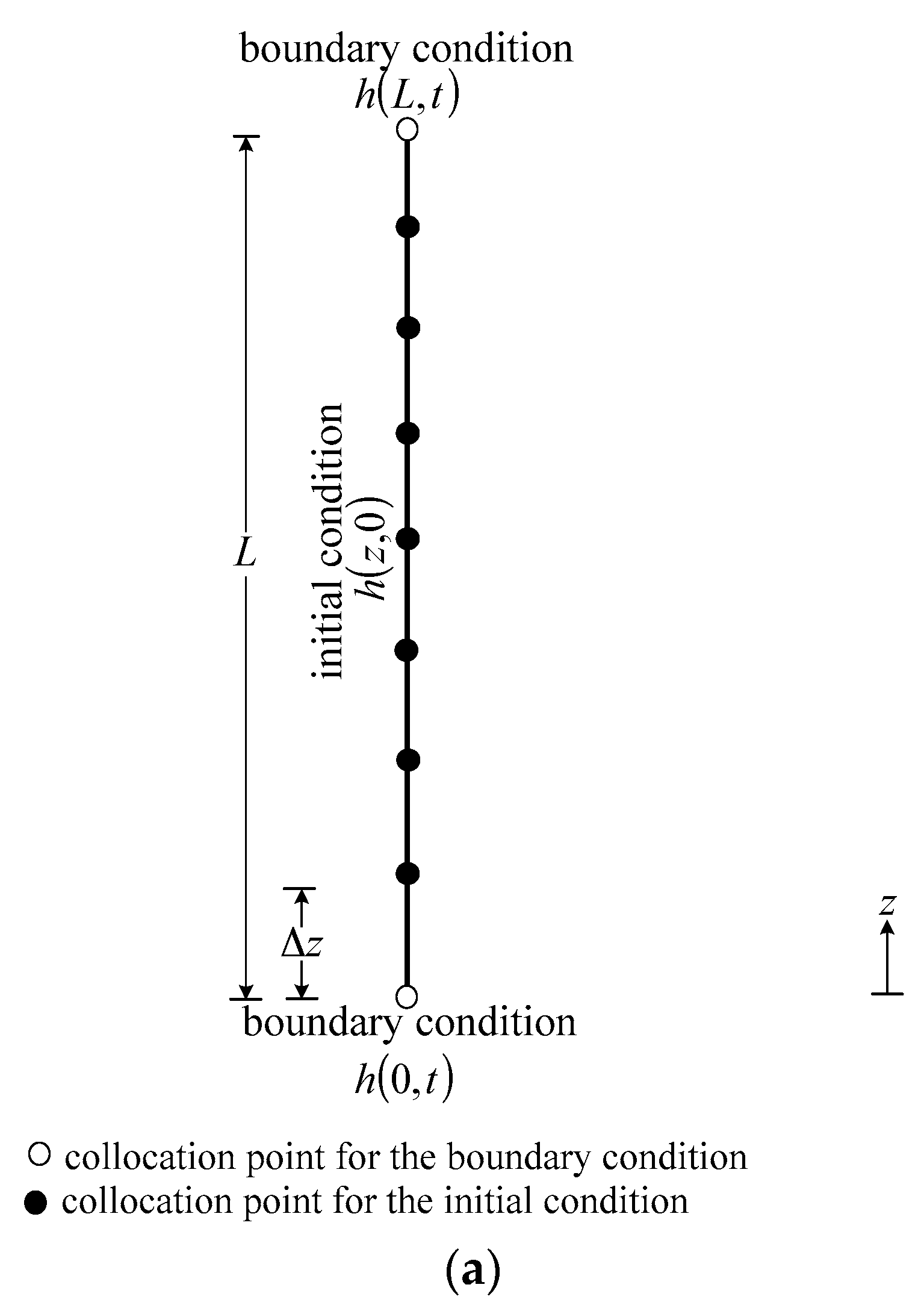
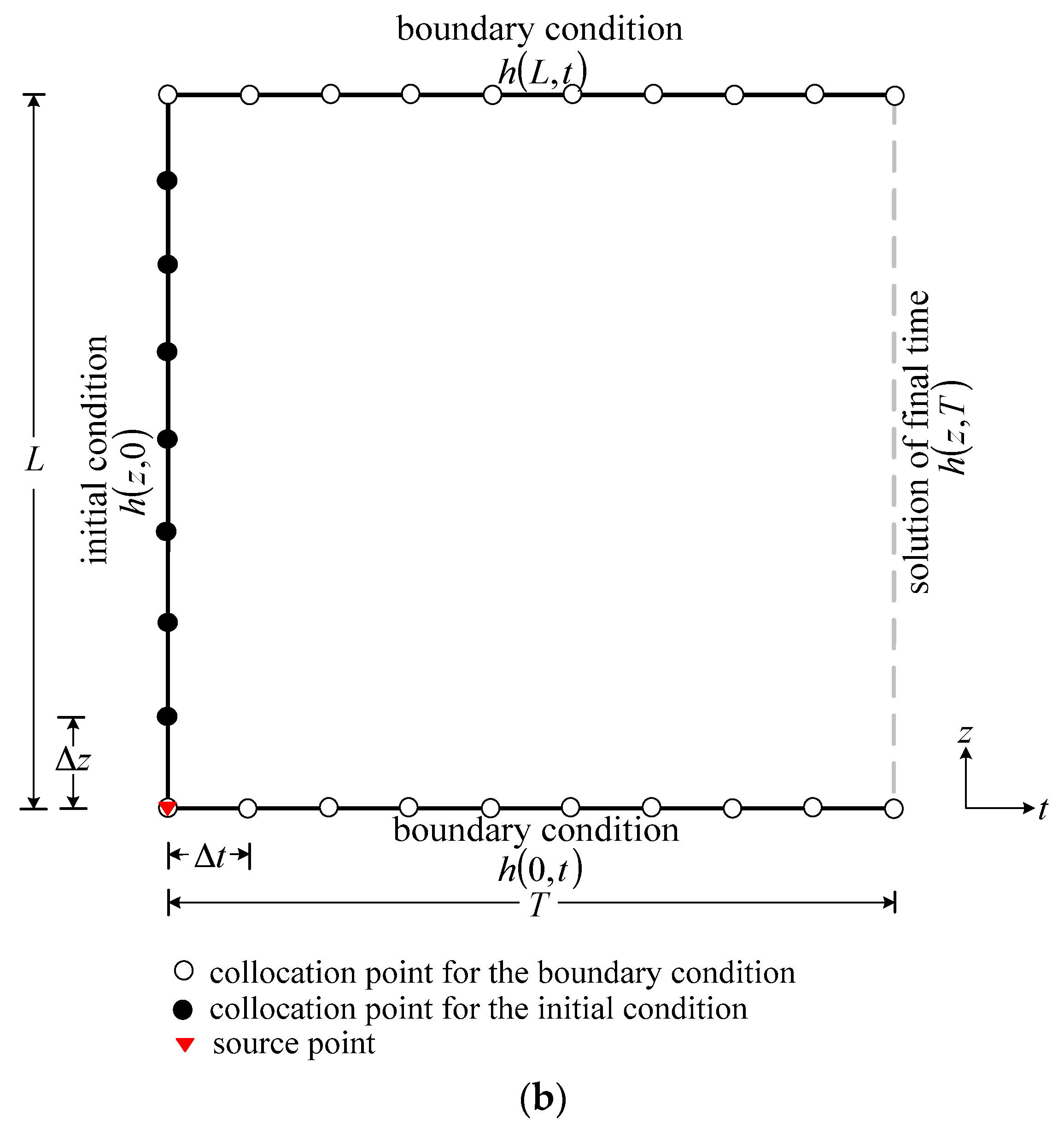
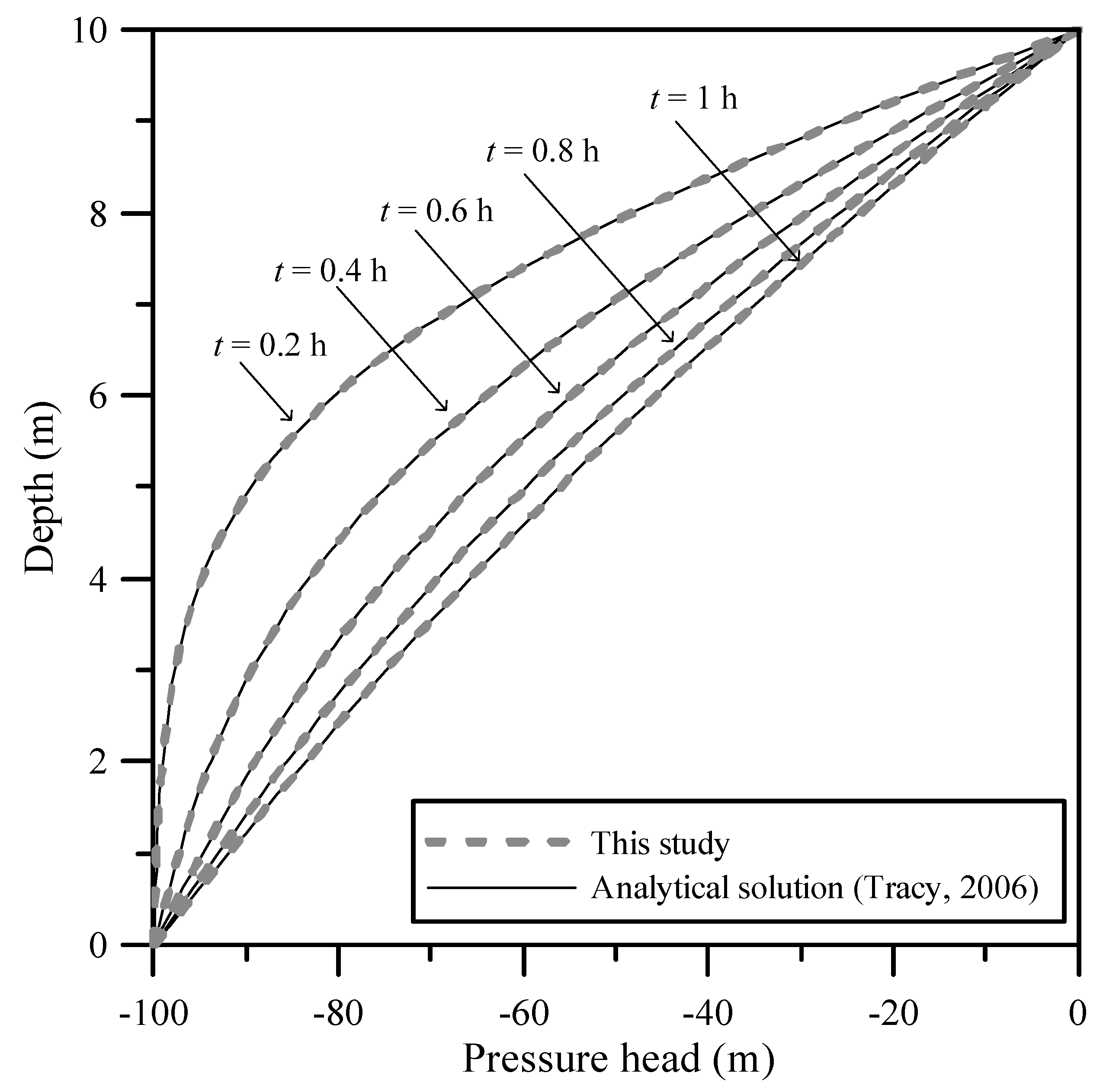
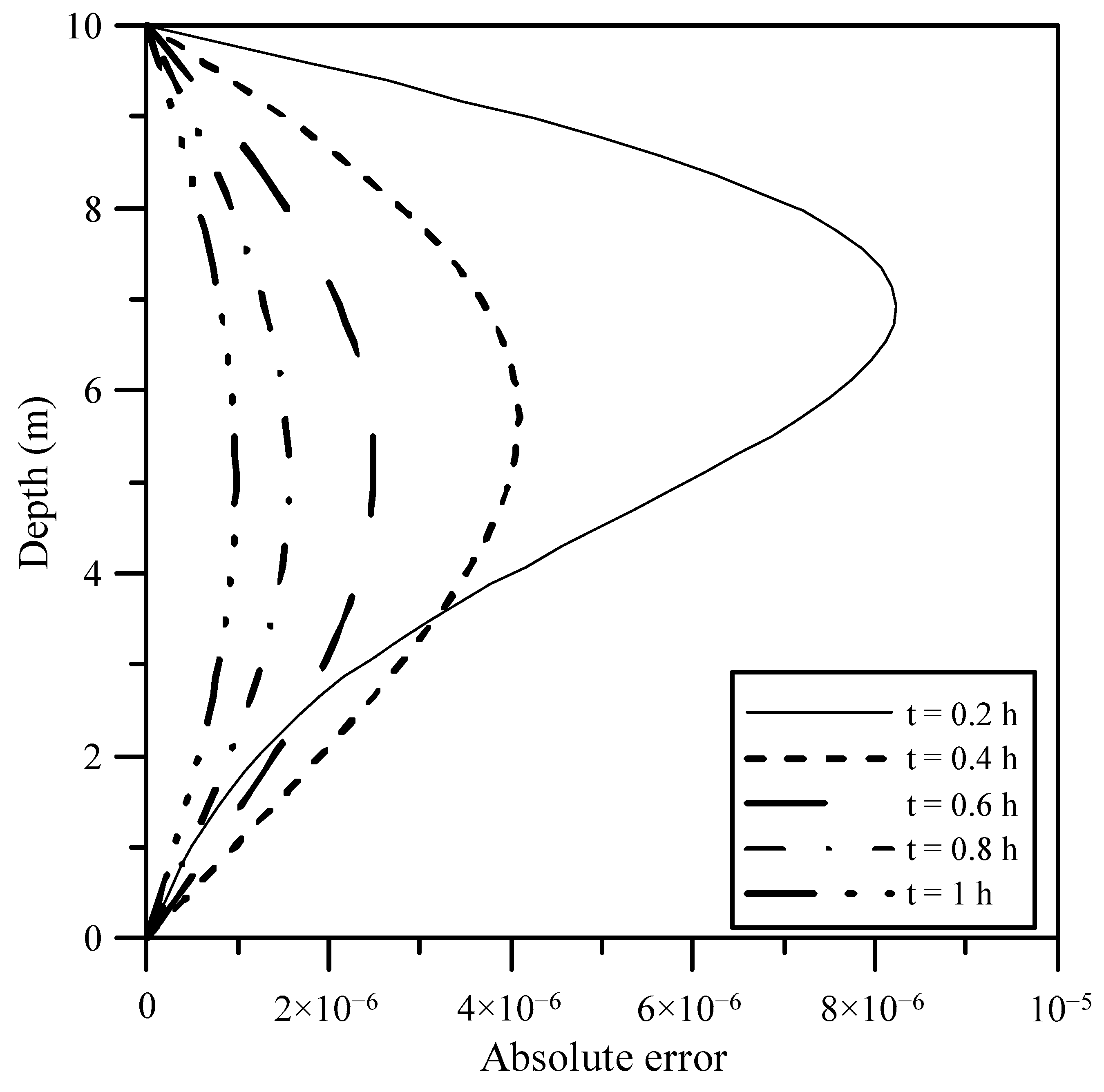
3.2. Transient Modeling of One-Dimensional Flow in Unsaturated Soil
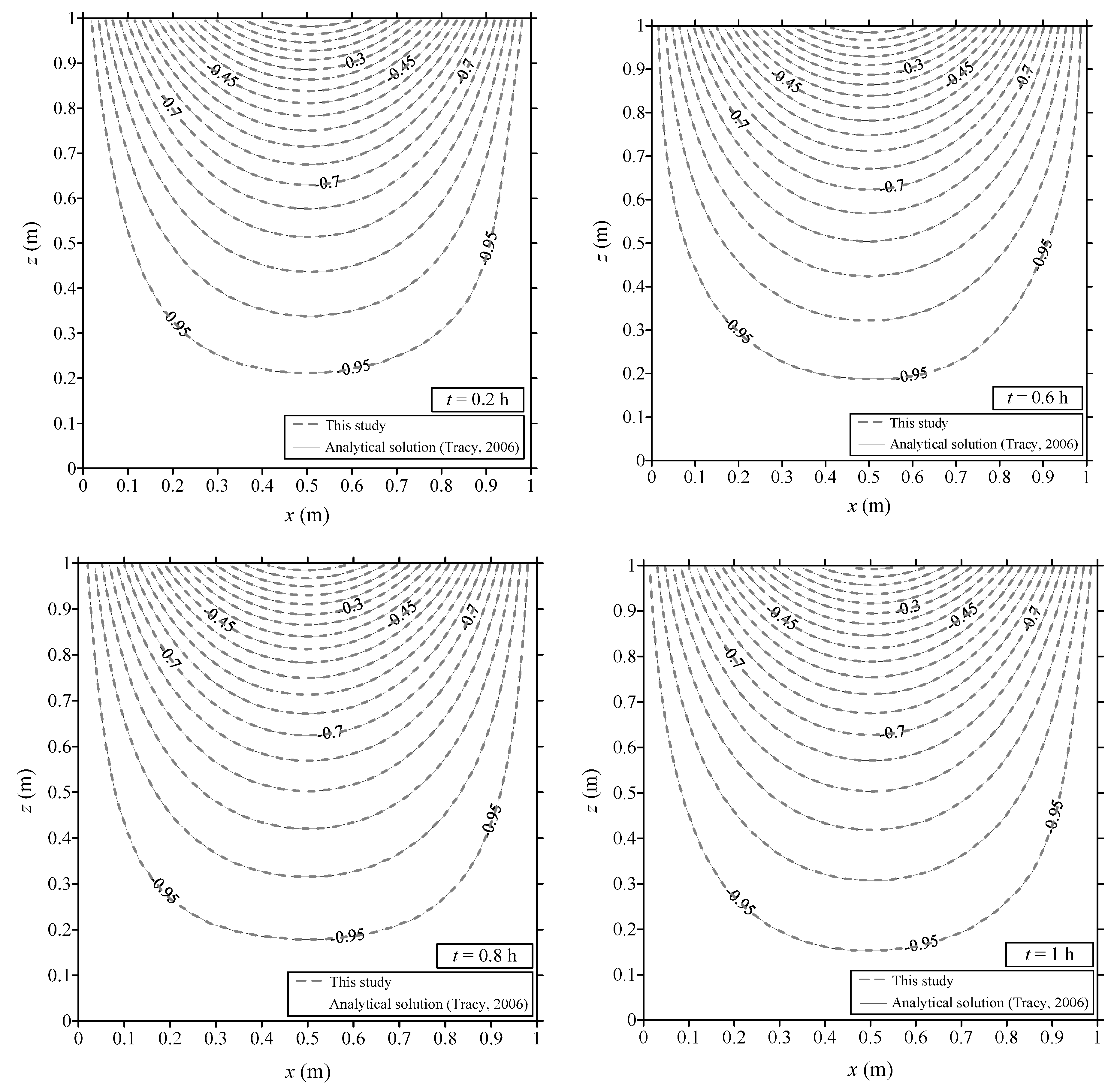
3.3. Transient Modeling of Two-Dimensional Flow in Unsaturated Soil
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sinai, G.; Dirksen, C. Experimental evidence of lateral flow in unsaturated homogeneous isotropic sloping soil due to rainfall. Water Resour. Res. 2006, 42, W12402. [Google Scholar] [CrossRef]
- Ebel, B.A. Simulated unsaturated flow processes after wildfire and interactions with slope aspect. Water Resour. Res. 2013, 49, 8090–8107. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Su, Y.; Xiao, J.E.; Huang, C.C. Transient modeling of regional rainfall-triggered shallow landslides. Environ. Earth Sci. 2017, 76, 1–18. [Google Scholar] [CrossRef]
- Huang, F.; Luo, X.; Liu, W. Stability analysis of hydrodynamic pressure landslides with different permeability coefficients affected by reservoir water level fluctuations and rainstorms. Water 2017, 9, 450. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Hydrology Paper No. 3; Colorado State University: Fort Collins, CO, USA, 1964; p. 27. [Google Scholar]
- Van Genuchten, M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A.; Huang, S. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 533–546. [Google Scholar] [CrossRef]
- Haverkamp, R.; Vauclin, M.; Touma, J.; Wierenga, P.J.; Vachaud, G. A comparison of numerical simulation models for one dimensional infiltration. Soil Sci. Soc. Am. J. 1977, 41, 285–294. [Google Scholar] [CrossRef]
- Kavetski, D.; Binning, P.; Sloan, S.W. Noniterative time stepping schemes with adaptive truncation error control for the solution of Richards equation. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Miller, C.T.; Abhishek, C.; Farthing, M.W. A spatially and temporally adaptive solution of Richards’ equation. Adv. Water Resour. 2006, 29, 525–545. [Google Scholar] [CrossRef]
- Li, H.; Farthing, M.W.; Dawson, C.N.; Miller, C.T. Local discontinuous Galerkin approximations to Richards’ equation. Adv. Water Resour. 2007, 30, 555–575. [Google Scholar] [CrossRef]
- Juncu, G.; Nicola, A.; Popa, C. Nonlinear multigrid methods for numerical solution of the variably saturated flow equation in two space dimensions. Transp. Porous Media 2012, 91, 35–47. [Google Scholar] [CrossRef]
- Carbone, M.; Brunetti, G.; Piro, P. Modelling the Hydraulic behaviour of growing media with the explicit finite volume solution. Water 2015, 7, 568–591. [Google Scholar] [CrossRef]
- Liu, X.; Zhan, H. Calculation of steady-state evaporation for an arbitrary matric potential at bare ground surface. Water 2017, 9, 729. [Google Scholar] [CrossRef]
- Celia, M.A.; Ahuja, L.R.; Pinder, G.F. Orthogonal collocation and alternating- direction procedures for unsaturated flow problems. Adv. Water Resour. 1987, 10, 178–187. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A General mass-conservation numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Chen, F.; Ren, L. Application of the finite difference heterogeneous multiscale method to the Richards’ equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Liu, C.Y.; Ku, C.Y.; Huang, C.C.; Lin, D.G.; Yeih, W. Numerical solutions of groundwater flow in unsaturated layered soil with extreme physical property contrasts. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 325–336. [Google Scholar] [CrossRef]
- Pan, L.; Warrick, A.W.; Wierenga, P.J. Finite elements methods for modeling water flow in variably saturated porous media: Numerical oscillation and mass distributed schemes. Water Resour. Res. 1996, 32, 1883–1889. [Google Scholar] [CrossRef]
- Bergamaschi, L.; Putti, M. Mixed finite elements and Newton-type linearizations for the solution of Richards’ equation. Int. J. Numer. Methods Eng. 1999, 45, 1025–1046. [Google Scholar] [CrossRef]
- Farthing, M.W.; Kees, C.E.; Miller, C.T. Mixed finite element methods and higher order temporal approximations for variably saturated groundwater flow. Adv. Water Resour. 2003, 26, 373–394. [Google Scholar] [CrossRef]
- Bause, M.; Knabner, P. Computation of variably saturated subsurface flow by adaptive mixed hybrid finite element methods. Adv. Water Resour. 2004, 27, 565–581. [Google Scholar] [CrossRef]
- Katsurada, M.; Okamoto, H. The collocation points of the fundamental solution method for the potential problem. Comput. Math. Appl. 1996, 31, 123–137. [Google Scholar] [CrossRef]
- Liu, C.S. A modified collocation Trefftz method for the inverse Cauchy problem of Laplace equation. Eng. Anal. Bound. Elem. 2008, 32, 778–785. [Google Scholar] [CrossRef]
- Chang, Y.S.; Chang, T.J. SPH simulations of solute transport in flows with steep velocity and concentration gradients. Water 2017, 9, 132. [Google Scholar] [CrossRef]
- Yeih, W.; Chan, I.Y.; Ku, C.Y.; Fan, C.M. Solving the inverse Cauchy problem of the Laplace equation using the method of fundamental solutions and the exponentially convergent scalar homotopy algorithm (ECSHA). J. Mar. Sci. Technol. 2015, 23, 162–171. [Google Scholar]
- Huyakorn, P.S.; Pinder, G.F. Computational Methods in Subsurface Flow; Academic Press: London, UK, 1983; pp. 354–401. ISBN 978-0-12-363480-1. [Google Scholar]
- Liu, C.S. A modified Trefftz method for two-dimensional Laplace equation considering the domain’s characteristic length. Comput. Model. Eng. Sci. 2007, 1, 53–65. [Google Scholar]
- Trefftz, E. Ein gegenstück zum ritzschen verfahren. In Proceedings of the 2nd International Congress for Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 131–137. [Google Scholar]
- Kita, E.; Kamiya, N. Trefftz method: An overview. Adv. Eng. Softw. 1995, 24, 3–12. [Google Scholar] [CrossRef]
- Kupradze, V.D.; Aleksidze, M.A. The method of functional equations for the approximate solution of certain boundary value problems. Comput. Math. Math. Phys. 1964, 4, 82–126. [Google Scholar] [CrossRef]
- Chen, C.S.; Karageorghis, A.; Li, Y. On choosing the location of the sources in MFS. Numer. Algorithms 2016, 72, 107–130. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Lin, H.; Atluri, S.N. Meshless Local Petrov-Galerkin (MLPG) method for convection-diffusion problems. Comput. Model. Eng. Sci. 2000, 1, 45–60. [Google Scholar]
- Kita, E.; Ikedab, Y.; Kamiya, N. Trefftz solution for boundary value problem of three-dimensional Poisson equation. Eng. Anal. Bound. Elem. 2005, 29, 383–390. [Google Scholar] [CrossRef]
- Fan, C.M.; Chan, H.F.; Kuo, C.L.; Yeih, W. Numerical solutions of boundary detection problems using modified collocation Trefftz method and exponentially convergent scalar homotopy algorithm. Eng. Anal. Bound. Elem. 2012, 36, 2–8. [Google Scholar] [CrossRef]
- Li, Z.C.; Lu, Z.Z.; Hu, H.Y.; Cheng, H.D. Trefftz and Collocation Methods; WIT Press: Southampton, UK, 2008. [Google Scholar]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Srivastava, R.; Yeh, T.-C.J. Analytical solutions for onedimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 1991, 27, 753–762. [Google Scholar] [CrossRef]
- Galison, P.L. Minkowski’s Space-Time: From visual thinking to the absolute world. Hist. Stud. Phys. Sci. 1979, 10, 85–121. [Google Scholar] [CrossRef]
- Naber, G.L. The Geometry of Minkowski Spacetime; Springer-Verlag: New York, NY, USA, 1992. [Google Scholar]
- Catoni, F.; Boccaletti, D.; Cannata, R.; Catoni, V.; Nichelatti, E.; Zampetti, P. The Mathematics of Minkowski Space-Time with an Introduction to Commutative Hypercomplex Numbers; Birkhäuser Verlag: Basel, Switzerland, 2008; pp. 5–17. ISBN 978-3-7643-8613-9. [Google Scholar]
- Segol, G. Classic Groundwater Simulations; Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Tracy, F.T. Clean two- and three-dimensional analytical solutions of Richards’ equation for testing numerical solvers. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Kita, E.; Kamiya, N.; Iio, T. Application of a direct Trefftz method with domain decomposition to two-dimensional potential problems. Eng. Anal. Bound. Elem. 1999, 23, 539–548. [Google Scholar] [CrossRef]
- Yeih, W.; Liu, C.S.; Kuo, C.L.; Atluri, S.N. On solving the direct/inverse cauchy problems of laplace equation in a multiply connected domain, using the generalized multiple-source-point boundary-collocation Trefftz method and characteristic lengths. Comput. Mater. Contin. 2010, 17, 275–302. [Google Scholar]
- Ku, C.Y. On solving three-dimensional Laplacian problems in a multiply connected domain using the multiple scale Trefftz method. Comput. Model. Eng. Sci. 2014, 98, 509–541. [Google Scholar]
- Ku, C.Y.; Kuo, C.L.; Fan, C.M.; Liu, C.S.; Guan, P.C. Numerical solution of three-dimensional Laplacian problems using the multiple scale Trefftz method. Eng. Anal. Bound. Elem. 2015, 50, 157–168. [Google Scholar] [CrossRef]
- Ku, C.Y.; Xiao, J.E.; Liu, C.Y.; Yeih, W. On the accuracy of the collocation Trefftz method for solving two and three dimensional heat equations. Numer. Heat Transf. Part B 2016, 69, 334–350. [Google Scholar] [CrossRef]
- Logan, J.D. Applied Mathematics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1987; pp. 275–360. ISBN 9780471165132. [Google Scholar]
- Green, W.H.; Ampt, G.A. Studies on soil physics I. The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; John Wiley & Sons, Inc.: Hoboken, NH, USA, 2004; pp. 494–527. ISBN 0-471-44731-5. [Google Scholar]



| Variable | Function | |
|---|---|---|
| Steady-State | ||
| Transient | ||
, | ||
| Variable | Function | |
|---|---|---|
| Transient | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Liu, C.-Y.; Xiao, J.-E.; Yeih, W. Transient Modeling of Flow in Unsaturated Soils Using a Novel Collocation Meshless Method. Water 2017, 9, 954. https://doi.org/10.3390/w9120954
Ku C-Y, Liu C-Y, Xiao J-E, Yeih W. Transient Modeling of Flow in Unsaturated Soils Using a Novel Collocation Meshless Method. Water. 2017; 9(12):954. https://doi.org/10.3390/w9120954
Chicago/Turabian StyleKu, Cheng-Yu, Chih-Yu Liu, Jing-En Xiao, and Weichung Yeih. 2017. "Transient Modeling of Flow in Unsaturated Soils Using a Novel Collocation Meshless Method" Water 9, no. 12: 954. https://doi.org/10.3390/w9120954





