An EMD-Based Chaotic Least Squares Support Vector Machine Hybrid Model for Annual Runoff Forecasting
Abstract
:1. Introduction
2. Data and Methods
2.1. Study Area and Data
2.2. Methods
2.2.1. Empirical Mode Decomposition
- Step 1)
- Identify all the extreme (maxima and minima) values of a time series .
- Step 2)
- Generate the upper and lower envelope ( and ) by applying cubic spline interpolation.
- Step 3)
- Compute a local mean curve of the two envelopes at the same time using
- Step 4)
- Calculate the difference,
- Step 5)
- Check the properties of ; it will be considered a valid IMF if it satisfies these two conditions:
- The number of extreme and zero crossings must be equal or differ at most by one.
- At any point, the local mean value of the envelope defined by the local extremes must be zero.
- Step 6)
- When is not qualified as an IMF, repeat Steps 1) to 5) by sifting the residual series. The sifting process stops when the residual (i.e., the trend term; ) satisfies the predetermined criteria.
2.2.2. Phase Space Reconstruction and Chaotic Characteristics Identification
2.2.3. Chaotic Least Squares Support Vector Machine Model
3. Model Results and Discussion
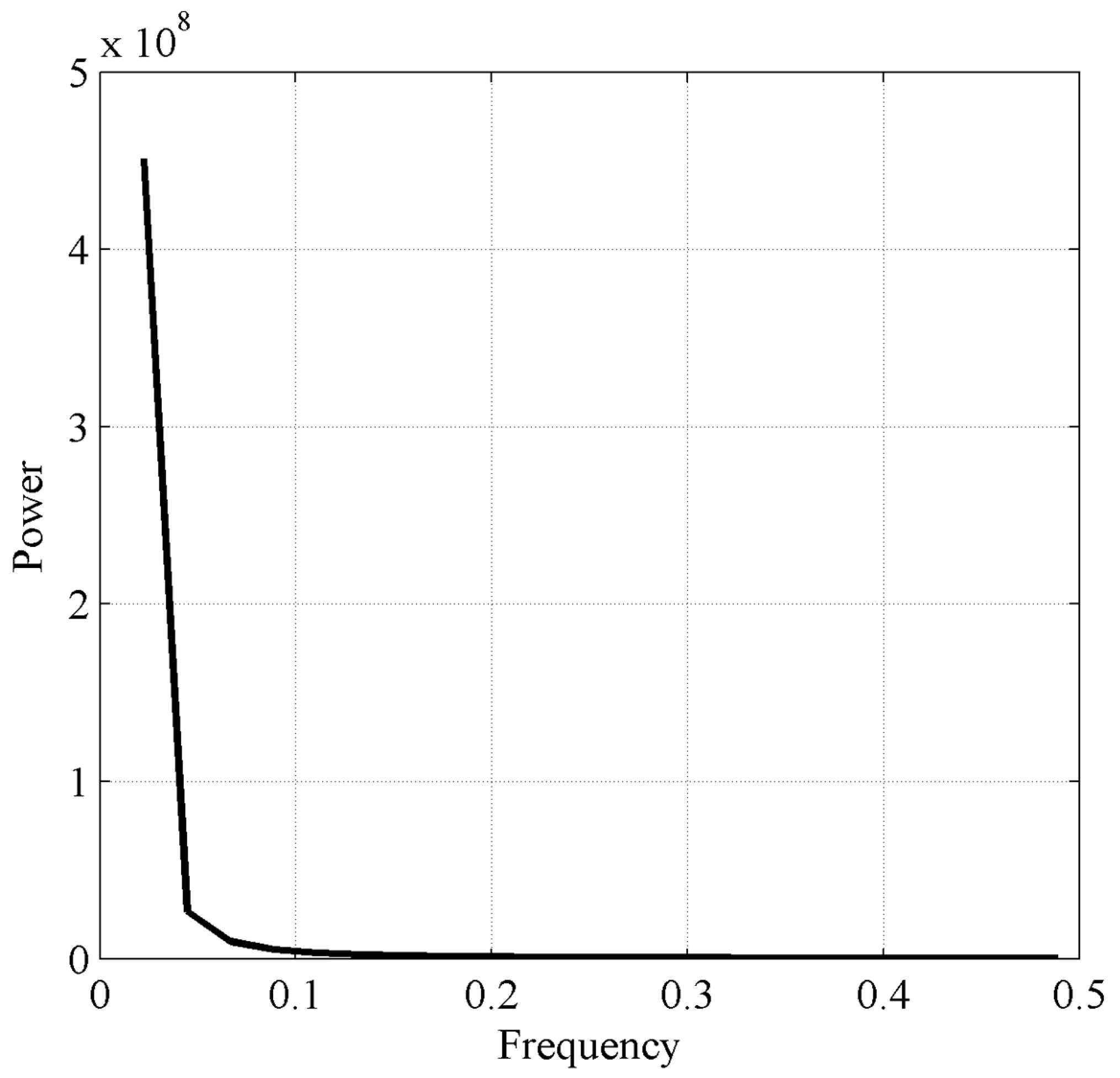
3.1. Stationarity Test of the Original Runoff Series
3.2. EMD of Runoff Series
3.3. Determination of Delay Time τ and Embedding Dimension m
3.4. Identification of Chaotic Characteristics
3.5. Hybrid Model
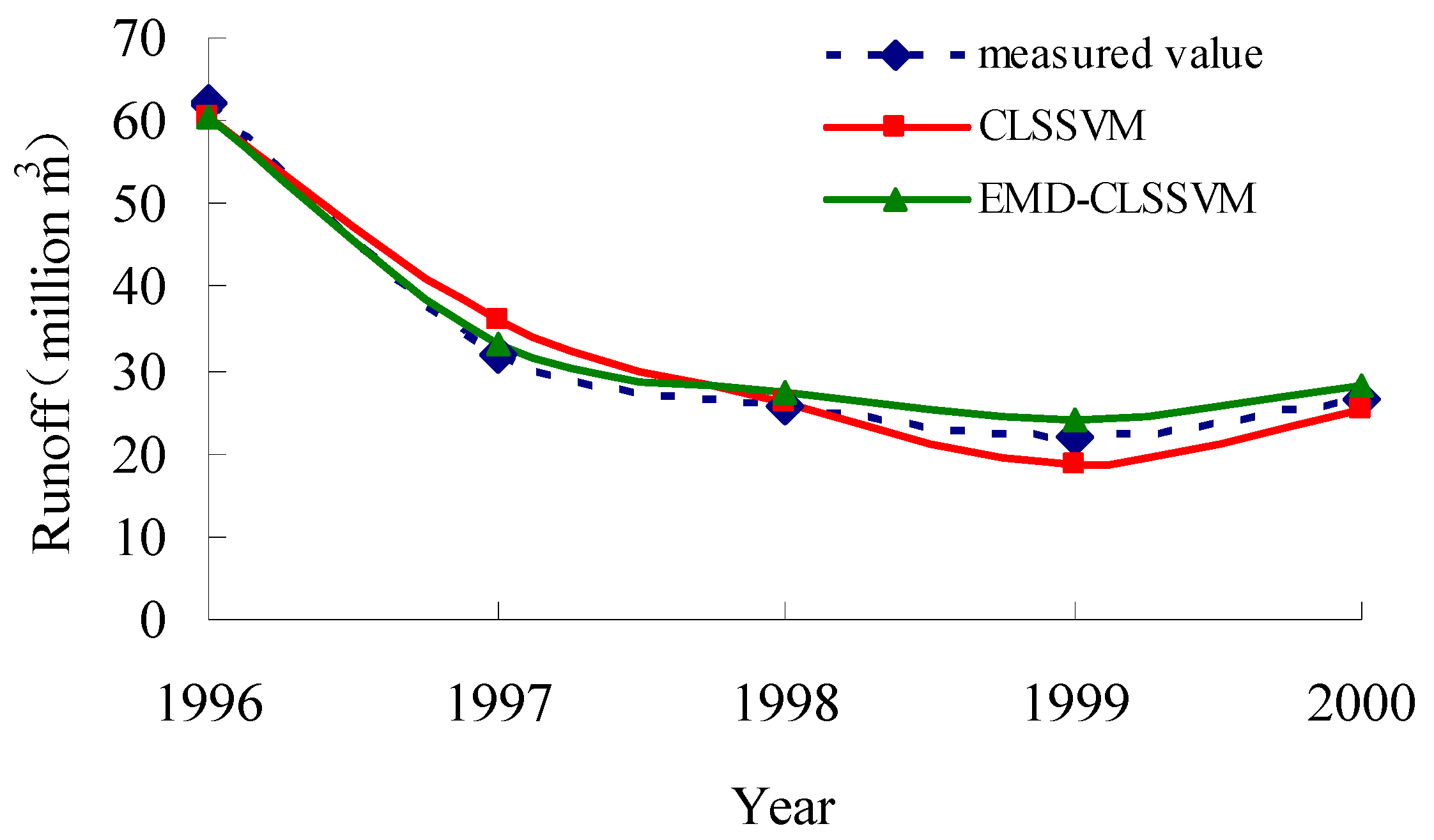
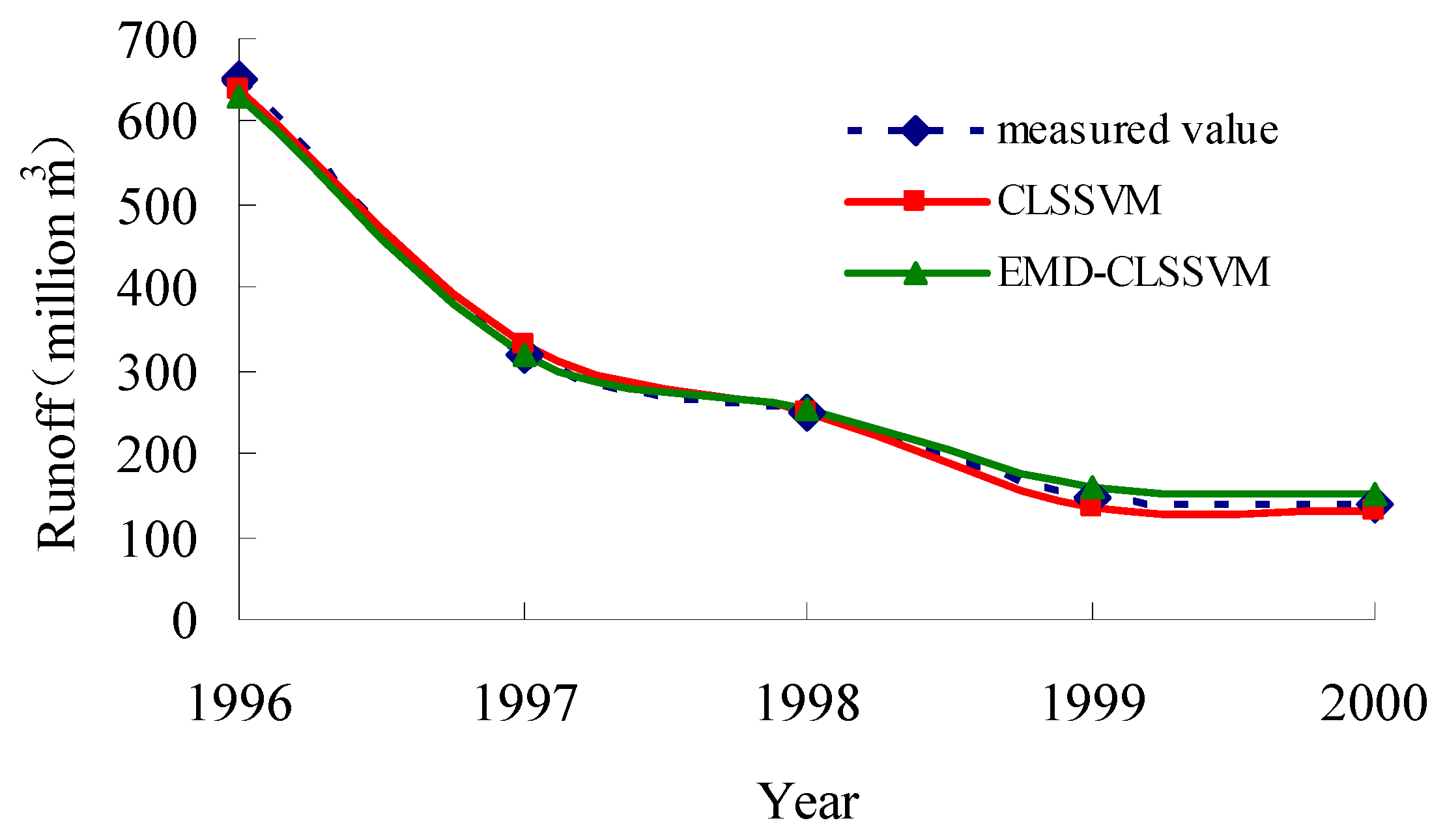
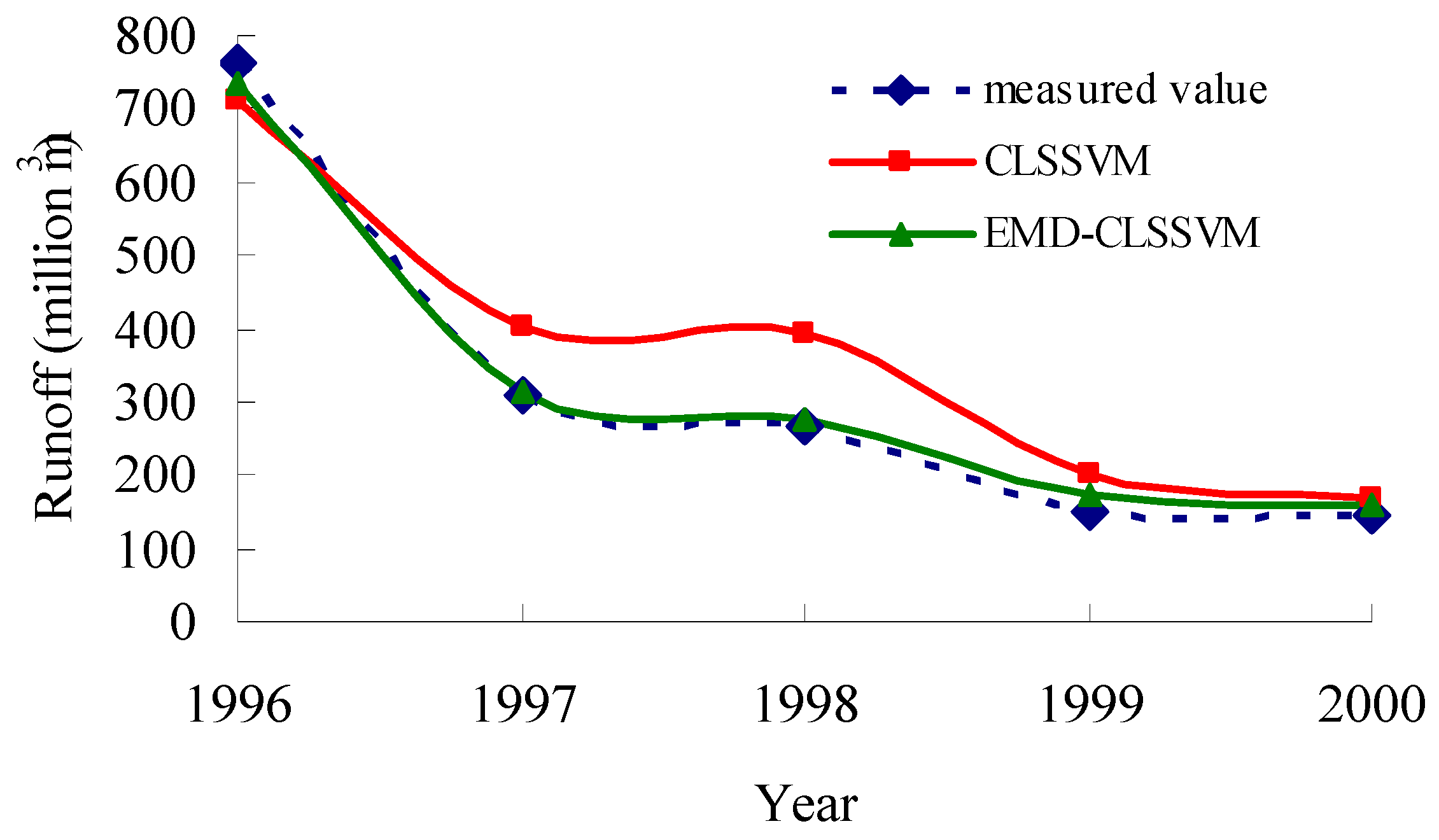
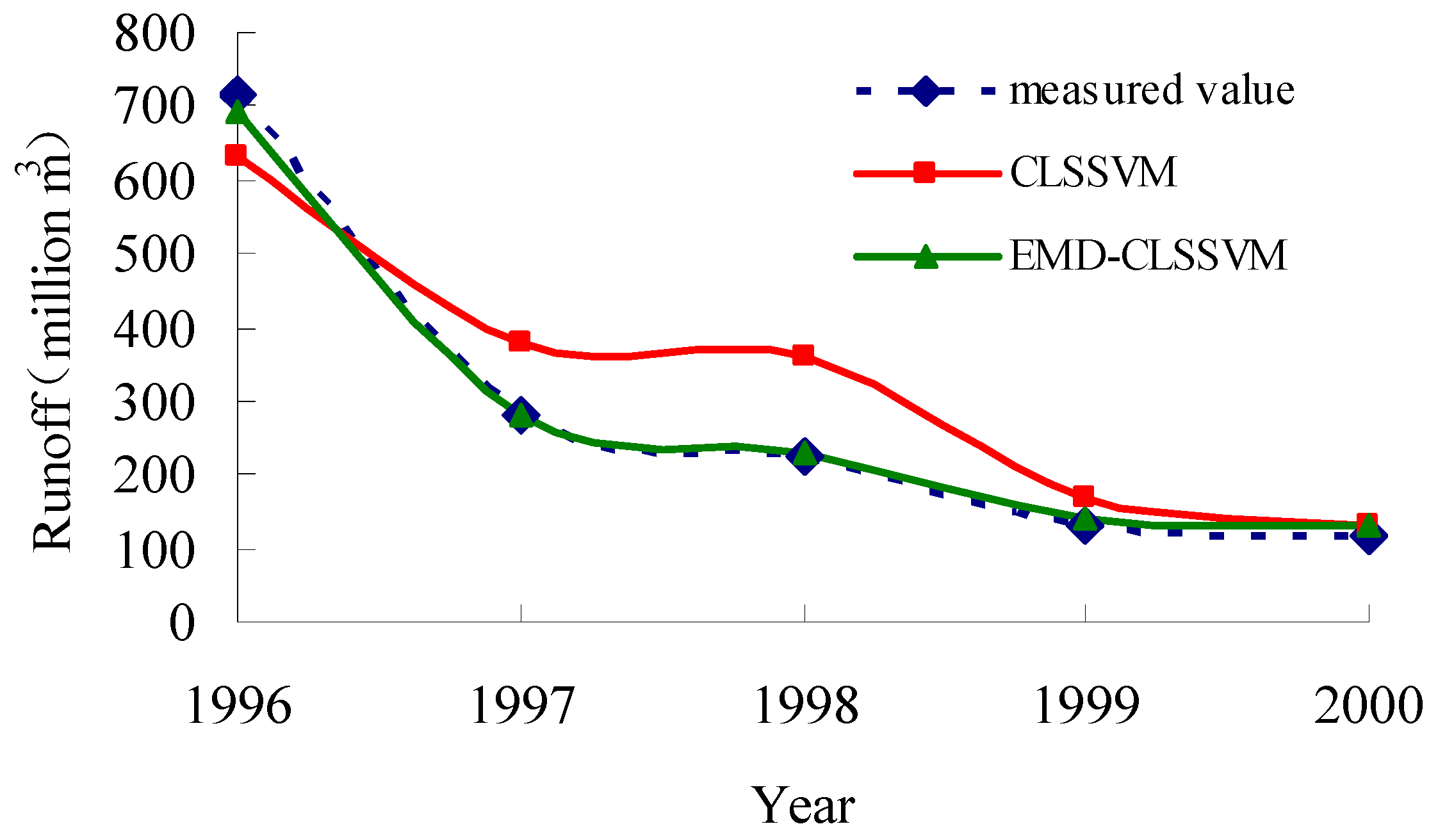
3.6. Comparative Analysis
3.7. Evaluation of Model Performance
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yaseen, Z.M.; El-Shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, M.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Kisi, O.; Nia, A.M.; Goshen, M.G.; Tajabadi, M.R.J.; Ahmadi, A. Intermittent streamflow forecasting by using several data driven techniques. Water Resour. Manag. 2012, 26, 457–474. [Google Scholar] [CrossRef]
- Barge, J.T.; Sharif, H.O. An ensemble empirical mode decomposition, self-organizing map, and linear genetic programming approach for forecasting River streamflow. Water 2016, 8, 247. [Google Scholar] [CrossRef]
- Chang, J.X.; Zhang, H.X.; Wang, Y.M.; Zhu, Y.L. Assessing the impact of climate variability and human activities on streamflow variation. Hydrol. Earth Syst. Sci. 2016, 20, 1547–1560. [Google Scholar] [CrossRef]
- Chen, C.S.; Liu, C.H.; Su, H.C. A nonlinear time series analysis using two-stage genetic algorithms for streamflow forecasting. Hydrol. Process. 2008, 22, 3697–3711. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Potter, N.J.; Vaze, J.; Petheram, C.; Zhang, L.; Teng, J.; Post, D.A. Observed hydrologic non-stationarity in far south-eastern Australia: Implications for modelling and prediction. Stoch. Environ. Res. Risk Assess. 2014, 28, 3–15. [Google Scholar] [CrossRef]
- Islam, M.N.; Sivakumar, B. Characterization and prediction of runoff dynamics: A nonlinear dynamical view. Adv. Water Resour. 2002, 25, 179–190. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Zhang, C.; Luo, G.P.; Teng, Z.D.; Jia, C.J. Characterizing cross-scale chaotic behaviors of the runoff time series in an inland river of Central Asia. Quat. Int. 2013, 311, 132–139. [Google Scholar] [CrossRef]
- Dhanya, C.T.; Kumar, D.N. Predictive uncertainty of chaotic daily streamflow using ensemble wavelet networks approach. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Sivakumar, B.; Bemdtsson, R.; Persson, M. Monthly runoff prediction using phase space reconstruction. Hydrol. Sci. J. 2001, 46, 377–387. [Google Scholar] [CrossRef]
- Tongal, H. Nonlinear forecasting of stream flows using a chaotic approach and artificial neural networks. Earth Sci. Res. J. 2013, 17, 119–126. [Google Scholar]
- Fathima, T.A.; Jothiprakash, V. Behavioural analysis of a time series—A chaotic approach. Sadhana-Acad. Proc. Eng. Sci. 2014, 39, 659–676. [Google Scholar] [CrossRef]
- Liu, Q.; Islam, S.; Rodriguez-lturbe, I.; Le, Y. Phase-space analysis of daily streamflow: Characterization and prediction. Adv. Water Resour. 1998, 21, 463–475. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, B.D.; He, B.; Peng, Y.; Ren, M.L. Singular spectrum analysis and ARIMA hybrid model for annual runoff forecasting. Water Resour. Manag. 2011, 25, 2683–2703. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Kumar, D.N. Predictability of nonstationary time series using wavelet and EMD based ARMA models. J. Hydrol. 2013, 502, 103–119. [Google Scholar] [CrossRef]
- Kisi, O.; Latifoglu, L.; Latifoglu, F. Investigation of empirical mode decomposition in forecasting of hydrological time series. Water Resour. Manag. 2014, 28, 4045–4057. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chang, J.X.; Huang, Q.; Chen, Y.T. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Di, C.L.; Yang, X.H.; Wang, X.C. A four-stage hybrid model for hydrological time series forecasting. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Mwale, F.D.; Adeloye, A.J.; Rustum, R. Application of self-organising maps and multi-layer perceptron-artificial neural networks for streamflow and water level forecasting in data-poor catchments: The case of the Lower Shire floodplain, Malawi. Hydrol. Res. 2014, 45, 838–854. [Google Scholar] [CrossRef]
- Alvaro, L.R.; Vicente, L.F.; David, P.V.; Joaquin, T.P. One-Day-Ahead Streamflow forecasting using artificial neural networks and a meteorological mesoscale model. J. Hydrol. Eng. 2015, 20, 05015001. [Google Scholar]
- Liu, Z.Y.; Zhou, P.; Chen, G.; Guo, L.D. Evaluating a coupled discrete wavelet transform and support vector regression for daily and monthly streamflow forecasting. J. Hydrol. 2014, 519, 2822–2831. [Google Scholar] [CrossRef]
- Sudheer, C.; Maheswaran, R.; Panigrahi, B.; Mathur, S. A hybrid SVM-PSO model for forecasting monthly streamflow. Neural Comput. Appl. 2014, 24, 1381–1389. [Google Scholar] [CrossRef]
- Shabri, A.; Suhartono, S. Streamflow forecasting using least-squares support vector machines. Hydrol. Sci. J. 2012, 57, 1275–1293. [Google Scholar] [CrossRef]
- Samsudin, R.; Saad, P.; Shabri, A. River flow time series using least squares support vector machines. Hydrol. Earth Syst. Sci. 2011, 15, 1835–1852. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Kugiumtzis, D. State space reconstruction parameters in the analysis of chaotic time series—The role of the time window length. Phys. D 1996, 95, 13–28. [Google Scholar] [CrossRef]
- Cao, L.Y. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y.C. Testing the null hypothesis of stationarity against the alternative of a unit-root-How sure are we that economic time series have a unit-root? J. Econometr. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Vallejos, R.O.; Anteneodo, C. Theoretical estimates for the largest lyapunov exponent of many-particle systems. Phys. Rev. E 2002, 66. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Water Resources. SL250–2000, Standard for Hydrological Information and Hydrological Forecasting; China Water and Power Press: Beijing, China, 2000.
- Karunanithi, N.; Grenney, W.J.; Whitley, D.; Bovee, K. Neural networks for river flow prediction. J. Comput. Civ. Eng. ASCE 1994, 8, 201–220. [Google Scholar] [CrossRef]
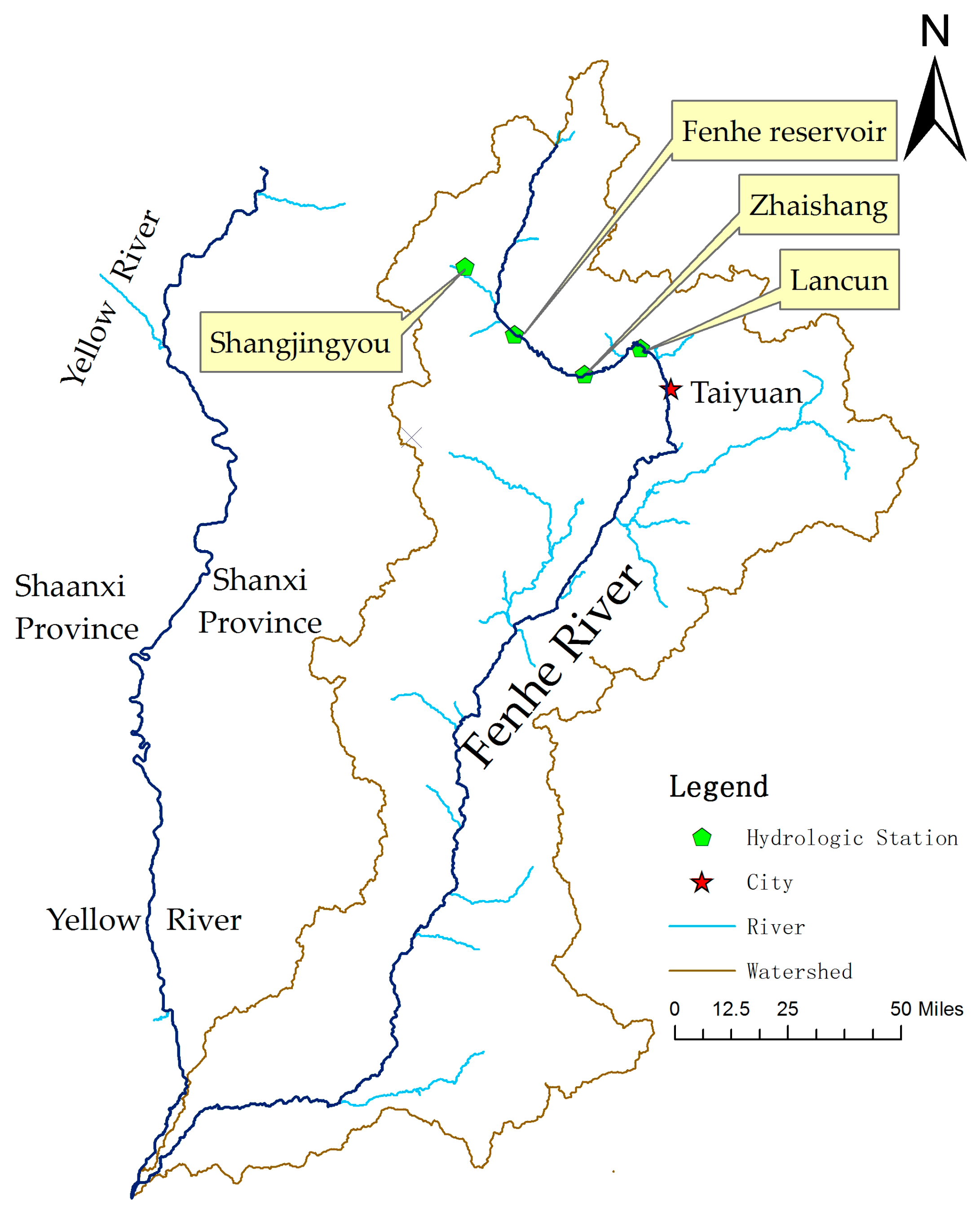

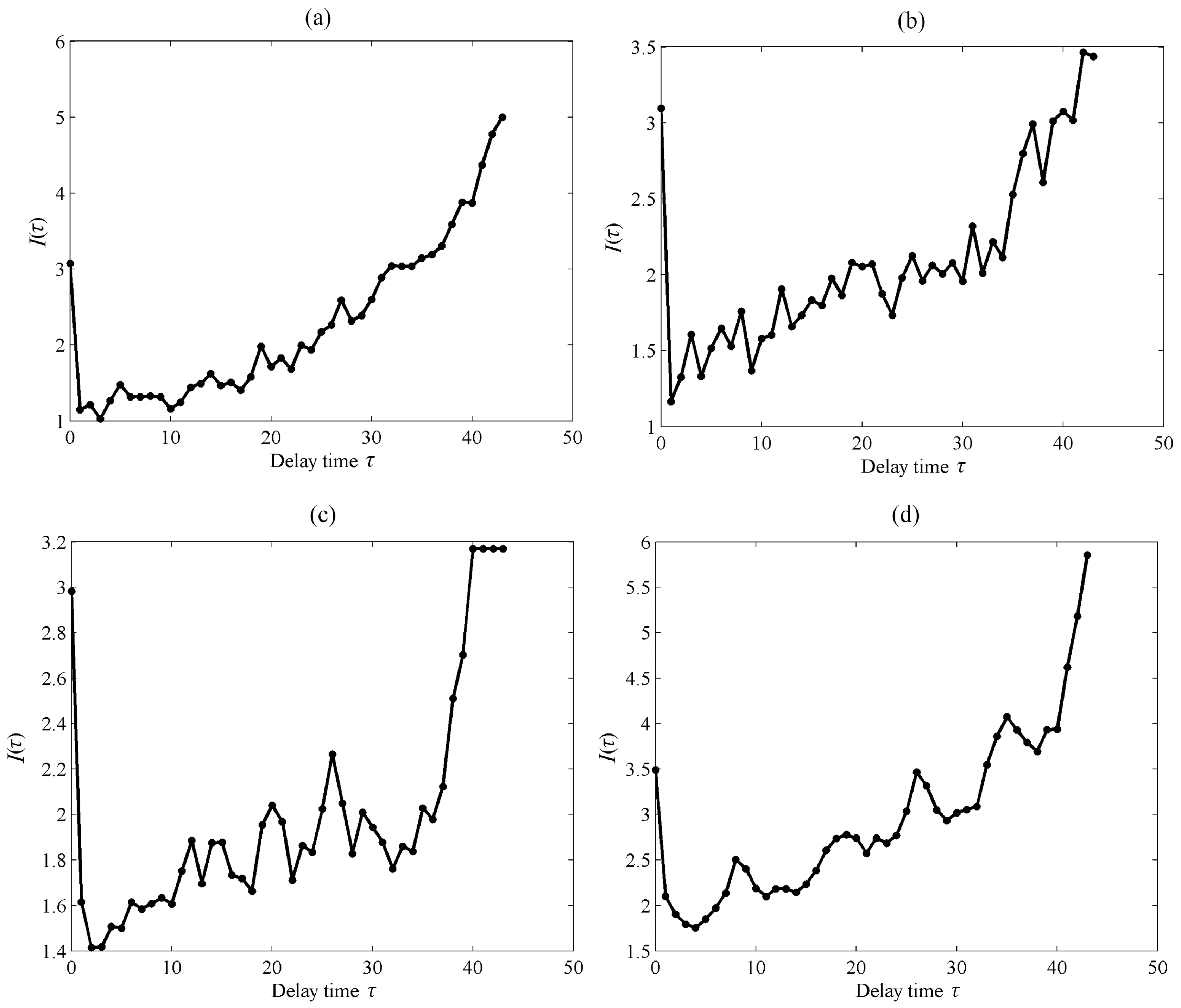
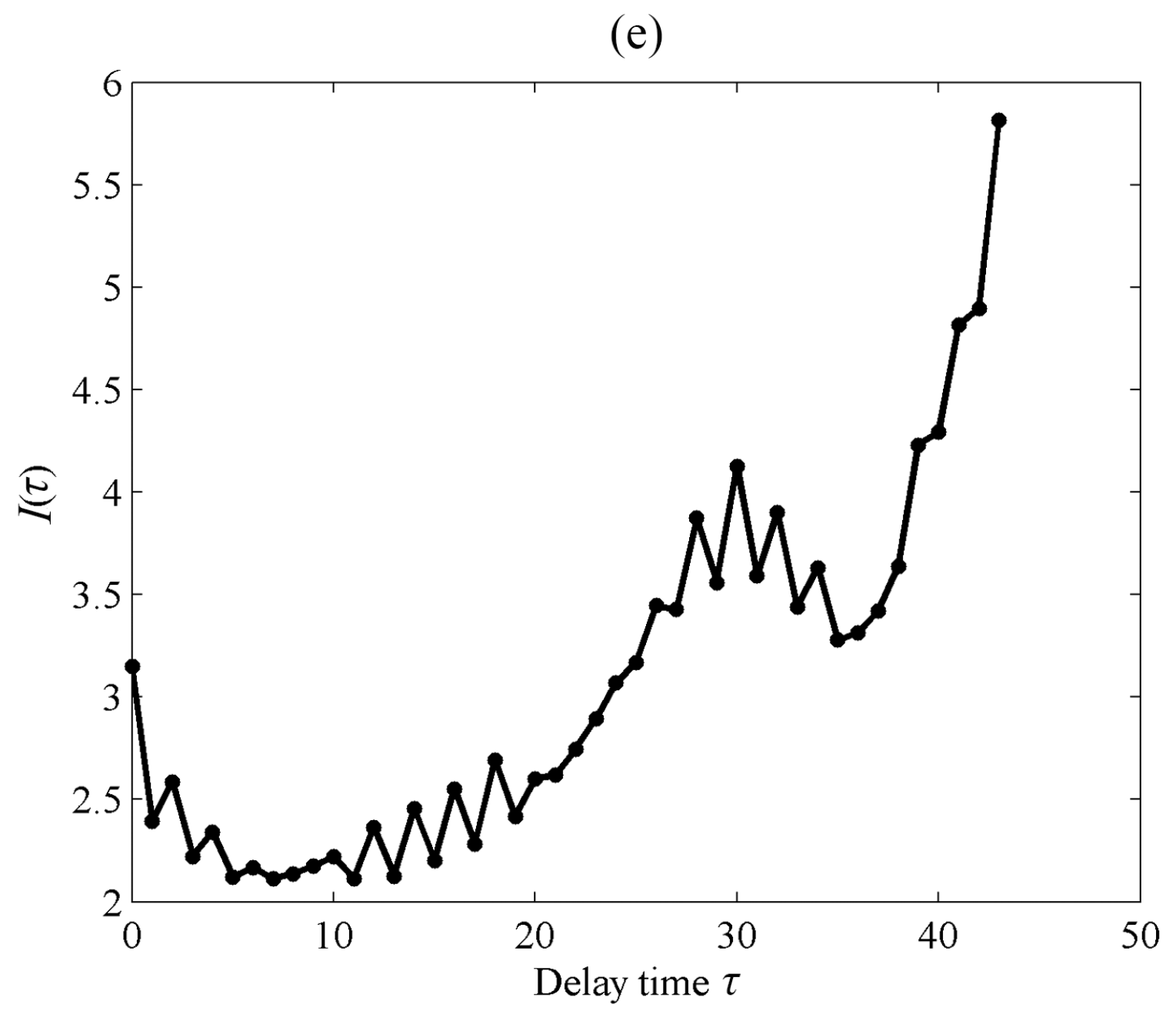
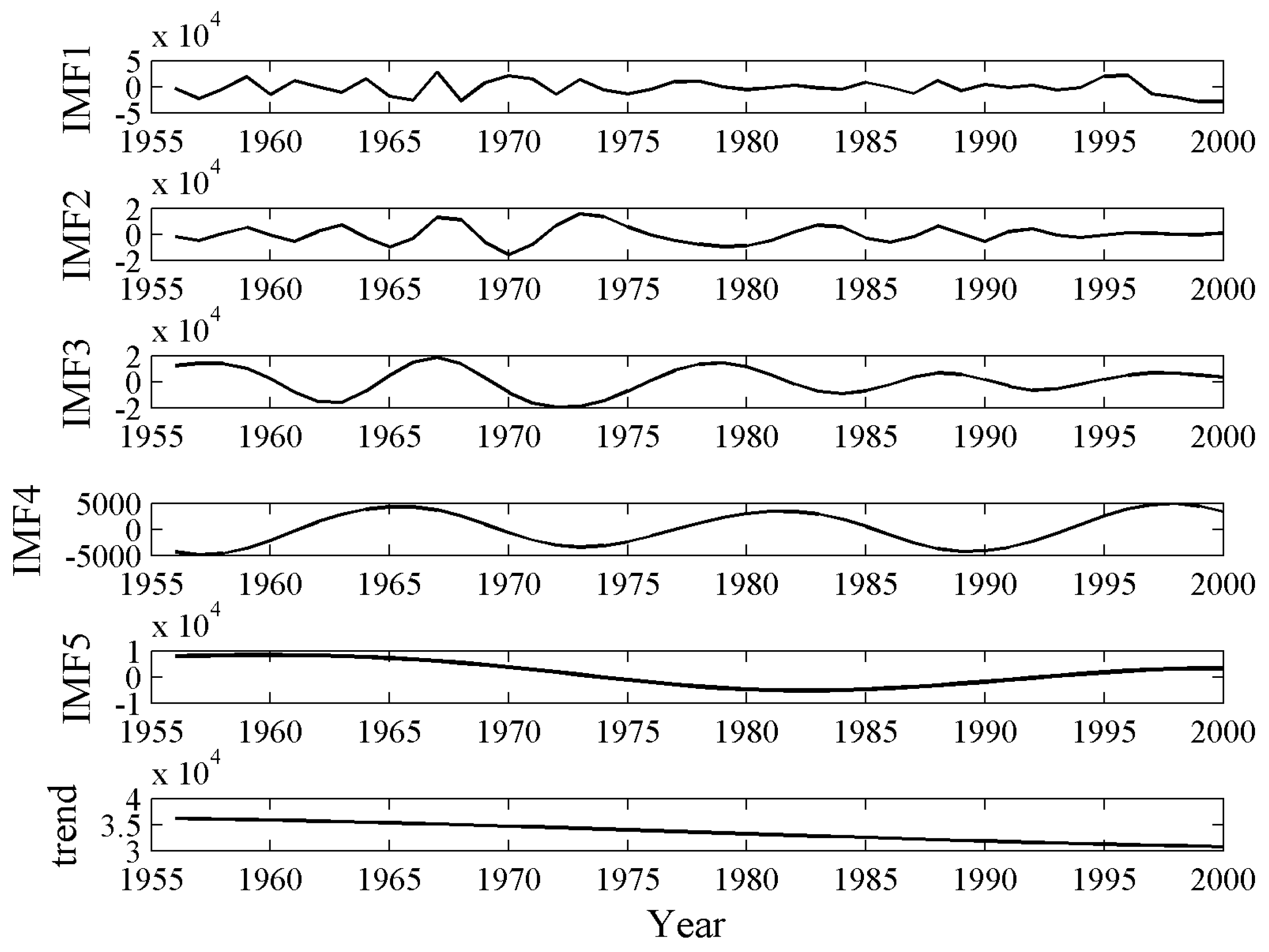
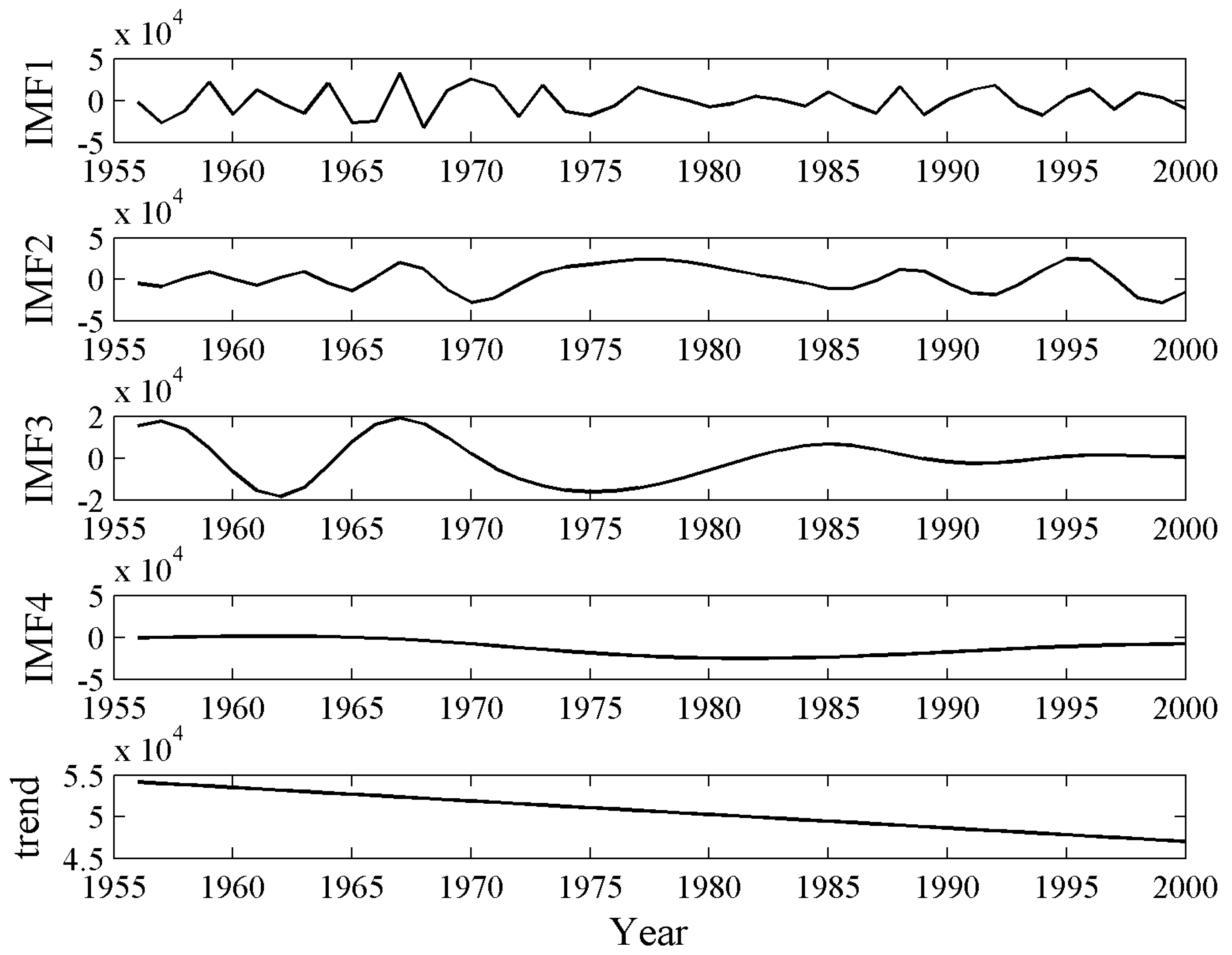
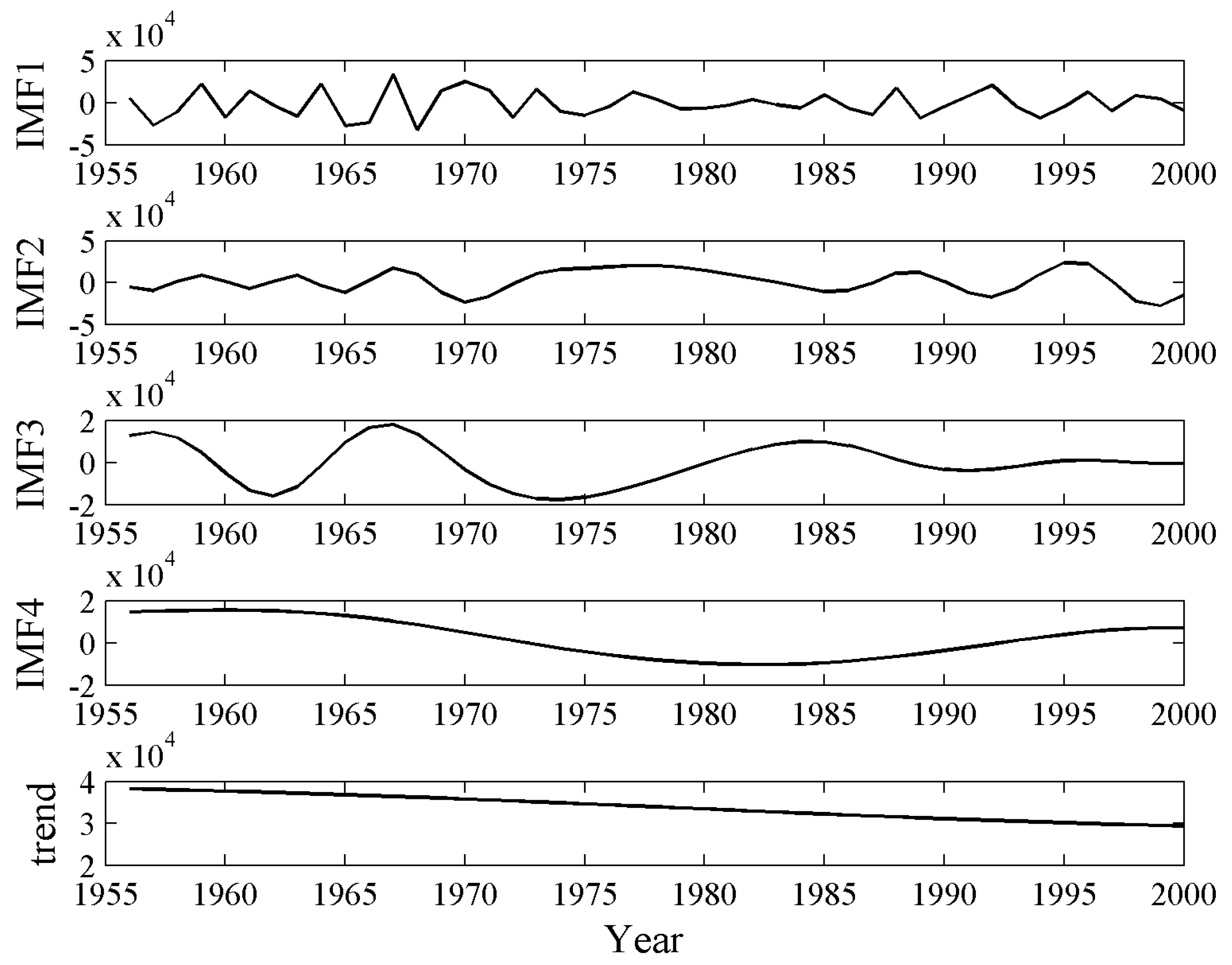
| IMFs | LM Statistic | τ | m | Average Period p | Lyapunov Exponent λ1 |
|---|---|---|---|---|---|
| IMF1 | 0.114 | 1 | 2 | 3 | 0.113 |
| IMF2 | 0.148 | 1 | 5 | 4 | 0.160 |
| IMF3 | 0.063 | 2 | 4 | 4 | 0.101 |
| IMF4 | 0.075 | 4 | 6 | 8 | 0.040 |
| IMF5 | 0.571 | 1 | 6 | 23 | — |
| IMFs | IMF1 | IMF2 | IMF3 | IMF4 |
|---|---|---|---|---|
| C | 625.2 | 316.0 | 68.1 | 18.1 |
| σ | 0.1 | 49.2 | 7.2 | 8.3 |
| Stations | IMFs | LM Statistic | τ | m | Average Period p | Lyapunov Exponent λ1 |
|---|---|---|---|---|---|---|
| Fenhe reservoir | IMF1 | 0.180 | 1 | 7 | 7 | 0.091 |
| IMF2 | 0.087 | 1 | 7 | 7 | 0.042 | |
| IMF3 | 0.105 | 3 | 6 | 6 | 0.023 | |
| IMF4 | 0.112 | 3 | 5 | 5 | 0.168 | |
| IMF5 | 0.363 | 2 | 4 | 23 | — | |
| Zhaishang | IMF1 | 0.248 | 1 | 7 | 7 | 0.01 |
| IMF2 | 0.119 | 2 | 7 | 7 | 0.169 | |
| IMF3 | 0.097 | 2 | 3 | 3 | 0.169 | |
| IMF4 | 0.335 | 1 | 4 | 23 | — | |
| Lancun | IMF1 | 0.129 | 1 | 7 | 7 | 0.163 |
| IMF2 | 0.129 | 2 | 7 | 7 | 0.017 | |
| IMF3 | 0.082 | 2 | 4 | 4 | 0.140 | |
| IMF4 | 0.329 | 2 | 4 | 23 | — |
| Station | Hybrid Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|---|
| QR | RMSE (106 m3) | MARE | MAE (106 m3) | QR | RMSE (106 m3) | MARE | MAE (106 m3) | ||
| Shangjingyou | CLSSVM | 61% | 10.19 | 0.21 | 8.12 | 100% | 2.49 | 0.07 | 2.03 |
| EMD-CLSSVM | 97% | 3.78 | 0.07 | 2.93 | 100% | 1.52 | 0.05 | 1.51 | |
| Fenhe reservoir | CLSSVM | 65% | 120.33 | 0.27 | 70.83 | 100% | 11.03 | 0.05 | 9.89 |
| EMD-CLSSVM | 97% | 75.17 | 0.21 | 53.43 | 100% | 9.93 | 0.03 | 7.95 | |
| Zhaishang | CLSSVM | 68% | 114.91 | 0.32 | 90.91 | 40% | 77.05 | 0.26 | 67.64 |
| EMD-CLSSVM | 97% | 40.19 | 0.09 | 30.33 | 100% | 17.71 | 0.07 | 15.72 | |
| Lancun | CLSSVM | 58% | 106.63 | 0.30 | 65.58 | 40% | 85.84 | 0.30 | 74.17 |
| EMD-CLSSVM | 97% | 24.18 | 0.07 | 19.11 | 100% | 12.16 | 0.05 | 10.18 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Chen, X.; Xu, Y.; Xi, D.; Zhang, Y.; Zheng, X. An EMD-Based Chaotic Least Squares Support Vector Machine Hybrid Model for Annual Runoff Forecasting. Water 2017, 9, 153. https://doi.org/10.3390/w9030153
Zhao X, Chen X, Xu Y, Xi D, Zhang Y, Zheng X. An EMD-Based Chaotic Least Squares Support Vector Machine Hybrid Model for Annual Runoff Forecasting. Water. 2017; 9(3):153. https://doi.org/10.3390/w9030153
Chicago/Turabian StyleZhao, Xuehua, Xu Chen, Yongxin Xu, Dongjie Xi, Yongbo Zhang, and Xiuqing Zheng. 2017. "An EMD-Based Chaotic Least Squares Support Vector Machine Hybrid Model for Annual Runoff Forecasting" Water 9, no. 3: 153. https://doi.org/10.3390/w9030153





