Effects of Pore-Scale Geometry and Wettability on Two-Phase Relative Permeabilities within Elementary Cells
Abstract
:1. Introduction
2. Materials and Methods
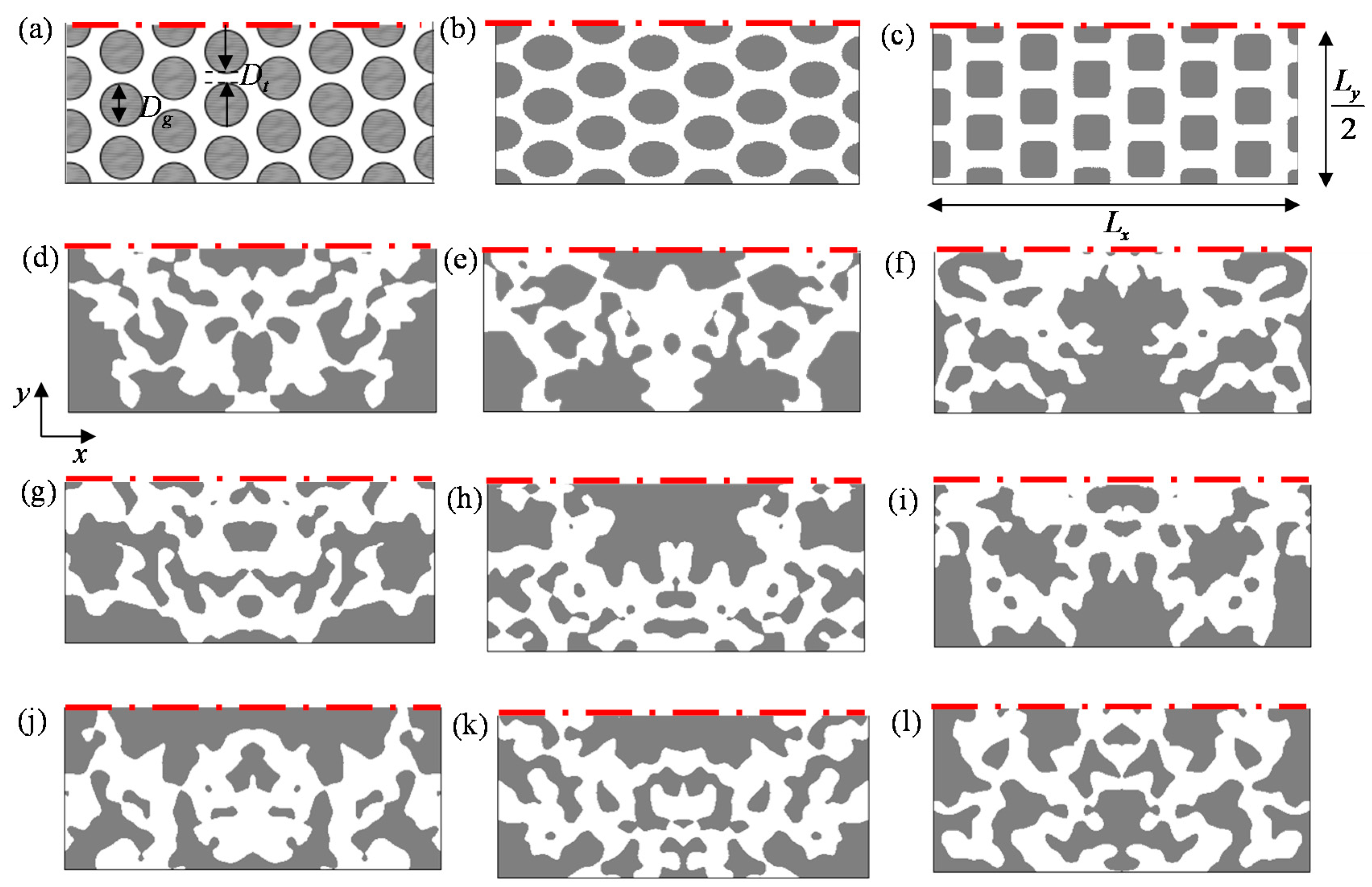
2.1. Generation of Regular and Random Elementary Cells
2.2. Pore Space Spatial Correlation
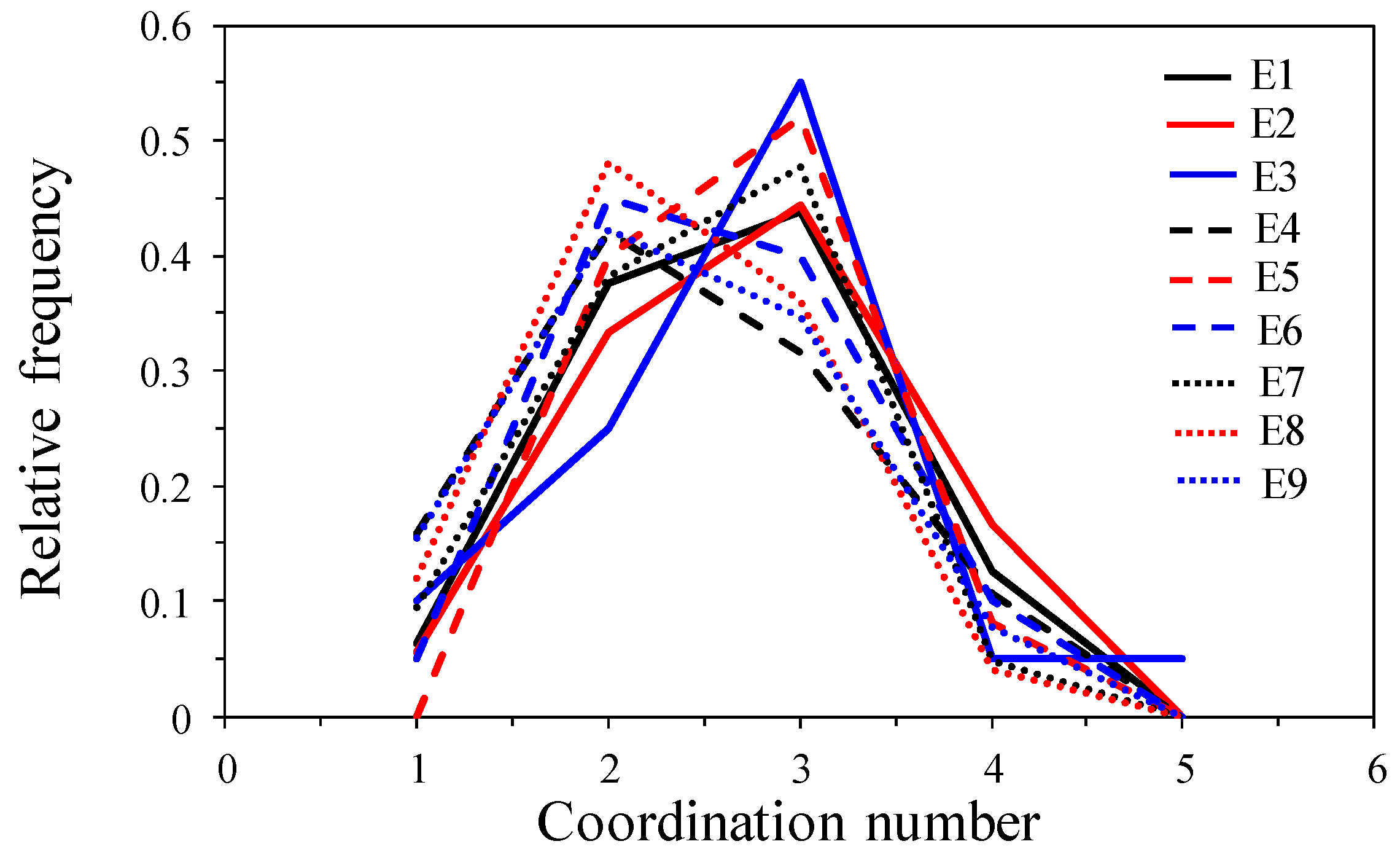
2.3. Topological/Morphological Analysis of the Elementary Cells
2.4. Single Phase Flow Simulations
2.5. Two-Phase Flow Simulations
3. Results and Discussion
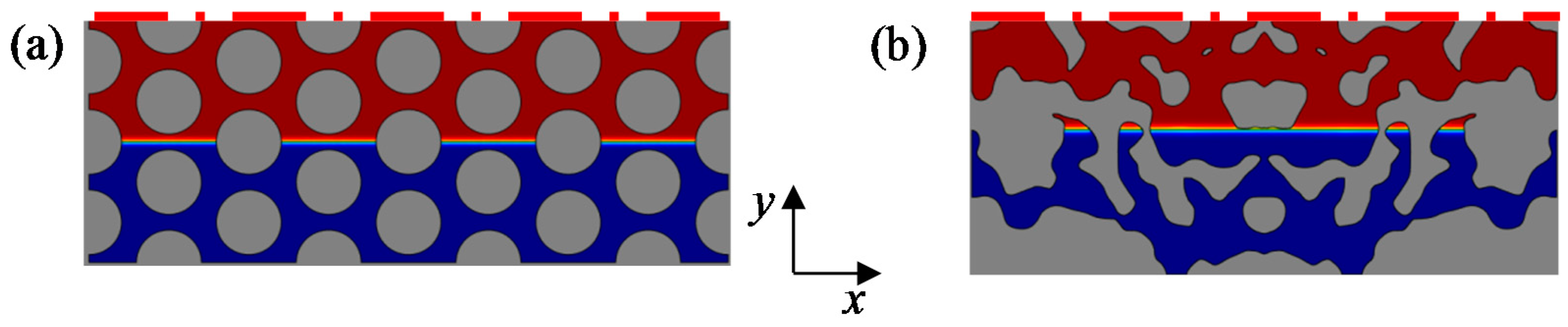
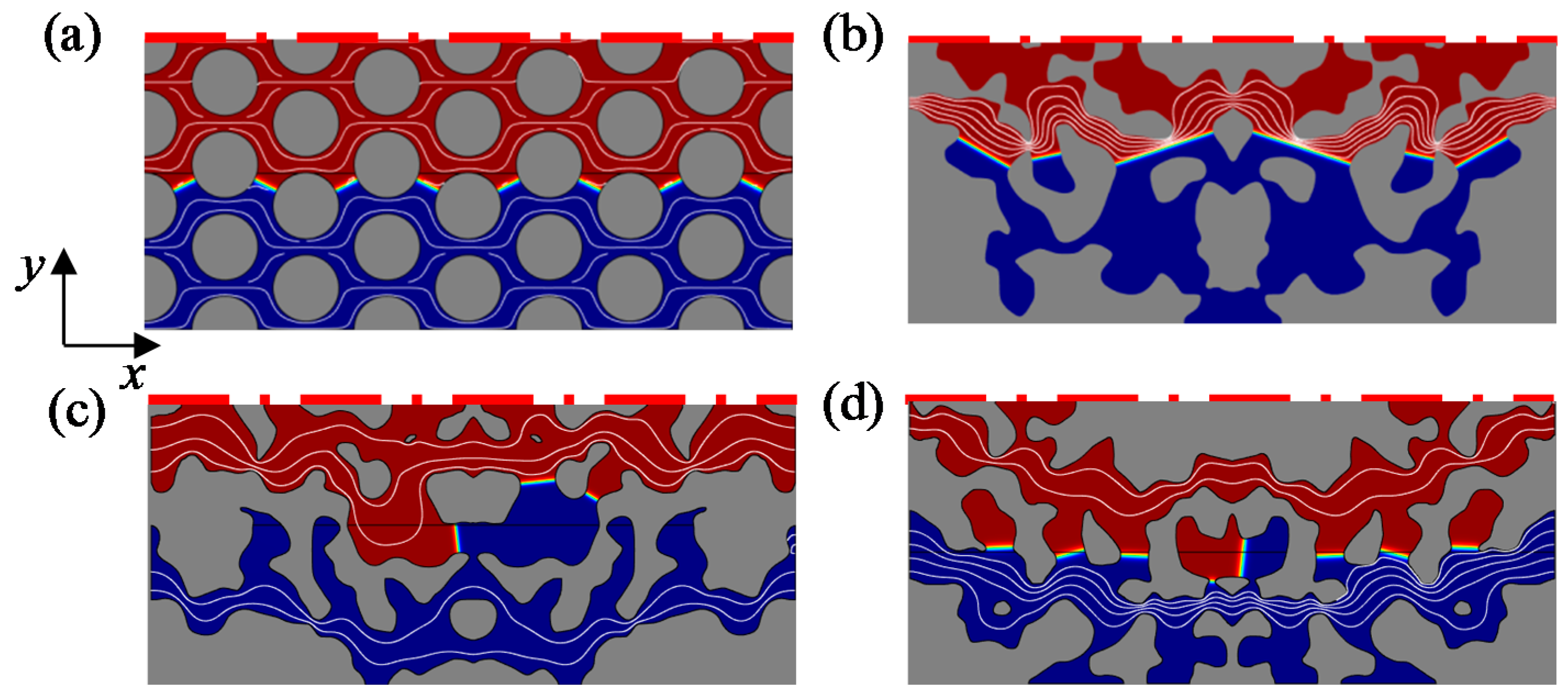
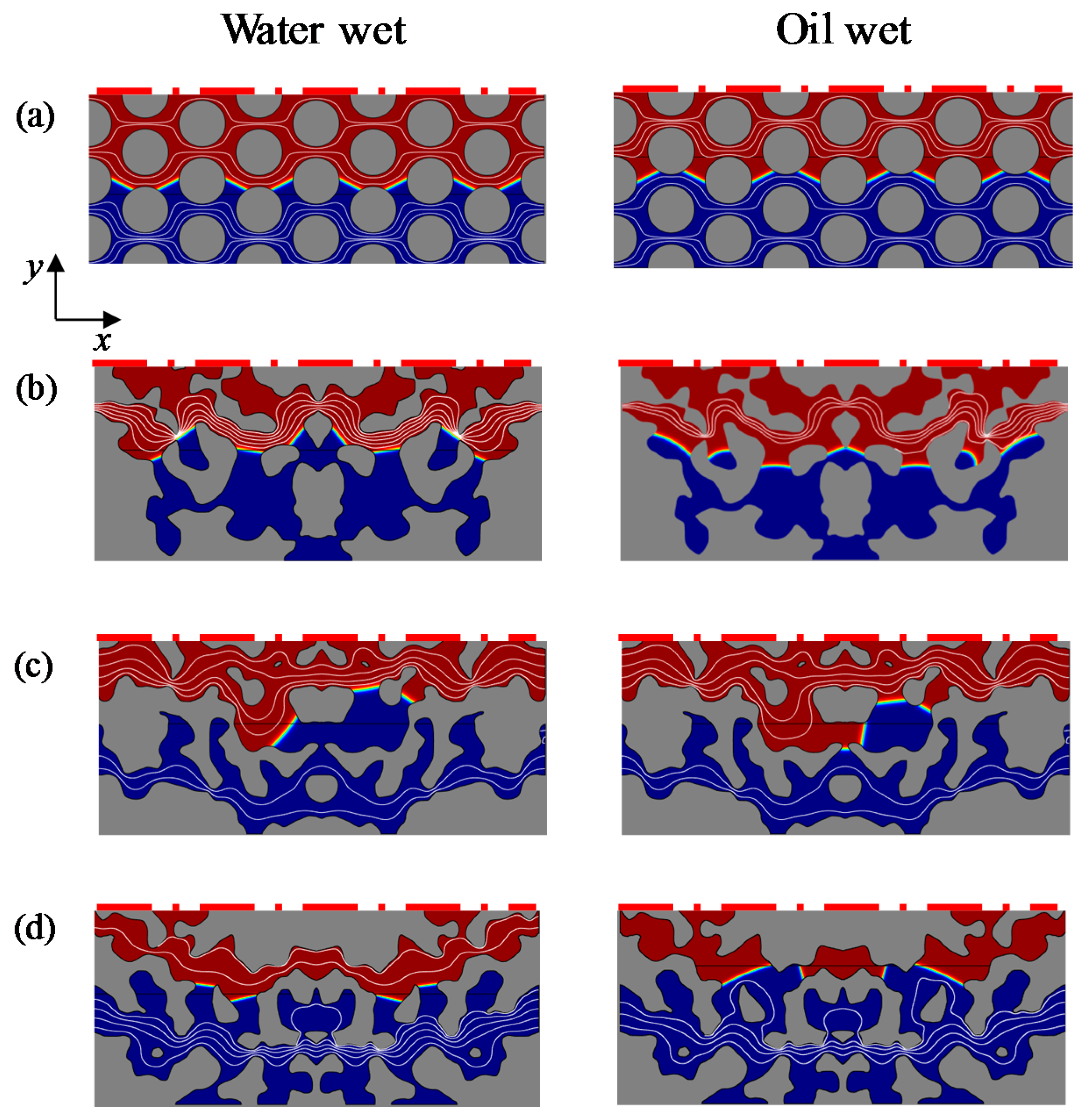
3.1. Equilibrium Two-Phase Distribution Patterns
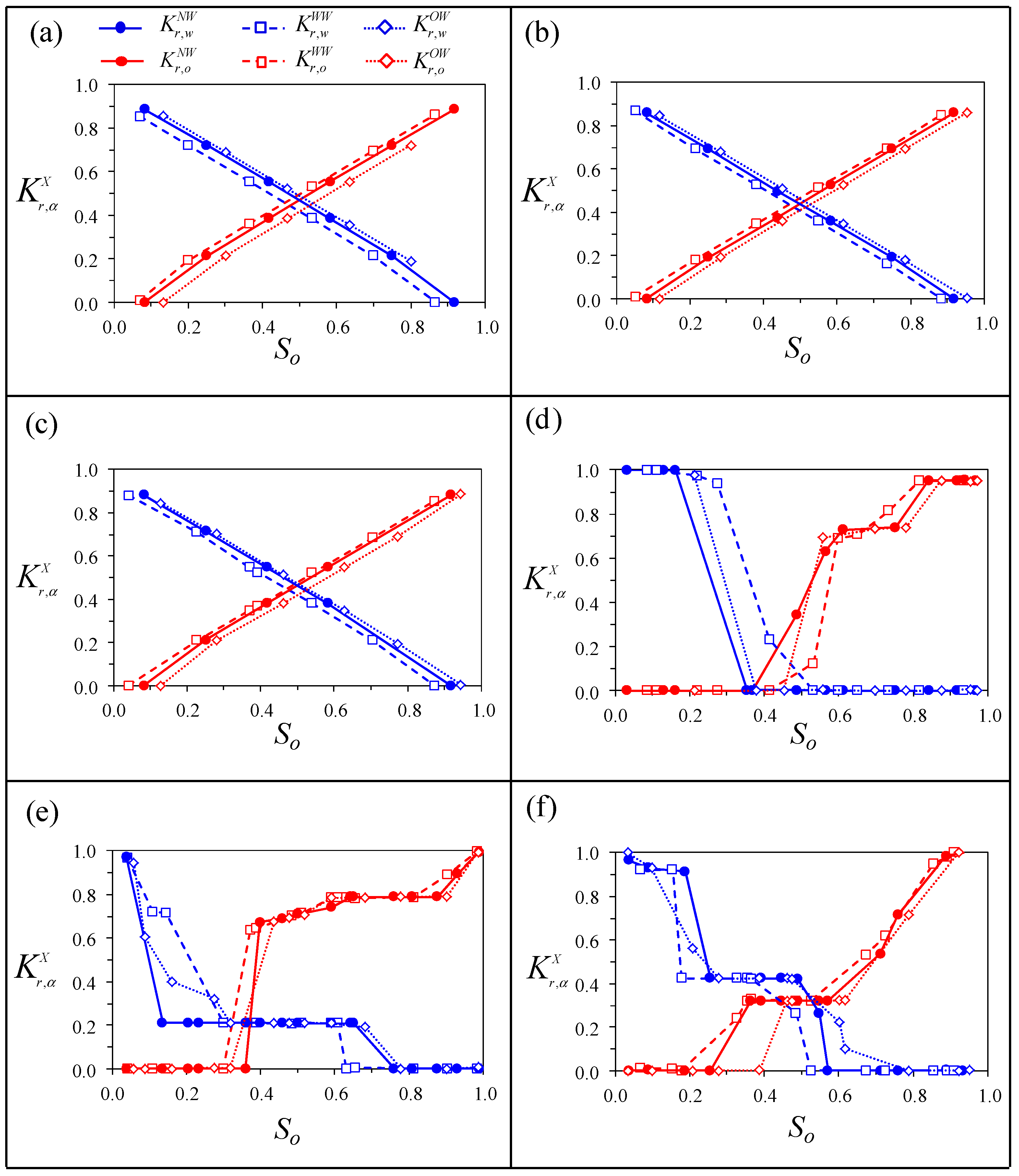
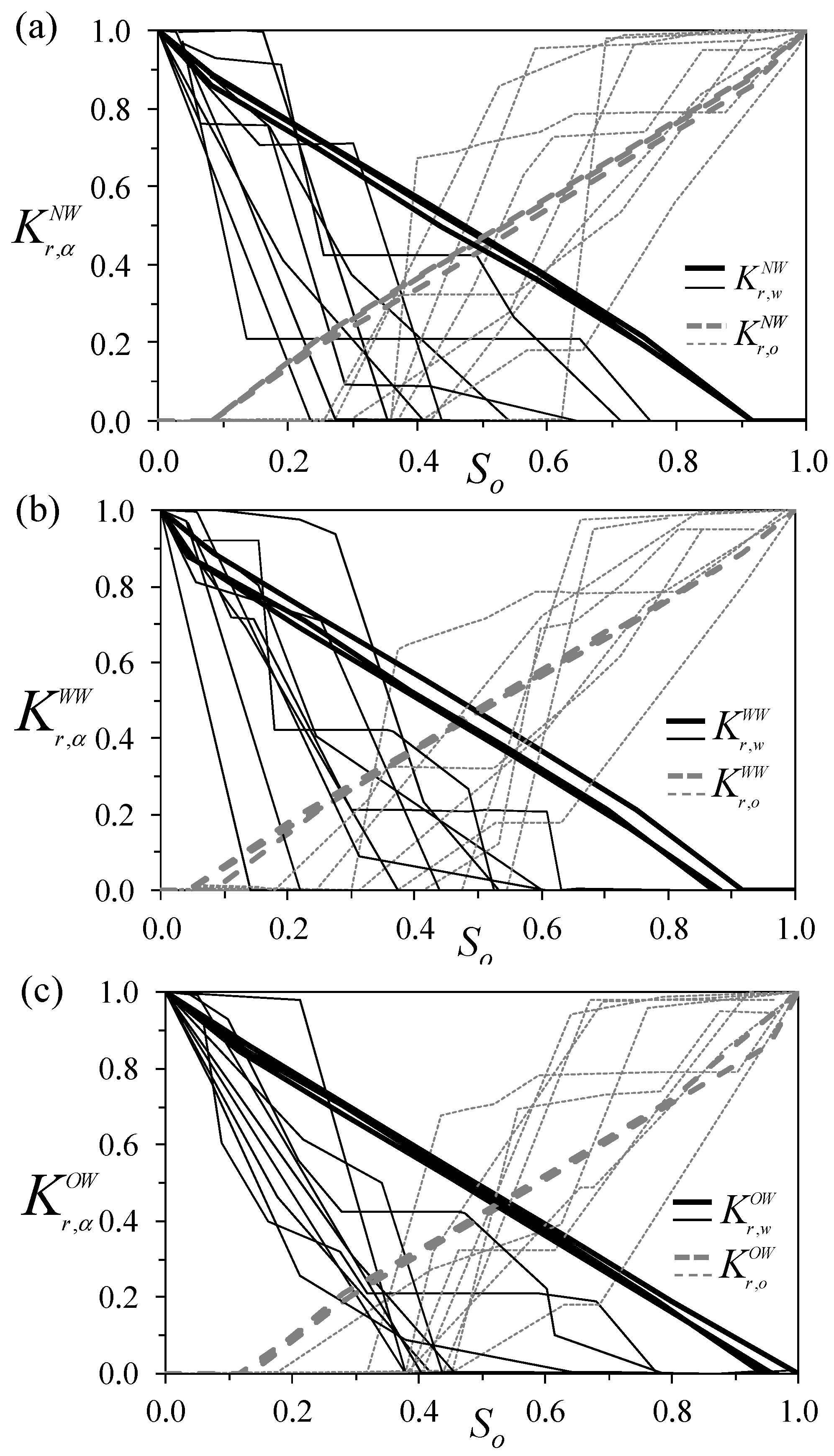
3.2. Relative Permeabilities
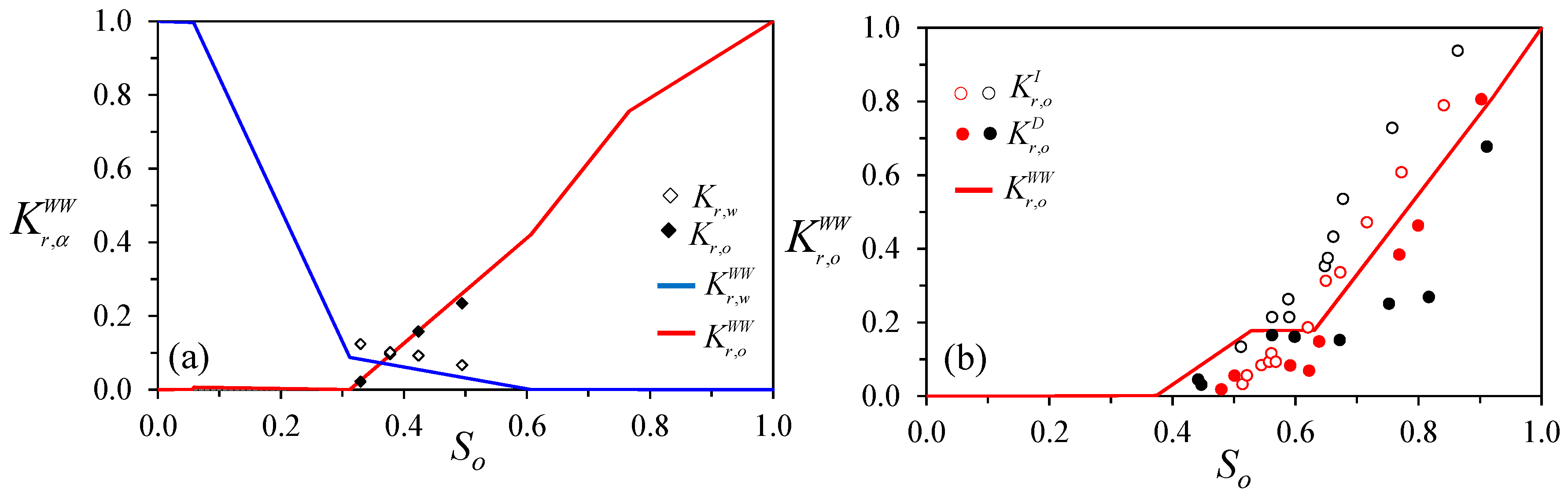
3.3. Qualitative Comparison of the Numerical Results against Experimental Data
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Probability Distribution of Velocity Fields
| Sample Identifier | So | Oil | |||||
| Mean | Mode | Median | Variance | CV (%) | Peak | ||
| HDa | 40 | 4.65 × 10−4 | 0.00 | 3.49 × 10−4 | 1.87 × 10−7 | 92.9 | 1.37 |
| 60 | 4.76 × 10−4 | 0.00 | 3.48 × 10−4 | 1.88 × 10−7 | 91.1 | 1.19 | |
| E4 | 40 | 6.28 × 10−4 | 0.00 | 5.68 × 10−4 | 2.75 × 10−7 | 83.5 | 1.06 |
| 60 | 4.68 × 10−4 | 0.00 | 2.90 × 10−4 | 2.52 × 10−7 | 107.3 | 2.08 | |
| Sample Identifier | So | Water | |||||
| Mean | Mode | Median | Variance | CV (%) | Peak | ||
| HDa | 40 | 9.52 × 10−4 | 0.00 | 6.96 × 10−4 | 7.54 × 10−7 | 91.2 | 1.01 |
| 60 | 9.29 × 10−4 | 0.00 | 6.97 × 10−4 | 7.49 × 10−7 | 93.1 | 1.42 | |
| E4 | 40 | 2.59 × 10−4 | 0.00 | 1.72 × 10−5 | 1.50 × 10−7 | 149.4 | 3.35 |
| 60 | 3.80 × 10−4 | 0.00 | 2.71 × 10−4 | 1.74 × 10−7 | 109.9 | 2.51 | |
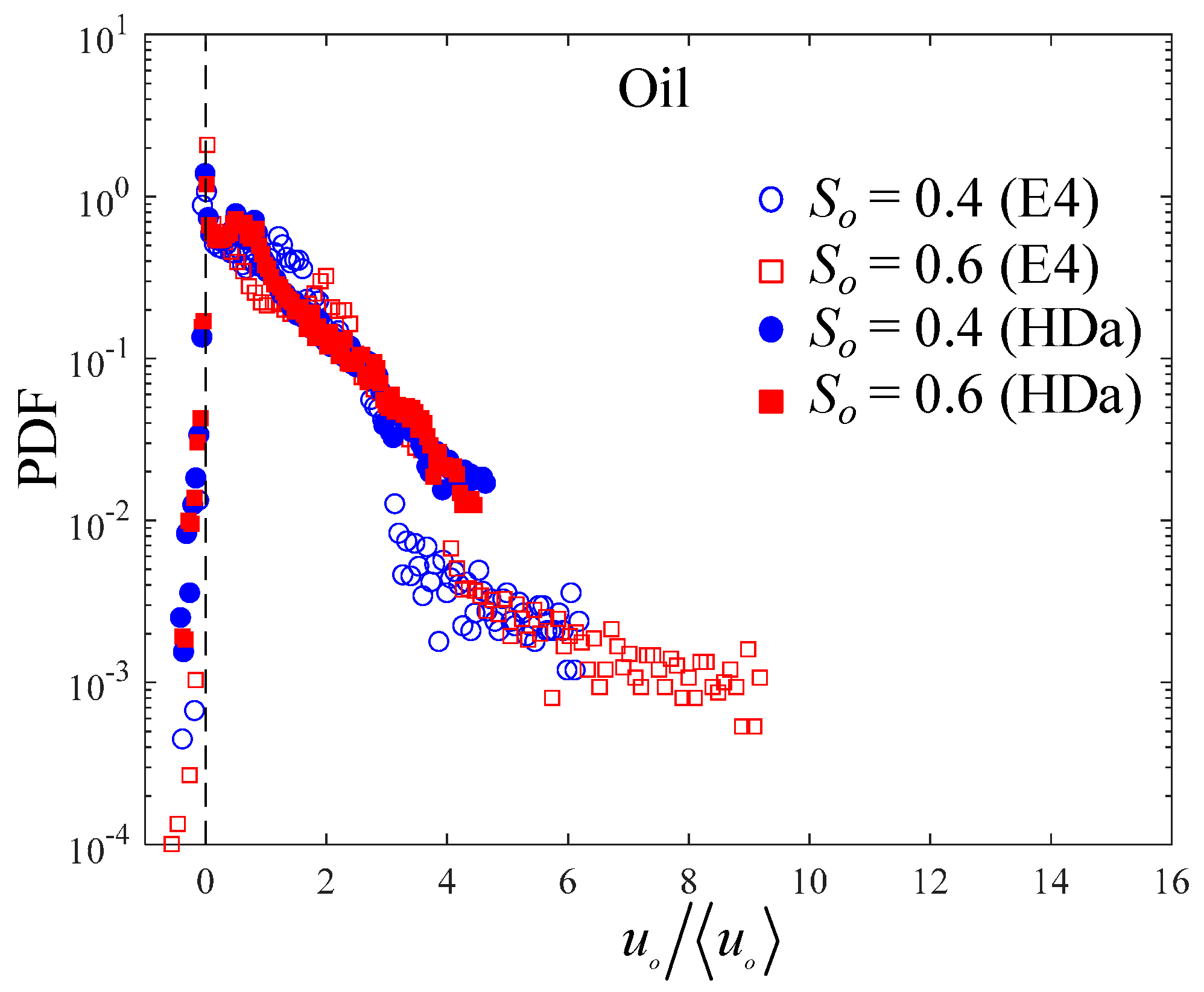
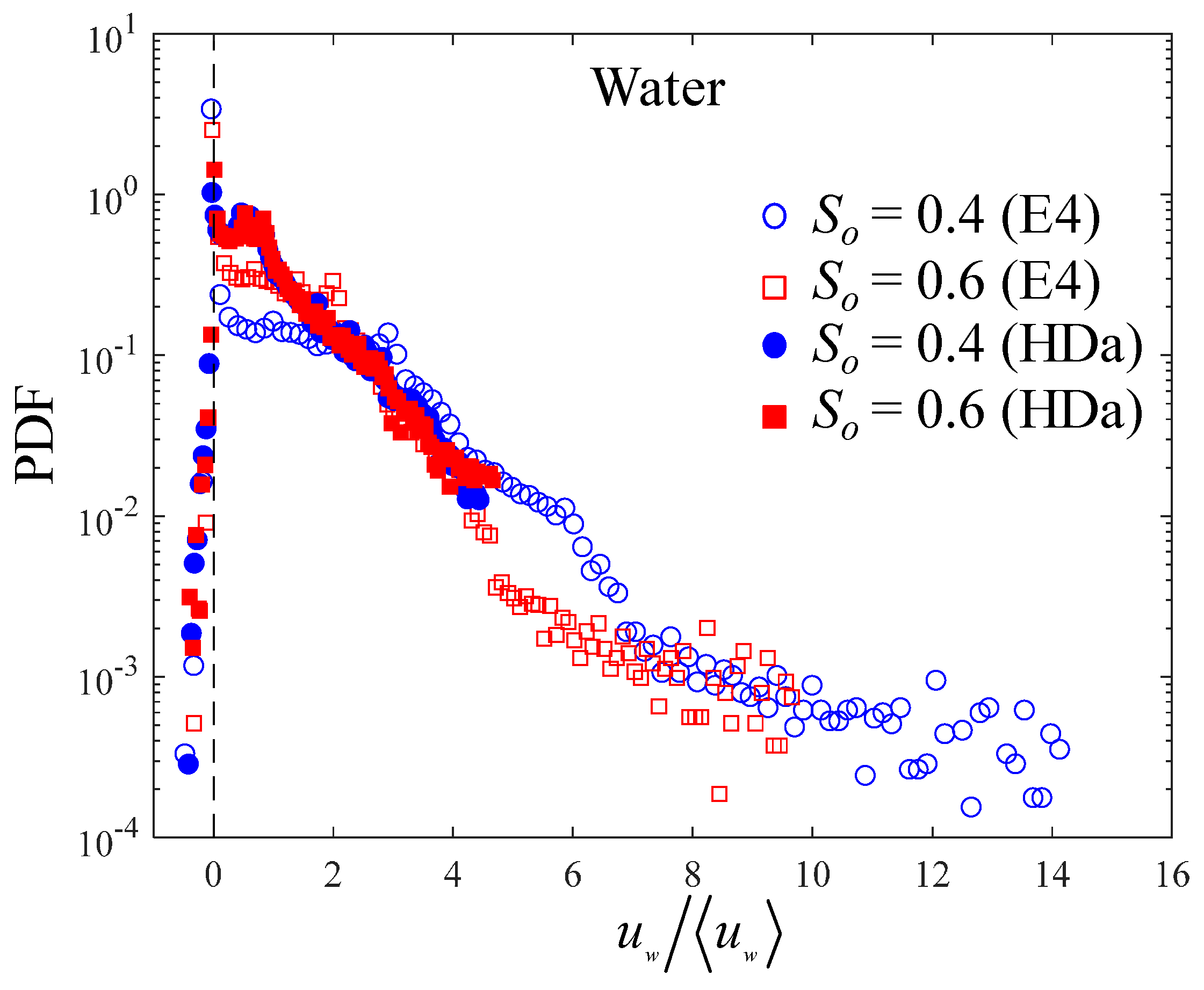
References
- Dullien, F.A.L. Porous Media Fluid Transport and Pore Structure, 2nd ed.; Academic: San Diego, CA, USA, 1992. [Google Scholar]
- Sahimi, M. Flow and Transport in Porous Media and Fractured Rock; Wiley VCH: Weinheim, Germany, 1995. [Google Scholar]
- Auriault, J.L.; Adler, P.M. Taylor dispersion in porous media: Analysis by multiple scale expansions. Adv. Water Resour. 1995, 4, 217–226. [Google Scholar] [CrossRef]
- Auriault, J.L. Non saturated deformable porous media: Quasistatic. Transp. Porous Media 1987, 2, 45–64. [Google Scholar] [CrossRef]
- Wood, B.D.; Valdès-Parada, F.J. Volume averaging: Local and nonlocal closures using a Green’s function approach. Adv. Water Resour. 2013, 51, 139–167. [Google Scholar] [CrossRef]
- Luévano-Rivas, O.A.; Valdés-Parada, F.J. Upscaling immiscible two-phase dispersed flow in homogeneous porous media: A mechanical equilibrium approach. Chem. Eng. Sci. 2015, 126, 116–131. [Google Scholar] [CrossRef]
- Alvarez-Ramirez, J.; Valdes-Parada, F.J.; Ibarra-Valdez, C. An Ohm’s law analogy for the effective diffusivity of composite media. Physica A 2016, 447, 141–148. [Google Scholar] [CrossRef]
- Auriault, J.L. Dynamics of two immiscible fluids flowing through deformable porous media. Transp. Porous Media 1989, 4, 105–128. [Google Scholar] [CrossRef]
- Withaker, S. Flow in porous media II: The governing equations for immiscible, two phase flow. Transp. Porous Media 1986, 105–125. [Google Scholar] [CrossRef]
- Whitaker, S. The closure problem for two-phase flow in homogeneous porous media. Chem. Eng. Sci. 1994, 49, 5. [Google Scholar] [CrossRef]
- Porta, G.M.; Chaynikov, S.; Riva, M.; Guadagnini, A. Upscaling solute transport in porous media from the pore scale to dual- and multi-continuum formulations. Water Resour. Res. 2013, 49, 2025–2039. [Google Scholar] [CrossRef]
- Gray, W.; Miller, C. Introduction to the Thermodynamically Constrained Averaging Theory; Springer: New York, NY, USA, 2014. [Google Scholar]
- Avraam, D.G.; Payatakes, A.C. Flow regimes and relative permeabilities during steady-state two-phase flow in porous media. J. Fluid Mech. 1995, 293, 207–236. [Google Scholar] [CrossRef]
- Tallakstad, K.T.; Knudsen, H.A.; Ramstad, T.; Løvoll, G.; Måløy, K.J.; Toussaint, R.; Flekkøy, E.G. Steady-state two-phase flow in porous media: Statistics and transport properties. Phys. Rev. Lett. 2009, 102, 074502. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Pan, C.; Miller, C.T. Pore-scale investigation of viscous coupling effects for two-phase flow in porous media. Phys. Rev. E 2005, 72, 026705. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Lu, X. Relative permeabilities and coupling effects in steady-state gas-liquid flow in porous media: A lattice Boltzmann study. Phys. Fluids 2009, 21, 092104. [Google Scholar] [CrossRef]
- Ahmadlouydarab, M.; Liu, Z.S.; Feng, J.J. Relative permeability for two-phase flow through corrugated tubes as model porous media. Int. J. Multiphas. Flow 2012, 47, 85–93. [Google Scholar] [CrossRef]
- Andrew, M.; Bijeljic, B.; Blunt, M.J. Pore-scale contact angle measurements at reservoir conditions using X-ray microtomography. Adv. Water Resour. 2014, 68, 24–31. [Google Scholar] [CrossRef]
- Scanziani, A.; Singh, K.; Blunt, M.J.; Guadagnini, A. Automatic method for estimation of in situ contact angle from X-ray micro tomography images of two-phase flow in porous media. J. Colloid Interface Sci 2017, in press. [Google Scholar] [CrossRef] [PubMed]
- Trojer, M.; Szulczewski, M.L.; Juanes, R. Stabilizing fluid-fluid displacements in porous media through wettability alteration. Phys. Rev. Appl. 2015, 3, 054008. [Google Scholar] [CrossRef]
- Dou, Z.; Zhou, Z.F. Numerical study of non-uniqueness of the factors influencing relative permeability in heterogeneous porous media by lattice Boltzmann method. Int. J. Heat Fluid Flow 2013, 42, 23–32. [Google Scholar] [CrossRef]
- Liu, H.; Valocchi, A.J.; Werth, C.; Kang, Q.; Oostrom, M. Pore-scale simulation of liquid CO2 displacement of water using a two-phase lattice Boltzmann model. Adv. Water. Resour. 2014, 73, 144–158. [Google Scholar] [CrossRef]
- Jiang, Z.; van Dijke, M.I.J.; Wu, K.; Couples, G.D.; Sorbie, K.S.; Ma, J. Stochastic pore network generation from 3D rock images. Transp. Porous Med. 2012, 94, 571–593. [Google Scholar] [CrossRef]
- Ahmadi, A.; Aigueperse, A.; Quintard, M. Calculation of the effective properties describing active dispersion in porous media: From simple to complex unit cells. Adv. Water Resour. 2001, 24, 423–438. [Google Scholar] [CrossRef]
- Bahar, T.; Golfier, F.; Oltéan, C.; Benioug, M. An upscaled model for bio-enhanced NAPL dissolution in porous media. Transp. Porous Med. 2016, 113, 653–693. [Google Scholar] [CrossRef]
- Lugo-Méndez, H.D.; Valdés-Parada, F.J.; Porter, M.L.; Wood, B.D.; Ochoa-Tapia, J.A. Upscaling diffusion and nonlinear reactive mass transport in homogeneous porous media. Transp. Porous Med. 2015, 107, 683–716. [Google Scholar] [CrossRef]
- Icardi, M.; Boccardo, G.; Tempone, R. On the predictivity of pore-scale simulations: Estimating uncertainties with multilevel Monte Carlo. Adv. Water Resour. 2016, 95, 46–60. [Google Scholar] [CrossRef]
- Hyman, J.D.; Smolarkiewicz, P.K.; Winter, C.L. Heterogeneities of flow in stochastically generated porous media. Phys. Rev. E 2012, 86, 056701. [Google Scholar] [CrossRef] [PubMed]
- Siena, M.; Riva, M.; Hyman, J.D.; Winter, C.L.; Guadagnini, A. Relationship between pore size and velocity probability distributions in stochastically generated porous media. Phys. Rev. E 2014, 89, 013018. [Google Scholar] [CrossRef] [PubMed]
- Hyman, J.D.; Winter, C.L. Stochastic generation of explicit pore structures by thresholding Gaussian random fields. J. Comput. Phys. 2014, 277, 16–31. [Google Scholar] [CrossRef]
- Hyman, J.D.; Smolarkiewicz, P.K.; Winter, C.L. Pedotransfer functions for permeability: A computational study at pore scales. Water Resour. Res. 2013, 49, 2080–2092. [Google Scholar] [CrossRef]
- Hyman, J.D.; Winter, C.L. Hyperbolic regions in flows through three-dimensional pore structures. Phys. Rev. E 2013, 88, 063014. [Google Scholar] [CrossRef] [PubMed]
- Guadagnini, A.; Blunt, M.; Riva, M.; Bijeljic, B. Statistical scaling of geometric characteristics in millimeter scale natural porous media. Trans. Porous Med. 2014, 101, 465–475. [Google Scholar] [CrossRef]
- Hyman, J.D.; Guadagnini, A.; Winter, C.L. Statistical scaling of geometric characteristics in stochastically generated pore microstructures. Computat. Geosci. 2015, 19, 845–854. [Google Scholar] [CrossRef]
- Dong, H.; Blunt, M.J. Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 2009, 80, 036307. [Google Scholar] [CrossRef] [PubMed]
- Mantz, H.; Jacobs, K.; Mecke, K. Utilizing Minkowski functionals for image analysis: A marching square algorithm. J. Stat. Mech. 2008, 2008, P12015. [Google Scholar] [CrossRef]
- Vogel, H.J.; Roth, K. Quantitative morphology and network representation of soil pore structure. Adv. Water Resour. 2001, 24, 233–242. [Google Scholar] [CrossRef]
- Vogel, H.J.; Weller, U.; Schlüter, S. Quantification of soil structure based on Minkowski functions. Comput. Geosci. 2010, 36, 1236–1245. [Google Scholar] [CrossRef]
- Schlüter, S.; Vogel, H.J. On the reconstruction of structural and functional properties in random heterogeneous media. Adv. Water Resour. 2011, 34, 314–325. [Google Scholar] [CrossRef]
- COMSOL Multiphysics®. CFD Module User’s Guide, Version 4.4; Comsol Inc.: Burlington, MA, USA, 2013. [Google Scholar]
- Badalassi, V.E.; Ceniceros, H.D.; Banerjee, S. Computation of multiphase systems with phase field models. J. Comput. Phys. 2003, 190, 317–397. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.J.; Liu, C.; Shen, J. A diffuse-interface method for simulating two-phase flows of complex fluids. J. Fluid Mech. 2004, 515, 293–317. [Google Scholar] [CrossRef]
- Amiri, H.A.A.; Hamouda, A.A. Evaluation of level set and phase field methods in modeling two phase flow with viscosity contrast through dual-permeability porous medium. Int. J. Multiphas. Flow 2013, 52, 22–34. [Google Scholar] [CrossRef]
- Amiri, H.A.A.; Hamouda, A.A. Pore-scale modeling of non-isothermal two phase flow in 2D porous media: Influences of viscosity, capillarity, wettability and heterogeneity. Int. J. Multiphas. Flow 2014, 61, 14–27. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Feng, J.J.; Ollivier-Gooch, C.F.; Hu, H.H. Phase-field simulations of interfacial dynamics in viscoelastic fluids using finite elements with adaptive meshing. J. Comput. Phys. 2006, 219, 47–67. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Feng, J.J. Spontaneous shrinkage of drops and mass conservation in phase-field simulations. J. Comput. Phys. 2007, 223, 1–9. [Google Scholar] [CrossRef]
- Beal, C. The viscosity of air, water, natural gas, crude oil and its associated gases at oil field temperature and pressure. Trans. AIME 1946, 165, 94–115. [Google Scholar] [CrossRef]
- Whitaker, S. The Method of Volume Averaging; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Auriault, J.L.; Boutin, C.; Geindreau, C. Homogenization of Coupled Phenomena in Heterogeneous Media; Iste Wiley: London, UK, 2009. [Google Scholar]
- Chang, L.C.; Chen, H.H.; Shan, H.Y.; Tsai, J.P. Effect of connectivity and wettability on the relative permeability of NAPLs. Environ. Geol. 2009, 56, 1437–1447. [Google Scholar] [CrossRef]
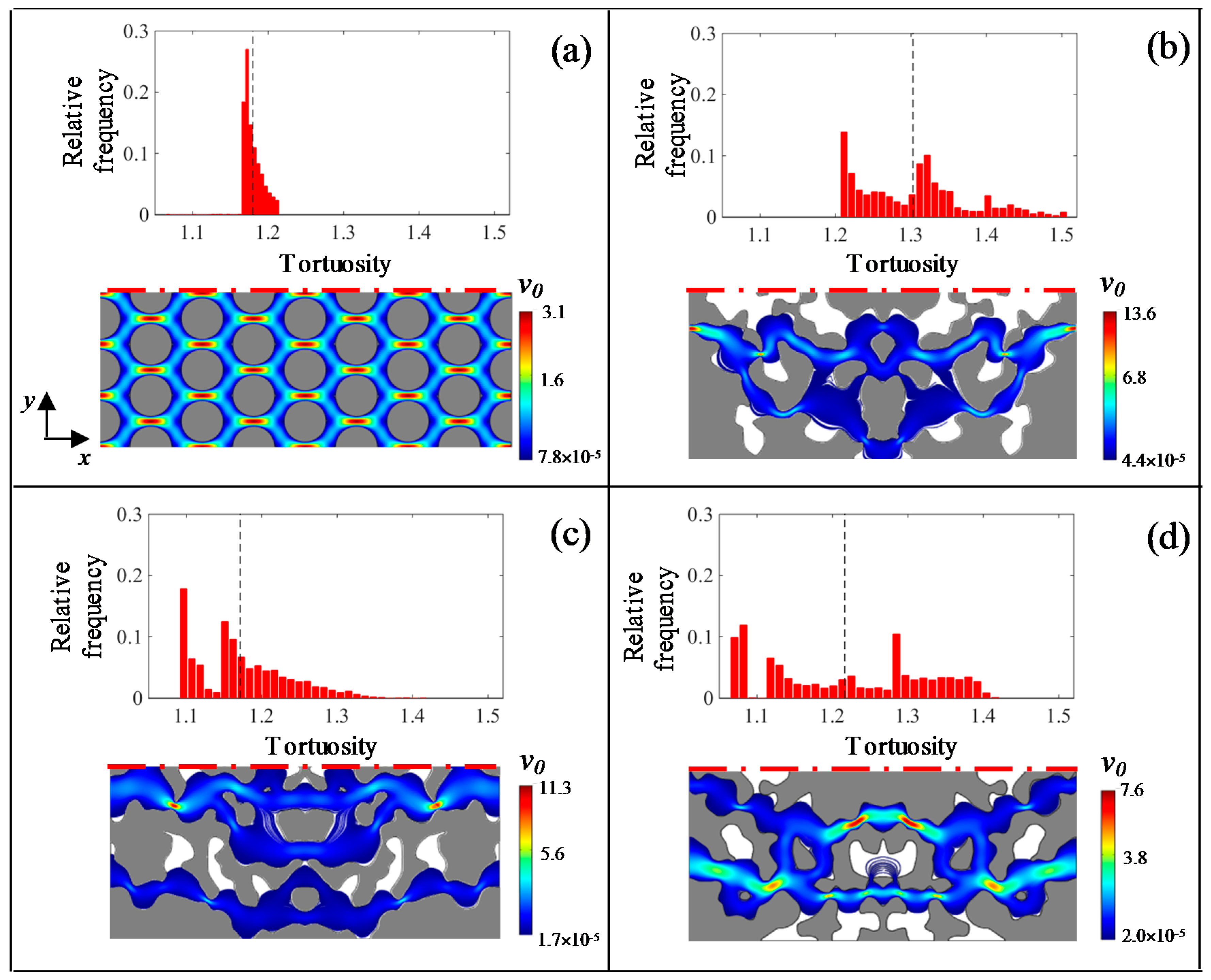
| Sample Identifier | n | SSA (10−3 m−1) | K (10−10 m2) | ||||
|---|---|---|---|---|---|---|---|
| HDa | 0.48 | 8.63 | 4.97 | - | - | - | - |
| HDb | 0.50 | 8.63 | 11.67 | - | - | - | - |
| HDc | 0.52 | 8.63 | 10.47 | - | - | - | - |
| Average HDa–HDc | 0.50 | 8.63 | 9.06 | - | - | - | - |
| E1 | 0.48 | 8.39 | 1.25 | 0.12 | 0.23 | 0.12 | 0.21 |
| E2 | 0.49 | 7.84 | 2.42 | 0.16 | 0.25 | 0.17 | 0.23 |
| E3 | 0.48 | 8.61 | 3.43 | 0.17 | 0.25 | 0.12 | 0.22 |
| E4 | 0.51 | 9.11 | 3.84 | 0.11 | 0.21 | 0.13 | 0.23 |
| E5 | 0.49 | 9.24 | 4.43 | 0.18 | 0.26 | 0.14 | 0.24 |
| E6 | 0.50 | 8.20 | 2.29 | 0.16 | 0.25 | 0.21 | 0.24 |
| E7 | 0.49 | 7.69 | 1.01 | 0.12 | 0.22 | 0.25 | 0.27 |
| E8 | 0.49 | 9.44 | 3.11 | 0.13 | 0.24 | 0.16 | 0.27 |
| E9 | 0.49 | 9.13 | 1.04 | 0.14 | 0.27 | 0.13 | 0.24 |
| Average E1–E9 | 0.49 | 8.63 | 2.54 | 0.14 | 0.24 | 0.16 | 0.24 |
| Sample Identifier | Npores | (%) | M0 (10−6 m2) | M1 (10−3 m) | M2 | |
|---|---|---|---|---|---|---|
| HDa | 112 | 3.00 | 2.68 | 8.10 | 69.91 | −173.25 |
| HDb | 112 | 3.00 | 2.68 | 8.53 | 73.19 | −181.00 |
| HDc | 112 | 3.00 | 2.68 | 10.73 | 80.77 | −64.25 |
| Average HDa–HDc | 112 | 3.00 | 2.68 | 9.12 | 74.62 | −139.50 |
| E1 | 64 | 2.63 | 4.10 | 7.20 | 60.45 | −145.25 |
| E2 | 72 | 2.72 | 3.78 | 7.03 | 55.10 | −133.25 |
| E3 | 80 | 2.70 | 3.38 | 7.16 | 61.61 | −147.50 |
| E4 | 76 | 2.37 | 3.12 | 6.74 | 61.39 | −160.75 |
| E5 | 100 | 2.68 | 2.68 | 6.95 | 64.24 | −151.00 |
| E6 | 80 | 2.55 | 3.19 | 6.87 | 56.28 | −134.25 |
| E7 | 84 | 2.48 | 2.95 | 7.06 | 54.30 | −135.75 |
| E8 | 100 | 2.32 | 2.32 | 9.44 | 65.62 | −162.50 |
| E9 | 104 | 2.35 | 2.26 | 9.13 | 63.93 | −157.75 |
| Average E1–E9 | 84.4 | 2.53 | 3.09 | 6.99 | 60.32 | −147.56 |
| Sample Identifier | Np | Mean | Variance | Minimum | Maximum | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| HDa | 4906 | 1.18 | 1.5 × 10−4 | 1.06 | 1.21 | 0.44 | 1.00 |
| HDb | 4947 | 1.14 | 6.5 × 10−5 | 0.96 | 1.16 | −9.33 | 197.76 |
| HDc | 4935 | 1.21 | 3.3 × 10−4 | 1.13 | 1.27 | 1.27 | 3.87 |
| Average HDa–HDc | 4929 | 1.18 | 1.8 × 10−4 | 1.05 | 1.21 | −2.54 | 67.54 |
| E1 | 4726 | 1.30 | 5.3 × 10−3 | 1.21 | 1.51 | 0.56 | 2.64 |
| E2 | 2305 | 1.32 | 2.0 × 10−2 | 1.15 | 1.92 | 0.71 | 3.46 |
| E3 | 2422 | 1.34 | 5.4 × 10−2 | 1.12 | 2.14 | 1.23 | 3.43 |
| E4 | 3729 | 1.17 | 3.7 × 10−3 | 1.09 | 1.42 | 0.63 | 2.81 |
| E5 | 3471 | 1.42 | 2.7 × 10−2 | 1.18 | 1.74 | 0.54 | 1.97 |
| E6 | 3730 | 1.80 | 2.6 × 10−2 | 1.15 | 2.11 | −1.32 | 7.85 |
| E7 | 3151 | 1.26 | 8.7 × 10−3 | 1.15 | 1.66 | 1.21 | 3.67 |
| E8 | 4480 | 1.21 | 1.2 × 10−2 | 1.06 | 1.42 | 0.06 | 1.59 |
| E9 | 4697 | 1.17 | 3.7 × 10−3 | 1.09 | 1.42 | 0.64 | 2.76 |
| Average E1–E9 | 3635 | 1.33 | 8.1 × 10−3 | 1.10 | 1.50 | 0.64 | 2.67 |
| Property | Experiments from Avraam and Payatakes [13] | Experiments from Chang et al. [50] | Our Computations | |
|---|---|---|---|---|
| Non wetting fluid | n-Dodecane | Diesel Fuel/Tetrachloroethane | Oil | |
| Wetting fluid | Water | Water | Water | |
| (Pa s) | 1.36 × 10−3 | not specified | 2.0 × 10−3 | |
| (Pa s) | 0.94 × 10−3 | not specified | 1.0 × 10−3 | |
| 1.45 | not specified | 2.0 | ||
| (kg/m3) | 730 | 820/1600 | 1000 | |
| (kg/m3) | 995 | 997 | 1000 | |
| (mN/m) | 25 | 48.7/38.75 | 40.0 | |
| (°) | 40 | 0 | 60 | |
| Capillary Number | 1.19 × 10−5 | not specified | 10−4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchi Janetti, E.; Riva, M.; Guadagnini, A. Effects of Pore-Scale Geometry and Wettability on Two-Phase Relative Permeabilities within Elementary Cells. Water 2017, 9, 252. https://doi.org/10.3390/w9040252
Bianchi Janetti E, Riva M, Guadagnini A. Effects of Pore-Scale Geometry and Wettability on Two-Phase Relative Permeabilities within Elementary Cells. Water. 2017; 9(4):252. https://doi.org/10.3390/w9040252
Chicago/Turabian StyleBianchi Janetti, Emanuela, Monica Riva, and Alberto Guadagnini. 2017. "Effects of Pore-Scale Geometry and Wettability on Two-Phase Relative Permeabilities within Elementary Cells" Water 9, no. 4: 252. https://doi.org/10.3390/w9040252






