1. Introduction
Modern water resource systems face water shortage risks from multiple uncertainties, which could cause negative social, economic, and ecological impacts. To alleviate the negative impacts of water shortage, management techniques such as increasing water supply and decreasing water demand are essential for the supply–demand balance. As a common component of a water resources system, reservoirs [
1,
2] can redistribute natural water resources over time by using water storage. However, during drought, total water availability may be insufficient to meet total demand, resulting in conflicts among competing water uses in different periods. In such cases, whether limited water is delivered for immediate use or kept for future use should be decided to best balance the consequences of current water use versus those in the future. For water supply reservoir, the consequence means that both the benefits of the current water delivery and carryover storage (for future water deliveries) can be jointly assessed. When potential drought is anticipated, the water delivery in the current period can be curtailed to alleviate the negative influence of water shortage in the future [
3], although the current availability is adequate to satisfy immediate water demand. This condition is a hedging policy [
4,
5], which is a water-saving approach to reducing maximum drought impacts.
Early studies have focused on developing various forms of hedging policies [
6] or models for reservoir operations. Hashimoto et al. [
7] analyzed the formulation of loss function and its corresponding optimal operational rules. Klemes [
8] verified that the standard operating policy (SOP) is the best policy given a linear loss function. For nonlinear loss or benefit functions, hedging rules vary with regard to various model formulations and purposes. Draper and Lund [
3] introduced a two-stage optimal hedging model that determines the optimal water delivery strategy for maximizing the summation of current and future benefits, and they found that the optimality condition for hedging is at which the marginal benefit of storage equals the marginal benefit of water release. They then derived the analytic hedging rules for monotonic increasing benefit functions. Shiau [
9] noted that either the release or the storage deviating from their targets could cause economic loss and used normalized deviations as loss functions to characterize competing water allocations. Zeng et al. [
10] extended the study of Draper and Lund [
3] to explore optimal hedging rules for multiple reservoirs that operate in parallel with a joint water demand.
Decision makers often rely on inflow forecasts [
11] to estimate potential water available for allocations, considering that water supply reservoir operations usually require scheduling releases and storage over several months. The influence of inflow forecast uncertainty should be incorporated into decision making, given that it is often difficult to precisely forecast the actual inflow at the beginning of the current time. Therefore, the hedging model turns out to be a stochastic optimization problem wherein the conventional objective [
12,
13] is to optimize the expected value (EV) of total benefit or total loss. This model yields a risk-neutral decision that is suited for all possible future inflow realizations, considering both cases wherein inflow is overestimated or underestimated. You and Cai [
14] examined how reservoir inflow uncertainty affects hedging operations using the EV of total benefit as the objective. They concluded that hedging should reduce the current release to face future risk induced by hydrological uncertainty. Zhao et al. [
15] developed optimal hedging rules for reservoir flood operations considering the influence of forecast uncertainty. To minimize the total expected flood damages, they analyzed how the expected flood-safety margin should be optimally allocated to the current and future time periods for different levels of flood events.
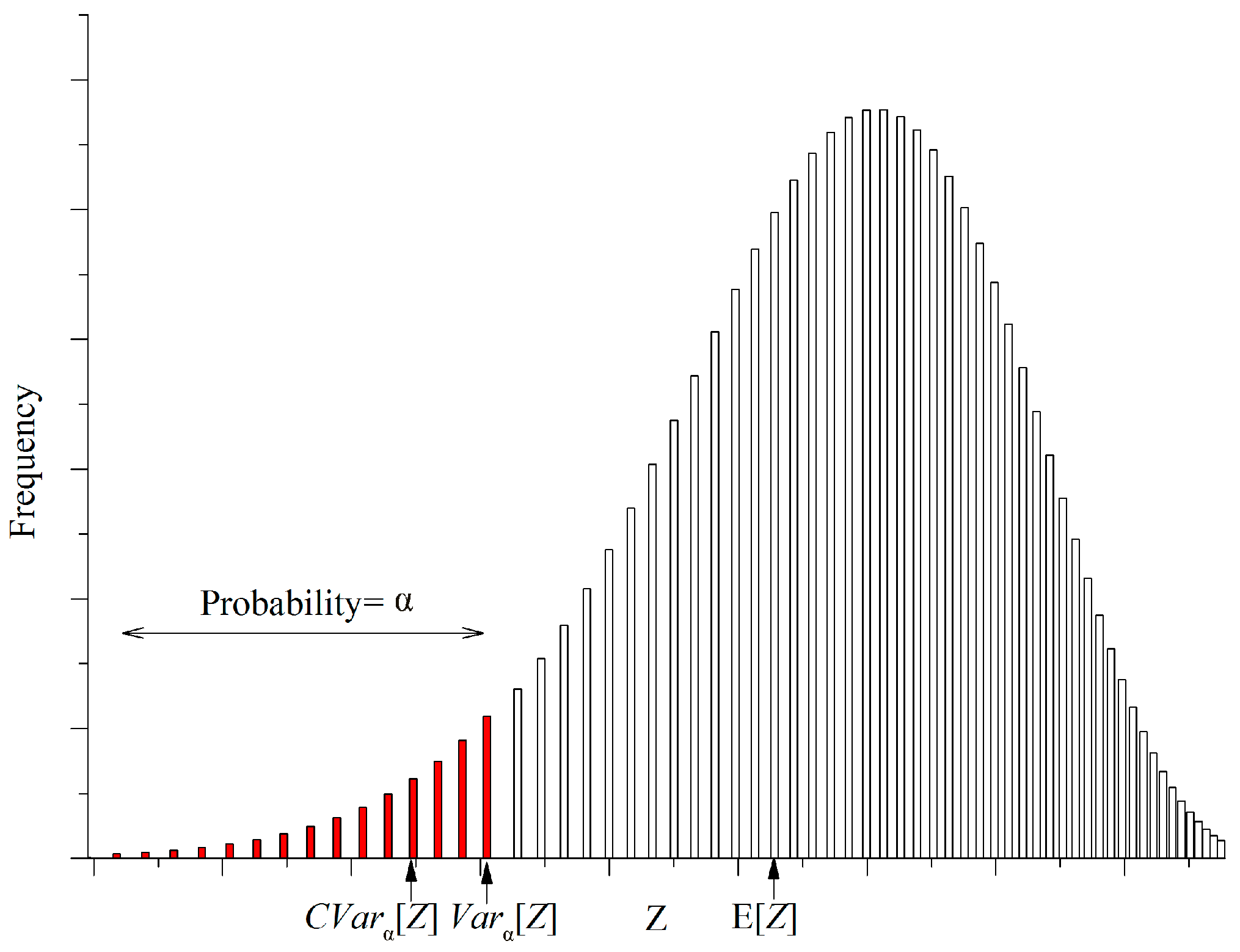
The expected value (EV) criterion provides a risk-neutral policy that is indifferent between gaining benefit in favorable realizations and suffering loss in unfavorable realizations because it seeks the best average outcome. Consequently, high benefit can be obtained when inflow is high, whereas high loss could also be a result of a low inflow. The optimal policy yielded from the EV criterion is often vulnerable to risks in unfavorable realizations. In water resource allocations, decision makers are often more concerned about the overall benefit in unfavorable realizations wherein water is less than anticipated [
16,
17]. This concern suggests a more conservative criterion, rather than EV, to focus on outcomes under unfavorable or even worst-case scenarios. The conditional value-at-risk (CVaR), or the expected shortfall, is a suitable criterion for assessing the mean value of outcome from undesirable cases, which is originally used in finance [
18,
19] to measure expected losses above a given loss threshold. Yamout et al. [
20] verified that applying the CVaR criterion to water allocation problems presents continuous and consistent model behavior compared with the modeling results under the value-at-risk (VaR) criterion. Piantadosi et al. [
21] proposed a model for managing the urban storm water to minimize CVaR, and they showed that the optimal policy under CVaR differs from the optimal policy obtained under expected loss minimization criterion. Hu et al. [
22] established a multiobjective model including water allocation equality and economic efficiency risk control, and the model incorporates a constraint to bind the CVaR of economic efficiency risk induced by the uncertainty of water availability. The optimal decision and model performance under the CVaR criterion differ from that under the expectation criterion. Thus, analytic derivations and analysis on the related formulations of hedging rules could provide decision makers intuitive and effective guidance in rationing water resource allocations.
The purposes of this study are: (1) to derive the hedging rules for water supply reservoir operations under the CVaR criterion considering inflow forecast uncertainty and (2) to explore the differences in rationing water deliveries and related performances under two criteria (CVaR and EV). Specifically, this study extends the studies of Draper and Lund [
3] and You and Cai [
14] and establishes a stochastic programming model for hedging under the consideration of inflow forecast uncertainty. Setting the objectives of maximizing the EV and the CVaR of total benefit, we derive the optimality condition of hedging policies and their analytic formulations. Comparative experiments and model simulations are conducted to investigate the differences. The methods are derived under the background of a reservoir solely for water supply, and the utility of water supply and water storage are evaluated in monetary values. These methods could limit the application of the methodologies to the operations of multipurpose reservoirs, except for the cases wherein the utility of operational purposes can be common-measured or converted into the same measuring unit using weights or conversion factors.
The remainder of this paper is organized as follows.
Section 2 reviews the classical two-period optimal hedging model under the EV criterion and extends it to a hedging model using the CVaR criterion. Thereafter, we derive the optimality condition for the hedging model under the CVaR criterion and obtain analytically formulated hedging rules.
Section 3 applies the methodology to a water supply reservoir, the Foziling Reservoir in China, and investigates the influences of parameters on the hedging rules and their statistical measures via sensitivity analysis.
Section 4 discusses the differences in performances of hedging rules when applied to guide real-time operations using numerical simulations. Finally,
Section 5 concludes the study.
3. Results
3.1. Hedging Decisions
Optimal hedging policies on
can be obtained using Equation (21) under different conditions. For a brief demonstration, in this section, we simulate the hedging policy of reservoir operations at the beginning of March, facing a water demand (
) of
. To address the influence of
on the results,
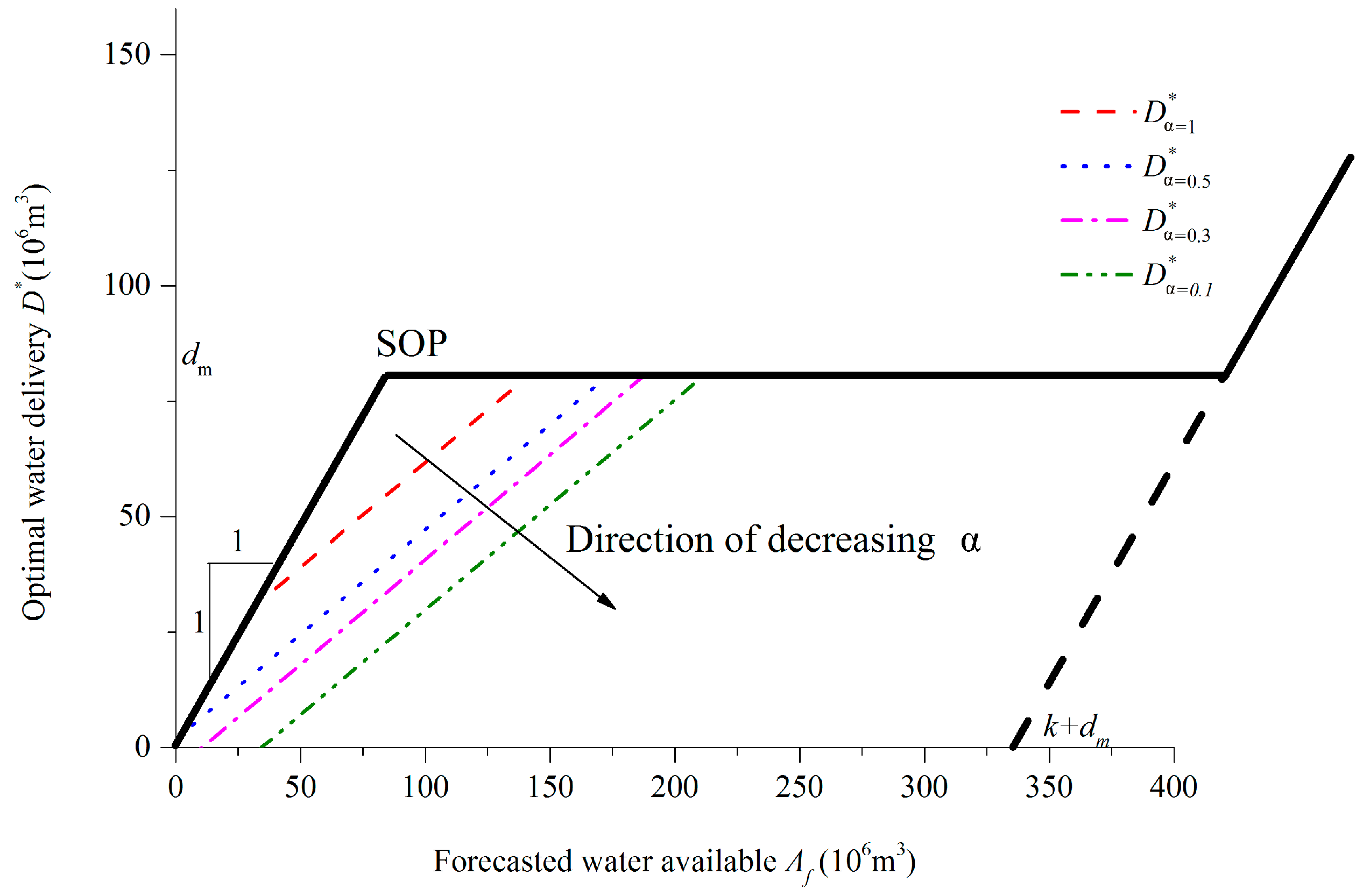
Figure 3 plots the optimal hedging rules under different values of
but the same value of
(
).
The hedging rule curves present linear trends with the increase in forecasted available water. Consistent with the analysis made in
Section 2.2.3, limited water would be delivered as
decreases. The starting water availability (SWA) [
25], which is the threshold of
for triggering hedging, increases as
decreases when
is less than or equal to 0.5. The ending water availability (EWA), which is the threshold of
for terminating hedging, increases as
decreases.
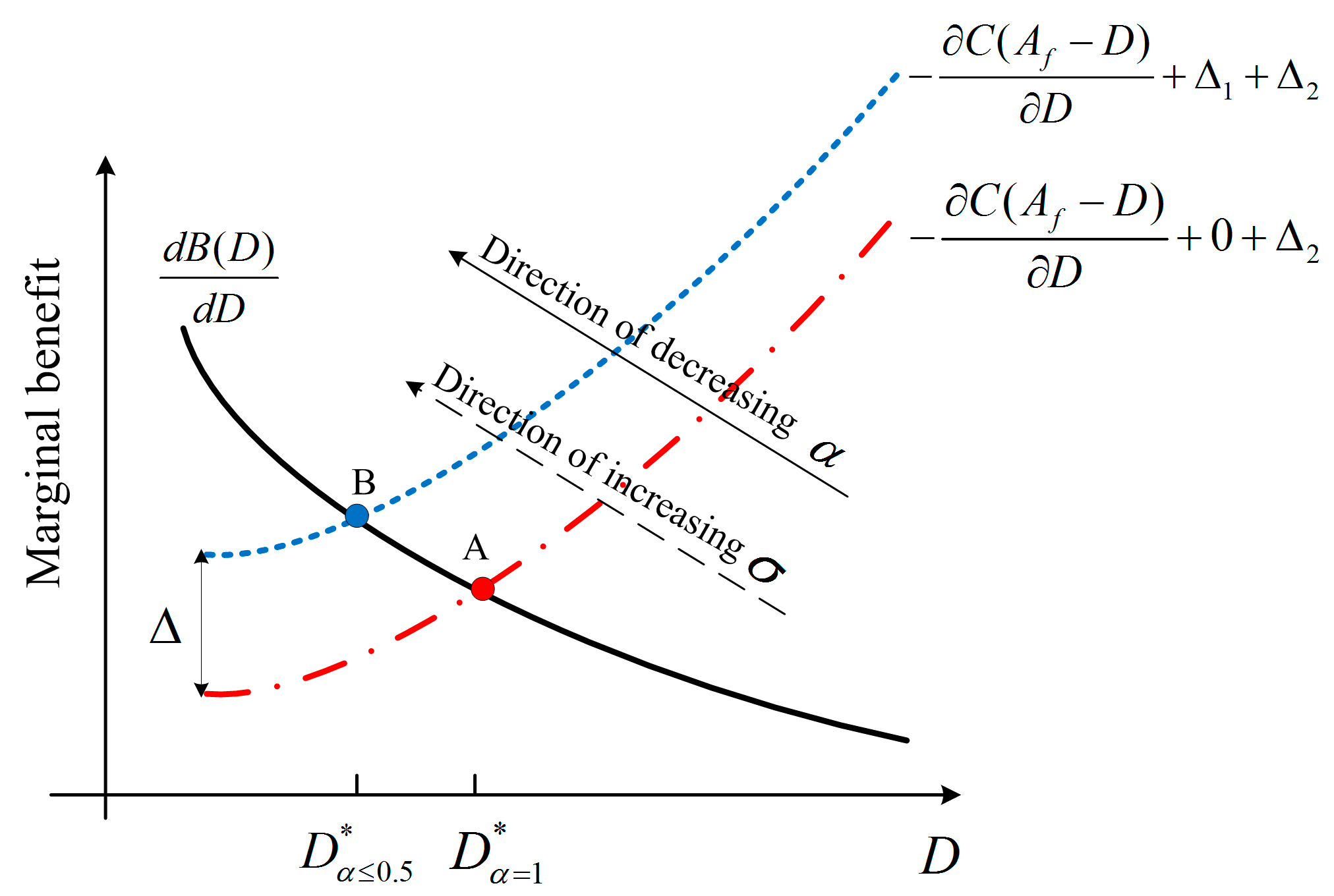
The variation ranges of SWA to EWA imply that the water delivery under the CVaR criterion is more conservative than that under the EV criterion. For instance, under the condition of , hedging would be triggered when varies from 0 to m3, whereas the triggered range of for varies from m3 to m3, indicating that hedging would be undertaken in a wide range of when is low. The “zero-release” range of would be great under a low value, which means water is strictly reserved for anti-adverse hydrological conditions in the future rather than delivered in the current.
The decrease in indicates that decision makers become risk-averse toward water shortage in the future, i.e., they would sacrifice current benefit to reduce the loss in the future benefit induced by potential drought. Reduced water delivery is a surrogate of insurance for the worst outcomes, and the most conservative decision upon the current water delivery would be made if approaches zero.
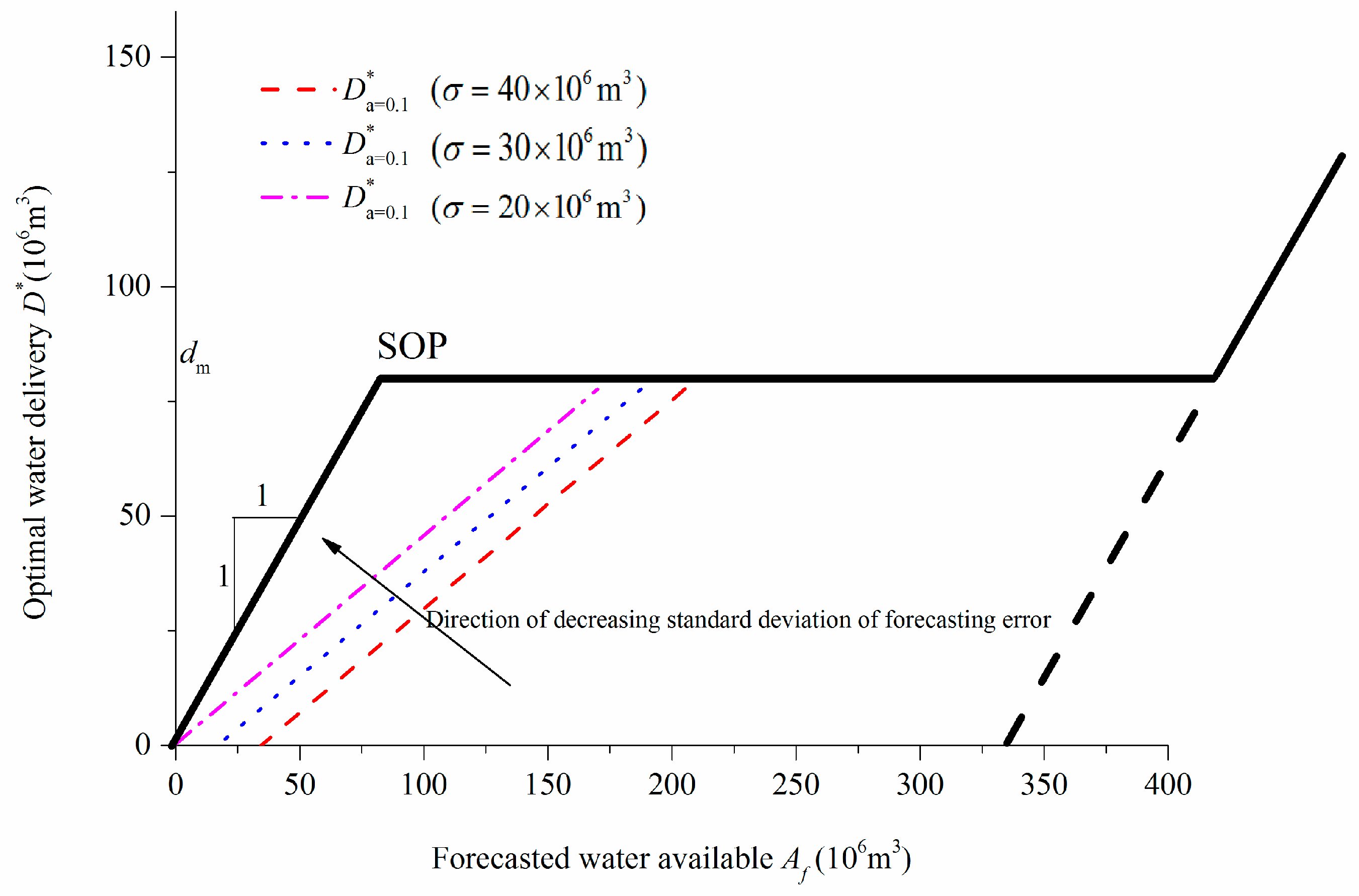
Figure 4 plots the optimal hedging curves under different values of
but with the same value of
. The optimal water delivery can be increased as
decreases, which means that abundant water can be delivered to ensure the current benefit if the influence of forecast uncertainty is reduced by improving the precision of inflow forecasts. The decrease in
results in a sharp forecasting error distribution, in which the probabilities of adverse situations (e.g., inflow is greatly overestimated) are low. Thus, substantial water can be delivered rather than reserved.
3.2. Statistical Measures of Total Benefit
To investigate the statistical measures of total benefit under different water delivery plans,
Table 2 lists the corresponding results for the case of
and
.
The results show that the optimal water delivery solution under the EV criterion () can only guarantee that () is maximized, but it does not ensure that the statistical results of total benefit under less-profitable situations () are maximized. Similarly, optimal water delivery under the CVaR criterion () guarantees that is maximized at the expense of degradation in the EV of total benefit. For instance, would result in the highest of CNY, but the lowest value of ( CNY), whereas produces the highest of CNY but the lowest value of ( CNY). Therefore, if decision makers select rather than , can be increased by CNY (5.3%) at the expense of a reduction in by CNY (2.7%). Tradeoffs exist among the indices.
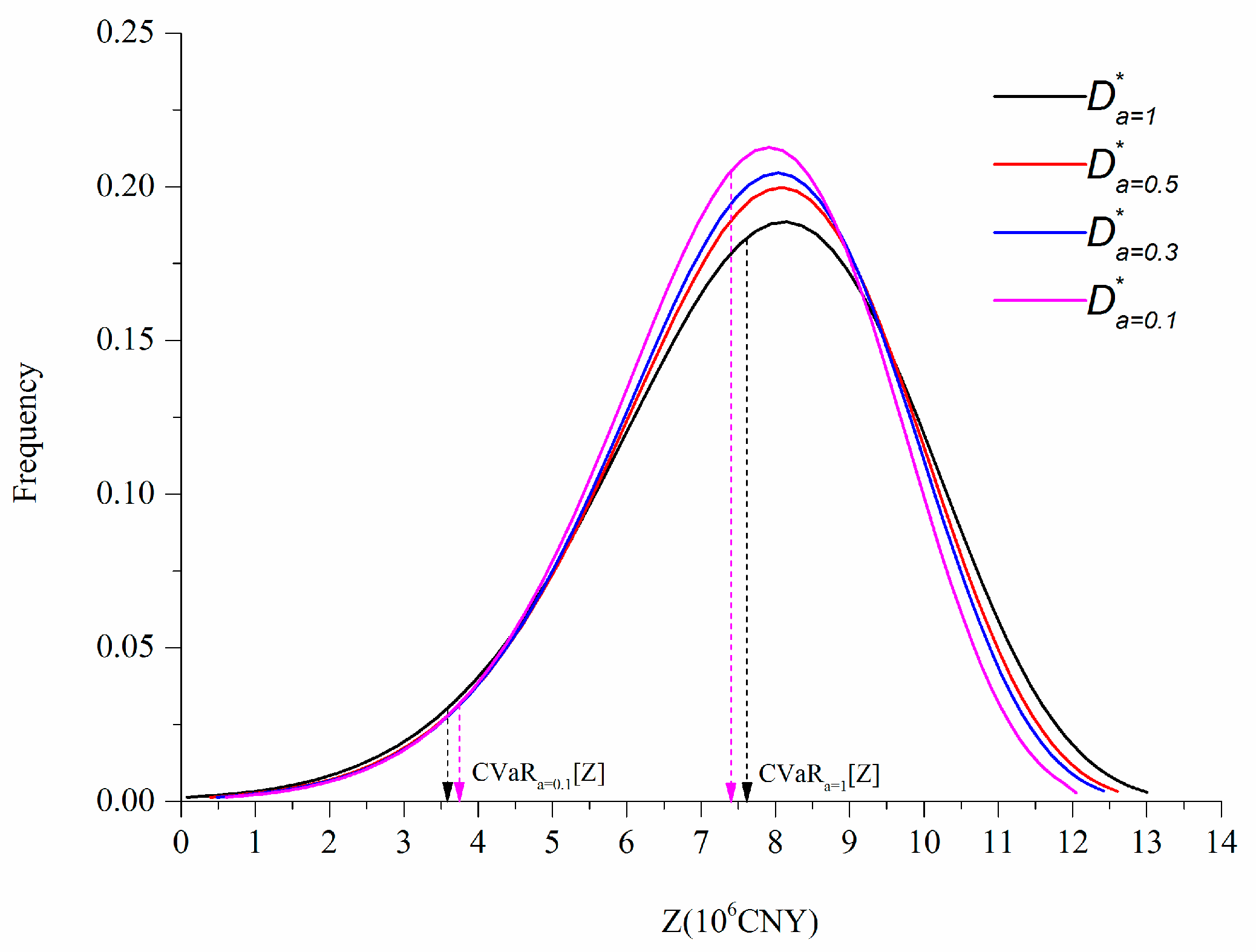
Figure 5 draws the probability density functions of
under different values of
to determine the reasons for the tradeoffs among different CVaR indices under various hedging policies.
The standard deviation of
(
) decreases as
diminishes. This result can be explained by a theoretical analysis of the variance of
, as analyzed in
Appendix B. The decrease in
could result in water-saving actions, which reduce water delivery
. Therefore, although actual inflow is less than anticipated and water shortage may occur in the future, the influence on
can be alleviated because reduced water delivery helps increase water storage. Correspondingly, the total benefit in dry hydrological scenarios is improved. If actual inflow is greater than anticipated and water that spills, the reduced water delivery could result in water surplus with minimal marginal benefit. Thus, the total benefit in those wet hydrological scenarios decreases. The probability density function of
sharpens due to the influence of a reduced
.
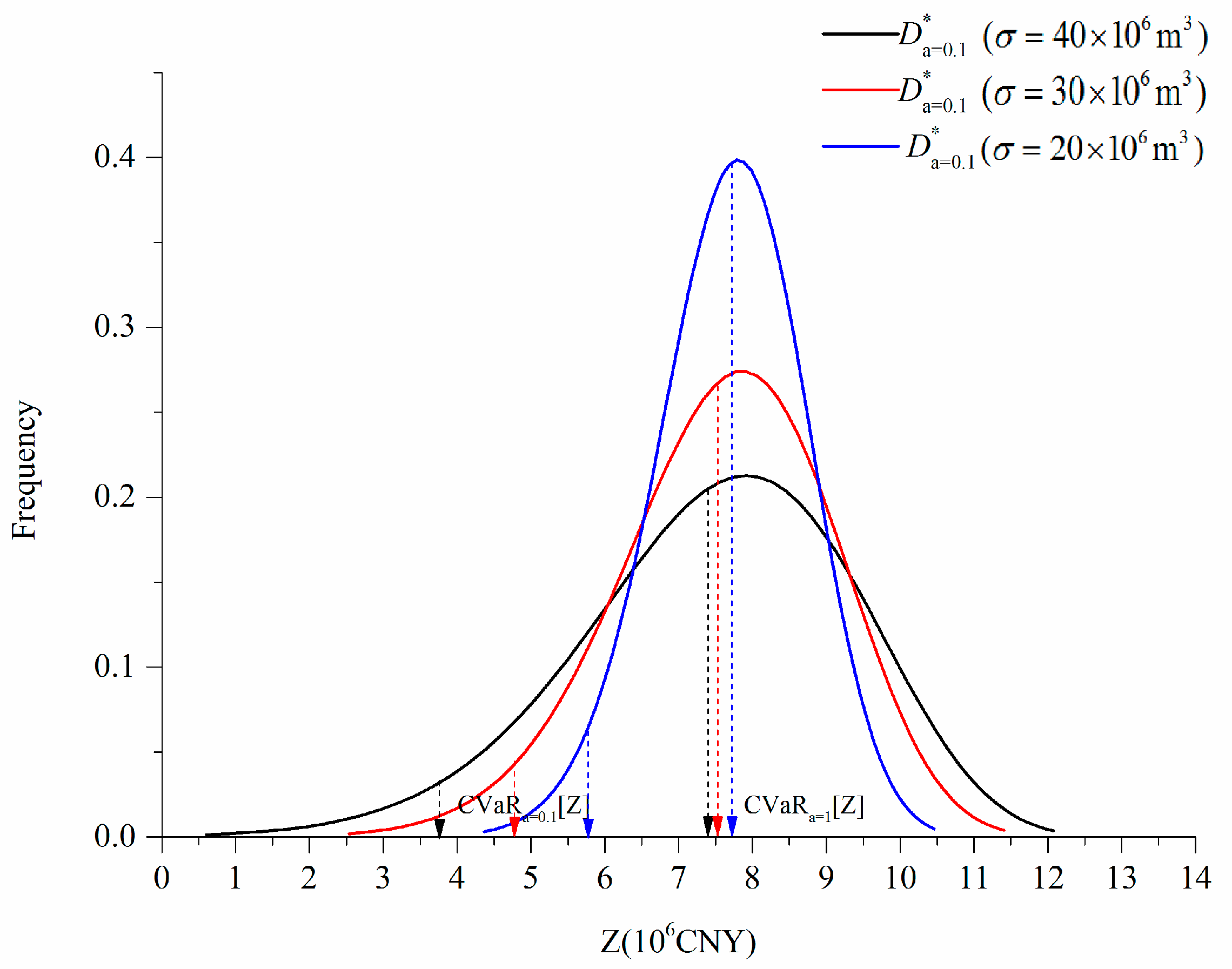
Figure 6 plots the probability density function of
under different values of
with
. This figure shows how the distribution of total benefit is influenced by improvements in forecasting accuracy.
and are improved as forecasting accuracy increases. If can be reduced from to , then can be increased by nearly 53%, whereas can be increased by 3.4%. The total benefit under a low confidence level of CVaR is more sensitive than the EV of total benefit considering the influence of forecasting accuracy. Therefore, improving the forecasting accuracy is an effective approach to improving total benefit, especially for the results under extremely dry hydrological conditions.
4. Discussion
The results under 49-year (1965–2013) actual streamflow sequences from observation records are simulated to validate the performances of hedging policies under different confidence levels when applied to guide real-time operations. Forecasted streamflow sequences are generated according to the current level of forecasting accuracy and used for guiding operations. Four indices, namely, the reliability
[
7], maximum one-month shortage percentage
[
9], total water spillage
, and actual total benefit during droughts
, are used to assess the performances, which can be characterized as follows:
where
is the number counting function;
is the index of time period;
is the total number of time periods;
is the index of critical drought time spans during which water shortfalls occur;
is the total number of drought events; and
and
are the starting and ending indices of time period during drought event
, respectively.
Long streamflow sequences are divided into four groups according to the frequency range of annual water volume, namely, the wet (0% to 25%), medium (25% to 50%), dry (50% to 75%), and extremely dry (75% to 100%) patterns to demonstrate the differences in the results under different hydrological patterns.
Table 3 presents the results of indices under different hedging decisions denoted by confidence levels.
Table 3 presents the following findings:
- (1)
Hedging decisions under the EV criterion () result in the highest reliability of water supply for all hydrological patterns. They could also cause the highest one-month water shortage level under dry and extremely dry conditions. By contrast, hedging decisions under the CVaR criterion () cause frequent but small water shortages, yet the highest one-month water shortages under dry and extremely dry conditions are all less than the results obtained under the hedging decisions using the expectation criterion. However, under wet and medium hydrological conditions, hedging decisions under the CVaR criterion could cause severe one-month water shortage. Hedging decisions under the CVaR criterion would be suited for dry and extremely dry hydrological conditions wherein the occurrence likelihood of drought is high.
- (2)
Substantial water would be spilled if the hedging policies under the CVaR criterion are implemented compared with the results of hedging under the expectation criterion. Hedging the loss of water shortage during drought by water conservation would have a side effect in increasing the water spilled considering the influence of forecasting error.
- (3)
The effect of hedging under the CVaR criterion can be explored under dry or extremely dry hydrological patterns. Consistent with theoretical analysis, the actual total benefit obtained from hedging decisions under the CVaR criterion is greater than the total benefit obtained from hedging decisions under the expectation criterion, during critical time periods of dry and extremely dry hydrological patterns. In facing wet or medium hydrological patterns, the difference in actual total benefit could be small.
The results of water shortage percentage and carryover storage for the reservoir during a typical dry hydrological time span (with the hydrology frequency of 87%) are compared for the four scenarios of hedging policies, as shown in
Figure 7.
During the critical time periods, the total inflows are overestimated by 1%. The highest one-month shortage percentage under the hedging policy using the EV criterion () would be 79.4%, whereas that obtained under the hedging policy using the CVaR criterion () would be 74.2%. Both the highest one-month shortages occurred in September 1976 as actual inflows from June to August 1976 are overestimated by 28%. Under the guidance of forecasted inflow, the policy () delivers 5.9% more water than the water delivered by the hedging policy using the CVaR () criterion. Compared with the result of actual benefit obtained from the hedging policy using the EV criterion (), the actual benefit can be increased by 0.4% if the policy of the CVaR criterion () is employed due to a successful water carryover.
5. Conclusions
This paper discusses the optimal hedging policy for a water supply reservoir considering the influence of inflow forecast uncertainty. An optimal hedging model for maximizing the overall benefit of water delivery (current benefit) and water storage (future benefit) is established. Inflow forecast uncertainty is addressed when estimating current water availability. Two different optimization criteria, the EV and CVaR criteria, are introduced to set different measures of total benefit of water delivery and carryover storage. The optimality conditions for the optimal hedging policies under the two criteria are analyzed, and the analytic solutions of hedging rules are derived. Differences in the hedging rules under the two criteria are highlighted with regard to varied inflow forecasting precisions and attitudes of decision makers toward risk hedging (the confidence level). Performances of hedging policies under the two criteria in real-time operations are analyzed by numerical simulations.
The methodology is applied to the Foziling Reservoir in China. The results are as follows:
- (1)
Under the influence of forecast uncertainty, the optimal value of water delivery reduces as increases or decreases. Therefore, decision makers will be conservative on current water delivery under a low inflow forecasting precision or a significant risk-averse attitude.
- (2)
The maximization of is at the expense of potential degradation in . Hedging the risk of water shortage in the future encourages water saving in the current, but it could also increase the chance of future water spill.
- (3)
In real-time operations, compared with the hedging policies using the EV criterion, hedging decisions using the CVaR criterion would be more suited for dry and extremely dry hydrological conditions wherein the occurrence likelihood of drought is high.
Although the optimal hedging rules under CVaR and EV criteria are systematically compared and analyzed via analytic derivations, more complex and practical modeling techniques are encouraged to bridge the gap between mathematical simplifications and real-world implementations. For example, extending the study to guide the operations of multiple-reservoir systems presents challenges in dealing with complex constraints that bind the physical and economic conditions of hedging. Future efforts can improve the current study.