The LHC Higgs Boson Discovery: Updated Implications for Finite Unified Theories and the SUSY Breaking Scale
Abstract
:1. Introduction
2. Theoretical Basis
Reduction of Dimension One and Two Parameters
3. Finiteness in N = 1 Supersymmetric Gauge Theories
- 1.
- There is no gauge anomaly.
- 2.
- The gauge β-function vanishes at one loop:
- 3.
- There exist solutions of the form:to the conditions of vanishing one-loop matter fields’ anomalous dimensions:
- 4.
- These solutions are isolated and non-degenerate when considered as solutions of vanishing one-loop Yukawa β-functions:
4. The SSB Sector of Reduced N = 1 SUSY and Finite Theories
All-Loop RGI Relations in the SSB Sector
5. A Successful Finite Unified Theory
- One-loop anomalous dimensions are diagonal, i.e., .
- Three fermion generations in the irreducible representations , which obviously should not couple to the adjoint .
- The two Higgs doublets of the MSSM should mostly be made out of a pair of Higgs quintet and anti-quintet, which couple to the third generation.
6. Phenomenological Constraints
6.1. Flavor Constraints
6.2. The Light Higgs Boson Mass
7. Numerical Analysis
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- ATLAS Collaboration; Aad, G. Combined Measurements of the Mass and Signal Strength of the Higgs-Like Boson with the ATLAS Detector Using up to 25 fb−1 of Proton-Proton Collision Data; ATLAS-CONF-2013-014; ATLAS Collaboration: Geneva, Switzerland, 2013. [Google Scholar]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; et al. Observation of a new boson with mass near 125 GeV in pp collisions at = 7 and 8 TeV. JHEP 2013, 1306, 81. [Google Scholar] [CrossRef] [Green Version]
- Pati, J.C.; Salam, A. Is Baryon Number Conserved? Phys. Rev. Lett. 1973, 31, 661. [Google Scholar] [CrossRef]
- Georgi, H.; Glashow, S.L. Unity of All Elementary Particle Forces. Phys. Rev. Lett. 1974, 32, 438. [Google Scholar] [CrossRef]
- Georgi, H.; Quinn, H.R.; Weinberg, S. Hierarchy of Interactions in Unified Gauge Theories. Phys. Rev. Lett. 1974, 33, 451. [Google Scholar] [CrossRef]
- Carlson, C.E. Particles and Fields: Williamsburg 1974. AIP Conference Proceedings No. 23; American INstitute of Physics: New York, NY, USA, 1975; 688p. [Google Scholar]
- Fritzsch, H.; Minkowski, P. Unified Interactions of Leptons and Hadrons. Ann. Phys. 1975, 93, 193–266. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Georgi, H. Softly Broken Supersymmetry and SU (5). Nucl. Phys. B 1981, 193, 150–162. [Google Scholar] [CrossRef]
- Sakai, N. Naturalness in Supersymmetric Guts. Z. Phys. C 1981, 11, 153–157. [Google Scholar] [CrossRef]
- Amaldi, U.; de Boer, W.; Furstenau, H. Comparison of grand unified theories with electroweak and strong coupling constants measured at LEP. Phys. Lett. B 1991, 260, 447–455. [Google Scholar] [CrossRef]
- Buras, A.J.; Ellis, J.R.; Gaillard, M.K.; Nanopoulos, D.V. Aspects of the Grand Unification of Strong, Weak and Electromagnetic Interactions. Nucl. Phys. B 1978, 135, 66–92. [Google Scholar] [CrossRef]
- Kubo, J.; Mondragon, M.; Olechowski, M.; Zoupanos, G. Testing gauge Yukawa unified models by M(t). Nucl. Phys. B 1996, 479, 25–45. [Google Scholar] [CrossRef]
- Kubo, J.; Mondragon, M.; Zoupanos, G. Unification beyond GUTs: Gauge Yukawa unification. Acta Phys. Polon. B 1997, 27, 3911–3944. [Google Scholar]
- Kobayashi, T.; Kubo, J.; Mondragon, M.; Zoupanos, G. Exact finite and gauge-Yukawa unified theories and their predictions. Acta Phys. Polon. B 1999, 30, 2013–2027. [Google Scholar]
- Fayet, P. Spontaneous Generation of Massive Multiplets and Central Charges in Extended Supersymmetric Theories. Nucl. Phys. B 1979, 149, 137–169. [Google Scholar] [CrossRef]
- Zimmermann, W. Reduction in the Number of Coupling Parameters. Commun. Math. Phys. 1985, 97, 211–225. [Google Scholar] [CrossRef]
- Oehme, R.; Zimmermann, W. Relation between Effective Couplings for Asymptotically Free Models. Commun. Math. Phys. 1985, 97, 569–582. [Google Scholar] [CrossRef]
- Kapetanakis, D.; Mondragon, M.; Zoupanos, G. Finite unified models. Z. Phys. C 1993, 60, 181–185. [Google Scholar] [CrossRef]
- Kubo, J.; Mondragon, M.; Zoupanos, G. Reduction of couplings and heavy top quark in the minimal SUSY GUT. Nucl. Phys. B 1994, 424, 291–307. [Google Scholar] [CrossRef]
- Kubo, J.; Mondragon, M.; Tracas, N.D.; Zoupanos, G. Gauge Yukawa unification in asymptotically nonfree theories. Phys. Lett. B 1995, 342, 155–162. [Google Scholar] [CrossRef]
- Kubo, J.; Mondragon, M.; Olechowski, M.; Zoupanos, G. Gauge Yukawa unification and the top–bottom hierarchy. arXiv, 1995; arXiv:hep-ph/9510279. [Google Scholar]
- Mondragon, M.; Zoupanos, G. Finite unified theories and the top quark mass. Nucl. Phys. Proc. Suppl. C 1995, 37, 98–105. [Google Scholar] [CrossRef]
- Kubo, J.; Mondragon, M.; Zoupanos, G. Perturbative unification of soft supersymmetry breaking terms. Phys. Lett. B 1996, 389, 523–532. [Google Scholar] [CrossRef]
- Piguet, O.; Sibold, K. Nonrenormalization Theorems of Chiral Anomalies and Finiteness in Supersymmetric Yang-Mills Theories. Int. J. Mod. Phys. A 1986, 1, 913–942. [Google Scholar] [CrossRef]
- Lucchesi, C.; Piguet, O.; Sibold, K. Vanishing Beta Functions in N = 1 Supersymmetric Gauge Theories. Helv. Phys. Acta 1988, 61, 321–344. [Google Scholar]
- Lucchesi, C.; Zoupanos, G. All order finiteness in N = 1 SYM theories: Criteria and applications. Fortsch. Phys. 1997, 45, 129–143. [Google Scholar] [CrossRef]
- Jack, I.; Jones, D.R.T. Renormalization group invariance and universal soft supersymmetry breaking. Phys. Lett. B 1995, 349, 294–299. [Google Scholar] [CrossRef]
- Zimmermann, W. Scheme independence of the reduction principle and asymptotic freedom in several couplings. Commun. Math. Phys. 2001, 219, 221–245. [Google Scholar] [CrossRef]
- Mondragón, M.; Tracas, N.D.; Zoupanos, G. Reduction of Couplings in the MSSM. Phys. Lett. B 2014, 728, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Jones, D.R.T.; Mezincescu, L.; Yao, Y.P. Soft Breaking of Two Loop Finite N = 1 Supersymmetric Gauge Theories. Phys. Lett. B 1984, 148, 317–322. [Google Scholar] [CrossRef]
- Jack, I.; Jones, D.R.T. Soft supersymmetry breaking and finiteness. Phys. Lett. B 1994, 333, 372–379. [Google Scholar] [CrossRef]
- Ibanez, L.E.; Lust, D. Duality anomaly cancellation, minimal string unification and the effective low-energy Lagrangian of 4-D strings. Nucl. Phys. B 1992, 382, 305–361. [Google Scholar] [CrossRef]
- Kaplunovsky, V.S.; Louis, J. Model independent analysis of soft terms in effective supergravity and in string theory. Phys. Lett. B 1993, 306, 269–275. [Google Scholar] [CrossRef]
- Brignole, A.; Ibanez, L.E.; Munoz, C. Towards a theory of soft terms for the supersymmetric Standard Model. Nucl. Phys. B 1994, 422, 125–171. [Google Scholar] [CrossRef]
- Casas, J.A.; Lleyda, A.; Munoz, C. Problems for supersymmetry breaking by the dilaton in strings from charge and color breaking. Phys. Lett. B 1996, 380, 59–67. [Google Scholar] [CrossRef]
- Kawamura, Y.; Kobayashi, T.; Kubo, J. Soft scalar mass sum rule in gauge Yukawa unified models and its superstring interpretation. Phys. Lett. B 1997, 405, 64–70. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kubo, J.; Mondragon, M.; Zoupanos, G. Constraints on finite soft supersymmetry breaking terms. Nucl. Phys. B 1998, 511, 45–68. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kubo, J.; Zoupanos, G. Further all loop results in softly broken supersymmetric gauge theories. Phys. Lett. B 1998, 427, 291–299. [Google Scholar] [CrossRef]
- Novikov, V.A.; Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. Instanton Effects in Supersymmetric Theories. Nucl. Phys. B 1983, 229, 407–420. [Google Scholar] [CrossRef]
- Novikov, V.A.; Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. Beta Function in Supersymmetric Gauge Theories: Instantons Versus Traditional Approach. Phys. Lett. B 1986, 166, 329–333. [Google Scholar] [CrossRef]
- Shifman, M.A. Little miracles of supersymmetric evolution of gauge couplings. Int. J. Mod. Phys. A 1996, 11, 5761–5784. [Google Scholar] [CrossRef]
- Kubo, J.; Mondragon, M.; Shoda, S.; Zoupanos, G. Gauge Yukawa unification in SO(10) SUSY GUTs. Nucl. Phys. B 1996, 469, 3–20. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Mondragon, M.; Zoupanos, G. Confronting Finite Unified Theories with Low-Energy Phenomenology. JHEP 2008, 807, 135. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Mondragon, M.; Zoupanos, G. Finite Theories after the discovery of a Higgs-like boson at the LHC. Phys. Lett. B 2013, 718, 1430–1435. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Mondragon, M.; Zoupanos, G. Finite Theories Before and After the Discovery of a Higgs Boson at the LHC. Fortsch. Phys. 2013, 61, 969–993. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Mondragon, M.; Zoupanos, G. The LHC Higgs boson discovery: Implications for Finite Unified Theories. Int. J. Mod. Phys. A 2014, 29, 1430032. [Google Scholar] [CrossRef]
- Oehme, R. Reduction and Reparametrization of Quantum Field Theories. Prog. Theor. Phys. Suppl. 1986, 86, 215–237. [Google Scholar] [CrossRef]
- Kubo, J.; Sibold, K.; Zimmermann, W. Higgs and Top Mass from Reduction of Couplings. Nucl. Phys. B 1985, 259, 331–350. [Google Scholar] [CrossRef]
- Kubo, J.; Sibold, K.; Zimmermann, W. New Results in the Reduction of the Standard Model. Phys. Lett. B 1989, 220, 185–190. [Google Scholar] [CrossRef]
- Piguet, O.; Sibold, K. Reduction of Couplings in the Presence of Parameters. Phys. Lett. B 1989, 229, 83–88. [Google Scholar] [CrossRef]
- Breitenlohner, P.; Maison, D. Gauge and mass parameter dependence of renormalized Green’s functions. Commun. Math. Phys. 2001, 219, 179–190. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. A Lagrangian Model Invariant under Supergauge Transformations. Phys. Lett. B 1974, 49, 52–54. [Google Scholar] [CrossRef]
- Iliopoulos, J.; Zumino, B. Broken Supergauge Symmetry and Renormalization. Nucl. Phys. B 1974, 76, 310–332. [Google Scholar] [CrossRef]
- Fujikawa, K.; Lang, W. Perturbation Calculations for the Scalar Multiplet in a Superfield Formulation. Nucl. Phys. B 1975, 88, 61–76. [Google Scholar] [CrossRef]
- Parkes, A.; West, P.C. Finiteness in Rigid Supersymmetric Theories. Phys. Lett. B 1984, 138, 99–104. [Google Scholar] [CrossRef]
- Rajpoot, S.; Taylor, J.G. On Finite Quantum Field Theories. Phys. Lett. B 1984, 147, 91–95. [Google Scholar] [CrossRef]
- Rajpoot, S.; Taylor, J.G. Towards Finite Quantum Field Theories. Int. J. Theor. Phys. 1986, 25, 117–138. [Google Scholar] [CrossRef]
- West, P.C. The Yukawa beta Function in N = 1 Rigid Supersymmetric Theories. Phys. Lett. B 1984, 137, 371–373. [Google Scholar] [CrossRef]
- Jones, D.R.T.; Mezincescu, L. The Chiral Anomaly and a Class of Two Loop Finite Supersymmetric Gauge Theories. Phys. Lett. B 1984, 138, 293–295. [Google Scholar] [CrossRef]
- Jones, D.R.T.; Parkes, A.J. Search for a Three Loop Finite Chiral Theory. Phys. Lett. B 1985, 160, 267–270. [Google Scholar] [CrossRef]
- Parkes, A.J. Three Loop Finiteness Conditions in N = 1 Superyang-mills. Phys. Lett. B 1985, 156, 73–79. [Google Scholar] [CrossRef]
- O’Raifeartaigh, L. Spontaneous Symmetry Breaking for Chiral Scalar Superfields. Nucl. Phys. B 1975, 96, 331–352. [Google Scholar] [CrossRef]
- Fayet, P.; Iliopoulos, J. Spontaneously Broken Supergauge Symmetries and Goldstone Spinors. Phys. Lett. B 1974, 51, 461–464. [Google Scholar] [CrossRef]
- Lucchesi, C.; Piguet, O.; Sibold, K. Necessary and Sufficient Conditions for All Order Vanishing Beta Functions in Supersymmetric Yang-Mills Theories. Phys. Lett. B 1988, 201, 241–244. [Google Scholar] [CrossRef]
- Ferrara, S.; Zumino, B. Transformation Properties of the Supercurrent. Nucl. Phys. B 1975, 87, 207–220. [Google Scholar] [CrossRef]
- Piguet, O.; Sibold, K. The Supercurrent in N = 1 Supersymmetrical Yang-Mills Theories. 1. The Classical Case. Nucl. Phys. B 1982, 196, 428–446. [Google Scholar] [CrossRef]
- Piguet, O.; Sibold, K. The Supercurrent in N = 1 Supersymmetrical Yang-Mills Theories. 2. Renormalization. Nucl. Phys. B 1982, 196, 447–460. [Google Scholar] [CrossRef]
- Piguet, O.; Sibold, K. Nonrenormalization Theorems of Chiral Anomalies and Finiteness. Phys. Lett. B 1986, 177, 373–376. [Google Scholar] [CrossRef]
- Ensign, P.; Mahanthappa, K.T. The Supercurrent and the Adler-bardeen Theorem in Coupled Supersymmetric Yang-Mills Theories. Phys. Rev. D 1987, 36, 3148. [Google Scholar] [CrossRef]
- Piguet, O. Supersymmetry, ultraviolet finiteness and grand unification. arXiv, 1996; arXiv:hep-th/9606045. [Google Scholar]
- Alvarez-Gaume, L.; Ginsparg, P.H. The Topological Meaning of Nonabelian Anomalies. Nucl. Phys. B 1984, 243, 449–474. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Zumino, B. Consistent and Covariant Anomalies in Gauge and Gravitational Theories. Nucl. Phys. B 1984, 244, 421–453. [Google Scholar] [CrossRef]
- Zumino, B.; Wu, Y.S.; Zee, A. Chiral Anomalies, Higher Dimensions, and Differential Geometry. Nucl. Phys. B 1984, 239, 477–507. [Google Scholar] [CrossRef]
- Leigh, R.G.; Strassler, M.J. Exactly marginal operators and duality in four-dimensional N = 1 supersymmetric gauge theory. Nucl. Phys. B 1995, 447, 95–133. [Google Scholar] [CrossRef]
- Mondragon, M.; Zoupanos, G. Higgs mass prediction in finite unified theories. Acta Phys. Polon. B 2003, 34, 5459–5468. [Google Scholar] [CrossRef]
- Delbourgo, R. Superfield Perturbation Theory and Renormalization. Nuovo Cim. A 1975, 25, 646–656. [Google Scholar] [CrossRef]
- Salam, A.; Strathdee, J.A. Feynman Rules for Superfields. Nucl. Phys. B 1975, 86, 142–152. [Google Scholar] [CrossRef]
- Grisaru, M.T.; Siegel, W.; Rocek, M. Improved Methods for Supergraphs. Nucl. Phys. B 1979, 159, 429–450. [Google Scholar] [CrossRef]
- Girardello, L.; Grisaru, M.T. Soft Breaking of Supersymmetry. Nucl. Phys. B 1982, 194, 65–76. [Google Scholar] [CrossRef]
- Hisano, J.; Shifman, M.A. Exact results for soft supersymmetry breaking parameters in supersymmetric gauge theories. Phys. Rev. D 1997, 56, 5475. [Google Scholar] [CrossRef]
- Jack, I.; Jones, D.R.T. The Gaugino Beta function. Phys. Lett. B 1997, 415, 383. [Google Scholar] [CrossRef]
- Avdeev, L.V.; Kazakov, D.I.; Kondrashuk, I.N. Renormalizations in softly broken SUSY gauge theories. Nucl. Phys. B 1998, 510, 289–312. [Google Scholar] [CrossRef]
- Kazakov, D.I. Exploring softly broken SUSY theories via Grassmannian Taylor expansion. Phys. Lett. B 1999, 449, 201–206. [Google Scholar] [CrossRef]
- Kazakov, D.I. Finiteness of soft terms in finite N = 1 SUSY gauge theories. Phys. Lett. B 1998, 421, 211–216. [Google Scholar] [CrossRef]
- Jack, I.; Jones, D.R.T.; Pickering, A. Renormalization invariance and the soft Beta functions. Phys. Lett. B 1998, 426, 73–77. [Google Scholar] [CrossRef]
- Jack, I.; Jones, D.R.T. RG invariant solutions for the soft supersymmetry breaking parameters. Phys. Lett. B 1999, 465, 148–154. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kubo, J.; Mondragon, M.; Zoupanos, G. Finite and gauge-Yukawa unified theories: Theory and predictions. AIP Conf. Proc. 1999, 490, 279–309. [Google Scholar] [CrossRef]
- Karch, A.; Kobayashi, T.; Kubo, J.; Zoupanos, G. Infrared behavior of softly broken SQCD and its dual. Phys. Lett. B 1998, 441, 235–342. [Google Scholar] [CrossRef]
- Mondragon, M.; Zoupanos, G. Finite unified theories. J. Phys. Conf. Ser. 2009, 171, 012095. [Google Scholar] [CrossRef]
- Hamidi, S.; Schwarz, J.H. A Realistic Finite Unified Theory? Phys. Lett. B 1984, 147, 301–306. [Google Scholar] [CrossRef]
- Jones, D.R.T.; Raby, S. A Two Loop Finite Supersymmetric SU(5) Theory: Towards a Theory of Fermion Masses. Phys. Lett. B 1984, 143, 137–141. [Google Scholar] [CrossRef]
- Leon, J.; Perez-Mercader, J.; Quiros, M.; Ramirez-Mittelbrunn, J. A Sensible Finite Su(5) Susy Gut? Phys. Lett. B 1985, 156, 66–72. [Google Scholar] [CrossRef]
- Misiak, M.; Asatrian, H.M.; Bieri, K.; Czakon, M.; Czarnecki, A.; Ewerth, T.; Ferroglia, A.; Gambino, P.; Gorbahn, M.; Greub, C.; et al. Estimate of at . Phys. Rev. Lett. 2007, 98, 22002. [Google Scholar] [CrossRef] [PubMed]
- Ciuchini, M.; Degrassi, G.; Gambino, P.; Giudice, G.F. Next-to-leading QCD corrections to B → X(s) gamma in supersymmetry. Nucl. Phys. B 1998, 534, 3–20. [Google Scholar] [CrossRef]
- Degrassi, G.; Gambino, P.; Giudice, G.F. B → X(s gamma) in supersymmetry: Large contributions beyond the leading order. JHEP 2000, 12, 9. [Google Scholar] [CrossRef]
- Carena, M.; Garcia, D.; Nierste, U.; Wagner, C.E.M. b → sγ and supersymmetry with large tan β. Phys. Lett. B 2001, 499, 141–146. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Giudice, G.F.; Isidori, G.; Strumia, A. Minimal flavor violation: An Effective field theory approach. Nucl. Phys. B 2002, 645, 155–187. [Google Scholar] [CrossRef]
- Asner, D.; Banerjee, S.; Bernhard, R.; Blyth, S.; Bozek, A.; Bozzi, C.; Cassel, D.G.; Cavoto, G.; Cibinetto, G.; Coleman, J.; et al. Averages of b-hadron, c-hadron, and τ-lepton properties. arXiv, 2010; arXiv:1010.1589. [Google Scholar]
- Buras, A.J. Relations between Δ M(s, d) and B(s, d) → μ in models with minimal flavor violation. Phys. Lett. B 2003, 566, 115–119. [Google Scholar] [CrossRef]
- Isidori, G.; Straub, D.M. Minimal Flavour Violation and Beyond. Eur. Phys. J. C 2012, 72, 2103. [Google Scholar] [CrossRef]
- Bobeth, C.; Gorbahn, M.; Hermann, T.; Misiak, M.; Stamou, E.; Steinhauser, M. Bs,d → l+l− in the Standard Model with Reduced Theoretical Uncertainty. Phys. Rev. Lett. 2014, 112, 101801. [Google Scholar] [CrossRef] [PubMed]
- Hermann, T.; Misiak, M.; Steinhauser, M. Three-loop QCD corrections to Bs → μ+μ−. JHEP 2013, 1312, 97. [Google Scholar] [CrossRef]
- Bobeth, C.; Gorbahn, M.; Stamou, E. Electroweak Corrections to Bs,d → ℓ+ℓ−. Phys. Rev. D 2014, 89, 34023. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Measurement of the → μ+μ− branching fraction and search for B0 → μ+μ− decays at the LHCb experiment. Phys. Rev. Lett. 2013, 111, 101805. [Google Scholar] [CrossRef] [PubMed]
- Quertenmont, L.; Beluffi, C.; Bruno, G.L.; Castello, R.; Caudron, A.; Ceard, L.; Da Silveira, G.G.; Delaere, C.; Du Pree, T.; Favart, D.; et al. Measurement of the B(s) to mu+ mu- branching fraction and search for B0 to mu+ mu- with the CMS Experiment. Phys. Rev. Lett. 2013, 111, 101804. [Google Scholar] [CrossRef]
- CMS and LHCb Collaborations. Combination of Results on the Rare Decays B0(s) → μ+μ− from the CMS and LHCb Experiments; Technical Report; CMS-PAS-BPH-13-007; CERN-LHCb-CONF-2013-012; CERN: Geneva, Switzerland, 2013. [Google Scholar]
- Isidori, G.; Paradisi, P. Hints of large tan(beta) in flavour physics. Phys. Lett. B 2006, 639, 499–507. [Google Scholar] [CrossRef]
- Isidori, G.; Mescia, F.; Paradisi, P.; Temes, D. Flavour physics at large tan(beta) with a Bino-like LSP. Phys. Rev. D 2007, 75, 115019. [Google Scholar] [CrossRef]
- Olive, K.A.; Particle Data Group. Review of Particle Physics. Chin. Phys. C 2014, 38, 90001. [Google Scholar] [CrossRef]
- Buras, A.J.; Gambino, P.; Gorbahn, M.; Jager, S.; Silvestrini, L. epsilon-prime/epsilon and rare K and B decays in the MSSM. Nucl. Phys. B 2001, 592, 55–91. [Google Scholar] [CrossRef]
- LHCb Collaboration. Precision measurement of the oscillation frequency with the decay → . New J. Phys. 2013, 15, 53021. [Google Scholar] [CrossRef]
- Goldberg, H. Constraint on the Photino Mass from Cosmology. Phys. Rev. Lett. 1983, 50, 1419. [Google Scholar] [CrossRef]
- Ellis, J.R.; Hagelin, J.S.; Nanopoulos, D.V.; Olive, K.A.; Srednicki, M. Supersymmetric Relics from the Big Bang. Nucl. Phys. B 1984, 238, 453–476. [Google Scholar] [CrossRef]
- Larson, D.; Dunkley, J.; Hinshaw, G.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Gold, B.; Halpern, M.; Hill, R.S.; Jarosik, N.; et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Komatsu, E.; Bennett, C.L.; Barnes, C.; Bean, R.; Bennett, C.L.; Doré, O.; Dunkley, J.; Gold, B.; Greason, M.R.; Halpern, M.; et al. Results from the Wilkinson Microwave Anisotropy Probe. PTEP 2014, 2014, 06B102. [Google Scholar] [CrossRef]
- Heinemeyer, S. MSSM Higgs physics at higher orders. Int. J. Mod. Phys. A 2006, 21, 2659–2772. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Hollik, W.; Weiglein, G. Electroweak precision observables in the minimal supersymmetric standard model. Phys. Rep. 2006, 425, 265–368. [Google Scholar] [CrossRef]
- Djouadi, A. The Anatomy of electro-weak symmetry breaking. II. The Higgs bosons in the minimal supersymmetric model. Phys. Rep. 2008, 459, 1–241. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Stal, O.; Weiglein, G. Interpreting the LHC Higgs Search Results in the MSSM. Phys. Lett. B 2012, 710, 201–206. [Google Scholar] [CrossRef] [Green Version]
- Bechtle, P.; Heinemeyer, S.; Stal, O.; Stefaniak, T.; Weiglein, G.; Zeune, L. MSSM Interpretations of the LHC Discovery: Light or Heavy Higgs? Eur. Phys. J. 2013, 73, 2354. [Google Scholar] [CrossRef]
- Bechtle, P.; Haber, H.E.; Heinemeyer, S.; Stål, O.; Stefaniak, T.; Weiglein, G.; Zeune, L. The Light and Heavy Higgs Interpretation of the MSSM. Eur. Phys. J. C 2017, 77, 67. [Google Scholar] [CrossRef]
- ATLAS and CMS Collaborations. Combined Measurement of the Higgs Boson Mass in pp Collisions at =7 and 8 TeV with the ATLAS and CMS Experiments. Phys. Rev. Lett. 2015, 114, 191803. [Google Scholar] [CrossRef]
- Degrassi, G.; Heinemeyer, S.; Hollik, W.; Slavich, P.; Weiglein, G. Towards high precision predictions for the MSSM Higgs sector. Eur. Phys. J. C 2003, 28, 133–143. [Google Scholar] [CrossRef]
- Buchmueller, O.; Dolan, M.J.; Ellis, J.; Hahn, T.; Heinemeyer, S.; Hollik, W.; Marrouche, J.; Olive, K.A.; Rzehak, H.; de Vries, K.J.; et al. Implications of Improved Higgs Mass Calculations for Supersymmetric Models. Eur. Phys. J. C 2014, 74, 2809. [Google Scholar] [CrossRef] [PubMed]
- Bahl, H.; Heinemeyer, S.; Hollik, W.; Weiglein, G. Reconciling EFT and hybrid calculations of the light MSSM Higgs-boson mass. Eur. Phys. J. C 2018, 78, 57. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Hollik, W.; Weiglein, G. FeynHiggs: A Program for the calculation of the masses of the neutral CP even Higgs bosons in the MSSM. Comput. Phys. Commun. 2000, 124, 76–89. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Hollik, W.; Weiglein, G. The Masses of the neutral CP—Even Higgs bosons in the MSSM: Accurate analysis at the two loop level. Eur. Phys. J. C 1999, 9, 343–366. [Google Scholar] [CrossRef] [Green Version]
- Frank, M.; Hahn, T.; Heinemeyer, S.; Hollik, W.; Rzehak, H.; Weiglein, G. The Higgs Boson Masses and Mixings of the Complex MSSM in the Feynman-Diagrammatic Approach. JHEP 2007, 702, 47. [Google Scholar] [CrossRef]
- Hahn, T.; Heinemeyer, S.; Hollik, W.; Rzehak, H.; Weiglein, G. FeynHiggs: A program for the calculation of MSSM Higgs-boson observables—Version 2.6.5. Comput. Phys. Commun. 2009, 180, 1426–1427. [Google Scholar] [CrossRef]
- Hahn, T.; Heinemeyer, S.; Hollik, W.; Rzehak, H.; Weiglein, G. High-Precision Predictions for the Light CP-Even Higgs Boson Mass of the Minimal Supersymmetric Standard Model. Phys. Rev. Lett. 2014, 112, 141801. [Google Scholar] [CrossRef] [PubMed]
- Bahl, H.; Hollik, W. Precise prediction for the light MSSM Higgs boson mass combining effective field theory and fixed-order calculations. Eur. Phys. J. C 2016, 76, 499. [Google Scholar] [CrossRef]
- ATLAS and CDF and CMS and D0 Collaborations. First combination of Tevatron and LHC measurements of the top-quark mass. arXiv, 2014; arXiv:1403.4427. [Google Scholar]
- Carena, M.; Garcia, D.; Nierste, U.; Wagner, C.E.M. Effective Lagrangian for the interaction in the MSSM and charged Higgs phenomenology. Nucl. Phys. B 2000, 577, 88. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Mondragon, M.; Zoupanos, G. Futs and the Higgs-boson. Int. J. Mod. Phys. Conf. Ser. 2012, 13, 118. [Google Scholar] [CrossRef]
- Heinemeyer, S.; Mondragon, M.; Zoupanos, G. Finite unified theories and their predicitions. Phys. Part. Nucl. 2013, 44, 299–315. [Google Scholar] [CrossRef]
- Supersymmetry Searches. Available online: https://twiki.cern.ch/twiki/bin/view/AtlasPublic/SupersymmetryPublicResults (accessed on 11 February 2017).
- CMS Supersymmetry Physics Results. Available online: https://twiki.cern.ch/twiki/bin/view/CMSPublic/PhysicsResultsSUS (accessed on 11 February 2017).
- Mangano, M. Physics at the FCC-hh, a 100 TeV pp Collider; CERN Yellow Report CERN 2017-003-M; CERN: Genève, Switzerland, 2017. [Google Scholar]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. MicrOMEGAs: A Program for calculating the relic density in the MSSM. Comput. Phys. Commun. 2002, 149, 103–120. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs: Version 1.3. Comput. Phys. Commun. 2006, 174, 577–604. [Google Scholar] [CrossRef]
- Barducci, D.; Belanger, G.; Bernon, J.; Boudjema, F.; da Silva, J.; Kraml, S.; Laa, U.; Pukhov, A. Collider limits on new physics within micrOMEGAs_4.3. Comput. Phys. Commun. 2018, 222, 327–338. [Google Scholar] [CrossRef]
- Valle, J.W.F. Neutrino mass: Theory, data and interpretation. PoS Corfu 1998, arXiv:hep-ph/990722298. [Google Scholar]
- Diaz, M.A.; Hirsch, M.; Porod, W.; Romao, J.C.; Valle, J.W.F. Solar neutrino masses and mixing from bilinear R parity broken supersymmetry: Analytical versus numerical results. Phys. Rev. D 2003, 68, 13009. [Google Scholar] [CrossRef]
- Dreiner, H.K. An Introduction to explicit R-parity violation. Adv. Ser. Direct. High Energy Phys. 2010, 21, 565–583. [Google Scholar] [CrossRef]
- Bhattacharyya, G. A Brief Review of R-Parity Violating Couplings; Presented at the ‘Beyond the Desert’; Castle Ringberg: Tegernsee, Germany, 1997. [Google Scholar]
- Allanach, B.C.; Dedes, A.; Dreiner, H.K. Bounds on R-parity violating couplings at the weak scale and at the GUT scale. Phys. Rev. D 1999, 60, 75014. [Google Scholar] [CrossRef] [Green Version]
- Romao, J.C.; Valle, J.W.F. Neutrino masses in supersymmetry with spontaneously broken R parity. Nucl. Phys. B 1992, 381, 87–108. [Google Scholar] [CrossRef]
- Lyth, D.H.; Stewart, E.D. Thermal inflation and the moduli problem. Phys. Rev. D 1996, 53, 1784. [Google Scholar] [CrossRef]
- Gelmini, G.B.; Gondolo, P. Neutralino with the right cold dark matter abundance in (almost) any supersymmetric model. Phys. Rev. D 2006, 74, 23510. [Google Scholar] [CrossRef]
- Mandelstam, S. Light Cone Superspace and the Ultraviolet Finiteness of the N = 4 Model. Nucl. Phys. B 1983, 213, 149–168. [Google Scholar] [CrossRef]
- Brink, L.; Lindgren, O.; Nilsson, B.E.W. The Ultraviolet Finiteness of the N = 4 Yang-Mills Theory. Phys. Lett. B 1983, 123, 323–328. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.; Dixon, L.J.; Johansson, H.; Roiban, R. The Ultraviolet Behavior of N = 8 Supergravity at Four Loops. Phys. Rev. Lett. 2009, 103, 81301. [Google Scholar] [CrossRef] [PubMed]
- Kallosh, R. On UV Finiteness of the Four Loop N = 8 Supergravity. JHEP 2009, 909, 116. [Google Scholar] [CrossRef]
- Bern, Z.; Carrasco, J.J.; Dixon, L.J.; Johansson, H.; Kosower, D.A.; Roiban, R. Three-Loop Superfiniteness of N = 8 Supergravity. Phys. Rev. Lett. 2007, 98, 161303. [Google Scholar] [CrossRef] [PubMed]
- Bern, Z.; Dixon, L.J.; Roiban, R. Is N = 8 supergravity ultraviolet finite? Phys. Lett. B 2007, 644, 265–271. [Google Scholar] [CrossRef]
- Green, M.B.; Russo, J.G.; Vanhove, P. Ultraviolet properties of maximal supergravity. Phys. Rev. Lett. 2007, 98, 131602. [Google Scholar] [CrossRef] [PubMed]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef] [Green Version]
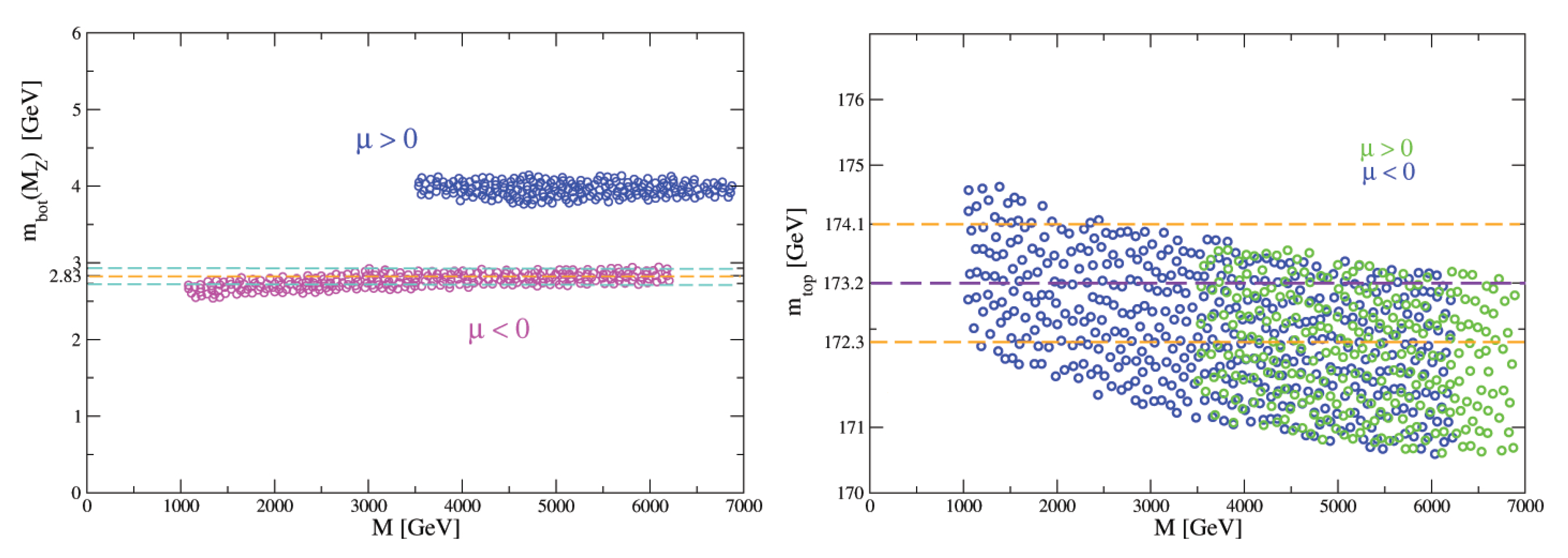
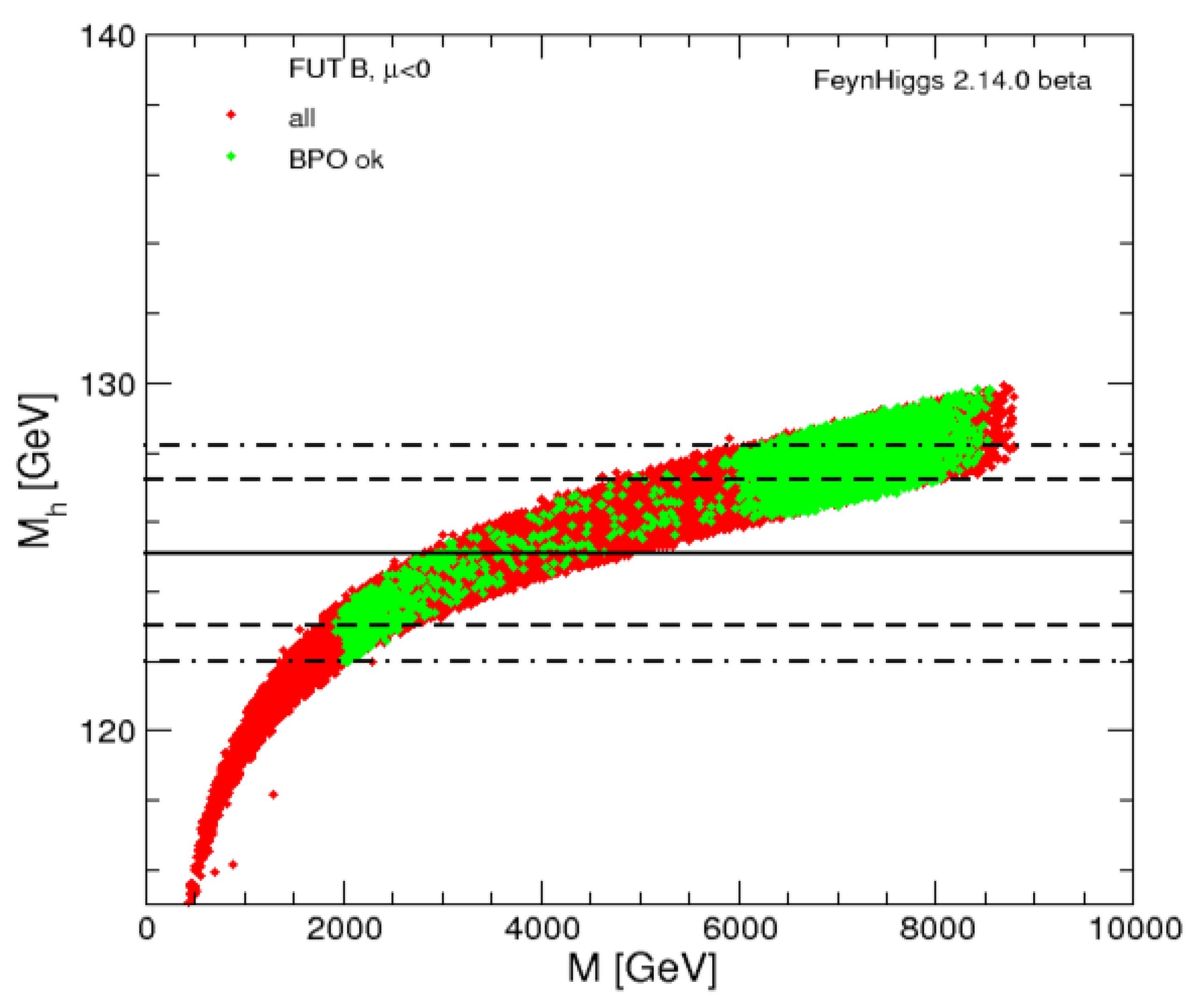
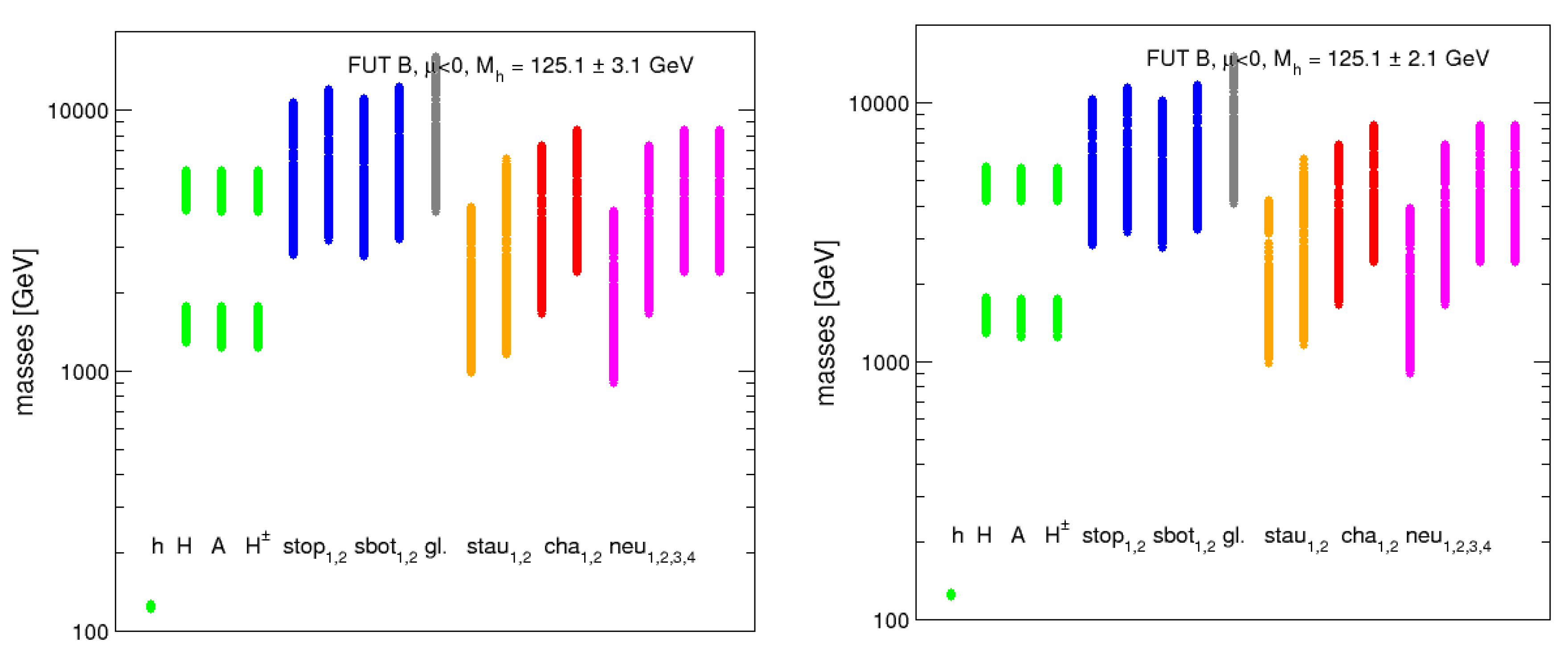
| lightest | 123.1 | 1533 | 1528 | 1527 | 2800 | 3161 | 2745 | 3219 | 4077 |
| heaviest | 127.2 | 4765 | 4737 | 4726 | 10,328 | 11,569 | 10,243 | 11,808 | 15,268 |
| lightest | 983 | 1163 | 1650 | 2414 | 900 | 1650 | 2410 | 2414 | 45 |
| heaviest | 4070 | 5141 | 6927 | 8237 | 3920 | 6927 | 8235 | 8237 | 46 |
| lightest | 122.8 | 1497 | 1491 | 1490 | 2795 | 3153 | 2747 | 3211 | 4070 |
| heaviest | 127.9 | 4147 | 4113 | 4103 | 10,734 | 12,049 | 11,077 | 12,296 | 16,046 |
| lightest | 1001 | 1172 | 1647 | 2399 | 899 | 647 | 2395 | 2399 | 44 |
| heaviest | 4039 | 6085 | 7300 | 8409 | 4136 | 7300 | 8406 | 8409 | 45 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinemeyer, S.; Mondragón, M.; Patellis, G.; Tracas, N.; Zoupanos, G. The LHC Higgs Boson Discovery: Updated Implications for Finite Unified Theories and the SUSY Breaking Scale. Symmetry 2018, 10, 62. https://doi.org/10.3390/sym10030062
Heinemeyer S, Mondragón M, Patellis G, Tracas N, Zoupanos G. The LHC Higgs Boson Discovery: Updated Implications for Finite Unified Theories and the SUSY Breaking Scale. Symmetry. 2018; 10(3):62. https://doi.org/10.3390/sym10030062
Chicago/Turabian StyleHeinemeyer, Sven, Myriam Mondragón, Gregory Patellis, Nicholas Tracas, and George Zoupanos. 2018. "The LHC Higgs Boson Discovery: Updated Implications for Finite Unified Theories and the SUSY Breaking Scale" Symmetry 10, no. 3: 62. https://doi.org/10.3390/sym10030062




